Numerical computation of the stochastic hepatitis B model using feed forward neural network and real data

Abstract

Hepatitis B is a global health burden and can persist for years, with nearly two billion infections worldwide, where its spread is influenced by environmental heterogeneity, host-pathogen interactions, and vaccination-induced immune variability. Proper understanding and developing models with a suitable framework is essential to accurately capture the complexity of the hepatitis B virus (HBV) and its transmission. In this work, we present a novel framework of a stochastic model and a forward neural network that combines neural networks and stochastic differential equations to analyze the dynamics of hepatitis B virus transmission, as it is important to capture the inherent uncertainty of disease spread in heterogeneous environments. We formulate the stochastic model with a saturated incidence rate, incorporating the long-term persistence of the disease following key characteristics of the disease transmission. The theoretical analysis of the model is proven to ensure the well-posedness and to determine the conditions for extinction and persistence of the disease. Further, a set of real data of hepatitis B reported cases will be used to produce stochastic simulations, and to train a feed-forward neural network (FFNN), while approximating the model dynamics more effectively. To evaluate the efficacy of the hybrid framework, we demonstrate its performance by the presenting mean squared error (MSE), absolute error (AE), and regression analysis showing strong agreement between the stochastic simulations and neural network predictions.

Introduction

Infectious diseases pose challenges to individuals and health-care systems worldwide, caused by parasites, viruses, bacteria, or fungi, which are typically communicable and spread directly through human contact, contaminated surfaces, water, air, or vectors. Common examples are tuberculosis, AIDS/HIV, influenza, malaria, SARS-CoV-2, and hepatitis B. Their spread can lead to epidemics or even a pandemic, making them a major focus in global health and epidemiology¹. The growing burden of infectious diseases presents a challenge, especially in low and middle-income countries, where resources are often limited. While vaccines, sanitation, and antibiotics have helped reduce the impact of many infectious diseases, modern lifestyles, aging populations, and environmental pollution have contributed to a sharp rise in infectious diseases. Seasonal changes in temperature, rainfall, and widespread resource scarcity can significantly influence the dynamics of infectious diseases². HBV is present in vaginal secretions and blood, and is a severe lifelong viral infection that produces liver inflammation due to exposure to the hepatitis B virus (HBV), which can be transmitted through different routes, with common sources being blood-related exposure and unprotected sexual practices. Since environmental variation and transmission mechanisms play critical roles in the temporal dynamics of HBV transmission, and it is a significant global health concern experiencing heightened death worldwide³. Although vaccines are available to prevent HBV infection, with approximately 95% of individuals developing protective immunity after completing the recommended three-dose vaccination series⁴. The disease transmission can vary from individual to individual and across regions, depending on environmental conditions, immune response, and vaccination mechanism, which ensures the inherently stochastic nature of the epidemic progression of hepatitis B transmission.

Epidemiological models consisting of deterministic, stochastic, and fractional-order differential equations are useful to illustrate the dynamics of infectious diseases. Several models are used to discuss the propagation and control of communicable infections (see, for instance^{5,6,7,8,9,10,11,12}). Each type of differential equation provides valuable insights and has its own limitations and advantages. Hepatitis B virus transmission and control vary across regions, showing the inherently stochastic nature of epidemic progression, which makes the stochastic differential equations suitable to study the inherent randomness associated with it¹³. The literature contains a variety of articles to study the dynamics of hepatitis B virus propagation. More precisely, a stochastic model of the classical extended SIR model has been studied in¹⁴. The SIS model has been studied to derive the disease elimination and persistence conditions by Zhao et al.¹⁵. To discuss the long-term behavior and to find the disease persistence condition, a model has been explored by Wei et al.¹⁶. Likewise, different authors studied the epidemiology of infectious diseases using stochastic differential equations^17,18. We noticed that the literature offers valuable insights; however, the mathematical analysis of biological models with more complexity often presents significant challenges. In addition, the chronic HBV infection is a lifelong illness, and people use controls as awareness grows. The saturated incidence rate better reflects realistic HBV transmission scenarios, where transmission does not grow indefinitely with infectious individuals due to limited contact rates, healthcare responses, and behavioral changes. As a result, there is a need for an alternative approach to overcome the limitations. Neural network-based models have been shown to be prominent tools for approximating the temporal dynamics of biological models.

In recent years, remarkable work has been done to integrate the differential equation with a neural network^19,20,21. Various physical problems have been modeled via differential equations, whose solution by neural networks has become a rapidly growing area of research²². Neural networks are inspired by the operational principles of the human brain, which enable them to learn complex patterns and approximate solutions to challenging problems^23,24. The operation of a neural network starts with input data and passes through one or many hidden layers, and undergoes a sequence of transformations to produce an output. To analyze stochastic differential equations, a feed-forward neural network (FFNN) is widely used and suitable to approximate the complex dynamics arising in the epidemic propagation. Various sources, such as environmental variability, demographic fluctuations, unpredictable outbreak patterns, and uncertainty, play an important role while modeling the temporal dynamics of HBV using stochastic differential equations to provide a mathematically rigorous framework, but often they are analytically intractable. However, FFNNs are capable of detecting complex patterns and providing accurate dynamics for the future trend propagation of hepatitis B virus transmission. Although network-based approaches are utilized to discuss the dynamics of epidemic models^25,26,27,28, but we believe that the integration of FFNNs with stochastic differential equations models is still unexplored, while bridging this gap is an innovative research direction to link complex epidemiological models with machine learning.

The objective of this research work is to present an innovative framework that combines stochastic differential equation models with a neural network to discuss the dynamics of HBV transmission. Keeping in view of the disease characteristics, the stochastic differential equation model with saturated incidence will better capture the inherent randomness and variability caused by random outbreaks, demographic fluctuations, and environmental factors, while the FFNN provides an accurate predictive analysis. The major contributions are summarized as follows.

• Saturated Incidence: A linear or bilinear incidence rate assumes that the new infections are directly proportional to the number of infectious and susceptible individuals, which looks unrealistic because it assumes infinite capacity for transmission while not accounting for immunity, behavioral changes, or healthcare saturation. Since HBV contains chronic carriers and has a complex nature of transmission, involving long infectious periods (usually persist in the body for years), behavioral changes, environmental contamination, and healthcare limitations. Saturation is common in HBV, and people take precautionary measures as awareness increases, as HBV includes indirect transmission routes, such as contaminated medical equipment. In this case, the saturated incidence rate is more appropriate and better reflects realistic HBV transmission scenarios. We therefore formulate a stochastic model with a realistic incidence of saturated type as chronically infected individuals having a long infectious period, while people apply control strategies with the increase of awareness.

• Random Perturbation: In the transmission of HBV the role of random perturbation is very important because the disease spread is inherently influenced by unpredictable factors. For example, contact variations, immunity changes, environmental fluctuations, and random demographic events are significant. To incorporate these uncertainties, incorporating random perturbations into the model, making it appropriate to show actual epidemiological patterns. Thus, we incorporate the random perturbation into each model state to represent the inherent randomness arising in the transmission of disease because of environmental variability, demographic heterogeneity, and behavioral differences, etc.

• Real data and SDE-FFNN: Real data of hepatitis B-infected cases will be used to parameterize the model parameters and present an annotative hybrid method to discuss the complex dynamics of the disease. The stochastic simulations will be produced using the real data of HBV, where the proposed network will be trained to enable us to capture the inherent nonlinear complex stochastic processes.

The organization of the paper is as follows. In Sect. "Mathematical model formulation", we present a formulation of the model with detailed biological significance. In Sect. "Well-posdness", we discuss the well-posedness of the proposed model to ensure the mathematical and biological feasibility of the problem. The conditions for disease elimination and persistence are derived in Sect. “Dynamical analysis”. Section "Parameters estimation and numerical experiments" presents the detailed numerical analysis of the proposed model. More precisely, the Sect. “Parameters estimation” is devoted to the estimation of the model parameters, while Sect. "Model discritization and the frame work of FFNN", presents the model discritization and the framework of the proposed network. We then present the detailed algorithm and its numerical implementation with discussion in Sect "Large scale numerical simulations and interpretation". Finally, concluding remarks and potential directions for future work are summarized in Sect. “Conclusion”.

Mathematical model formulation

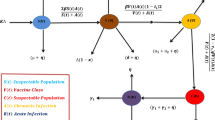
We present a stochastic model to study the dynamics of hepatitis B virus (HBV) by incorporating the key characteristics of the disease using stochastic perturbation and saturated incidence rate. Using stochastic perturbation, we want to capture the inherent randomness that arises in the disease dynamics under varying population environments. HBV is a complex disease, involving chronic carriers, behavioral changes, healthcare limitations, environmental contamination, and lengthy infectious phase. HBV can be present in individual body for long time, and as awareness grows (e.g., in families, clinics), people take precautionary measures. Screening, diagnosis, and vaccination services are not infinitely scalable. HBV transmission includes indirect routes like contaminated medical equipment, where saturation is common. Moreover, it leads to contact saturation in closed communities or households. Incidence rate in biological models is a key concept and plays a crucial role. Bilinear incidence rate, generally denoted by $\beta {SI}$, assumes that the rate of new infections is proportional to the number of susceptible and infectious individuals, which looks unrealistic because it assumes infinite capacity for transmission, while it does not account for behavioral changes, immunity, or healthcare saturation. The saturated incidence rate symbolized by $\frac{\beta {SI}}{1+\gamma {I}}$ better reflects realistic HBV transmission scenarios, especially in endemic regions, where transmission does not grow indefinitely with infectious individuals due to limited contact rates, healthcare responses, and behavioral changes. More precisely, the sum of the total population - N(t), that is under consideration, has been divided into three epidemiological groups of susceptible - S(t), infected with HBV - I(t), and recovered/immune - R(t). To incorporate the random perturbation, we assume variation in each group of population connected to various information sources denoted by Brownian motion filtration $\mathcal {F}=\{\mathcal {F}_t\}_{t \ge 0}$ (where $\mathcal {F}_t:=\xi (W(t))$ is the $\sigma$ algebra generated by W(t), and is a right-continuous and complete filtration). Thus the state variables $S(t), I(t), R(t)$ are taken as stochastic processes on a filtered probability space $(\Omega , \mathcal {F}_T, \{\mathcal {F}_t\}_{t \ge 0}, \mathbb {P})$ contain a 3D Brownian motion $W:=(W(t))_{t\ge 0}$, and $W(t)=\left( W_1(t),W_2(t),W_3(t)\right)$ and with dynamics interpreted in the mean-square Itô sense. The model parameters and the states are assumed to have non-negative values. Also, incorporated that those susceptible who are vaccinated against HBV will lead to immune individuals because 95% of the vaccinated population develops protective immunity. In light of these, the proposed epidemiological problem looks like:

$$\begin{aligned} \begin{aligned} dS(t)&=\left\{ \Lambda -\frac{\xi S(t)I(t)}{1+\gamma I(t)}-(\vartheta _0+\eta )S(t)\right\} dt+\xi _1S(t)dW_1(t),\\ dI(t)&=\left\{ \frac{\xi S(t)I(t)}{1+\gamma I(t)}-(\vartheta _0+\vartheta _1+\zeta )I(t)\right\} dt+\xi _2I(t)dW_2(t),\\ dR(t)&=\left\{ \zeta I(t)+\eta S(t)-\vartheta _0R(t)\right\} dt+\xi _3R(t)dW_3(t). \end{aligned} \end{aligned}$$

(1)

The details of descriptions of the model parameters, along with their fitted/estimated numerical value, have been provided in the following Table 1.

Table 1 Model parameters with explanations, estimated values and confidence intervals obtained from reported infected cases of HBV.

Noted that the proposed epidemiological model will take its associated deterministic version by taking $\xi _i=0$ for $i=1,2,3$, whose disease free equilibrium, basic reproductive number and the endemic equilibrium, say $E_1=\left( \frac{\Lambda }{\vartheta _0+\eta },0,\frac{\Lambda \eta }{\vartheta _0(\vartheta _0+\eta )}\right)$, $R_{d}$ and $E_{*}=\left( S_{*},I_{*},R_{*}\right)$, where

$$\begin{aligned} R_{d}=\frac{\xi \Lambda }{\left( \vartheta _0+\eta \right) \left( \vartheta _0+\vartheta _1+\zeta \right) }, \end{aligned}$$

and

$$\begin{aligned} S_{*}=\frac{1}{\xi }\left( \vartheta _0+\vartheta _1+\zeta \right) ,\quad I_{*}=\frac{\vartheta _0+\eta }{(\vartheta _0+\eta +1)}(R_{d}-1),\quad R_{*}=\frac{1}{\vartheta _0}\left( \zeta {I}_{*}+\eta {S}_{*}\right) . \end{aligned}$$

Generally, stochastic epidemiological models do not possess equilibria like deterministic models because of the continuous fluctuations introduced by random perturbations. Therefore, to study the long-term temporal dynamics, a probabilistic framework has been used rather than classical analysis. The key tools include stopping time, Lyapunov function, Itô formula, expectations of the model states, derivation of extinction and persistence conditions using the well-known Itô formula, and long-term averages.

Having formulated the model, we discuss the stochastic model using the tools as described. First, we will discuss the feasibility of the model to ensure that the problem is a well-posed dynamical system.

Well-posdness

In this section, we investigate whether the model is well posed. To do so, we perform the solution existence, boundedness, and positivity. We use the Lyapunov function with the implementation of Itô formula for this purpose. Let as assume that $N(t) = S(t) + I(t) + R(t)$, and $Y(t) = (S(t), I(t), R(t))^{t}$ and K is any positive constant, we then introduce

$$\begin{aligned} \mathbb {R} = \left\{ Y \in \mathcal {R}_+^3 : R,S> 0,I\ge 0, N(t) \le {K} \right\} , \end{aligned}$$

is an invariant region. To prove that the model possesses a unique and positive global solution confined to the set $\mathbb {R}$ for $t \ge 0$, we state the following result.

Theorem 3.1

Let Y(t) is the solution of the model (1), then for initial data within $\mathcal {R}^3_{+}$, a unique solution Y(t) exists, and remains in $\mathcal {R}^3_{+}$ for $t\ge 0$, satisfying

$$\begin{aligned} q\left\{ Y\in \mathbb {R},~\hbox { for all non-negative}\ t\right\} =1. \end{aligned}$$

Proof

To provide a clear and structured arguments, we organized the proof into the following steps: local existence and stopping times, developing a Lyapunov function, implementing the Itô formula, calculating the drift term, expectation, and using a contradiction argument to show global existence. For simplicity and clarity, the various steps are given below. $\square$

1. Local existence with stopping time

Following the methodology adopted by Lei et al. in²⁹, we first show the condition of local Lipschitz continuity. Let $t_e$ is the explosion time, and let $Y(t)$ is the solution of the model defined over the interval $[0, t_e)$, with initial data $Y(0) = Y_0 \in \mathcal {R}_{+}^{3}$. It maybe observed that the coefficients of the governing equation of the model for an initial population sizes $Y_0 \in \mathcal {R}_{+}^{3}$ are locally Lipschitz continuous. This indicates the existence and uniqueness of a local solution Y(t). To extend the result and show the global existence, it is enough to prove $t_e = \infty$.

To proceed, let us assume $\frac{1}{\varrho _0}< Y_0 < \varrho _0$, where $\varrho _0 \ge 0$ is a sufficiently large constant, which ensures that the initial data remain in a bounded domain. Defining the stopping time $t_\varrho$ as:

$$\begin{aligned} t_\varrho = \inf \left\{ t \in [0, t_e) : \min Y(t) \le \frac{1}{\varrho } \; \text {or} \; \max Y(t) \ge \varrho \right\} . \end{aligned}$$

It is clear that $\inf t_\varrho = \infty$ almost surely. Since $t_\varrho$ depends on $\varrho$, we note that, as $\varrho \rightarrow \infty$, $t_\varrho \rightarrow t_\infty$. Thus, we prove that $t_\infty = \infty$.

Suppose $T> 0$ and $0< \zeta < 1$, then, we assume that:

$$\begin{aligned} P\{t_\infty \le T\}> \zeta . \end{aligned}$$

(2)

This implies that there exists some $\varrho _1 \ge \varrho _0$ such that for all $\varrho \ge \varrho _1$, the following inequality holds:

$$\begin{aligned} P\{t_\varrho \le T\} \ge \zeta . \end{aligned}$$

2. Lyapunov function

To proceed, we define a Lyapunov function that ensures growth and Lipschitz conditions are satisfied globally, and ultimately the stochastic model admits a well-defined and unique solution for all t. In light of this, we assume a function $\mathcal {G}$, which is continuous and twice differentiable, such that

$$\begin{aligned} \mathcal {G}=S+I+R-3-\log \left\{ SIR\right\} . \end{aligned}$$

Obviously, the function $\mathcal {G}\ge 0$.

3. Application of Itô formula

To differentiate a function of It$\hat{o}$ process, we use It$\hat{o}$ formula. Before implementing of Itô formula to the function $\mathcal {G}$, it is worthy to outline its general form using the following lemma.

Lemma

Let us assume that $Y=\left( y_1,y_2,y_3,\ldots ,y_m\right)$ shows stochastic process contained in $R^n$, and $\mathcal {H}$ is a continuous and twice differentiable function i.e. $\mathcal {H}\in {C}^2\left( R^n\right)$ and $\langle ,\rangle$ represents the quadratic variation, then the implantation of Itô formula gives

$$\begin{aligned} d\mathcal {H} = \sum _{j=1}^{m} \frac{\partial \mathcal {H}}{\partial y_j} dY_j + \frac{1}{2} \sum _{j,i=1}^{m} \frac{\partial ^2 \mathcal {H}}{\partial y_j \partial y_i}\langle dY_j, dY_i\rangle . \end{aligned}$$

Let $\varrho _0\le \varrho$ and $T\ge 0$, then the use of Itô formula gives

$$\begin{aligned} d\mathcal {G}(S,I,R)=U\mathcal {G}dt+\xi _1(S-1)dW_1+\xi _2(I-1)dW_2+\xi _3(R-1)dW_3. \end{aligned}$$

(3)

Step 4. The calculation of drift term

Calculating the drift term to find the deterministic rate of change in a stochastic process. Let $U\mathcal {G}$ is the drift term, then from Eqn.(3), we can write

$$\begin{aligned} & U\mathcal {G}=\left\{ 1-\frac{1}{S}\right\} \left\{ \Lambda -\frac{\xi S(t)I(t)}{1+\gamma I(t)}-(\vartheta _0+\eta )S(t)\right\} +\frac{1}{2}\xi _1^2\\ & \quad +\left\{ 1-\frac{1}{I}\right\} \left\{ \frac{\xi S(t)I(t)}{1+\gamma I(t)}-(\vartheta _0+\vartheta _1+\zeta )I(t)\right\} +\frac{1}{2}\xi _2^2\\ & \quad +\left\{ 1-\frac{1}{R}\right\} \left\{ \zeta I(t)+\eta S(t)-\vartheta _0R(t)\right\} +\frac{1}{2}\xi _3^2. \end{aligned}$$

Expanding the equation by multiplying each term, we get

$$\begin{aligned} & U\mathcal {G}=\Lambda -\frac{\xi S(t)I(t)}{1+\gamma I(t)}-(\vartheta _0+\eta )S(t)-\frac{\Lambda }{S(t)}+\frac{\xi I(t)}{(1+\gamma I(t))}+(\vartheta _0+\eta )+\frac{1}{2}\xi _1^2\\ & \quad +\frac{\xi S(t)I(t)}{1+\gamma I(t)}-(\vartheta _0+\vartheta _1+\zeta )I(t)-\frac{\xi S(t)}{(1+\gamma I(t))}+(\vartheta _0+\vartheta _1+\zeta )+\frac{1}{2}\xi _2^2\\ & \quad +\zeta I(t)+\eta S(t)-\vartheta _0R(t)-\zeta \frac{I(t)}{R(t)}-\eta \frac{S(t)}{R(t)}+\vartheta _0+\frac{1}{2}\xi _3^2. \end{aligned}$$

Simplifying the equation by canceling the like terms, and removing the negative terms from the right-hand side, the equation reduces to the following inequality:

$$\begin{aligned} U\mathcal {G}\le \Lambda +\frac{\xi I(t)}{1+\gamma I(t)}+(\vartheta _0+\eta )+\frac{1}{2}\xi _1^2+(\vartheta _0+\vartheta _1+\zeta )+\frac{1}{2}\xi _2^2 +\vartheta _0+\frac{1}{2}\xi _3^2. \end{aligned}$$

Since the total population $N=S+I+R$ is bounded, therefore $\frac{\xi I(t)}{1+\gamma I(t))}\le \xi I(t)\le \xi N(t)\le \xi K$, the above inequality takes the following form:

$$\begin{aligned} \begin{aligned} U\mathcal {G}\le \Lambda +\xi {K}+\vartheta _0+\eta +\frac{1}{2}\xi _1^2+\vartheta _0+\vartheta _1+\zeta +\frac{1}{2}\xi _2^2+\frac{1}{2}\xi _3^2+\vartheta _0:=M. \end{aligned} \end{aligned}$$

Introducing the above inequality into Eqn.(3), we may lead to the following expression

$$\begin{aligned} d\mathcal {G}\le {M}dt-(1-S)\xi _1dW_1(t)-(1-I)\xi _2dW_2(t)-(1-R)\xi _3dW_3(t). \end{aligned}$$

Step 5. Expectation

Let us assume that $T\wedge {t}_\varrho =\kappa$, the integration of the last inequality gives

$$\begin{aligned} \int _0^{\kappa }d\mathcal {G}\le \int _0^{\kappa }M dt-\int _0^{\kappa }(1-S)\xi _1dW_1(t)-\int _0^{\kappa }(1-I)\xi _2dW_2(t)-\int _0^{\kappa }(1-R)\xi _3dW_3(t). \end{aligned}$$

By taking the expectation, we obtain

$$\begin{aligned} E\bigg [\mathcal {G}\left( S(\kappa ),I(\kappa ),R(\kappa )\right) \bigg ]\le E\bigg [\int ^{\kappa }_0Mdt\bigg ]+\mathcal {G}(Y(0)), \end{aligned}$$

implies

$$\begin{aligned} E\bigg [\mathcal {G}\left( S(\kappa ),I(\kappa ),R(\kappa )\right) \bigg ]\le {M}{T}+\mathcal {G}(Y(0)). \end{aligned}$$

(4)

Step 6. Use of contradiction

Let $\Omega _\varrho =\{T\ge t_\varrho \}$ for every $\varrho \ge \varrho _1$, then $p(\Omega _\varrho )\ge \zeta$. Since, for any outcome $\epsilon \in \Omega _\varrho$, there exists a component $S(\epsilon ,t_\varrho )$ or $I(\epsilon ,t_\varrho )$ or $R(\epsilon ,t_\varrho )$ that equals $\varrho$ or $1/\varrho$, so

$$\begin{aligned} \mathcal {G}\big (S(\epsilon ,t_\varrho ),I(\epsilon ,t_\varrho ),R(\epsilon ,t_\varrho )\big )\ge \bigg (\frac{1}{\varrho }-1+\log \varrho \bigg )\wedge \big (\varrho -\log \varrho -1\big ). \end{aligned}$$

Now, from Eqn.(2) and Eqn.(4), we obtain

$$\begin{aligned} & \mathcal {G}(Y_0)+TM\ge E\bigg [1_{\Omega \varrho (\epsilon )}G\big (S(\kappa ),I(\kappa ),R(\kappa )\big )\bigg ],\\ & \quad \ge E\bigg [1_{\Omega \varrho (\epsilon )}\bigg (-1+\log \varrho +\frac{1}{\varrho }\bigg ) \wedge (-1+\varrho -\log \varrho \big )\bigg ]\\ & \quad =\bigg (-1+\frac{1}{\varrho }\log \varrho \bigg )\wedge (-1+\varrho -\log \varrho \big )E\big [1_{\Omega \varrho (\epsilon )}\big ], \end{aligned}$$

implies that

$$\begin{aligned} \begin{aligned} \mathcal {G}(Y(0))+TM&\ge \zeta \bigg (\frac{1}{\varrho }+\log \varrho -1\bigg )\wedge (\varrho -\log \varrho -1). \end{aligned} \end{aligned}$$

In equation above $1_{\Omega \varrho (\epsilon )}$ denotes the indicator function for the event $\Omega _\varrho (\epsilon )$. However, as $\rho$ increases without bound, the expression $\infty>\mathcal {G}\big (Y_0\big )+\mathcal {K}T=\infty$ leads to a contradiction; therefore, we conclude that $t_\infty =\infty$, and hence, the solution exists globally. $\square$

We now investigate the positivity of the model by proving that all states of the model have non-negative or positive values. For this, we establish the following result.

Theorem 3.2

For initial data Y(0) remains in $\mathcal {R}_{+}^3$, the model (1) posses positive solutions.

Proof

Since the proposed epidemiological model possesses a solution. Let I is the interval of solution contained in $[0,+\infty )$, then the solution of the first state of the system (1) becomes

$$\begin{aligned} & S(t)=\exp \bigg \{-(\vartheta _0+\eta )t-\int _0^t\left( \frac{\xi {I}(x)}{1+\gamma {I}(x)}+\frac{1}{2}\xi _1^2+\xi _1dW_1(x)\right) \bigg \}\\ & \quad \times \bigg \{S(0)+\Lambda \int _0^t\exp \left\{ (\vartheta _0+\eta )x+\int _0^x\left( \frac{\xi {I}(x)}{1+\gamma {I}(x)}+\frac{1}{2}\xi _1^2+\xi _1dW_1(y)\right) dy\right\} dx. \end{aligned}$$

As a result, we obtained that $S(t)>0$. A similar argument proves that I(t) and R(t) respectively have non-negative and strictly positive values, thus we conclude that the epidemiological model gives a solution having non-negative or positive values and remains in $\mathcal {R}^3_{+}$, for all $t\ge 0$. $\square$

The existence analysis and positivity of the model confirm that the epidemiological model is well-posed; therefore, we can now discuss the temporal dynamics, including extinction and persistence analysis, and ultimately obtain the conditions for these outcomes.

Dynamical analysis

In this section, we will focus on discussing the model extinction and persistence, and find the conditions under which the disease persists and becomes extinct. First, we define the stochastic reproductive number for the proposed stochastic model as $R_{s}=R_e+R_p$, where

$$\begin{aligned} R_e=\frac{\xi \Lambda }{\left( \vartheta _0+\eta \right) \left( \vartheta _0+\vartheta _1+\zeta +\frac{\xi _2^2}{2}\right) },\quad R_p=\frac{\xi \Lambda }{\left( 1+\gamma K\right) \left( \vartheta _0+\eta \right) \left( \vartheta _0+\vartheta _1+\zeta +\frac{\xi _2^2}{2}\right) }. \end{aligned}$$

We then characterize the model extinction by establishing the result as described below.

Theorem 4.1

If $R_{e}<1$, then the disease dies out i.e.

$$\begin{aligned} \lim _{t\rightarrow \infty }\sup \frac{\log {I}(t)}{t}\le \left( \vartheta _0+\vartheta _1+\zeta +\frac{\xi _{2}^2}{2}\right) \left( R_e-1\right) <0, \end{aligned}$$

and

$$\begin{aligned} \lim _{t\rightarrow \infty }S(t)=\frac{\Lambda }{\vartheta _0+\eta },\quad \lim _{t\rightarrow \infty } I(t)=0,\quad \lim _{t\rightarrow \infty }R(t)=\frac{\eta \Lambda }{\vartheta _0(\vartheta _0+\eta )}. \end{aligned}$$

On the other hand, if $R_e>1$ and $R_p>1$, and $t\rightarrow \infty$, the persistent occurs and the proposed epidemiological model (1) possess

$$\begin{aligned} I_2\le \lim {\inf }\langle I(t)\rangle \le {\sup }\langle I(t)\rangle \le I_1, \end{aligned}$$

where

$$\begin{aligned} I_1=\frac{\vartheta _0+\eta }{\xi \left( \vartheta _0+\vartheta _1+\zeta \right) }\bigg \{\left( \vartheta _2+\vartheta _1+\zeta +\frac{\xi _2^2}{2}\right) (R_e-1)\bigg \}, \end{aligned}$$

and

$$\begin{aligned} I_2=\frac{(1+\gamma {K})(\vartheta _0+\eta )}{\xi \left( \vartheta _0+\vartheta _1+\zeta \right) }\bigg \{\left( \vartheta _2+\vartheta _1+\zeta +\frac{\xi _2^2}{2}\right) (R_p-1)\bigg \}. \end{aligned}$$

Proof

To perform the extinction analysis of the model, we begin by taking the integral form of the proposed epidemiological model, which becomes

$$\begin{aligned} \begin{aligned}&\int _0^tdS(x)=\Lambda {t}-\int _0^t\left\{ \frac{\xi {I}(x)}{1+\gamma I(x)}+(\vartheta _0+\eta )\right\} S(x)dx+\xi _1\int _0^t S(x)dW_1(x),\\&\int _0^tdI(x)=\int _0^t\left\{ \frac{\xi S(x)I(x)}{1+\gamma I(x)}-(\vartheta _0+\vartheta _1+\zeta )I(x)\right\} dx+\xi _2\int _0^t I(x)dW_2(x),\\&\int _0^tdR(x)=\int _0^t\left\{ \zeta I(x)+\eta S(x)-\vartheta _0R(x)\right\} dx+\xi _3\int _0^t R(x)dW_3(x). \end{aligned} \end{aligned}$$

The evaluation of the integral system may lead to the following system of equations

$$\begin{aligned} \begin{aligned}&S(t)-S(0)=\left\{ \Lambda -\frac{\xi \langle {I}(t)S(t)\rangle }{1+\gamma \langle I(t)\rangle }-(\vartheta _0+\eta )\langle S(t)\rangle +\frac{\xi _1}{t}\int _0^t S(x)dW_1(x)\right\} t,\\&I(t)-I(0)=\left\{ \frac{\xi \langle {I}(t)S(t)\rangle }{1+\gamma \langle I(t)\rangle }-(\vartheta _0+\vartheta _1+\zeta )\langle I(t)\rangle +\frac{\xi _2}{t}\int _0^t I(x)dW_2(x)\right\} t,\\&R(t)-R(0)=\left\{ \zeta \langle I(t)\rangle +\eta \langle S(t)\rangle -\vartheta _0\langle R(t)\rangle +\frac{\xi _3}{t}\int _0^t R(x)dW_3(x)\right\} t. \end{aligned} \end{aligned}$$

From the above system of equations, we may obtain

$$\begin{aligned} & \frac{S(t)+I(t)-S(0)-I(0)}{t}=\Lambda -\left( \vartheta _0+\eta \right) \langle {S}(t)\rangle -\left( \vartheta _0+\vartheta _1+\zeta \right) \langle {I}(t)\rangle \\ & \quad +\frac{\xi _{1}}{t}\int _0^tS(x)dW_{1}(x)+\frac{\xi _{2}}{t}\int _0^tI(x)dW_{2}(x). \end{aligned}$$

It is easy to write that

$$\begin{aligned} & \langle {S}(t)\rangle =\frac{1}{\left( \vartheta _0+\eta \right) }\bigg \{\Lambda -\left( \vartheta _0+\vartheta _1+\zeta \right) \langle {I}(t)\rangle \\ & \quad +\frac{\xi _{1}}{t}\int _0^tS(x)dW_{1}(x)+\frac{\xi _{2}}{t}\int _0^tI(x)dW_{2}(x)-\left( \frac{S(t)+I(t)-S(0)-I(0)}{t}\right) \bigg \}. \end{aligned}$$

To further proceed, we can write from the proposed epidemiological model as

$$\begin{aligned} d\log {I}(t)=\frac{\xi {S}(t)}{1+\gamma {I}(t)}-\vartheta _0-\vartheta _1-\zeta -\frac{\xi _{2}^2}{2}+\xi _{2}dW_{2}(t). \end{aligned}$$

Applying the integral on both sides, we obtain

$$\begin{aligned} \frac{1}{t} \log {I}(t)|_{0}^{t}=\xi \left\langle \frac{{S}(t)}{1+\gamma {I}(t)}\right\rangle -\vartheta _0-\vartheta _1-\zeta -\frac{\xi _{2}^2}{2}+\frac{1}{t}\xi _{2}dW_{2}(t). \end{aligned}$$

(5)

Since, $\gamma>0$ and $I(t)\ge 0$, so $1+\gamma {I}(t)\ge 1$ implies that $\left\langle \frac{{S}(t)}{1+\gamma {I}(t)}\right\rangle \le \langle S(t)\rangle$, thus the above equation may takes the following form:

$$\begin{aligned} \frac{1}{t} \log {I}(t)|_{0}^{t}\le \xi \left\langle {S}(t)\right\rangle -\vartheta _0-\vartheta _1-\zeta -\frac{\xi _{2}^2}{2}+\frac{1}{t}\xi _{2}dW_{2}(t). \end{aligned}$$

Substituting the value of $\langle {S(t)}\rangle$, the above inequality becomes

$$\begin{aligned} & \frac{1}{t} \log {I}(t)|_{0}^{t}\le \frac{\xi }{\left( \vartheta _0+\eta \right) }\bigg \{\Lambda -\left( \vartheta _0+\vartheta _1+\zeta \right) \langle {I}(t)\rangle +\frac{\xi _{1}}{t}\int _0^tS(x)dW_{1}(x)+\frac{\xi _{2}}{t}\int _0^tI(x)dW_{2}(x)\\ & \quad -\left( \frac{S(t)+I(t)-S(0)-I(0)}{t}\right) \bigg \}-\vartheta _0-\vartheta _1-\zeta -\frac{\xi _{2}^2}{2}+\frac{1}{t}\xi _{2}dW_{2}(t), \end{aligned}$$

which implies that

$$\begin{aligned} & \frac{1}{t} \log {I}(t)|_{0}^{t}\le \frac{\xi }{\left( \vartheta _0+\eta \right) }\bigg \{\Lambda +\frac{\xi _{1}}{t}\int _0^tS(x)dW_{1}(x)+\frac{\xi _{2}}{t}\int _0^tI(x)dW_{2}(x)\\ & \quad -\left( \frac{S(t)+I(t)-S(0)-I(0)}{t}\right) \bigg \}-\vartheta _0-\vartheta _1-\zeta -\frac{\xi _{2}^2}{2}+\frac{1}{t}\xi _{2}dW_{2}(t). \end{aligned}$$

Let us define the threshold parameter in case of extinction for the proposed epidemiological model as

$$\begin{aligned} R_e=\frac{\xi \Lambda }{\left( \vartheta _0+\eta \right) \left( \vartheta _0+\vartheta _1+\zeta +\frac{\xi _2^2}{2}\right) }, \end{aligned}$$

then the preceding inequality can be rewritten as

$$\begin{aligned} & \frac{1}{t} \log {I}(t)|_{0}^{t}\le \left( \vartheta _0+\vartheta _1+\zeta +\frac{\xi _{2}^2}{2}\right) \left( R_e-1\right) + \frac{\xi }{\left( \vartheta _0+\eta \right) }\bigg \{\frac{\xi _{1}}{t}\int _0^tS(x)dW_{1}(x)+\frac{\xi _{2}}{t}\int _0^tI(x)dW_{2}(x)\\ & \quad -\left( \frac{S(t)+I(t)-S(0)-I(0)}{t}\right) \bigg \}+\frac{1}{t}\xi _{2}dW_{2}(t). \end{aligned}$$

We now apply the strong law of large numbers, whose general form is described by the lemma given below.

Lemma

Let $M = \{M_t\}_{t \ge 0}$ represents a continuous and real-valued local martingale such that $M_0 = 0$. If

$$\begin{aligned} \lim _{t \rightarrow \infty } \langle M, M \rangle _t = \infty \quad \text {then}\quad \lim _{t \rightarrow \infty } \frac{M_t}{\langle M, M \rangle _t}=0\quad \text {a.s.} \end{aligned}$$

If

$$\begin{aligned} \limsup _{t \rightarrow \infty } \frac{\langle M, M \rangle _t}{t}<\infty \quad \text {then}\quad \lim _{t \rightarrow \infty } \frac{M_t}{t} = 0 \quad \text {a.s.} \end{aligned}$$

Using the fact as provided in the above lemma, the last inequality can be written as follows:

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t} \log {I}(t)|_{0}^{t}\le \left( \vartheta _0+\vartheta _1+\zeta +\frac{\xi _{2}^2}{2}\right) \left( R_e-1\right) . \end{aligned}$$

From the last equation, we observe that if the value of the stochastic reproductive number is less than one ($R_{e}<1$), $\lim {I}(t)=0$ as t increases without bounds. In addition, by taking the associated limiting system of the epidemiological model that is under consideration, it is easy to shows that $S(t) \rightarrow \frac{\Lambda }{\vartheta _0+\eta }$ and $R(t) \rightarrow \frac{\Lambda \eta }{\vartheta _0(\vartheta _0+\eta )}$ as time grows without bound. Hence, we conclude that if $R_{e}<1$, the extinction of the disease occurs.

We now analyze the model persistence, which provides, under conditions disease persists. Since we know that

$$\begin{aligned} & \frac{1}{t} \log {I}(t)|_{0}^{t}\le \frac{\xi }{\left( \vartheta _0+\eta \right) }\bigg \{\Lambda -\left( \vartheta _0+\vartheta _1+\zeta \right) \langle {I}(t)\rangle +\frac{\xi _{1}}{t}\int _0^tS(x)dW_{1}(x)+\frac{\xi _{2}}{t}\int _0^tI(x)dW_{2}(x)\\ & \quad -\left( \frac{S(t)+I(t)-S(0)-I(0)}{t}\right) \bigg \}-\vartheta _0-\vartheta _1-\zeta -\frac{\xi _{2}^2}{2}+\frac{1}{t}\xi _{2}dW_{2}(t). \end{aligned}$$

Re-arranging and then simplifying, we obtain

$$\begin{aligned} & \langle {I}(t)\rangle \le \frac{\vartheta _0+\eta }{\xi \left( \vartheta _0+\vartheta _1+\zeta \right) }\bigg \{\left( \vartheta _2+\vartheta _1+\zeta +\frac{\xi _2^2}{2}\right) (R_e-1)\\ & \quad +\frac{\xi }{\left( \vartheta _0+\eta \right) }\bigg \{\frac{\xi _{1}}{t}\int _0^tS(x)dW_{1}(x)+\frac{\xi _{2}}{t}\int _0^tI(x)dW_{2}(x)\\ & \quad -\left( \frac{S(t)+I(t)-S(0)-I(0)}{t}\right) \bigg \}+\frac{1}{t}\xi _{2}dW_{2}(t)-\frac{1}{t} \log {I}(t)|_{0}^{t}\bigg \}. \end{aligned}$$

Taking the limit as t approaches infinity and applying the supremum, the above inequality looks like:

$$\begin{aligned} \lim _{t\rightarrow \infty }\sup \langle {I}(t)\rangle \le \frac{\vartheta _0+\eta }{\xi \left( \vartheta _0+\vartheta _1+\zeta \right) }\bigg \{\left( \vartheta _2+\vartheta _1+\zeta +\frac{\xi _2^2}{2}\right) (R_e-1)\bigg \}=I_1. \end{aligned}$$

(6)

Since, $\gamma>0$ and $I(t)\le K$ implies that $\frac{1}{1+\gamma {I}(t)}\ge \frac{1}{1+\gamma {K}}$, then from Eqn. (5), we can write

$$\begin{aligned} \frac{1}{t} \log {I}(t)|_{0}^{t}\ge \frac{\xi }{1+\gamma {K}}\left\langle {S}(t)\right\rangle -\vartheta _0-\vartheta _1-\zeta -\frac{\xi _{2}^2}{2}+\frac{1}{t}\xi _{2}dW_{2}(t). \end{aligned}$$

Plugging the value of $\left\langle {S}(t)\right\rangle$ and defining the threshold parameter in case of persistence as

$$\begin{aligned} R_p=\frac{\xi \Lambda }{\left( 1+\gamma {K}\right) \left( \vartheta _0+\eta \right) \left( \vartheta _0+\vartheta _1+\zeta +\frac{\xi _2^2}{2}\right) }. \end{aligned}$$

Performing the same steps as above, we obtain

$$\begin{aligned} & \langle {I}(t)\rangle \ge \frac{(1+\gamma {K})(\vartheta _0+\eta )}{\xi \left( \vartheta _0+\vartheta _1+\zeta \right) }\bigg \{\left( \vartheta _2+\vartheta _1+\zeta +\frac{\xi _2^2}{2}\right) (R_p-1)\\ & \quad +\frac{\xi }{(1+\gamma {K})\left( \vartheta _0+\eta \right) }\bigg \{\frac{\xi _{1}}{t}\int _0^tS(x)dW_{1}(x)+\frac{\xi _{2}}{t}\int _0^tI(x)dW_{2}(x)\\ & \quad -\left( \frac{S(t)+I(t)-S(0)-I(0)}{t}\right) \bigg \}+\frac{1}{t}\xi _{2}dW_{2}(t)-\frac{1}{t} \log {I}(t)|_{0}^{t}\bigg \}. \end{aligned}$$

Applying infimum and taking the limit as t approaches infinity, we get

$$\begin{aligned} \lim _{t\rightarrow \infty }\inf \langle {I}(t)\rangle \ge \frac{(1+\gamma {K})(\vartheta _0+\eta )}{\xi \left( \vartheta _0+\vartheta _1+\zeta \right) }\bigg \{\left( \vartheta _2+\vartheta _1+\zeta +\frac{\xi _2^2}{2}\right) (R_p-1)\bigg \}=I_2. \end{aligned}$$

(7)

Combining the results from Eqns. (6) and (7), we conclude that

$$I_2 \le \liminf \langle I(t) \rangle \le \limsup \langle I(t) \rangle \le I_1,$$

as t increase without bound, which completes the proof. $\square$

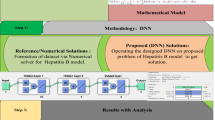
Parameters estimation and numerical experiments

This section provides comprehensive numerical experiments to validate the theoretical findings and efficiency of the hybrid framework through graphical representations. Specifically, we estimate the model parameters using real hepatitis B infection data to ensure biological relevance and practical applicability. In addition, the framework of the FFNN is described, followed by a detailed calibration of the model using the procedure in the adopted hybrid approach.

Parameters estimation

For parameter estimation, we employed real hepatitis B infection data obtained from various hospitals in District Swabi, Khyber Pakhtunkhwa, Pakistan, covering the period from January 2022 to August 2023, as illustrated in Fig. 1. Using the reported data and nonlinear optimization to fit model parameters by computing its value from real data.

Fig. 1

The graphs show the comparison of reported hepatitis B infection cases (bar graph) with simulated data (dashed line), along with the corresponding absolute error.

To do so, let us assume that a parameter vector $\phi \in {\mathbb {R}}^{p}$ and $\hat{I}(t_i;\phi )$, $i=1,2,\ldots ,n$ represent the number of infected individuals produced by the proposed model at times $t_1,t_2,\ldots ,t_n$, while the observed data are denoted by $I_{data}(t_i)$. To estimate $\phi$ using nonlinear least squares, we have:

$$\begin{aligned} \hat{\phi }=\arg \min _{\phi \in \Omega }\sum _{i=1}^{n}\left\{ I_{data}(t_i)-\hat{I}(t_i;\phi )\right\} ^2, \end{aligned}$$

where $\Omega$ is the feasible set. The mean square error and absolute mean square error are defined by the following equations:

$$\begin{aligned} \text {MSE}=\frac{1}{n}\sum _{i=1}^{n}\left\{ \hat{I}(t_i)-I_{data}(t_i)\right\} ^2,\quad \text {MAE}=\frac{1}{n}\sum _{i=1}^{n}\left| \hat{I}(t_i)-I_{data}(t_i)\right| . \end{aligned}$$

To calculate the coefficient of determination ($R^2$), let us assume $\bar{I}_{data}$ represents the mean of actual infected data, then

$$\begin{aligned} R^2=1-\sum _{i=1}^{n}\left\{ \frac{\left( I_{data}(t_i)-\hat{I}(t_i)\right) ^2}{\left( I_{data}(t_i)-\bar{I}\right) ^2}\right\} . \end{aligned}$$

To proceed further, we use MATLAB lsqcurvefit to solve the optimization problem numerically and to estimate the fitted values of the model parameters as provided by Table 1. To construct confidence intervals based on the estimated values of the model parameters, let us define the residual variance estimate as:

$$\begin{aligned} \hat{\sigma }^2=\frac{1}{n-p}\sum _{i=1}^{n}r_i^2, \end{aligned}$$

where $r_i=I_{data}(t_i)-\hat{I}(t_i;\phi )$, and assume a $n\times {p}$ Jacobian matrix denoted by $J(\phi )$ and define as:

$$\begin{aligned} J_{i,j}(\phi )=\frac{\partial {\hat{I}(t_i,\phi )}}{\partial \phi _j}. \end{aligned}$$

Using Moore-Penrose pseudo-inverse to avoid numerical instability and calculating the estimated covariance with the aid of nonlinear least squares approximation given by

$$\begin{aligned} \hat{Cov}(\hat{\phi })\approx \hat{\sigma }^2\left( J(\hat{\phi })^{T}J(\hat{\phi })\right) ^{-1}. \end{aligned}$$

Thus, approximating 95% confidence interval $\hat{\phi }_j\pm {t}_{{n-p},0.975}SE(\hat{\phi }_J)$, where $SE(\hat{\phi }_j)=\sqrt{(\hat{Cov}(\hat{\phi }))_{jj}}$. Further, the detail implementation procedure of parameters estimation and calculating confidence intervals is concluded via Algorithm 1.

Model discritization and the frame work of FFNN

Let $[0, T]$ be the time interval and the time step $\Delta t = T / K$, then the discretized time points become $L_m = m \Delta t$. To make our symbolic representation simple, using $(S_m, I_m, R_m)$ for $(S(L_m), I(L_m), R(L_m))$ and $W_m(L_n) = W_{mn}$ for $m = 1, 2, 3$. The implementation of the Itô–Taylor expansion provides the following discretization form of the proposed model:

$$\begin{aligned} \begin{aligned} S_m&=S_{m-1}+\left\{ \Lambda -\frac{\xi {S}_{m-1}I_{n-1}}{1+\gamma {I}_{n-1}}-(\vartheta _0+\eta )S_{m-1}\right\} \Delta t\\&\qquad +\xi _1 S_{m-1}(W_{1_{{m}}}-W_{1_{{m-1}}})-\frac{1}{2}\xi _1^2 S_{m-1}\left\{ (W_{1_{{m}}}-W_{1_{{m-1}}})^2-\Delta t\right\} ,\\ I_{m}&=I_{m-1}+\left\{ \frac{\xi {S}_{n-1}I_{m-1}}{1+\gamma {I}_{m-1}}-(\vartheta _0+\vartheta _1+\zeta )I_{m-1}\right\} \Delta t\\&\qquad +\xi _1 I_{m-1}(W_{2_{{m}}}-W_{2_{{m-1}}})+\frac{1}{2}\xi _1^2 I_{m-1}\left\{ (W_{2_{{m}}}-W_{2_{{m-1}}})^2-\Delta t\right\} ,\\ R_{m}&=R_{m-1}+\left\{ \eta {S}_{n-1}-\vartheta _0 R_{m-1}+\zeta {I}_{n-1}\right\} \Delta t\\&\qquad +\xi _3 R_{m-1}(W_{3_{{m}}}-W_{3_{{m-1}}})-\frac{1}{2}\xi _1^2 R_{m-1}\left\{ (W_{3_{{m}}}-W_{3_{{m-1}}})^2-\Delta t\right\} . \end{aligned} \end{aligned}$$

Algorithm 1

Estimation of parameter and computation of confidence interval.

To illustrate the discretization of the Brownian paths used in $W_{n}(L_m)-W_{n}(L_{m-1})$, taking the increment $\delta {t}$ and defining $\Delta t$ is an integral multiple of $\mathcal {R}\ge 1$, $W_{n}(L_m)-W_{n}(L_{m-1})$ looks like

$$\begin{aligned} W_{n}(L_n)-W_{m}(L_{n-1})=\sum _{k=m\mathcal {R}-\mathcal {R}+1}^{m\mathcal {R}}dW_k. \end{aligned}$$

To apply the procedure for the proposed model, we first divide the interval [0, T] into sub-intervals, and define $L_m=m\delta t$ and $\delta t=\frac{T}{K}>0$: $0=L_0<L_1<L_2<L_3<\cdots <L_K=T$. Defining the initial data $(S_0,I_0,R_0)$ as an initial guess/input for the next model states and using the recursive formulas $(S_m,I_m,R_m)$ for $1\le m \le K$ as reported above, derived by following Milstein’s numerical procedure. We also discretize the Brownian paths to use in the formula $W_{n}(L_m)-W_{n}(L_{m-1})$ and increment $\Delta t$, $\mathcal {R}\ge 1$. Finally calculating $W_{n}(L_m)-W_{m}(L_{n-1})=W_{m}(m\mathcal {R}\delta t)-W_{m}((m-1)\mathcal {R}\delta t)=\sum _{k=m\mathcal {R}-\mathcal {R}+1}^{m\mathcal {R}}dW_k$.

We now outline the modeling framework of the neural network to approximate the model that is under consideration. We implement FFNN using supervised learning to generate the stochastic simulations. For this purpose, first, we apply the Milstein procedure and the estimated parameter values derived from the number of reported hepatitis B cases as reported in Table 1. To proceed, as we know that

$$\begin{aligned} Y(t)=\left( \begin{array}{c} S(t) \\ I(t) \\ R(t) \\ \end{array} \right) , \end{aligned}$$

then the next state is given by

$$\begin{aligned} Y(t+\Delta {t})=\left( \begin{array}{c} S(t+\Delta {t}) \\ I(t+\Delta {t}) \\ R(t+\Delta {t}) \\ \end{array} \right) . \end{aligned}$$

Let ${\theta }$ represent the learnable (biases or weights) parameters of the network function, denoted by $G_{\theta }$, which is given by

$$\begin{aligned} G_{\theta }:Y(t)\mapsto {Y(t+\Delta {t})}. \end{aligned}$$

The FFNN network is a multilayer perceptron (MLP), which will be trained to approximate the above nonlinear function. The network will learn the nonlinear stochastic dynamics represented by the mapping between the current and predicted states of the proposed model (1). The number of input layer are three representing S(t) - the susceptible, HBV infected - I(t), and recovered populations - R(t) at time t, while the network output layers are the predicted states $S(t+\Delta {t})$, $I(t+\Delta {t})$ and $R(t+\Delta {t})$ at time $t+\Delta {t}$. Moreover, the network is a fully connected neural network of two hidden layers, each containing 20 and 30 neurons respectively (see the architecture in Fig. 2), by following the work having similar complexity in the literature³⁰. For $i=1,2,3$, if $a_i$ and $H_i$ are the biases and weights of the layer, and $\eta _i$ $(i=1,2)$ are the activation functions, then the network function can be written as:

$$\begin{aligned} \hat{Y}(t+\Delta {t})=G_{\theta }(Y(t))=H_3\eta _2(H_2\eta _1(H_1x(t)+a_1)+a_2)+a_3, \end{aligned}$$

where in the hidden layers a hyperbolic tangent sigmoid function $\left( \eta (x)=\tanh (x)\right)$ is used as a activation function and $\eta _{out}(Y)=Y$ is used as a linear activation function. The network is then trained over simulated data $(Y(t_i),Y(t_i+\Delta {t}))$ produced by stochastic simulations, and the optimization takes the form:

$$\begin{aligned} \min _{\theta }L(\theta )=\frac{1}{N}\sum _{i=1}^{N}\Vert G_{\theta }(Y(t_i))-Y(t_i+\Delta {t})\Vert ^2, \end{aligned}$$

where $\Vert .\Vert$ is the Euclidean norm and N is the number of training samples. The loss function is defined to be the Mean Squared Error (MSE) as:

$$\begin{aligned} MSE=\frac{1}{3N}\sum _{i=1}^{N}\sum _{j=1}^{3}\left( Y_{j}^{true}(t_i+\Delta {t})-Y_{j}^{pred}(t_i+\Delta {t})\right) ^2. \end{aligned}$$

Solving the nonlinear least square problem using Levenberg–Marquardt optimization algorithm with the training configuration as: the maximum epochs is 1000, performance goal (MSE) is $10^{-6}$, minimum gradient threshold is $10^{-7}$, and early stopping to prevent overfitting. To ensure reliable training and performance, the dataset generated from the stochastic trajectories will be divided into 80% and 20% for training and testing. The overall implementation procedure is concluded by Algorithm 2.

Large scale numerical simulations and interpretation

To conduct large-scale numerical simulations, we utilized a dataset representing the reported cases of hepatitis B virus (HBV) infection in District Swabi, Khyber Pakhtunkhwa, Pakistan, spanning the period from January 2022 to August 2023. The model parameters are estimated with their confidence intervals using a least-squares optimization procedure as concluded by Algorithm 1, and the result is illustrated in Fig. 1, which compares the reported cases (bar graph) with the simulated model trajectory (line graph) and the corresponding absolute error.

Algorithm 2

SDE–FFNN

Fig. 2

The plot represents the architecture of the feed-forward neural network which learns the nonlinear stochastic mapping: $(S(t), I(t), R(t)) \longrightarrow (S(t+\Delta t), I(t+\Delta t), R(t+\Delta t))$.

These estimated parameters with confidence intervals, summarized in Table 1, were then employed for large-scale simulations within the proposed hybrid SDE–FFNN framework, as outlined in Algorithm 2. The stochastic dynamics were simulated using Milstein’s higher-order numerical scheme over a time horizon of 2000 days, with initial conditions specified as $S(0)=500$, $I(0)=50$, and $R(0)=30$. The resulting stochastic realizations generated both simulation outputs and datasets used for training the feed-forward neural network (FFNN). Finally, the complete algorithm was implemented in MATLAB, and the outcomes of the hybrid approach are presented in Figs. 3,4,5,6,7,8. These results provide validation of the theoretical results established for the proposed stochastic model (1) and investigate the efficiency of the hybrid framework by showing a close match between the stochastic trajectories and FFNN outputs with low mean square errors. Thus, we consider the following two examples for disease extinction and persistence.

Example 5.1

This example aims to numerically support the theoretical results of disease extinction for the model (1) established in Theorem 4.1. We consider a vaccination rate $\eta =0.7254$ and a recovery rate $\zeta =0.5218$, and set all other epidemic parameters as in Table 1. Ultimately, we calculated the value of the basic reproductive number as $\mathcal {R}_0=0.7196<1$ revels that if the value of the basic reproductive numbers is less than one predict extinction of the HBV in the long run substantiated by Figs. 3(a), 4 (a) and 5 (a), respectively demonstrate that there will be susceptible and recovered population. At the same time, the HBV-infected population vanishes. Under these parameter adjustments, a comparative analysis of stochastic trajectories and FFNN outputs is presented to show the temporal dynamics of the model compartments, with associated absolute error depicted in Figs. 3,4,5. The performance of the hybrid approach is also evaluated by presenting the mean squared error (MSE), training diagnostics, error histogram, and regression analysis, as shown by Figs. 6,7,8,9. From the temporal dynamics of the model compartment, we observed that they closely agree with certain noticeable deviations, highlighting regions where FFNN struggles to generalize adequately. Moreover, mean absolute error and error distribution between outputs and targets across testing, validation, and training are given by Fig. 6 (a) and (b), respectively. The FFNN model achieves the best validation performance of 95126.5954 at epoch 15, as illustrated in Fig. 7. The training diagnostics are evaluated with a declining gradient of 414739.6408, learning rate 100, and validation check 6 at epoch 21, as shown in Fig. 8. The regression performance is approximately 0.999 for all (validation, testing, and training) as given by Fig. 9. Thus, in the case of disease extinction, comparative analysis of the model performance highlights that the proposed hybrid framework can capture the disease dynamics effectively.

Fig. 3

FFNN trajectories (red-dashed line) vs stochastic trajectories (blue line) for the model compartment - S(t), and its associated absolute error under parameter setting of extinction analysis.

Fig. 4

The graphs show the comparative analysis of the stochastic simulations and FFNN outputs for the model state - I(t), with its absolute error analysis against parameter setting of extinction.

Fig. 5

The temporal dynamics of the model state R(t) at extinction setting, where the blue line represents the solution trajectories provided by stochastic simulations, while the red dashed line represents the FFNN outputs with its associated absolute error.

Fig. 6

The graphs show the total mean absolute error and mean square error of the validation as well as datasets training against the training epochs under extinction setting.

Fig. 7

The plot shows the best validation performance of MSE against epochs in case of extinction of the model.

Fig. 8

The figure illustrates insight into the optimization stability, learning behavior, and generalization control of the training process against parameter setting of extinction.

Fig. 9

The graphs visualize the regression performance of the network outputs and the target values for the validation, testing, training and overall datasets in case of extinction analysis.

Example 5.2

In this example, we illustrate the persistence of the disease to validate the result established in Theorem 4.1. According to the sufficient condition for HBV persistence derived in model (1), this numerical experiment serves to confirm the theoretical analysis. Using the estimated parameter values provided in Table 1, the computed basic reproduction number $\mathcal {R}_0=1.2242>1$ indicates that the disease persists, implying the continual presence of infected individuals. This outcome is further supported by the simulation results shown in Figs. 10 (a), 11 (a), and 12 (a), which visually confirm the persistence of the disease anticipated by the theory. Under these parameter settings, we present the dynamical behavior of the compartmental population, as illustrated in Figs. 10,11,12, respectively showing the temporal evolution of S(t), I(t), and R(t), along with their associated absolute errors. Moreover, to assess the model performance, MSE, error histogram, training and validation performance, as well as regression analysis, are provided in Figs. 13, 14, 15, and 16, respectively. The mean square error analysis and the distribution of prediction errors during the training, validation, and testing phases, where the concentration of errors around zero demonstrates that the model is well-calibrated and achieves high predictive accuracy, as shown in Fig. 13. In this case, the best validation performance is 133039.1699 at epoch 12 as shown by Fig. 14, the gradient, learning parameter and validation check are 1742944.0486, 100 and 6 respectively at epoch 14 as depicted by Fig. 15 which show that the training progress of the neural network further illustrates the evaluation of the gradient, damping parameter, and validation performance, confirming effective convergence of the hybrid framework. The R-value for training, testing, validation, and overall is approximately equal to 1, as provided in Fig. 16, validating the predictive capacity of the network, showing that the FFNN generalizes well and accurately approximates the solution of the stochastic HBV model.

Fig. 10

The graphs shows the comparative analysis of FFNN outputs (red-dashed line) vs stochastic simulations (blue line) for the state - S(t), along with their associated absolute error in case of persistence.

Fig. 11

The graphs show the comparative analysis of the stochastic simulations and FFNN outputs for the model state - I(t), with its absolute error analysis against parameters setting for persistence.

Fig. 12

The temporal dynamics of the model state - R(t) in case of persistence setting, where the blue line represents the solution trajectories provided by stochastic simulations, while the red dashed line represents the FFNN outputs with its associated absolute error.

Fig. 13

The graphs show the total mean absolute error and mean square error of the validation as well as datasets training against the training epochs for persistence setting.

Fig. 14

At the persistence analysis, the plot shows the best validation performance of MSE against epochs in case of persistence of the model.

Fig. 15

The figure illustrates insight into the optimization stability, learning behavior, and generalization control of the training process against persistence parameter adjustment.

Fig. 16

The graphs visualize the regression performance at persistence of the network outputs and the target values for the validation, testing, training and overall datasets.

Conclusion

We discussed the dynamics of hepatitis B using an annotative hybrid approach of stochastic differential equation and feed forward neural network. Formulating the model, we then studied the mathematical and biological feasibility to ensure the theoretical soundness of the proposed epidemic problem. We also investigated the extinction and persistence of the model to find the conditions for disease extinction and persistence which corresponds to the number of infected individuals decreases over time and ultimately vanishes whenever $R_e<1$, while if $R_p>1$, the number of HBV infected individuals are positive and the disease continues to exist in the population. The model parameters are parameterized using real data of HBV reported cases and generated a data to train the feed forward neural network and predicted the model dynamics. A close agreement have been observed between the stochastic simulations and the neural network outputs, with relatively low error values highlighting the effectiveness of the proposed hybrid framework. This suggests that the integration of SDEs and FFNNs can enhance the predictive capacity of the model under the considered conditions. Based on the reported data, the long-run behavior of the hybrid framework suggests the potential persistence of infection, which could offer useful insights for public health practitioners.

However, while the predictive capacity with low mean square error suggests the usefulness of the proposed hybrid approach, several limitations should be acknowledged. First, the analysis have been conducted within a restricted set of parameter assumptions and a relatively limited dataset of reported cases. Hepatitis B virus transmission, however, is a complex disease having multi-infection stages and is a global health problem. Second, the present work assumes only white noise, which restricted the noise effects. To enhance the results, future work should focus on incorporating multiple infection phases of hepatitis B together with broader noise structures, such as Lévy or colored noise, and employ more comprehensive datasets of reported cases. We also find the relationship between the neural network parameters and those of the epidemiological model to determinate that the model is biological feasibility of the hybrid framework. With these modification, the framework could be further strengthened to provide more reliable predictions of HBV outbreaks.