Sybil-resistant and privacy-preserving authentication based on short-term pseudonym for internet of vehicles

Abstract

By sharing basic safety messages (BSMs) containing driving information, internet of vehicles becomes an important part in cooperative intelligent transportation systems. Designing a secure, privacy-preserving and efficient authentication scheme is an imperative and challenging issue. Vehicles should use different anonymous identities to send BSMs to resist trajectory tracking attacks. However, malicious vehicles may use multiple identities at the same time to launch Sybil attacks. In terms of efficiency, some schemes use time-consuming computation operations such as bilinear pairing and have very costly computation time for verifying signatures. To solve these problems, we construct a Sybil-resistant and privacy-preserving (SRPP) authentication scheme. In SRPP, vehicles use different short-term pseudonyms in different road side unit (RSU) jurisdictions, and short-term pseudonyms need to be authorized by RSUs. In terms efficiency, SRPP scheme mainly uses computationally efficient multiplication operations and point addition operations on elliptic curve, and realizes batch verification. Security proof and analysis show that SRPP scheme can meet security requirements and resist multiple types of attacks such as replay and DoS. The performance evaluation demonstrates that compared with recent proposed schemes, SRPP scheme is practical in terms of computation time and communication overhead while resisting Sybil attacks and trajectory tacking attacks.

Introduction

To improve driving experience, road safety and traffic management, researchers have proposed internet of vehicles (IoVs). In IoVs, each vehicle includes real-time location, speed, and other driving information in basic safety messages (BSMs), which are shared with surrounding vehicles and infrastructure via wireless connection^1,2,3. However, by exploiting BSM, attackers can launch several types of attacks, such as impersonation and Sybil attacks^4,5. Therefore, in IoVs, ensuring the correctness and reliability of the exchanged BSMs are essential considerations that must be addressed^6,7,8. In addition, since BSMs contain vehicle’s identity, position, direction, etc., if the information is exploited by attackers, they may disclose vehicle’s travel trajectory, occupation, etc., and hijack a vehicle⁹. Thus, the protection of vehicle’s privacy is also an important part in the research field of message authentication in IoVs⁷.

Pseudonym and digital signature are widely used techniques to address the above security and privacy issues in IoVs, and researchers proposed some anonymous message authentication schemes^10,11. However, existing schemes still suffer some limitations⁸. Generally, traditional PKI-based schemes exist certificate management burden^12,13, and key escrow issue^14,15. In addition, the security of some existing schemes depends on strong assumptions about the ideal tamper-proof devices (TPDs)^16,17. Besides, some schemes are only designed for vehicle-to-infrastruction (V2I) communication. In fact, vehicle-to-vehicle (V2V) communication is also an important mode for vehicles to share traffic data, and it is urgent to propose authentication scheme for V2V communication. Moreover, existing authentication schemes are less concern about Sybil attacks and trajectory privacy simultaneously. For these reasons, security and privacy protection are still the critical factors restricting the development of IoVs¹⁸.

Considering the above security, privacy protection and efficiency issues in IoVs, we proposes a Sybil-resistant and privacy-preserving (SRPP) authentication scheme. The principal contributions of our work are summarized as follows:

• 1. We construct a lightweight anonymity message authentication scheme by utilizing computationally efficient multiplication operations and point addition operations on elliptic curve, hash functions and XOR operations. By supporting batch mode, thus receivers can verify multiple signatures simultaneously and efficiently.

• 2. Furthermore, based on two hash chains, vehicles can generate short-term pseudonyms on demand, and short-term pseudonyms need to be authorized by RSUs. In this way, vehicles can use multiple pseudonyms during their travel, while limiting the abuse of pseudonyms. Thus, SRPP scheme can resist both trajectory tracking and Sybil attacks.

• 3. Based on random oracle model, the security of SRPP scheme is proved, and the security in message authentication, dynamic pseudonym, un-linkability and conditional traceability, and resistance to various common attacks such as Sybil and tracking are illustrated. Moreover, the performance evaluation demonstrates that compared with other related work recently proposed, SRPP scheme has reasonable computation time cost in generating signature and verifying BSMs, and practical communication overhead in sending BSMs.

Related works

Public key infrasturcture (PKI)-based schemes

In PKI-based schemes, when a vehicle sends a BSM, it attaches a corresponding certificate to the message. The receiver needs to verify the certificate in BSM. In a traditional PKI-based scheme¹², each vehicle loads a large number of certificates from a trusted authority (TA) to its own TPD. To minimize the required storage for certificates, RSUs are used to assign short-lifetime pseudonyms and corresponding certificates to requesting vehicles¹⁹. By introducing fog computing, Kang et al.²⁰ transfered pseudonym management to resources at the network edge. Certificate revocation is also an issue in PKI based schemes. Wasef and Shen²¹ realized revocation by updating the global key used to calculate hash message authentication code (HMAC). The time and resource cost of updating the global key is relatively high. Overall, in such schemes, certificate management increases the storage, communication and computation burden¹³.

Identity (ID)-based schemes

The ID-based schemes avoid the burden of certificate management, because the public key of each vehicle can be easily calculated from its identity¹⁴. In most ID-based schemes, each vehicle preloads system master secret key (SMSK), its real identity, and password from TA into its own TPD in initialization phase. He et al.²² proposed a scheme that does not use bilinear pairing. Ali et al.²³ proposed an ID-based batch verification scheme for V2I communication by using bilinear pairing and general hash functions. Without using bilinear pairng, Ali et al.²⁴ proposed a scheme for V2V communication, but Song et al.²⁵ demonstrated that this scheme²⁴ is insecure.

On the whole, most ID-based schemes strongly assume that SMSK must be pre-loaded into each vehicle’s TPD and that no attacker will be able to obtain SMSK from TPD¹⁶. In fact, by launching a side channel attack, an attacker may get SMSK¹⁴. As a result, using SMSK, the adversary can launch impersonation attacks, bogus message attacks, etc., and the whole system could be exposed to serious security risks¹⁷. In addition, ID-based schemes generally require a TA to generate and manage vehicles’ private keys, which brings the new key escrow problem²⁶.

Certificateless signature (CLS)-based schemes

CLS-based scheme is considered to have the potential to solve the certificate management problem of the PKI-based schemes and the key escrow problem of the ID-based schemes²⁶. To achieve secure V2I communication, scholars proposed some schemes. Based on bilinear paring, Horng et al.²⁶ proposed a CLAS-based scheme with conditional privacy-preserving in which each BSM uses a different pseudonym. Zhong et al.¹⁶ used a trace authority (TRA) responsible for generating pseudonyms for vehicles and, if necessary, tracking real identities of vehicles. Han et al.²⁷ proposed a CLAS scheme that does not use bilinear pairing, named eCLAS, and proved the security of eCLAS in the random oracle model based on the computational difficulty of elliptic curve discrete logarithm problem (ECDLP). Zhu et al.¹ devised a pairing-free authentication scheme, which has better computational performance than previous authentication schemes, but Yang et al.²⁸ showed that the proposed scheme¹ is susceptible to coalition assaults launched by malicious RSUs and vehicles, as well as being insecure against public-key replacement (PKR) attacks. Yang et al.²⁹ put forward a re-cryptanalysis to the security of the CLAS scheme proposed by Zhu et al.¹, and then proposed a provably secure CLAS scheme with a new aggregate algorithm for IoVs. The main difference between the two schemes is that Yang et al.’s scheme²⁹ changes the input space of a hash function in the signature generation phase. However, the improved scheme²⁹ still only supports V2I communication, and a vehicle uses only one pseudonym, which makes the vehicle potentially vulnerable to trajectory tracking attacks.

Elliptic curve cryptography (ECC) can provide the same or even higher security level as RSA, achieving a smaller key size, faster computing speed, lower bandwidth and storage overhead. These features perfectly match the demanding requirements of low latency, high throughput and resource constraints in the IoVs. Based on ECC, Kamil and Ogundoyin³⁰ proposed a CLAS scheme for vehicular communications, and the security of this scheme was reduced to the computational difficulty assumption of ECDLP. Through analysis, Xiong et al.¹⁵ found that the scheme³⁰ could not resist collusion attacks, and put forward an improvement scheme to resist collusion attacks, however, in this scheme, a vehicle uses only one pseudonym for a long time, so the vehicle’s trajectory privacy is not protected³¹. Ali et al.³² also proposed an ECC-based scheme for V2V communication that uses efficient general hash functions instead of time-consuming MapToPoint hash functions, but it does not provide unforgeability¹⁸. Thus, Zhou et al.¹⁸ designed a new provably secure scheme that does not use time-consuming bilinear pairing and MapToPoint opereations, however, there is also the problem of travel trajectory disclosure. Based on ECC, Wu and Ye³³ proposed a CLAS scheme that does not use bilinear pairing, but there is also a risk of leaking travel trajectory.

Wu et al.⁷ proposed a CLS scheme for V2V communication, whose batch verification method is based on bilinear pairing, so its computation time cost is higher compared with those schemes that do not use bilinear paring. During the registration phase, a vehicle applies to TA for a pool of pseudonyms. This provides an opportunity for malicious users to launch Sybil attacks. Based on CLAS and paring-free operations, Zhu et al.⁸ proposed a lightweight conditional privacy-preserving identity authentication (LCPIA) scheme with fewer operations and less communication overhead. In LCPIA scheme, vehicles collaborate with TA to generate dynamic pseudonyms and public/private key pairs, and each vehicle may hold multiple usable pseudonyms which can be used by attackers to launch Sybil attacks. In addition, they did not discuss how TA sent the relevant cryptographic materials to a vehicle.

In general, although many important results have been achieved in the research of privacy-preserving authentication scheme for vehicular communications, how to resist Sybil attacks and trajectory tracking attacks while improving verification efficiency is still a challenge.

Preliminaries

System model

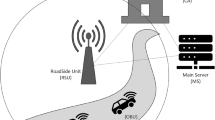
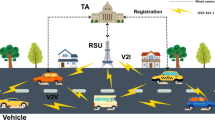
The system model of the proposed SRPP scheme is comprised of a TA, several RSUs and intelligent vehicles^34,35, as shown in Fig. 1.

TA is the upper layer management center having the highest authority, storage, communication and computation capabilities, and has the highest level of security, that is, will not be compromised by attackers. It completes the system setup and the registration of RSUs and vehicles by offline means. TA generates long-term anonymous identities for each vehicle and reveals the true identities of malicious vehicles when needed. TA generally adopts the secure socket layer (SSL) protocol to communicate with RSUs³⁶.

RSUs are base-stations fixed along roadsides. They have less capabilities than TA and more capabilities than vehicles. In our SRPP scheme, RSUs are responsible for authorizing vehicles’ short-term pseudonyms. A RSU communicates with TA as well as other RSUs in real time through secure SSL protocol, and with vehicles through dedicated short range communication (DSRC) protocol.

Each vehicle is required to register its real identity information in TA, and each vehicle can establish a secure channel for the registration. Vehicles periodically broadcast BSMs including driving-related status data (e.g., speed and location) through DSRC protocol. The secret materials used by vehicles to sign and verify messages are kept secret in their respective on-board TPD. Vehicles are untrusted and can launch fake messages, Sybil and other attacks.

Fig. 1

System model.

Security requirement

To meet the security and privacy requirements of vehicular communications, a practical BSM authentication scheme need to satisfy the following security goals⁸.

• 1. Message Authentication In V2V and V2I communications, vehicles and RSUs are exposed to wireless communication channels. To prevent adversaries in open channels from forging and tampering, any receiver in IoVs must have the capability to ensure that the received BSMs are sent from authorized devices and have not been modified by adversaries.

• 2. Dynamic Pseudonym Pseudonym provides some protection for vehicles’ real identity. However, if a vehicle uses only one pseudonym for a long time, adversaries can use that pseudonym to launch a trajectory tracking attack. Therefore, dynamic pseudonyms should be guaranteed in IoVs, so that different pseudonyms can be used in different areas to ensure greater privacy and security.

• 3. Un-Linkability Any adversary cannot correctly link two or more pseudonyms to the same vehicle. In IoVs, unlinkability ensures that BSMs sent under different pseudonyms are uncorrelated.

• 4. Conditional Traceability Conditional traceability requires that TA be able to track the real identity of a vehicle, and that no other entity has this ability.

• 5. Resistance Against Attacks In this complex system environment, by analyzing or broadcasting BSMs, an attacker may launch multiple attacks such as tracking, replay, Sybil and denial of service (DoS). Resistance to these attacks is also a fundamental requirement for a BSM authentication scheme.

Mathematical knowledge

The ECC belongs to public-key cryptography (PKC) designed on elliptic curves over finite fields³⁷. The ECC requires a shorter key size than other PKC-oriented approaches while providing the same level of security.

Consider a finite field ${{F}_{p}}$ with a large prime order p. Elliptic curve $E\left( a,b \right) :{{y}^{2}}={{x}^{3}}+ax+b(\bmod p)$ is defined on ${{F}_{p}}$, where $a,b\in {F}_{p}$ and $4{{a}^{3}}+27{{b}^{2}}\ne 0$ . Let ${{G}_{q}}$ be a finite cyclic additive group on $E\left( a,b \right)$ with a generator point G, where q is a large prime order. Especially, the scalar multiplication on ${{G}_{q}}$ is given as $mH=H+H+\cdots +H$ (m times), where $m\in Z_{q}^{*}$ and H is a random point on $E\left( a,b \right)$. Our SRPP scheme is based on the following computational complexity assumptions³⁸.

Definition 1

ECDLP: Given two random points ${H,K}\in {{G}_{q}}$, finding $x\in Z_{q}^{*}$ such that $K=x\cdot H$ is computationally hard.

Definition 2

Computational diffie-hellman problem (CDHP): Given $H,K\in {{G}_{q}}$, the computation of $(x\cdot y)\cdot G$ is hard, where $H=x\cdot G$, $K=y\cdot G$ with $x,y\in Z_{q}^{*}$.

Definition 3

Collision-resistance: Given a hash function $H():X\rightarrow Y$ , if it is impossible to find two distinct values a and b, where $a,b\in {X}$ and ${a}\ne {b}$, such that $H\left( {a} \right) =H\left( {b} \right)$, then it possesses collision-resistance.

Proposed SRPP scheme

In this section, the overall framework of our proposed SRPP scheme and the implementation details are introduced.

Framework of SRPP

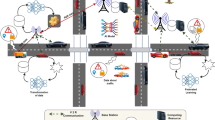
To protect privacy and defend against Sybil attacks, SRPP scheme supports each vehicle to use different short-term anonymous identities in different RSU jurisdictions. The framework of SRPP scheme consists of six phases, namely: (1) system setup; (2) registration; (3) mutual authentication and short-term pseudonym generation; (4) authorizing short-term pseudonym; (5) signing and broadcasting BSM; (6) authenticating BSM, as shown in Fig. 2. For illustration purpose, we show in Table 1 the definitions of notations used in the following descriptions.

Fig. 2

Framework of SRPP.

Table 1 Notations and definitions.

System setup

The system setup is accomplished by TA, which inputs a security parameter l and generates system parameters sypas and system secret key ${{s}_{TA}}$ for the authentication system.

• 1. TA selects a cyclic additive group ${{G}_{q}}$ with order q on the elliptic curve $E({{F}_{p}})$ according to the selected security parameter l, where p, q are large primes of length l-bits, and G is a generator point of ${{G}_{q}}$.

• 2. TA chooses a number ${{s}_{TA}}\in Z_{q}^{*}$ at random and computes ${{S}_{TA}}={{s}_{TA}}\cdot G$ as its private key and public key respectively.

• 3. TA selects six one-way collision-resistant hash functions: ${{H}_{1}}:{{\{0,1\}}^{*}}\times {{G}_{q}}\times {{\{0,1\}}^{*}}\rightarrow Z_{q}^{*}$, ${{H}_{2}}:{{G}_{q}}\times {{\{0,1\}}^{*}}\rightarrow Z_{q}^{*}$, ${{H}_{3}}:{{\{0,1\}}^{*}}\times {{G}_{q}}\times {{G}_{q}}\times {{\{0,1\}}^{*}}\times {{\{0,1\}}^{*}}\rightarrow Z_{q}^{*}$, ${{H}_{4}}:{{\{0,1\}}^{*}}\rightarrow Z_{q}^{*}$, ${{H}_{5}}:{{\{0,1\}}^{*}}\times {{G}_{q}}\times {{G}_{q}}\times {{\{0,1\}}^{*}}\rightarrow Z_{q}^{*}$, ${{H}_{6}}:{{\{0,1\}}^{*}}\times {{\{0,1\}}^{*}}\times {{G}_{q}}\times {{\{0,1\}}^{*}}\rightarrow Z_{q}^{*}$. It is worth noting that vehicles communicate through wireless means and are facing long-term and complex threats. A system that relies on a single hash function, once this function is breached, will lead to large-scale and catastrophic security failures. Our approach of using multiple hash functions has significantly raised the threshold and cost of attacks, providing a stronger guarantee for secure vehicle communication and meeting the fundamental requirements of the IoV for high reliability and security resilience.

• 4. TA publishes the system public parameters $\{q,{{G}_{q}},G,{{S}_{TA}},{{H}_{1}},{{H}_{2}},{{H}_{3}},{{H}_{4}},{{H}_{5}},{{H}_{6}}\}$ , and keeps the ${{s}_{TA}}$ secret.

Registration

Before communicating with other entities in IoVs, any RSU and vehicle must register with TA. TA generates public key and secret key for RSUs and vehicles. TA provides long-term public key ${{R}_{i}}$ and corresponding secret key $RS{{K}_{i}}$ for a RSU, and provides long-term public key ${{V}_{i}}$, corresponding secret key $VS{{K}_{i}}$ and two hash seeds for a vehicle.

RSU registration

For the $RS{{U}_{i}}$, TA chooses a number ${{r}_{i}}\in Z_{q}^{*}$ at random and computes ${{R}_{i}}={{r}_{i}}\cdot G$, $h_{RSU}^{i}={{H}_{1}}\left( RI{{D}_{i}},{{R}_{i}},\Delta t_{R}^{i} \right)$, $RS{{K}_{i}}=( {{r}_{i}}+{{s}_{TA}}\cdot h_{RSU}^{i} ) \bmod \,q$, where ${{R}_{i}}$ is long-term public key of $RS{{U}_{i}}$, $RI{{D}_{i}}$ is identification code of $RS{{U}_{i}}$, $\Delta t_{R}^{i}$ is expiration date of ${{R}_{i}}$, and $RS{{K}_{i}}$ is secret key of $RS{{U}_{i}}$. Then, the TA sends $\left\{ {{R}_{i}},h_{RSU}^{i},RS{{K}_{i}},\Delta t_{R}^{i} \right\}$ to $RS{{U}_{i}}$ via a secure channel.

Vehicle registration

For the vehicle $Ve{{h}_{i}}$ with real identity $VI{{D}_{i}}$, TA generates two random hash seeds $Seed_{i}^{1}$ and $Seed_{i}^{2}$, and selects a random number ${{v}_{i}}\in Z_{q}^{*}$, and computes ${{V}_{i}}={{v}_{i}}\cdot G$, $h_{Veh}^{i}={{H}_{2}}({{V}_{i}}, \Delta t_{V}^{i})$, $VS{{K}_{i}}=\left( {{v}_{i}}+{{s}_{TA}}\cdot h_{Veh}^{i} \right) \bmod \,q$, where ${{V}_{i}}$ is long-term public key of $Ve{{h}_{i}}$, $\Delta t_{V}^{i}$ is the expiration date of ${{V}_{i}}$, and $VS{{K}_{i}}$ is the long-term secret key of $Ve{{h}_{i}}$. Then, TA stores $\left\{ VI{{D}_{i}},{{V}_{i}},Seed_{i}^{1},Seed_{i}^{2},h_{Veh}^{i},VS{{K}_{i}},\Delta t_{V}^{i} \right\}$ in its database, and sends $\left\{ {{V}_{i}},Seed_{i}^{1},Seed_{i}^{2},h_{Veh}^{i},VS{{K}_{i}},\Delta t_{V}^{i} \right\}$ to $Ve{{h}_{i}}$ via a secure channel.

Mutual authentication and short-term pseudonym generation

In SRPP scheme, short-term pseudonyms, which are used by vehicles when sending BSMs, should be authorized by RSUs. In this way, SRPP scheme prevents malicious users from abusing pseudonyms, thus making it resistant to Sybil attacks. Before a RSU authorizes a short-term pseudonym, the RSU and the vehicle authenticate that each other’s identities are legitimate. Also, the vehicle generates short-term pseudonym $SPI{{D}_{i,k}}$ and partial private key $v{{a}_{i}}$.

RSU broadcasting hello message

The corresponding RSU, noted as $RS{{U}_{i}}$, broadcasts hello messages periodically, e.g., every 5s, which contain information such as identity and public key. Specifically, $RS{{U}_{i}}$ randomly selects $r{{a}_{i}}\in Z_{q}^{*}$, computes $R{{A}_{i}}=r{{a}_{i}}\cdot G$, $R{{H}_{i}}={{H}_{3}}(RI{{D}_{i}}, {{R}_{i}}, R{{A}_{i}},$ $\Delta t_{R}^{i}, ti{{m}_{h}})$ and $\delta _{R}^{i}$ $=\left( \ RS{{K}_{i}}+R{{H}_{i}}\cdot \ r{{a}_{i}}\ \right) mod \,q$, where $ti{{m}_{h}}$ is timestamp, and then broadcasts hello message ${{M}_{h}}:\{ RI{{D}_{i}},{{R}_{i}},R{{A}_{i}},\Delta t_{R}^{i},ti{{m}_{h}},$ $\delta _{R}^{i} \}$.

Vehicle authenticating hello message

To resist replay attacks, when $Ve{{h}_{i}}$ receives a hello message, it first checks $ti{{m}_{h}}$ to make sure the message is fresh, and checks $\Delta t_{R}^{i}$ to make sure the RSU identity is unexpired. Next, $Ve{{h}_{i}}$ calculates $h_{RSU}^{i}={{H}_{1}}(RI{{D}_{i}},{{R}_{i}},\Delta t_{R}^{i})$ and $R{{H}_{i}}={{H}_{3}}(RI{{D}_{i}},{{R}_{i}},R{{A}_{i}},\Delta t_{R}^{i},ti{{m}_{h}})$. Then, $Ve{{h}_{i}}$ checks if $\delta _{R}^{i}\cdot G\overset{?}{\mathop {=}}\,{{R}_{i}}+h_{RSU}^{i}\cdot {{S}_{TA}}+R{{H}_{i}}\cdot R{{A}_{i}}$ holds. The proof of the formula is demonstrated bellow.

$$\begin{aligned} \begin{aligned} \delta _{R}^{i}\cdot G&=\left( RS{{K}_{i}}+R{{H}_{i}}\cdot r{{a}_{i}} \right) \cdot G \\&=\left( {{r}_{i}}+{{s}_{TA}}\cdot h_{RSU}^{i}+R{{H}_{i}}\cdot r{{a}_{i}} \right) \cdot G \\&={{r}_{i}}\cdot G+{{s}_{TA}}\cdot G\cdot h_{RSU}^{i}+R{{H}_{i}}\cdot r{{a}_{i}}\cdot G \\&={{R}_{i}}+h_{RSU}^{i}\cdot {{S}_{TA}}+R{{H}_{i}}\cdot R{{A}_{i}} \\ \end{aligned} \end{aligned}$$

(1)

If the formula holds, $Ve{{h}_{i}}$ stores $\{RI{{D}_{i}},{{R}_{i}},\Delta t_{R}^{i}\}$ into its TPD.

Vehicle generating short-term pseudonym and sending request message

Using two hash seeds distributed by TA, $Ve{{h}_{i}}$ can locally generate many short-term pseudonyms as needed. Note that, vehicles can request fresh hash seeds from TA when the regular maintenance of the system is coming, or the current hash seeds are no longer secure. Successively applying ${{H}_{4}}(\cdot )$ on $Seed_{i}^{1}$ and $Seed_{i}^{2}$, two hash chains can be formed as follows.

$$\begin{aligned} \begin{aligned} S_{i,k}^{1} =H_{4}^{k}(Seed_{i}^{1}),\\ S_{i,k}^{2} =H_{4}^{k}(Seed_{i}^{2}) \end{aligned} \end{aligned}$$

(2)

The kth short-term pseudonym of $Ve{{h}_{i}}$ is generated by computing $SPI{{D}_{i,k}}={{H}_{4}}(S_{i,k}^{1}\oplus S_{i,k}^{2})$. Next, $Ve{{h}_{i}}$ sends a request message to $RS{{U}_{i}}$. Given that once an attacker obtains $Ve{{h}_{i}}$’s public key ${{V}_{i}}$, it can track $Ve{{h}_{i}}$’s trajectory. In order to avoid disclosing ${{V}_{i}}$, our scheme utilize XOR operation and CDHP based operation to conceal ${{V}_{i}}$. Specific operations are as follows.

$Ve{{h}_{i}}$ randomly chooses a number $v{{a}_{i}}\in Z_{q}^{*}$ with secrecy, and computes $V{{A}_{i}}=v{{a}_{i}}\cdot G$, $VA{{R}_{i}}=v{{a}_{i}}\cdot {{R}_{i}}$, $A{{V}_{i}}={{V}_{i}}\oplus VA{{R}_{i}}$, $V{{H}_{i}}={{H}_{3}}(SPI{{D}_{i,k}},V{{A}_{i}},A{{V}_{i}}, \Delta t_{V}^{i},ti{{m}_{r}})$, and $\delta _{V}^{i}=\left( VS{{K}_{i}}+V{{H}_{i}}\cdot v{{a}_{i}} \right) \bmod \,q$, where $v{{a}_{i}}$ is short-term partial private key, $V{{A}_{i}}$ is short-term public key, $ti{{m}_{r}}$ is time-stamp. Then, $Ve{{h}_{i}}$ sends message ${{M}_{r}}:\left\{ SPI{{D}_{i,k}},V{{A}_{i}},A{{V}_{i}},\Delta t_{V}^{i},ti{{m}_{r}},\delta _{V}^{i} \right\}$ to $RS{{U}_{i}}$.

RSU authenticating request message

When receiving the request message ${{M}_{r}}$, $RS{{U}_{i}}$ first checks the timestamp $ti{{m}_{r}}$ in ${{M}_{r}}$, and then computes ${{V}_{i}}$ $=A{{V}_{i}}\oplus {{r}_{i}}\cdot V{{A}_{i}}$, $h_{Veh}^{i}={{H}_{2}}({{V}_{i}}, \Delta t_{V}^{i})$ and $V{{H}_{i}}={{H}_{3}}(SPI{{D}_{i,k}}, V{{A}_{i}}, A{{V}_{i}}, \Delta t_{V}^{i}, ti{{m}_{r}})$. After that, $RS{{U}_{i}}$ checks if $\delta _{V}^{i}\cdot G\overset{?}{\mathop {=}}\,{{V}_{i}}+h_{Veh}^{i}\cdot {{S}_{TA}}+V{{H}_{i}}\cdot V{{A}_{i}}$ holds to authenticate the signature $\delta _{V}^{i}$. The proof of the formula is demonstrated bellow.

$$\begin{aligned} \begin{aligned} \delta _{V}^{i}\cdot G&=\left( VS{{K}_{i}}+V{{H}_{i}}\cdot v{{a}_{i}} \right) \cdot G \\&=\left( {{v}_{i}}+{{s}_{TA}}\cdot h_{Veh}^{i}+V{{H}_{i}}\cdot v{{a}_{i}} \right) \cdot G \\&={{v}_{i}}\cdot G+h_{Veh}^{i}\cdot {{s}_{TA}}\cdot G+V{{H}_{i}}\cdot v{{a}_{i}}\cdot G \\&={{V}_{i}}+h_{Veh}^{i}\cdot {{S}_{TA}}+V{{H}_{i}}\cdot V{{A}_{i}} \\ \end{aligned} \end{aligned}$$

(3)

Authorizing short-term pseudonym

In this phase, RSU generates short-term secret key $SVS{{K}_{i}}$ for vehicle $Ve{{h}_{i}}$. SRPP scheme uses XOR operation and CDHP based operation to secure the secret key $SVS{{K}_{i}}$. Specifically, $RS{{U}_{i}}$ generates the authentication materials associated with the short-term pseudonym for ${{V}_{i}}$. $RS{{U}_{i}}$ sets the expiration date $\Delta t_{VS}^{i,k}$ for $SPI{{D}_{i,k}}$, selects $r{{v}_{i}}\in Z_{q}^{*}$ randomly, and computes $R{{V}_{i}}=r{{v}_{i}}\cdot G$, $r{{h}_{i}}={{H}_{5}}(SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},\Delta t_{VS}^{i,k})$, $SVS{{K}_{i}}=(RS{{K}_{i}}+r{{h}_{i}}\cdot r{{v}_{i}})\bmod q$, $ASVS{{K}_{i}}=SVS{{K}_{i}}\oplus r{{v}_{i}}\cdot V{{A}_{i}}$ . Then, $RS{{U}_{i}}$ sends $\{R{{V}_{i}},ASVS{{K}_{i}},\Delta t_{VS}^{i,k}\}$ to $Ve{{h}_{i}}$. When $Ve{{h}_{i}}$ receives the reply message from $RS{{U}_{i}}$, it calculates $SVS{{K}_{i}}=ASVS{{K}_{i}}\oplus v{{a}_{i}}\cdot R{{V}_{i}}$. $SVS{{K}_{i}}$ is the short-term secret key of $Ve{{h}_{i}}$ with short-term pseudonym $SPI{{D}_{i,k}}$. Then, the short-term private key of $Ve{{h}_{i}}$ is set as $vp{{r}_{i}}=\{v{{a}_{i}},SVS{{K}_{i}}\}$. $Ve{{h}_{i}}$ sets its corresponding public key $VP{{U}_{i}}=\{V{{A}_{i}},R{{V}_{i}}\}$.

Signing and broadcasting BSM

Assume that, $Ve{{h}_{i}}$ generates a plain-text $M_{i}^{'}$ containing driving information such as position, speed and direction. $Ve{{h}_{i}}$ selects a random number $v{{b}_{i}}\in Z_{q}^{*}$ and calculates $V{{B}_{i}}=v{{b}_{i}}\cdot G$, $h_{M}^{i,1}={{H}_{6}}(M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},ti{{m}_{M}})$, $h_{M}^{i,2}={{H}_{6}}(M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},h_{M}^{i,1})$ and $\delta _{M}^{i}=(v{{b}_{i}}+h_{M}^{i,1}\cdot v{{a}_{i}}+h_{M}^{i,2}\cdot SVS{{K}_{i}})\bmod \,q$, where $ti{{m}_{M}}$ is the timestamp and $\delta \ _{M}^{i}$ is the signature. Then, $Ve{{h}_{i}}$ broadcasts the message ${{M}_{i}}:\{M_{i}^{'},SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},V{{B}_{i}},ti{{m}_{M}},h_{M}^{i,1},\Delta t_{VS}^{i,k},\delta _{M}^{i}\}$.

Authenticating BSM

If a RSU or vehicle receives a BSM, it first uses an operation based on hash function to quickly check whether the BSM has been tampered. Next, the receiver authenticates the authenticity of the signature in the BSM to achieve message authentication and thus ensure accountability.

Quick check

For the BSM ${{M}_{i}}$ sent by $Ve{{h}_{i}}$, the receiver generates a new value of $h_{M}^{i,1}$ using $(M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},ti{{m}_{M}})$ which is included in ${{M}_{i}}$, and hash function ${{H}_{6}}\left( \right)$. The receiver compared the calculated new $h_{M}^{i,1}$ value with the original $h_{M}^{i,1}$ value in the BSM. If the two values are equal, the receiver continues to authenticate message signature; otherwise, it discards the BSM.

Signature verification

The proposed SRPP scheme supports BSM authentication both individually and in batches.

(a) Single mode

First, we introduce the single signature verification mode as follows. The receiver calculates $h_{M}^{i,2}={{H}_{6}}(M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},h_{M}^{i,1})$, $h_{RSU}^{i}={{H}_{1}}(RI{{D}_{i}}, {{R}_{i}}, \Delta t_{R}^{i})$ and $r{{h}_{i}}={{H}_{5}}(SPI{{D}_{i,k}}, V{{A}_{i}}, R{{V}_{i}}, \Delta t_{VS}^{i,k})$. The receiver then checks if the following equation holds, and if it does, the signature is correct, otherwise the BSM is discarded.

$$\begin{aligned} \begin{aligned} \delta _{M}^{i}\cdot G=V{{B}_{i}}+h_{M}^{i,1}\cdot V{{A}_{i}}+h_{M}^{i,2}\cdot {{R}_{i}}+h_{M}^{i,2}\cdot h_{RSU}^{i}\cdot {{S}_{TA}}+h_{M}^{i,2}\cdot r{{h}_{i}}\cdot R{{V}_{i}} \end{aligned} \end{aligned}$$

(4)

The correctness of Eq. 4 is proved as:

$$\begin{aligned} \begin{aligned} \delta _{M}^{i}\cdot G&=(v{{b}_{i}}+h_{M}^{i,1}\cdot v{{a}_{i}}+h_{M}^{i,2}\cdot SVS{{K}_{i}})\cdot G \\&=(v{{b}_{i}}+h_{M}^{i,1}\cdot v{{a}_{i}}+h_{M}^{i,2}\cdot RS{{K}_{i}}+h_{M}^{i,2}\cdot r{{h}_{i}}\cdot r{{v}_{i}})\cdot G \\&=(v{{b}_{i}}+h_{M}^{i,1}\cdot v{{a}_{i}}+h_{M}^{i,2}\cdot {{r}_{i}}+h_{M}^{i,2}\cdot {{s}_{TA}}\cdot h_{RSU}^{i}+h_{M}^{i,2}\cdot r{{h}_{i}}\cdot r{{v}_{i}})\cdot G \\&=V{{B}_{i}}+h_{M}^{i,1}\cdot V{{A}_{i}}+h_{M}^{i,2}\cdot {{R}_{i}}+h_{M}^{i,2}\cdot h_{RSU}^{i}\cdot {{S}_{TA}}+h_{M}^{i,2}\cdot r{{h}_{i}}\cdot R{{V}_{i}} \\ \end{aligned} \end{aligned}$$

(5)

(b) Batch mode

In $RS{{U}_{i}}$ jurisdiction region, when receiving n message tuples ${{M}_{j}}:\{M_{j}^{'},SPI{{D}_{j,k}},V{{A}_{j}},R{{V}_{j}},V{{B}_{j}},ti{{m}_{M}},h_{M}^{j,1},\Delta t_{VS}^{j,k},\delta _{M}^{j}\}$ for $j=1,2,...,n$, the receiver computes ${{\delta }_{\sum }}=\sum \nolimits _{j=1}^{n}{\delta _{M}^{j}}$. The receiver then checks if the following equation holds, if it does, then the n signatures are correct, otherwise there is an incorrectly signed message. After the signature authentication is completed, other processing is performed on these messages.

$$\begin{aligned} \begin{aligned} {{\delta }_{\sum }}\cdot G&=\sum \nolimits _{j=1}^{n}{(V{{B}_{j}}+h_{M}^{j,1}\cdot V{{A}_{j}}+h_{M}^{j,2}\cdot r{{h}_{j}}\cdot R{{V}_{j}}})+\sum \nolimits _{j=1}^{n}{h_{M}^{j,2}}\cdot ({{R}_{i}}+h_{RSU}^{i}\cdot {{S}_{TA}}) \end{aligned} \end{aligned}$$

(6)

The correctness of Eq. 6 is proved as:

$$\begin{aligned} \begin{aligned} {{\delta }_{\sum }}\cdot G&=\sum \nolimits _{j=1}^{n}{\delta _{M}^{j}}\cdot G \\&=\sum \nolimits _{j=1}^{n}{(v{{b}_{j}}+h_{M}^{j,1}\cdot v{{a}_{j}}+h_{M}^{j,2}\cdot SVS{{K}_{j}})\cdot G} \\&=\sum \nolimits _{j=1}^{n}{(v{{b}_{j}}+h_{M}^{j,1}\cdot v{{a}_{j}}+h_{M}^{j,2}\cdot RS{{K}_{i}}+} h_{M}^{j,2}\cdot r{{h}_{j}}\cdot r{{v}_{j}})\cdot G\\&=\sum \nolimits _{j=1}^{n}{(v{{b}_{j}}+h_{M}^{j,1}\cdot v{{a}_{j}}+h_{M}^{j,2}\cdot {{r}_{i}}+h_{M}^{j,2}\cdot {{s}_{TA}}\cdot h_{RSU}^{i}} \,+h_{M}^{j,2}\cdot r{{h}_{j}}\cdot r{{v}_{j}})\cdot G \\&=\sum \nolimits _{j=1}^{n}{(V{{B}_{j}}+h_{M}^{j,1}\cdot V{{A}_{j}}+h_{M}^{j,2}\cdot {{R}_{i}}+} h_{M}^{j,2}\cdot h_{RSU}^{i}\cdot {{S}_{TA}}+h_{M}^{j,2}\cdot r{{h}_{j}}\cdot R{{V}_{j}}) \\&=\sum \nolimits _{j=1}^{n}{(V{{B}_{j}}+h_{M}^{j,1}\cdot V{{A}_{j}}+h_{M}^{j,2}\cdot r{{h}_{j}}\cdot R{{V}_{j}}})+ \sum \nolimits _{j=1}^{n}{h_{M}^{j,2}}\cdot ({{R}_{i}}+h_{RSU}^{i}\cdot {{S}_{TA}}) \\ \end{aligned} \end{aligned}$$

(7)

Security proof and analysis

In this section, the security of the proposed SRPP scheme is proved. In addition, security analysis demonstrates that the SRPP scheme can satisfy security requirements.

Security proof

By using two games played between an adversary and a challenger, we modeled the security of the SRPP scheme. Two types of adversaries are considered: Type I and Type II^30,32.

Type-I Attacker: This kind of attacker simulates a common entity as a malicious vehicle to replace the public key or private key of any vehicle. However, it cannot get the master secret key of TA.

Type-II Attacker: This kind of attacker simulates a curious but honest TA and can approach the TA’s master secret key. However, it cannot replace the public key of a vehicle or access a vehicle’s private key.

Theorem 1

In the random oracle model, the proposed SRPP scheme is existentially unforgeable against a Type-I adversary ${{A}_{1}}$, if the ECDLP assumption holds.

Proof

Suppose the adversary ${{A}_{1}}$ can forge a BSM ${{M}_{i}}:\{M_{i}^{'},SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},V{{B}_{i}},ti{{m}_{M}},\Delta t_{VS}^{i,k},\delta _{M}^{i}\}$. By utilizing ${{A}_{1}}$ as a subroutine, we construct a challenger C that can solve the ECDLP with a non-negligible probability. Given a random instance $W={{s}_{TA}}\cdot G$ of the ECDLP to C , where ${{s}_{TA}}\in Z_{q}^{*}$ and W, G are points on $E/{{F}_{q}}$, the ultimate goal of C is to output ${{s}_{TA}}$ by interacting with ${{A}_{1}}$.

• 1. Setup: C generates $sypas:\{q,{{G}_{q}},G,{{S}_{TA}},{{H}_{1}},{{H}_{2}},{{H}_{3}},$ ${{H}_{4}},{{H}_{5}},{{H}_{6}}\}$ and sends sypas to ${{A}_{1}}$. Note that ${{A}_{1}}$ does not know secret key ${{s}_{TA}}$.

• 2. ${{H}_{2}}$-query: By inputting $\{{{V}_{i}},\Delta t_{V}^{i}\}$, ${{A}_{1}}$ submits ${{H}_{2}}$-query to C. If the input exists in the list ${{L}_{{{H}_{2}}}}$, C returns $h_{Veh}^{i}$ to ${{A}_{1}}$. Otherwise, C computes $h_{Veh}^{i}={{H}_{2}}({{V}_{i}}, \Delta t_{V}^{i})$. C forwards $h_{Veh}^{i}$ to ${{A}_{1}}$, and adds the element $\{{{V}_{i}},\Delta t_{V}^{i},h_{Veh}^{i}\}$ to the list ${{L}_{{{H}_{2}}}}$.

• 3. RevealLongtermSecetKey: By inputting ${{V}_{i}}$, ${{A}_{1}}$ requests this query to C. When receiving the query, C checks list ${{L}_{LSK}}$. If ${{V}_{i}}$ already exists in ${{L}_{LSK}}$, C returns $\{VS{{K}_{i}},\Delta t_{V}^{i}\}$ to ${{A}_{1}}$. Otherwise, C chooses $VS{{K}_{i}},\Delta t_{V}^{i}\in Z_{q}^{*}$ randomly. Then, C forwards $\{VS{{K}_{i}},\Delta t_{V}^{i}\}$ to ${{A}_{1}}$ and adds the element $\{{{V}_{i}},VS{{K}_{i}},\Delta t_{V}^{i}\}$ to ${{L}_{LSK}}$.

• 4. ${{H}_{5}}$-query: ${{A}_{1}}$ submits this query with an input $\{SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},\Delta t_{VS}^{i,k}\}$. Then, C checks list ${{L}_{{{H}_{5}}}}$. If the input exists in ${{L}_{{{H}_{5}}}}$, C returns $r{{h}_{i}}$ to ${{A}_{1}}$. Otherwise, C computes $r{{h}_{i}}={{H}_{5}}(SPI{{D}_{i,k}}, V{{A}_{i}}, R{{V}_{i}}, \Delta t_{VS}^{i,k})$. C forwards $r{{h}_{i}}$ to ${{A}_{1}}$ and adds the element $\{SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},\Delta t_{VS}^{i,k},r{{h}_{i}}\}$ to ${{L}_{{{H}_{5}}}}$.

• 5. RevealShorttermPartialPrivateKey: ${{A}_{1}}$ requests this query with an input $\{SPI{{D}_{i,k}},{{R}_{i}}\}$. When receiving the request, C checks list ${{L}_{SPPK}}$. If $\{SPI{{D}_{i,k}},{{R}_{i}}\}$ already exists in ${{L}_{SPPK}}$, C returns $v{{a}_{i}}$ to ${{A}_{1}}$. Otherwise, C selects $v{{a}_{i}}$ randomly and computes $V{{A}_{i}}=v{{a}_{i}}\cdot G$. Finally, C adds the element $\{SPI{{D}_{i,k}},{{R}_{i}},v{{a}_{i}},V{{A}_{i}}\}$ to ${{L}_{SPPK}}$ and outputs $\{v{{a}_{i}},V{{A}_{i}}\}$ to ${{A}_{1}}$.

• 6. RevealShorttermPrivateKey: By inputting $\{SPI{{D}_{i,k}},$ ${{R}_{i}}\}$, ${{A}_{1}}$ requests this query to C. When receiving the request, C checks list ${{L}_{SPK}}$ as follows.

  (a) If $\{SPI{{D}_{i,k}},{{R}_{i}}\}$ exists in ${{L}_{SPK}}$, C returns short-term private key $vp{{r}_{i}}=\{v{{a}_{i}},SVS{{K}_{i}}\}$ to ${{A}_{1}}$.

  (b) If $\{SPI{{D}_{i,k}},{{R}_{i}}\}$ does not exist in ${{L}_{SPK}}$, C submits a query on RevealShorttermPartialPrivateKey($SPI{{D}_{i,k}},{{R}_{i}}$) to produce $\{SPI{{D}_{i,k}},{{R}_{i}},v{{a}_{i}},V{{A}_{i}}\}$, and adds returned values to ${{L}_{SPPK}}$. Next, C randomly selects $r{{v}_{i}},RS{{K}_{i}},$ $\Delta t_{VS}^{i,k}\in Z_{q}^{*}$, calculates $R{{V}_{i}}=r{{v}_{i}}\cdot G$, $r{{h}_{i}}$ $={{H}_{5}}(SPI{{D}_{i,k}}, V{{A}_{i}}, R{{V}_{i}}, \Delta t_{VS}^{i,k})$ and $SVS{{K}_{i}}=(RS{{K}_{i}}+r{{h}_{i}}\cdot r{{v}_{i}})\bmod q$. Finally, C adds the element $\{ SPID_{{i,k}} ,R_{i} ,va_{i} ,VA_{i} ,rv_{i} ,$$RV_{i} ,\Delta t_{{VS}}^{{i,k}} ,rh_{i} ,SVSK_{i} \}$ to ${{L}_{SPK}}$ and outputs the private key $vp{{r}_{i}}=\{v{{a}_{i}}, SVS{{K}_{i}}\}$ to ${{A}_{1}}$.

• 7. RevealPublicKey: By inputting $\{SPI{{D}_{i,k}},{{R}_{i}}\}$, ${{A}_{1}}$ submits this query to C. When receiving the request, C checks ${{L}_{SPK}}$ as follows.

  (a) If the input value exists in ${{L}_{SPK}}$, C outputs $\{V{{A}_{i}},R{{V}_{i}}\}$ to ${{A}_{1}}$.

  (b) If there is no $\{SPI{{D}_{i,k}},{{R}_{i}}\}$ in ${{L}_{SPK}}$, C submits a query on RevealShorttermPrivateKey($SPI{{D}_{i,k}},{{R}_{i}}$) to generate $\{SPI{{D}_{i,k}},$ ${{R}_{i}},v{{a}_{i}},V{{A}_{i}},r{{v}_{i}},R{{V}_{i}},\Delta t_{VS}^{i,k},r{{h}_{i}},SVS{{K}_{i}}\}$ and adds the element to ${{L}_{SPK}}$. Finally, C outputs $\{V{{A}_{i}},R{{V}_{i}}\}$ to ${{A}_{1}}$.

• 8. RepalcePublicKey: ${{A}_{1}}$ submits $\{SPI{{D}_{i,k}},{{R}_{i}},\Delta t_{VS}^{i,k},VA_{i}^{'},RV_{i}^{'}\}$, where $VA_{i}^{'}=va_{i}^{'}\cdot G$, $RV_{i}^{'}=rv_{i}^{'}\cdot G$. Then, C uses $\{SPI{{D}_{i,k}},{{R}_{i}},\Delta t_{VS}^{i,k},VA_{i}^{'},RV_{i}^{'}\}$ to replace the corresponding old tuple in ${{L}_{SPK}}$. In addition, ${{A}_{1}}$ keeps $\{va_{i}^{'},rv_{i}^{'}\}$.

• 9. ${{H}_{6}}$-query: By inputting $\{M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},ti{{m}_{M}}\}$, ${{A}_{1}}$ submits this query to C. Then, C checks list ${{L}_{{{H}_{6}}}}$. If there is a record in ${{L}_{{{H}_{6}}}}$ that matches the input value. C outputs $(h_{M}^{i,1},h_{M}^{i,2})$ to ${{A}_{1}}$. Otherwise, C computes $h_{M}^{i,1}={{H}_{6}}(M_{i}^{'}, SPI{{D}_{i,k}}, V{{B}_{i}}, ti{{m}_{M}})$ and $h_{M}^{i,2}={{H}_{6}}(M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},h_{M}^{i,1})$. C forwards $(h_{M}^{i,1},h_{M}^{i,2})$ to ${{A}_{1}}$ and adds the element $\{M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},ti{{m}_{M}},h_{M}^{i,1},h_{M}^{i,2}\}$ to ${{L}_{{{H}_{6}}}}$.

• 10. Signing-query: ${{A}_{1}}$ submits this query with $\{SPI{{D}_{i,k}},{R}_{i},M_{i}^{'}\}$. C selects $\{v{{a}_{i}},SVS{{K}_{i}}\}$ from the list ${{L}_{SPK}}$. Next, it chooses $v{{b}_{i}},ti{{m}_{M}}\in Z_{q}^{*}$ randomly and calculates $V{{B}_{i}}=v{{b}_{i}}\cdot G$. C selects $h_{M}^{i,1}$ and $h_{M}^{i,2}$ from the list ${{L}_{{{H}_{6}}}}$ by inputting $\{M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},ti{{m}_{M}}\}$. C calculates $\delta _{M}^{i}=(v{{b}_{i}}+h_{M}^{i,1}\cdot v{{a}_{i}}+h_{M}^{i,2}\cdot SVS{{K}_{i}})\bmod \,q$, and returns $\delta _{M}^{i}$ to ${{A}_{1}}$. The response to the signing query satisfies Eq. 8

  $$\begin{aligned} \begin{aligned} \delta _{M}^{i}\cdot G&=V{{B}_{i}}+h_{M}^{i,1}\cdot V{{A}_{i}}+h_{M}^{i,2}\cdot {{R}_{i}}+h_{M}^{i,2}\cdot h_{RSU}^{i}\cdot {{S}_{TA}}+h_{M}^{i,2}\cdot r{{h}_{i}}\cdot R{{V}_{i}} \end{aligned} \end{aligned}$$

  (8)

  Finally, ${{A}_{1}}$ outputs the tuple $\{M_{i}^{'},SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},$ $V{{B}_{i}},ti{{m}_{M}},h_{M}^{i,1},\Delta t_{VS}^{i,k},\delta _{M}^{i}\}$. According to Forgery Lemma³⁷. ${{A}_{1}}$ can forge another valid tuple $\{M_{i}^{'},SPI{{D}_{i,k}},$ $V{{A}_{i}},R{{V}_{i}},V{{B}_{i}},ti{{m}_{M}},h_{M}^{i,1},\Delta t_{VS}^{i,k},\delta _{M*}^{i}\}$ that satisfies the following equation:

  $$\begin{aligned} \begin{aligned} \delta _{M}^{i*}\cdot G&=V{{B}_{i}}+h_{M}^{i,1}\cdot V{{A}_{i}}+h_{M}^{i,2*}\cdot {{R}_{i}}+h_{M}^{i,2*}\cdot h_{RSU}^{i}\cdot {{S}_{TA}} +h_{M}^{i,2*}\cdot r{{h}_{i}}\cdot R{{V}_{i}} \end{aligned} \end{aligned}$$

  (9)

  Based on Eq. 8 and Eq. 9, we have

  $$\begin{aligned} \begin{aligned} (\delta _{M}^{i}-\delta _{M}^{i*})\cdot G&=(h_{M}^{i,2}-h_{M}^{i,2*})\cdot {{R}_{i}}+(h_{M}^{i,2}-h_{M}^{i,2*})\cdot h_{RSU}^{i}\cdot {{S}_{TA}}+(h_{M}^{i,2}-h_{M}^{i,2*})\cdot r{{h}_{i}}\cdot R{{V}_{i}}\\&=(h_{M}^{i,2}-h_{M}^{i,2*})({{R}_{i}}+h_{RSU}^{i}\cdot {{S}_{TA}}+r{{h}_{i}}\cdot R{{V}_{i}}) \\&=(h_{M}^{i,2}-h_{M}^{i,2*})(r_{i}^{'}\cdot G+h_{RSU}^{i}\cdot {{s}_{TA}}\cdot G+r{{h}_{i}}\cdot rv_{i}^{'}\cdot G) \end{aligned} \end{aligned}$$

  (10)

  Hence, C returns $[(\delta _{M}^{i}-\delta _{M}^{i*}){{(h_{M}^{i,2}-h_{M}^{i,2*})}^{-1}}-r_{i}^{'}-r{{h}_{i}}\cdot rv_{i}^{'}]{{(h_{RSU}^{i})}^{-1}}$ as the solution to the given instance of ECDLP; otherwise, the game is terminated. However, this contradicts with the difficult assumption of ECDLP. Therefore, in the security model, the proposed SRPP scheme is existentially unforgeable against a Type I adversary ${{A}_{1}}$. $\square$

Theorem 2

In the random oracle model, the proposed SRPP scheme is existentially unforgeable against an Type-II adversary ${{A}_{2}}$ based on the ECDLP assumption holds.

Proof

Suppose the adversary ${{A}_{2}}$ can forge a BSM ${{M}_{i}}:\{M_{i}^{'},SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},V{{B}_{i}},ti{{m}_{M}},\Delta t_{VS}^{i,k},\delta _{M}^{i}\}$. By utilizing ${{A}_{2}}$ as a subroutine, we construct a challenger C that can solve the ECDLP with a non-negligible probability. Given a random instance $W=v{{a}_{i}}\cdot G$ of the ECDLP to C , where $v{{a}_{i}}\in Z_{q}^{*}$ and W, G are points on $E/{{F}_{q}}$, the ultimate goal of C is to output $v{{a}_{i}}$ by interacting with ${{A}_{2}}$.

• 1. Setup: C generates $sypas=\{q,{{G}_{q}},G,{{S}_{TA}},{{H}_{1}},{{H}_{2}},$ ${{H}_{3}},{{H}_{4}},{{H}_{5}},{{H}_{6}}\}$, and sends sypas and master secret key ${{s}_{TA}}$ to ${{A}_{2}}$. C randomly selects $\{{{V}^{*}},SPI{{D}^{*}}\}$ as challenge long-term public key and short-term pseudonym for ${{A}_{2}}$.

• 2. ${{H}_{2}}$-query: By inputting $\{{{V}_{i}},\Delta t_{V}^{i}\}$, ${{A}_{2}}$ submits ${{H}_{2}}$-query to C. If there is a record in list ${{L}_{{{H}_{2}}}}$ that matches $\{{{V}_{i}},\Delta t_{V}^{i}\}$. C outputs $h_{Veh}^{i}$ to ${{A}_{2}}$. Otherwise, C computes $h_{Veh}^{i}={{H}_{2}}({{V}_{i}}, \Delta t_{V}^{i})$. C forwards $h_{Veh}^{i}$ to ${{A}_{2}}$, and adds the element $\{{{V}_{i}},\Delta t_{V}^{i},h_{Veh}^{i}\}$ to the list ${{L}_{{{H}_{2}}}}$.

• 3. RevealLongtermSecetKey: By inputting ${{V}_{i}}$, ${{A}_{2}}$ requests this query to C. When receiving the request, C checks ${{L}_{LSK}}$ as follows.

  (a) If there is a tuple that matches ${{V}_{i}}$ in ${{L}_{LSK}}$, C outputs the corresponding $\{VS{{K}_{i}},\Delta t_{V}^{i}\}$ to ${{A}_{2}}$.

  (b) If ${{V}_{i}}\ne {{V}^{*}}$ and there is no tuple matching ${{V}_{i}}$ in ${{L}_{LSK}}$, C chooses $VS{{K}_{i}},\Delta t_{V}^{i}\in Z_{q}^{*}$ randomly. Then, C forwards $\{VS{{K}_{i}},\Delta t_{V}^{i}\}$ to ${{A}_{2}}$ and adds the element $\{{{V}_{i}},VS{{K}_{i}},\Delta t_{V}^{i}\}$ to ${{L}_{LSK}}$.

  (c) If ${{V}_{i}}={{V}^{*}}$, C aborts the game process.

• 4. ${{H}_{5}}$-query: ${{A}_{2}}$ submits this query with an input $\{SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},\Delta t_{VS}^{i,k}\}$. Then, C checks list ${{L}_{{{H}_{5}}}}$. If there is a tuple matching the input value in ${{L}_{{{H}_{5}}}}$. C returns $r{{h}_{i}}$ to ${{A}_{2}}$. Otherwise, C computes $r{{h}_{i}}={{H}_{5}}(SPI{{D}_{i,k}}, V{{A}_{i}}, R{{V}_{i}}, \Delta t_{VS}^{i,k})$. C forwards $r{{h}_{i}}$ to ${{A}_{2}}$ and adds the element $\{SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},\Delta t_{VS}^{i,k},r{{h}_{i}}\}$ to ${{L}_{{{H}_{5}}}}$.

• 5. RevealShorttermPartialPrivateKey: By inputting $\{SPI{{D}_{i,k}},$ ${{R}_{i}}\}$, ${{A}_{2}}$ requests this query to C. When receiving the request, C checks list ${{L}_{SPPK}}$ as follows.

  (a) If there is a tuple matching $\{SPI{{D}_{i,k}},{{R}_{i}}\}$ in ${{L}_{SPPK}}$, C outputs $v{{a}_{i}}$ to ${{A}_{2}}$.

  (b) If $SPI{{D}_{i,k}}\ne SPI{{D}^{*}}$ and $SPI{{D}_{i,k}}$ does not exist in the ${{L}_{SPPK}}$, C selects $v{{a}_{i}}$ randomly and computes $V{{A}_{i}}=v{{a}_{i}}\cdot G$. Finally, C adds the element $\{SPI{{D}_{i,k}},{{R}_{i}},v{{a}_{i}},V{{A}_{i}}\}$ to ${{L}_{SPPK}}$ and outputs $\{v{{a}_{i}},V{{A}_{i}}\}$ to ${{A}_{2}}$.

  (c) If $SPI{{D}_{i,k}}=SPI{{D}^{*}}$, C aborts the game process.

• 6. RevealShorttermPrivateKey: ${{A}_{2}}$ requests this query with an input $\{SPI{{D}_{i,k}},{{R}_{i}}\}$. Then, C checks list ${{L}_{SPK}}$ as follows.

  (a) If $\{SPI{{D}_{i,k}},{{R}_{i}}\}$ already exists in the ${{L}_{SPK}}$, C returns short-term private key $vp{{r}_{i}}=\{v{{a}_{i}},SVS{{K}_{i}}\}$ to ${{A}_{2}}$.

  (b) If there is no tuple matching $\{SPI{{D}_{i,k}},$ ${{R}_{i}}\}$ in ${{L}_{SPK}}$, C makes a query on RevealShorttermPartialPrivateKey ($SPI{{D}_{i,k}},{{R}_{i}}$) to produce $\{SPI{{D}_{i,k}},{{R}_{i}},v{{a}_{i}},{{VA}_{i}}\}$, and adds the element to ${{L}_{SPPK}}$. Next, C selects $r{{v}_{i}},RS{{K}_{i}},\Delta t_{VS}^{i,k}\in Z_{q}^{*}$ randomly, calculates $R{{V}_{i}}=r{{v}_{i}}\cdot G$, $r{{h}_{i}}={{H}_{5}}(SPI{{D}_{i,k}}, V{{A}_{i}}, R{{V}_{i}}, \Delta t_{VS}^{i,k})$ and $SVS{{K}_{i}}=(RS{{K}_{i}}+r{{h}_{i}}\cdot r{{v}_{i}})\bmod q$. Finally, C adds the element $\{SPI{{D}_{i,k}}, {{R}_{i}}, v{{a}_{i}}, V{{A}_{i}}, r{{v}_{i}},$$R{{V}_{i}},\Delta t_{VS}^{i,k},r{{h}_{i}},SVS{{K}_{i}}\}$ to ${{L}_{SPK}}$ and outputs the private key $vp{{r}_{i}}=\{v{{a}_{i}},SVS{{K}_{i}}\}$ to ${{A}_{2}}$.

• 7. RevealPublicKey: By inputting $\{SPI{{D}_{i,k}},{{R}_{i}}\}$, ${{A}_{2}}$ requests this query to C. When receiving the request, C checks list ${{L}_{SPK}}$ as follows.

  (a) If there is a tuple matching the input value in ${{L}_{SPK}}$. C outputs $\{V{{A}_{i}},R{{V}_{i}}\}$ to ${{A}_{2}}$.

  (b) If there is no tuple matching the input value in ${{L}_{SPK}}$, C makes a query on RevealShorttermPrivateKey ($SPI{{D}_{i,k}},{{R}_{i}}$) to generate $\{SPI{{D}_{i,k}},{{R}_{i}},v{{a}_{i}},V{{A}_{i}},$ $r{{v}_{i}},R{{V}_{i}},\Delta t_{VS}^{i,k},r{{h}_{i}},SVS{{K}_{i}}\}$ and adds the element to ${{L}_{SPK}}$. Finally, C outputs the $\{V{{A}_{i}},R{{V}_{i}}\}$ to ${{A}_{2}}$.

• 8. ${{H}_{6}}$-query: By inputting $\{M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},ti{{m}_{M}}\}$, ${{A}_{2}}$ submits ${{H}_{6}}$-query to C. Then, C checks list ${{L}_{{{H}_{6}}}}$. If there is a tuple matching the input value in ${{L}_{{{H}_{6}}}}$. C returns $(h_{M}^{i,1},h_{M}^{i,2})$ to ${{A}_{2}}$. Otherwise, C computes $h_{M}^{i,1}={{H}_{6}}(M_{i}^{'}, SPI{{D}_{i,k}}, V{{B}_{i}}, ti{{m}_{M}})$ and $h_{M}^{i,2}={{H}_{6}}(M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},h_{M}^{i,1})$. C forwards $(h_{M}^{i,1},h_{M}^{i,2})$ to ${{A}_{2}}$ and adds the element $\{M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},ti{{m}_{M}},h_{M}^{i,1},h_{M}^{i,2}\}$ to ${{L}_{{{H}_{6}}}}$.

• 9. Signing-query: ${{A}_{2}}$ submits this query with $\{SPI{{D}_{i,k}},R_{i},M_{i}^{'}\}$. C selects $\{v{{a}_{i}},SVS{{K}_{i}}\}$ from the list ${{L}_{SPK}}$. Next, it chooses $v{{b}_{i}},ti{{m}_{M}}\in Z_{q}^{*}$ randomly and calculates $V{{B}_{i}}=v{{b}_{i}}\cdot G$. C selects $h_{M}^{i,1}$ and $h_{M}^{i,2}$ from the list ${{L}_{{{H}_{6}}}}$ by inputting $\{M_{i}^{'},SPI{{D}_{i,k}},V{{B}_{i}},ti{{m}_{M}}\}$. C calculates $\delta _{M}^{i}=(v{{b}_{i}}+h_{M}^{i,1}\cdot v{{a}_{i}}+h_{M}^{i,2}\cdot SVS{{K}_{i}})\bmod \,q$, and returns $\delta _{M}^{i}$ to ${{A}_{2}}$ as a valid signature. The response to the signing query satisfies Eq. 11.

  $$\begin{aligned} \begin{aligned} \delta _{M}^{i}\cdot G&=V{{B}_{i}}+h_{M}^{i,1}\cdot V{{A}_{i}}+h_{M}^{i,2}\cdot {{R}_{i}}+h_{M}^{i,2}\cdot h_{RSU}^{i}\cdot {{S}_{TA}}+h_{M}^{i,2}\cdot r{{h}_{i}}\cdot R{{V}_{i}} \end{aligned} \end{aligned}$$

  (11)

  Finally, ${{A}_{2}}$ outputs the tuple $\{M_{i}^{'},SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},$ $V{{B}_{i}},ti{{m}_{M}},h_{M}^{i,1},\Delta t_{VS}^{i,k},\delta _{M}^{i}\}$. According to Forgery Lemma³⁷. ${{A}_{2}}$ can forge another valid tuple $\{M_{i}^{'},SPI{{D}_{i,k}},$ $V{{A}_{i}},R{{V}_{i}},V{{B}_{i}},ti{{m}_{M}},h_{M}^{i,1*},\Delta t_{VS}^{i,k},\delta _{M*}^{i}\}$ that satisfies the following equation:

  $$\begin{aligned} \begin{aligned} \delta _{M}^{i*}\cdot G&=V{{B}_{i}}+h_{M}^{i,1*}\cdot V{{A}_{i}}+h_{M}^{i,2}\cdot {{R}_{i}}+h_{M}^{i,2}\cdot h_{RSU}^{i}\cdot {{S}_{TA}}+h_{M}^{i,2}\cdot r{{h}_{i}}\cdot R{{V}_{i}} \end{aligned} \end{aligned}$$

  (12)

  Based on Eq. 11 and Eq. 12, we have

  $$\begin{aligned} \begin{aligned} (\delta _{M}^{i}-\delta _{M}^{i*})\cdot G&=(h_{M}^{i,1}-h_{M}^{i,1*})\cdot V{{A}_{i}} =(h_{M}^{i,1}-h_{M}^{i,1*})\cdot v{{a}_{i}}\cdot G \\ \end{aligned} \end{aligned}$$

  (13)

  Hence, C returns $(\delta _{M}^{i}-\delta _{M}^{i*}){{(h_{M}^{i,1}-h_{M}^{i,1*})}^{-1}}$ as the solution of the given instance of ECDLP; otherwise, the game is terminated. However, this contradicts with the difficult assumption of the ECDLP. Therefore, in the security model, the proposed SRPP scheme is existentially unforgeable against a Type II adversary ${{A}_{2}}$. $\square$

Security analysis

We analyze the security of the proposed SRPP scheme in this part.

(1) Message Authentication In the SRPP scheme, to generate a BSM signature $\delta _{M}^{i}$, $(SVS{{K}_{i}},h_{M}^{i,1},h_{M}^{i,2},v{{a}_{i}},v{{b}_{i}})$ are required, among which $SVS{{K}_{i}}$ is generated by RSU and is securely transmitted to $Ve{{h}_{i}}$ based on XOR operation and CDHP. $h_{M}^{i,1}$ and $h_{M}^{i,2}$ are hash values. $v{{a}_{i}}$ and $v{{b}_{i}}$ are random numbers generated by $Ve{{h}_{i}}$ secretly. Also, the SRPP scheme can verify the integrity and validity of the BSM ${{M}_{i}}:\{M_{i}^{'},SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},V{{B}_{i}},ti{{m}_{M}},h_{M}^{i,1},\Delta t_{VS}^{i,k},\delta _{M}^{i}\}$ by checking whether the condition $\delta _{M}^{i}\cdot G=V{{B}_{i}}+h_{M}^{i,1}\cdot V{{A}_{i}}+h_{M}^{i,2}\cdot {{R}_{i}}+h_{M}^{i,2}\cdot h_{RSU}^{i}\cdot {{S}_{TA}}+h_{M}^{i,2}\cdot r{{h}_{i}}\cdot R{{V}_{i}}$ is true. In this way, only vehicle $Ve{{h}_{i}}$ can generate correct message signature, and BSM signature is unforgeable. Therefore, the proposed SRPP scheme satisfies message authentication.

(2) Dynamic Pseudonym In our scheme, based on two hash chains, vehicles use various short-term pseudonyms in different RSU jurisdictions to send BSMs.

(3) Un-Linkability In the SRPP scheme, attackers cannot link two or more short-term pseudonyms to the same vehicle. Suppose $SPI{{D}_{i,k}}={{H}_{4}}(H_{4}^{k}(Seed_{i}^{1})\oplus H_{4}^{k}(Seed_{i}^{2}))$ and $SPI{{D}_{i,k+1}}={{H}_{4}}(H_{4}^{k+1}(Seed_{i}^{1})\oplus H_{4}^{k+1}(Seed_{i}^{2}))$ belong to the same vehicle, to validate their relationship, the attacker should calculate ${{x}_{1}}=H_{4}^{k}(Seed_{i}^{1})$, ${{x}_{2}}=H_{4}^{k}(Seed_{i}^{2})$, ${{y}_{1}}={{H}_{4}}({{H}_{4}}({{x}_{1}})\oplus {{H}_{4}}({{x}_{2}}))$ for each possible values of $Seed_{i}^{1}$ and $Seed_{i}^{2}$ until the condition $SPI{{D}_{i,k+1}}={{y}_{1}}$ is established. Because, hash function is unidirectional, it is computational hardness to link the relationship between two short-term pseudonyms.

(4) Conditional Traceability In the SRPP scheme, $Ve{{h}_{i}}$ uses long-term public key to execute mutual authentication with RSU, and uses short-term pseudonyms to broadcast BSMs. The real identity $VI{{D}_{i}}$ and long-term public key ${{V}_{i}}$ are stored in TA database. Long-term public key and short-term pseudonym are stored in RSU’s database. In special cases, RSU can trace long-term public key ${{V}_{i}}$ based on short-term pseudonym in BSM, and then TA reveals the real identity $VI{{D}_{i}}$ based on ${{V}_{i}}$. In summary, our scheme can provide conditional traceability.

(5) Resistance Against Attacks As in the previous analysis, short-term pseudonyms for vehicles are not linkable in our scheme. Therefore, the SRPP scheme has the ability to resist tracking attacks. When a BSM is signed, the SRPP scheme uses a timestamp $ti{{m}_{M}}$. Upon receiving a BSM, the receiver first check its freshness. The receiver will only proceed to the next step on the BSM whose timestamp has not expired. Thus, our scheme can effectively resist replay attacks. Short-term pseudonyms used by vehicles require authorization from RSUs first. Vehicles cannot use short-term pseudonyms arbitrarily. So, our SRPP scheme can resist Sybil attacks. Our proposed scheme provides batch mode to authenticate message signatures. A vehicle or RSU can verify the correctness of the signatures of a large number of BSMs in a short period of time. Therefore, the SRPP scheme can effectively resist DoS attacks.

Performance evaluation

This section evaluates the performance of the proposed SRPP scheme from the aspects of security feature, computation time cost and communication overhead.

Security feature

In this section, we evaluate and compare security features including resistance to Sybil attacks and resistance to trajectory tracking attacks. If a vehicle uses an anonymous identity for a long time, it is vulnerable to trajectory tracking attacks. If a vehicle can use multiple pseudonyms at the same time, a malicious user may launch Sybil attacks. According to the security analysis in the previous section and the description of related works, Table 2 summarizes the security features of the proposed SRPP scheme and other relevant schemes in terms of resistance against Sybil (RS) and trajectory tracking attacks (RTT), whether online TA or RSU is needed. From table 2, we can see that our scheme provides better Sybil attack defense and trajectory tracking defense capabilities.

Table 2 Comparison of security features of related schemes.

Computation time cost

We compare the proposed SRPP scheme with the recent related schemes^1,7,8,18,29 in terms of computation time cost in vehicular communications. We set security level to 80 bits. For ECC-based schemes, the ECC is instance as an additive group G with prime order q on the $E:{{y}^{2}}={{x}^{3}}+ax+b\,(\bmod p)$, where p, q are both 160 bits primes and $a,b\in Z_{p}^{*}$. For bilinear pairing-based schemes, the bilinear pairing is instanced as $e:{{G}_{1}}\times {{G}_{1}}\rightarrow {{G}_{T}}$, where ${{G}_{1}}$ is an additive group of prime order q on $E:{{y}^{2}}={{x}^{3}}+x\,(\bmod q)$, q is a 160 bits Solinas prime number and p is a 512 bits prime number. The execution time of cryptographic operations have been obtained using the MIRACL library³⁹ on the hardware platform which contains 4-GB memory, an Intel I7-4770 processor, and runs on Windows 7 operating system. Table 3 lists out the time of executing following cryptographic operations^32,40.

Table 3 Execution time of cryptographic operations.

In our comparison, we mainly consider the computation time cost for generating one signature and verifying $n(n>1)$ signatures. In our SRPP scheme, to generate one signature for BSM, one scale multiplication operation based on elliptic curve and 2 general hash function operations are involved, and the computation time cost is $1{{T}_{sm-ecc}}+2{{T}_{h}}=0.4422\,ms$. In terms of signature verification, our scheme involves $(2n+3)$ scalar multiplication operations, $(3n+1)$ point addition operations related to elliptic curve and $(3n+1)$general hash function operations. Therefore, the total cost of verifying n signatures is $(2n+3){{T}_{sm-ecc}}+(3n+1){{T}_{pa-ecc}}+(3n+1){{T}_{h}}=(0.8897n+1.3279)\,ms$. So the total cost of execution is $(0.8897n+1.7701)\, ms$. In the similar way, we analyze the computation time cost of other schemes and summarize the results in Table 4 and Fig. 3. Because the scheme⁷ proposed by Zhu et al. is based on pairing operations, the computation time cost is significantly higher than that of other schemes. To make the comparison of computation time costs among other schemes clearer, we do not present the computation time cost of this scheme in Fig. 3.

Table 4 Comparison on computation cost of related schemes.

Fig. 3

Computation time cost comparison of schemes.

As shown in Table 4 and Fig. 3, in terms of signing one message, the performance of our scheme is similar to other four schemes^1,8,18,29. In terms of verifying messages, the computation time cost of our scheme is lower than Yang’s scheme²⁹, similar to other two schemes^1,18, and slightly higher than Zhu’s scheme⁸. In Zhu’s scheme¹, a vehicle has only one pseudonym, which makes it vulnerable to trajectory tracking attacks, and this scheme only supports V2I communication. Although Zhu’s scheme⁸ has a lower computation time cost than ours, their dynamic pseudonym scheme relies on online TA, which can become a system bottleneck when there is a high traffic follow.

Communication overhead

We analyze and compare our SRPP scheme with other recent related schemes in terms of communication overhead when vehicles send BSMs. To analyze bilinear pairing-based scheme, the size of $|{{G}_{1}}|$ is set to $64\times 2=128$ bytes. For ECC-based schemes, the size of |G| is set to $20\times 2=40$ bytes. In both types of schemes, the elements in $Z_{q}^{*}$, the size of hashing value and the field related to time are 20 bytes, 20 bytes and 4 bytes, respectively. Because all schemes have the same plain-text driving data, we exclude this overhead when comparing performance.

In our scheme, the transmitted message is ${{M}_{i}}:\{M_{i}^{'},$ $SPI{{D}_{i,k}},V{{A}_{i}},R{{V}_{i}},V{{B}_{i}},ti{{m}_{M}},h_{M}^{i,1},\Delta t_{VS}^{i,k},\delta _{M}^{i}\}$, where $M_{i}^{'}$ is plain-text; $SPI{{D}_{i,k}},h_{M}^{i,1},\delta _{M}^{i}\in Z_{q}^{*}$; $V{{A}_{i}},R{{V}_{i}},V{{B}_{i}}\in$ G; $ti{{m}_{M}},\Delta t_{VS}^{i,k}$ are fields related to time. Therefore, the communication overhead for sending a BSM is $20\times 3+40\times 3+4\times 2=188$ bytes. The communication overhead of other schemes^1,7,8,18,29 to send one message is 208 bytes, 116 bytes, 164 bytes, 228 bytes and 148 bytes respectively. We summarize the results in Fig. 4. As can be seen from Fig. 4, the communication overhead of our proposed scheme is lower than the schemes in studies^1,18 and is higher than other three schemes^7,8,29. Although the communication overhead of our scheme is not the lowest, based on the previous analysis, Wu’s scheme⁷ has high computational cost and Zhu’s scheme⁸ exists the risk of system bottleneck. In addition, compared with Yang’s scheme²⁹, our scheme has the advantage of resisting trajectory tracking.

Fig. 4

Comparison of communication cost in sending messages.

In general, our proposed scheme, assisted by RSU, provides security capabilities against Sybil attacks and trajectory tracking attacks, which are not fully considered in other schemes. Although our scheme is slightly higher than Zhu’s scheme⁸ in terms of computation time, their scheme relies on an online TA, which can be a system performance bottleneck. On the other hand, although Wu’s scheme⁷ has lower communication cost than our proposed scheme, their operations of signing and authenticating messages are time-consuming.

Conclusion

IoVs is a complex system due to features such as wireless communication channels and high-speed movements of vehicles. The research of message authentication scheme for IoVs involves many problems such as computing efficiency, communication cost, identity authentication and privacy protection, trajectory privacy protection, anti-Sybil attacks and so on. Based on ECDLP, CDHP, hash operations and XOR operations, we proposed an efficient anonymous BSM authentication scheme with batch verification for vehicular communications. In addition, a dynamic pseudonym method is used to resist Sybil attacks and trajectory tracking attacks. Security proof and analysis show that the proposed SRPP scheme can meet the security requirements of message authentication, dynamic pseudonym, un-linkability and conditional traceability, and resist multiple attacks such as replay and DoS. Moreover, compared with other related work, the proposed SRPP scheme is practical in terms of computation time cost in generating signature and verifying BSMs and communication overhead in sending BSMs.