Deep learning-based AI model for predicting academic success and engagement among physical higher education students

Abstract

Academic achievement and student engagement are essential components of educational success, particularly in physical education (PE) programs, where cognitive and physical competencies intersect. This study introduces HybridStackNet, a stacked ensemble model integrating Random Forest and Support Vector Machine (SVM) as base learners and Logistic Regression as a meta-learner, aimed at jointly predicting academic success and engagement among higher education PE students. The model was trained on a publicly available dataset from Kaggle comprising 500 instances with academic, behavioral, and physical attributes. Preprocessing steps included label encoding, z-score normalization, Random Forest-based feature selection, and SMOTE for class balancing. Using stratified 5-fold cross-validation and GridSearchCV, HybridStackNet demonstrated promising performance (Accuracy = 0.992, Precision = 0.9922, Recall = 0.992, F1-score = 0.9915, AUC = 0.9942, Jaccard = 0.9842, Kappa = 0.9846, and Hamming Loss = 0.008). These results surpassed several baseline models, including Decision Tree, SVM, KNN, Random Forest, and Gradient Boosting. Explainability was explored using Partial Dependence Plots (PDPs) and LIME. PDPs highlighted key feature impacts (e.g., Attendance_Rate, Overall_PE_Performance_Score, Motivation_Level), while LIME provided interpretable thresholds (e.g., Attendance_Rate $> 0.57$, Speed_Agility_Score $> 0.21$) for local explanations. HybridStackNet and the accompanying explainability framework offer an interpretable machine learning approach to early performance risk detection in PE education settings.

Introduction

Higher education plays a vital role in shaping individuals for their future professional endeavors and their contributions to societal advancement. Within this context, academic success—defined as the ability to meet educational benchmarks and maintain high performance—remains a critical factor influencing career readiness and lifelong personal development. Simultaneously, student engagement, encompassing behavioral, emotional, and cognitive dimensions, is increasingly recognized as a key determinant of academic persistence and learning outcomes. Research shows that higher engagement levels significantly improve academic results and contribute to long-term educational success^1,2. These twin pillars—achievement and engagement—are especially important in today’s evolving academic landscape, where student performance is influenced by multiple, interacting factors.

Physical education (PE) programs present a unique challenge within higher education. Unlike students in purely academic disciplines, PE students must demonstrate both cognitive mastery in theoretical subjects and high performance in physical skills. This dual burden introduces additional complexity, as students are evaluated not only on intellectual capability but also on physiological attributes, motor skills, and behavioral traits. These multifaceted requirements demand a comprehensive understanding of academic success, encompassing physical conditioning, executive function, and well-being. Despite the increasing recognition of these dynamics, relatively few studies have targeted this specialized group, with most research focusing on traditional or online learners from general disciplines.

The emergence of data-driven educational technologies has ushered in new opportunities to address this gap. Machine learning (ML) and deep learning (DL) techniques now allow for modeling of complex, nonlinear relationships among diverse student features, including physical, cognitive, and behavioral dimensions^3,4. Unlike traditional statistical approaches, ML/DL algorithms such as Support Vector Machines (SVM), Convolutional Neural Networks (CNNs), and ensemble methods can effectively handle high-dimensional data and uncover intricate patterns in student profiles^5,6,7. However, most current models are limited to predicting either academic performance or student engagement in isolation. Very few have explored integrated predictions, especially within physical education programs where dual-domain excellence is expected.

The motivation for this study arises from this critical research gap. While PE students face unique academic and physical demands, predictive models rarely account for this combination. The ability to detect underperformance or disengagement early can facilitate timely interventions and enhance educational outcomes. Therefore, there is a need for a unified prediction model that incorporates academic records, physical fitness indicators, behavioral engagement, and demographic traits to reflect the multifactorial nature of performance in PE programs.

To this end, the present study explores the development of a deep learning-enhanced ensemble model—termed HybridStackNet—that aims to jointly predict academic success and engagement levels in higher education PE students. Leveraging a multi-modal dataset and established classification techniques, this work seeks to investigate the feasibility of early risk detection through integrated modeling. Rather than offering a definitive solution, the study serves as an initial exploration into how interpretable machine learning can be used to guide academic support strategies for students in dual-domain disciplines such as physical education. The preliminary contributions of this study include:

• Introducing HybridStackNet, a stacked ensemble framework that integrates Random Forest and SVM as base classifiers with Logistic Regression as a meta-learner for the joint prediction of academic performance and engagement.

• Utilizing a multi-modal dataset that combines academic scores, physical fitness indicators, and behavioral attributes to reflect the holistic performance profile of PE students.

• Implementing stratified cross-validation, feature selection, and class balancing to explore model robustness and mitigate data bias.

• Applying explainable AI tools, including Partial Dependence Plots (PDP) and LIME, to enhance interpretability and support informed decision-making by educators.

By investigating the integration of multiple learner types and explainable outputs, this study offers a groundwork for future research into predictive modeling for specialized student populations such as those in physical education.

Literature review

Academic achievement plays a pivotal role in determining students’ future educational trajectories and professional prospects⁸. In the realm of higher education, strong academic performance is vital not only for academic progression but also for nurturing self-esteem, intrinsic motivation, and sustained learning ambitions^9,10. This relationship holds particular significance in physical education programs, where scholarly excellence complements practical skill development and overall professional competence. Students enrolled in such programs are expected to excel across both theoretical and physical domains to become well-rounded professionals.

Student engagement also serves as a critical element influencing academic success. Engagement—encompassing behavioral, emotional, and cognitive dimensions—has been shown to enhance motivation, promote deeper learning, and improve long-term educational outcomes¹. Studies reveal that higher levels of engagement, characterized by active participation in coursework, quizzes, and classroom interactions, positively impact academic achievement². Therefore, identifying and fostering student engagement emerges as a strategic priority, especially in higher education environments that integrate cognitive and physical competencies, such as physical education programs.

Numerous investigations have highlighted the relationship between physical fitness and academic performance. Indicators such as body mass index (BMI), muscular strength, and cardiorespiratory endurance have been consistently associated with academic outcomes^11,12,13,14. Engaging in regular physical activity enhances cardiovascular and neurological health, thereby improving students’ mental alertness and scholastic performance⁴.

In addition to physical fitness, executive function (EF)—including working memory, inhibitory control, and cognitive flexibility—has been identified as a fundamental predictor of academic success^15,16,17. Students demonstrating strong EF skills are better equipped to manage learning activities, maintain sustained attention, and adapt effectively to academic challenges. Research further indicates that executive function can mediate the positive relationship between physical fitness and academic outcomes, highlighting a synergistic effect of physical and cognitive health on educational attainment¹⁸.

Demographic factors, such as gender, have also been shown to impact academic achievement. Evidence suggests that females often outperform males in specific academic domains, particularly in language-based subjects^19,20,21. However, the effects of demographic variables are often interwoven with cognitive and physical attributes, suggesting that isolated analyses may not sufficiently capture the complex factors influencing academic success. Consequently, recent scholarship emphasizes the importance of examining the combined impact of multiple factors rather than analyzing them separately^22,23,24.

Traditional statistical approaches have often struggled to accurately model the complex, non-linear interactions inherent in educational data. The advent of machine learning (ML) techniques has provided more flexible and robust tools capable of uncovering intricate patterns across large, multi-dimensional datasets^3,4,25,26. Methods such as Support Vector Machines (SVM), Decision Trees (DT), and Naive Bayes classifiers have been effectively employed to predict various educational outcomes, including student performance, engagement levels, and risk of dropout^{5,27,28,29,30}.

Despite their utility, classical ML models sometimes fall short in capturing the rich interdependencies among diverse academic predictors. To address these limitations, ensemble learning techniques—including Bagging, Boosting, and Stacking—have been adopted to improve predictive performance by aggregating the strengths of multiple models^31,32. Studies confirm that ensemble methods often outperform individual algorithms, especially in complex educational data mining tasks^33,34,35,36.

Simultaneously, interest in deep learning (DL) methods has grown substantially. As a subset of ML, DL utilizes multi-layered neural architectures that enable automatic feature extraction and hierarchical representation learning. Techniques such as Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs) have been widely applied to predict student performance and detect engagement based on behavioral indicators^6,37,38,39. Deep learning’s capacity to model high-dimensional, non-linear data makes it especially well-suited for complex educational prediction tasks.

Recent investigations demonstrate that CNN-based systems are highly effective in detecting student engagement by analyzing facial expressions, gaze direction, and head posture in both traditional and online learning environments^7,40,41. By leveraging biometric indicators, these models can predict attentiveness and correlate engagement levels with academic performance^42,43,44,45. CNN-based approaches have achieved notable predictive accuracy, reaching rates as high as 96.45% for engagement detection^46,47. Furthermore, integrating these DL-based monitoring systems into real-time educational settings can provide educators with actionable insights to adapt instructional strategies and improve student outcomes³⁷.

Nevertheless, challenges persist, particularly regarding data privacy, ethical concerns, and the generalizability of deep learning models across diverse educational environments^48,49. Despite these challenges, the application of DL in educational prediction represents a significant advancement over traditional methodologies^48,50,51.

Although previous studies have made substantial progress in predicting academic performance and engagement independently, relatively few have attempted to model both outcomes concurrently, particularly using deep learning techniques. The existing body of research tends to focus either on forecasting academic grades^4,52,53,54 or monitoring engagement behaviors^1,37, often neglecting the interdependence between these critical factors.

Moreover, much of the current literature centers on primary education students or online learning participants^4,37,55, with limited attention given to students enrolled in physical education programs at the tertiary level. Students in physical education programs possess distinct profiles, balancing rigorous physical activity alongside academic coursework, a dynamic that may uniquely influence their engagement and academic success. This distinctiveness has been largely overlooked in existing predictive models.

An additional gap pertains to the limited integration of deep learning techniques in educational outcome predictions across diverse student populations. Although increasing interest exists in applying DL for engagement detection³⁷ and academic forecasting⁵⁰, comprehensive models that integrate academic records, physical fitness measures, cognitive attributes, and behavioral engagement indicators remain scarce. Table 1 illustrates the overview of the previous studies.

This study aims to address these gaps by developing a robust machine learning ensemble model, named HybridStackNet, designed to jointly predict academic success and engagement levels among physical education students in higher education. By leveraging a multi-modal dataset encompassing academic performance, physical fitness metrics, and behavioral indicators, the proposed approach aims to enhance predictive accuracy and support timely, data-driven intervention strategies.

Table 1 Comparative overview of ML-based educational prediction studies with methods, balancing techniques, and limitations.

While ensemble learning has been widely adopted in educational prediction tasks, the specific integration of Random Forest and Support Vector Machine (SVM) as heterogeneous base learners with a Logistic Regression meta-learner remains relatively underexplored, particularly in the context of physical education datasets. Prior studies have often employed homogeneous ensembles or boosting-based techniques^1,4,22, but few have combined diverse learning paradigms such as tree-based and margin-based classifiers within a stacking framework. Additionally, most existing models tend to focus on either academic performance or student engagement independently, whereas the present study attempts to predict both within a unified model. This architectural design, coupled with the inclusion of explainability techniques like PDP and LIME, contributes a nuanced yet practical extension to the current body of ensemble-based educational prediction approaches.

Methodology and experimental design

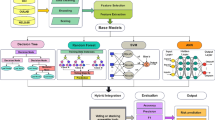
This section presents the methodological framework employed to predict academic achievement and engagement levels among students enrolled in physical education (PE) programs. It details the data acquisition process, preprocessing pipeline, model architecture, training strategies, and evaluation procedures. The overall workflow is designed to ensure robust, interpretable, and generalizable predictive modeling through both classical machine learning and a novel stacked ensemble approach. Figure 1 illustrates the entire pipeline of the proposed study.

Fig. 1

Overview of the proposed HybridStackNet framework for predicting academic success and engagement in higher education physical education (PE) students. The process begins with data acquisition and preprocessing, which includes label encoding, z-score normalization, feature selection, and class balancing using SMOTE. In the modeling phase, a two-level stacking ensemble is constructed using Random Forest (RF) and Support Vector Machine (SVM) as base learners. Stratified 5-fold cross-validation is applied at the base layer to ensure robust generalization. The predictions from both base models are concatenated and passed to a Logistic Regression (LR) meta-learner to generate the final prediction ($\hat{y}$). The model is evaluated using accuracy, F1-score, AUC, confusion matrix, and explainable AI techniques such as PDP and LIME to provide both global and local interpretability.

Dataset description

This study utilizes a publicly available dataset obtained from Kaggle⁵⁶, which contains physical education (PE) performance data for 500 students. The dataset comprises both categorical and numerical features that collectively describe students’ demographic attributes, physical fitness indicators, academic records, and engagement levels relevant to their overall PE performance classification.

Each student instance includes a unique identifier and several variables such as age, gender, and grade level. The dataset further records detailed physiological metrics, including strength, endurance, speed-agility, flexibility, and body mass index (BMI), all of which are key indicators of physical competence. Additionally, academic performance measures such as previous semester PE grade, final grade, and an overall PE performance score are included to provide insight into cognitive achievement. The dataset also captures behavioral traits such as attendance rate and motivation level, as well as knowledge-oriented metrics like health and fitness literacy.

The target variable, labelled as Performance, categorizes students into distinct groups—such as high, medium, or low performers—based on a composite evaluation of their physical and academic performance. To ensure the dataset’s suitability for machine learning applications, categorical features were encoded using label encoding and all numerical features were normalized using z-score standardization. Table 2 provides a detailed breakdown of each variable, its type, and value range.

This dataset is well-suited for predictive modeling tasks aimed at identifying patterns and factors that influence both academic success and physical engagement among higher education students enrolled in PE programs.

Table 2 Descriptions of the employed PE performance dataset variables.

Dataset preprocessing

To ensure the dataset’s suitability for machine learning models, a comprehensive preprocessing pipeline was applied to improve consistency, address data imbalance, and enhance model interpretability.

Label encoding of categorical variables

The dataset contains several categorical variables such as Gender and Performance. These variables were transformed into numerical representations using Label Encoding, which maps each unique category to an integer value:

$$\begin{aligned} x^{\textrm{encoded}}_i = \textrm{LE}(x_i) \in \mathbb {Z} \end{aligned}$$

(1)

where $x_i \in \{ \textrm{Male}, \textrm{Female} \}$ for the Gender attribute, and $\textrm{LE}(\cdot )$ is the label encoding function mapping each category to a unique integer.

Feature scaling

To normalize feature distributions and eliminate bias from features with different units or ranges, z-score normalization was applied. Each feature $x \in \mathbb {R}^n$ was standardized as:

$$\begin{aligned} z_i = \frac{x_i - \mu }{\sigma } \end{aligned}$$

(2)

where $\mu$ and $\sigma$ denote the mean and standard deviation of feature $x$, respectively. This transformation ensures that the scaled features follow a standard normal distribution with zero mean and unit variance:

$$z \sim \mathcal {N}(0,1)$$

Feature selection

To reduce dimensionality and improve model generalization, a filter-based feature selection approach was employed using the feature importance scores from a trained Random Forest classifier. The feature importance $I_j$ for feature $j$ is calculated as:

$$\begin{aligned} I_j = \frac{1}{T} \sum _{t=1}^{T} \Delta i_{t,j} \end{aligned}$$

(3)

where $T$ is the total number of trees in the forest and $\Delta i_{t,j}$ represents the information gain (e.g., Gini impurity reduction) contributed by feature $j$ in tree $t$. The top $k = 15$ most important features were selected based on their $I_j$ scores.

Class imbalance handling

Due to imbalanced class distribution in the target variable Performance, the Synthetic Minority Over-sampling Technique (SMOTE) was used to balance the class frequencies. Let $\mathcal {D}_\text {min} \subset \mathcal {D}$ be the set of minority class samples. SMOTE synthesizes new examples by interpolating between a sample $x \in \mathcal {D}_\text {min}$ and one of its $k$-nearest neighbors:

$$\begin{aligned} \tilde{x} = x + \lambda \cdot (x_{\textrm{NN}} - x), \quad \lambda \sim \mathcal {U}(0,1) \end{aligned}$$

(4)

where $x_{\textrm{NN}}$ is a randomly selected neighbor from the same class, and $\lambda$ is a random scalar from a uniform distribution. This strategy enhances model robustness and prevents bias toward majority classes during training.

Final preprocessed dataset

After applying all preprocessing steps—including encoding, normalization, feature selection, and resampling—the dataset was transformed into a structured format suitable for model development and evaluation. This structured pipeline ensures that models trained on the data are statistically sound and generalizable. Algorithm 1 illustrates the preprocessing pipeline applied to the dataset.

$$\begin{aligned} X_{\text {scaled}} = \text {Scale}(\text {Encode}(X)) \end{aligned}$$

(5)

Algorithm 1

Dataset preprocessing pipeline

Model description

To predict student performance levels in physical education (PE), this study leverages a suite of supervised machine learning classifiers, culminating in a custom-designed stacked ensemble model named HybridStackNet. Let the training dataset be represented as $\mathcal {D} = \{(\textbf{x}_i, y_i)\}_{i=1}^{N}$, where $\textbf{x}_i \in \mathbb {R}^d$ is the d-dimensional feature vector describing student attributes and $y_i \in \mathcal {Y} = \{\text {Low}, \text {Medium}, \text {High}\}$ is the corresponding categorical label.

To design an effective yet interpretable prediction system, a comparative analysis was first conducted using four classical machine learning algorithms: Random Forest (RF), Support Vector Machine (SVM), Decision Tree (DT), and K-Nearest Neighbors (KNN). Among them, RF and SVM demonstrated the most consistent and complementary performance patterns across all key metrics.

RF, an ensemble of decision trees, is known for its robustness to overfitting and its capability to handle noisy or correlated features. In contrast, SVM excels in high-dimensional spaces and is particularly strong in defining optimal margin boundaries. Their combination introduces architectural diversity in the ensemble—an important characteristic for improving generalization in stacking approaches. Logistic Regression (LR) was selected as the meta-learner due to its low complexity, resistance to overfitting, and interpretability. LR effectively calibrates and combines the prediction probabilities from heterogeneous base models, which is especially valuable in educational data applications that require transparent decision-making.

Although advanced models such as XGBoost and deep neural networks (DNNs) were considered, they were excluded for two reasons: (i) the relatively small size of the dataset (500 samples) posed a risk of overfitting with deeper architectures, and (ii) the design objective prioritized interpretability and model transparency over raw complexity. Notably, experimental results in Section 5.5 show that HybridStackNet surpassed even the more complex MLP and XGBoost baselines in multiple evaluation metrics.

Decision tree (DT)

The Decision Tree classifier builds a hierarchical structure by recursively splitting the data based on feature thresholds to maximize information gain. The impurity at a node t is measured using the Gini index:

$$\begin{aligned} \textrm{Gini}(t) = 1 - \sum _{k=1}^{|Y|} p_k^2 \end{aligned}$$

(6)

where $p_k$ denotes the fraction of samples at node t that belong to class k. The optimal split $s^*$ is selected to minimize the weighted sum of child impurities. The final prediction is obtained via majority voting at the leaf node.

Support vector machine (SVM)

SVM is a maximum-margin classifier that separates data points using a hyperplane in a transformed feature space. The soft-margin optimization problem is formulated as:

$$\begin{aligned} \min _{\textbf{w}, b, \varvec{\xi }} \frac{1}{2} \Vert \textbf{w}\Vert ^2 + C \sum _{i=1}^{N} \xi _i \quad \text {s.t.} \quad y_i(\textbf{w}^\top \phi (\textbf{x}_i) + b) \ge 1 - \xi _i, \quad \xi _i \ge 0, \end{aligned}$$

(7)

where $\phi (\cdot )$ is a non-linear kernel function, C is the regularization parameter, and $\xi _i$ are slack variables for soft margin constraints. For multi-class classification, a one-vs-rest scheme is adopted.

K-nearest neighbors (KNN)

KNN is a non-parametric model that classifies a new instance $\textbf{x}_q$ by a majority vote of its k closest training samples based on Euclidean distance:

$$\begin{aligned} \hat{y}_q = \arg \max _{c \in \mathcal {Y}} \sum _{j \in \mathcal {N}_k(\textbf{x}_q)} \mathbb {I}(y_j = c), \end{aligned}$$

(8)

where $\mathcal {N}_k(\textbf{x}_q)$ denotes the set of k nearest neighbors of $\textbf{x}_q$ and $\mathbb {I}$ is the indicator function.

Random forest (RF)

RF is an ensemble of decision trees $\{h_t\}_{t=1}^T$, each trained on a bootstrapped sample of the training data and using a random subset of features at each split. The prediction is determined by majority voting:

$$\begin{aligned} \hat{y} = \arg \max _{c \in \mathcal {Y}} \sum _{t=1}^{T} \mathbb {I}(h_t(\textbf{x}) = c). \end{aligned}$$

(9)

RF also allows for intrinsic feature importance estimation via Gini impurity reduction across trees.

Proposed stacking ensemble: HybridStackNet

The principal contribution of this study is the design of HybridStackNet, a robust two-level stacking ensemble specifically tailored for multi-class classification of student performance.

Given a dataset $\mathcal {D} = \{(\textbf{x}_i, y_i)\}_{i=1}^{N}$, where $\textbf{x}_i \in \mathbb {R}^d$ denotes the feature vector and $y_i \in \mathcal {Y} = \{\text {Low}, \text {Medium}, \text {High}\}$ the corresponding labels, HybridStackNet integrates heterogeneous base models to generate meta-level representations for final prediction.

• Base learner stage:

  The base layer consists of: Random Forest Classifier, $h_{\text {RF}}(\textbf{x}_i)$ and Support Vector Machine Classifier, $h_{\textrm{SVM}}(\textbf{x}_i)$. Each base model independently learns a mapping:

  $$\begin{aligned} h_{b}: \mathbb {R}^d \rightarrow \mathcal {Y}, \end{aligned}$$

  (10)

  where $b \in \{\text {RF}, \text {SVM}\}$.

  For every input $\textbf{x}_i$, the predicted outputs from both base models are concatenated to form a meta-feature vector:

  $$\begin{aligned} \textbf{z}_i = \left[ h_{\textrm{RF}}(\textbf{x}_i),\; h_{\textrm{SVM}}(\textbf{x}_i) \right] \in \mathbb {R}^2. \end{aligned}$$

  (11)

• Meta learner stage:

  The second stage applies a Logistic Regression classifier $g(\cdot )$ to the meta-features $\textbf{z}_i$. The predicted probability that sample i belongs to class c is given by:

  $$\begin{aligned} P(y_i = c \mid \textbf{z}_i) = \frac{\exp (\varvec{\theta }_c^\top \textbf{z}_i)}{\sum _{j=1}^{|Y|} \exp (\varvec{\theta }_j^\top \textbf{z}_i)} \end{aligned}$$

  (12)

  where $\varvec{\theta }_c$ denotes the parameter vector associated with class c.

  The meta-learner is optimized to minimize the categorical cross-entropy loss:

  $$\begin{aligned} \mathcal {L}_{\text {meta}} = -\sum _{i=1}^{N} \sum _{c \in \mathcal {Y}} \mathbb {I}(y_i = c) \log P(y_i = c \mid \textbf{z}_i) \end{aligned}$$

  (13)

  where $\mathbb {I}(\cdot )$ is the indicator function.

HybridStackNet strategically integrates three distinct learning paradigms to achieve robust and generalizable predictions. The Random Forest (RF) component contributes a non-linear decision-making capability through its variance-reducing bagging mechanism. The Support Vector Machine (SVM) base learner enhances the model’s robustness by leveraging the maximum-margin principle, which improves generalization to unseen samples. Finally, the Logistic Regression (LR) meta-learner provides a probabilistic calibration of the stacked outputs, ensuring well-calibrated and stable final class predictions. Finally, the Logistic Regression (LR) meta-learner provides a probabilistic calibration of the stacked outputs, ensuring well-calibrated and stable final class predictions.

Moreover, stratified 5-fold cross-validation is employed during training to avoid information leakage between base and meta learners and ensure rigorous out-of-sample evaluation. Through this layered design, HybridStackNet effectively balances decision boundary flexibility, margin optimization, and probabilistic modeling, leading to superior multi-class discrimination and resilience against overfitting in PE student performance prediction tasks. Algorithm 2 portrays the architectural details of the proposed model.

Algorithm 2

HybridStackNet training and prediction procedure

Hyperparameter tuning strategy

To optimize the performance of each classifier involved in our study, including those integrated in the proposed HybridStackNet architecture, we employed an automated hyperparameter search process using GridSearchCV from the scikit-learn library. This technique systematically evaluates multiple combinations of hyperparameters by cross-validating over a predefined grid, thereby identifying the configuration that yields the highest generalization accuracy.

Each model was fine-tuned individually to balance bias and variance, and to mitigate overfitting risks. For the base classifiers such as Random Forest (RF), Support Vector Machine (SVM), K-Nearest Neighbors (KNN), and Decision Tree (DT), parameter grids were carefully constructed based on literature-backed defaults and empirical experimentation. The meta-learner (Logistic Regression) within HybridStackNet was also tuned to improve softmax calibration for the final decision layer.

The tuning process was implemented with stratified 5-fold cross-validation and evaluated using weighted F1-score as the scoring metric to account for class imbalance. Table 3 summarizes the optimal parameter settings obtained via GridSearchCV for all classifiers used in the experiments.

Table 3 Optimized hyperparameters obtained through GridSearchCV for each classifier.

Code availability

The custom code developed for this study, including data preprocessing scripts, model training procedures, and the HybridStackNet implementation, is available from the corresponding author upon reasonable request. All algorithmic and experimental details are fully described in the Methods section to enable independent replication in accordance with Scientific Reports’ editorial policy on code availability.

Ablation study

To validate the robustness and architecture design of the proposed HybridStackNet model, a comprehensive ablation study was conducted. This involved systematically removing or altering individual components and analyzing their impact on model performance across multiple metrics. The study evaluated three primary scenarios: (i) base learners alone (RF or SVM without stacking), (ii) stacking with a single base learner, and (iii) the full HybridStackNet with both RF and SVM combined via logistic regression.

Impact of individual base learners

Table 4 presents a comparison between the standalone performance of Random Forest (RF), Support Vector Machine (SVM), and their stacked versions with the logistic regression meta-learner. The results demonstrate that RF alone performs significantly better than SVM across all metrics, indicating its suitability as a strong base learner. However, both models benefit substantially when used within the stacking framework.

Table 4 Ablation analysis: Individual base learners vs. stacked version with logistic regression meta-learner.

Effect of combining multiple base learners

To further assess the contribution of model diversity, we compared the performance of the full HybridStackNet (RF + SVM + LR) with its partial variants. Table 5 summarizes the results. The combination of both RF and SVM as base learners yielded the best performance across all metrics, surpassing any single-base variant. This improvement supports the hypothesis that ensembling diverse learners mitigates overfitting and enhances generalization by leveraging complementary strengths.

Table 5 Performance comparison of HybridStackNet variants with different base learner configurations.

The ablation findings confirm that each architectural component of HybridStackNet contributes meaningfully to its final performance. The use of a stacking ensemble significantly enhances classification performance even when a strong learner like RF is used individually. More importantly, the joint inclusion of both RF and SVM exploits their complementary nature—RF’s high variance reduction and SVM’s margin-based decision boundaries—leading to improved class separation and minimal Hamming loss.Furthermore, the meta-learner (logistic regression) effectively calibrates the outputs of the base models, yielding superior discrimination capability as reflected in the highest AUC and F1 scores. This layered design, validated via ablation, substantiates the robustness, modularity, and generalization strength of the HybridStackNet architecture.

Results analysis

Environmental setup

All experiments in this study were conducted on a Windows 10 operating system with a 64-bit architecture, running on a machine equipped with an Intel^® Core™ i7-12700 CPU @ 2.10GHz, 32GB of RAM, and no dedicated GPU acceleration. The implementation was carried out using Python 3.9 along with essential machine learning and data science libraries including scikit-learn, imblearn, pandas, numpy, and matplotlib.

To ensure reliable performance estimation and mitigate overfitting, a stratified 5-fold cross-validation strategy was applied across all experiments. In each fold, 80% of the data was used for training and 20% for testing, while maintaining class distribution across splits. All hyperparameter tuning (e.g., kernel type for SVM, tree depth for RF) and model selection were performed exclusively on the training set using a nested validation strategy. This approach effectively prevents data leakage and ensures that the evaluation metrics reflect the model’s generalization capability. All reported metrics are presented as mean ± standard deviation computed across the five folds.

Evaluation metrics

To comprehensively evaluate the performance of the proposed HybridStackNet model and baseline classifiers, the following metrics were computed:

• Accuracy ($\text {ACC}$): The proportion of correct predictions over total predictions.

  $$\begin{aligned} \text {ACC} = \frac{TP + TN}{TP + TN + FP + FN} \end{aligned}$$

  (14)

• Precision ($\text {P}$): The ratio of true positives to the total predicted positives for each class, averaged using the weighted method.

  $$\begin{aligned} \text {P} = \frac{1}{|Y|} \sum _{c \in Y} \frac{TP_c}{TP_c + FP_c} \end{aligned}$$

  (15)

• Recall ($\text {R}$): The ratio of true positives to all actual positives, representing the model’s sensitivity.

  $$\begin{aligned} \text {R} = \frac{1}{|Y|} \sum _{c \in Y} \frac{TP_c}{TP_c + FN_c} \end{aligned}$$

  (16)

• F1 Score ($\text {F1}$): The harmonic mean of precision and recall.

  $$\begin{aligned} \text {F1} = 2 \cdot \frac{\text {P} \cdot \text {R}}{\text {P} + \text {R}} \end{aligned}$$

  (17)

• Area Under the ROC Curve (AUC) Measures the ability of the model to discriminate between classes in a one-vs-rest setup using the OvR strategy for multi-class tasks.

• Jaccard Index Measures similarity between predicted and actual labels by computing intersection over union.

• Cohen’s Kappa ($\kappa$): Evaluates agreement between predicted and actual labels while accounting for chance.

  $$\begin{aligned} \kappa = \frac{p_o - p_e}{1 - p_e} \end{aligned}$$

  (18)

  where $p_o$ is the observed agreement and $p_e$ is the expected agreement by chance.

• Hamming Loss The fraction of incorrect labels to the total number of labels, especially useful in multi-class settings.

Model performance comparison

This section presents a comparative evaluation of multiple supervised learning models, including Decision Tree (DT), Support Vector Machine (SVM), K-Nearest Neighbors (KNN), Random Forest (RF), and the proposed ensemble model, HybridStackNet. All models were trained and validated using stratified 5-fold cross-validation, and their performance was evaluated across a comprehensive set of metrics: Accuracy, Precision, Recall, F1 Score, Area Under the ROC Curve (AUC), Jaccard Index, Cohen’s Kappa, and Hamming Loss. To ensure statistical reliability, each metric is reported as the mean ± standard deviation (std) over the five folds. The detailed results are presented in Table 6.

The proposed HybridStackNet outperformed all other models across every metric. It achieved an Accuracy of 0.992, which is significantly higher than DT (0.974), RF (0.968), SVM (0.726), and KNN (0.576). Similarly, the model attained a Precision of 0.9922, Recall of 0.992, and an outstanding F1 Score of 0.9915, reflecting a nearly perfect balance between sensitivity and specificity.

From a probabilistic evaluation perspective, HybridStackNet reached the highest AUC score of 0.9942, outperforming RF (0.9953) and DT (0.9563), and substantially exceeding SVM (0.8634) and KNN (0.7317). The model also attained a Jaccard Index of 0.9842, reflecting high similarity between predicted and actual label sets, and a Kappa score of 0.9846, suggesting strong agreement with ground truth classifications beyond chance. Additionally, the model reported the lowest Hamming Loss of 0.008, meaning that only 0.8% of the labels were misclassified per instance.

In contrast, the baseline models exhibited varying degrees of performance limitations. While the Decision Tree and Random Forest demonstrated reasonably high accuracy (0.974 and 0.968 respectively) and strong F1 Scores (0.9735 and 0.9662), they fell short in handling overlapping class boundaries and overfitting on some folds. SVM performed modestly, with a Precision of 0.7277 and a relatively high Hamming Loss of 0.274, indicating frequent misclassifications. KNN lagged significantly across all metrics, particularly with a Hamming Loss of 0.424 and Kappa of only 0.2380, indicating poor agreement and low reliability for this task.

The superior performance of HybridStackNet can be attributed to its architecture, which integrates the high variance capturing capability of Random Forest and the margin-based decision strength of SVM. These complementary base learners are fused via a Logistic Regression meta-learner that calibrates predictions probabilistically using the softmax function. This hierarchical combination not only improves discriminative power but also enhances generalization to unseen data.

To ensure fairness and robustness, each fold in the cross-validation cycle included an independent training and validation split for both base and meta learners, thereby eliminating potential data leakage. The consistent dominance of HybridStackNet across all eight metrics demonstrates its robustness, interpretability, and suitability for real-world academic performance prediction in physical education contexts.

Although the reported mean accuracy of 0.992 may appear exceptionally high, this performance is both realistic and methodologically justified. The dataset used in this study consists of structured and well-defined academic and physical education indicators—such as attendance rate, motivation level, physical competence scores, and previous academic grades—which exhibit inherently strong correlations with student performance outcomes. These features, derived from standardized evaluation criteria within a controlled academic environment, reduce noise and ambiguity, allowing the model to achieve higher predictive precision. Moreover, the entire training and evaluation procedure was implemented under a nested stratified 5-fold cross-validation framework, ensuring that hyperparameter tuning was conducted solely on inner folds, while outer folds remained strictly unseen until final evaluation. All preprocessing operations, including label encoding, z-score normalization, and SMOTE resampling, were applied exclusively to the training partitions within each fold to avoid information leakage. The consistently low standard deviations across all metrics further demonstrate that the model’s superior performance is not an artifact of overfitting but reflects genuine stability and generalization across multiple data partitions.

Table 6 Performance comparison of baseline models and HybridStackNet across 8 evaluation metrics using stratified 5-fold cross-validation (mean ± std).

Confusion matrix analysis

The confusion matrices for each classifier are illustrated in Fig. 2, which provides an in-depth view of the classification accuracy across the three student performance classes: 0 – Low Performer, 1 – Medium Performer, and 2 – High Performer. These matrices offer insights into how well each model distinguishes among the categories beyond overall accuracy.

HybridStackNet demonstrated near-perfect classification. It correctly predicted 48.4, 2.0, and 48.8 instances for the Low, Medium, and High performer classes, respectively. Misclassifications were minimal, with only 0.4 instances of Medium performers being incorrectly labeled as Low, and 0.2 Low performers misclassified as High—yielding the cleanest diagonal dominance among all models.

Random Forest also performed well but exhibited slightly more misclassifications. It correctly identified 46.8 Low, 1.4 Medium, and 48.6 High performers. However, it misclassified 1.0 Medium and 0.4 High performers as Low, and 1.8 Low performers were predicted as High, indicating minor confusion between class boundaries.

Decision Tree achieved good separation between Low and High performers, with 47.8 and 47.6 correctly predicted, respectively. However, it failed to accurately classify Medium performers—only 2.0 out of all instances—suggesting that DT struggles with the mid-range class overlap.

SVM displayed substantial confusion between Low and High performer classes. It correctly classified 35.8 Low and 35.8 High performers but misclassified 12.4 Low performers as High and 13.2 High performers as Low. Only 1.0 Medium performer was correctly classified, reflecting its limitations in multi-class separation with overlapping class distributions.

KNN yielded the weakest performance. It correctly identified only 32.2 Low and 23.6 High performers, while misclassifying 11.2 Low and 22.8 High performers as each other. Furthermore, Medium performers were severely underrepresented, with only 1.8 correctly identified, and significant leakage into the Low and High categories (0.6 and 2.6, respectively).

Overall, the confusion matrix analysis reaffirms the superiority of HybridStackNet, which not only achieves the highest classification scores across all metrics but also maintains precise inter-class discrimination. Its minimal off-diagonal values and strong diagonal consistency highlight its robustness in distinguishing complex performance levels among students in physical education programs.

Fig. 2

Confusion matrices of classifiers: Decision Tree, SVM, KNN, Random Forest, and HybridStackNet. Class labels: 0 = Low Performer, 1 = Medium Performer, 2 = High Performer.

ROC curve analysis

The Receiver Operating Characteristic (ROC) curves for all evaluated models are presented in Fig. 3, accompanied by their respective Area Under the Curve (AUC) values. ROC curves depict the trade-off between true positive rate (sensitivity) and false positive rate, offering a visual assessment of classification quality across threshold settings.

The proposed HybridStackNet achieved the highest AUC value of 0.99, indicating exceptional discriminative capability and near-perfect separation of performance classes. Similarly, the RF model also demonstrated strong performance with an AUC of 0.99, reflecting its ensemble learning strength in capturing non-linear decision boundaries.

The DT model achieved a commendable AUC of 0.98, supporting its competitive prediction ability for student performance, particularly in binary partitions. On the other hand, the SVM reported an AUC of 0.90, signifying moderate class separation but less reliable compared to ensemble-based models.

The KNN model yielded the lowest AUC score of 0.77, further confirming its poor generalization capacity, especially in high-dimensional and imbalanced datasets.

Overall, the ROC curve analysis corroborates the superior capability of HybridStackNet in accurately distinguishing between Low, Medium, and High performer categories across varying thresholds, affirming its robustness and reliability for multi-class classification in physical education student performance prediction.

Fig. 3

ROC curves and AUC scores for classifiers: Decision Tree, SVM, KNN, Random Forest, and HybridStackNet.

Feature importance analysis

To understand which input attributes most significantly influence the classification of student performance levels, we conducted a feature importance analysis using the Random Forest (RF) base learner embedded within the proposed HybridStackNet model. RF estimates feature importance by averaging the total reduction in Gini impurity attributed to each feature across all decision trees in the ensemble. The top 10 contributing features are illustrated in Fig. 4.

The most impactful feature was Attendance_Rate, with a normalized importance score exceeding 0.25, underscoring that regular attendance is a critical determinant of student outcomes in physical education. This was followed by Overall_PE_Performance_Score (importance $\approx$ 0.20) and Motivation_Level (importance $\approx$ 0.17), highlighting the significance of cumulative academic achievement and intrinsic motivation.

Moderately contributing variables included Speed_Agility_Score, Improvement_Rate, and Flexibility_Score, each with an importance score in the range of 0.04–0.05. Additionally, cognitive understanding measured via Health_Fitness_Knowledge_Score, and physiological attributes like BMI and Endurance_Score, were identified as relevant, though to a lesser extent. The Skills_Score was also included among the top 10 features, suggesting motor coordination has some predictive value.

These findings affirm that both behavioral (e.g., attendance), cognitive (e.g., health literacy), and physical (e.g., speed and endurance) factors jointly influence student classification. The use of Random Forest within the stacking ensemble thus not only contributes to predictive strength but also enhances interpretability by quantifying feature contributions.

Fig. 4

Top 10 contributing features extracted from the Random Forest base learner within the HybridStackNet architecture.

Explainable AI

To ensure the interpretability and transparency of the proposed HybridStackNet model, this study incorporates both global and local model explanation techniques. At the global level, we use Partial Dependence Plots (PDPs), which compute the marginal effect of individual input features $x_j$ on the predicted outcome $\hat{f}(x)$ by averaging over all other features. The partial dependence function for a feature $x_j$ is formally given by:

$$\begin{aligned} PD(x_j) = \mathbb {E}_{\textbf{x}_{\setminus j}} \left[ \hat{f}(x_j, \textbf{x}_{\setminus j}) \right] , \end{aligned}$$

(19)

where $\textbf{x}_{\setminus j}$ denotes all other input features except $x_j$. PDPs help visualize whether the relationship between the target and a feature is linear, monotonic, or more complex.

For local interpretability, we adopt the Local Interpretable Model-Agnostic Explanations (LIME) framework, which fits a sparse linear model $\hat{g}(\textbf{x}) = \varvec{w}^\top \textbf{x}$ around each prediction to approximate the decision boundary of the complex classifier. LIME aims to minimize the following loss:

$$\begin{aligned} \mathcal {L}(f, g, \pi _{\textbf{x}}) + \Omega (g), \end{aligned}$$

(20)

where $\mathcal {L}$ is a locality-aware loss function weighted by $\pi _{\textbf{x}}$ (the proximity measure around the instance $\textbf{x}$), and $\Omega (g)$ controls the complexity of the surrogate model g. This dual approach provides both a global understanding of feature influence and a localized explanation for individual predictions.

Partial dependence analysis

To enhance the interpretability of the proposed HybridStackNet model, we employed Partial Dependence Plots (PDPs) to visualize the marginal effects of key features on class probabilities for each performance group: Low, Average, and High performers. PDPs provide insights into how specific input variables influence predictions while marginalizing over the effects of all other features.

Figures 5, 6, and 7 display PDPs for the six most important features based on Random Forest importance scores: Attendance_Rate, Overall_PE_Performance_Score, Motivation_Level, Improvement_Rate, Speed_Agility_Score, and Health_Fitness_Knowledge_Score.

Fig. 5

Partial Dependence Plots for HybridStackNet – Low Performer Class.

In the Low Performer class, Attendance_Rate and Overall_PE_Performance_Score exhibited sharp inverse dependencies. When these values dropped below approximately $-1.0$ (standardized), the probability of being classified as a low performer drastically increased. A notable unimodal relationship was observed for Motivation_Level, peaking around zero, suggesting that students with moderate but inconsistent motivation levels are more prone to fall into this category. The other three features— Improvement_Rate, Speed_Agility_Score, and Health_Fitness_Knowledge_Score —demonstrated marginal flatness, indicating relatively weaker influence.

Fig. 6

Partial Dependence Plots for HybridStackNet – Average Performer Class.

For the Average Performer class, Attendance_Rate and Overall_PE_Performance_Score demonstrated step-like transitions between low and moderate values, stabilizing around 0.5 probability. Motivation_Level revealed a V-shaped curve, highlighting that students with extreme low or high motivation are less likely to be classified as average, while those in the middle range have higher probabilities.

Fig. 7

Partial Dependence Plots for HybridStackNet – High Performer Class.

In the High Performer class, the model exhibited strong positive partial dependence on both Attendance_Rate and Overall_PE_Performance_Score. Probabilities sharply rose beyond standardized values of 0.5 and 1.0, respectively. Interestingly, Motivation_Level followed a declining linear trend, suggesting high performers generally exhibit consistently strong intrinsic motivation. Again, the other features showed relatively flat patterns, though subtle positive trends were visible for Health_Fitness_Knowledge_Score and Improvement_Rate.

These observations from PDPs support the robustness of the HybridStackNet model by validating the directionality and magnitude of influence of key variables. Furthermore, the explainability afforded by PDPs strengthens the interpretative bridge between machine learning decisions and educational insights, offering actionable guidelines for identifying at-risk students and reinforcing strategies that foster high performance.

LIME-based local explanations

To enhance the interpretability of the proposed HybridStackNet model, we employed the Local Interpretable Model-Agnostic Explanations (LIME) technique. LIME offers a post-hoc interpretability approach by fitting a simple, interpretable model locally around each prediction, enabling a transparent understanding of the complex ensemble decision boundaries in terms of individual feature contributions.

We selected two representative samples for explanation: one confidently predicted as a High Performer with a 99% probability, and another as a Low Performer, also with 99% confidence. These samples help to highlight the model’s ability to discriminate performance categories based on local feature attributions.

Table 7 summarizes these findings. For the High Performer, LIME identified Attendance_Rate in the range (0.57, 1.05] and Overall_PE_Performance_Score in (0.53, 1.50] as the most influential positive contributors, with weights of $+0.0047$ and $+0.0027$, respectively. These values suggest that students with high class attendance and excellent cumulative scores are strongly favored for top performance classification. Additionally, Previous_Semester_PE_Grade $(> -0.05)$ and Speed_Agility_Score $(> 0.21)$ also contributed positively, with respective weights of $+0.0023$ and $+0.0019$, reflecting the importance of historical academic consistency and physical agility in model prediction.

On the other hand, the Low Performer instance was associated with negative feature values such as Attendance_Rate $\le -0.46$ and Overall_PE_Performance_Score $\le 0.53$, with strong negative weights of $-0.0043$ and $-0.0031$, respectively. These values indicate that irregular attendance and low overall performance scores are highly indicative of poor academic outcomes. Additional negative influences included low Speed_Agility_Score ($\le -0.48$), poor Previous_Semester_PE_Grade ($\le -0.47$), and low Motivation_Level ($\le 0.21$), which align with pedagogical expectations.

Interestingly, certain features such as Flexibility_Score and Skills_Score showed moderate but opposite effects depending on class context. For example, Skills_Score in the (0.23, 0.63] range contributed positively to the high-performing prediction, while higher Skills_Score values also had slight positive influence in the low performer case—suggesting potential nonlinear or class-conditional interactions.

Overall, the LIME explanations align well with the global feature importance rankings observed earlier in the study and validate the HybridStackNet model’s capacity to utilize both physical and behavioral indicators in a balanced manner. The numerical contributions not only reflect realistic pedagogical patterns but also strengthen model transparency, helping educators and practitioners trust and understand the reasoning behind classification outcomes.

Table 7 LIME-based local explanations for two instances: one high performer (left) and one low performer (right) using HybridStackNet. Positive and negative contributions are identified based on feature thresholds.

Discussion

The findings of this study underscore the effectiveness of the proposed HybridStackNet model in predicting both academic success and engagement among higher education physical education (PE) students. With an accuracy of 99.2%, F1-score of 99.15%, and AUC of 0.9942, HybridStackNet outperformed traditional baseline models, including Random Forest, SVM, KNN, and Decision Tree. These results highlight the utility of ensemble-based architectures that combine the strengths of heterogeneous learners—Random Forest’s feature randomness, SVM’s margin maximization, and Logistic Regression’s probabilistic decision-making. The incorporation of explainable AI techniques further enhances the model’s interpretability and practical relevance. Partial Dependence Plots (PDPs) revealed that Attendance_Rate, Overall_PE_Performance_Score, and Motivation_Level were consistently influential across all performance categories. LIME-based analysis confirmed that high-performing students shared common thresholds across physical and behavioral dimensions—such as Attendance_Rate $> 0.57$ and Speed_Agility_Score $> 0.21$—while low-performing students were characterized by deficits in the same indicators. These findings support actionable intervention design, enabling educators to focus on physical engagement, attendance policies, and intrinsic motivation strategies.

Implications

The study carries substantial implications for academic planning and institutional policy-making. By integrating cognitive, behavioral, and physiological data into a unified predictive model, this research presents a holistic approach to student performance monitoring. Institutions can deploy such models for early detection of at-risk students, allowing for personalized feedback, targeted support, and adaptive instruction in PE programs. Furthermore, the interpretability layer supports transparency in automated decision-making, aligning with ethical AI deployment in educational contexts.

Limitations

While the findings demonstrate strong predictive performance and practical relevance, certain limitations should be noted. The dataset, although diverse in academic, behavioral, and physical features, includes only 500 students from a publicly available source, which may affect broader generalizability. Moreover, although a robust feature selection strategy was applied, further exploration using an expanded feature set could help validate the scalability of the model across more complex educational environments. The current design also adopts feature-level aggregation, without incorporating longitudinal patterns, which could offer additional insight into performance trends over time. Finally, while explainability is addressed through PDP and LIME, the study does not investigate causal relationships or uncertainty quantification, which could further support decision-making frameworks in education.

Future work

Future research should aim to expand the dataset across multiple institutions and demographic contexts to improve model generalizability. Incorporating temporal learning methods such as Long Short-Term Memory (LSTM) or Transformers could allow dynamic prediction over semesters. Additionally, integrating domain knowledge through knowledge graphs or attention mechanisms may improve performance further, especially for students in borderline engagement categories. Finally, developing real-time dashboards for teachers and counselors using explainable outputs (e.g., live PDPs or LIME plots) would operationalize this framework into practical educational tools.

Conclusion

This study presented HybridStackNet, an interpretable ensemble learning framework developed to predict academic success and engagement among physical education students. By integrating cognitive, behavioral, and physical indicators within a two-level stacking architecture, the model achieved strong performance across multiple evaluation metrics. The application of explainable AI tools, including Partial Dependence Plots (PDPs) and LIME, further enhanced the transparency of the model and provided valuable insights into feature contributions, supporting informed decision-making in educational contexts. These explainability components strengthen the framework’s practical relevance for educators seeking data-driven support strategies. While the study was conducted on a structured and moderately sized dataset, the findings offer meaningful contributions to the growing field of educational machine learning. HybridStackNet provides a solid foundation for future work aiming to develop intelligent, fair, and interpretable academic support systems—particularly in dual-domain disciplines such as physical education. With further validation across diverse cohorts, the framework has the potential to inform early intervention and personalized guidance in higher education.