Introduction

Coastal boulders are frequently deposited by coastal inundation events such as tsunamis and storm surges1,2,3,4,5,6,7 and thus provide critical insights for disaster science and coastal engineering. The distribution of these boulders is determined by a complex combination of factors that include geographical features, flow velocity and direction, inundation depth, and duration, making them an important indicator for understanding the processes of past inundation events8,9,10. These boulders, which can occasionally weigh several hundred tons, often record catastrophic events that should be considered in disaster mitigation. While tsunamis are a well-established transport mechanism, recent research increasingly highlights the capacity of storm waves to quarry and transport massive boulders6,7,11,12,13. According to the 6th Assessment Report of the Intergovernmental Panel on Climate Change (IPCC), climate change will increase the frequency of tropical cyclones14. Therefore, information derived from boulder distribution, particularly in low- to mid-latitude regions, is becoming increasingly important. Of particular interest are the larger boulders because they serve as a geological record of past extreme events, thus providing direct physical evidence required for reliable hazard assessments and "worst-case" scenario identification.

Among the various attributes of coastal boulders, weight and location are particularly important when evaluating past inundation events. Direct measurement of the location and shape of boulders distributed along the coast is the most fundamental approach for their identification15,16. Because boulders are extremely heavy, it is impractical to measure their weight directly in the field. Therefore, their weight is typically estimated from the volume. The traditional method for this involves measuring the boulder’s three principal axes (a, b, c) and approximating its volume as a rectangular prism or ellipsoid17. However, this simplification often results in overestimation of the true volume because it systematically ignores irregularities in the boulder, such as complex surfaces and concavities. While such overestimations provide a conservative margin of safety for risk assessment, they introduce a significant scientific bias that compromises the reliability of back-calculated hydrodynamic forces and prevents precise assessment. Consequently, structure-from-motion (SfM) technology has been used to obtain more realistic boulder volumes18. These ground-based measurements yield realistic volume assessments, although their efficiency becomes a limiting factor when mapping numerous boulders over a large area.

Recently, the development of satellite technology, unmanned aerial vehicles (UAVs), and light detection and ranging (LiDAR) has facilitated the mapping of boulders over wider areas19,20,21,22. UAV-based photogrammetry, in particular, provides cost-effective and flexible means of acquiring high-resolution image data rapidly, even in regions with limited infrastructure or under challenging conditions, such as immediately following an inundation event. While these technologies yield an unprecedented amount of precise geomorphological data, the identification of boulders from the generated digital models is still largely a manual task. The distinction in orthoimages is often ambiguous because boulders and the bedrock benches from which they detach are typically of the same lithology. When viewed from directly above in orthophotos, the distinction between boulders and visually similar landforms, such as pedestal rocks connected to underlying benches, is a particular challenge. Consequently, the interpretation of orthoimages is heavily dependent on operator experience and training, which represents a major bottleneck for efficient, large-scale boulder mapping.

Recent advances in deep learning offer a powerful tool for identifying specific objects in images, including those that are visually complex or numerous and thus difficult for human observers to recognise. A critical aspect of this technology is that the detection accuracy depends on the model and training data rather than operator experience. This allows boulders to be identified using consistent criteria, which in turn makes it possible to obtain large-scale distribution data of uniform quality. Furthermore, it offers a way to update and share a technique for boulder detection with other researchers because the model can be incrementally improved by adding training data from new regions.

In this study, we propose and demonstrate a novel approach that integrates UAV-based SfM technology with deep learning techniques to enable the efficient and precise mapping of large boulders and the determination of their volumes. Our approach was developed using a rigorous training dataset from Ishigaki Island, Japan, a coast with numerous boulders transported by multiple large inundation events, such as past tsunamis and storms. The approach uses a deep learning model to automatically detect boulders in high-resolution imagery and then calculates their volumes using the associated digital elevation data. The proposed framework provides not only a practical tool for monitoring and field investigation but also a foundational baseline for future studies. Since the performance of the model inherently depends on its training data, we provide our trained model and analytical procedures in a reusable format. This facilitates further development in other regions, thereby enhancing the reproducibility and scalability of boulder research.

Research area

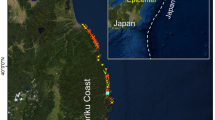
In this study, we developed and validated mapping techniques for coastal boulders using a deep-learning approach. The boulders distributed on Ishigaki Island, Okinawa, Japan, served as the study objects. Ishigaki Island is located in southwestern Japan, with the Ryukyu Trench to the south (Fig. 1a). This study focused on the southeastern coastal region of Shiraho, Ishigaki Island, which is composed of uplifted limestone of the Ryukyu Group. Beyond this bench lies a coral reef with a moat extending approximately 1 km (Fig. 1b)23. Numerous boulders are distributed between the reef edge and coastline16. Boulders distributed along the coast are significantly larger than those in the other groups16. Based on their distribution, size, and radiocarbon age, some of these boulders may have originated from the Meiwa tsunami of 177124,25. In this study, we integrated drone photography with deep learning to analyse a reef-flat area within 200 m of the coastline where these boulders are distributed.

Fig. 1
figure 1

Location map and DSM of study area. (a) Location map of Ishigaki Island, southwestern Japan. The base map imagery is from the Blue Marble Next Generation layer, provided by the National Aeronautics and Space Administration (NASA). (b) Detailed map of the Shiraho coastal area, Southeast Ishigaki Island drawn using Mapping Toolbox in MATLAB, showing the training (red polygon) and testing (blue polygon) areas for detecting boulders in this study. The inset shows the location within the island. The base map tiles are from the Geospatial Information Authority of Japan (GSI). Both maps were created using the Mapping Toolbox in MATLAB (Version R2024a, The MathWorks Inc., Natick, MA, USA, https://www.mathworks.com) and QGIS (Version 3.36, a project of the Open Source Geospatial Foundation, https://qgis.org). (c) Orthoimage (Ortho 202205) and (d) Digital Surface Model (DSM 202205) of the Shiraho area. The southern part (outlined in red) was used for training, and the northern part (outlined in blue) was used for testing the boulder detection model.

Full size image

Methods

Drone survey

In this study, we used deep learning to identify the distribution of coastal boulders, focusing on an area extending 200 m from the coastline and approximately 1.5 km in length along the coastline, where boulders are prominently distributed16. The boulders were primarily distributed in the intertidal zone; therefore, the surveys were conducted during low tides around the spring tide on 18–21 December 2021, 29–31 May 2022, and 7–8 October 2022.

Photographs were taken using a DJI Mavic Air 2 drone from an altitude of approximately 50 m, with 80% forward overlap and 70% side overlap. Depending on the shooting conditions (date, time, and weather), the shutter speed was set between 1/2000 s and 1/1500 s to minimise motion blurring caused by drone vibration. The ISO sensitivity (a parameter controlling the amplification of the image sensor signal) was adjusted within a low range of 100–400 to ensure sufficient brightness. The primary target of this research was large coastal boulders, as they are the most reliable indicators of high-energy inundation events. Therefore, the image acquisition was designed to prioritise wide-area coverage rather than the high resolution required to identify smaller boulders. The captured images were 3000 × 4000 pixels, corresponding to a resolution of approximately 1.91 cm/pixel.

Construction of ortho and DSM

Using 1292, 1802, and 1833 images captured during each survey, we created orthoimages and Digital Surface Model (DSM) for each survey. These were designated Ortho202112, Ortho202205, Ortho202210, and DSM202205, respectively.

The models were generated using two versions of Agisoft Metashape (v.1.8.4 for Ortho202205 or v.2.1.1 for others)26 due to software updates. Although the software versions have algorithmic differences, the resulting variations in the orthoimages and DSMs were visually minor and did not affect the representation of the essential geomorphological characteristics of the target boulders. We took advantage of these minor variations as a form of data augmentation. This approach enhances the robustness of the deep learning model by preventing overfitting to the specific software version, thereby improving its generalisability. To generate high-resolution digital models of extensive areas within a practical timeframe, we constructed DSMs. By definition, a DSM is a 2.5D height field that represents the surface with a single height value for each horizontal coordinate. This simplified data structure does not preserve complex 3D shapes, such as overhangs (the undersides of boulders). However, it enables computationally efficient processing and analysis across extensive areas. It is thus the standard and practical choice for large-scale UAV-based mapping. The edges of the constructed orthoimages and DSMs with insufficient coverage were clipped. Ultimately, we created orthoimages and DSMs with areas of approximately 0.54 km2 and resolutions of 1.91 and 3.81 cm/pixel, respectively. The orthoimages were 256-level RGB images containing no data other than colour information.

Training datasets

We defined independent training and test areas to train our deep learning model (Fig. 1b–d). The training area, located in the southern part of the study region, covered approximately 0.17 km2 and accounted for 31.5% of the total area. The test area, located in the northern part, covered approximately 0.37 km2 and accounted for 68.5% of the total area.

Only orthoimages were used for training and testing. We divided the orthoimages into 4000 × 4000-pixel segments (ca. 78 × 78 m) to facilitate the handling and annotation of boulder contours using CVAT27, an open-source image annotation tool. In this analysis, we focused on larger coastal boulders related to extreme inundation events. Therefore, smaller boulders, which can be moved by more frequent wave conditions, were deliberately excluded from the training targets. We applied this annotation to all boulders with an approximate maximum diameter of ≥ 0.5 m within the segmented images from the training and evaluation areas. This threshold was chosen as a practical lower limit for reliable identification and verification in the field. The annotations were also limited to terrestrial areas, excluding submerged zones due to practical constraints that made direct verification infeasible.

The training dataset was compiled using all the available orthoimages: Ortho202112 (4.7%), Ortho202205 (48.4%), and Ortho202210 (46.9%). The orthoimages were captured under varying conditions, such as different levels of sunlight, to allow the model to learn from boulders under diverse conditions. The training area predominantly consisted of reef flats, sandy beaches, and coastal vegetation, with minimal artificial structures or moats. The annotations in this area included 110 unique boulders with maximum diameters of approximately 0.4 to 6.1 m.

In contrast, the testing dataset was created using only Ortho202205, which had the most uniform lighting across the entire area. To highlight the model limitations, the test area was intentionally selected to include features not present in the training data. The test area included reef flats, sandy beaches, and coastal vegetation, as well as a significant number of artificially relocated boulders, artificial structures, and moats (submerged area) (Fig. 6a, b). The annotations in this area included 281 unique boulders with maximum diameters of approximately 0.4 to 6.5 m.

Training the detection model for boulders

In this study, we used a mask region-based convolutional neural network (Mask R-CNN28), which is an instance segmentation framework, to detect the locations and contours of boulders from the generated orthoimages. Mask R-CNN is an extension of R-CNN, which is a method for object detection enhanced by a segmentation function that identifies objects at the pixel level. This enables instance segmentation, allowing precise identification of the contours of each object.

We applied a Mask R-CNN using Detectron229. Detectron2 is a Python library developed by Meta Research that provides algorithms for object detection and segmentation. It also provides pre-trained baselines29 that have been trained and evaluated on Common Objects in Context (COCO)30,31, a large-scale dataset for object segmentation.

In this study, we fine-tuned the pre-trained baseline “mask_rcnn_R_50_FPN_3x”29 to detect boulders in the orthoimage. The training process used 2000 × 2000-pixel images cropped from annotated 4000 × 4000-pixel divided orthoimages of the training area. These images were divided into two groups, with approximately 90% used for training and 10% used for validation. To ensure a fully consistent and reproducible training set for all experiments, we opted to pre-generate a static set of 9144 augmented images using a dedicated MATLAB program. The augmentation process included operations such as scaling (with a random scaling factor of 0.7–1.0), horizontal and vertical flipping, grayscale conversion, random adjustments to saturation (with a random gain in the range of 0.95–1.60) and brightness (with a random gain in the range of 0.4–1.5), and the application of motion blur (with a random distance of up to 5 pixels at a random angle), Gaussian blur (with a fixed sigma of 2.0), and JPEG noise. Training was conducted using an NVIDIA GPU (TITAN V). After the warm-up phase, the model was trained for approximately 10 h with a mini-batch size of 2 and a learning rate of 0.00008.

Detection of boulders from the orthoimage

To evaluate the developed deep learning model, we used it to detect boulders from an orthoimage of the test area. The orthoimage in the test area was relatively large (42,754 × 56,150 pixels), making it difficult to process it in a single operation. Therefore, we used a moving window approach to sequentially process the images. The window size was set to 2000 × 2000 pixels, which was consistent with the size used during training. We applied a 50% overlap, vertically and horizontally, to extract the shape of the boulders at the image boundaries precisely.

The performance of the trained model was quantitatively evaluated in two stages. First, the primary evaluation was conducted on the output of the individual sliding windows before the merging process. This stage utilised the standard COCO evaluation metrics, including mean average precision (AP) and mean average recall (AR), across a range of intersection over union (IoU) thresholds. Second, to provide a more intuitive understanding of the practical model performance on the final merged map, we also reported the absolute counts of true positives (TPs), false positives (FPs), and false negatives (FNs), along with the calculated F1 score, which provides a single metric balancing precision and recall, at a fixed IoU threshold of 0.50. Both evaluations were conducted for each boulder size category, following a common object detection metric implemented in Detectron2. Boulders were classified by area as small (s: area < 322 pixels2; area < 0.37 m2), medium (m: 322 ≤ area < 962 pixels2; 0.37 ≤ area < 3.36 m2), or large (l: ≥ 962 pixels2; ≥ 3.36 m2) using the default settings of Detectron2.

Calculations of shapes and volumes

To provide a quantitative evaluation of the results obtained by the deep learning model, we compared the shapes and volumes calculated from the detected contours with those derived from actual measurements. It was assumed that the boulders were in contact with the basement surface at their maximum projected surfaces. We also defined “a-axis length” as the length of the longest cross-section of the maximum projected surface, “b-axis length” as the length of the longest cross-section perpendicular to the a-axis, and “c-axis length (or height)” as the longest perpendicular distance from the basement surface. In this study, a-, b-, and c-axis lengths, as defined here, are used unless otherwise specified.

As actual boulders are typically very large and irregular in shape, obtaining precise measurements is challenging. Therefore, we conducted verification using the volume calculated from the DSM (Vdsm) and that approximated by a rectangular prism (Vabc).

Detectron2 returns the shape of each detected object as a binary image. To facilitate post-processing, we converted binary images into coordinates using Python code and exported them in JSON format. Owing to the 50% overlap in the images used for detection, the exported contour data contained many duplicates. To remove duplicates, we first converted the detected contours into a planar Cartesian coordinate system and then calculated the IoU for each pair of boulders. In this study, we merged contours with an IoU above a certain threshold to represent the same boulder. Merged contours were defined as the union of the respective contours. If the threshold is set excessively high, the required merges may not be applied, particularly in the case of boulders with diameters exceeding 1000 pixels. Conversely, if the threshold is excessively low, adjacent albeit distinct boulders may merge incorrectly. Therefore, in this study, a threshold of 15% was applied for merging using a custom MATLAB program31.

From the merged contours of each boulder, we calculated the centroid coordinates, a-axis length, b-axis length, aspect ratio, orientation of the a-axis, and area using built-in functions in MATLAB. Notably, the a- and b-axis lengths were approximate values, representing the axial length of an ellipse with the same second central moment as the contour.

Furthermore, based on the merged contours, we calculated the height and volume of each boulder from the DSM using MATLAB (Fig. 2)31. First, we extracted the DSM of each boulder and its surrounding area and applied a median filter to remove noise from the extracted DSM. Next, we isolated the surrounding smoothed DSM that formed the basement surface by masking based on the shape of the boulders in the extracted DSM. As the actual basement surface is significantly complex, we approximated it using a cubic surface. We then calculated the surface and maximum heights (c-axis length) of the boulders from the approximated basement surface. Finally, Vdsm was calculated by integrating the heights of the boulder surfaces. In contrast, the volume approximated by a rectangular prism (Vabc) was calculated by multiplying the a-, b-, and c-axis lengths (heights).

Fig. 2
figure 2

Workflow for calculating the shape and volume of boulders from the orthoimage and DSM. The a- and b-axis lengths were directly calculated from the detected contour. The height (c-axis) was estimated from the surface heights of boulders relative to the approximated basement surface, with the DSM-based volume (Vdsm) calculated via integration of these heights.

Full size image

Field measurements of shapes

As mentioned in the Study Area section, we validated our detected results against field measurement data. To validate our approach, we used new measurement results obtained using a tape measure in addition to the results directly measured by Goto et al.16. In our new measurements, we assumed that boulders were in contact with the basement surface at their maximum projected surfaces. In contrast, while Goto et al.16 also used volume approximations based on a rectangular prism, their definitions of the a-axis length, b-axis length, and height differed. Goto et al.16 estimated the original orientation of boulders before transportation based on their characteristics and measured the a-axis length, b-axis length, and height relative to the original plane.

Results

Preliminary evaluation of unmerged detections

After approximately 10 h of training using Detectron2, 12 models were obtained, one for each training epoch. Detection tests were conducted on the output of the individual sliding windows using the built-in functions of Detectron2 to evaluate the performances of the models. The evaluation was based on the AP and AR using the built-in function of Detectron2. The AP/AR was calculated across multiple IoU thresholds, ranging from 0.50 to 0.95 in increments of 0.05. The evaluation was conducted according to the boulder area (small, medium, and large).

The AP and AR of our models from each training epoch exhibited the following trends: The overall AP ranged from 0.422 to 0.483. The AP for large (APl), medium (APm), and small (APs) boulders ranged from 0.661 to 0.702, 0.351 to 0.408, and 0.011 to 0.077, respectively. For AR, the overall AR ranged from 0.559 to 0.595. The AR for large (ARl), medium (ARm), and small (ARs) boulders ranged from 0.726 to 0.759, 0.503 to 0.549, and 0.037 to 0.090, respectively (Supplementary Table S1). AP increased slightly from the 4th to the 5th training epoch. However, models trained beyond the 5th epoch exhibited decreasing AP. Using an earlier checkpoint, we mitigated the risk of overfitting. Although the 5th epoch model showed a slight improvement, we selected the 4th epoch model because performance for our primary targets—boulders larger than approximately 0.5 m—had already stabilised. Notably, the AP and AR scores for small boulders remained low, as expected. This is because smaller boulders were explicitly excluded from both the training and evaluation and are outside the scope of this study. We therefore do not interpret metrics for this small size range. The AP/AR scores, calculated from the tile-based predictions of the selected model before the merging process, are as follows: overall AP of 0.475, APl of 0.684, APm of 0.408, APs of 0.048, overall AR of 0.586, ARl of 0.742, ARm of 0.540, and ARs of 0.087 (Supplementary Table S1). All subsequent detailed analyses were therefore conducted using this selected model.

Performance evaluation of merged detections

In this study, we used the selected model to detect boulders in the test area by applying a moving window with a 50% overlap to the orthoimage for more detailed and practical verification. The size of the moving window was 2000 × 2000 pixels, which is equivalent to approximately 39 × 39 m. Although the test area had an irregular shape with an area of 0.37 km2, the orthoimage was cropped into squares using the moving window aligned in the north–south direction, resulting in some pixels lacking RGB data. Including the surrounding blank area, the total area size of the test area was equivalent to 0.87 km2. In our environment, the detection of boulders within each window averaged 0.24 s, with a total detection time of 562 s for the entire test area.

A total of 1434 objects were detected within the windows, including duplicates. The final output of our workflow is a single, unified distribution map of the entire area, which requires merging numerous overlapping and duplicate detections from the sliding windows. Therefore, MATLAB was used to merge the detected objects with an IoU of 15% or higher, resulting in the detection of 419 boulders. Each boulder was detected an average of 3.4 times, and most commonly 4 times, which is close to the theoretical value.

To assess the practical, end-to-end performance of our workflow, we then conducted a detailed evaluation of the final merged results. This performance was therefore evaluated on the merged detections of the entire test area, which contained diverse geomorphological contexts that were not present in the training data.

The evaluation of the entire test area yielded an F1-score of 0.604 for the target boulder sizes (medium and large combined) (details provided in Fig. 3 and Supplementary Table S2). An analysis of this result reveals that the moderate score was due to a markedly low precision (0.492), caused by a very high number of FPs (n = 211). Spatially, these FPs were not evenly distributed. The selected model accurately detected boulders on the coastal bench (Fig. 3b) but struggled to detect them in submerged (Fig. 3c) and artificial zones, where most errors were concentrated.

Fig. 3
figure 3

Merged results of the detected boulders within the testing area using the selected model. (a) Overview of the testing area. Solid lines show the contours of the detected boulders. Blue, red, and yellow contours indicate true positives, false positives, and false negatives, respectively. (b) Enlarged view of the bench zone. (c) Enlarged view of the submerged zone.

Full size image

To assess the model performance specifically within its intended operational domain, we conducted a second evaluation focused only on areas analogous to the training environment. The results of this filtered evaluation are presented in Table 1. Under these conditions, the model demonstrated a significant improvement in performance. For large-sized boulders, the model achieved perfect scores with a precision, recall, and F1-score of 1.000. Overall, for the target boulder sizes (medium and large combined), the model achieved a high F1-score of 0.863.

Table 1 Instance segmentation performance on the test dataset.
Full size table

Boulder dimensions and volumes

The height of each boulder was calculated using the DSM of the detected boulders. The edges of the orthoimage and the submerged areas in the test area lacked feature points for constructing the DSM, leading to gaps and noise in the DSM. To calculate the height and Vdsm of the boulders from their shapes and DSM, we approximated the complex basement surface using a cubic surface. The root mean square error (RMSE) of the approximations ranged from 0.0062 to 1.3018 (median: 0.0382), indicating that the overall approximations of the basement surface were estimated with sufficient precision. However, two boulders were excluded from the analysis because the RMSE of their basal surface approximations exceeded 1, suggesting that the surface may not have been precisely estimated. We also considered boulders with a maximum height calculated from the DSM between 0.1 and 10 m to reduce the noise impacts. A total of 408 boulders were detected by the model (Fig. 3a). Notably, this set included several objects that were challenging for human annotators to identify visually from only the orthoimage during the creation of the ground truth.

The 408 boulders detected by the model had maximum projection areas varying between 0.27 and 17.77 m2 (median 1.34 m2; Fig. 4d), a-axis lengths between 0.67 and 6.32 m (median 1.48 m; Fig. 4a), b-axis lengths between 0.38 and 4.50 m (median 1.11 m; Fig. 4b), and maximum heights between 0.11 and 4.25 m (median 0.53 m; Fig. 4c). Additionally, the boulders had volumes ranging from 0.049 to 51.408 m3 (median 0.867 m3; Fig. 4e) for Vabc and from 0.002 to 28.769 m3 (median 0.522 m3; Fig. 4f) for Vdsm.

Fig. 4
figure 4

Distributions of geometric properties for the model-detected boulders from the orthoimage (Ortho202205) and the DSM (DSM202205). The histograms show the distributions of the (a) a-axis length, (b) b-axis length, (c) height (c-axis length), (d) area of the maximum projection plane of boulders, (e) volume approximated by a cuboid (Vabc), and (f) DSM-based volume (Vdsm).

Full size image

Field measurements

To validate the detection results, we directly measured the actual boulder size in the field using a tape measure. In May 2022, we measured 70 boulders and used 64 of them for analysis. The boulders had a-axis lengths ranging from 0.7 to 5.8 m (median 2.2 m; Fig. 5a), b-axis lengths ranging from 0.6 to 3.9 m (median 1.6 m; Fig. 5b), and heights ranging from 0.4 to 2.2 m (median 1.1 m; Fig. 5c).

Fig. 5
figure 5

Distributions of boulder dimensions from field measurements. (a–c) Distributions of a-axis, b-axis, and heights from new field measurements in this study. (d–f) Distributions for boulders in the test area identifiable from the dataset of Goto et al.16.

Full size image

We also compared the detection results with those of the dataset measured by Goto et al.16 We identified 38 boulders in the study area, as documented by Goto et al.16 The boulders had a-axis lengths ranging from 1.1 to 5.3 m (median 2.3 m; Fig. 5d), b-axis lengths ranging from 0.8 to 3.2 m (median 1.6 m; Fig. 5e), and heights ranging from 0.5 to 2.1 m (median 1.3 m; Fig. 5f).

Discussion

Evaluation of the deep learning model

We validated the detection performance of the deep learning model by comparing the merged detection results with a manually annotated ground truth dataset created from an orthoimage of the same test area.

A preliminary evaluation using the built-in functions of Detectron2 showed that the AR of the selected model in this study was 0.586. Considering boulder size, the model showed relatively good sensitivity, detecting 0.742 of boulders larger than approximately 180 cm and 0.54 of those between 0.60 and 1.80 m. However, the AR for small boulders was low (0.087) as anticipated. Note that this calculation used the detection results on the output of the individual sliding windows before merging, which included small split boulders that were partially cut off because of their location at the edges of each window. The discrepancy in detection performance between large and small objects is a common issue observed in many models. Difficulty in detecting and identifying small objects often results from a lack of information to distinguish them from the background32. In addition, it is important to note that the scope of this research was intentionally focused on boulders of significant size. As such, boulders smaller than approximately 0.5 m were deliberately excluded from the training dataset by design. Therefore, the resulting low sensitivity for small boulders was an expected outcome.

The precision of boulder detections was also evaluated. The overall AP on the output of the individual sliding windows before merging of the selected model was 0.475. The AP was 0.684 for large boulders, 0.408 for medium boulders, and 0.048 for small boulders, which was expected. Therefore, the model performed better with larger boulders.

Furthermore, the merging process refined these detections. This step resolves issues inherent in the sliding-window approach, where boulders located at the edges of grids could be partially cut off, leading to either FNs or fragmented, FP detections. By integrating these partial detections into a single object, the performance metrics for the merged detection results became more robust. As shown in Table 1, the F1-score for the merged results on target boulders (medium and large boulders) across the entire test area reached 0.604. This reflects an improvement in precision to 0.492 and in recall to 0.785, confirming the value of the merging step in producing a more reliable final detection set. To diagnose the factors influencing this overall performance, we divided the merged detections of the test area into grids of 4000 × 4000 pixels (ca. 78 × 78 m) and calculated AP50 and AR50 for each grid (Fig. 6a). This spatial analysis allowed us to identify specific geographic areas where the model exceled or struggled. Here, AP50 (Fig. 6c) and AR50 (Fig. 6d) represent precision and recall for each grid at a 50% IoU threshold, respectively. The results showed that AP50 and AR50 varied significantly across different areas.

Fig. 6
figure 6

Spatial distribution of model performance across the test area. (a) Testing area was divided into 4000 × 4000-pixel grids (ca. 78 × 78 m). (b) Grid classification. Grids with artificial objects or submerged zones are hatched by red and blue, respectively. (c) AP50 of each grid. (d) AR50 of each grid.

Full size image

The analysis of AP50 showed a mean of 0.415 across all grids. The distribution of these values was polarised, suggesting that the overall mean AP50 was lowered by specific, very low-performing grids. The spatial distribution reveals that the lower AP50 grids were concentrated in submerged and artificial zones (Fig. 6b, c). This confirms that the model errors were not random but rather were concentrated in these specific, out-of-scope environments for which it was not trained.

In contrast, the grids with low AR50 values were concentrated near the sandy beach and the boundary between the beach and reef flat, where the AR50 ranged from 0.2 to 0.7. As smaller boulders are more likely to be transported, they are distributed further inland. During the survey period, the area contained not only sand but also a large amount of pumice that had drifted from the August eruption of Fukutoku-Oka-no-Ba33. This sand and pumice made detection more difficult by burying some of the boulders. However, since these undetected boulders were both relatively few in number and predominantly small (Table 1), their impact on the detection of larger boulders was considered limited.

The analysis of AP50 and AR50 indicates that the overall performance was primarily constrained by low precision due to the high concentration of FPs within submerged and artificial zones (Fig. 6a–d). In these specific environments, this lower precision is not a flaw but rather a result of the research design, which intentionally focused on large boulders. Notably, submerged zones were intentionally excluded from our primary quantitative evaluation because of the inherent technical limitations. These limitations included optical distortions at the air–water interface that compromises SfM model generation and the difficulty of conducting direct measurements in a submerged environment. Therefore, when the model performance was evaluated within its intended operational domain—the natural reef-flat environment—the results demonstrated the true effectiveness of the approach. Indeed, after excluding these zones, the final metrics of the test area showed a significant improvement, with the precision, recall, and, F1-score all reaching 0.863 (Table 1). These high metrics indicate a well-balanced model that minimised both FPs (n = 25) and FNs (n = 25), confirming that the overall approach is robust and highly effective for its designed purpose.

In summary, the model developed in this study shows strong potential as an effective tool for its designed purpose. While the model produced a higher rate of false detections when applied to unrestricted entire orthoimages, this was an expected consequence of a research design that intentionally focused on a natural reef-flat environment. The model achieved a high F1-score of 0.863 when evaluated within its intended operational domain, confirming the model enables rapid and reliable boulder mapping. These findings establish two key performance characteristics: first, the practical lower size limit for reliable detection with this base model is approximately 0.5 m; second, the current performance should be considered a strong baseline, which could be readily improved by utilising higher-resolution imagery. This baseline demonstrates the key advantages of the deep learning approach: the potential for repeated application to the same area for temporal monitoring with high efficiency and consistent, objective criteria, scalability to other similar coastal regions, and a significant reduction in long-term manual analysis costs.

Boulder measurements

We measured the shape of the boulders from the contours detected from the orthoimage (Ortho202205) using the trained model and evaluated the results by comparing them with the shapes of the boulders measured manually in the field. For this comparison, we used field measurements from 2022, the dataset measured by Goto et al.16, and our dataset annotated on an orthoimage of the testing area. The boulder parameters defined by Goto et al.16 differed from those used in this study. Additionally, some boulders on the bench fractured and changed shape owing to gravitational forces since the 2008–2009 measurements. Therefore, making precise comparisons between individual parameters is challenging. However, the overall trends were considered reliable because most boulders retained their initial positions and orientations.

First, we compared the lengths of the a- and b-axes calculated from the contours detected by the trained model with those obtained from the manual annotation of the orthoimage (Fig. 7a, b). The comparison included cases where two touching boulders were mistakenly detected as a single boulder, as indicated by the outliers in Fig. 7a. The a- and b-axis lengths obtained from manual annotation and detection showed very high correlation coefficients of 0.99 and 0.98, respectively (Fig. 7a, b). The mean difference (MD) between the annotated and detected values was 0.02 m for the a-axis and 0.05 m for the b-axis. These differences corresponded to approximately 1–2 pixels, indicating that the shape parameters were determined with a precision close to the theoretical limit, considering the resolution of the orthoimage.

Fig. 7
figure 7

Comparisons of boulder dimensions derived from detected contours, manual annotations, and field measurements. (a, b) Comparisons between the manual annotations and detected contours. (c, d, e) Comparisons between field measurements and detected contours. (f, g, h) Comparisons of the field measurements between our measurements and those by Goto et al.16.

Full size image

The mean absolute error (MAE) was 0.09 m (4.5 pixels) for the a-axis and 0.094 m (4.9 pixels) for the b-axis. The contours of the boulders are not always sharp and are often composed of a few pixels that could be described as a "transition zone”. As there was no evident systematic error dependent on size, these errors were mainly caused by the ambiguous contours within the “transition zone”. Considering the inherent variability in the annotations, the errors of 4.5 and 4.9 pixels suggest that the boulder parameters were estimated with a precision close to the limits imposed by the resolution of the orthoimage.

Next, we compared the detection results with our field measurements for 2022. The a- and b-axis lengths of the detected boulders were calculated from the orthoimage (Ortho202205), whereas the height was calculated as the maximum height from the DSM (DSM202205). The average differences between the detected values and the measured values for the a-axis length, b-axis length, and height were 0.03, 0.04, and 0.02 m, respectively (Fig. 7c–e). Overall, the average error was 1–2 pixels, indicating that the parameters of the detected contours were in good agreement with the measured values with a precision close to the theoretical limit.

In contrast, when comparing the detected and measured values, the MAEs for the a-axis length, b-axis length, and height were 0.18, 0.18, and 0.08 m, respectively, which were twice as large as those between the detected and annotated values. Similarly, when comparing the detected values with field measurement values from Goto et al.16, the MAEs for the a-axis length, b-axis length, and height were 0.24, 0.21, and 0.08 m, respectively, indicating significantly larger MAEs. Additionally, when comparing our measured values with those from Goto et al.16, the MAEs for the a-axis length, b-axis length, and height were 0.25, 0.32, and 0.07, respectively (Fig. 7f–h). The boulders distributed in the study area were often large, with heights exceeding 1 m, making it difficult to assess boulder shapes visually in the field. Considering that the average aspect ratio was close to 0.7, variability possibly existed in determining the a-axis during field measurements. However, the errors in height were relatively smaller than the others because the height was easier to measure precisely in this case. Therefore, the larger MAEs of the a- and b-axis lengths between the detected and measured values were likely due to measurement errors during the field measurements. As the MAEs between the detected and field-measured values were smaller than those between our measurements and those of Goto et al.16, orthoimage-based measurements may be more suitable for achieving higher precision.

In summary, the average values of the boulder parameters estimated from the detected contours showed an error of only a few pixels when compared with the average values of manual annotations on the orthoimage and field measurements, indicating that the shape parameters can be estimated with high precision close to the theoretical limit. The MAE between the parameters estimated from the detected contours and the measured values was approximately 0.18 m, which likely included detection and manual measurement errors in the field. The MAE between the parameters estimated from the detected contours and those estimated from the manual annotations was approximately 9 cm, suggesting that the errors in the detection process were likely less than this value, considering the errors caused by the annotation process.

Volumes

We evaluated the boulder volumes calculated using our approach by comparing the Vabc and Vdsm values derived using the respective approaches.

First, we compared the Vabc calculated from the detected contours with that calculated from the directly measured values in the field (Fig. 8c). The detected Vabc showed a high correlation (0.96) with the measured Vabc. The difference between the mean values of each method was 0.08 m3, indicating that the detection method using deep learning can measure with a precision close to the field measurements. However, the MAE was larger at 1.06 m3. The MAE for the height comparison was sufficiently small at 0.08 m, suggesting that the larger MAE between the volumes was primarily due to errors in estimating the a- and b-axis lengths. This trend of a larger MAE was also observed when annotated contours were used instead of detected contours. Therefore, a large MAE between the detected and measured Vabc values was likely to be more influenced by the measurement precision in the field than by the precision of the detected contours. Thus, calculations from the detected contours may be able to achieve volume measurements with a precision comparable to or even higher than that of field measurements using orthoimages.

Fig. 8
figure 8

Comparisons of boulder volume estimations. (a, b) Comparisons of the volumes calculated from the detected contours and annotated contours. (c, d) Comparisons of the volumes from the detected contours and field measurements.

Full size image

Additionally, while the MAE between the detected Vabc and the annotated Vabc was 0.50 m3, the MAE between the detected Vdsm (Fig. 8a) and the annotated Vdsm was 0.15 m3 (Fig. 8b). This indicates that Vdsm provides more robust and precise measurements than that of Vabc when assessing minor alterations in boulder contours. Therefore, Vdsm may be more suitable for precisely estimating boulder volumes from orthogonal images. In this study, we used the DSM for volume calculation. As a 2.5D data structure, it cannot model complex geometrics like undercuts, which may lead to a slight overestimation of Vdsm. However, this potential difference is less significant than the difference from approximating the complex boulder shape into a basic geometric form, such as a cuboid. By integrating the actual upper surface, Vdsm more faithfully captures the irregular boulder shape far compared with the simplistic approximations. Therefore, it represents a pragmatic compromise, balancing the need for a realistic volume with the practical limitations of measurement. Consequently, Vdsm likely provides a more realistic volume than the commonly used Vabc and can contribute to advancing research on inundation events.

Finally, the detected Vdsm was compared with the field-measured Vabc, revealing a high correlation (0.96; Fig. 8d). Notably, the Vdsm constituted, on average, 54.6% of the Vabc closely matching the ratio of an ellipsoid to its circumscribing cuboid. The rounding of boulders is considered a result of their unique transport and abrasion histories. It follows that the volume likely captured by this approach is not merely a geometric volume, but a more representative physical quantity reflecting this history. This approach provides detailed morphological data that reflect the actual and often complex surface topology of boulders. Although this study focuses only on volume, accurately quantifying these complex morphological features with the proposed approach could be a step toward a more detailed understanding of inundation and transport history of boulders.

Conclusion

In this study, we developed a novel approach that integrates UAV photogrammetry with deep learning technologies to achieve more efficient mapping and high-precision volume estimations of coastal boulders.

The Mask R-CNN model trained in this study demonstrated high effectiveness for boulder mapping along the coastline within its intended operational domain—the terrestrial coastal environment. By strategically focusing the training dataset on specific target objects and environments, it is possible to develop a practical model that achieves the required precision and recall within realistic time and effort. This highlights that precisely defining the target is an essential strategy for developing a practical model, especially when available training data are limited. Moreover, a model developed with such a clear focus provides a foundation for future expansion, such as adaptation to new environments through transfer learning.

Shape measurements of boulders, in combination with a practical model, have the potential to achieve precision and reproducibility comparable to or even greater than those of field measurements. Furthermore, when using the same orthoimage and DSM, Vdsm provides more robust and precise measurements than Vabc when assessing minor alterations to boulder contours. Therefore, Vdsm provides a more realistic and practical volume than the traditionally used Vabc, providing more precise information for understanding the transport processes of boulders during inundation events.

In conclusion, the novel mapping approach proposed in this study enables precise and rapid mapping of boulders, making it an effective tool for rapid mapping and monitoring post-event changes, such as those caused by tsunamis and large tropical cyclones. This approach offers a key advantage of providing large-scale data over extensive coastal areas, making it possible to map at a scale that is impractical with traditional surveys. Such large-scale data can help researchers estimate the magnitude of past inundation events, leading to a deeper understanding of coastal hazards and more accurate risk assessments.