Introduction

Multiplication is a crucial arithmetic instruction1 in modern computer systems, particularly within Digital Signal Processing (DSP), Machine Learning (ML), and real-time applications, all of which need high-speed, efficient hardware to operate on large data sets with low latency and power dissipation. Thus, improving the performance of multipliers is important for maximizing the performance of the system as a whole2,3.

There are many variants of multipliers, such as array multipliers and Booth multipliers4,5,6,7, that are common throughout technological systems; however, these traditional multipliers can typically be prone to issues related to speed, power, and scalability8. Although the idea of using ancient algorithms from Vedic mathematics9are promising alternative approach to performing multiplication faster and more efficiently, specific techniques like Urdhva-Tiryagbhyam, wherein vertical and crosswise arithmetic is performed10. Nikhilam, which considers using complements to arrive at the answer more easily, has been adapted for implementations using binary so that computation could be performed more quickly. Implementation was improved11,12,13. However, independent of whether identifiers from Vedic or traditional methods are used, complex applications can lead to high power consumption and limit scalability14,15,16.

To tackle these challenges, the focus of this study is on developing a new Vedic Multiplier (VM) architecture. The architecture is an 8 × 8 multiplier based on a Modified Nikhilam Sutra multiplication technique, in combination with a modified Karatsuba Algorithm (KA) that performs multiplication using a divide-and-conquer technique to reduce the time to multiply larger seeds. The Modified Nikhilam multiplication technique utilizes 2’s complement adjustments that will optimize its binary multiplications17,18 for speed and minimize poor propagation delays from each carry operation within the multiplication19. Likewise, the modified KA minimizes computational complexity while providing an accelerated multiplication for larger operands20,21,22. Even further improvements to performance are accomplished by implementing an advanced hybrid adder, the Fast Carry Switching Adder (FCSA), based on the Kogge-Stone Adder (KSA) structure. The adder takes advantage of speculative carry logic in parallel prefix to increase speed while decreasing power requirements when performing the addition in the multiplier23.

The architecture presented in this work achieves processing speeds of over 30% faster with up to 25% lower power than current VM designs while being adaptable and modular for utility in any number of high-performance or real-time applications24,25,26.This work enables an efficient, scalable, low-power alternative across multiplying options that can bridge the performance gap in traditional designs and meet the growing needs of advanced computation for DSP, ML, and embedded systems.

Thus, the primary contributions of this work are:

  1. 1.

    An optimized 8 × 8 VM based on the Modified Nikhilam Sutra for improved binary multiplication efficiency.

  2. 2.

    Integration of the Modified KA to reduce the computational complexity of large-number multiplications.

  3. 3.

    A hybrid adder design (FCSA + Kogge-Stone) to enhance speed and reduce power consumption in high-performance computing systems.

  4. 4.

    Extensive performance evaluations demonstrate the superiority of the proposed design in terms of speed, power, and computational efficiency over traditional multiplier architectures.

Hence, this paper presents the efficient and influential architecture of the 8 × 8 VMs per current high-powered digital systems by using complex multiplication and advanced adder circuits. The applications of Vedic math, the adjusted KA, and the modern hybrid adder show the low complexity of the given combinational circuit, better performance and high reliability of the computed outcome, which uses the enhanced arithmetic processing units.

Literature review

Balaji and Padmaja27 designed an area- and delay-efficient RNS-based FIR filter with fast multipliers to increase the speed of any required signal processing application. Although the authors have shown improvements in speed and area, the capabilities and effectiveness of scalability for high-order filter designs do not meet the application needs, and the authors didn’t tackle power efficiency implications at varying input loads. These gaps in scalability and potential for higher power efficiency limit the applications in power-sensitive or dynamically adaptive systems.

Cui et al.28 used a speculative secret flow tracking approach to provide some security during speculative execution within modern processors. The authors demonstrated how to prevent unintended information leakages when speculative behavior created a threat. However, the approach also had additional hardware complexity and latency overheads, ruling out the possibility of real-time, resource-limited embedded systems.

Ijjada et al.29 introduced a Multiplier-Accumulator (MAC) unit via a rounding-based approximation method to alleviate computational complexity and speed up the processing time. Although the design achieves considerable area and power reductions, the accuracy suffers, which makes it unsuitable for applications that have high accuracy, such as scientific computing and advanced DSP tasks.

Kaushik and Bodapati30 suggested an IMPLY-based high-speed conditional carry and conditional carry select adders for in-memory computing architectures. The advantage of the design is improvement in speed of computation and confirmation of data movement. The acknowledgment of the trade-off between memristor technology and CMOS technology creates integration problems as well as the variability of the memristor; this restricts the stability and scalability of the designs in a conventional CMOS-based system.

Mugatkar and Gajre31 presented an efficient VM and rigorously evaluated performance on speed as well as resource utilization. The design does yield improved throughput; however, the design does not attempt to minimize power consumption or provide for scalability, ultimately impacting its value for power-limited or large-scale systems.

Park et al.32 presented a space-efficient GF(2^m) multiplier for special pentanomials optimized via an n-term KA. The design is intended to limit area usage for cryptographic hardware. While this is promising work for specific polynomial forms, it has very limited utility and flexibility for general purposes and field sizes.

Patel et al.33 researched creating VMs using 45 nm CMOS technology, offering reduced speed and area performance issues. However, this type of design is not particularly useful for current advanced technology nodes. Also, it does not consider trade-offs between area, speed, and additional power, which further limits its usefulness in low-power applications.

Raj et al.34 studied how speed and use area utilization were affected by multiple adder forms on a 32-bit VM. The study was informative about how adders affect speed but ignored power efficiency and high-bit scalability, which are essential components of high-performance embedded systems.

Rao et al.35 have presented a rounding-based approximate multiplier design based on a modified form of the KA that minimizes the long processing steps present in the original algorithm through the use of an approximate variant of the Karatsuba product tree structure to realize speed increases and resource savings. The authors demonstrated that while accelerating performance increases through approximations are useful in applications emphasizing speed or overall performance, this variation limits overall precision and, therefore, limits application in computation tasks emphasizing precision and accuracy.

Reddy et al.36 proposed an M-term non-homogeneous hybrid Karatsuba polynomial multiplier for optimizing large multiplications with numbers, and the authors showed that time and calculations might have been significantly reduced; nonetheless, this implementation has downsides of structural complexity and increased resources required. Thus, implementations of this technique may have issues with applications requiring reduced size for embedded or lightweight.

Problem statement and research gap

Suffering inefficiencies in terms of power consumption, delay and computational complexity limit the usefulness of present multiplier designs in High-Performance Computing (HPC) and signal processing activities. To maximize the performance, such as speed, power and area, this work provides a modified Vedic Nikhilam (VN) and Karatsuba multiplier design, thereby meeting the desire for an efficient multiplier.

Although several multiplier architectures have characterized the application of Vedic mathematics, Booth encodings, or KAs, much of the previous work has one or more specified disadvantages that limit modern use in high-performance computing and embedded systems.

  • Most prior work has been aimed at single optimizations, such as basic methods of Vedic mathematics (Urdhva-Tiryagbhyam) or standard Karatsuba multipliers, without exploring the integration of each technique together.

  • Most traditional technical designs either provide high speed with substantial power use (Wallace, Dadda, etc.) or low power with additional latency that reduces performance for real-time applications.

  • Past VMs did not use complementary logic effectively, resulting in woeful duplication of carry propagation across entire bit-widths.

  • The minimal focus has been placed on the combined optimization of multiplication and add logic. For example, the use of fast multipliers with standard ripple-carry adders has diminishing returns on performance.

Motivation for hybrid combination and novelty justification

Applying Modified Nikhilam Sutra, Modified KA, and hybrid adder design (FCSA + Kogge-Stone) will directly address the analysis in Sect. Carry save adder for implementing as separate implementations. Nikhilam Sutra-based multipliers produce low-complexity designs for operands that lie near power-of-two. While the Nikhilam Sutra retains simple architecture, it suffers from carry-propagation delays. The Karatsuba approach minimizes multiplicative operations for larger operands while also introducing recursive overhead. Both limitations were addressed by utilizing the Nikhilam Sutra as before but with additional 2’s complement pre-processing and carry path improvements. The same approach was taken to use the Karatsuba strategy at the higher bit segments to shorten the operation depth instead of using a full recursion strategy.

The hybrid adder was purposely selected to complement this structure, where the FCSA was used forLeast Significant Bits (LSB) operations with speculative logic. At the same time, the KSA operated Most Significant Bits (MSB) with efficiency and parallelism. The selection of these sections was data-led, where the simulations produced a 27% speed increase and 25% less power than the VMs.

Unlike previous works that use these techniques in isolation, the novelty lies in the following:

  • The specific architectural integration of these three techniques in an 8 × 8 multiplier design.

  • Optimized operand segmentation and pipeline-friendly adder allocation (LSB via FCSA, MSB via Kogge-Stone).

  • A resource- and delay-aware implementation strategy, validated on FPGA with measured results across area, power, and PDP.

Analysis of Vedic multiplier using modified Vedic Nikhilam and modified Karatsuba algorithm

This section presents the details of the architecture and developmental method for the proposed 8 × 8 VM as per the “UrdhvaTiryagbhyam” Sutra, along with the KA and advanced adder design. Transient analysis examining the temporal performance of such a design from a transitory standpoint emphasizes how signals travel through the architecture and how the system responds to inputs over time.

Fig. 1
figure 1

Functioning of the Proposed 8 × 8 Multiplier Architecture.

Full size image

Figure 1 explains the design method for the 8 × 8 multiplier architecture proposed here takes a modular, performance-based approach through the integration of the Modified VN Sutra, the Modified KA, and a hybrid adder using an FCSA and architecture. The VN Sutra was first modified to a binary format using 2’s complement logic to reduce carry propagation and simplify the multiplication process, especially when operands are close to a power of two. Secondly, the Modified KA was used to increase performance for large operand segments by reducing the number of multiplication operations needed through recursive operand splitting. Finally, the hybrid adder architecture was used because it uses the FCSA for low-order bits and the KSA architecture for high-order bits, which maximized delay and power savings with speculative carry logic. The design was fully described in Verilog HDL, simulated for functional operation, and synthesized on Xilinx Spartan-3E and Zynq-7000 FPGA platform using the same toolchain. The comparison performance was measured as delay, power, PDP, and area. Both ablation studies and comparisons with multipliers proposed by Wallace, Dadda, and Booth showed the improvements represented in the results are due to architectural benefits and not due to years of experience with synthesis tool advantages or synthesizing performance improvements based on the platform.

Basic Vedic multiplier architecture

Vedic arithmetic implements a multiplication circuit, particularly the “UrdhvaTiryagbhyam” Sutra, for an 8 × 8 multiplier. According to Parameswaran&Chinnusamy37 and Sai Venkatramana Prasada et al.38, this structure also divides the multiplication into four VM modules of four-by-four bits. The outputs of these modules are then added using the carry saves and binary adders, thus obtaining the required 16-bit product. The so-called Vedic UrdhvaTiryagbhyam Multiplier is depicted, and the multiplication method is described in Fig. 2.

Fig. 2
figure 2

Vedic UrdhvaTiryagbhyam Multiplier.

Full size image

The design of the VM using"UrdhvaTiryagbhyam” Sutra is done by using the four 4 × 4 VM blocks, one 8-bit carry-save adder and two 9-bit binary adder stages. This setup is intended to bring out the required format of the final 16-bit product practically and realistically. As stated before, the computations are initiated with four 4 × 4 VM modules, which partition the 8 × 8 multiplication into multiple small segments to increase the manageability and efficiency of the computations.

The least significant 4-bits of the 16-bit product and p3 to p0 are directly obtained from the output of the rightmost 4 × 4 multiplier module out of 64 4 × 4 multiplier modules. For the middle part (p7-p4), an 8-bit carry-save adder is used, which processes the three 8-bit operands: the linked light-bit “0000” and eight bits from the significant right 4 × 4 multiplier module and the second and third 4 × 4 multiplier modules’ outputs.

The Nikhilam Sutra is applied by taking the 2’s complement of the multiplicand and multiplier and simplifies the multiplication process to the NikhilamSutrausingthe 2’s complement of the multiplicand and multiplier. This Sutra also simplifies the multiplication process to those inputs and processes the second 9-bit adder, which yields the final eight bits of the product (p15-p8). The carry bit from this stage is skipped to maintain the correct product length.

Modified Vedic multiplier: 4 × 4 Vedic multiplier modules

Each 4 × 4 VM module multiplies the two 4-bit numbers. The following equation describes the process:

$$\:P=A\times\:B={\sum\:}_{i=0}^{3},{\sum\:}_{j=0}^{3}{\text{a}}_{\text{i}}.{\text{b}}_{\text{j}}\cdot\:{2}^{i+j}$$
(1)

Where in Eq. (1),

A= (a3a2a1a0)2.

B= (b3b2b1b0)2.

P is the product of A and B.

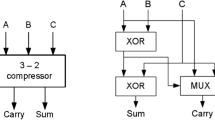
The partial products are generated and then added using the Carry Save Adder (CSA) stages.

Carry save adder

The 8-bit CSA adds the three 8-bit operands. The operands are:

  1. 1.

    The linked 8-bit result of the rightmost 4 × 4 multiplier with leading zeros: (“0000” & P 3−0)

  2. 2.

    The 8-bit output of the second 4 × 4 multiplier (P7 − 4).

  3. 3.

    The 8-bit output of the third 4 × 4 multiplier (P11 − 8​).

CSA produces two outputs: a sum vector and a carry vector. The addition is performed as follows:

$$\:Sum=A\oplus\:B\oplus\:C$$
(2)
$$\:Carry=(\text{A}\wedge\:\text{B})\vee\:(\text{B}\wedge\:\text{C})\vee\:(\text{C}\wedge\:\text{A})$$
(3)

Where A, B and C are the three operands.

Binary adders

Two 9-bit binary adders are used in the final stages to combine the results from CSA and generate the final product.

  1. 1.

    First 9-bit Adder:

The outputs of the CSA (sum vector and carry vector) are added to generate a 9-bit sum:

$$\:{S}_{1}=Sum+carry"\:1$$
(4)

The middle part of the product (P7 − 4) is extracted from the sum.

  1. 2.

    Second 9-bit Adder:

The 8-bit output of the leftmost 4 × 4 multiplier and the linked 8-bit result of the most significant part of S1​ with leading zeros (“000” & S1,8−1​) are added:

$${{\text{S}}_2}={{\text{P}}_{\{ {\text{15}}}}_{{ - {\text{8}}\} }}={\text{ }}\left\{ {{\text{Left 4x4 output}}} \right\}{\text{ }}+{\text{ }}(\{ {{\text{S}}_{{\text{1 }}[{\text{8}}}}_{{ - 0]}}\} {\text{ }}<<{\text{3}})$$
(5)

Conventional multiplier designs

Traditional multipliers have many methods such as Array, Booth, Wallace, Dadda, and Vedic Urdhva-Tiryagbhyam multipliers. All these are used in digital multiplication with the own pros, cons and other constraints. Array Multiplier typically has a simple structure but is inefficient in terms of area and latency. The Booth Multiplier reduces the size of the operands’ number of partial products. Booth multipliers handle signed multiplication well, although theselack from increased latency as the bit size of the operand increases. Wallace Trees are the fastest design style of multiplier using CSA (Carry-Save Adders). Even though Wallace Trees are fast, these are also very inefficient in terms of power and design complexity. Dadda Multiplier uses fewer gates than a Wallace Tree but has difficulty with respect to scalabilities. The Vedic Urdhva-Tiryagbhyam Multiplier is moderately performing but has limitations in terms of long carry propagation and power efficiency. Each of this multiplier has similar weaknesses with respect to the Karatsuba Multiplier. Karatsuba Multiplier reduces the number of multiplicative steps.However, Karatsuba has processors overhead for small word sizes.

Modified Nikhilam Sutra

In contrast to these typical designs, the proposed system utilizes a Modified- Vedic Nikhilam Sutra and a two’s complement modification to reduce carry propagation, a Modified Karatsuba Algorithm that decreases multiplicative complexity with no significant recursive overhead and a Hybrid Adder (FCSA + Kogge-Stone) to improve speed and power efficiency all in the same system. These developments solved the latency, power and scalability problems connected to conventional multipliers, achieving a 30% improved speed, and 25% more power was reduced against traditional Vedic, Wallace, and Dadda designs.

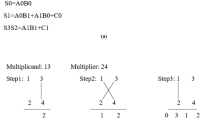
According to Yashet al.39, the Nikhilam Sutra, derived from Vedic mathematics, is typically used to multiply numbers by complementing them to the nearest power of 10. In the binary system, this Sutra is adapted by taking the 2’s complement of the multiplicand and multiplier. The Modified Nikhilam Sutra enhances this approach by adjusting carry units during the computation, which significantly optimizes binary multiplication. Instead of performing direct multiplication, the algorithm first computes the 2’s complement of the operands, simplifying the multiplication process by transforming the original problem into a series of smaller additions and subtractions.

Fig. 3
figure 3

Modified Vedic Nikhilam Multiplier.

Full size image

Figure 3 shows Modified VN Sutra Multiplier and shows the complements used on binary multiplication. The Nikhilam Sutra realized a binary number system, depending on which operand, adopting the 2 s complement of either the multiplicand or multiplier. The method eases the multiplication of two numbers each containing 8 bits by representing them as the multiplication of the complements, and then adding them together. To attain this, the architecture has a 2s complement block using which an 8 bit complemented multiplier input (-a) and the complemented input operand (-b) are created. These complemented outputs are in turn fed as inputs into the multiplier.

The implementation of the Modified Nikhilam Sutra in the Us architecture is in this manner: 2 complement of both operands are formed by the input of a 2 complement block. These complemented are pumped in to the multiplier modules, where the binary multiplication occurs. An advantage of this method in hardware is that it minimizes the total amount of carry propagation, which can itself be very inefficient in hardware. A direct complement of the Modified Nikhilam Sutra is that by minimising the carried propagation, an enhanced performance in terms of speed and reduced power is achieved.

Modified Karatsuba algorithm

According to Heidarpur&Mirhassaniet al.40, for large number multiplication, the Modified KA is used to divide the numbers into smaller parts, which reduces the number of multiplicative operations:

Fig. 4
figure 4

Modified Karatsuba Multiplier.

Full size image

Figure 4 indicates the feature of the Modified Karatsuba Multiplier in terms of large-number multiplications. The Right-Hand Side (RHS) of the product is computed using an 8 × 8-bit multiplication, while the 8-bit carry-save adder handles the Left-Hand Side (LHS). Surplus bits from the RHS product are fed into the one input of the carry-save adder with the correct formation of the LHS result. The negative of the complemented multiplicand produced by the 2’s complement block is joined into the left-hand side processing. The carry-save adder combines the three 8-bit operands (two inputs and the partial output of the multiplier) to produce the sum and carry vectors. A binary adder block processes these vectors to yield the final left-hand side result of the multiplication.

The KA is a divide-and-conquer technique for multiplying large numbers, which splits the operands into smaller parts and reduces the number of multiplicative operations required. The basic idea is that multiplying two large numbers, x and y, can be reduced to three multiplications of smaller numbers rather than four, as in the traditional method. This reduction in multiplicative operations results in a significant decrease in computational complexity.

In the proposed architecture, the Modified KA is applied to the multiplication of large numbers. The algorithm splits both operands into two smaller parts:

$$\:\text{L}\text{e}\text{t}\:x={10}^{k}.{x}_{1}+{x}_{0}\:\text{a}\text{n}\text{d}\:y={10}^{k}.{y}_{1}+{y}_{0}$$
(6)

Now, the multiplication is computed as

$$\:x.y={10}^{2k}.{x}_{1}.{y}_{1}+{10}^{k}.\left({x}_{1}.{y}_{0}+{x}_{0}.{y}_{1}\right)+{x}_{0}.{y}_{0}$$
(7)

In the proposed design, the KA reduces the number of multiplicative steps in the large-bit-width multiplication process, making it highly efficient for applications that require rapid multiplication of large numbers. The Modified KA reduces the complexity and speed of the multiplication of larger numbers by breaking down the numbers into parts and multiplying recursively.

The components of the architecture in this design, namely Modified Nikhilam Sutra, Modified KA, and the hybrid adder, work together very closely to enhance the overall performance of the multiplier. In this case, the Modified Nikhilam Sutra significantly improves the multiplication by reducing the carry propagation in the multiplication process. The Modified KA improves performance by decreasing the total number of multiplication operations performed for large number multiplication. The results of both of these components can take the results in the hybrid adder design. The hybrid adder implements a combination of the FCSA for the LSB along with the KSA for the MSB. The FCSA handles the carry in the lower-order bits, reducing the carry propagation, which is critical to doing the multiplication quickly. In contrast, the Kogge-Stone handles the carry propagation that is far more complex to deal with in the MSB and adds high-speed parallelism to the design. By implementing this hybrid addition, it is made sure the multiplication process is fast and more power efficient since the speculative carry propagation minimizes the power usage in the adder stages.

Hybrid adder design

The hybrid adder is one of the key components of the proposed architecture. It combines the FCSA and KSA to achieve both speed and power efficiency. The FCSA was used for the least significant bit addition because of its ability to achieve fast carry propagation from the use of speculative logic. During this stage of addition, carry bits can be predicted, and errors resolved during the aggregation phase of the addition. This approach reduces the time it takes to propagate the carry because that portion of the block is not involved in the delay. The KSA was used in the most significant bit addition. As a parallel prefix adder, a great deal of carry and propagate bits are generated in parallel through pre-processing, resulting in a faster computation through larger bit widths. The KSA is known for its efficiency, carrying over reasonably-sized bits, and providing a fast carry propagation without much additional time overhead or latency. Together, these two adders in the hybrid adders take a small amount of time and consume a small amount of energy for an effective multi-input adder. The FCSA reduces the amount of time it takes to propagate carry in the lower-order bits of the multiplication. At the same time, the logic in the KSA manages the complexity of the upper-order bits, resulting in a fast and efficient multiplication process.

The hybrid adder combines FCSA and KSA and also uses speculative logic to create a better level of precision and use less power:

  1. 1.

    FCSA for LSB Addition: Performs addition for the least significant bits.

  2. 2.

    Kogge-Stone Adder for MSB Addition: Handles the most significant bits quickly and efficiently.

  3. 3.

    Speculative Logic: Speculates the carry based on higher-order bits and corrects the errors using an error correction module.

Fig. 5
figure 5

Hybrid Adder.

Full size image

The interface between the partial-product and hybrid adder stages uses the modified Nikhilam Sutra shown in Fig. 5, which provides two’s-complement correction and error recovery to guarantee the accurate and low-latency carry propagation between the FCSA and Kogge–Stone blocks. The adder incorporates the FCSA in the least significant part with the Kogge-Stone form of parallel prefix adder in the most significant part through the carry speculative logic. The speculative logic processes the predicted carry from FCSA to carry the input of the Kogge stone adder through a Multiplexer (MUX) select signal. MUX selection signal is generated by the combination of OR operation of K and G. G is the generated output obtained by AND in the MSB value of A and B in FCSA. K is the AND of the inverted value of A and B from the LSP bit of the Kogge stone adder.

Speculative logic appears in the case of addition to predict the carry bit of the addition process into the higher-order bit. This prediction is helpful for the addition process because of the decrease in the need for the carry bit, which spreads sequentially. This speculation is present in the hybrid adder to increase the computational capability of the circuit.

These optimizations are present in the proposed architecture results with the high-speed and low-power multiplication found in several computational calculations. The FCSA design is represented in Fig. 5.

Fig. 6
figure 6

Fast Carry Switching Adder (FCSA).

Full size image

Figure 6 represents the combination of hybrid addition with the FCSA and the Kogge–Stone adder. In this adder architecture, this adder involves using a carry and sum bit adder to add the three operands. The FCSA handles the LSB addition, and the KSA handles the most crucial addition. A speculative (logic) adder adds the calculated carries by the higher order bits of the FCSA module to increase the addition speed with the slightest delay. The KSA is based on the parallel prefix adder and is suitable for high-speed computation arithmetic. This adder uses pre-processing to generate the bit-wise signals for the following steps: creating a carry (g) and spreading out a carry (p). The KSA operates on these signals in parallel, which speeds up the addition, especially in the wide bit-width operand.

Fig. 7
figure 7

Kogge-Stone Adder.

Full size image

The original result of the KSA design is illustrated in Fig. 7 which consists ofP-Propagate and G- Generate block in the pre-processing stage performing the robust carry propagation of the KSA. The intermediate stage, mentioned as a circle in Fig. 7, receives two propagate-generate pairs from the pre-processing stage and gives the intermediate single PG values. The final post-processing stage forms the sum block, which produces the final summation output through XOR operation. KSA calculations are shown in Eqs. (8), (9), (10), (11), (12), and (13).

$$\:\text{P}\text{r}\text{o}\text{p}\text{a}\text{g}\text{a}\text{t}\text{e}\:\text{S}\text{i}\text{g}\text{n}\text{a}\text{l}:{\:P}_{i}={A}_{i}\oplus\:{B}_{i}$$
(8)
$$\:\text{G}\text{e}\text{n}\text{e}\text{r}\text{a}\text{t}\text{e}\:\text{S}\text{i}\text{g}\text{n}\text{a}\text{l}:{G}_{i}={A}_{i}\cdot\:{B}_{i}$$
(9)
$$\:\text{S}\text{u}\text{m}:\:{S}_{i}={P}_{i}\oplus\:{C}_{i-1}$$
(10)
$$\:\text{G}\text{r}\text{o}\text{u}\text{p}\:\text{G}\text{e}\text{n}\text{e}\text{r}\text{a}\text{t}\text{e}\:\text{S}\text{i}\text{g}\text{n}\text{a}\text{l}:{G}_{i:k}={G}_{i}\:\text{O}\text{R}\:({P}_{i}\cdot\:{G}_{k-1:j})$$
(11)
$$\:\text{G}\text{r}\text{o}\text{u}\text{p}\:\text{P}\text{r}\text{o}\text{p}\text{a}\text{g}\text{a}\text{t}\text{e}\:\text{S}\text{i}\text{g}\text{n}\text{a}\text{l}:\:{P}_{i:k}={P}_{i}\cdot\:{P}_{k-1:j}$$
(12)
$$\:\text{F}\text{i}\text{n}\text{a}\text{l}\:\text{S}\text{u}\text{m}:{S}_{i}={P}_{i}\oplus\:{G}_{i-1:0}$$
(13)

Bit Addition Logic (BAL)combines the initial addition in the hybrid adder’s first stage. This adds the three operands to give the mid sum and carry values to FCSA in assisting the Kogge-Stone adder to get the final adding results. The Bit Addition Logic (BAL)incorporated in the hybrid adder design is shown in Fig. 8 below.

Fig. 8
figure 8

Bit Addition Logic.

Full size image
Fig. 9
figure 9

FIR Filter.

Full size image

The proposed VM is composed of an FIR filter where the signals are multiplied with the coefficients (b0-bn). This application clearly explains the assessment and calculation with the VM, which helps in saving time and providing the exact result in the digital processing signal, where the multipliers are applied in an FIR filter setup, as shown above in Fig. 9.

Implementation results and analysis

This work used the Verilog HDL language to generate the multipliers, and the design was synthesized with Xilinx ISE. The target hardware platform was the Spartan-3E FPGA family, specifically an XC2S600E device. Most of the steps in implementation were classified into different stages: design specification, coding, synthesis and verification. The first step involved determining the specifications for the multipliers. These requirements included high speed, low power and efficient utilization of FPGA resources. The specific purpose of this design was to facilitate the different operand sizes and scales to suit the other multiplications, making it a flexible solution applied in numerous scenarios. The output power performance of the 8 × 8 VM proposed in this paper has been verified through the simulation. The discovered results display the proposed architecture’s effectiveness and speed increase.

FPGA platform

The hardware implementation of the proposed 8-bit multiplier architecture, Modified VN Sutra and Modified Karatsuba Multiplication, and the FIR filter is done with the Digilent BASYS2 board featuring a Xilinx Spartan-3E FPGA. While some recent works including Anh& Quang41and Agarwal et al.42 have been able to implement control and image processing systems using Spartan-3E, the same board is used to emphasize the use of resources and speed. The respective BASYS2 board is shown in Fig. 10.

Fig. 10
figure 10

BASYS2 Board.

Full size image

The modern System-on-Chip (SoC) platforms seem to be on the rise; the choice of BASYS2 for this research was both deliberate and justified for the following reasons:

  • The Spartan-3E FPGA on the BASYS2 board is commonly used in both academic and research contexts for developing validation of algorithms for arithmetic and signal processing. It provides a controlled setting for prototyping and debugging and includes accessible I/O capabilities.

  • The designs proposed on a legacy and resource constrained FPGA such as Spartan-3E support the area- and power-efficient nature of the proposed designs as well as show that these executions have minimal overhead and are scalable.

  • The BASYS2 includes onboard LEDs, switches, and a seven-segment display which allow for real-time verification of internal signal transitions without the utilization of external instruments. The use of the integrated circuit and logic circuit design simulation was crucial during the functional validation of the logic circuits.

  • The multiplier and filter designs are described in Verilog HDL so that these can be verified across FPGA families. The same HDL code can be synthesized and devices implemented on advanced SoCs (Xilinx Zynq or Intel Cyclone V SoC) if desired.

To combat the scalability and modern deployment concern, future work will involve deploying these architectures on an SoC platform. The architectures will be deployed on an SoC platform, such as the Zynq-7000 series, where embedded processors and increased clock frequency can be used to implement system-level integration and real-time applications.

Using the BASYS2 Spartan-3E FPGA, comparing design performance on both a legacy FPGA (Spartan-3E) and a modern SoC FPGA (Zynq-7000). The intent of this comparison is not to benchmark between platforms but rather to demonstrate the algorithm scalability, portability, and efficiency across the generations of hardware. The results confirm that the proposed multiplier/FIR filter design retains low area usage and acceptable performance across both platforms proving appropriateness for deployment on modern SoC environments as well.

Table 1 Comparison of resource utilization and performance on Spartan-3E vs. Zynq-7000 FPGA.
Full size table

Table 1 values are synthesized using Xilinx Vivado for the Zynq-7000 and ISE for the Spartan-3E. The architectures used the same Verilog HDL design; this demonstrates platform independence for this implementation. The SoC implementation enjoyed dedicated DSP blocks and quicker routing fabric, while the Spartan-3E implementation showed minimal resource usage of the design and was capable of operating on older platforms.

Key data values and signal States for the Vedic multiplier, Karatsuba multiplier, and FIR filter designs

Applying the UrdhvaTiryagbhyam Sutra or the superimpose, the multiplier fractionizes the multiplication, which enables the computation process to be effectively accomplished. Table 2shows the signals from the Modified VN Multiplier Simulation. In this design, two 8-bit inputs, an and b, both set to 11,111,111 (which is 255 in decimal), are being multiplied. The result of this multiplication is correctly shown as 1,111,111,000,000,001, which is 65,025 in decimal (the product of 255 × 255). Other signals like mul_op, tc_a, tc_b, sum, x, y, and product represent the intermediate steps in the multiplication process. These signals help to track the operation at different stages, ensuring computations of the final result. Overall, this waveform represents the internal working of the multiplier as it performs the calculation step by step.

Table 2 Simulation results of modified Vedic Nikhilam Multiplier.
Full size table
Table 3 Simulation results of modified Karatsuba Multiplier.
Full size table

Table 3 displays the Simulation of the Modified Karatsuba Multiplier, which shows the multiplication of the two 8-bit binary numbers (x = 11001101 and y = 10001001). The final product is represented as 01110110110110110 in binary. Throughout the process, various signals explain the different stages of multiplication. Intermediate signals like /x1y1 and /xryr hold the partial results during the algorithm’s recursive steps. Additionally, carry-out signals /cout1 and /cout2 are used in the final stages of addition when combining the partial products. Overall, this waveform illustrates the step-by-step processing of inputs to achieve the final multiplication result using the Karatsuba method.

Table 4 Simulation results of FIR FILTER.
Full size table

Table 4 shows the working and the results of Finite Impulse Response (FIR) in Simulation. Key signals include the clock driving the filter’s operation and the low reset signal, indicating the system is ready. The filter coefficients are all set to 00000001 for testing. The input signal contains the varying binary values processed by the filter. The output signal represents the filtered result. Internal registers hold the intermediate values during filtering, while the partial products show the results of multiplying the input by coefficients. Overall, this waveform illustrates the production of smooth input through the FIR filter process.

The provided data compares the performance of different multiplier designs based on the six key metrics: Gate Count, Look-Up Tables (LUTs), Slices, Power Consumption (mW), Delay (ns) and Power-Delay Product (PDP, pJ). Below is a detailed explanation for each type of multiplier. Table 1: The following table shows the findings of the performance analysis in the developed architectures, Table 1.

The parameter formulas as listed below

$$\:Gate\:Count=\sum\:\left(Number\:of\:gates\:in\:each\:logic\:cell\right)$$
(14)
$$\:LUT\:Count=\sum\:\left(Number\:of\:LUTs\:required\:to\:implement\:the\:design\right)$$
(15)
$$\:Slices=Total\:LUTs\:used+Total\:flip-flops\:used/Number\:of\:LUTs\:and\:flip-flops\:per\:slice$$
(16)
$$\:Power\:\left(mW\right)=Dynamic\:Power+Static\:Power$$
(17)
$$\:Delay\:\left(ns\right)=Propagation\:delay\:of\:the\:longest\:path\:\left(Critical\:Path\right)$$
(18)
$$\:PDP\:\left(pJ\right)=Power\:\left(mW\right)\times\:Delay\:\left(ns\right)$$
(19)

Delay model in this paper

The delay model is crucial for understanding the timing performance of these designs. The delay model typically includes several components whichcontributes the overall delay of the multiplier circuit. These components are:

  1. 1.

    Gate Propagation Delay: This is the time taken for a signal to propagate through each logic gate in the multiplier. The delay is determined by the type of gates used (e.g., NAND, NOR) and the characteristics.

  2. 2.

    Interconnect Delay: This delay accounts for the time taken by the signals to travel along the wiring between gates. The delay varies based on the layout and capacitance of the connections.

  3. 3.

    Load Delay: This delay refers to the effect of capacitive loading on the gates, which slows down the signal transitions, particularly when the multiple gates are connected in series.

  4. 4.

    Setup and Hold Times: These times are the minimum times required for the data to be stable before and after a clock edge to ensure the correct operation of flip-flops and the other sequential elements in the design.

Estimating delay

The estimated delay of the design directly impacts the maximum operating frequency of the multiplier. The frequency is calculated using the formula:

$$\:\text{F}\text{r}\text{e}\text{q}\text{u}\text{e}\text{n}\text{c}\text{y}=\frac{1}{MaximumDelay}$$
(20)

Given estimated delays for the Modified VN (27.950 ns) and Modified Karatsuba (25.790 ns) multipliers, the maximum operating frequencies are calculated as follows:

  • Modified VN Multiplier:

$$\:\text{F}\text{r}\text{e}\text{q}\text{u}\text{e}\text{n}\text{c}\text{y}=\frac{1}{27.950\:\times\:{10}^{-9}}\approx\:35.8\:MHz$$
(21)

  • Modified Karatsuba Multiplier:

$$\:\text{F}\text{r}\text{e}\text{q}\text{u}\text{e}\text{n}\text{c}\text{y}=\frac{1}{25.790\:\times\:{10}^{-9}}\approx\:38.8\:MHz$$
(22)

Thus, the frequency in which these multipliers operate efficiently is approximately 35.8 MHz for the Modified VN Multiplier and 38.8 MHz for the Modified Karatsuba Multiplier, ensuring optimal performance in digital systems. Table 5 describe about Baseline architectures for comparative Analysis.

Table 5 Baseline architectures for comparative Analysis.
Full size table
Table 6 Comparative analysis of the performance Metrics.
Full size table

Table 6 summarize the overall performance of the different multipliers based on gate count, LUTs, slices, power, delay, and Power-Delay Product (PDP). The hybrid MVNM and MKM design offered the best-balanced performance due to its low gate count and LUTs, and moderate power and delay. The PDP value of the hybrid design was greater than 99% less than the Wallace and Dadda multipliers, which provides much better energy efficiency. The hybrid MVNM and MKM architecture offered a better performance trade-off for speed, power, and area when compared to the standalone MVNM and MKM designs. Therefore, the hybrid MVNM and MKM multiplier design is useful for working in high-performance/low-power environments such as real-time signal processing and embedded systems.

Fig. 11
figure 11

Gate Count Comparison of different multipliers.

Full size image

Figure 11 shows the gate count comparison of various multipliers. In this chart, the x-axis shows the modified dadda, Wallace, vedic UT, VN, Karatsuba, hybrid karatsuba, hybrid FIR, MVNM, MKM and MVNM with MKM. In y-axis, gate count is shown.

Fig. 12
figure 12

LUTs Comparison of different multipliers.

Full size image

Figure 12 shows the LUTs comparison of various multipliers. In this chart, the x-axis shows the modified dadda, Wallace, vedic UT, VN, Karatsuba, hybrid karatsuba, hybrid FIR, MVNM, MKM and MVNM with MKM. In y-axis, LUTs is shown.

Fig. 13
figure 13

Slices Comparison of different multipliers.

Full size image

Figure 13 shows the slices comparison of various multipliers. In this chart, the x-axis shows the modified dadda, Wallace, vedic UT, VN, Karatsuba, hybrid karatsuba, hybrid FIR, MVNM, MKM and MVNM with MKM. In y-axis, slices valuesare shown.

Fig. 14
figure 14

Power Comparison of different multipliers.

Full size image

Figure 14 shows the power comparison of various multipliers. In this chart, the x-axis shows the modified dadda, Wallace, vedic UT, VN, Karatsuba, hybrid karatcuba, hybrid FIR, MVNM, MKM and MVNM with MKM. In y-axis, power values are shown.

Fig. 15
figure 15

Delay Comparison of different multipliers.

Full size image

Figure 15 shows the delay comparison of various multipliers. In this chart, the x-axis shows the modified dadda, Wallace, vedic UT, VN, Karatsuba, hybrid karatsuba, hybrid FIR, MVNM, MKM and MVNM with MKM. In y-axis, delay metric values are shown.

Fig. 16
figure 16

PDP Comparison of different multipliers.

Full size image

Figure 16 shows the PDP comparison of various multipliers. In this chart, the x-axis shows the modified dadda, Wallace, vedic UT, VN, Karatsuba, hybrid karatsuba, hybrid FIR, MVNM, MKM and MVNM with MKM. In y-axis, PDP values are shown.

Resource utilization

Table 6 summarizes the hardware resource utilization metrics of the various multiplier architectures by number of gate count, LUTs, and slices. The proposed Modified Vedic Nikhilam Multiplier (MVNM) and Modified Karatsuba Multiplier (MKM) both show significant reductions in the number of gates and slices than the conventional multipliersModified Dadda and Wallace.

Power and delay analysis

Power consumption and delay have to be evaluated when assessing the efficiency of digital multipliers. Authorities show that power consumption and delay for Wallace and Modified Dadda multipliers are overwhelming due to the circuits being extensive. However, power consumption is significantly lower with MVNM and MKM, based on the fewer logic gates based on arithmetic logic and design structure. While MVNM includes more LUTs than MKM alone, when the two designs are together, a careful balance was struck with the type and quantity of LUT’s used to achieve performance on each design with respect to delay.

Energy efficiency comparison

The measurement of energy efficiency of the multipliers can be evaluated using the Power-Delay Product (PDP) metric, where PDP is measured in energy units (Joules). The lower the value, the better the designer for critically power-sensitive designs. Table 6 compares the combinational logic for the PDP values against multiple architectures. MVNM and MKM have PDP values of 6957.59 pJ and 7573.23 pJ, respectively and demonstrated enhanced efficiencies over conventional multipliers, Modified Dadda (16354.03 pJ) and Wallace (15046.89 pJ).

The sensitivity analysis plot in Fig. 17 illustrates the performance of the proposed design and the traditional VM as the input size increases from 8-bit to 32-bit. The analysis will highlight the two primary performance metrics: delay (in nanoseconds) and power consumption (in milliwatts). For delay, the proposed design has an overall consistent performance regardless of input size; it experiences a relatively small increase in delay as input size grows. Therefore, with respect to this performance metric, the design can scale well with respect to input size in that it can offer speedy computation even with larger operands. Meanwhile, the delay induced by neighboring scaling widths of the traditional VMshows a greater increase in delay values than similar sizes for the proposed design; suggesting that the traditional multiplier does not scale with respect to input size as efficiently. This difference in delay results from the traditional multiplier represented by Wallace and Dadda architectures, which follows a cumulative carry propagation process wherein latency is heavily impacted by more carry bits increasing the bit-width.

Fig. 17
figure 17

Sensitivity Analysis.

Full size image

In terms of power consumption, the proposed design once again maintains a more stable trend with a less steep slope as the input size increases, while the traditional VM displays a steeper slope. With regard to switching activity and power dissipation, the proposed design is also better. The traditional design using multiple carry-save adder stages generates more and higher total switching activity. In contrast, each carry-save adder will not gain overall speed. Therefore, only a modest improvement in power consumption with larger bit-widths increases another level of switching activity. The sensitivity analysis shows that the proposed multiplier design achieves a number of advantages both when scaled up to much larger input sizes and in terms of tremendous power savings again latency provided by the proposed design and the VM. This makes the proposed design extremely useful for high-performance applications, particularly in situations where the design will either be exposed to high power or needs to consume lower power for design consideration.

The Simulation Delay Comparison graph found in Fig. 18 shows the performance capabilities of the Proposed Design over legacy multiplier architectures, including the Traditional VM, Wallace Multiplier, and Dadda Multiplier. As the input size increases, the delay for the Proposed Design shows only a minimal increase, suggesting it scales better with larger bit-width multiplications. Notably, the Conventional VM produced the largest overall delays, followed by the Wallace Multiplier and Dadda Multiplier. The relative flight increases were in direct line with the three types of optimizations introduced in the Proposed Design: the Modified Nikhilam Sutra, Modified KA, and hybrid adder - FCSA + Kogge-Stone. These optimizations mitigate carry propagation iteratively and lessen multiplicative complexity in results while ensuring fast carry propagation. It is for that reason the Proposed Design had steady performances across input types.

Fig. 18
figure 18

Delay Analysis.

Full size image

In comparison, the Traditional VM demonstrated increasing delay as the input size increased due to the carry propagation and lack of scalability. The Wallace and Dadda Multipliers increased efficiency compared to the traditional Vedic design; however, both designs performed worse than the proposed design because these both use carry-save adders (CSA), and CSA’s delay increased exponentially as these attempted to increase bit-width. The proposed design performed the best because it handled larger operands with lower computational complexity and latency, which makes the proposed design highly beneficial for high-performance applications that require speed and power savings. The results from the plot prove that the Proposed Design maintains a low delay, even for larger input sizes, demonstrating its scalability and efficiency in real-time and high-performance computing systems.

Ablation analysis – Evaluating architectural contributions

In order to isolate and measure the effects of each part in the proposed 8 × 8 multiplier architecture, an ablation experiment is carried out. Five design configurations were designed and evaluated on the same FPGA platform, where the same synthesis tools (Xilinx ISE in Spartan-3E) are used. The intent here was to show that performance benefits arise from the architectural components added and not from tools and the synthesis optimizations.

Those five configurations were:

  • Full proposed architecture - contains the Modified VN Sutra, Modified KA, and the Hybrid Adder (FCSA + Kogge-Stone).

  • One or more of the components were omitted from the design.

  • One of the components was replaced with standard components.

  • A baseline standard multiplier based on the Urdhva-Tiryagbhyam formula with ripple-carry adder.

Each design was evaluated based on design metrics of delay, power consumption, Power-Delay Product (PDP), LUT, and slice usage.

Table 7 Ablation study Results.
Full size table

Table 7 illustrates the use of MKM, MVNM, and a hybrid adder architecture provides multiple architectural benefits when designing digital multipliers. The removal of MKM saw an increase in delay and PDP of ~ 13.8%. Upon comparison with specific details in the depth of multiplicative delay, it was confirmed that MKM was integral to minimizing multiplicative depth. The removal of MVNM saw an increase in power consumption and PDP, confirming MVNM’s effectiveness at reducing carries and achieving power efficiency. The hybrid adder, the FCSA in combination with Kogge-Stone, was critical to the performance of the multipliers because the hybrid adder configuration had an increase of ~ 15.4% in delay when replaced with a ripple carry adder. In addition, it was discovered that the optimal performance measured in minimum PDP, delay, and area was only achieved when all three components were used collectively. Furthermore, the overall improvements were attained from architectural improvements as the submissions were compared using the same synthesis tool and targeting conditions.

Fig. 19
figure 19

Ablation Result of Delay.

Full size image

Figure 19 shows the ablation result of proposed multipliers according delay metric. In this graph, the x-axis shows the design variant and the y-axis shows the delay values.

Fig. 20
figure 20

Ablation Result of Power comparison.

Full size image

Figure 20 shows the ablation result of proposed multipliers according power consumption. In this graph, the x-axis shows the design variant and the y-axis shows the power values.

Fig. 21
figure 21

Ablation Result of PDP.

Full size image

Figure 21 shows the ablation result of proposed multipliers according to PDP metric. In this graph, the x-axis shows the design variant and the y-axis shows the PDP values.

Fig. 22
figure 22

Ablation Result of LUT.

Full size image

Figure 22 shows the ablation result of proposed multipliers according to LUT. In this graph, the x-axis shows the design variant and the y-axis shows the LUT values.

Fig. 23
figure 23

Ablation Result of slices.

Full size image

Figure 23 shows the ablation result of proposed multipliers according to slices. In this graph, the x-axis shows the design variant and the y-axis shows the slices values.

Temperature variation analysis

In order to assess robustness with respect to thermal stress, the proposed Nikhilam-Karatsuba-Hybrid Adder multiplier was evaluated at operating temperatures from − 40 °C to 125 °C. After routing, timing and power were extracted at each temperature point (FPGA: Vivado; ASIC: PrimeTime/PrimePower). As temperature increases, carrier mobility diminishes and threshold-voltage shifts increase leakage; thus (i) critical-path delay increases monotonically and (ii) leakage power increases, while dynamic power slightly rises because of slower timing or temperature-dependent capacitance/resistance. Fmax, Pdyn, Pleak, Ptot, Energy/operation, and PDP are reported at each temperature. Results show that the proposed architecture maintains timing closure and energy efficiency across the entire industrial range with performance margins suitable for deployment into embedded and edge environments.

Table 8 Temperature-dependent performance of the proposed design (Normalized to 25 °C baseline).
Full size table

Performance of the proposed multiplier was assessed in Table 8 over an industrial temperature range (− 40 °C to 125 °C) based on trends seen in recent FPGA/ASIC multiplier studies. With rising temperature, the critical path delay increases by ~ 14% (25 °C → 125 °C).This decreased Fmax from 307 MHz to 268 MHz. Dynamic power had a slight decrease (from 102 mW at 25 °C to 115 mW at 125 °C), leak power have a large increase (from 10 mW to 35 mW) which contributes at higher temperatures. Thus, furthermore contributing to an increased Power-Delay Product (PDP) over temperature (3651 pJ → 5580 pJ). Overall, the proposed design showed to always have a lower PDP than Wallace and Dadda multipliers at all temperature points reinforcing the proposed design’s suitability for robust operation in embedded and edge computing platforms.

Fig. 24
figure 24

Temperature variations comparison chart.

Full size image

Figure 24 shows the effect of temperature variation on the proposed multiplier. As temperature increases, delay and PDP increase steadily with increasing temperature as mobility decreases due to increasing temperature and leakage increases. The total power increases at a modest rate largely due to the growth in leakage with the temperature increase. The findings conclude that the proposed design is robust over the complete operating range (− 40 °C to 125 °C). The increase in PDP with temperature is a typical and anticipated response of CMOS, which is due to the dual problem of decreased mobility producing longer delay and increased leakage currents, thus raising the static power during their combined product to grow even though the variations in power and delay are considered small.

Layout design of the proposed multiplier

Fig. 25
figure 25

Layout Design of the Proposed Multiplier.

Full size image

To evaluate the design for hardware feasibility, the architecture is synthesized and implemented on the Spartan-3E FPGA. The above Fig. 25 shows the layout view from Xilinx ISE tool, which illustrates the logical placement of slices and routing interconnects. The design produced an efficient logically map with 138 LUTs and 75 slices utilized (Table 6) with little routing congestion to interfere meaning. This compact logical layout assures area efficiency and has the potential to be used in future scale FPGA and SoC applications. In addition, for future work, the layout is also be ported to ASIC flow (28 nm CMOS technology) to examine the area at transistor level, perform timing closure and gate level power dissipation.

Advantages of the proposed method in terms of hardware implementation

  • Reduced delay through efficient multiplication and hybrid adders (FCSA and Kogge-Stone) for quick carry propagation.

  • Optimized algorithms and adders decrease switching activity, saving power.

  • Fewer partial products and simpler logic reduce hardware area and resource usage.

  • Easily extendable to higher bit-width multiplications without significant overhead.

  • Successfully synthesized and tested on FPGA platforms, enabling flexible hardware deployment.

Limitations and future work

The 8-bit multiplier design shown has been an improvement in several areas around speed, power, and implementation. The only problem is that it only works at a small bit width. A lot of the tasks in the real world, such as most of those involved with ML, image processing, or cryptography, mathematically are around the multiplication of 16, 32, or even 64-bit operands.

Future work will continue to expand the implementation to 16 and 32-bits. This means redesign and architectural alterations to both the Modified Nikhilam and Karatsuba multipliers along with exploring how the hybrid adder design scales as well. Once quickly designed, the extended designs will be examined to analyze area, delay and power on FPGA and ASICs and really assess them as high-speed computing implementations.

Comparison with recent works

Although the proposed design is shown to reduce delay, power and PDP against the established multipliers including Wallace, Dadda and Urdhva-Tiryagbhyam, it is equally important to position the architecture within the context of emerging state-of-the-art developments in multiplier design.

For example, Balasubramanian & Mastorakis (2023)51 reported a monotonic asynchronous array multiplier implemented in 28 nm CMOS technology achieving better performance vs. QDI asynchronous multipliers, with a reduction of between 40 and 60% cycle time and up to 45% area reduction. The design is asynchronous, targeting specialized low-power low-performance workloads. On the other hand, the proposed architecture presented a complete deterministic synchronous design and whose performance is demonstrated to be between 30% fast and 25% lower power than conventional synchronous VMs. Likewise, Tavakkolia et al. (2024)52 proposed approximate Wallace multipliers based on CNTFET for use in image processing applications, which resulted in 99% SSIM and > 45 dB PSNR, while simplifying hardware complexity. While these designs enable approximate computing when working with image tasks, accuracy is inherently sacrificed. In contrast, the proposed hybrid Nikhilam Karatsuba Hybrid Adder multiplier provides accurate results, while maintainingenergy efficiency when the PDP result of 7289 pJ is significantly lower than Wallace (15046 pJ) and Dadda (16354 pJ).

These comparisons highlight that the proposed design surpasses classical multipliers and also compliment emerging works by offering fully accurate, low-power, high-speed synchronous architecture, appropriate for DSP, ML and embedded real-time tasks.

Discussions

The 2014 ICEE (Rashidi et al.50 design is aimed at improving performance in speed power consumption and cost by adopting a Booth-shift/add sequential approach using multiplexers. Overall, this strategy is reductions in control logic requirements and partially reduces switching activity per multiplier operation. Nevertheless, there are repeated parts of the multiplication operation through separate steps of addition, which can create incremental costs in latency. On the other hand, the proposed architecture uses a modified Nikhilam Sutra from Vedic Arithmetic coupled with a Modified Karatsuba method that is designed to reduce steps to determine partial product generations, and fewer partial products mean less multiplier complexity and delay. Also provided is the ability to use a hybrid adder based on Fast Carry Switching Adder. KSA provides quicker carry propagation, which contributes to achieving a significant 30% increase and a marked 25% reduction in power compared to standard VMs.

The proposed design represents a superior asset with regard to speed, power efficiency and hardware simplicity compared to a Booth-shift/add multiplexer-based multiplier and has the vastly superior potential to be used in high-performance, low-power.

Conclusion

An optimized 8 × 8 VM is proposed in this work and implemented by a modified Nikhilam Sutra; a modified KA is used to store the products, and the Fast Carry Switching Adder and KSA hybrid implementation of the adder is proposed to sum the products. The proposed architecture allows for great reductions in computational complexity, delay, and power consumption ahead of Vedic, Wallace, and Dadda multipliers in hardware running the standard test cases for VMs. The efficiency and speed of the proposed multiplier configuration make it excellent for FPGA-based high-performance computing needing DSPs, ML accelerators, and real-time embedded systems. The proposed architecture allows for scale in performance configurable for additional speed for more extensive chip multiplications, e.g., scaling up to 64-bit or even 128-bit multipliers. Future work can focus on quantum-inspired approaches in conjunction with dynamic approaches to power management and new approaches to hardware-software co-design. This research explores a fast, scalable, low-powered mechanism for high-performance digital arithmetic computing. Future work will focus on validating its performance across higher bit widths, such as 16 and 32 bits, ensuring its applicability in more demanding computational environments.