Introduction

Change of direction (COD) is a core technical movement in many competitive sports, such as football and basketball, and plays a crucial role in athletes’ performance. It requires athletes to quickly and accurately change their direction of movement while maintaining body balance and stability at high speeds. Statistical data show that football players can change direction more than 700 times in a single match1. Research indicates that the ability to change direction is a key indicator distinguishing elite from sub-elite athletes2,3, and its quality directly determines the effectiveness of breaking through, defending, and executing tactics in a game.

Deceleration, as one of the three phases of COD (acceleration, deceleration, and re-acceleration)4,5 ,has been proven to be the foundation of athletes’ rapid COD6,7. Rapid deceleration enables players to quickly transition to other movements, thereby facilitating the success of both offense and defense8,9. However, there are significant differences in the deceleration strategies required for different COD angles. Larger COD angles typically require longer deceleration distances, stronger braking capabilities10, and higher levels of muscle activation11. This indicates that in training, precise training should be conducted according to the characteristics of different COD angles to better meet the needs of athletes in various situations.

Current research on deceleration mainly focuses on horizontal deceleration12,13, with insufficient attention to deceleration in anticipated COD scenarios. Meanwhile, studies on COD primarily analyze the entire COD phase rather than the deceleration preparation phase, which is a component of the COD11,13. For instance, Falch et al.11 investigated the changes in muscle activation and kinematic characteristics under different approach distances and COD angles, but their research focus was not on the neuromuscular control mechanisms during the deceleration phase. Pan et al.14 used non-negative matrix factorization (NMF) to study muscle synergies during lateral cutting movements. However, their analysis unit was the entire stance phase, without specifically focusing on the key deceleration step. These limitations in methodology and analytical perspective have led to a lack of understanding of the neuromuscular control mechanisms during the deceleration phase in anticipated COD situations, thereby restricting the scientific formulation of targeted training strategies.

Muscle synergy refers to the coordinated activation of groups of muscles, which allows the central nervous system to control movement through a smaller number of core variables rather than individual muscles15,16. The coordination and stability of movement depend on the regularity of the synergy modules17. In tasks that require instantaneous coordination of multi-joint braking, such as COD deceleration, muscle synergies are also affected differently. Therefore, it is necessary to clarify the modular control characteristics of the central nervous system and the changes in lower limb muscle synergies during deceleration at different COD angles.

Based on this, this study intends to use surface electromyography (sEMG) combined with the Non-negative Matrix Factorization (NMF) method to investigate the muscle synergy characteristics during the deceleration step under different anticipated COD angles. Referring to the findings of Falch et al.11, this study will primarily focus on the differences in muscle synergy patterns during the deceleration step before speed-dominant directional changes (\(45^{\circ }\,\hbox {and}\, 90^{\circ }\)). The research hypothesis is that \(45^{\circ }\,\hbox {and}\, 90^{\circ }\) directional changes share common synergy modules during the deceleration step but exhibit significant differences in the weightings of certain muscles and their activation characteristics.

Materials and methods

Experimental participants

From April to May 2025, 16 male collegiate athletes were recruited at Wuhan Sports University (age 20.60±1.05year, height 179.60±3.94 cm, body mass 76.53±7.11 kg, 6–10 year training history, 3–5 sessions \(\hbox {wk}^{-1}\), \(120\,\hbox {min ssession}^{-1}\)). All participants were right-leg dominant and had sustained no lower-limb injuries that could affect performance in the six months preceding testing.

Prior to the testing, all participants were fully informed in writing about the potential risks and safety guidelines related to the testing procedures and signed informed consent forms. Participants wore wireless surface electromyography sensors and completed the \(45^{\circ }\,\hbox {and}\, 90^{\circ }\) COD tests. The study protocol was approved by the Ethics Committee of Wuhan Sports University (approval number: 2025101) and followed the ethical guidelines of the Helsinki Declaration.

Experimental instruments

Wireless surface electromyography was recorded with the U.S.-made Delsys Trigno™ system. Following the electrode-placement guidelines of Hermens et al.18, wireless Surface Electromyography sensors were positioned precisely on each participant. Consistent with previous work19, signals were collected from the vastus lateralis (VL), rectus femoris (RF), vastus medialis (VM), biceps femoris (BF), semitendinosus (ST), tibialis anterior (TA), and gastrocnemius lateralis (GL) at a sampling frequency of 2,000 Hz.

A three-dimensional motion capture system (SIMIMO-TION, Germany) was employed. In this study, five high-speed cameras were positioned around the COD area to record the athletes’ movements during the COD process in order to identify the changes in the phases of the COD. After the test, the video data were imported into the motion capture system analysis software and filtered using a Butterworth low-pass filter with a cutoff frequency of 10 Hz20.

Experimental protocol

Prior to the test, the subjects are required to complete the following preparations: First, the electromyography electrodes are attached. Then, a 5-minute jog is conducted to warm up, increase heart rate and body temperature. Subsequently, a 5-minute dynamic stretching is performed to activate the muscle groups, enhance joint mobility, and prevent sports injuries. After the warm-up, the subjects complete several practice trials at full speed to familiarize themselves with the testing procedure.

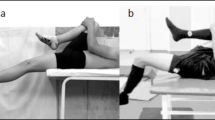
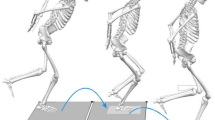
The testing method was designed in reference to the experiments conducted by Falch et al.11 and Schreurs et al.21 (see Fig. 1). The COD test included \(45^{\circ }\,\hbox {and}\, 90^{\circ }\) left turns, which were primarily executed by the participants’ dominant foot (right foot). The specific procedure was as follows: Participants started from a standing position with their front foot 20 centimeters away from the timing gate. They first sprinted 5 meters in a straight line, then turned left, and finally sprinted another 5 meters to reach the finish line. Infrared timing gates were set at both the starting point and the finish line to measure the time taken for the COD. Each direction was tested three times, and the best trial was used for subsequent EMG analysis.Because different COD angles impose distinct muscular loads10, the order of these blocks was randomized across participants to eliminate sequence effects. To prevent fatigue, participants were given adequate rest (5 min) between each trial block. The definition of the deceleration phase in this study is based on gait definitions. Specifically, the deceleration phase is defined as a braking gait cycle occurring before the plant step11, analyzing the electromyographic (EMG) indicators from the initial contact of the heel on the side opposite to the change of direction angle until the same heel contacts the ground again, covering a complete gait cycle.

Fig. 1
figure 1

Measurement setup and equipment placement.

Full size image

Data processing

The raw EMG signals were first processed with a band-pass filter of 10–500 Hz and then full-wave rectified. The rectified signals were enveloped using a 4th -order low -pass Butterworth filter with a cutoff frequency of 10 Hz22. Referring to previous research14, the signals were normalized using their maximum values. The time axis was normalized to the range of 0–100% by linear interpolation, making signals of different lengths comparable in time23. Surface electromyography (EMG) signals were collected from seven target muscles (VM, RF, VL, BF, ST, GL, TA) and processed to form a 7\(\times\)101 -dimensional feature matrix E (where m = 7 represents the number of muscles and n = 101 is the length of the time sequence) in the aforementioned order. Subsequently, the non - negative matrix factorization algorithm24 (Formula 1) was applied to decompose this matrix into a k - dimensional synergy matrix W representing muscle synergy patterns and an activation coefficient matrix H reflecting temporal activation characteristics. The feature matrix E’(Formula 2) was reconstructed through matrix multiplication (W\(\times\)H) for subsequent analysis.

$$\begin{aligned} \textrm{E} = \sum _{i=1}^{N}W_iH_i + e, \quad W_i \ge 0, \quad H_i \ge 0 \end{aligned}$$
(1)
$$\begin{aligned} E^\prime = \sum _{i=1}^{N} W_i H_i, \quad W_i \ge 0, \quad H_i \ge 0 \end{aligned}$$
(2)

Note: N is the number of muscle synergies, and e is the residual.

Subsequently, key synergy features were extracted from the original feature matrix E and its reconstructed matrix E’ of muscle activation patterns. The specific analysis indicators and criteria are as follows:

  1. (1)

    Number of muscle synergies involved: The variance accounted for (VAF) analysis method was used to compare the variance and its rate of change between the reconstructed feature matrix E’ and the original matrix E (Formula 3). The criterion for determining the number of synergies involved is a VAF value greater than 90%25,26,27.

    $$\begin{aligned} \text {VAF} = 1 - \frac{\sum _{i=1}^{m}\sum _{j=1}^{n}\left( E_{ij} - E_{ij}^\prime \right) ^2}{\sum _{i=1}^{m}\sum _{j=1}^{n}\left( E_{ij}\right) ^2} \end{aligned}$$
    (3)
  2. (2)

    Muscle Relative Weight. The contribution of muscles is derived from the decomposition of the original matrix E, which can be used to compare the differences in muscle contributions within the same synergy for different gait COD angles28.

  3. (3)

    Time to Peak Activation of Muscle Synergies. The coefficient matrix H, which is decomposed from the original matrix E, can reflect the activation intensity of each synergy. The time at which the activation intensity of each muscle synergy reaches its peak is recorded26.

  4. (4)

    Activation Level of Muscle Synergies and Overall Activation Level. The coefficient matrix H can also be used to evaluate the muscle activation intensity of each synergy and the overall activation level of the synergy structure30. The activation level of each muscle synergy is defined as(Formula 4):

    $$\begin{aligned} E_i(Activation\ Level) = \frac{1}{n} \sum _{j=1}^{n} H_{ij} \end{aligned}$$
    (4)

    Note: Hij is the element in the i-th row and j-th column of the activation coefficient matrix H, representing the activation intensity of the i-th muscle synergy at the j-th time point. n is the length of the time sequence.

  5. (5)

    Duration of Significant Activation and Co-activation of Muscle Synergies. The duration of significant activation of a muscle synergy refers to the length of time during which the activation level of a particular muscle synergy exceeds 50% of its maximum activation level. Co-activation refers to the proportion of time during which two or more muscle synergies are simultaneously in an activated state.

Statistical analysis

In this study, SPSS 21.0 software was used for statistical analysis. First, the K-means clustering algorithm was applied to cluster the synergy modules before and after the experiment. Based on this, Pearson correlation analysis (with a threshold set at r=0.6) was used to categorize the extracted synergy modules. Synergy modules with \({r}>0.6\) were grouped together to identify types of muscle synergies31. In the analysis of differences before and after the experiment, since the synergy modules participated by individuals were not entirely consistent before and after the experiment, only the synergy modules that existed in both periods were selected for paired analysis. The specific methods are as follows: First, the Shapiro-Wilk test was used for normality analysis. If the data conformed to a normal distribution, paired sample t-tests were employed to compare the differences in various indicators between the two groups; if the data did not conform to a normal distribution, the Wilcoxon signed-rank test was used for comparison. The significance level for statistical analysis was set at \({P}<0.05\), and differences were considered statistically significant.The datasets generated during this study are available in the Figshare repository: (DOI: https://doi.org/10.6084/m9.figshare.30092332.v1).

Results

Matrix decomposition results

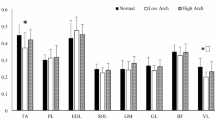
In this study, non-negative matrix factorization was performed on the electromyographic signals of the deceleration step for \(45^{\circ }\,\hbox {and}\, 90^{\circ }\) change of direction sprints. Although there were significant differences in the synergy weights between the two angles (\({P}>0.05\)), overall, two sets of synergy modules could be extracted under both COD angles (see Figs. 2 and 3). Synergy 1 was dominated by the biceps femoris, semitendinosus, and vastus lateralis, while Synergy 2 was dominated by the rectus femoris, vastus medialis, and tibialis anterior.

Fig. 2
figure 2

Synergy matrix W and activation coefficient matrix H for the \(45^{\circ }\) Deceleration.

Full size image
Fig. 3
figure 3

Synergy matrix W and activation coefficient matrix H for the \(90^{\circ }\) Deceleration.

Full size image

Matrix Decomposition ResultsWhen the Variance of Functional Activation (VFA) was greater than 90%, the number of muscle synergy modules for the deceleration steps at \(45^{\circ }\,\hbox {and}\, 90^{\circ }\) was mostly 2. When the number of synergy modules was 3, the VFA of all individuals’ synergy modules was greater than 90% (see Fig. 4). There was no significant difference in the number of synergy modules between different angles \({P}>0.05\) (P>0.05).

Fig. 4
figure 4

Variation of VFA values with the number of synergies at different angles.

Full size image

Comparison of Synergy Parameters As the COD angle increased from \(45^{\circ }\,\hbox {to}\, 90^{\circ }\), significant changes were observed in the muscle weightings across different synergy modules. In Synergy Module 1, the weighting of tibialis anterior (TA) significantly decreased (\(45^{\circ }\): 0.460 ± 0.252, \(90^{\circ }\): 0.324 ± 0.204, P = 0.029). In Synergy Module 2, the weightings of both vastus lateralis (VL) and biceps femoris (BF) showed significant increases (VL: \(45^{\circ }\) 0.203 ± 0.224, \(90^{\circ }\) 0.395 ± 0.281, P = 0.014; BF: \(45^{\circ }\) 0.142 ± 0.124, \(90^{\circ }\) 0.276 ± 0.249, P = 0.049). The weightings of the remaining muscles showed no statistically significant differences between the two COD angles (\(\hbox {P} > 0.05\)) (see Table 1).

Table 1 Muscle synergy analysis for \(45^{\circ }\,\hbox {and}\,90^{\circ }\) change of direction sprints. The table presents the mean and standard deviation (Mean±SD) of muscle activation levels for two different change of direction angles (\(45^{\circ }\,\hbox {and}\,90^{\circ }\)) and their corresponding P values, effect sizes, and other data.
Full size table

Although some muscles exhibited changes in their weights within the synergy modules across the two change of direction angles, other synergy parameters, such as the time to peak activation, Activation Level of Synergy, the proportion of Significant activation duration, the overall activation level, and the duration of co-activation, showed no significant differences (\(\hbox {P}>0.05\)) (see Table 2)

Table 2 Differences in synergy parameters. This table outlines the differences in various synergy parameters for \(45^{\circ }\,\hbox {and}\, 90^{\circ }\) change of direction sprints, including the mean and standard deviation (Mean±SD) of the parameters and their corresponding P values, effect sizes, and other data.
Full size table

Discussion

This study found that during the deceleration phase of both \(45^{\circ }\,\hbox {and}\,90^{\circ }\) COD maneuvers, two distinct muscle synergy modules were consistently identified. This structural characteristic reflects the presence of a neurocontrol template in anticipatory directional changes. The modular organization suggests that the central nervous system employs predefined synergy templates, adapting to different COD demands by modulating activation timing and intensity rather than reconstructing new synergy modules to optimize motor performance, which aligns with the findings of Pan et al.14on synergy patterns during various side-step cuttings.

Specifically, Synergy Module 1 was dominated by the biceps femoris (BF), semitendinosus (ST), and vastus lateralis (VL), while Synergy Module 2 was primarily composed of the rectus femoris (RF), vastus medialis (VM), and tibialis anterior (TA). As the COD angle increased from \(45^{\circ }\) to \(90^{\circ }\), significant changes in muscle weightings were observed during the deceleration step. At \(90^{\circ }\), the weighting of the tibialis anterior (TA) in Synergy Module 1 significantly decreased (P = 0.029). In Synergy Module 2, the weightings of the vastus lateralis (VL) and biceps femoris (BF) showed significant increases (P = 0.014 and P = 0.049). In contrast, no significant differences were found in other synergy parameters, such as time to peak activation and co-activation duration. Notably, the integration of anatomically antagonistic muscles such as the biceps femoris (BF) and vastus lateralis (VL) within the same synergy module demonstrates a distinct muscle co-activation pattern during COD maneuvers. This pattern serves as a crucial neural control strategy, closely associated with regulating joint stiffness, maintaining postural stability, and optimizing energy efficiency32,33. Therefore, while this study provides evidence for understanding the efficient and stable synergy modules control strategies employed by the central nervous system during rapid deceleration in directional changes, the specific mechanisms warrant further investigation through biomechanical modeling and analysis of neural drive signals.

When the COD angle increased, corresponding adjustments were observed in the muscle synergy patterns. During \(90^{\circ }\) COD maneuvers, the demand for hip and knee joint moments surged significantly. This study found a notable reduction in the weighting of the tibialis anterior (TA) within Synergy Module 1 (P=0.029). This phenomenon suggests that under larger COD angles, the central nervous system may temporarily reduce resource allocation for ankle joint control. Future research could integrate techniques such as electroencephalography (EEG) to further validate the adaptive mechanisms of neural control strategies.

The quadriceps serve as a key muscle group during the deceleration phase of COD maneuvers10,34, with their neuromuscular control patterns demonstrating significant alterations as the COD angle increases. Havens et al.35 found that the deceleration demands during \(90^{\circ }\,\hbox {COD}\) are not uniformly distributed across all joints, but rather place greater emphasis on the knee joint . During deceleration, the knee joint is subjected to increased shear forces and torsional moments, with anterior shear forces also rising correspondingly36. Hader et al.10 further confirmed that the vastus lateralis exhibits greater muscular activity during sharper COD maneuvers. At \(90^{\circ }\,\hbox {COD}\), generating greater lateral center of mass-center of pressure distance and subsequent lateral propulsion requires increased hip abduction35,37, which redirects the force vector more laterally relative to the knee joint center35,38 and potentially elevates knee abduction moments. Based on this context, the current study proposes that the significant increase in the weighting of the vastus lateralis (VL) within Synergy Module 2 primarily serves a dual requirement for knee joint stability: it must enhance the knee extension moment to counteract greater centrifugal loads, while simultaneously modulating the abduction moment to balance the increased knee valgus tendency resulting from lateral displacement of the center of mass. However, the above interpretation still requires future validation through integration with actual biomechanical data (such as lower limb kinematics, kinetics, and joint moments).

Numerous training studies have demonstrated that enhancing hamstring strength can effectively improve COD performance39,40. For example, Siddle et al.41 found that six weeks of Nordic hamstring curl (NHC) training simultaneously improved COD speed and reduced injury risk; Adıgüzel et al.42 also reported that an eight-week NHC program led to an 8% improvement in COD capacity. These long-term training benefits underscore the fundamental role of the hamstrings in COD movements. The observed increase in biceps femoris (BF) activation during \(90^{\circ }\,\hbox {COD}\) in this study further confirms the central functional importance of the hamstrings: it indicates that the nervous system immediately upregulates hamstring recruitment when confronting greater deceleration loads and stability demands.

During the \(90^{\circ }\,\hbox {COD}\) test, the observed significant reduction in tibialis anterior (TA) weighting within Synergy Module 143 warrants attention. As a primary ankle dorsiflexor, diminished TA activation may compromise dynamic foot stability during the deceleration phase43, consequently elevating the risk of ankle inversion injuries. Therefore, in COD training, it is necessary to specifically strengthen the control ability of the ankle joint in deceleration scenarios, such as combining dorsiflexion eccentric training with an unstable surface.

In the COD movement, athletes must rapidly decelerate their body’s momentum after high-speed sprinting before promptly reaccelerating. In this process, the eccentric contraction capacity of synergistic muscle groups such as the hamstrings, gluteus maximus, and soleus becomes the fundamental guarantee for deceleration efficiency and knee joint stability44. Among these, the hamstrings, as one of the core synergistic muscle groups, together with the gluteus maximus and soleus, form a mechanical buffer system that counteracts body inertia44, with eccentric strength serving as the key factor ensuring both deceleration performance and knee stability.

From the perspective of neuromuscular control, the activation pattern of the hamstring muscles has a significant impact on knee joint stability. Studies have confirmed that the strength ratio of the hamstrings to the quadriceps is a core indicator for reducing the risk of secondary ACL injuries45. When the knee joint approaches full extension, the shear force on the ACL reaches its peak, significantly increasing the risk of injury46. The hamstrings can generate a posterior moment, which can create a mechanical balance with the quadriceps. This co-activation pattern helps maintain the dynamic stability of the knee joint47 . Therefore, in deceleration training, it is necessary to strengthen the co-working ability and eccentric contraction ability of the core muscle groups (hamstrings, quadriceps, etc.) in different angle COD scenarios (such as Nordic hamstring training48), to meet the needs of turning.

Although this study initially revealed the impact of change-of-direction angles on the lower limb muscle coordination patterns during deceleration, several limitations still exist. First, the study only compared two change-of-direction angles, \(45^{\circ }\) and \(90^{\circ }\), and did not cover other angles or more complex multi-gait cycle deceleration scenarios. Therefore, the generalizability of the conclusions needs further validation. Second, the sample size was limited (n=16), and the differences in neuromuscular control strategies among individuals may have had some impact on the stability of the overall results. In terms of statistical analysis, this study did not perform statistical correction for multiple comparisons. Although this was based on the exploratory nature of the study to avoid missing potentially meaningful findings due to excessive correction, it may have increased the risk of Type I errors (false positives). Therefore, the significant differences reported in the text (especially those with P values close to 0.05) should be regarded as preliminary evidence, and their robustness needs to be confirmed by subsequent larger-sample validation studies. In addition, regarding electromyography collection, this study only placed a single pair of electrodes in the middle segment of each muscle. Although this is in line with the conventional operation specifications of surface electromyography, it cannot reflect the functional zoning phenomena caused by differences in fiber orientation, activation timing, and motor unit recruitment strategies in the proximal and distal parts of the same muscle. In recent years, studies on muscle regional differences by Sahinis et al.49 and on functional zoning of the semitendinosus muscle50 have indicated that this spatial heterogeneity of muscles may affect the interpretation of muscle synergies. Therefore, single-point recording may underestimate the true neuromuscular control strategies. In future studies, it is necessary to use high-density surface EMG or multi-site synchronous acquisition technology to more comprehensively and accurately characterize the overall muscle synergy features51.

Conclusion

This study, through comparative analysis of the muscle synergy patterns during deceleration steps in \(45^{\circ }\) and \(90^{\circ }\,\hbox {COD}\) sprints, has revealed the adaptive regulatory mechanisms of the nervous system in response to different turning requirements. The findings are as follows: 1) In both COD angles, two stable muscle synergy modules were identified. Synergy 1 was dominated by the biceps femoris, semitendinosus, and vastus lateralis, while synergy 2 was centered on the rectus femoris, vastus medialis, and tibialis anterior. These modules collectively contribute to deceleration, initial direction change, and joint stability maintenance. 2) As the COD angle increased from \(45^{\circ }\) to \(90^{\circ }\), the weight of the tibialis anterior (TA) in synergy module 1 significantly decreased, while the weights of the vastus lateralis (VL) and biceps femoris (BF) in synergy module 2 significantly increased. This change reflects that the nervous system, in response to the higher deceleration demands, strengthens knee joint stability while relatively reducing ankle joint control.3) During \(90^{\circ }\) changes of direction, the risk of ACL injury increases and ankle joint stability decreases. Therefore, targeted training should focus on: optimizing knee joint stability; strengthening the eccentric power of the hamstrings; and enhancing dynamic control of the ankle joint.