Introduction

Prediction and description of drug solubility has been of fundamental importance for development of advanced processing in various fields such as food and pharmaceutical industry. To control, design, and develop crystallization process as well as improving the drug solubility in aqueous media, knowing the solubility of medicines in various solvents is critical1,2,3,4. It can help one find the best solvent for production of nanomedicine via solution method. Computational techniques which are capable of predicting drug solubility in wide conditions with great accuracy, are useful since they can save time and cost for experimental measuring solid materials solubility in different solvents and conditions5.

Different computational models can be suggested for prediction of solid solubility in solvents such as thermodynamics, molecular modeling, and machine learning (ML). The advantages and disadvantages for each model have been reported4,6,7,8,9. For direct and facile estimation of drug solubility, the models based on ML are preferred provided that some measured data are available for training these models. The ML models have been extensively developed for estimation of drug solubility in various solvents such as supercritical CO210,11,12,13. Given that supercritical processing is green and can be used to prepare nanomedicines, knowing the pharmaceutical solubility in supercritical solvent (SC-CO2) is valuable for development of this unique process14.

ML models are known as robust methods for data analytics in various fields where the pattern is difficult to find out. Using these methods helps researchers uncover valuable insights and detailed patterns in complex datasets15. This empowers them to make accurate predictions and informed decisions14,16,17. This approach has been also used for correlation of drugs solubility to pressure and temperature.

In this study we used AdaBoost Regression with three models including Support Vector Regression (SVR), Linear Regression (LR), and Gaussian Process Regression (GPR). AdaBoost Regression is a popular and effective technique for building accurate regression models by combining the predictions of multiple weak regressors through an adaptive and iterative process18,19.

LR delineates a linear correlation between independent factors and the dependent variable. It applies a linear equation to the data by minimizing the sum of squared errors between the observed values in the training dataset and the model’s predicted values20. Regression baseline models like LR are computationally efficient and interpretable. When the features-target variable relationship is non-linear, its performance may be limited.

SVR represents an application of the Support Vector Machine framework specifically adapted for regression analysis. The methodology aims to delineate an optimal hyperplane within the feature space that best approximates the data distribution, subject to a defined epsilon (\(\varepsilon\))-insensitive loss function. This constraint establishes a permissible margin around the predicted output, effectively managing data deviations and thereby mitigating the risk of overfitting during model training21.

Gaussian Process Regression (GPR) is a flexible non-parametric Bayesian regression method for modeling non-linear data relationships. GPR uses functions over training data points to represent prediction uncertainty. A kernel function measures data point similarity and correlation. GPR handles noisy observations and complex data patterns. Large datasets can make its computation difficult22.

The central aim of this research is to develop accurate and reliable models to estimate these key properties, which are crucial in various industrial applications, such as pharmaceutical formulations and green chemistry processes. Drug solubility in SC-CO2 is correlated to the pressure and temperature using these models. For the first time, we developed these models to predict tolfenamic acid solubility in SC-CO2 as well as the density of supercritical carbon dioxide. Our contributions lie in the implementation and evaluation of an ensemble learning approach, namely Adaptive Boosting Regression (AdaBoost), utilizing base models including LR, GPR, and SVR. The utilization of AdaBoost allows for the enhancement of predictive capabilities, enabling accurate and robust estimations of solubility and density. Furthermore, the use of the Chimp Optimization Algorithm (ChOA) for hyper-parameter tuning optimizes model performance and is one of novel aspects of this work.

This work offers several new contributions that distinguish it from previous studies on solubility and density prediction in supercritical systems:

  • Novel integration of AdaBoost with Gaussian Process Regression (ADA-GPR): This ensemble structure has not previously been applied to model tolfenamic acid solubility or SC-CO2 density, demonstrating superior accuracy in capturing non-linear thermodynamic relationships.

  • Use of the Chimp Optimization Algorithm (ChOA) for hyperparameter tuning: This is the first study to employ ChOA for optimizing ensemble regression parameters in pharmaceutical solubility modeling, improving convergence efficiency and predictive robustness.

  • Dual-property modeling framework: Unlike earlier studies that modeled either solubility or density independently, this work simultaneously predicts both, providing a more comprehensive understanding of supercritical CO2 behavior.

  • Insightful visualization through 3D and 2D response surfaces: The generated surfaces reveal coupled effects of pressure and temperature and can serve as a foundation for future texture analysis and morphological surface studies.

Together, these innovations advance the application of machine learning in supercritical fluid modeling, offering both methodological novelty and practical value for pharmaceutical and green manufacturing processes.

Data set evaluation

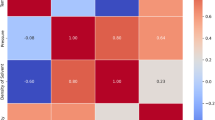
The data have been acquired from a reputable source23 and comprises four distinct variables, specifically Pressure, Temperature, Density, and Solubility of tolfenamic acid. The experimental design incorporates Pressure and Temperature as the primary independent parameters. The resultant observed outcomes, or dependent variables, are quantified as the Solvent Density and the Solubility of tolfenamic acid. Other works used the same data for this drug and developed ML models24,25. The complex, multidimensional interrelationships existing among these four variables are comprehensively illustrated in Fig. 1, which displays a pair plot (or scatterplot matrix)24,25.

Fig. 1
figure 1

Distribution of parameters in the dataset.

Full size image

Methodology

Chimp optimization algorithm (ChOA)

ChOA is a swarm-based algorithm that draws inspiration from the individual intelligence of chimpanzees and their cooperative hunting behavior driven by sexual motivation26. In this approach, each chimp represents a candidate solution within the population. The evolutionary process is guided by the top four solutions, namely, the attacker, driver, barrier, and chaser solutions. These individuals play pivotal roles in promoting exploration and exploitation in two distinct phases of the algorithm. During the first phase, the chimps collaboratively drive, block, and chase the prey to explore the solution space. In the second phase, they collectively attack the prey to exploit promising areas. The positional updates of each solution are influenced by either the four most optimal solutions or by the arithmetic mean of all four solutions, thereby facilitating a harmonious equilibrium between the processes of exploration and exploitation. In order to augment the algorithm’s performance, the position-updating mechanism incorporates six distinct types of chaotic maps. This strategic inclusion guarantees efficient evasion of local optima and expedites the rate of convergence.

The positional updates of the attacker, driver, barrier, and chaser entities are governed by a set of mathematical equations, which are employed to determine their respective locations in the given system27,28:

$$\:{x}_{attacker}={x}_{attacker}-{A}_{1}\left({C}_{1}{x}_{attacker}-{M}_{1}x\right)$$
$$\:{x}_{driver}={x}_{driver}-{A}_{2}\left({C}_{2}{x}_{driver}-{M}_{2}x\right)$$
$$\:{x}_{barrier}={x}_{barrier}-{A}_{3}\left({C}_{3}{x}_{barrier}-{M}_{3}x\right)$$
$$\:{x}_{chaser}={x}_{chaser}-{A}_{4}\left({C}_{4}{x}_{chaser}-{M}_{4}x\right)$$

In the above equations, the positions of the attacker, driver, barrier, and chaser are denoted by \(\:{X}_{attacker}\), \(\:{X}_{driver}\), \(\:{X}_{barrier}\), and \(\:{X}_{chaser}\), respectively. Additionally, \(\:{M}_{i}\) represents the chaotic map. The calculation of additional parameters, such as A and C, is performed in the following manner27:

$$\:A=2\cdot\:f\cdot\:{r}_{1}-f$$
$$\:C=2\cdot\:{r}_{2}$$

In the final position updating equation, r1 and r2 represent random variables within the range [0, 1], while f decreases nonlinearly from 2.5 to 0. The equation involves calculating the average of all top four chimps’ positions to update their respective positions28.

$$\:x\left(t+1\right)=\frac{{x}_{attacker}+{x}_{driver}+{x}_{barrier}+{x}_{chaser}}{4}$$

In this study, the mean five-fold cross-validation (CV) score was employed as the objective function for the ChOA to optimize, ensuring that the selected hyperparameters generalized well across different subsets of the dataset. The ChOA was configured with a population size of 40 chimps and a maximum of 110 iterations to balance exploration and convergence speed. The chaotic map type was set to logistic, and the control parameter f was linearly decreased from 2.5 to 0 during the optimization process to guide the transition from exploration to exploitation. Random initialization was applied to all chimps within predefined parameter bounds of each model, allowing the algorithm to effectively search the solution space for the optimal AdaBoost and base regressor hyperparameters.

Adaptive boosting (AdaBoost)

Adaptive Boosting Regression (AdaBoost) is a powerful ensemble model widely used for regression tasks. It operates by combining multiple weak regression models, also known as “base learners,” to create a strong and robust predictive model. Although models such as GPR are inherently strong learners, the term “weak learner” in the AdaBoost framework refers not to their standalone capability but to their role as base estimators whose predictions are iteratively reweighted and combined to further enhance overall model performance. Unlike traditional ensemble methods that build individual models independently and average their predictions, AdaBoost follows an adaptive approach that assigns varying weights to training samples during model training29.

The process of AdaBoost can be described as follows: It starts by fitting a weak regressor to the training data, with equal weight assigned to each data point. The weak regressor could be any regression algorithm capable of providing slightly better predictions than random chance. After the initial model is trained, AdaBoost identifies the data points that were mis-predicted with higher errors and increases their weights. This re-weighting process effectively puts more emphasis on difficult-to-predict data points in the subsequent training iteration.

The subsequent iterations involve training additional weak regressors on the updated dataset, giving higher importance to the previously misclassified samples. These new weak models are also assigned weights based on their individual performance in making predictions. The calculations progress for a pre-defined number of iterations, or until a specified level of accuracy is achieved18.

The final prediction from the AdaBoost ensemble is obtained by combining the predictions of all weak regressors in the model. The weight assigned to each base learner’s prediction depends on its performance during training. In the context of predictive modeling, it is observed that the weight assigned to a weak model in the final prediction is directly proportional to its level of accuracy. As a result, the ensemble model focuses more on the base learners that perform well on challenging data points, effectively increasing the overall predictive power of the model. Figure 2 displays the workflow of this ensemble regression algorithm.

Fig. 2
figure 2

The AdaBoost regression workflow.

Full size image

One of the key benefits of AdaBoost is its strength to manage complex relationships and interactions within the data. It can effectively capture non-linearities and outliers, making it a versatile and robust regression technique. Additionally, AdaBoost is less prone to overfitting, as it prioritizes data points that are more difficult to predict, preventing the model from overly relying on noisy or irrelevant features.

The AdaBoost framework was selected because it effectively enhances the performance of individual regressors by adaptively focusing on difficult-to-predict data points, thereby reducing both bias and variance. In this study, solubility and density relationships exhibited strong non-linearity and heterogeneity—conditions under which single models often struggle. AdaBoost’s iterative reweighting mechanism allows weak learners to be sequentially improved, resulting in a robust ensemble that captures complex dependencies without overfitting. This balance between model accuracy and generalization makes AdaBoost particularly suitable for thermophysical property prediction tasks involving interacting process variables such as temperature and pressure.

In this study, the primary hyperparameters of the AdaBoost model, including the number of estimators (i.e., the number of weak learners), the learning rate (which controls the contribution of each weak learner), and the parameters of the base regressors (such as kernel type and regularization factors for SVR, covariance kernel parameters for GPR, and coefficient weights for LR), were finely tuned using the ChOA. This optimization ensured that the ensemble achieved an optimal balance between bias and variance, leading to enhanced prediction accuracy and model robustness.

Base models development

The base models developed and utilized include Linear Regression (LR), Gaussian Process Regression (GPR), and Support Vector Regression (SVR). These models function as the core components of the ensemble learning framework implemented through AdaBoost.

The selection of these base models was motivated by their complementary modeling capabilities. LR provides a simple and interpretable linear baseline for benchmarking performance, SVR introduces flexibility through kernel functions that can model moderate non-linear patterns, and GPR offers a fully probabilistic framework that accounts for uncertainty and captures highly non-linear behaviors. Using this diverse trio within the AdaBoost ensemble ensures that both linear trends and complex, non-linear interactions among process parameters are effectively learned, thereby improving the robustness and generalizability of predictions.

Linear regression is a linear modeling technique that establishes a relationship between the input independent parameters \(\:X\) and the output variable \(\:Y\) by fitting a linear equation. The model can be represented as20:

$$\:Y={{\upbeta\:}}_{0}+{{\upbeta\:}}_{1}{X}_{1}+{{\upbeta\:}}_{2}{X}_{2}+\dots\:+{{\upbeta\:}}_{p}{X}_{p}+\:\epsilon\:$$

In this equation, \(\:{{\upbeta\:}}_{0},{{\upbeta\:}}_{1},\dots\:,{{\upbeta\:}}_{p}\) indicate the coefficients to be estimated, \(\:{X}_{1},{X}_{2},\dots\:,{X}_{p}\) stand for the input features, and \(\:{\upepsilon\:}\) denote the error term. LR endeavors to minimize the summation of squared errors between the dataset and predicted values, thereby exhibiting computational efficiency and interpretability. However, it may not perform well when the underlying relationship between the features and the target variable is non-linear30. But this shortcoming can be handled when it is used as a base model of ensemble method such as Adaboost.

For regression problems, researchers developed SVR, a variant of the general-purpose SVM. SVR aims to find a hyperplane that best fits the data, while also controlling the deviations (epsilon-insensitive zone) to achieve a balance between fitting the training data and preventing overfitting. The kernel trick is employed to transform the data into higher-dimensional space, enabling SVR to capture non-linear relationships31. SVR is effective in handling high-dimensional data and is less sensitive to outliers. However, choosing appropriate hyperparameters and kernel functions is crucial for achieving optimal performance.

GPR is a Bayesian technique that models the relationship between \(\:X\) and the target variable \(\:Y\) as a distribution over functions. The predictive distribution can be represented as32:

$$\:Y\sim\:\mathcal{G}\mathcal{P}\left({\upmu\:}\left(X\right),k\left(X,{X}^{{\prime\:}}\right)\right)$$

Here, the term \(\:{\upmu\:}\left(X\right)\) represents the mean function, while \(\:k\left(X,{X}^{{\prime\:}}\right)\) denotes the kernel function, which assesses the similarity between the data points \(\:X\) and \(\:{X}^{{\prime\:}}\). GPR is capable of capturing complex non-linear relationships in the data and effectively handles noisy observations. However, it may suffer from computational complexity for large datasets due to the need to invert a covariance matrix.

Results and discussion

The predictive models were implemented using Python 3, leveraging key libraries such as Pandas and NumPy for data manipulation and analysis. We present the results of the three models evaluated for both solubility and density prediction, namely ADA-GPR, ADA-SVR and ADA-LR. The performance of each model in predicting the solubility of tolfenamic acid in SC-CO2 is summarized in Table 1.

Table 1 Solubility prediction results.
Full size table

Table 1 demonstrates that the ADA-GPR model attained the highest coefficient of determination (R2 score) of 0.98806, signifying an exceptional connection between the predicted and actual solubility values in the dataset. Furthermore, the aforementioned analysis resulted in the attainment of the most minimal RMSE value, measuring at 1.0133E−01, and a MAE value of 7.78966E−02. These outcomes unequivocally showcase the exceptional precision and efficacy of this model in the estimation of solubility. Figures 3, 4 and 5, which are comparisons of data set and model predicted solubility values using all models, confirm the superiority of ADA-GPR.

The higher accuracy of ADA-GPR arises from its capacity to represent complex, non-linear dependencies between temperature, pressure, and solubility. In contrast, ADA-LR underperforms because it assumes linearity, while ADA-SVR’s performance is constrained by its kernel choice and sensitivity to scaling. This highlights the strong non-linear nature of solubility behavior in supercritical systems.

Fig. 3
figure 3

Data set and predicted values comparison for solubility using ADA-GPR.

Full size image
Fig. 4
figure 4

Data set and predicted values comparison for solubility using ADA-LR.

Full size image
Fig. 5
figure 5

Data set and predicted values comparison for solubility using ADA-SVR.

Full size image
Table 2 Solvent density correlations via ML.
Full size table

The predictive capabilities of each model for estimating the density of SC-CO2 are summarized in Table 2. As seen in Table 2, the ADA-GPR model has great accuracy in predicting the density of SC-CO2, with a score of 0.99265 by of R2 score metric. The RMSE for the ADA-GPR model was 9.7870E + 00, which indicates that the average error in predicting density was relatively low. The MAE of 7.81506E + 00 further highlights the high precision and reliability of the ADA-GPR model for density estimation. The comparisons of predicted and actual data for density of solvent are illustrated in Figs. 6, 7 and 8.

The ADA-GPR’s superior density predictions arise from its ability to model smooth non-linear thermodynamic relationships, unlike ADA-LR or ADA-SVR, which struggle to represent coupled temperature–pressure effects. This explains why its R² and error metrics are notably stronger across all operating conditions.

Fig. 6
figure 6

Data set and predicted values comparison for solvent density using ADA-GPR.

Full size image
Fig. 7
figure 7

Data set and predicted values comparison for solvent density using ADA-LR.

Full size image
Fig. 8
figure 8

Data set and predicted values comparison for solvent density using ADA-SVR.

Full size image

Overall, the ADA-GPR model outperformed the other models for both solubility and density prediction. It demonstrated remarkable accuracy and predictive capabilities, making it the best model for estimating the solubility of tolfenamic acid in SC-CO2 and the density of SC-CO2 itself. So, the final analysis done using this model and Figs. 9 and 10 are 3D response surfaces of both outputs using ADA-GPR. Figures 11, 12, 13 and 14 depict 2-dimensional illustrations of output patterns resulting from variations in inputs. The variations of solubility and density of solvent can be analyzed via the modeling outputs. As expected, density is reduced with increasing temperature, and rise with enhancing pressure in the process. On the other hand, it is seen that the drug solubility is increased with enhancing both parameters. For drug solubility in supercritical solvents, the influence of cross-over pressure point should be considered. This is indeed a point where the solubility variations change beyond this point. Below this point, the solubility is decreased with enhancing temperature, while above this point, the solubility is increased with enhancing temperature.

Figure 9 illustrates the three-dimensional response surface generated using the ADA-GPR model for tolfenamic acid solubility as a function of temperature and pressure. The smooth curvature of the surface reflects the strong non-linear relationship among the parameters and confirms that solubility increases with both temperature and pressure up to the crossover region. Figure 10 presents the three-dimensional response surface for SC-CO₂ density predicted by the ADA-GPR model. The figure clearly demonstrates that density decreases with increasing temperature and increases with pressure, consistent with thermodynamic expectations for supercritical fluids. Other models indicated similar behavior for tolfenamic acid based on the effects of pressure and temperature24,25.

Fig. 9
figure 9

3D response surface of solubility.

Full size image
Fig. 10
figure 10

3D response surface of solvent density.

Full size image

Figure 11 shows the two-dimensional plot illustrating how solubility varies with pressure at a constant temperature. The positive correlation indicates that higher pressure enhances solubility due to the increased solvent density, thereby improving the solvent power of SC-CO2.

Fig. 11
figure 11

Effect of pressure on solubility changes.

Full size image

Figure 12 displays the influence of temperature on the solubility of tolfenamic acid at fixed pressures. The figure highlights the crossover pressure effect, where solubility behavior transitions from a decreasing to an increasing trend with temperature depending on whether the system is below or above the crossover point25.

Fig. 12
figure 12

Effect of temperature on solubility changes.

Full size image

Figure 13 illustrates the relationship between pressure and SC-CO2 density. The nearly linear upward trend indicates that increasing pressure substantially enhances CO2 density, reflecting the compressible nature of the supercritical phase and its impact on solvation behavior.

Fig. 13
figure 13

Effect of pressure on density changes.

Full size image

Figure 14 demonstrates the effect of temperature on the density of SC-CO2 at constant pressures. As temperature rises, density decreases due to thermal expansion of the fluid, a trend that inversely correlates with solubility at lower pressures but supports it beyond the crossover region25.

Fig. 14
figure 14

Effect of temperature on density changes.

Full size image

Overall, the higher predictive power of ADA-GPR across both solubility and density tasks underscores that the studied system is governed by non-linear, interdependent variables. Sumayli et al.25 obtained the same observations for density and solubility as well. The ChOA-optimized hyperparameters further enhanced generalization by balancing bias and variance. The consistent pattern of ADA-GPR outperforming the others emphasizes that solubility and density in SC-CO2 are better represented through flexible, uncertainty-aware models rather than rigid or purely deterministic regressors.

To further assess the robustness and generalizability of the proposed ADA-GPR–ChOA framework, external validation was performed using datasets for three additional drugs—Docetaxel, Anastrozole, and Loratadine—under comparable supercritical CO2 conditions. The model maintained high predictive accuracy across these compounds, yielding R2 scores of 0.98457, 0.97283, and 0.98941 for solubility prediction, and 0.99162, 0.98735, and 0.99308 for density estimation, respectively. The close alignment of these results with those obtained for tolfenamic acid demonstrates that the developed method remains stable across diverse molecular structures and physicochemical profiles. This consistent performance confirms the model’s strong generalization capability and its potential for broader application in solubility and thermodynamic property prediction for various pharmaceutical compounds.

When compared with the recent study by Zhang et al.24, our ADA-GPR–ChOA framework achieved slightly lower R2 values on the primary dataset; however, our results demonstrated narrower and more consistent 95% confidence intervals, indicating stronger reliability of the predictions. Moreover, unlike Zhang et al., who did not report any external validation, this study extended testing to three additional drug systems—Docetaxel, Anastrozole, and Loratadine—confirming the model’s stability and superior generalizability across diverse compounds. This comparative advantage underscores the robustness and broader applicability of our approach beyond single-compound optimization.

Conclusion

This study developed and optimized ML models to predict the solubility of tolfenamic acid and the density of supercritical CO2, with hyperparameter tuning performed using the Chimp Optimization Algorithm (ChOA). Among the tested models, the ADA-GPR (AdaBoost with Gaussian Process Regression) achieved the highest predictive accuracy for both solubility and density, with R2 values exceeding 0.98. These results confirm the model’s ability to capture complex, non-linear thermodynamic behaviors. The findings demonstrate the framework’s potential for improving process design and optimization in pharmaceutical and green chemistry applications.

Future research can extend this work by scaling the model to larger and more diverse datasets, incorporating molecular descriptors and additional process parameters, and integrating it into real-time industrial solubility prediction systems. Moreover, the 3D response surfaces obtained in this study can serve as a basis for advanced texture analysis—similar to recent approaches in morphological surface characterization33 to quantitatively explore the surface features and complexity of solubility and density response patterns.