Introduction

With the increasing difficulty of mining deep mineral resources, coastal and continental shelf sea-based metal mines have now become a new direction for mineral resource mining in China1,2,3. According to statistical data, there are fewer metal mines mined on the seabed in the world, mainly in Newfoundland iron ore in Canada, Kruva iron ore in Finland, the Levant tin mine in the UK, and the Sanshandao gold mine in China4. However, subsea metal ore mining is deep mining. Due to the complex mining environment it faces, coupled with external dynamic disturbances, it may induce geological hazards and safety problems such as large-scale rock explosions in the mining area, fault slip, rock movement deformation, and sudden water, so how to safely and efficiently mine deep subsea metal ore has been a difficult problem5,6. It has been documented that in-situ stress levels in certain deep-sea mining areas, including the Clarion-Clipperton Fracture Zone, can attain 40–60 MPa, representing a high-risk environment for rockburst7. The severe implications of such geo-stresses are illustrated by the Mponeng Gold Mine in South Africa, where at approximately 3,000 m depth, stresses surpass 100 MPa and have been associated with several hundred rockburst events over the lifecycle of an individual stope8. Furthermore, substantial water inflows present a parallel hazard, as observed at the West Rand Gold Field, where inflows of up to 80,000 m³ per day resulted in complete mine flooding and caused irreversible impacts on regional groundwater regimes and surface stability9. Currently, subsea metal mines are usually mined by the filling method, and the differences in mining methods, recovery sequences and other factors are likely to affect the transfer of deep stresses and recreate the unloading environment, which in turn results in different ways of regulating deep ground pressure in subsea metal mines. Therefore, the selection of a reasonable ground pressure control mining method is of great research significance for deep mining10,11.

Recently, relevant research on the ground pressure control aspects of deep mining has been conducted by numerous scholars, and the common research methods are mainly theoretical analysis12, numerical simulation analysis13,14 and physical model tests15,16. For example, Qian et al.17 used a numerical simulation analysis method to establish a geological model of highly inclined coal seams, predicted surface subsidence and set up safe mine pillars, which effectively controlled surface subsidence and surrounding rock damage. Wang et al.18 applied the physical similarity model to study the surface settlement of mining in composite strata and summarized the movement characteristics and rules of roof settlement in various regions. To predict the ground settlement caused by deep mining, Li et al.19 established a theoretical model for the prediction and analysis of dynamic settlement in deep mining by using a theoretical analysis model, and the comparison with the measured results showed that the model was effective. Zheng et al.20 used a physical model test to obtain a bed separation grouting simulation. Cui et al.21 utilized a physical model test to study the comparative analysis of energy release under different mining methods. Li et al.22 carried out a similar material-physical model simulation of column instability damage in a slowly dipping medium-thick phosphate rock quarry, and the results showed that column damage exhibited a significant “domino effect”. Although the above research methods have achieved good results, they all have their own limitations. For example, although the theoretical analysis method can reveal the nature and law of the problem, it is mainly suitable for simple engineering problems, and it is not good for solving most complex engineering problems. Although the numerical simulation method has a high degree of flexibility and expansibility, there are several problems, such as calculation error and algorithm instability. Although the physical model test method has the directness and repeatability of the test, it may be affected by the experimental conditions and environment and has certain limitations. Because practical engineering problems are complex and changeable, a single method cannot fully reflect the actual effect. Therefore, more comprehensive, rich and reliable results can be obtained by using theoretical analysis, experimental analysis and numerical simulation analysis methods23.

To achieve a better research effect, many combinations of research methods have often been applied to analyze the ground pressure control of deep well mining by many scholars and have achieved better results24,25,26. For example, Xu et al.27 proposed a ground pressure energy control scheme through engineering verification based on a physical model test and three-dimensional numerical simulation for the energy propagation problem caused by rock mass instability in a steep slope coal seam in the Urumqi mining area of Xinjiang. Wang et al.28 used a physical model test and theoretical analysis to study the reasonable width of waterproof coal pillars and determined the optimal width of the pillars. Zhang et al.29 studied the dynamic formation movement characteristics of open pit and underground combined mining through physical model tests and numerical simulation analysis and revealed the internal movement laws of rock strata. Lu et al.30 used numerical simulation analysis and physical model tests to study the stability of the surrounding rock structure under filling mining of steeply inclined coal seams. Li et al.31used a physical model test to study the spatial distribution characteristics and evolution rules of the overlying water-conducting fault zone in deep coal mining. Zhang et al32. used a physical model test and numerical simulation analysis to study the stability of weakly consolidated water-bearing areas in coal mining and analyze the decompression effect of aquifers.

Therefore, considering the complexity of ground pressure control in deep subsea metal mining, the deformation characteristics of the physical model surface are observed by the DIC method by conducting a physical model test on the deep-960 middle mining area, and then a numerical model is established according to the engineering conditions of deep subsea mining in the Sanshandao gold mine. In addition, the test results of the physical model are compared and analyze with the numerical analysis results. Finally, the mining method is verified by field industrial tests of the ground pressure control mining method, which verifies the effectiveness and rationality of this ground pressure control method.

Engineering background

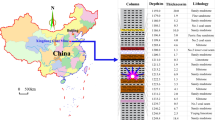
The Sanshandao gold mine has three mining areas: Xinli, Xishan and Xiling. The current production is mainly in Xinli and Xishan, while Xiling is located 2 km east of Xishan, with the ore body’s assigned elevation between − 500 and − 2600 m, which is a deep mining body and is currently in the infrastructure period. The specific location of the mine is shown in Fig. 1. The mining scale of the Xinli mine is 6,500 t/d, using the combined shaft + auxiliary ramp development method, and the mining method adopts the plate mechanized chamber-column cross-stratification filling mining method and mechanized upwards approach filling mining method. The diagram of mining method in Xishan mining area is shown in Fig. 2. After three phases of technical transformation, the mining scale of the Xishan mine is 1500 t/d, and the ramp has been extended to −960 m. Currently, the Xishan mine has been explored to the middle section of −960 m, and the deep mining of the Xishan mine faces a high-temperature, high-pressure and high-humidity operating environment and complicated mining technical conditions.

Fig. 1
figure 1

The location of the mine.

Full size image
Fig. 2
figure 2

Diagram of the mining methods used in the Xishan mining area.

Full size image

The deep ore body of the Xishan mining area has an average dip of 44° and a horizontal thickness of 40 m. The F1 fault is revealed in the middle of the ore body, and its production is basically the same as that of the ore body. The ore body of this fault is broken, which is a typical inclined thick and broken ore body. Based on geological investigations and rock mechanics tests, the upper plate is fractured serialized granitic rock, the ore body is fractured pyritic serialized granitic rock, and the lower plate is granite. The lithological stabilities of the upper and lower plates are different; moreover, the upper plate is a more broken and unstable ore body, and the lower plate is a stable ore body. A schematic diagram of the ore body and the F1 fault assignment is shown in Fig. 3.

Fig. 3
figure 3

Schematic diagram of the ore body and F1 fault assignment.

Full size image

In view of the mining technology characteristics of deep mining, large differences in the lithological stability of the upper and lower plates, high ground stress and obvious ground pressure, combined with the actual situation of the Xishan mine, based on the mining method of backfilling in the downwardsard direction after the segmentation of the upper and lower plates in the medium depth hole, a deep mining ground pressure control method was proposed. Therefore, for this mining ground pressure control method, a physical model test is carried out, and a physical model test is established. Additionally, relevant research on the mechanical behavior of the model is conducted during the excavation process.

Physical model test

For the ground pressure control model of deep subsea metal mining, the model dimensions and excavation steps were simplified to facilitate physical model test33,34.

Test system

In Fig. 4(a), the physical model test system consists of a test stand, a hydraulic servo pump station, horizontal and vertical pressure servo loading devices, a top water pressure servo loading device, a static strain test system, and a DIC. The static strain testing system includes strain gauges, testing hardware (strain signal conditioner, data collector), and professional testing and analysis software. The DIC is a method to measure the deformation by correlating the images taken before and after the deformation of the object, which has the advantages of noncontact, full field, and easy operation35,36,37,38

The DIC system includes a high-speed camera, two light sources and a set of DIC analysis software. The high-speed camera has a shooting speed of 8 fps and a resolution of 1344 × 888 pixels (1 pixel is approximately 0.22 mm). The physical model needs to be sprayed with white matte paint before the marker points, and the scattered marker points are sprayed with black matte paint. The scattered spot size is controlled at 3–4 mm, and the scattered spot spacing is 1.5 mm. The hydraulic servo loading device is composed of a hydraulic cylinder and pressure head, which can realize two loading modes of position control and force control and can apply horizontal and vertical load pressure to the model, and the maximum horizontal and vertical load is 300 kN. The hydraulic servo device applies water pressure directly to the top of the model through the combined action of vertical pressure and the hydraulic loading device.

Fig. 4
figure 4

The physical model test system: (a) schematic diagram of the DIC test system; (b) physical model diagram; (c) loading device diagram and boundary conditions; (d) physical model test system field diagram.

Full size image

Principle of similarity

The design of similar ratios for similar materials includes parameters such as the geometric ratio, density, vertical stress, horizontal stress, Poisson’s ratio, elastic modulus, tensile strength, and uniaxial compressive strength39,40,41. Equation (1) is the formula for the geometric similarity ratio.

$${K_L}=\frac{{{L_p}}}{{{L_m}}}$$
(1)

where \({K_L}\), \({L_p}\), and \({L_m}\) are the geometric ratio, the actual stope size of the project, and the dimensions of similar material models, respectively.

Equation (2) is the density similarity ratio calculation method42,43,44.

$${K_\rho }=\frac{{{\rho _p}}}{{{\rho _m}}}$$
(2)

where\({K_\rho }\), \({\rho _p}\), and \({\rho _m}\) are the density similarity ratio, the density of the actual rock mass of the project, and the density of the similar material model, respectively.

Equation (3) is the stress similarity ratio calculation.

$${K_{\sigma s}}=\frac{{{\sigma _{ps}}}}{{{\sigma _{ms}}}}={K_L}{K_\rho }$$
(3)

where \({K_{\sigma s}}\), \({\sigma _{ps}}\), and \({\sigma _{ms}}\) are the stress similarity ratio, the stress on the actual rock mass of the project, and \({\sigma _{ms}}\) is the stress on a similar material model, respectively.

By calculating and analyzing the ground stress data from multiple measurement points in each middle section of the Sanshandao mine, the regression characteristic Eq. (4) to (6) for the variations in \({\sigma _{\hbox{max} }}\), \({\sigma _{\hbox{min} }}\), and \({\sigma _z}\) with burial depth can be obtained, and the results are shown below:

$${\sigma _{\hbox{max} }}=0.11+0.0539H$$
(4)
$${\sigma _{\hbox{min} }}=0.13+0.0181H$$
(5)
$${\sigma _z}=0.08+0.0315H$$
(6)

where H is the burial depth of the measurement point, in m.

Physical model test Preparation and steps

In the test process, the test model should first be constructed in the model box according to a certain similarity ratio and then loaded according to the predesigned loading mode45,46,47.

Figure 4(b) and Fig. 4(c) show the physical model diagram and the physical model loading device schematic, respectively. As shown in Fig. 4(b), the model test bench is 2500 mm long and 2100 mm high, and it is in the form of a frame structure, which is welded by steel sections and has sufficient rigidity. A hydraulic cylinder for applying a horizontal force is fixed to the test frame column at one end, and two hydraulic cylinders for vertical loading are installed on the test frame beam at the top. The maximum model box size is 1600 mm in length, 800 mm in width and 200 mm in height. According to the situation of the Sanshandao gold mining process, the mining prototype in this experiment is a 112 m long and 45 m wide mining area, and some widths need to be reserved from the simulated mining area to the edges of both sides of the model. In addition, the geometric similarity ratio KL =150 is used in this experiment, namely, the simulated excavation area with a central length of 746.67 mm and a width of 300 mm is selected in the similar model.

As shown in Fig. 4(c), the bottom of the water tank at the top of the physical model is not closed, and a rectangular hollow sealing rubber is fitted between the bottom of the water tank and the top of the model specimen. The seal rubber ring is 10 mm thick, as large as the bottom of the water tank, 1300 mm × 200 mm, and the rectangular hollow size is slightly smaller than the size of the top of the model specimen, 1100 mm × 120 mm. The width of the ring band of the seal rubber ring is 30 mm, which is slightly larger than the thickness of the water tank wall to ensure that the water tank wall completely passes through the seal rubber ring on the top of the model and that the body of water inside the tank is directly on the top of the model. In this test, construction gypsum with quartz sand and water is taken as the raw material for the preparation of similar materials. According to a physical model test with construction gypsum and quartz sand as similar material raw materials, a quartz sand: gypsum ratio of 1:6 was configured with similar simulation material mechanical indexes: bulk density of 1.7–2.0.kN/m3 and compressive strength of 0.4–2.2 MPa. According to the physical and mechanical indicators of the original rock at the site, the bulk weight is 2.6 kN/m3, and the compressive strength is 80–127 MPa. From formula (2) and formula (3), the density similarity ratio \({K_\rho }\) is selected as 1.44. Therefore, the ratio of construction gypsum to quartz sand is selected as 1:6, and the prepared similar material has a bulk weight of 1.8 kg/m3 and a compressive strength of 0.5 MPa. The similar materials can effectively simulate the failure behavior of rock masses. The Physical model test system field diagram is shown in Fig. 4(d). And the stress-strain curves of specimens are shown in Fig. 5. And the Physical and mechanical properties of similar materials is shown in Table 1.

Table 1 Physical and mechanical properties of similar materials.
Full size table
Fig. 5
figure 5

Stress-strain curves of specimens: (a) the similar materials; (b) the orebody(granite).

Full size image

In a physical model test, the prototype depth of the Sanshandao gold mining area was 960 m, and according to Eq. (4)~(6), \({\sigma _{\hbox{max} }}\) is 51.854 MPa, \({\sigma _{\hbox{min} }}\) is 17.506 MPa, and \({\sigma _z}\) is 30.32 MPa. According to Eq. (3), the stress similarity ratio \({K_{\sigma s}}\) is 216. According to the model similarity principle, the physical model should be subjected to a compressive force of 0.240. In the horizontal direction, the force area in the horizontal direction is 0.16 m2; namely, the equipment should apply a force of 38.4 kN in the horizontal direction of the model. Similarly, the vertical direction should be subjected to a compressive force of 0.140 MPa, and the force area in the vertical direction should be 0.32 m2; namely, the equipment should exert a force of 44.92 kN in the vertical direction of the model.

To better study and analyze the rock stability under the mining disturbance of the physical model, strain gauges were installed around the physical model test to verify the strain. In this experiment, a total of 16 strain gauges were designed and arranged around the physical model, numbered from 1 to 16, among which 5 strain gauges were arranged at the top of the model, numbered from 1 to 5, 6 at the side helpers, numbered from 6 to 8 for the left helper and 14 to 16 for the right helper, and 5 strain gauges were arranged at the bottom, numbered from 9 to 13, as shown in Fig. 6. Due to the strain gauges falling off at some locations (at 14 ~ 16) during the experiment, the actual arrangement of the strain gauges and excavation-filling sequence is shown in Fig. 6, with immediate filling after mining, followed by the next excavation step after filling, where the specific excavation-filling sequence is 1–12. The excavation-filling sequence diagram of the physics model test is shown in Fig. 7.

Fig. 6
figure 6

Schematic diagram of the actual arrangement of the strain gauges and excavation scheme.

Full size image
Fig. 7
figure 7

Diagram of the excavation-filling sequence used in the physics model test.

Full size image

Numerical simulation

FLAC3D is widely used to solve complex engineering problems48,49,50. For the mining process of the relatively solid ore body in the lower plate of the Sanshandao deep ore body by a medium-deep hole drop and subsequent filling mining method after splitting the upper and lower plates, a three-dimensional numerical model is established in this paper to explore the stress release in the back mining ground under this ground pressure control method and to study the effect of back mining ground pressure control.

Modelling

Due to the complexity of the deep mining site process of the Sanshandao gold mine subsea metal ore, the model was simplified. The established numerical model is 224 m in length along the vertical strike of the ore body and 174 m in the vertical direction with the ore body as the centre. The X direction has been selected as the vertical strike of the ore body, while the Y direction is vertical and the Z direction is along strike of the ore body. In the established stope model, fourteen chambers are arranged along the direction of the ore body. Each chamber is 8 m in width, 55 m in thickness, 87 m in height, and 6 m in the top and bottom columns. Moreover, a 3D numerical model was established, and the ore body model was divided into 130 groups, including 1 group of top columns, 1 group of bottom columns, and 128 groups in the ore body area. Finally, the ore body model is meshed again, 2 m is divided into a grid, and the computational grid model is shown in Fig. 8.

Fig. 8
figure 8

Internal grouping and meshing of ore body.

Full size image

Mechanical parameters of materials

The numerical analysis in this research was implemented with FLAC3D. The Mohr-Coulomb elastoplastic constitutive model was utilized to represent the rock mass, a model prevalent in geotechnical engineering for its capability to replicate both pre-yield elastic deformation and post-yield plastic failure. The yield criterion of the model is defined by the material’s cohesion (c) and internal friction angle (Φ). And the mechanical parameters of the materials are shown in Table 1.

Table 2 Mechanical parameters of the materials.
Full size table

Simulation of the excavation process

In the excavation process, stope number 1 was first mined and then immediately filled. Then, stope 2 was mined and immediately filled to complete the 18 mining steps, as shown in Fig. 9, to represent the model excavation sequence.

Fig. 9
figure 9

Excavation sequence of the 3D numerical model.

Full size image

Results and discussion

Analysis of the physical model test results

The strain changes at the monitoring points of the top slab during the test are shown in Fig. 10. It can be concluded that the strains of monitoring points 1 and 5 decrease after the first filling is completed in steps 1 and 2, while the strains at monitoring point 3 continue to increase steadily. In the remaining 10 steps, the strain patterns at the three monitoring points of the top slab are basically the same. During the excavation process, the strain increases significantly, while it remains relatively stable after filling, which proves the good effect of the filling body on ground pressure control. Its strain reaches the maximum value during the excavation process of step 7 and step 8, and the maximum strain values at the three monitoring points are 4.2 × 10− 4, 6 × 10− 4, and 2.9 × 10− 4. In addition, it can be concluded that among the influences of the test on the strain of the rock mass in the roof, the influence on monitoring point 5 is higher than that on monitoring point 1, and the influence on monitoring point 1 is higher than that on monitoring point 5. It can be seen from the values that the test has minimal interference on the rock mass in the whole roof and will not cause damage.

Fig. 10
figure 10

Strain diagram of the top plate monitoring points during the whole excavation step.

Full size image

The strain diagram of the lateral monitoring points during the whole process of the excavation step is shown in Fig. 11. Through the overall analysis of all the monitoring points, the change pattern of the strain curve of each monitoring point is similar, showing a low-high-low change pattern. The maximum strain value in each of these steps appeared after excavation when the exposed area was the largest. With the completion of filling, the expansion and supporting effect of the filling body decrease the strain. Among all monitoring points, the strain change of monitoring point 6 is the largest, indicating that excavation has the greatest impact on monitoring point 6. The strain change at monitoring point 8 is the smallest, indicating that the excavation has the least influence on monitoring point 8.

Fig. 11
figure 11

Strain diagram of lateral monitoring points during the whole excavation process.

Full size image

The strains of the bottom monitoring points during the whole excavation step with respect to the excavation time are shown in Fig. 12. Through the overall analysis of all the monitoring points, the change pattern of each monitoring point is similar, showing a low-high-low shape in each excavation step, and the maximum strain generally appears after excavation. With the completion of filling, the strain gradually decreased, but the overall trend increased. Among them, the strain change at monitoring point 13 is the largest, and the strain change at monitoring point 9 is the smallest, indicating that the excavation disturbance at monitoring point 13 is the largest and the disturbance at monitoring point 9 is the smallest.

Fig. 12
figure 12

Strain diagram of the bottom plate monitoring points during the whole excavation step.

Full size image

The numerical simulation results analysis

Vertical stress variation analysis

Figure 13 represents the vertical stress at excavation steps 1–9. When excavation is carried out, the stress concentration area is mainly concentrated in part of the excavated filled area, and as the excavation steps continue, the stress concentration phenomenon in part of the excavated filled area is lifted. During excavation steps 1–3, the top and bottom column stress concentration phenomenon is not obvious, and after excavation steps 4–6, the stress concentration area is smaller. As mining proceeds to steps 7–9, the stress concentration phenomenon of the surrounding rock on both sides of the stope is further highlighted, and the stress concentration area continues to expand.

Fig. 13
figure 13

Excavation steps 1–9 vertical stresses.

Full size image

As shown in Fig. 14, the vertical stress concentration phenomenon is more serious in excavation steps 10–12, and upwards stress concentration occurs in the bottom plate of certain mine houses. In excavation steps 13–15, the vertical stress direction is vertically downwards, and the downwards deformation of the stope roof needs to be noted at this time. In addition, after backfilling in step 17 and mining in step 18, the stress concentration area of the peripheral rock on both sides of the ore body was reduced, showing a better effect of ground pressure control.

Fig. 14
figure 14

Excavation steps 10–18 vertical stresses.

Full size image

The vertical stress evolution calculation results show that the verticalstress is relatively small, the stress distribution is relatively uniform, the local stress concentration phenomenon is relatively insignificant, and the control effect of the ground pressure control method is relatively good.

Horizontal stress variation analysis

The horizontal stress variation diagram of steps 1–9 of the excavation step is shown in Fig. 15. Figure 15 shows that with the progress of excavation steps 1–3, the horizontal stress concentration area continues to expand, and the stress concentration area is mainly concentrated in the backfill and the roof and bottom plate of the mine house, and the stress concentration value of the backfill body is smaller than that of the roof and bottom plate of the mine house. In this case, all the values of the horizontal stress concentration area are negative, and the direction is the opposite direction of the z-axis. With the excavation steps 4–6, the stress concentration area does not expand significantly, but large stress concentration areas appear on both sides of the mining house. However, it is observed that extensive areas of concentration of stress emerge on both sides of the mining house. During the excavation process, from steps 7 to 9, the horizontal stress concentration area expands, and the horizontal stress concentration phenomenon occurs on both sides of the mine.

Fig. 15
figure 15

Excavation steps 1–9 horizontal stresses.

Full size image

Figure 16 illustrates the horizontal stress variation diagram for steps 10–18 of the excavation process. As illustrated in Fig. 16, with the progress of the excavation steps, the horizontal stress concentration areas have appeared and are constantly expanding, and the horizontal stress concentration areas are mainly concentrated in the areas that have been mined and filled and the surrounding areas of the mining houses. Concurrently, the horizontal stress concentration area is more extensive and the horizontal stress value is higher during the 10–12 steps of excavation. Additionally, the horizontal stress concentration area of some filling areas is interconnected. During the excavation steps 13–15, the horizontal stress concentration area continues to expand, and the backfill between the ore houses exhibits a pronounced stress concentration phenomenon. During the excavation steps 16–18, the horizontal stress concentration area of the entire model attains its maximum extent, with the greatest concentration occurring in the filling area and the surrounding rock.

Fig. 16
figure 16

Excavation steps 10–18 horizontal stresses.

Full size image

The results of horizontal stress evolution show that the vertical stress shows a trend of concentrated expansion with the continuous progress of the excavation steps, and the local stress concentration phenomenon is relatively insignificant on the whole, and the initial stress in the excavation process is mainly concentrated in the backfill and the roof and bottom of the mine. In the middle stage of the excavation process, the horizontal stress is mainly concentrated in the area that has been mined and filled and the area around the mine house that is being mined. In the subsequent phase of the excavation process, the area of horizontal stress concentration continues to expand, with the backfill between the ore houses exhibiting a distinct stress concentration phenomenon. The horizontal stress is predominantly concentrated within the filling area and the surrounding rock, with an overall effective control of ground pressure.

Comparison of the results of numerical simulation and physical model tests

The conclusion regarding the agreement between the physical model’s strain measurements and the numerical stress contours is supported by the fundamental constitutive relationship used in the simulation. The numerical simulation employs the Mohr-Coulomb elastoplastic constitutive model, which intrinsically couples the stress state with the development of plastic strain through its yield criterion. This intrinsic relationship thereby ensures a close spatial correspondence between the high-stress zones predicted by the simulation and the large-strain zones observed in the physical experiments. This observed alignment provides strong, albeit indirect, validation that the numerical model is accurately replicating the internal mechanical response of the physical model, as the simulated stress fields are the direct computational result of the deformation patterns that the physical model visually exhibits.

As seen in Fig. 17, according to the numerical simulation horizontal stress cloud diagram, the surrounding rock on both sides of the excavation area is under compressive stress, and there is stress concentration. Based on the direction of compressive stress, it can be determined that the surrounding rock on both sides tends to move towards the excavation area. In addition, the horizontal strain values range from 4.9 × 10− 3~5.6 × 10− 3 on both sides of the horizontal strain contour diagram of the physical model test, which can be judged to be consistent with the numerical simulation of the horizontal stress contour diagram according to the strain direction, which proves the consistency between the numerical simulation and physical model test.

In addition, according to Fig. 17, after excavation and filling, the horizontal strain of the surrounding rock on both sides of the excavation area is negative, the value is small, and the distribution area is small, which indicates that the high ground stress of the surrounding rock during excavation has been well controlled.

Fig. 17
figure 17

Comparison of numerical simulation horizontal stress and similar simulation horizontal strain after completion of mining: (a) Numerical simulation horizontal stress cloud diagram; (b) Similar simulation horizontal strain cloud diagram.

Full size image

As seen in Fig. 18, according to the vertical stress cloud of the numerical simulation analysis, there are obvious stress concentrations on both sides and below the excavation area after the completion of excavation and backfilling, especially the concave compressive stress below the excavation area, which coincides with the vertical strain in the negative direction below the excavation area of the physical model test, which also proves the consistency between the numerical simulation and physical model test.

In addition, Fig. 18(a) shows that there are vertical stress concentrations in the surrounding rock on both sides of the stope excavation area, while the vertical strain on both sides of the excavation area in the vertical strain diagram of the physical model test is a small vertical strain, and the value range is between − 5.2 × 10− 4 and − 1.8 × 10− 3, which is somewhat different.

According to Fig. 18(b), the strain around the excavation area changes to a lesser extent after excavation and backfilling are completed, which indicates that the high ground stress in the surrounding rock is well controlled during the excavation process.

Fig. 18
figure 18

Comparison of numerically simulated vertical stress and similar simulation vertical strain after mining is completed: (a) Numerical simulation vertical stress cloud diagram; (b) Similar simulation vertical strain cloud diagram.

Full size image

As shown in Fig. 19, according to the numerical simulation maximum principal stress distribution cloud diagram, the surrounding rock in the edge area of the numerical simulation model is mainly affected by compressive stress, while the edge of the excavation and filling area of the physical model test observes a positive maximum principal strain concentration with values ranging from 7.0 × 10− 3 to 8.4 × 10− 3, indicating that this area is subject to compressive stress, which is consistent with the physical model test where the maximum principal strain is all in the negative direction. The test results are consistent with those of a physical model test where the maximum principal strain is in the negative direction.

Moreover, both the physical model test and the numerical simulation model are affected by compressive stresses in the parts outside the excavation area, and the results of the physical model test and the numerical simulation analysis are consistent.

Fig. 19
figure 19

Comparison of the maximum principal stress of the numerical simulation and the similar simulation maximum principal strain after the completion of mining: (a) Numerical simulation maximum principal stress cloud diagram; (b) Similar simulation maximum principal strain cloud diagram.

Full size image

As shown in Fig. 20, the surrounding rock at the edge of the numerical simulation is mainly affected by compressive stress, which coincides with the physical model test where the maximum principal strain at the edge of the excavation and filling area is in the negative direction.

From Fig. 20(a) and Fig. 20(b), the surrounding rock outside the excavation area is subjected to larger compressive stress, while in the area outside the excavation area of the physical model test, the left and right sides are affected by slight tensile stress, the top and bottom are more affected by compressive stress, and there is a certain difference between the two, but the results of the minimum principal strain (compressive stress) in the negative direction of the arc that exists below the mining area are in complete agreement.

Fig. 20
figure 20

Comparison of the minimum principal stress of the numerical simulation and the similar simulation minimum principal strain after the completion of mining: (a) Numerical simulation minimum principal stress cloud diagram; (b) Similar simulation minimum principal strain cloud diagram.

Full size image

Engineering application and validation

The determined deep mining ground pressure control method was adopted for the field industrial test, and after the field research, the test area was selected between the 1600 line and 1800 line from the − 915 m to −975 m level. The test area is divided into three zones: the first mining false top mining zone, the first mining site of the lower plate medium-deep hole and the high section mining site of the lower plate medium-deep hole. The specific test area is shown in Fig. 21. The industrial field test shows that the proposed ground pressure control method is scientific and reasonable, and the average production capacity of intelligent mining with medium-deep hole segmented empty field subsequent backfilling is 385 t/d, the mining loss rate is 7.62%, the mining depletion rate is 6.18%, and 53,400 t of ore is safely extracted during production at the test site. During the indicator calibration phase conducted in the experimental mining sector, a total of 53,400 metric tons of ore were successfully extracted under controlled safety conditions. The extracted material exhibited an average gold grade of 2.35 g/t, corresponding to a total contained metal content of 125.49 kg. Applying a metallurgical recovery rate of 94%, which reflects standard processing performance for this deposit type, the recoverable gold is calculated to be 117.96 kg. Based on the current gold price of 782.7 RMB/g, the potential gross revenue from metal sales is estimated at approximately 92.33 million RMB. Assuming project implementation proceeds as planned, with operating costs maintained within 430 RMB/t through optimized mining and processing strategies, the projected pre-tax profit would reach approximately 69.37 million RMB, demonstrating favorable economic viability for the mining method under evaluation. To facilitate a comparison of the medium and deep hole test area, the area of the Sanshandao gold mine was originally used by the approach method, with an average production capacity of 175t/d for the approach and fill mining method. Consequently, the production capacity has been increased from 175t/d to 385t/d of the original approach method, which has greatly improved the stope production capacity, and the field industrial test has achieved the expected results, which shows that the ground pressure control mining mode has certain promotion and application value, and possesses favourable engineering practicability.

Fig. 21
figure 21

Cross-section of the test stope.

Full size image

Study limitations and discussion

However, there are certain limitations to the study. Firstly, this study did not account for the influence of the F1 fault. Future work would benefit from a detailed investigation into the fault’s effects, particularly by examining the spatial relationships between the fault, backfill, and surrounding rock mass. And the guidance provided by the new model in relation to engineering applications is a challenging area of investigation. Secondly, this paper focuses on the ground pressure regulation techniques employed in the deep mining of subsea gold deposits at the Sanshandao mine. Further studies on the general adaptability of the new ground pressure control mode could be conducted by analysing the results of similar deep mining operations at other metal mines. Besides, the detachment of strain gauges at locations 14–16 during the experiment resulted in the loss of strain data from these critical zones, particularly in the vicinity of the F1 fault. This gap potentially limits a complete understanding of the local strain field and its evolution during the failure process. To solve this limitation, the strain fields in these regions can be reasonably interpreted by combining numerical simulation results with data from adjacent functional strain gauges in future studies. Furthermore, a synthesis of the regulations governing the novel ground pressure control mode in deep mining could provide more comprehensive guidance for future deep mining operations.

Conclusion

  1. (1)

    The results of the numerical simulation indicate that the vertical stress is relatively minor throughout the excavation process, with a relatively uniform stress distribution and insignificant local stress concentration. Nevertheless, as the excavation process continues, the horizontal stress demonstrates a tendency towards concentrated expansion, with the local stress concentration phenomenon remaining relatively insignificant. The results of the numerical simulation demonstrate that the novel mining mode is effective in controlling ground pressure.

  1. (2)

    The analysis results of the physical model test show that the similar material model has an obvious disturbance to the surrounding area during the excavation process, and the strain value continues to increase as the disturbance gradually intensifies with continuous excavation. Meanwhile, the backfilling of the extraction area helps to control the further development of the strain at the monitoring points around the excavation area, which indicates the good effect of the backfilling body on ground pressure control. In addition, the strain values at the monitoring points are approximately one in ten thousand, indicating that this ground pressure regulation mining method has a good control effect on the high ground stress.

  1. (3)

    The field industrial test shows that the production capacity of continuous mining after filling in the downwards directional segmented vacant field in the lower plate reaches 385 t/d, the mining loss rate is 7.62%, the mining depletion rate is 6.18%, and 53,400 t of ore is safely extracted during production at the test site, which also shows that the ground pressure control method is reasonable and effective. This method can be effectively applied to subsea and deep underground mining, where it demonstrates a significant capability in optimizing stress distribution and mitigating hazardous stress concentrations, thereby enhancing overall geomechanical stability.