Introduction

The global energy crisis and environmental degradation have intensified the shift from conventional energy sources to renewable alternatives1,2. In aeronautical applications, lithium-ion batteries have become the primary power source for unmanned aerial vehicles (UAVs) owing to their high energy density, extended cycle life, and lightweight properties3,4,5. However, UAV performance and safety are heavily dependent on accurate state of charge (SOC) estimation, as SOC directly governs operational efficiency, mitigates power failures, and prolongs battery lifespan6,7. SOC prediction is inherently complex due to dynamic factors such as temperature fluctuations, aging effects, and varying operational conditions, which alter internal battery dynamics8. Consequently, precise SOC estimation is essential for optimizing charge/discharge cycles and enhancing overall system reliability9.

Existing SOC prediction methods, including recurrent neural networks (RNN) and long short-term memory (LSTM) models, have demonstrated partial success10 but remain limited by their inability to explicitly model temporal dynamics and adapt to rapidly changing UAV flight conditions11. These approaches often focus solely on battery-specific parameters while neglecting temporal dependencies, further compromising accuracy. To address these challenges, a temporal-aware transformer networks (TATNS) is proposed, integrating localized spatio-temporal feature extraction with long-range dependency modeling. The framework employs a temporal encoder and a sliding window-based multi-output mechanism to improve adaptability and prediction robustness in real-world UAV applications. To rigorously evaluate the proposed framework, extensive experiments are conducted on a publicly available, large-scale dataset.

This study presents three key contributions:

  1. (1)

    A hybrid temporal-aware transformer networks is developed, combining transformer architecture with deep feature fusion to enhance SOC prediction accuracy. TATNS achieves a mean absolute percentage error (MAPE) of 4.320%, outperforming the best baseline by 7.97%.

  2. (2)

    A temporal enhancement strategy is introduced to capture time-series dependencies without additional parameters. This method significantly strengthens temporal representation and enhances prediction reliability.

  3. (3)

    A multi-output sliding window framework is proposed to overcome the limitations of single-output forecasting. This framework effectively aligns predictions with the practical operational requirements of UAVs.

The remainder of this paper is structured as follows: Sect. 2 reviews existing SOC estimation methods. Section 3 details the proposed TATNS framework and theoretical foundations. Section 4 outlines experimental methodologies, while Sect. 5 presents results and analysis. Finally, Sect. 6 concludes the study and discusses future research directions.

Literature review

Generally, the SOC of a battery is defined as the ratio of the remaining capacity to its total capacity12,13 is critical for lithium-ion battery management. Existing SOC estimation methods are broadly categorized into coulomb counting14, open circuit voltage (OCV) analysis15, model-based approaches16, and data-driven techniques17. This study focuses on data-driven methods due to their adaptability and accuracy potential.

The coulomb counting method estimates SOC by integrating the current flowing into and out of the battery over time. Kong et al.18 proposed a smart prediction method based on coulomb counting method to improve the prediction accuracy. Zhang et al.19 proposed a model-free state of health (SOH) calculation method by fusion of coulomb counting method and differential voltage analysis. While this method is relatively straightforward and easy to implement, it is susceptible to cumulative errors arising from inaccuracies in current measurement and variations in battery capacity due to factors such as temperature fluctuations. These cumulative errors can significantly degrade the reliability of SOC estimates over prolonged usage periods. Furthermore, the method is highly sensitive to initial SOC conditions, which are often difficult to determine accurately.

The OCV method estimates SOC by measuring the battery voltage when it is in a resting state and comparing it against a predefined lookup table or mathematical model. Pattipati et al.20 proposed a robust normalized OCV modeling approach that dramatically reduces the number of OCV-SOC parameters and as a result simplifies and generalizes the BFG across temperatures and aging. Birkl et al.21 present an OCV model for lithium-ion cells which can be parameterized by measurements of the OCV of positive and negative electrode half-cells and a full cell. Although this method is simpler compared to coulomb counting, it is also influenced by temperature variations and the dynamic aging properties of the battery22. Tian et al.23 propose a method to estimate the results of offline OCV based ageing diagnosis, the error is less than 1%. Moreover, the nonlinear relationship between SOC and OCV necessitates precise calibration and high-precision sensors to minimize prediction errors, thereby imposing stringent requirements on the prediction conditions24. The method assumes that the battery reaches a fully relaxed state, which is impractical in dynamic UAV applications where continuous operation prevents sufficient rest periods. These limitations hinder the scalability and adaptability of the OCV method in real-world scenarios.

To enhance SOC prediction accuracy, various model-based methods have been proposed, including electrochemical models25, equivalent circuit models (ECM)26, Kalman filter-based models27, and hybrid models. For instance, Lai et al.26 introduced a first and second-order resistance-capacitance model to capture the dynamic behavior of the battery. Lim et al.28 developed a fading Kalman filter approach to estimate OCV from model parameters, achieving SOC prediction errors below 3%. Additionally, Li et al.29 proposed an adaptive unscented Kalman filter based on an extended single particle model, which accurately and robustly estimates SOC, lithium-ion concentration, and potential. Despite their accuracy, model-based methods are often overly complex, particularly when dealing with the nonlinear characteristics of battery systems. These methods require specific calibration for each battery type or configuration, limiting their generalizability across different systems. Additionally, they struggle to adapt to new battery technologies or changing environmental conditions, which is a critical limitation for UAV applications operating in dynamic and unpredictable environments.

Coulomb counting, OCV, and model-based approaches are primarily intended to estimate the current SOC under quasi-steady-state conditions using instantaneous or short-term historical measurements. These methods are inherently reactive and cannot predict future battery states. In contrast, SOC prediction aims to forecast the SOC over multiple future steps. For UAVs operating in real-world scenarios, multi-step SOC prediction is essential for proactive energy allocation, safe path replanning, and real-time battery health monitoring. The use of data-driven methods enables more accurate prediction of multi-step SOC data. Data-driven methods, encompassing machine learning and neural network techniques, offer a promising alternative by eliminating the need for intricate modeling processes. These methods directly establish and train a mapping between monitored data, such as voltage, current, temperature, and SOC30. The reliance solely on directly measurable parameters allows for greater flexibility and the potential to generalize across various battery types for SOC prediction. Within the realm of machine learning, Li et al.31 employed the least squares support vector machine (LSSVM) to develop a battery model, while Zhao et al.32 introduced an extreme learning machine (ELM) approach for SOC prediction, constructing an ECM based on a recursive least squares method. Their results demonstrated that the ELM-based model significantly outperformed traditional methods, reducing the mean absolute error (MAE) and root mean square error (RMSE) by at least 50%. Furthermore, Zhou et al.33 proposed a combined data-driven modeling approach that integrates LSSVM with particle swarm optimization and unscented Kalman filter, achieving maximum SOC errors constrained to within 0.5% under various operating conditions. However, traditional machine learning techniques often require manual feature extraction, which can introduce unnecessary errors and limit model performance. Moreover, these methods typically focus on short-term dependencies and fail to capture long-range temporal patterns effectively. This limitation is particularly problematic in UAV applications, where dynamic operating conditions demand robust multi-output predictions.

Deep neural network approaches offer substantial improvements over traditional machine learning methods by obviating the need for manual feature extraction and thereby enhancing the capability to capture the complex nonlinear features inherent in lithium-ion batteries34,35,36. For example, Song et al.37 developed a hybrid CNN and LSTM network to infer SOC from measurable data, achieving a maximum average error below 1.5% and a maximum RMSE below 2%. Chatterjee et al.38 proposed a Bi-LSTM model to make real-time decisions on power distribution and operation modes. Liu et al.39 introduced a Multiscale and fast Fourier gating mechanism for sodium-ion batteries, integrating multi-scale temporal branches with a fast Fourier transform based gating mechanism to suppress high-frequency noise and enhance modeling of nonlinear voltage-SOC dynamics. Separately, a MConvTCN-Informer framework40 combines multi-scale temporal convolutions with the Informer’s efficient attention to jointly capture short-term fluctuations and long-range dependencies in lithium-ion cells. Existing research underscores that CNNs are adept at extracting essential features from data, while transformer networks excel in capturing comprehensive information from entire input sequences, particularly benefiting the handling of long-sequence data. Consequently, both CNN and transformer models exhibit significant advantages in enhancing the accuracy and reliability of battery SOC predictions. Despite advancements, existing frameworks often neglect temporal dependency awareness-a critical gap under fluctuating UAV conditions. To address these limitations, the proposed TATNS integrates a parameter-efficient temporal encoder for explicit time-series dependency modeling. Unlike single-output methods, TATNS employs a sliding window-based multi-output strategy to predict SOC across 60 future time steps, aligning with real-world battery management system (BMS) requirements. This approach enhances adaptability and robustness in dynamic environments, as validated in subsequent experiments. A summary of reviewed methodologies is provided in Table 1.

Table 1 Comparison of available relevant studies.
Full size table

Methods

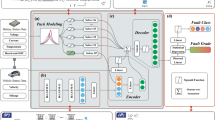
The main objective of the proposed TATNS model is to predict SOC from historical data while overcoming the limitations of existing methods. A deep learning architecture is developed by integrating CNN, temporal encoding, transformer, and a Kalman filter to improve accuracy and adaptability. Accurate and timely SOC prediction is essential for maintaining battery operation and planning maintenance, especially in dynamic UAV environments where conditions change rapidly. In this study, typical UAV battery models are selected as the source of battery data. A detailed description of the TATNS architecture and its components is provided in the following sections. The overall framework is shown in Fig. 1. As shown in Fig. 1, the overall process consists of four consecutive stages: (1) local spatio-temporal feature extraction through 1D CNN, (2) explicit time coding, (3) long-distance dependency modeling through the converter encoder, and (4) noise-aware refinement using Kalman filtering.

Fig. 1
figure 1

Proposed SOC prediction process for li-ion batteries.

Full size image

Convolutional neural network

CNNs are deep learning models designed for processing data with spatial structures. They are widely used in image processing and computer vision tasks. CNNs are also effective for handling time-series data with local dependencies by efficiently extracting local features. The core component of a CNN is the convolutional layer, where learnable kernels perform sliding window operations to extract features across spatial locations. In this study, a 1D CNN architecture with small kernels and adaptive stride is adopted, the small kernel focuses on local voltage-current correlations during current pulses, while adaptive stride adjusts according to current change rate to balance feature detail and computational efficiency, with the addition of batch normalization (BN) and activation layers. The BN layer is placed before the activation function to accelerate training convergence.

The core operation involves 1D convolution, where the kernel slides along the time axis to capture local temporal dependencies. The convolution is mathematically expressed as:

$$Conv1d(X)={W_{conv}} * X+{b_{conv}}$$
(1)

where \({W_{conv}}\) represents the weights of the convolutional kernel, and \({b_{conv}}\) is the bias term.

The complete convolution operation, including batch normalization and ReLU activation, is expressed as:

$${X_{cnn}}=ReLU(BatchNorm1d(Conv1d(X)))$$
(2)

This CNN module captures local temporal dependencies in the SOC sequence, allowing the model to learn key features that are critical for accurate SOC prediction.

Temporal-aware encoding module

In time-series prediction tasks, such as battery SOC estimation, the sequential order and temporal dependencies between time steps are critical. Although 1D CNNs are shift-invariant and effective at local feature extraction, they lack awareness of absolute time position, which is critical in UAV scenarios where identical current patterns may correspond to different SOC trajectories depending on flight phase. The proposed sinusoidal temporal encoding. Standard neural networks often fail to capture this order, leading to a loss of temporal information. To address this issue, a temporal-aware encoding module is incorporated, can explicitly inject time-step information, enabling the model to distinguish contextually similar but temporally distinct events based on the approach used in transformer models. To address this issue, a temporal-aware encoding module is incorporated, based on the approach used in transformer models.

The core idea is to generate sinusoidal embedding vectors that vary with each time step, encoding temporal order into a fixed-length representation. The periodic nature of sine and cosine functions allows long sequences to be encoded without explicitly memorizing each position. For a time-series of maximum length \({L_{\hbox{max} }}\), the temporal encoding vector \({{\mathbf{T}}_i} \in {{\mathbb{R}}^{{d_{{\text{model}}}}}}\) for time step i is computed as:

$${{\mathbf{T}}_i}=\left[ {\sin \left( {\frac{i}{{{{10000}^{\frac{{2k}}{{{d_{{\text{model }}}}}}}}}}} \right),\cos \left( {\frac{i}{{{{10000}^{\frac{{2k+1}}{{{d_{{\text{model }}}}}}}}}}} \right)} \right]_{{k=0}}^{{{d_{{\text{model }}}}/2 - 1}}$$
(3)

where \({d_{{\text{model}}}}\) is the model dimension, i is the position of the time step. The scaling factor 10,000 is an empirically determined constant that balances the modeling of short-term and long-term temporal dependencies. By testing 1000 and 100,000 equivalents, it is found that they are the most suitable coefficients for the framework. In our ablation tests, this value yielded optimal performance across the 128-step input window. Other architectural parameters are fine-tuned via grid search. The indices i and j denote the time-step position and embedding dimension, respectively, enabling the model to encode temporal order through a combination of high and low frequency sinusoidal functions. These encodings are added to input features (Fig. 2), enabling the model to learn relative temporal relationships while preserving local spatial features.

Fig. 2
figure 2

Temporal encoding mechanism for sequential data.

Full size image

The temporal encoding vector is then added to the input features to generate a feature representation that incorporates temporal information. This addition allows the model to learn not only the local features of the input data but also the relative position of each time step in the sequence.

Temporal encoding enables the model to effectively understand the temporal dependencies in time-series data. This explicit temporal awareness enables the model to distinguish identical electrical patterns occurring at different operational phases, thereby enhancing its adaptability to non-stationary and dynamic UAV environments. This allows the model to make more accurate predictions at different positions in the sequence, improving the overall accuracy of the time-series forecast.

Transformer module

The transformer is a deep learning model based on the self-attention mechanism, originally proposed by Vaswani et al.50 for natural language processing tasks. Due to its strong sequence modeling capability and efficient parallelization, it has been widely applied in time-series prediction. In this study, the transformer module is employed to capture long-term dependencies and nonlinear dynamics in battery SOC sequences. The self-attention mechanism is shown in Fig. 3.

Fig. 3
figure 3

Self-attention mechanism in transformer model.

Full size image

Self-attention mechanism

The self-attention mechanism dynamically assigns weights by computing the relevance between each time step and all others in the sequence. Given an input sequence \(X \in {{\mathbb{R}}^{T \times d}}\) (where T is the sequence length and d is the feature dimension), the self-attention mechanism is computed as follows:

Linear transformation

The input sequence X is mapped to queries (Q), keys (K), and values (V) using learnable weight matrices \({W_Q}\), \({W_k}\), and \({W_V}\).

Attention score calculation

The similarity between queries and keys is computed via dot product, resulting in an attention score matrix \(A \in {{\mathbb{R}}^{T \times T}}\).

Weighted summation

The attention scores are used to compute a weighted sum of the values V, yielding the self-attention output:

$$Attention(Q,K,V)=softmax(\frac{{Q{K^T}}}{{\sqrt {{d_k}} }})V$$
(4)

here, \(\sqrt {{d_k}}\) is used to scale the dot product results, preventing gradient vanishing issues.

Multi-head attention mechanism

To improve model expressiveness, queries, keys, and values are projected into multiple subspaces. Attention is computed independently in each subspace and the results are concatenated before a final projection:

$$MultiHead(Q,K,V)=Concat(hea{d_1},hea{d_2}, \ldots ,hea{d_h}){W_O}$$
(5)

where \(hea{d_i}=Attention(Q{W_{{Q_i}}},K{W_{{K_i}}},V{W_{{V_i}}})\), and \({W_O}\) is the output projection matrix.

Feedforward neural network (FFN)

Each position in the sequence goes through the same feed-forward network consisting of two linear transformations with a ReLU activation in between:

$$FFN(x)=max(0,x{W_1}+{b_1}){W_2}+{b_2}$$
(6)

This FFN is applied independently and identically to each position in the sequence, following the self-attention layer.

Transformer decoder

In conventional applications, the transformer decoder generates sequences by combining masked multi-head self-attention, encoder-decoder attention, and feedforward networks. Masked attention ensures that each position attends only to previous positions. Encoder-decoder attention allows integration of encoder outputs, enhancing the model ability to generate contextually coherent predictions. Layer normalization, residual connections, and dropout are applied for regularization and stability.

In this study, only the transformer encoder is utilized. It processes the local features extracted by the CNN and the temporal information provided by the encoding module, capturing the complex dynamics of battery SOC sequences. The encoder output is further refined using a Kalman filter, which is discussed in the next section.

Kalman filter module

The Kalman filter is a recursive state estimation algorithm widely employed to predict and smooth noisy data. In this study, the Kalman filter is applied as a post-processing step to the sequence generated by the Transformer module, it treats the TATNS output as the prior state estimate. By incorporating the Kalman filter, the impact of measurement noise is reduced, and the overall prediction accuracy is improved.

The Kalman filter operates in two primary phases: the prediction phase and the update phase. In the prediction phase, the filter uses the previous state estimate \({\hat {x}_{k - 1}}\) and the state transition matrix F to predict the next state \({\hat {x}_k}\). In the update phase, the filter adjusts the prediction by incorporating the new measurement \({z_k}\), which in this case corresponds to the predicted SOC value from the transformer model. The measurement is combined with the predicted state using a gain matrix \({K_k}\), computed based on the measurement noise R and the process noise covariance Q. The update is given by:

$${K_k}=\frac{{{P_{k - 1}}{H^T}}}{{H{P_{k - 1}}{H^T}+R}}$$
(7)

where \({K_k}\) is the Kalman gain, \({P_{k - 1}}\) is the error covariance matrix, and H is the measurement matrix.

Through recursive updates, the Kalman filter continuously refines the SOC prediction by combining the model prior prediction with the latest measurement. This process effectively filters out random noise and enhances the stability of the predictions.

In this study, the Kalman filter is applied to the SOC outputs from the transformer encoder. As a result, the final SOC estimates are smoother, more robust against noise, and more reliable for long-term forecasting tasks. By adopting this approach, the adaptability and accuracy of the proposed TATNS model in dynamic environments are significantly improved. The computational complexity of TATNS is approximately 7.12 million FLOPs. Thanks to its parallelizable architecture, the model achieves an inference latency typically below 10 ms on representative embedded AI platforms used in UAVs, satisfying the real-time requirement for onboard battery management systems.

Experimental platform and data

Simulation platform

The model is implemented based on Pytorch 2.4.1 deep learning framework using Python 3.9.0. All experiments are conducted on a workstation with an AMD R7 5800 H CPU and a NVIDIA GeForce RTX 3060 Laptop GPU. Although the current hardware setup is sufficient for offline training and validation, future work will focus on optimizing the model for deployment on embedded systems with limited computational resources, such as those used in UAVs.

Dataset acquisition

One typical battery model for UAVs is the 18,650 lithium-ion battery, which has been applied to certain models of DJI drones and the UAVs developed by our research team. To validate the effectiveness of the battery SOC prediction method proposed in this study, experiments were conducted using publicly available datasets. The dataset used in this experiment is the LG 18650HG2 Li-ion battery data, made publicly available by Dr. Phillip Kollmeyer from McMaster University51. The data can be accessed through the following link: https://data.mendeley.com/datasets/cp3473x7xv/3. This dataset is based on a brand-new LG 18650HG2 Li-ion battery and records voltage, current, temperature, and SOC data under various charge and discharge conditions, making it particularly suitable for deep learning-based battery SOC prediction tasks. Notably, voltage, current, and temperature are standard measurements in virtually all modern UAV battery management systems. Their acquisition requires only low-cost, off-the-shelf sensors, and thus imposes no significant hardware burden on practical UAV deployments.The core advantage of this dataset lies in its high-resolution time-series data and diverse experimental conditions, which effectively support the modeling of complex nonlinear relationships required by the model. Data were collected at ambient temperatures ranging from − 10 °C to 25 °C, covering UAV outdoor flight environment, enabling robust evaluation of thermal effects on battery dynamics. The dataset granular temporal resolution and operational variability support modeling of nonlinear SOC relationships critical for UAV applications. Although the cycle curves are generated in the laboratory, they provide a standardized benchmark that can first verify the effectiveness of the algorithm’s core in a controlled environment. The basic parameters of the batteries used in the dataset are shown in Table 2.

Table 2 LG HG2 cell basic performance parameters.
Full size table

Evaluation metrics

This study uses MAE, RMSE and MAPE as evaluation metrics52. MAE represents the average absolute error between all predicted SOC values and actual SOC values. RMSE measures the square root of the average squared differences between predicted SOC values and actual SOC values, imposing a higher penalty on larger errors, as it squares the errors in its calculation. Therefore, RMSE is highly sensitive to large discrepancies. MAPE is used to measure the deviation of the predicted SOC from the actual SOC as a percentage of the actual value. The formulas are as follows:

$$MAE=\frac{1}{n}\sum\limits_{{i=1}}^{n} {|SO{C_i} - {{\widehat {{SOC}}}_i}} |$$
(8)
$$RMSE=\sqrt {\frac{1}{n}\sum\limits_{{i=1}}^{n} {{{\left( {SO{C_i} - {{\widehat {{SOC}}}_i}} \right)}^2}} }$$
(9)
$$MAPE=\frac{{100\% }}{n}\sum\limits_{{i=1}}^{n} {\left| {\frac{{SO{C_i} - \widehat {{SO{C_i}}}}}{{SO{C_i}}}} \right|}$$
(10)

where \(SO{C_i}\) is the actual value, \({\widehat {{SOC}}_i}\) is the predicted value, and n is the number of samples. Smaller MAE, RMSE, MAPE values indicate better predictive performance of the model.

Results and discussion

A sliding window technique was employed to capture temporal dependencies in battery time series data through sequence generation. Input sequences were mapped to corresponding outputs, enabling historical pattern recognition while maintaining computational efficiency. The input window length is set to 128 time steps, which is consistent with recent studies on real-world battery SOC prediction53 and adjusted to a power of two to improve training efficiency on GPU-based platforms. The predicted output is determined to be 60 steps through the grid search method. The parameters optimally determined by grid search are shown in Table 3.

Table 3 Key parameters configuration for model training.
Full size table

Under the same condition, comparative experiments were conducted with mainstream and state-of-the-art methods. Subsequently, ablation experiments as well as testing and analyzing the ability of the proposed model to predict the SOC of the battery under a variety of temperature conditions were performed.

Comparison experiments

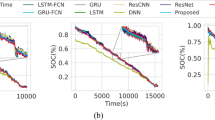
The proposed architecture was benchmarked against five neural network frameworks (Stacked CNN, MLP, RNN, LSTM, transformer, PatchTST, TimesNet) under standardized conditions. Performance metrics (MAE, RMSE, MAPE), all expressed as percentages, are summarized in Fig. 4; Table 4.

Fig. 4
figure 4

Comparison of predicted and actual SOC for various experimental conditions.

Full size image
Table 4 The comparison of SOC prediction errors of different existing methods.
Full size table

Table 4 presents the SOC prediction errors for different models. The TATNS model achieved the lowest prediction errors across all metrics, with a MAE of 2.165, RMSE of 2.703, and MAPE of 4.320, outperforming all baseline models. The transformer model ranked second overall, with a MAE of 2.488, RMSE of 3.131, and MAPE of 4.694, demonstrating its strength in capturing long-term dependencies. Stacked CNN also showed competitive performance with a MAE of 2.664, RMSE of 3.199, and MAPE of 5.572. In contrast, traditional sequential models such as LSTM, RNN and MLP exhibited higher error rates, indicating limitations in handling complex temporal patterns.

The transformer parallel structure allowed faster training compared to sequential models. This advantage is critical for real-time BMS. In Fig. 4, the predicted SOC values (blue) by TATNS closely follow the actual SOC (red), with minimal deviation, unlike other models.

The superior performance of TATNS can be attributed to its advanced temporal encoding mechanism, which effectively captures time-series dynamics. By integrating this with the transformer architecture, the model leverages both local and global temporal patterns, enhancing predictive accuracy. Additionally, the use of temporal encoders facilitates more precise sequence modeling, allowing the TATNS framework to adapt dynamically to changes in input data, thus ensuring high accuracy even under fluctuating operational conditions.

Ablation study

An ablation study was conducted to evaluate the contribution of individual components within the proposed TATNS model. Key elements, including the transformer, CNN, and temporal encoding modules, were systematically removed to assess their respective impacts on model performance. Additionally, the effectiveness of multi-output prediction was compared against single-output prediction under identical conditions. The results are illustrated in Fig. 5 and summarized in Tables 5 and 6.

Fig. 5
figure 5

Impact of model components on SOC prediction.

Full size image
Table 5 Ablation study results for SOC prediction.
Full size table

The results clearly indicate that each component plays a vital role in the overall predictive performance of the TATNS model. The full model achieved the lowest error metrics, with a MAE of 2.165, RMSE of 2.703, and MAPE of 4.320, reflecting exceptional predictive accuracy.

The removal of the CNN module resulted in a noticeable decline in performance, underscoring its critical role in local feature extraction. The omission of the temporal encoding module led to a slight reduction in predictive accuracy, highlighting its importance in modeling time dependencies. The transformer module was found to be particularly essential, contributing substantially to the model ability to capture long-range dependencies and complex dynamic behaviors.

Table 6 Results of different prediction methods under the same step condition.
Full size table

Moreover, the comparison between single-output and multi-output prediction strategies reveals that multi-output prediction significantly outperforms its single-output counterpart. The multi-output approach achieved lower MAE, RMSE, and MAPE values, demonstrating superior capability in capturing the evolving nature of SOC over time.

Overall, the ablation study confirms that the CNN, temporal encoding, and transformer modules jointly enhance SOC prediction by addressing feature extraction and long-term dependency modeling. Furthermore, multi-output prediction improves forecasting accuracy by capturing temporal dynamics across multiple future steps. These findings emphasize the necessity of integrating advanced neural network structures and temporal modeling techniques to achieve high-performance SOC estimation in real-world applications.

Sensitivity analysis

The temperature sensitivity of the proposed model was evaluated under four distinct temperature conditions: − 10 °C, 0 °C, 10 °C, and 25 °C. The performance metrics for each temperature condition are summarized in Fig. 6; Table 7.

The TATNS model demonstrates a high degree of robustness across the tested temperature range. the model shows a slight drop in performance, yielding a MAE of 2.874, RMSE of 3.784, and MAPE of 4.879. Nevertheless, this result still reflects a high level of accuracy, indicating the model capability to adapt to cold-temperature conditions where battery dynamics become more nonlinear and challenging to predict.

Fig. 6
figure 6

SOC prediction condition for different temperatures.

Full size image
Table 7 Performance metrics for SOC prediction at different temperatures.
Full size table

As the temperature increases to 0 °C, the model performance improves significantly, achieving its best performance across all tested conditions, with MAE of 1.474, RMSE of 1.781, and MAPE of 2.989. This suggests enhanced predictive capability under slightly cold but more stable conditions. At moderate temperatures of 10 °C and 25 °C, the model continues to perform reliably, with errors remaining low. The MAE and RMSE values remain within 2.2–2.6%, and MAPE under 5%, confirming that the TATNS model maintains stable and accurate predictions under typical operating temperatures. This consistent performance across diverse thermal conditions underscores the model’s strong dynamic adaptability, a critical requirement for UAVs operating in real-world, rapidly changing environments.

In Fig. 7, the error analysis, defined as the difference between actual and predicted SOC, provides further insight into the model performance. At lower temperatures, the prediction error exhibits greater variability, which can be attributed to the more complex dynamics of battery behavior in colder environments. However, despite these challenges, the model maintains relatively low errors, demonstrating resilience in extreme thermal conditions. At higher temperatures (10 °C and 25 °C), the prediction errors are significantly reduced, reflecting enhanced consistency and accuracy under less thermally restrictive conditions.

Fig. 7
figure 7

Prediction error of battery SOC at different temperatures.

Full size image

These findings collectively highlight the robustness and reliability of the TATNS framework, making it well-suited for real-world applications where batteries are exposed to diverse and varying environmental conditions. By effectively capturing the temperature-dependent relationships inherent in battery SOC prediction, the model ensures accurate and dependable performance across a broad range of thermal environments, emphasizing its practical value and adaptability in dynamic operational scenarios.

Conclusion

In UAV operations, accurate SOC prediction for lithium-ion batteries is critical for safe flight planning but complicated by dynamic loads, temperature variations, and nonlinear electrochemical behavior. This study presents a novel deep learning framework, TATNS, designed to predict the SOC in UAV lithium-ion batteries. TATNS integrates CNNs, transformer-based attention mechanisms, and temporal encoding strategies for dynamic error correction. This hybrid architecture effectively captures both localized electrochemical characteristics and long-term temporal dependencies, significantly improving the prediction robustness under dynamic operating conditions. The Transformer module in the TATNS framework can handle dynamic feature problems, and the Kalman filter can suppress noise. The model sliding window processing and multi-output forecasting methods could adapt to battery dynamic change and SOC nonlinear change.

Experimental validation on a large-scale UAV battery dataset demonstrates the superior performance of TATNS, with a MAE of 2.165, RMSE of 2.703 and MAPE of 4.320. Compared to the second-best model, the TATNS method reduces MAE by 12.98%, RMSE by 13.66%, and MAPE by 7.97%. These results reflect a significant reduction in error compared to existing models, including LSTM, RNN, and standalone CNN/transformer models. Additionally, the TATNS framework shows robust performance against environmental perturbations and thermal fluctuations, which are essential for UAV applications where ambient temperature variations can degrade battery performance.

Despite these advancements, TATNS has some certain limitations. The model performance decreases under ultra-low temperature conditions, indicating the demand for further enhancement in its adaptability to extreme thermal environments. While lightweight models offer higher computational efficiency, TATNS prioritizes prediction accuracy over speed, aligning with UAV safety-critical BMS requirements. Experiments are conducted on laboratory cycling data. Real UAV flight data are not yet included. Validating TATNS on actual UAV telemetry data is therefore the highest priority in our future work. Current research focuses on the deployment of a single UAV. In future studies, the model deployment issue of UAV swarms can be further explored. This expansion to swarm operations would necessitate addressing critical challenges in distributed computing communication protocols. Successfully overcoming these hurdles could enable more complex missions through collaborative intelligence and resource sharing among multiple autonomous platforms. These improvements could further enhance the framework scalability and applicability, providing a more robust solution for next-generation UAVs that demand enhanced operational intelligence and reliability.