Evolution mechanism of deformation and failure energy in composite rock mass with structural planes of different inclinations

Abstract

In order to investigate the mechanical properties and energy evolution patterns of composite rock masses with structural planes of different inclinations, this study selected composite rock samples made from coal and sandstone, with structural plane inclinations of 0°, 30°, 45°, 60°, and 90°. Uniaxial compression tests were conducted, and energy theory was applied to analyze the energy transformation characteristics during the deformation and failure process. The results show that the structural plane inclination significantly influences the compressive strength, peak strain, and elastic modulus of the composite rock masses. The compressive strength exhibits a “U-shaped” trend, first decreasing and then increasing, with the minimum at 45° and the maximum at 90°. The peak strain decreases monotonically as the angle increases, while the elastic modulus increases exponentially. The energy evolution process can be divided into four stages: compaction, elastic deformation, plastic deformation, and failure. The total peak strain energy and elastic energy percentages exhibit a pattern of first decreasing and then increasing with changes in the inclination angle. A piecewise damage constitutive model considering the compaction stage was established based on the experimental results. The model curve aligns well with the experimental data and can accurately characterize the stress-strain evolution characteristics of composite rock masses with structural planes of different inclinations. The findings of this study provide theoretical insights for disaster prevention and control in deep mines, as well as the stability analysis of composite rock masses.

Introduction

Due to the depletion of shallow coal resources, coal mining in China is gradually advancing to deeper regions, where it faces higher geostress and more complex geological environments¹. Coal bodies naturally exhibit a layered distribution, and during deep mining, composite coal-rock columns or composite surrounding rocks often appear. After coal pillars are left, composite rock masses are prone to the initiation, propagation, and penetration of cracks under static loads, which weakens their overall stability². The coal damage and failure in stress states are fundamentally driven by energy transfer and exchange, which is a phenomenon of state instability³. Focusing on the energy evolution in the deformation and failure processes of coal-rock bodies provides a more accurate reflection of the essential characteristics of deformation and failure⁴. Additionally, under the influence of various geological factors, especially tectonic actions, significant coal layer inclinations often occur⁵. Therefore, studying the deformation and failure energy evolution mechanisms of composite rock masses with structural planes of different inclinations is valuable for disaster prevention in deep mines.

In recent years, numerous scholars have conducted extensive research on composite coal-rock bodies. Zuo et al.⁶ compared the mechanical responses of monolithic rocks, monolithic coal, and coal-rock composite bodies under uniaxial compression, revealing the differences in their failure mechanisms using acoustic emission technology. Fan et al.⁷ focused on the deformation and failure characteristics of coal-rock contact surfaces, emphasizing that the mechanical properties of coal-rock bodies and the characteristics of the interface are key factors influencing the assessment of composite bodies’ susceptibility to impact. Cheng et al.⁸ explored the strength characteristics of coal-rock composite bodies through uniaxial compression experiments, investigating the role of the coal-rock height ratio, interface parameters, and material properties of the individual layers. Yang et al.⁹ analyzed the energy evolution characteristics of coal-rock composite bodies throughout the uniaxial loading process, clarifying the dominant mechanisms of energy transformation during their deformation and failure. Yin et al.¹⁰ conducted a systematic study on the mechanical behavior of coal-rock composite bodies under uniaxial loading, investigating the influence of lithological factors from multiple perspectives, including strength, energy evolution path, and macro-failure modes. Li et al.¹¹ used SHPB testing systems to study the energy response and failure modes of coal-rock-like composite bodies under impact loading, and analyzed the impact of fracture characteristics on the failure mechanisms. Li et al.¹² performed uniaxial loading, incremental cyclic loading and unloading, and steady-state cyclic loading and unloading tests on various rock samples, comparing the acoustic emission responses and failure precursors under different loading paths. Li et al.¹³ conducted uniaxial compression tests on various coal-rock composite specimens, investigating the impact of coal-rock ratios and lithological conditions on their mechanical properties and energy accumulation behavior, and concluded that the overall strength of the composite body is mainly dominated by the strength of the coal. Chen et al.¹⁴ used an energy-based approach to prepare composite specimens with different coal-rock ratios and proposed a method for evaluating the impact susceptibility based on the index of residual energy release rate. Zhang et al.¹⁵ developed a multi-factor coupling damage model for rock masses considering the direction of structural planes based on the D-P criterion, and derived theoretical expressions for model parameters.

Although the above studies have yielded valuable results, most existing research on composite rock masses neglects the systematic influence of the inclination angle of the coal-rock structural planes, leading to a vague understanding of their role in the entire energy evolution process. Additionally, most damage constitutive models focus on intact rocks or homogeneous jointed rock masses, and fail to fully consider the significant compaction characteristics at the early stages of loading for coal-rock composites, as well as their coupling relationship with the inclination of the structural planes. This results in limitations in representing the mechanical behavior of such materials. Therefore, it is essential to clarify the mechanical and energy evolution laws under different structural plane inclinations and establish constitutive models that accurately reflect the compaction phase and damage evolution characteristics. This would be key to advancing the understanding of the failure mechanisms of composite rock masses and enhancing engineering practices.

To address these issues, this study, based on energy evolution theory, systematically analyzes the mechanical properties and energy evolution characteristics of composite rock masses with structural planes of different inclinations (0°, 30°, 45°, 60°, and 90°) through uniaxial compression tests. A piecewise damage constitutive model that takes into account the compaction phase is developed to reveal the influence of structural plane inclination on the damage and failure mechanisms of composite rock masses, providing theoretical support for disaster prevention and control in deep mines.

Experimental design

To control the variables in the experiment, the coal-rock samples used were all collected from the same location in the 12th mining district of a coal mine. The preparation and testing of the samples strictly followed the relevant specifications and procedures for uniaxial compression tests outlined in the national standard of the People’s Republic of China, GB/T 23561.12–2024, Methods for Determining the Physical and Mechanical Properties of Coal and Rocks. The samples were processed into standard cylindrical specimens of 50 mm × 100 mm.

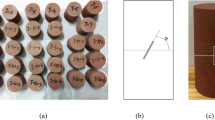
To ensure the reliability of the results, samples with no visible joints, cracks, and deviations in parallelism (≤ 0.05 mm) or height (≤ 0.2 mm) were selected. In addition, to reduce sample variability, ultrasonic testing was conducted on the samples, and those with similar wave velocities were chosen for the tests. After secondary polishing, the composite rock samples with different inclinations of structural planes were prepared. Given that the coal-rock interface formed naturally under different surface conditions through continuous deposition, without considering interlayer displacement, the interface between coal and rock needs to meet the requirements of high strength and thin thickness. To achieve this, a high-strength cloudstone adhesive was used to bond the coal and rock interface, with a bonding strength of 103 MPa. This strength is sufficient to meet the interface strength requirements, ensuring that the adhesive thickness during bonding remains less than 1 mm^16,17. The final result was the preparation of composite rock mass specimens, as shown in Fig. 1.

Fig. 1

Composite rock mass sample.

The testing equipment used in this study was the UTM4204 electronic universal testing machine, as shown in Fig. 2. To achieve a quasi-static loading rate and to avoid inertia effects caused by overly rapid loading as well as creep effects induced by excessively slow loading, a displacement-controlled loading mode was adopted in this test, with a loading rate of 0.02 mm/s until specimen failure^18,19,20.

Fig. 2

Testing equipment.

This experiment employed five different structural plane inclinations (0°, 30°, 45°, 60°, and 90°). To reduce experimental errors, three tests were conducted for each structural plane inclination, resulting in a total of 21 tests. The basic design of the experiment is shown in Table 1.

Table 1 Experimental design for samples with different structural plane inclinations.

Mechanical properties of composite rock mass with structural planes of different inclinations

The mechanical parameters of the composite rock samples with different structural plane inclinations, obtained from the uniaxial compression tests, are presented in Table 2.

Table 2 Mechanical parameters of composite rock mass with different inclinations.

From Table 2, the comparison between rock samples, coal samples, and composite rock mass samples reveals the following trends. The average compressive strength of the rock samples is 42.341 MPa, with a peak strain of 0.924 × 10⁻². The average compressive strength of the coal samples is 17.154 MPa, with a peak strain of 1.871 × 10⁻², which is significantly lower than that of the rock samples. The compressive strength is highest for the rock samples, followed by the composite rock masses, and the lowest for the coal samples. Peak strain is inversely related, with rock samples having the smallest peak strain, followed by composite rock masses, and coal samples exhibiting the largest. The stress-strain curves obtained from the uniaxial compression tests for samples with different structural plane inclinations (0°, 30°, 45°, 60°, and 90°) are shown in Fig. 3.

Fig. 3

Stress–strain curves of composite rock mass samples with different structural plane inclinations.

Using the data from the stress-strain curves, the compressive strength, peak strain, and elastic modulus were fitted for each sample with different structural plane inclinations. The fitted curves are shown in Fig. 4.

Fig. 4

Fitted curves for three mechanical parameters of composite rock mass. (a) Compressive strength fitting curve, (b) peak strain fitting curve, (c) elastic modulus fitting curve.

The relationships between compressive strength, peak strain, and elastic modulus with different structural plane inclinations were derived from the fitted functions as shown in Table 3.

Table 3 Mechanical parameter fitting functions.

As indicated by Fig. 3, the compressive strength of the composite rock masses is as follows for different structural plane inclinations: 30.938 MPa (0°), 24.135 MPa (30°), 19.268 MPa (45°), 22.205 MPa (60°), and 41.953 MPa (90°). The curve shows that compressive strength follows a “U-shaped” distribution²¹, decreasing until 45° and then increasing as the inclination reaches 90°.

Energy evolution in the loading and failure process

Energy calculation principle

During loading until failure, rocks experience multiple forms of energy conversion, primarily in the following forms: energy input, accumulation, dissipation, and release²². If a unit volume of rock is simplified as a closed system, ignoring heat exchange with the outside environment, according to the first law of thermodynamics, the work done by the external force will be entirely converted into the total energy of the system, U (in kJ·m⁻³)²³. The relationship can be expressed as:

$$U={U_e}+{U_d}$$

(1)

Where U_e represents elastic strain energy (kJ·m⁻³) and U_d represents dissipation energy (kJ·m⁻³). The rock unit energy in the principal stress space²⁴ is:

$$U = \int\limits_{0}^{{\varepsilon _{1} }} {\sigma _{1} {\text{d}}\varepsilon _{1} } + \int\limits_{0}^{{\varepsilon _{2} }} {\sigma _{2} {\text{d}}\varepsilon _{2} } + \int\limits_{0}^{{\varepsilon _{3} }} {\sigma _{3} {\text{d}}\varepsilon _{3} }$$

(2)

$${U_e}=\frac{1}{2}{\sigma _1}{\varepsilon _{e1}}+\frac{1}{2}{\sigma _2}{\varepsilon _{e2}}+\frac{1}{2}{\sigma _3}{\varepsilon _{e3}}$$

(3)

Where, ${\varepsilon _i}(i=1,2,3)$ is the total strain in the direction of the principal stress ${\sigma _i}(i=1,2,3)$ and ${\varepsilon _{ei}}$ is the elastic strain. The relationship between U_e and U_d in a rock cell at a certain stress level is shown in Fig. 5.

Fig. 5

Relationship between elastic strain energy and dissipation energy.

For a uniaxial stress state, ${\sigma _2}={\sigma _3}=0$, so Eqs. (2) and (3) can be simplified to:

$$U = \int\limits_{0}^{{\varepsilon _{1} }} {\sigma _{1} {\text{d}}\varepsilon _{1} }$$

(4)

$${U_e}=\frac{1}{2}{\sigma _1}{\varepsilon _{e1}}=\frac{{\sigma _{1}^{2}}}{{2{E_u}}} \approx \frac{{\sigma _{1}^{2}}}{{2{E_0}}}$$

(5)

where E₀ is the initial modulus of elasticity, the dissipated energy U_d can be expressed as:

$${U_d}=U - {U_e}=\int_{0}^{{{\varepsilon _1}}} {{\sigma _1}} d{\varepsilon _1} - \frac{{{\sigma _1}^{2}}}{{2{E_0}}}$$

(6)

Energy evolution law of specimens with different structural plane inclinations

During the loading process, the specimens undergo failure due to structural instability, driven by the accumulation of energy. The evolution of cracks, from initiation to propagation and eventual penetration, continuously dissipates energy. The variation in energy consumption during the fracturing process reveals the failure mechanism of the coal body²⁵. Based on the aforementioned principles of energy calculation, and by integrating the experimental stress-strain data, the energy conversion curves from loading to failure for the specimens with different structural plane inclinations are plotted in Fig. 6.

Fig. 6

Energy conversion curves for specimens with different structural plane inclinations. (a) 0° joint angle, (b) 30° joint angle, (c) 45° inclination structural plane, (d) 60° inclination structural plane, (e) 90° inclination structural plane.

The energy conversion process can be divided into the following four stages based on the stress-strain curves and energy evolution:

Compaction Stage (OA): During this phase, internal natural fissures and pores of the specimen close, leading to densification of the overall structure. The total input energy, elastic strain energy, and dissipation energy all accumulate slowly with minimal increases. A portion of the input energy is converted into elastic strain energy, which is stored within the specimen, while the remaining energy is dissipated in the form of dissipative energy²⁶.

Elastic Deformation Stage (AB): In this phase, the specimen’s structure remains essentially intact, and it predominantly exhibits elastic behavior. Both the total input energy and the elastic strain energy accumulate rapidly, while the increase in dissipative energy remains relatively moderate. This indicates that the internal fissures of the specimen have been closed, and the damage accumulation has stabilized, with most of the input energy stored as elastic potential energy, demonstrating high energy conversion efficiency.

Plastic Deformation Stage (BC): During this stage, the specimen’s ability to store elastic energy approaches its limit, causing a sharp increase in dissipative energy, while the increase in elastic strain energy significantly slows. Although input energy continues to accumulate, the stress-strain response starts to diverge, indicating the formation of significant internal cracks and even macro fractures. A large amount of energy is consumed in the processes of crack propagation and structural damage.

Failure Stage (CD): Once the stress reaches the peak value, the specimen becomes structurally unstable, and internal cracks rapidly propagate through the specimen. The previously accumulated elastic strain energy is released suddenly, resulting in a sharp drop in the stress-strain curve. Concurrently, dissipative energy increases sharply, and the release curve of elastic energy intersects with the dissipative energy curve, marking the complete loss of bearing capacity. Experimental measurements show that when the angle is 0°, the total strain energy of the composite rock mass is 382.8 kJ·m^− 3; when the angle increases to 30°, 45°, 60°, and 90°, the total strain energy is 247.3 kJ·m^− 3, 176.7 kJ·m^− 3, 270.4 kJ·m^− 3, and 306.8 kJ·m^− 3, respectively.

The energy values and their respective proportions at the peak point of the composite rock mass specimens with different structural plane inclinations are shown in Fig. 7.

Fig. 7

Changes in energy values and proportions at the peak of composite rock mass samples from different inclinations.

From Fig. 7, it can be seen that under uniaxial compression, as the angle increases, the total strain energy, elastic energy, and the proportion of elastic energy first decrease and then increase. In contrast, the dissipative energy and its proportion first increase and then decrease as the angle increases. Specifically, when the angle increases from 0° to 45°, the total strain energy decreases from 245.64 kJ·m⁻³ to 124.50 kJ·m⁻³, a reduction of 49.32%. The elastic energy decreases from 197.27 kJ·m⁻³ to 73.94 kJ·m⁻³, a decrease of 62.52%. Meanwhile, the dissipative energy increases from 48.37 kJ·m⁻³ to 50.56 kJ·m⁻³, an increase of 4.53%. The proportion of elastic energy decreases from 0.80 to 0.59, while the proportion of dissipative energy increases from 0.20 to 0.41. When the angle increases to 90°, the total strain energy increases from 124.50 kJ·m⁻³ to 195.20 kJ·m⁻³, an increase of 56.79%. The elastic energy rises from 73.94 kJ·m⁻³ to 155.10 kJ·m⁻³, a growth of 109.76%. However, the dissipative energy decreases from 50.56 kJ·m⁻³ to 40.10 kJ·m⁻³, a decrease of 20.69%. The proportion of elastic energy increases from 0.59 to 0.79, while the proportion of dissipative energy decreases from 0.41 to 0.21. These results clearly demonstrate that the inclination angle of the structural plane has a significant impact on the energy evolution of the specimen during loading and failure.

The impact of inclination on energy release rate and kinetic energy risk

To quantitatively characterize the dynamic instability tendency of the specimens, this study introduces the kinetic energy index K_e, defined as:

$${K_e}=\frac{G}{{{G_c}}}$$

(7)

where G_c represents the critical fracture energy.

The calculation results are shown in Table 4. When the inclination angle α = 90°, the specimen has the highest elastic energy storage before peak, amounting to 107.14 kJ/m³, indicating that it accumulates a higher amount of strain energy before failure. However, the energy release rate after the peak is relatively low, at only 5.90 kJ/m³·s, reflecting a more gradual energy dissipation process. In contrast, specimens with α = 0° and 45° have higher values for G, and the energy release is more intense. It can be observed that, although the specimen with 90° has a lower instantaneous energy release rate, it has the highest K_e value, meaning it has a higher “energy-storage-to-energy-dissipation ratio.” This suggests that once local structural instability or external disturbances trigger failure, the accumulated elastic energy is more likely to be converted into kinetic energy, leading to an impact-type failure.

Table 4 Energy storage and release characteristics for specimens with different structural plane angles.

Different inclination structural plane composite rock mass damage evolution constitutive model

Model establishment

In the field of rock and soil mechanics, a one-dimensional elastic–brittle damage model is commonly used to characterize the damage behavior of rocks under uniaxial loading. This model regards the composite rock mass as an aggregate composed of a large number of microscopic elements, and assumes that the strength of each element follows the Weibull statistical distribution²⁷. Based on the relationship between the number of failed elements and the damage variable, the expression of the damage variable under axial load can be derived as follows²⁸:

$$D = \frac{{N_{d} }}{N} = \frac{{\int_{0}^{\varepsilon } {NPd\varepsilon } }}{N} = 1 - \exp \left[ { - \left( {\frac{\varepsilon }{v}} \right)^{u} } \right]$$

(8)

In the equation: N_d is the number of damaged elements, N is the total number of elements, P is the probability density function of the element under static loading, Ɛ is strain, and u and v are Weibull distribution parameters.

In the rock mass, the initiation and development of macroscopic cracks are essentially the results of the continuous generation and propagation of internal microcracks. Relevant studies have pointed out that under axial loading, the propagation of microcracks inside the rock mass mainly occurs along the axial direction. On this basis, the relationship between the internal microcrack distribution of the rock mass and the external loading can be explained with the aid of fracture mechanics theory:

$$\sigma ={E_\alpha }\varepsilon \left( {1 - D} \right)={E_\alpha }\varepsilon \exp \left[ { - {{\left( {\frac{\varepsilon }{v}} \right)}^u}} \right]$$

(9)

Here, E_α represents the fitted elastic modulus of composite rock masses with different structural plane inclinations.

According to the parameter determination methods proposed by Yang et al.²⁹ and Wu et al.³⁰, the Weibull distribution strength parameters v and u can be determined based on key experimental parameters such as elastic modulus E, peak stress σ_c, and peak strain Ɛ_c, as shown in Eqs. (10) and (12).

$$u=\frac{1}{{\ln \frac{{E{\varepsilon _p}}}{{{\sigma _p}}}}}$$

(10)

$$v={\varepsilon _p}{u^{\frac{1}{u}}}$$

(11)

As shown in Fig. 8, the composite rock mass exhibits a significant compaction stage during uniaxial compression. However, the constitutive curve calculated from Eq. (9) presents a concave shape, which fails to accurately represent the compaction phase during the loading process and deviates considerably from the experimental data. Therefore, a piecewise damage constitutive model considering the compaction phase was established.

Constitutive model correction

BIAN et al.²⁸ found that constructing constitutive relationships for the compaction phase and other deformation phases helps to more accurately represent the stress-strain curves of rocks under axial load. Therefore, based on Eq. (9), a piecewise damage constitutive model was established, which incorporates both the compaction phase and other deformation phases.

$$\sigma ={E_\alpha }\varepsilon (1 - \exp \left[ { - {{(\frac{\varepsilon }{{{v_c}}})}^{{u_c}}}} \right]{\text{ }}(\varepsilon \leqslant {\varepsilon _c})$$

(12)

$$\sigma ={E_\alpha }(\varepsilon - {\varepsilon _c}){\text{exp}}\left[ { - {{(\frac{{\varepsilon - {\varepsilon _c}}}{{{v_p}}})}^{{u_p}}}} \right]+{\sigma _c}{\text{ }}(\varepsilon >{\varepsilon _c})$$

(13)

In the equation, u_c and v_c are the Weibull distribution parameters for the compaction phase, Ɛ_c and σ_c are the stress and strain at the boundary point between the compaction phase and the elastic stage, and u_p and v_p are the Weibull distribution parameters for other stages.

During the entire loading deformation process of the composite rock mass, the boundary point between the compaction phase and the elastic stage and the stress peak point satisfy:

$$\left\{ {\begin{array}{*{20}{c}} {\sigma \left| {_{{\varepsilon ={\varepsilon _c}}}} \right.={\sigma _c}} \\ {\frac{{\partial \sigma }}{{\partial \varepsilon }}\left| {_{{\varepsilon ={\varepsilon _c}}}} \right.={E_\alpha }} \\ {\sigma \left| {_{{\varepsilon ={\varepsilon _p}}}} \right.={\sigma _p}} \\ {\frac{{\partial \sigma }}{{\partial \varepsilon }}\left| {_{{\varepsilon ={\varepsilon _p}}}} \right.=0} \end{array}} \right.$$

(14)

The following parameters can be obtained:

$${u_c}= - \frac{1}{{\ln \left( {1 - \frac{{{\sigma _c}}}{{{E_\alpha }{\varepsilon _c}}}} \right)}}$$

(15)

$${u_p}=\frac{1}{{\ln \frac{{{E_\alpha }({\varepsilon _p} - {\varepsilon _c})}}{{{\sigma _p} - {\sigma _c}}}}}$$

(16)

$${v_c}={\varepsilon _{_{c}}}u_{c}^{{\frac{1}{{{u_{_{c}}}}}}}$$

(17)

$${v_p}=({\varepsilon _{_{p}}} - {\varepsilon _{_{c}}})u_{{_{p}}}^{{\frac{1}{{{u_{_{p}}}}}}}$$

(18)

Model validation

In order to validate the accuracy of the proposed damage constitutive model, the stress-strain curves of composite rock specimens with different structural plane angles were analyzed. Based on the experimental data, the model parameters were derived, as shown in Table 5.

Table 5 Parameters for the damage constitutive model.

Figure 8 shows the comparison between the experimental stress-strain curves and the theoretical model curves for composite rock specimens with different structural plane angles. As observed, the overall trend of the theoretical curves predicted by the model aligns well with the experimental results. At 0° angle, the theoretical curves for the compaction, elastic, and plastic stages before the peak match the experimental curves with an RMSE of 0.52 and R² of 0.962. However, as the structural plane angle increases, some deviations are observed in specific regions, with the RMSE increasing.

As the structural plane angle increases, the configuration becomes more favorable for shear slippage. In this case, the failure behavior is controlled not only by macroscopic stress but also by the inherent heterogeneity of the coal mass and the local mechanical properties of the interface cement layer. The current Weibull-based macroscopic model is unable to fully capture this angle-dependent, micro-scale failure mechanism. Additionally, while our segmented model introduces the compaction phase, it is still based on continuous medium mechanics and statistical damage theory. For failure behaviors at intermediate angles, potentially dominated by interface delamination and shear in the coal mass, the continuous medium model’s simulation capacity has inherent limitations. This results in deviations between the model and experimental data, particularly in the stress hardening and softening rates during the plastic phase.

In classical constitutive models, the Hoek-Brown model, based on empirical parameters, is typically used to describe the strength evolution of homogeneous rock masses. The Drucker-Prager (D-P) model, widely applied in geotechnical plasticity analysis, approximates elastic-plastic behavior. Both models lack explicit consideration for the initial fracture closure process during loading and the statistical heterogeneity introduced by interfaces or bedding differences. The segmented damage constitutive model proposed in this study, by incorporating the Weibull statistical description of the compaction phase, significantly improves the accuracy of fitting the entire stress-strain curve, especially in the compaction and elastic phases. The compaction segment reflects the non-linear increase in stiffness due to the closure of primary pores, while the elastic and plastic segments are governed by distinct Weibull parameters to characterise the material’s strength distribution and damage accumulation.

In classical constitutive models, the Hoek-Brown model, based on empirical parameters, is typically used to describe the strength evolution of homogeneous rock masses. The Drucker-Prager (D-P) model, widely applied in geotechnical plasticity analysis, approximates elastic-plastic behavior. Both models lack explicit consideration for the initial fracture closure process during loading and the statistical heterogeneity introduced by interfaces or bedding differences. The segmented damage constitutive model proposed in this study, by incorporating the Weibull statistical description of the compaction phase, significantly improves the accuracy of fitting the entire stress-strain curve, especially in the compaction and elastic phases.

Compared to the Hoek-Brown and D-P models, which lack specific physical terms or statistical descriptions to capture the low stiffness initial phase due to crack closure, the segmented model accurately reflects this process through an independent compaction phase. In the elastic-plastic transition and peak evolution, traditional models rely on empirical or yield criterion parameters, making it difficult to map material micro-strength distribution directly to macroscopic stress-strain curves. Our model, through statistical parameters, directly reflects micro-heterogeneity, offering clearer physical meaning for the parameters.

In terms of parameter interpretability, Hoek-Brown and D-P parameters typically require extensive regression or empirical tables for determination, whereas segmented Weibull parameters can be derived or preliminarily estimated using macroscopic quantities such as experimental modulus of elasticity, peak stress, and peak strain. This enhances the physical guidance for parameter acquisition. Consequently, from the perspective of theoretical mechanisms and physical interpretability, the segmented damage model is more suitable than the typical Hoek-Brown and D-P models for composite rock masses exhibiting distinct interfaces/bedding planes and undergoing compaction processes.

Overall, this theoretical constitutive model effectively characterises the stress-strain evolution patterns of composite rock masses with differently inclined structural planes during uniaxial compression tests. It accurately describes the changes in both the consolidation and elastic-plastic stages as the angle increases. However, due to the model’s limitations, its simulation of progressive failure behaviour following the peak remains inadequate, a matter that warrants further investigation in subsequent research.

Fig. 8

Comparison between test curves and theoretical calculations. (a) 0° Inclination Structural Plane, (b) 30° Inclination Structural Plane, (c) 45° Inclination Structural Plane, (d) 60°Inclination Structural Plane, (e) 90° Inclination Structural Plane.

Parameter analysis

To further verify the rationality and feasibility of the proposed model, a parameter analysis was conducted based on the results of the uniaxial compression tests. Figure 9 illustrates the influence of the parameters u_c、v_c、u_p, and v_p on the theoretical stress-strain curves, showing how variations in these parameters affect the segmented damage constitutive model when other variables remain constant.

Fig. 9

Effect of different parameters on model curves. (a) Effect of uc on the model curve, (b) Effect of vc on the model curves, (c) Effect of up on the model curve, (d) Effect of vp on the model curves.

From Fig. 9(a) and (b), it can be seen that u_c and v_c reflect the shape characteristics of the compaction stage in the theoretical curve. As u_c and v_c increase, the compaction segment of the model curve gradually changes from steep to gentle, resulting in a decrease in stress magnitude and a reduction in the stress growth rate. From Fig. 9(c) and (d), it can be observed that as u_p increases, the plastic phase of the stress-strain curve becomes more linear, and the starting point of this stage shifts to the right. The difference between the peak strain and the starting strain of the plastic phase decreases, indicating a negative correlation between u_p and this strain difference. Changes in v_p do not alter the linearity of the elastic stage before the peak; however, when v_p decreases, the peak of the stress–strain curve shifts along the elastic segment toward the lower left. In this case, the difference between the peak strain and the ending strain of the compaction stage decreases, showing that the variation trend of v_p is consistent with the change in the strain difference between the peak and the end of the compaction stage.

Discussion

Physical meaning and limitations of the damage variable

Although the proposed segmented damage model can reproduce the macroscopic stress–strain behavior of the composite rock mass with good accuracy, the scalar damage variable D is calibrated solely based on macroscopic mechanical data and currently lacks independent microscopic validation (such as AE event density or CT-derived fracture volume fraction). Therefore, at this stage, D should be regarded as a statistical indicator of macroscopic mechanical degradation, rather than a strictly observable physical measure of material damage.

We explicitly acknowledge this limitation and plan to incorporate microscopic verification in future research. Specifically, acoustic emission (AE) monitoring and CT imaging will be used to obtain quantifiable fracture evolution data. By establishing a physically observable damage index D_obs and performing regression analysis between D_obs and the model-derived D(ε), the correlation and consistency between the two can be evaluated. If a significant linear or power-law relationship is observed, it would validate that the model-defined D possesses physical representativeness. Otherwise, further modification of the model will be necessary to explicitly account for the influence of microstructural evolution.

Accordingly, in the current stage of this study, the term damage degree refers only to its macroscopic statistical meaning, and should not be interpreted as a direct mapping of the microcrack volume fraction. All conclusions presented in this work are drawn under this assumption.

Notes on specimen design and size effect

In this study, the structural plane length of the prepared specimens was only 50 mm, whereas in situ coal–rock pillars or roadway surrounding rocks typically contain discontinuous structural planes several meters long. Thus, the current experimental results cannot yet be directly extrapolated to engineering-scale column design. According to Bažant’s size effect law³¹, when the structural characteristic size increases, the nominal strength decreases significantly; neglecting this effect may lead to overestimation of design values. This study has not yet conducted large-scale or field-scale tests (e.g., specimens with dimensions of φ150 × 300 mm or larger). Therefore, the strength parameters and damage model proposed herein are applicable only within the laboratory-scale range.

Potential impact of cementation layer strength on experimental results

In this study, high-strength marble glue (approximately 103 MPa) was used to bond the coal–rock interface, with the main purpose of preventing premature debonding and thereby highlighting the influence of joint inclination on the overall mechanical behavior of the composite rock mass. However, the bonding strength and roughness of natural sedimentary interfaces are generally much lower than those of the artificial adhesive layer, and their heterogeneity, weak cementation characteristics, and frictional properties may lead to differences between the failure modes observed in laboratory specimens and those occurring in the field. Therefore, the results of this study are more representative of composite rock masses with strongly bonded interfaces. Future work will consider using weakly cemented materials that better simulate natural interfaces or preparing specimens containing actual natural interfaces, in order to improve the engineering representativeness of the experimental conditions.

Conclusion

This study aims to systematically investigate the influence of structural plane inclination on the mechanical properties, energy evolution characteristics, and damage–failure mechanisms of composite rock masses. The objective is to address the current gaps in understanding the inclination effect of structural planes and to overcome the limitations of traditional damage models, which fail to accurately represent the compaction phase and the full damage evolution process of such composites. Through uniaxial compression tests on composite rock specimens with different structural plane inclinations, combined with energy theory and statistical damage mechanics, the following major findings and conclusions are obtained:

• (1) The structural plane inclination is a key geometric factor controlling the macroscopic mechanical behavior of composite rock masses. The compressive strength exhibits a distinct “first decreases, then increases” U-shaped trend with increasing inclination, reaching a minimum at 45°, while the strength remains relatively high at 0° and 90°. This indicates that when the inclination direction forms a specific angle with the loading direction, shear slip is most likely to occur, resulting in weakened strength. The peak strain decreases approximately linearly with increasing inclination, whereas the elastic modulus increases exponentially. These results suggest that as the proportion of rock in the loading direction increases, the composite’s resistance to deformation is enhanced, while its overall plastic deformation capacity is reduced.

• (2) From an energy perspective, the study reveals the regulatory effect of structural plane inclination on the failure mechanism of composite rock masses. Under uniaxial compression, the energy evolution process can be clearly divided into four stages: compaction, elastic deformation, plastic deformation, and failure. The peak total strain energy and elastic energy ratio both exhibit a “first decrease, then increase” trend with increasing inclination, while the dissipated energy ratio shows the opposite trend. Particularly, the 45° specimen displays the weakest energy storage capacity and the highest energy dissipation proportion, indicating a higher tendency for stable plastic failure. Although the specimen with α = 90° has a lower post-peak energy release rate, its energy storage level is the highest, resulting in the largest kinetic energy index. This combination of high storage and delayed release implies a greater potential for dynamic instability.

• (3) Based on the experimental findings, a segmented damage constitutive model incorporating the compaction phase was successfully established and verified. By introducing separate Weibull statistical functions for the compaction and other deformation stages, the model significantly improves the fitting accuracy of the entire stress–strain curve, particularly for the compaction and elastic phases. Compared with classical models such as the Hoek–Brown empirical criterion and the Drucker–Prager yield criterion, the proposed segmented model provides clearer physical interpretation and stronger mechanism-based representation. It explicitly captures the low-stiffness initial stage caused by crack closure and better accounts for the statistical heterogeneity induced by structural plane inclination. Parameter analysis shows that u_c and v_c primarily control the shape of the compaction phase, while u_p and v_p govern the evolution of the plastic phase and the location of the peak stress. The model effectively reproduces the stress–strain evolution of composite rock masses under different structural plane inclinations, especially showing high predictive accuracy at lower angles. However, deviations observed at higher angles indicate that for failure processes dominated by strong interface effects and material heterogeneity, the model’s predictive capability still needs further improvement. Future research may consider incorporating independent parameters capable of characterising interface properties to further optimise the model. Additionally, as this study aimed to establish and validate the theoretical framework and applicability of the segmented damage model, global parameter identifiability or sensitivity analysis was not pursued. Subsequent work will undertake parameter uncertainty assessments based on multiple experimental and numerical inversion sets to enhance the model’s generalisability.

• (4) Although the proposed segmented model has been validated under laboratory loading conditions, certain limitations remain. First, the number of specimens was relatively small, and the current experimental data mainly correspond to specific structural plane inclinations under uniaxial static loading. Thus, broader experimental verification is required to confirm the model’s applicability across different rock types and loading conditions. Second, this study focuses on static loading; the model’s performance under dynamic or impact loading conditions has not yet been fully examined, and its applicability in such scenarios needs to be further extended.

• (5) Future studies will expand the experimental database by testing a wider variety of rock types, structural plane inclinations, and loading modes to verify the universality and reliability of the proposed model. In addition, parameter uncertainty and sensitivity analyses—such as Monte Carlo simulations and Sobol sensitivity assessments—will be conducted to evaluate parameter identifiability and model stability under varying conditions. Finally, the model will be applied to different coalfields and mining areas, and validated against real engineering data, to assess its transferability and provide a more solid theoretical basis for predicting damage evolution of rock masses under diverse geological conditions.

• (6) It should be noted that the conclusions of this study and the applicability of the proposed damage constitutive model have clear limitations. Because the specimens were fabricated using a coal–rock ratio of 1:1, with dimensions of φ50 mm × 100 mm, and were tested under uniaxial static loading conditions, without considering the influence of structural stress, confining pressure, dynamic disturbance, or size effects, the strength characteristics, energy evolution behavior, and applicability of the segmented damage model presented in this paper are valid only within the material conditions, interface characteristics, and laboratory-scale range used in this study. Under larger specimen sizes, different coal–rock ratios, or alternative loading paths (such as triaxial loading, cyclic loading, or impact loading), the conclusions of this study may not remain consistent and will require further experimental verification.

In summary, through a systematic experimental and theoretical investigation, this study quantitatively elucidates the controlling effect of structural plane inclination on the mechanical and energy characteristics of composite rock masses. Furthermore, it develops a segmented damage constitutive model capable of accurately describing the mechanical behavior of such materials. The results offer valuable theoretical guidance for understanding instability mechanisms and improving disaster prevention in deep mining engineering.