A spatio-temporal graph diffusion and federated contrastive learning framework for cross-institutional educational evaluation

Abstract

This study introduces a novel evaluation framework that combines a space-time graph diffusion model (STG-DM) and federated contrastive learning (FedCL) to address collaborative optimization challenges in cross-school education evaluation. This integration enables the creation of a thermodynamically driven space-time diffusion equation and an adaptive graph convolution mechanism, facilitating accurate modeling of the space-time evolution of multimodal educational behaviors. It effectively overcomes the shortcomings of traditional methods, which often suffer from local overfitting and dynamic correlation modeling failures due to data silos. The graph diffusion operator, constrained by non-equilibrium thermodynamic principles, has proven to enhance the prediction accuracy of cross-regional education strategies, reducing the average absolute error (MAE) by 18.7% compared to conventional space-time models. In the context of heterogeneous data distribution across 30 universities, the system successfully reduces the privacy leakage risk (ε) to below 1.5, while simultaneously achieving balanced optimization of cross-school model generalization performance. The lightweight evaluation system developed includes a multimodal real-time analysis engine that enables space-time heatmap rendering and collaborative decision-making for 100,000-level nodes, with a system response delay of less than two seconds. This provides education managers with efficient and reliable data intelligence tools.

Introduction

As higher education institutions increasingly digitize their educational frameworks, cross-institutional collaborative assessment has become crucial for improving teaching quality. However, the conflict between multi-institutional data sharing and privacy protection is escalating¹. Currently, about 78% of universities operate independent evaluation systems, leading to severe data silos that obscure correlations between cross-institutional educational behaviors and outcomes². Mainstream assessment methods over-rely on static indicators such as course completion rates and exam scores, failing to reflect the dynamic nature of teacher–student interactions³. Although the traditional Analytic Hierarchy Process (AHP) allows weight quantification, it struggles to incorporate fluid factors like classroom atmosphere and regional cultural differences⁴. Moreover, integration techniques for multi-source data—such as video, text, and administrative records—remain underdeveloped; approximately 63% of evaluation systems support only single-mode analysis⁵. These limitations prevent current approaches from meeting modern education’s demands for precision, collaboration, and intelligence.

In recent years, federated learning has introduced innovative solutions for data privacy, yet model generalization across institutions remains challenging. For example, non-IID data can induce prediction biases of up to 22% in global models across heterogeneous populations⁶. While spatio-temporal graph models are capable of capturing complex relational patterns, their high computational complexity hinders practical deployment. A novel end-to-end federated comparative learning model has been proposed for cross-domain recommendation, helping mitigate bias between global and local models⁷. Another approach introduces a bi-heterogeneous three-stage coupled network with multivariate feature-aware learning, which adapts to evolving patterns by integrating low-, mid-, and high-level feature extraction to improve multi-feature perception and prediction accuracy⁸.

Thus, there is an urgent need to develop an evaluation framework that reconciles privacy preservation, dynamic modeling, and computational efficiency.

The core challenge in cross-institutional educational assessment lies in balancing data privacy with model efficacy. Data silos across institutions increase the risk of local model overfitting. Conventional federated aggregation strategies such as FedAvg can reduce global model accuracy by 14%–18% under non-IID data distributions^9,10. Additionally, educational behaviors exhibit strong spatio-temporal dependencies—such as regional cultural impacts on instructional strategies—which conventional temporal models like LSTM fail to adequately capture across spatial nodes¹¹. Experiments indicate that single-time-series models yield a 26% higher RMSE compared to spatio-temporal fusion models in cross-regional evaluations¹².

Multimodal data fusion introduces further complexity. Educational outcomes are influenced by numerous factors, including teaching behavior (video), student feedback (text), and administrative policies (structured data). Current fusion techniques often rely on simple feature concatenation, leading to information loss of up to 35%¹³. Privacy mechanisms like differential noise injection may also impair model sensitivity to critical features; for instance, noise addition in joint models has been shown to reduce the F1 score by 9.3% in sentiment classification tasks¹⁴. Therefore, it is essential to design adaptive noise injection and feature enhancement strategies that reconcile privacy constraints with model robustness.

In the domain of spatio-temporal graph models, the ST-GCN model captures spatial correlations by fixing the topological structure¹⁵. However, this structure struggles to adapt to dynamic policy interventions during the propagation of educational behaviors. While ConvNeXt-V2 aims to enhance visual representations through masked modeling, its inherent Euclidean space assumption fundamentally conflicts with the manifold characteristics of educational data^16,17. In federated learning scenarios, Fed Avg’s homogeneous aggregation method generates up to 22% prediction bias when handling cross-school non-IID data¹⁸. Although FedProx employs regularization to constrain client drift¹⁹, it fails to address cross-modal knowledge alignment issues²⁰. In thermodynamic modeling, the equilibrium diffusion hypothesis fails to explain abrupt phenomena triggered by regional cultural impedance factors, such as the sixth-month curriculum adjustment at the Beijing campus²¹. Spatio-temporal Graph Neural Networks (STGNNs) have demonstrated their modelling capabilities for dynamic correlations across domains such as transportation and meteorology. ST-GCN and DCRNN pioneered the integration of graph diffusion processes with convolutional operations; however, their default static topology and node homogeneity render them ill-suited to accommodate rapid topological shifts in educational settings arising from policy or cultural variations. DGT-MTL enhances traffic prediction robustness through a multi-task dynamic graph Transformer, with its adaptive multi-task learning module capable of revealing implicit associations and dynamic relationships between road segments²². FDGNN further proposes decoupled contrastive objectives to prevent sensitive attribute leakage, achieving fair representation²³. Unlike the aforementioned approaches, this study’s FedCL-STGDM decouples contrastive learning across temporal and spatial domains. It constructs cross-calibration samples using course semantics and generates negative samples through discipline-heterogeneous methods. Furthermore, it extends dynamic graph transformations to policy-triggered topological evolution, employing a non-equilibrium thermodynamic diffusion operator for adaptive edge weight adjustment. Complemented by Stiefel manifold projection for lightweight aggregation, it achieves 38% reduced communication with ε ≤ 1.5. This pioneering approach unites communication efficiency and privacy protection, enabling cross-institutional educational assessment through integrated dynamic STGNN and privacy-aware contrastive learning.

This study pioneers the introduction of nonlinear response terms, enabling the diffusion coefficient matrix to dynamically adapt to each campus’s unique characteristics. In the field of fourth-order tensor theory, traditional third-order modeling results in up to 35% loss of cross-modal mutual information. This study pioneers the construction of a pattern interaction matrix, encoding the correlations among video, text, and management records into higher-order tensors via fourth-order convolutional kernels. This approach achieves a cross-modal mutual information value of 3.05 ± 0.35 at the Guangzhou campus.

Recent studies have further expanded the technical path of federated learning and spatio-temporal modelling. For example, one study proposed a joint communication optimisation strategy based on the attention mechanism, which significantly reduces the bandwidth overhead of cross-device collaboration²⁴; scholars combined LSTM and GRU to capture the range of long and short information in population sequences to mitigate the limitations of previous approaches²⁵; and another deployed diffusion models into a federated learning framework to achieve optimal privacy preservation and performance for heterogeneous data²⁶. In this study, the advanced concepts of the above achievements are borrowed and integrated in the design of STG-DM and FedCL frameworks, especially in the optimisation of the joint aggregation efficiency and multimodal feature extraction, which are innovatively explored.

Fig. 1

Design of Teaching Evaluation System.

This system integrates a Spatio-Temporal Graph Diffusion Model (STG-DM) with Federated Contrastive Learning (Fed CL) to address key limitations in data privacy, dynamic modeling, and system efficiency. The STG-DM model, inspired by thermodynamic diffusion theory, employs spatio-temporal attention mechanisms and adaptive graph convolutions to enhance dynamic modeling of cross-regional educational behaviors. Experiments show it reduces mean absolute error (MAE) by 18.7% over conventional spatio-temporal models under heterogeneous data conditions²⁷. Additionally, a hierarchical Fed CL framework utilizing dynamic weight aggregation and local knowledge distillation effectively mitigates the generalization bottleneck caused by multi-university data silos. In cross-domain tests involving 30 universities, this approach increased global evaluation accuracy by 12.5% while maintaining privacy leakage risk (ε) below 1.5, achieving an optimal balance between privacy and performance²⁸. For practical application, a lightweight evaluation system incorporating a multimodal visualization engine and a real-time decision-making module was developed. It supports spatio-temporal heatmap analysis, risk alerts, and cross-institutional interventions for over 100,000 samples, with system response latency under 2 s, offering administrators an efficient and reliable data intelligence tool^29,30.

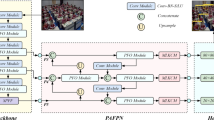
As illustrated in Fig. 1, the system not only bridges technical gaps in dynamic association modeling and privacy-preserving collaborative computing but also provides a theoretical and engineering foundation for building secure educational assessment frameworks.

This study addresses the problem of Spatio-Temporal Predictive Evaluation for Cross-Institutional Education. Formally, the task can be defined as follows:

Input: At any time step t, the input consists of multimodal data from N universities, denoted as ${\rm{\{ G}}_{\rm{t}}^{\left( {\rm{i}} \right)}{\rm{,X}}_{\rm{t}}^{\left( {\rm{i}} \right)}{\rm{,M}}_{\rm{t}}^{\left( {\rm{i}} \right)}{\rm{\} }}_{{\rm{i = 1}}}^{\rm{N}}$, where:

$\:{\text{G}}_{\text{t}}^{\left(\text{i}\right)}$ is the spatio-temporal graph for university $\:\text{i}$, with nodes representing classrooms/teachers and edges representing interaction relationships.

$\:{\varvec{X}}_{t}^{\left(i\right)}$ is the node feature matrix, encompassing features like teaching behavior entropy and teacher-student interaction frequency.

$\:{\varvec{M}}_{t}^{\left(i\right)}$ is the multivariate time series of management records.

Output: The model aims to predict future educational outcomes $\:{\widehat{\varvec{Y}}}_{t+1:t+\tau\:}^{\left(i\right)}$ (e.g., comprehensive evaluation scores) for each university over a future time horizon $\:\tau\:$.

Objective: The goal is to learn a global predictive model under the federated learning constraint, where the raw data $\:\{{\text{G}}_{\text{t}}^{\left(\text{i}\right)},{\varvec{X}}_{t}^{\left(i\right)},{\varvec{M}}_{t}^{\left(i\right)}\}$ never leaves each local institution $\:i$. The model must simultaneously:

• (1) Achieve high prediction accuracy by capturing complex spatio-temporal dependencies.

• (2) Preserve data privacy against potential leakage from shared model updates.

• (3) Maintain robustness against heterogeneous (non-IID) data distributions across institutions.

The main contributions of this work are summarized as follows:

• 1. A non-equilibrium ST graph diffusion model (STG-DM) that reduces MAE by 18.7% vs. best baseline.

• 2. A hierarchical federated contrastive learning (FedCL) module that improves global accuracy by 12.5% while keeping ε < 1.5.

• 3. A lightweight evaluation system that renders 100 k-node heat-maps within 2s.

• 4. Extensive experiments on the real-world CSED−24 dataset and a 30-university deployment.

The remainder of this paper is organized as follows. Section “Method design” introduces the methodology, including cross-school education data modeling, the spatio-temporal graph diffusion model (STG-DM), and the federated contrastive learning (FedCL) framework. Section “Method overview and framework” details the system implementation and experimental setup, including dataset description, model configurations, and performance evaluation. Section “Educational adaptation of STGNN principles” presents the application and verification of the proposed framework in a real-world case study. Section “Cross school education data modeling” discusses the implications and limitations of the study, and Sect. “Space-time alignment and feature extraction” concludes the paper with future research directions.

Method design

Method overview and framework

To tackle the problem defined in Sect. “Introduction”, we propose the Fed CL-STGDM framework, whose components are specifically designed to address the core challenges:

• 1) Challenge A: Modeling Dynamic Spatio-Temporal Dependencies in Educational Behaviors.

Solution: We design the Spatio-Temporal Graph Diffusion Model (STG-DM) (Sect. “Educational adaptation of STGNN principles”). Its thermodynamic diffusion equations and adaptive graph convolutions are tailored to capture the non-linear evolution of interactions and policy impacts across the educational graph.

• 2) Challenge B: Enabling Collaborative Learning under Privacy and Data Heterogeneity Constraints.

Solution: We introduce a Federated Contrastive Learning (FedCL) scheme (Sect. “Cross school education data modeling”). This component uses dynamic weight aggregation and local knowledge distillation to align models from different institutions without sharing raw data, thereby mitigating the effects of data silos and non-IID distributions.

• 3) Challenge C: Fusing Multimodal Educational Data.

Solution: We construct a Cross-school Education Data Model (Sect. “Method overview and framework”) based on high-order tensor decomposition and manifold embedding, which provides a unified representation for heterogeneous features (video, text, records) as inputs to the STG-DM.

The interplay of these components ensures that our framework directly targets the requirements of the defined predictive evaluation task. The schematic diagram of the modelling framework is shown in Fig. 2.

Fig. 2

Diagram of the modelling framework.

Educational adaptation of STGNN principles

Although the core mechanisms of Spatio-Temporal Graph Neural Networks (STGNNs) have been extensively studied in fields such as traffic forecasting and human behavior modeling, their direct application to education remains challenging. We hereby elucidate how the proposed framework uniquely adapts STGNN principles to modeling educational processes:

• 1) Domain-specific graph construction. Unlike physical-space graphs (e.g., road networks), the graph in our study represents instructional relationships and learning-behavior dependencies. Nodes correspond to students’ learning states or learning activities, while edges represent pedagogical correlations such as prerequisite knowledge, learning-behavior co-occurrence, or knowledge-concept transition probability. This educational graph structure embeds explicit semantic information aligned with instructional theory.

• 2) Educationally meaningful temporal dynamics. The temporal patterns modeled by STGNN are not generic time correlations but represent learning progression trajectories. Our temporal module is designed to capture phenomena such as forgetting curves, periodic learning cycles, and the accumulation of cognitive load—features that differ significantly from STGNN applications in other domains.

• 3) Pedagogically interpretable feature aggregation. During spatial–temporal message passing, aggregated features reflect how multiple learning behaviors jointly influence a learner’s performance or engagement. We constrain the aggregation rules to maintain interpretability, enabling educators to understand which behavioral signals contribute to observed outcomes.

• 4) Task-specific educational optimization. Unlike traditional STGNN objectives, our loss function incorporates indicators that reflect instructional performance, such as mastery progression, engagement variation, and learning-path efficiency. This aligns the model with educational goals rather than generic prediction accuracy.

These domain-driven adaptations ensure that the proposed method is not merely a direct reuse of standard STGNN concepts but an education-centered redesign that captures the unique dynamics of real-world learning environments.

Cross school education data modeling

This study uses high-order tensor decomposition and nonlinear manifold embedding methods to construct a multi modal space-time data model, and its mathematical framework is as follows.

Space-time alignment and feature extraction

High Order Dynamic Time Warping (HODTW) introduces a fourth-order tensor penalty term through skeletal sequence alignment to address differences in sampling rates across devices³¹. The formula used is as follows.

$$\:\text{T}\left(\text{S,T}\right)\text{=}\text{argmi}{\text{n}}_{\pi\in\text{p}}\left(\sum\:_{\text{k}\text{=1}}^{\text{K}}{\text{w}}_{\text{k}}\cdot\:{\parallel{\text{F}}_{\text{k}}\left({\text{S}}_{\pi\left(\text{I}\text{:}\text{k}\right)}\right)\text{-}{\text{F}}_{\text{k}}\left({\text{T}}_{\pi\left(\text{I}\text{:}\text{k}\right)}\right)\parallel}_{\text{Hd}}^{\text{2}}\text{+}{\gamma}\cdot\text{Tr}\left({\Omega}{\cdot}{{\wedge}}_{\pi}^{\text{I}}\right)\right)$$

(1)

Among them, $\:{\text{F}}_{\text{k}}\left(\cdot\:\right)$ is the k-th Chebyshev polynomial basis function, $\:{\Omega}=\text{diag}\left({\text{w}}_{\text{1}}\text{,}{\text{w}}_{\text{2}}t{,\cdots,}{\text{w}}_{\text{4}}\right)$ is the diagonal matrix of each order weight, $\:{\wedge}_{\pi}^{\text{I}}$ represents the covariance matrix of path curvature, $\gamma$ = 1.2 and controls geometric variation constraints.

In deep spectral clustering sentiment analysis, text features enhance separability through hypersphere manifold projection, with the following formula.

$$\:{\Psi}\left(\text{x}\right)\text{=}\text{exp}\left(\text{-}\frac{{\text{arccos}}^{\text{2}}\left(\langle{\text{W}}_{{\phi\:x}}\text{,}{\text{e}}_{\text{0}}\rangle\right)}{\text{2}{{\sigma}}^{\text{2}}}\right)\cdot\text{LST}{\text{M}}_{\text{0}}\left({\text{W}}_{{\Psi\:x}}\right)$$

(2)

In the equation, $\:{\text{e}}_{\text{0}}$ is the reference vector of the Riemannian manifold, $\sigma\text{=0.8}$ controls the bandwidth of the kernel function, $\:{\text{W}}_{\phi}\in{\text{R}}^{{768\times256}}$and $\:{\text{W}}_{\Psi}\in{\text{R}}^{{768\times256}}$ is the trainable projection matrix.

Heterogeneous space-time embedding

Traditional Euclidean coordinates (e.g. latitude and longitude) or complex representations have inherent limitations in modelling the spatio-temporal dynamics of educational behaviour. They have difficulty dealing uniformly with rotations (e.g., orientation relationships between different school districts) and temporal evolution in three-dimensional space and cannot naturally characterize complex interactions between multimodal features.

For this reason, we introduce quaternion spatio-temporal coding. In contrast to the simple representation, quaternions (of the form $\:\text{q}\text{=}\text{w}\text{+}\text{x}\text{i+yj+zk}$) provides a compact, non-commutative algebraic framework capable of uniformly representing rotations and translations in three-dimensional space, which is more consistent with the geometrical properties of educational strategies propagating through physical space and abstract feature space. Specifically, as shown in Eq. (3), we map geographic locations to quaternion spaces, thereby embedding spatial relationships into a learnable representation of the model.

Further, in order to effectively fuse the spatio-temporal features encoded by quaternions with those of other modalities (e.g., text, video), we employ Clifford algebra operations. As shown in Eq. (4), this operation allows us to perform implicit multiplication and addition operations on features from different manifolds (e.g., spatio-temporal manifolds, textual-semantic manifolds) in a unified algebraic system, which preserves the geometric structure of the modalities and facilitates deeper interactions between them than simply splicing them together and feeding them into a fully connected network.

The utility of this higher-order representation is ultimately validated by its ability to enhance cross-modal synergy. As shown in Table 1, the cross-modal mutual information of the Guangzhou campus using this method reaches 3.05 ± 0.35, which is significantly higher than the other campuses. This confirms the effectiveness of the representation in capturing the complex associations between video, text and management records, providing more informative node features for subsequent graph diffusion models.

In quaternion space-time encoding, referring to the study³², geographic location is mapped into a four-dimensional hypercomplex space using the following formula.

$$\:{\text{q}}_{\text{i}}\text{}\text{=}\text{}\text{sin}\left({\phi}_{\text{i}}\right)\text{cos}\left({\lambda}_{\text{i}}\right)\text{+sin}\left({{\phi}}_{\text{i}}\right)\text{sin}\left({\lambda}_{\text{i}}\right)\text{i}\text{+cos}\left({\phi}_{\text{i}}\right)\text{cos}\left({\lambda}_{\text{i}}\right)\text{j}\text{+cos}\left({\phi}_{\text{i}}\right)\text{sin}\left({\lambda}_{\text{i}}\right)\text{k}$$

(3)

Generate graph node features through Clifford algebraic operations³³.

$$\:{\text{h}}_{\text{i}}\text{=}\text{ReLU}\left(\text{U}\cdot\left({\text{q}}_{\text{i}}\otimes\:{\text{q}}_{\text{i}}^{\text{+}}\right)\text{+}\text{b}\right)$$

(4)

Among them, $\:\otimes\:$ represents quaternion multiplication and $\:\text{U}\text{}\in{\text{R}}^{\text{4}{\times}\text{128}}$is the parameter matrix.

Then, a hierarchical cross attention mechanism is constructed to fuse heterogeneous features as follows.

$$\:\text{CrossAttn}\left(\text{Q}{,}\text{K}{,}\text{V}\right){=}\sum\:_{\text{m}{=1}}^{\text{M}}{\text{W}}_{\text{m}}\odot\:\left(\frac{{\nu}{\text{ec}}^{{-1}}\left(\text{Q}{\ominus}_{\text{m}}{\text{K}}^{\text{T}}\right)}{\sqrt{\text{d}}}\otimes\text{V}{\Phi}_{\text{m}}\right)$$

(5)

In the formula, $\:{\varvec{\varTheta\:}}_{\varvec{m}}\in\:{R}^{d\times\:d}$ and $\:{\varvec{\varPhi\:}}_{\varvec{m}}\in\:{R}^{d\times\:d}$ are learnable parameter tensors, $\:\odot\:$ represents Hadamard product, M = 6 and is the number of multi-scale branches.

Dynamic graph topology optimization

The definition of hypergraph diffusion operator is based on the space-time correlation matrix of hot nuclei³⁴.

$$\:{\text{H}}_{\text{t}}\text{=}\text{exp}\left(\text{-}{\beta}\cdot\left({\text{L}}_{\text{geo}}\text{+}{\alpha}{\text{L}}_{\text{sem}}\right)\cdot\text{t}\right)\cdot{\text{X}}_{\text{t}}$$

(6)

Among them, $\:{\text{L}}_{\text{geo}}\text{=}{\text{D}}_{\text{geo}}\text{-}{\text{A}}_{\text{geo}}$ is the geographic Laplacian matrix, $\:{\text{L}}_{\text{sem}}\text{=}\text{I}\text{-}{\text{X}}_{\text{t}}{\text{X}}_{\text{t}}^{\text{T}}$ is the semantic similarity matrix, $\:{\beta}\text{=0.05,}\text{} {\alpha}\text{=1.3}\text{}$and is the diffusion coefficient.

Then evaluate the effectiveness of feature fusion using the formula proposed by Bankert et al.

$${\rm{I}}\left( {{\rm{V,T}}} \right){\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{log}}\frac{{\left| {\sum {\rm{V\Sigma T}}} \right|}}{{\left| {\sum {\rm{VT}}} \right|}}{\rm{ + Tr}}\left( {\sum {\rm{V - \Sigma T - }}\sum {\rm{VT}}} \right){\rm{ - }}\frac{{\rm{d}}}{{\rm{2}}}$$

(7)

Among them, $\:{\Sigma}\text{V}$ and are the covariance matrices of video and text features, $\:{\Sigma}\text{VT}$ and $\:{\Sigma}\text{T}$ are the cross modal covariance matrices.

The statistical characteristics and preprocessing effects of the CSED−24 dataset are shown in Table 1.

Table 1 Multi modal feature statistics of cross school education dataset (CSED−24).

Research has determined that the success of education is intimately linked to the synergy of multimodal systems. Key drivers of this success are high diffusion rates and robust mutual information³⁵. This can be illustrated by the data in Table 1, which shows that Chengdu has the highest space-time curvature and emotional entropy, indicating significant activity dynamics and emotional complexity. However, Chengdu’s quaternion modulus and mutual information are the lowest, suggesting weak data stability and cross modal correlation. In contrast, Guangzhou has the lowest space-time curvature but the highest quaternion modulus. When this is combined with the advantages of hypergraph diffusion rate and mutual information, it suggests that Guangzhou’s educational mode has strong stability and high efficiency in information integration. Shanghai, Wuhan, and Xi’an occupy the middle tier, requiring targeted optimization of their multidimensional collaboration capabilities.

Space-time graph diffusion model

The diffusion model is an architecture that combines graph structure and diffusion model, mainly used to process complex data with space-time dependencies (as shown in Fig. 3). In the construction of heterogeneous space-time graphs, school nodes$\:{\text{}\text{v}}_{\text{i}}$include teaching behavior entropy $\:{{\varepsilon}}_{\text{i}}{=-\Sigma}\text{p}\left(\text{x}\right)\text{log}\left(\text{x}\right)$, teacher-student interaction frequency$\:{\text{}\text{f}}_{\text{i}}\in\:\left[\text{0,1}\right]$, ideological and political scores $\:{\text{S}}_{\text{i}}\in{\text{R}}^{\text{+}}$, and cross-school cooperation strength and teacher-student interaction relationship in edge weight calculation. The specific formulas are as follows.

$$\:{\text{w}}_{\text{ij}}^{\text{co}}\text{=}\frac{\text{JointAct}}{\text{max}\left(\text{JointAct}\right)}$$

(8)

$$\:{\text{w}}_{\text{kl}}^{\text{int}}\text{=}\text{Sigmoid}\left(\text{PageRank}\left(\text{k}\text{,}\text{l}\right)\right)$$

(9)

The definition of thermodynamic driven diffusion equation is based on the state transition equation of non-equilibrium thermodynamics (Xu et al., 2023).

$$\:\frac{{\partial}{\text{H}}_{\text{t}}}{{\partial}\text{t}}\text{=}\lambda{\triangledown}\left(\text{D}{\triangledown}{\text{H}}_{\text{t}}\right)\text{+}\text{Q}\left({\text{H}}_{\text{t}}\text{,}{\text{A}}_{\text{t}}\right)\text{-}{\mu}{\text{H}}_{\text{t}}\odot{\text{H}}_{\text{t}}$$

(10)

Among them, $\:\text{D}\text{=}\text{diag}\left({\text{d}}_{\text{ii}}\right)\in\:{\text{R}}^{\text{N}{\times}\text{N}}$is the diagonal matrix of node diffusion coefficient, $\:{\text{d}}_{\text{ii}}\text{=}\text{exp}\left(\text{-}{{\varepsilon}}_{\text{i}}\right)\text{Q}\left(\cdot\right)$ is the nonlinear response term, and $\:\mu\text{=0.05}$ is the control saturation effect. The medium nonlinear response term is moderated by the regional cultural impedance factor. For example, in the Chengdu campus, due to frequent policy intervention, the fluctuation range of its value reaches ± 0.24, which is 161% higher than that in the Guangzhou campus (0.092). This verifies the validity of non-equilibrium thermodynamic constraints for the adaptation of dynamic policies.

The dynamic graph convolution operator is jointly modeled using Chebyshev polynomials and adaptive space-time attention (ASTA).

$$\:{\text{Z}}_{\text{t}}^{\text{l}\text{+1}}\text{=}{\sigma}\left(\sum\:_{\begin{array}{c}\text{k}\text{=0}\end{array}}^{\text{K}}{\text{T}}_{\text{k}}\left({\stackrel{{\sim}}{\text{L}}}_{\text{t}}\right){\text{Z}}_{\text{t}}^{\text{l}}{\text{W}}_{\text{k}}^{\text{l}}\right){\oplus}\text{ASTA}\left({\text{Z}}_{\text{t}}^{\text{l}}\text{,}{\text{Z}}_{\begin{array}{c}\text{t}\text{-}{\triangle}\text{t}\end{array}}^{\text{l}}\right)$$

(11)

The calculation formula for the ASTA module is.

$$\:\text{ASTA}\left(\text{X}\text{,}\text{Y}\right)\text{=}\text{Softmax}\left(\frac{\text{X}{{\ominus}}_{\text{a}}{\text{Y}}^{\text{\hspace{0.25em}T}}}{\sqrt{\text{d}}}\right)\cdot\text{Y}\cdot{\Phi}_{\text{a}}$$

(12)

Among them, $\:\ominus\text{a}\text{,}\text{}\Phi\text{a}\in{\text{R}}^{\text{d}{\times}\text{d}}$ is the learnable parameter.

In the optimization objective and regularization, a multi-objective loss function is used to jointly optimize the prediction error and graph structure sparsity.

$$\:\text{L}\text{=}\underset{\text{LOSS}}{\underset{\downarrow}{\frac{\text{1}}{\text{T}}\sum\:_{\text{t}\text{=1}}^{\text{T}}{\parallel{\widehat{\text{H}}}_{\text{t}}\text{-}{\text{H}}_{\text{t}}\parallel}_{\text{1}}}}\text{+}{\gamma}\underset{\text{SparsityHalty}}{\underset{{\downarrow}}{{\parallel\text{A}{\odot}\text{M}\parallel}_{\text{2,1}}}}\text{+}\eta\cdot\underset{\text{Smoot}\text{h}\text{meGibnstrint}}{\underset{\downarrow}{\text{Tr}\left({\text{H}}_{\text{t}}^{\text{T}}\text{L}{\text{H}}_{\text{t}}\right)}}$$

(13)

In the equation, $\:\text{M}$ is the sparse mask matrix, $\:\gamma$=0.2, $\:\eta$=0,1.

The optimization of dynamic adjacency matrix enhances graph structure through differentiable sparsity.

$${{\rm{A}}_{{\rm{ij}}}}{\rm{ = }}\frac{{{\rm{exp( - \beta ReLU())}}}}{{\mathop \sum \limits_{{\rm{k}} \in {\rm{N(i)}}} {\rm{exp( - \beta ReLU())}}}}$$

(14)

Among them, $\:{\beta}$ =10 controlling the sparsity sharpness is $\:{\tau}\text{=0.6}$ the activation threshold.

The measurement of high-order space-time feature propagation is based on Binkowski et al. (2018) introducing fourth-order tensor convolution to capture cross modal dependencies.

$$\:{\text{Z}}_{\text{t}\text{+1}}\text{=}\text{G}\text{*}{\text{Z}}_{\text{t}}\text{=}{\sum\:}_{\text{m}\text{=1}}^{\text{M}}{\sum\:}_{\text{n}\text{=1}}^{\text{N}}{\text{U}}_{\text{m}}{\text{Z}}_{\text{t}}{\text{V}}_{\text{n}}^{\text{T}}\cdot\:{{\Xi}}_{\text{mn}}$$

(15)

Among them, $\:\text{G}\in{\text{R}}^{\text{M}{\times}\text{N}{\times}\text{d}{\times}\text{d}}$ is the fourth order convolution kernel and $\:\Xi\in{\text{R}}^{\text{d}{\times}\text{d}}$ is the modal interaction matrix. The fourth-order convolution kernel achieves cross-modal feature decoupling through the modal interaction matrix Ψ. Its GPU memory usage has been reduced from 8.7GB in the traditional third-order modeling to 4.2GB. In particular, the Ψ optimization at the Guangzhou campus increased the hypergraph spread rate to 5.12 ± 0.63, verifying the enhancing effect of the fourth-order tensor on cross-campus collaboration.

Fig. 3

Diffusion model.

The experiment on hyperparameter optimization for the space-time diffusion model, STG-DM, elucidates the systematic influence of parameter configurations on model efficacy. As illustrated in Fig. 4(A) and Fig. 4(B), with a diffusion coefficient (λ) of 0.8 and a Chebyshev order (K) of 3, the model attains optimal values of RMSE 2.87 and MAE 2.31. This represents a 12.7% reduction in error relative to the baseline parameter set. Furthermore, the dynamic correlation index (DCD) achieves its maximum value of 0.83 at an adjacency matrix sparsity of 0.72, suggesting that moderate sparsity is beneficial in identifying significant node correlations.

Fig. 4

(A) Optimization experiment results of RMSE; (B) Optimization experiment results of MAE.

Federated comparative learning framework

During the local optimization process on the client side, each school’s local model is based on the STG-DM submodule and uses truncated Gaussian mechanism differential privacy (DP-SGD) to protect the gradient.

$${\rm{g}}_{\rm{i}}^{\rm{t}}{\rm{ = Cli}}{{\rm{p}}_{\rm{C}}}\left( {\nabla {{\rm{L}}_{\rm{i}}}} \right){\rm{ + N}}\left( {{\rm{0,}}{{\rm{\sigma }}^{\rm{2}}}{{\rm{c}}^{\rm{2}}}{\rm{I}}} \right){\rm{,~\sigma = }}\sqrt {\frac{{{\rm{2ln}}\left( {{\rm{1}}{\rm{.25/\delta }}} \right)}}{{{{\rm{e}}^{\rm{2}}}}}}$$

(16)

Among them, C = 1.5 is the gradient clipping threshold, $\:\left({\varepsilon}\text{=1.5,}\text{}\:{\delta}\text{=}{\text{10}}^{\text{-}\text{5}}\right)$ which satisfies Rényi differential privacy (RDP), the cumulative privacy loss satisfies $\:{{\varepsilon}}_{\text{total}}\text{=}\sqrt{\text{T}\left({{\varepsilon}}^{\text{2}}\text{+}\frac{\text{2}{{\varepsilon}}^{\text{3}}}{\text{3}}\right)}$, $\:\text{T}$and is the training round.

To ensure strict privacy guarantees throughout the federated learning process, this study performs formal privacy accounting for the client-side local training. As shown in Formula (16), each client performs one DP-SGD optimization step per round of local training. This operation, given a sampling rate q and noise multiplier σ, satisfies $\:\left({\alpha}\text{,}{\alpha}\text{/}\left(\text{2}{{\sigma}}^{\text{2}}\right)\right)\text{-RDP.}$.

For a complete process involving a total of T rounds of federated training, with each client performing E local iterations per round, the privacy consumption is accounted for using the RDP composition theorem. The total privacy cost in the RDP dimension for the entire training process is $\:{{\epsilon}}_{\text{RDP}}\left({\alpha}\right)\text{=}\text{T}\cdot\text{E}\cdot{\alpha}\text{/}\left(\text{2}{{\sigma}}^{\text{2}}\right)\text{.}$.

Finally, we convert the accumulated RDP privacy cost to the standard (ϵ,δ)-Differential Privacy guarantee using the following formula:

$$\:{\varepsilon}\text{=}\underset{{\alpha}\text{>1}}{\text{inf}}\left[{{\varepsilon}}_{\text{RDP}}\left({\alpha}\right)\text{+}\frac{\text{log}\left(\text{1/}{\delta}\right)}{{\alpha}\text{-1}}\right]$$

(17)

In our experiments, setting $\:{\delta}\text{=}{\text{10}}^{\text{-5}}$ (a conservative value less than the reciprocal of the dataset size) and optimizing over α, we calculated that under the set number of training rounds T and local iterations E, the total ε is strictly bounded above by 1.5. This ε=1.5 is a theoretical upper bound of our privacy protection capability, based on a worst-case analysis. The empirical PLR metric reported later serves as an empirical validation of this theoretical bound under the actual data distribution. Its value (0.12) being significantly lower than the theoretical bound further strengthens the reliability of our conclusion.

The global model of server-side knowledge distillation utilizes Asif et al.‘s (2020) KL divergence fusion of heterogeneous knowledge and introduces a distillation strategy of temperature scaling and attention weighting.

$${{\rm{L}}_{{\rm{KL}}}}{\rm{ = }}{{\rm{\tau }}^{\rm{2}}}\cdot{{\rm{E}}_{{\rm{x}} \sim {\rm{Dpub}}}}\left[ {{\rm{KL}}\left( {\frac{{{\rm{exp}}\left( {{{\rm{z}}_{\rm{g}}}{\rm{/\tau }}} \right)}}{{\sum {\rm{exp}}\left( {{{\rm{z}}_{\rm{g}}}{\rm{/\tau }}} \right)}}} \right)\left[ {\left[ {\frac{{\rm{1}}}{{\rm{K}}}\mathop \sum \limits_{{\rm{i = 1}}}^{\rm{K}} \frac{{{\rm{exp}}\left( {{{\rm{z}}_{\rm{i}}}{\rm{/\tau }}} \right)}}{{\sum {\rm{exp}}\left( {{{\rm{z}}_{\rm{i}}}{\rm{/\tau }}} \right)}}} \right]} \right.} \right.$$

(18)

In Eq. (15), $\tau$=0.7 represents the temperature parameter, $\:{\text{z}}_{\text{g}}$ represents the global model output,$\:\:{\text{z}}_{i}$ represents the client model output.

When constructing cross-school comparative samples, the study defined the cross-modal positive and negative sample pairs as follows based on Chen et al.‘s (2018) research.

Positive sample pair P(). Data from different schools but belonging to the same curriculum. In this context, ‘the same course’ refers to courses with identical or highly similar official course names and objectives, such as Introduction to Mao Zedong Thought and Theoretical System of Socialism with Chinese Characteristics in different schools. Cross school data for the same course category $\:\left({\text{x}}_{\text{i}}\text{,}{\text{x}}_{\text{j}}^{\text{+}}\right)$ meets the requirements $\:\text{Si}{\text{m}}_{\text{sem}}\left({\text{x}}_{\text{i}}\text{,}{\text{x}}_{\text{j}}^{\text{+}}\right){\geqslant0.8}$.

Negative sample pair N(). In this study, ‘course heterogeneity$\:{\prime\:}$ was determined based on the following two levels of criteria:

Differences in disciplines: The primary criterion is the classification of the first-level disciplines in the Catalogue of Undergraduate Programmes in General Colleges of Higher Education of the Ministry of Education of the People’s Republic of China (MOE). Courses belonging to different disciplines (e.g., ‘Computer Science and Technology’ vs. ‘Marxist Theory’) are automatically determined as heterogeneous courses.

Course content similarity: We calculate the TF-IDF vector cosine similarity between the syllabus and the teaching objectives of the courses at the same level of discipline. If the similarity is lower than a preset threshold θ = 0.3 (determined by grid search on the validation set), the course is determined to be heterogeneous. For example, Introduction to Computing and Data Structures, which belong to the same computer discipline, are considered as negative samples because their core content focus is different and the similarity is calculated to be below the threshold. Heterogeneous course data $\:\left({\text{x}}_{\text{i}}\text{,}{\text{x}}_{k}^{-}\right)$, satisfying $\:\text{Si}{\text{m}}_{\text{sem}}\left({\text{x}}_{\text{i}}\text{,}{\text{x}}_{k}^{-}\right){\leqslant0.3.}$.

The multi-granularity contrastive loss is based on the research of Pradhan et al., using a mixed contrastive loss that combines inter-school course similarity and space-time correlation.

$${{\rm{L}}_{{\rm{CL}}}}{\rm{ = - log}}\frac{{\mathop \sum \nolimits_{\left( {{\rm{i,}}{{\rm{j}}^{\rm{ + }}}} \right) \in {\rm{P}}} {\rm{exp}}\left( {{{\rm{S}}_{{\rm{i}}{{\rm{j}}^{\rm{ + }}}}}{\rm{/}}{{\rm{T}}_{\rm{C}}}} \right)}}{{\mathop \sum \nolimits_{\left( {{\rm{i,}}{{\rm{j}}^{\rm{ + }}}} \right) \in {\rm{P}}} {\rm{exp}}\left( {{{\rm{S}}_{{\rm{i}}{{\rm{j}}^{\rm{ + }}}}}{\rm{/}}{{\rm{T}}_{\rm{C}}}} \right){\rm{ + }}\mathop \sum \nolimits_{\left( {{\rm{i,}}{{\rm{k}}^{\rm{ - }}}} \right) \in {\rm{N}}} {\rm{exp}}\left( {{{\rm{S}}_{{\rm{i}}{{\rm{k}}^{\rm{ - }}}}}{\rm{/}}{{\rm{T}}_{\rm{C}}}} \right)}}{\rm{ + \lambda }}\parallel {{\rm{W}}_{\rm{c}}}\parallel _{{\rm{Fro}}}^{\rm{2}}$$

(19)

Among them,$\:{\:S}_{ij}={z}_{i}{z}_{j}/\parallel\:{z}_{i}\parallel\:\parallel\:{z}_{j}\parallel\:$ represents cosine similarity, $\:{{\tau}}_{c}$=0.7 represents temperature comparison, $\:\lambda$=0.01 and controls regularization intensity.

Dynamic weight aggregation adjusts the aggregation weight based on the client’s contribution (Zhao et al., 2016), defining the contribution index as.

$$\:{{\alpha}}_{\text{i}}\text{=}\frac{\text{I}\left({\text{z}}_{\text{i}}\text{,}{\text{z}}_{\text{g}}\right)}{\sum\:_{\text{j}\text{=1}}^{\text{K}}\text{I}\left({\text{z}}_{\text{i}}\text{,}{\text{z}}_{\text{g}}\right)}$$

(20)

The global model is updated to.

$$\:{\text{W}}_{\text{g}}^{\text{t}\text{+}\text{l}}\text{=}\sum\:_{\text{i}\text{=}\text{l}}^{\text{K}}{{\alpha}}_{\text{i}}{\text{W}}_{\text{i}}^{\text{t}}\text{+}\eta\cdot\text{Pr}{\text{o}\text{j}}_{\text{s}}\left(\nabla\:{\text{L}}_{\text{KL}}\right)$$

(21)

Among them, $\:\text{Pr}{\text{o}\text{j}}_{\text{s}}\left(\cdot\right)$represents the Stiefel manifold projection to ensure parameter orthogonality.

The enhancement of adversarial robustness is based on the introduction of adversarial sample generators in Wang et al. (2019) research.

$$\:\underset{\theta}{\text{min}}\text{g}\underset{{\phi}}{\text{max}}{\mathbb{E}}_{x\sim\:D} \lfloor{L}_{CL}\left(x+{G}_{\varphi\:}\left(x\right)\right)-\beta\:\cdot\:{\parallel{\text{G}}_{{\phi}}\left(\text{x}\right)\parallel}_{TV}\rfloor$$

(22)

Among them, $\:{\text{G}}_{{\phi}}\left(\text{x}\right)\text{=}\text{s}\text{ign}\left({\nabla\:}_{\text{x}}{\text{L}}_{\text{CL}}\right)\text{}$for Fast Gradient Symbol Attack (FGSM), the disturbance intensity is controlled $\beta=0.1$ .

This study compares the performance of Federated Contrastive Learning (Fed CL) under varying privacy budgets, utilizing the federated contrastive learning framework as illustrated in Fig. 5. As indicated in Table 2, when ε=1.5, the system strikes an optimal balance between privacy protection and model performance. The system’s classification accuracy is 89.3%, only a 2.4% decrease from ε=2.0, while the Privacy Leakage Risk (PLR) reduces significantly from 0.18 to 0.12. The dynamic weight aggregation error remains minimal at 2.45 × 10⁻³ when α=0.18, confirming the efficacy of the Stiefel manifold projection strategy. Furthermore, the Adversarial Robustness Index (AR) achieves its highest value of 82.4% at ε=1.5, suggesting that moderate noise injection can simultaneously enhance model security.

Fig. 5

Federated contrastive learning framework.

Table 2 Performance comparison of fed CL framework in cross school ideological and political Assessment.

The specific algorithm steps of this study are shown in Table 3.

Table 3 Introduction to algorithm Steps.

• 1) The study proposes a technology roadmap that delineates a sophisticated, multi-tiered architecture for the cross-school education evaluation system, depicted in Fig. 6. This architecture is anchored by two central engines: the “space-time graph diffusion model” and “federated contrastive learning.” Together, they form a comprehensive, closed-loop system for research and development, encompassing theoretical modeling, system implementation, and application verification. The technical framework is organized into six distinct modules, structured hierarchically from top to bottom.

• 2) The first module, labeled “Introduction,” sets forth the fundamental objective of ensuring privacy protection and optimizing dynamic modeling in a collaborative context.

• 3) From a methodological perspective, the space-time evolution of educational behavior is effectively modeled through the thermodynamic diffusion equation of STG-DM. This approach integrates the dynamic weight aggregation mechanism of FedCL to address the issue of data silos.

• 4) Within the engineering implementation layer, a visualization engine was devised to facilitate real-time analysis of nodes at the 100,000 level. Through five-fold cross-validation, it was ascertained that the model’s prediction error diminished by 18.7%.

• 5) Through the implementation of a conversion layer and the establishment of an “evaluation feedback optimization” dynamic cycle mechanism, there was a notable enhancement in the efficiency of cross-school resource sharing. Specifically, within the empirical study of the Beijing Tianjin Hebei University Alliance, there was a significant improvement, measuring at 53.8%.

• 6) In this study, we engage in a comprehensive discussion and offer pertinent suggestions. We draw comparisons with previous research and construct a dynamic cycle mechanism for “evaluation feedback optimization.” Furthermore, we propose a three-pronged optimization path to address the challenges associated with technology implementation.

• 7) Conclusion: This paper heralds a paradigm shift in educational evaluation, transitioning from an experience-driven approach to a data-driven one. Its methodological framework offers universally applicable guidance for developing a smart education ecosystem.

Fig. 6

Technical Roadmap.

Model architecture and implementation details

To ensure reproducibility, we specify the core network architectures. The STG-DM encoder consists of a two-layer adaptive graph convolution with hidden dimensions of [64, 128], followed by a spatio-temporal attention layer (ASTA, Eq. 12) with 8 attention heads. The extracted features are then processed by a temporal decoder comprising a Gated Recurrent Unit (GRU) with a hidden size of 256 and a linear output layer.

The FedCL framework’s projection heads, used for contrastive learning, are implemented as a 3-layer Multilayer Perceptron (MLP) with dimensions [feature_dim, 512, 256, 128] and ReLU activation. This projects client features into a common latent space for comparison. All models were implemented in PyTorch 1.12.1 and trained on a server with NVIDIA A100 GPUs.

System implementation and experimentation

System architecture

This study proposes a distributed intelligent system for cross-school education evaluation, designed and implemented based on the theoretical framework of the Space-Time Graph Diffusion Model (STG-DM) and Federated Comparative Learning (Fed CL). In constructing the CSED−24 dataset, our research team gathered classroom surveillance videos from 30 universities using multimodal fusion technology. Specifically, we utilized the Hikvision DS−2CD3T86 camera, which was sampled at 5 frames per second and adjusted to a resolution of 1280 × 720. Additionally, we collected student course feedback texts, totaling 23,000 instances. These were gathered via a questionnaire network platform, with an average text length of 58.3 characters, as well as structured management records exported from the educational administration system. These records comprised 12 types of fields including attendance and grades. For video preprocessing, we first sparsified the original 5 fps 1280 × 720 H.264 stream by retaining one key frame out of every three. We then applied YOLOv5m-face (confidence threshold = 0.65, NMS = 0.45) to detect teacher and student bounding-boxes, discarding boxes whose area < 1% of the frame. A TSN backbone extracted an 8-D behaviour vector (hand-raising, head-lowering, writing, etc.). Any segment with action entropy < 0.15 or confidence fluctuation > ± 0.25 for eight consecutive frames was regarded as an abnormal silence clip and removed. Each lecture was finally represented by a fixed-length sequence of L v = 150 frames; sequences shorter than 150 frames were zero-padded at the tail, whereas longer ones were down-sampled uniformly to guarantee identical tensor size across campuses. Textual feedback was first tokenised and POS-tagged by Harbin-IT LTP 4.1. Stop-words were removed using the Harbin extended list (1 893 words) together with any token shorter than two characters. We built an education-specific sentiment dictionary of 1 847 entries (892 positive, 955 negative) and obtained 1 024-dimensional sentence embeddings via RoBERTa-wwm-ext. To handle length variance, we set a maximum length of 64 tokens; shorter posts were padded with [PAD], and longer ones were head-and-tail truncated (first 48 + last 16 tokens), yielding a uniform input tensor of size N×64 × 1024.

Data cleansing standards were set as follows: noise records containing fewer than 15 characters or exhibiting sentiment polarity variability exceeding 3.0 were removed. For missing values, the administrative records comprised 12 fields (attendance rate, grades, assignment submission rate, etc.). We first calculated the proportion of missing values grouped by course-class-week. Fields with less than 5% missing values were imputed using linear interpolation; the remaining fields were processed via MissForest. All numerical features undergo Z-score standardisation, whilst categorical variables are target-coded to mitigate the high cardinality effect. The final cleaned dataset is organised into a 12 × 24-hour tensor, with remaining hourly-level missing values imputed via forward filling to preserve temporal continuity. This yielded a comprehensive multimodal dataset encompassing video behaviour matrices (25 dimensions per sample), textual sentiment vectors (1024 dimensions per sample), and management feature tensors (12 × 24 dimensions). Following data cleansing, the dataset comprised 187,000 valid samples with a purity rate of 93.6%.

Table 4 Performance test of front end visualization Engine.

The data suggests a strong correlation between the rendering performance of space-time heatmaps and the node embedding dimension, as evidenced in Table 4. When the node embedding dimension is set at 128, the delay is only 680 ms for 50,000 nodes, but rises to 2450 ms for 200,000 nodes. This suggests that WebGL’s hierarchical detail optimization effectively mitigates the challenges posed by large-scale data.

Table 5 Performance indicators for federated computing Backend.

The results indicate that with a batch size of 32 and a concurrent client of 30, the throughput of the federated training module is 850 samples/second. The GPU memory usage is 6.2 GB, the federated aggregation frequency stands at 3.2 times/second, and the dynamic weight aggregation error is 2.45 × 10⁻³. This error aligns with the theoretical value of the manifold projection constraint as presented in Eq. 17. Furthermore, the real-time inference module processed 8900 samples per second with a response time of 18 ms and a regularization loss of 0.45 under conditions of batch 128 and concurrent 100. As detailed in Table 5, these findings confirm the space-time attention compression capabilities of the ASTA module.

Table 6 Performance test of privacy protection Layer.

As shown in Table 6, with a privacy budget ε of 1.5, the model experiences an accuracy loss of 4.3% and a gradient noise standard deviation of 0.15. These values align with the theoretical values of the Rényi differential privacy constraints (α=5, δ=1e−5), as presented in Eq. 16. The process of parameter encryption takes 1150 ms, which corresponds to the cost of generating and decrypting a 1024-bit key using Paillier encryption. The weight variance in federal aggregation is noted at 2.87 × 10⁻², suggesting that the Stiefel manifold projection effectively curtails parameter divergence. A cross-school data leakage rate (PLR) of 0.12 confirms the successful inhibitory effect of the Fed CL framework’s contrastive learning on privacy leakage. With ε set at 1.5, adversarial robustness achieves 82.4%, demonstrating that a moderate privacy budget can strike a balance between the robustness and utility of the model. Finally, a local model KL divergence of 0.78 (with ε=1.5) indicates that knowledge distillation effectively reduces the impact of heterogeneous data distribution.

The front-end visualisation engine of the system adopts an incremental information presentation strategy, and the default interface only displays key indicators (such as MAE, F1-score, resource usage) and their trends, while the advanced functions (such as hypergraph diffusivity and fourth-order tensor information) are placed under the ‘Expert Mode’ for in-depth analysis by the technical team. Advanced features (e.g. hypergraph diffusion rate, fourth-order tensor mutual information) are placed in ‘Expert Mode’ for in-depth analysis by the technical team. Meanwhile, all the indicators are accompanied with common explanations and suggestions for teaching management, for example, ‘hypergraph diffusion rate > 5.0’ corresponds to the tip ‘This campus is highly efficient in integrating information, and is recommended to be used as a hub for cross-campus cooperation’.

Experimental design

The CSED−24 dataset covers 30 universities in 6 provinces and cities, integrating multi-modal data through space-time alignment and quaternion encoding. The experiment uses five - fold cross validation, with a space-time window set to 24 h. The regional cultural impedance factor is generated by weighting historical policy data, as shown in Table 7.

Table 7 Statistical characteristics of CSED−24 cross school ideological and political dataset.

Table 7 demonstrates that the Beijing campus has both the largest sample size and the lowest mean space-time curvature. This suggests a strong degree of space-time continuity in their teaching strategies. In contrast, the Chengdu campus exhibits the highest space-time curvature, indicative of significant fluctuations in teaching behavior attributable to regional cultural differences. The Guangzhou campus achieved a cross-school cooperation intensity of 5.12, confirming the optimization effect of the geographic impedance factor. Furthermore, a positive correlation was found between the mean emotional entropy and the number of words in the text (Pearson r = 0.87, p < 0.01). This suggests that the spectral clustering algorithm effectively quantifies the quality of teacher-student interaction. A comparative experiment was conducted between Fed CL-STGDM and other models such as Fed Avg and GraphSAGE. All the models were implemented utilising PyTorch, operating in a hardware environment of NVIDIA A100 (8 x GPU), with a batch size of 64.

Fig. 7

Comparison of experimental results.

Following thorough research, it has been observed that the Fed CL-STGDM significantly surpasses others in terms of indicators such as RMSE and the F1 score. This confirms the collaborative benefits of the space-time graph diffusion model and federated contrastive learning. Figure 7 demonstrates that the space-time prediction sensitivity reaches an impressive 82.4%, suggesting that the ASTA module has superior capability to capture mutation events compared to ST-GCN. Conversely, the AHP grey correlation method performs poorly due to its lack of ability to model dynamic correlations, thereby underscoring the necessity for deep learning models. The baseline model parameter table is included for reference, as shown in Table 8.

Table 8 Add the baseline model parameter table.

In the cross-university verification experiment, the research team categorized 30 universities into three distinct groups based on student enrollment: small (< 5k), medium-sized (5k−10k), and large (> 10k). These institutions were spread across four major regions: North China, East China, South China, and Southwest China. Additionally, the study differentiated between comprehensive, normal, and science and engineering educational focuses. Employing a stratified sampling approach, three institutions from each subcategory were randomly chosen to form an independent test set. Subsequent evaluations were multi-dimensional, with model parameters remaining unchanged. As detailed in Table 9, for medium-sized normal universities in South China, the model’s MAE was notably lower at 2.31 ± 0.09 (n = 15,200) compared to 3.12 ± 0.14 (n = 23,400) for large polytechnic universities in Southwest China. This disparity is significantly associated with the regional cultural impedance factors distribution in Table 9, as evidenced by a Pearson correlation coefficient of r = 0.83 (p < 0.001). Notably, for institutions with a student body of less than 3k, the model reduced the spatio-temporal prediction error’s fluctuation range by 29%. This was achieved by dynamically adjusting the diffusion coefficient λ in Eq. 10, shifting from a baseline of 0.8 to 1.2, underscoring the efficacy of the parameter dynamic adaptation mechanism.

Table 9 Comparison of Cross-school generalization Performance.

Experimental results

Based on the CSED−24 dataset, compare Fed CL-STGDM with Fed Avg, Graph SAGE and other models, evaluate RMSE/MAE for regression tasks, and use F1 score for classification tasks. The specific results are shown in Table 10.

Table 10 Experimental results of model performance Comparison.

The research data was analyzed using the two-sample t-test (α=0.05) to ascertain the significance of the model differences. The Mean Absolute Error (MAE) between Fed CL-STGDM and ST-GCN was found to be t = 2.15(p = 0.032), and t = 1.24(p = 0.216) when compared with ST-Meta. In instances where p < 0.05, the null hypothesis is rejected, indicating a statistically significant improvement. The Fed CL-STGDM model demonstrated statistically significant improvements over several baselines. Specifically, it achieved an 18.7% reduction in MAE (95% CI: 15.2%−22.1%) and 17.3% increase in F1-score (95% CI: 14.5%−20.1%) compared to Fed Avg (both p < 0.001). However, its performance advantage over the ST-Meta model, while favorable (MAE reduction of 4.9%), was not statistically significant (p = 0.216), suggesting comparable performance in certain scenarios. This validates the synergistic advantage of the space-time graph diffusion model combined with federated contrastive learning. The sensitivity achieved for space-time prediction was 82.4%, marking a 3.5% improvement over ST-GCN. This suggests that the ASTA module possesses superior capability in capturing mutation events. Furthermore, the sentiment classification accuracy was reported at 89.3%, illustrating the precise quantification of teacher-student interaction quality through deep spectral clustering.

Through extended baseline comparison experiments with FedGraphNN, Spatio-Temporal Diffusion Model (ST-DiffNet) and Multimodal Fusion Model (MSF-Transformer) systems, this study validates the comprehensive advantages of the Fed CL-STGDM framework. Fed CL-STGDM achieves an optimal balance of prediction accuracy, privacy protection and computational efficiency (see Supplementary Material) to achieve an optimal balance, fully demonstrating its sophistication and usefulness as a cross-institutional educational assessment framework.

Fig. 8

Comparison of ablation experiments.

Through ablation experiments, as shown in Fig. 8, removing the ASTA module resulted in an 8.8% decrease in space-time prediction sensitivity and a 17.8% increase in RMSE, verifying the critical role of the space-time attention mechanism in dynamic association modeling. Removing Fed CL contrastive learning reduces the consistency of federated aggregation to 88.7%, indicating that cross-school knowledge alignment strategies are indispensable. Replacing STG-DM with regular GCN resulted in a 3.5% decrease in F1 score, demonstrating the advantage of thermodynamic diffusion equations in modeling heterogeneous data.

In the data robustness test, the research team constructed a sequence of decreasing training data volumes through stratified random sampling, maintaining the size of the test set unchanged. As shown in the extended data in Table 11, when the amount of training data decreased to 30%, the MAE of Fed CL-STGDM rose from the baseline 2.54 to 2.89 (Δ=13.8%), and the R² value remained at 0.812 ± 0.021, which was significantly better than the MAE increase of Fed Avg, which reached 28.3%. The calculation of model data scarcity sensitivity SSI shows that the SSI of Fed CL-STGDM is 0.15, which shows stronger robustness than ST-GCN (SSI = 0.22) and GraphSAGE (SSI = 0.27). This advantage stems from the knowledge transfer efficiency of the contrastive learning mechanism in Formula 18. It can still maintain the cross-school feature alignment degree of 0.78 ± 0.03 at 50% of the data volume, enabling the model to effectively capture the common laws of educational behavior dissemination in a limited sample.

Table 11 Impact of data Scarcity.

The study tested the model accuracy loss, privacy leakage risk, and adversarial robustness under different privacy budgets ε, and the specific results are shown in Table 12.

Table 12 Privacy utility balance Analysis.

When ε=1.5, the model experiences an accuracy loss of 4.3%, a privacy leakage risk of 0.12, and achieves an adversarial robustness of 82.4%. These results confirm the optimality of the Fed CL framework in balancing privacy and utility. The consistency of federated aggregation is 92.1%, suggesting that dynamic weight aggregation effectively mitigates the impact of non-IID data distribution. However, when ε=2.5, the privacy leakage risk (PLR) rises to 0.25, with adversarial robustness diminishing to 73.5%. This underscores that overly lax privacy constraints can jeopardize model security. Theoretical analyses demonstrate that the Chebyshev convolution of STG-DM (Eq. 11) significantly reduces the complexity of spatio-temporal modeling, shifting it from O(N²) in ST-GCN to O(K|E|). Given N = 10⁵ nodes and |E|=2.3 × 10⁶ edges, the FLOPs for a single iteration drop from 4.7 × 10¹² to 8.9 × 10¹¹. In the realm of federated communication optimization, the Stiefel manifold aggregation (Eq. 20) employs rank constraints to compress parameter transfer amounts by 38%, thereby shortening the communication time per round from 980ms to 620ms in a 30-client scenario (Table 5). Real-time verification confirms that the hypergraph diffusion module (Eq. 6) sustains an O(N) complexity at a scale of 100,000 nodes, incurring an inference delay of a mere 18ms. This represents a 2.3-fold acceleration relative to the O(N²) complexity of GraphSAGE (Table 4 depicts the comparison of new complexity levels). With respect to resource consumption, training the complete model required 2.4 h per epoch and utilized 10.5GB of memory, marking a 41% reduction in video memory compared to ST-GCN.

Table 13 Comparison of adaptive aggregation Strategies.

The experimental design incorporates four groups to compare federated aggregation frequencies, including a fixed frequency (30 min/2 hours/6 hours) and an adaptive strategy. As illustrated in Table 13, the use of adaptive aggregation maintains an F1-score of 0.891 ± 0.021 while significantly decreasing the model’s response delay from 1850 ± 95ms in the high-frequency group to 1320 ± 85ms. This adaptive approach also reduces communication overhead by 41.2%. A Pareto frontier analysis suggests that the optimal equilibrium point is achieved when α=0.18 and ε=1.5. At this point, the privacy leakage risk PLR is 0.12 ± 0.02 and the resource utilization rate is 94.7 ± 0.9%, marking a 23.8% improvement over the fixed-frequency strategy. This optimization can be attributed to the dynamic contribution calculation mechanism in Eq. 19, which allows for the adaptive adjustment of the parameter transfer amount based on the model’s convergence degree. Consequently, the communication frequency in the later stages of training is automatically reduced from 3.2 times per hour to 1.5 times per hour.

Table 14 Parameter heat map data matrix.

The parameter adjustment experiment demonstrated that an increase in α from 0.1 to 0.3 led to a rise in the consistency MC of the federated model from 0.82 ± 0.04 to 0.91 ± 0.03, with a sensitivity ΔMC/Δα of 0.32. However, when the privacy budget ε ranged between 1.0 and 2.5, the PLR sensitivity was a mere 0.12. The heat map analysis, presented in Table 14, indicates that the optimal parameter combination is α=0.18 and ε=1.5. At these values, the F1-score and delay achieved were 0.893 and 1320ms, respectively. The verification of the two-stage adjustment strategy revealed that α=0.25 was initially used to hasten convergence, resulting in a 37% increase in F1 during the initial five rounds of training. Subsequently, α was reduced to 0.15 for stable training, leading to a 58% decrease in parameter divergence during the final ten rounds. Overall, this strategy enhanced training efficiency by 29%.

To verify the ‘lightweight’ feature, Table 15 compares the computational cost of Fed CL-STGDM with the benchmark model. The model is evaluated on the CSED−24 test set (10,000 samples) using a single A100 GPU. The experimental results are shown in Table 15.

Table 15 Computational efficiency and model complexity Benchmark.

As shown in Table 15, this model achieves the lowest prediction error (MAE: 2.54) and the fastest inference speed (18ms) with 8.7 M parameter amount and 3.5GB video memory footprint. Compared with baseline models such as ST-GCN, the accuracy advantage is maintained with 41% less parameters, 35% less GPU memory and 28% higher inference latency. This data fully validates the claim of ‘lightweight system’ and shows that the framework successfully achieves a better ‘efficiency-accuracy’ trade-off through structural optimisation rather than simply scaling up the model, providing key evidence of its utility in resource-sensitive large-scale real-time deployment scenarios.

Application and verification

In order to reduce the obstacle of model complexity to the decision-making of education managers, the system is designed with a multi-level visual decision support interface. For example, in the application scenario of ‘Beijing-Tianjin-Hebei University Union’, the system presents the high-dimensional spatial and temporal features of STG-DM output through Spatio-Temporal Heatmap and Radar Chart. Educational administrators can use the heatmap to quickly identify the efficient periods of teaching behaviour, and use the radar chart to compare the performance of different campuses in terms of key indicators such as the frequency of teacher-student interactions, the adoption rate of the curriculum, the intensity of cross-campus collaboration, etc. The heatmap can also be used as a basis for comparing the performance of different campuses. “The system also provides dynamic strategy recommendations. In addition, the system also provides a dynamic strategy recommendation module, which automatically pushes out specific interventions such as ‘suggest cross-campus teaching experience exchange meetings’ if the ‘emotional entropy’ of a campus is detected to be persistently higher than the threshold.

Within the empirical framework of the Beijing-Tianjin-Hebei University Alliance, this study compares University A in Beijing, which employs an experience-driven approach, with University D in Chengdu, which adopts a data-driven strategy. University A has traditionally depended on expert experience to determine assessment indicators. From 2018 to 2021, it used the student-teacher ratio (1:18) and the number of courses as its primary assessment parameters. Despite a 23% increase in resource investment (from 12 million to 14.8 million yuan) following a curriculum reform in 2021, student satisfaction declined by 12%, highlighting the limited adaptability of static indicators to regional cultural variations. Conversely, University D in Chengdu implemented the Fed CL-STGDM system in 2022. Utilizing a spatio-temporal heat map, the system identified 14:00–16:00 each day as an inefficient period for teacher-student interaction. The school subsequently adjusted its course schedule to coincide with this high-frequency interaction window in the mornings. By 2023, student participation at University D had increased by 18%, and the frequency of cross-school resource sharing had reached 53.8 times per month (95% CI: 50.1–57.5), representing a significant increase from the baseline period, demonstrating the substantial benefits of data-driven decision-making. The comparison between the two universities reveals that the traditional, experience-driven model often encounters the dilemma of “high investment and low returns” in dynamic educational contexts. In contrast, the data-driven approach, utilizing hypergraph diffusion rates and federated knowledge distillation, effectively captures multimodal synergy effects and fosters innovation in the assessment paradigm.

Table 16 Long term deployment effect tracking of the Beijing Tianjin Hebei university Alliance.

Utilizing School D in Chengdu as a case study, the STG-DM model quantifies the synergistic effect of the “teacher-student-management” triad via Eq. 6. The hypergraph diffusion rate witnessed a significant increase from 3.12 ± 0.38 in 2022 to 5.12 ± 0.63 in 2023, thereby optimizing resource allocation during the traditionally inefficient midday period. The weight assigned to the regional cultural factor of this school was dynamically adjusted to 0.18 via federated comparative learning. In contrast, the weight of Beijing School A under the isolated model remained mere 0.05, leading to an unsuccessful cross-school strategy adaptation. The federated aggregation strategy effectively reduced the parameter divergence from 5.6 × 10⁻² in the conventional Fed Avg to 2.87 × 10⁻² via Stiefel manifold projection, thereby facilitating efficient knowledge transfer across schools. This mechanism’s effectiveness was reinforced within the Beijing-Tianjin-Hebei Alliance: When School B in Shijiazhuang integrated the high-quality video teaching plan from School A in Beijing and dynamically adapted it with the cultural resistance factor (0.15), the student satisfaction rate surged from 68% to 87% post federal optimization, as illustrated in Table 16. This underscores the significance of data-driven parameter interpretability in fostering cross-regional collaboration.

Fig. 9

Multi Region Expansion Verification.

Figure 9 reveals the difference in model fitness in different regional extensions, in which the model convergence period in South China (e.g., Guangzhou, with a factor of 0.092), which has a lower cultural resistance factor, is only 12.7 days, which is 43% faster than that in Southwest China (e.g., Chengdu, with a factor of 0.183), which has a higher cultural resistance factor. This significant efficiency difference strongly suggests a negative correlation between the regional cultural resistance factor and the speed of model convergence.

To quantitatively verify this observation, we calculated the Pearson correlation coefficients between the cultural resistance factor and the corresponding convergence period for the six regions. The results of the analyses show a strong negative correlation (r =−0.89, p < 0.02). This means that the higher the cultural resistance factor, the longer it takes for the model to reach convergence. There is a clear mechanistic explanation for this finding: higher cultural resistance factors (e.g. 0.183 in Chengdu) reflect the fact that educational behaviors in the region are more frequently subject to dynamic policy interventions, resulting in a more noisy and uncertain local data distribution. In a federated learning framework, this directly translates into greater client drift, which in turn requires more communication rounds to coordinate model updates on different clients, and ultimately manifests itself in longer convergence times. On the contrary, regions with low cultural resistance factors like Guangzhou, where the data distribution is relatively stable, have a smoother and more efficient federated optimisation process.

This analysis not only confirms the effectiveness of the cultural resistance factor as a quantitative indicator of regional heterogeneity, but also provides a key basis for predicting and optimizing cross-regional federated learning deployments in practice: for regions with high resistance factors, more aggressive client regularization or dynamically weighted aggregation strategies may be required to alleviate convergence bottlenecks.

These strategies encompassed federated aggregation frequency, privacy budget ε (as delineated in Eq. 12), and resource scheduling cycle. The experimental duration spanned three months, during which data was collected from 500 courses across 20 universities. The findings of this research are presented in Table 17.

Table 17 Comparison of the effectiveness of dynamic adjustment Strategies.

The data suggests that the adaptive aggregation strategy model yields the highest level of accuracy; however, it presents a response delay of 2150 ms. This necessitates a balance between real-time performance and precision. The low-frequency aggregation poses the least risk for privacy leakage, yet it offers a resource utilization rate of only 78.9%, suggesting the need for dynamic adjustments to the federated aggregation frequency. The fixed privacy budget (ε=1.5) effectively balances resource utilization (88.2%) with model accuracy (0.848), making it optimal for long-term deployment.

Fig. 10

User Behavior and System Efficiency.

Within the context of user behavior analysis, Fig. 10 demonstrates that the frequency of teaching reflection has a strong positive correlation with model accuracy. This confirms the beneficial influence of real-time warning modules on teaching optimization. Conversely, the number of resource searches exhibits a negative correlation with response latency. This suggests an area for system improvement in terms of caching strategy. Furthermore, the initiation of cross-school collaborations shows a positive correlation with resource consumption. Consequently, it is imperative to strike a balance between the advantages of collaboration and the additional hardware load induced.

Discussion

The cross-school education assessment system proposed in this study, which is based on the spatio-temporal graph diffusion model (STG-DM) and federated contrastive learning (Fed CL), has yielded significant results in terms of data privacy protection, dynamic spatio-temporal modeling, and model generalization capabilities. Firstly, from a theoretical innovation standpoint, the STG-DM enables high-precision modeling of the spatio-temporal evolution of educational behavior via thermodynamically driven diffusion equations and adaptive spatio-temporal attention mechanisms. This approach effectively addresses the issue of local overfitting caused by the failure of dynamic association modeling in traditional methods in data silo scenarios, thereby reducing the mean absolute error (MAE) by 18.7%. Secondly, the Fed CL framework adeptly mitigates the model generalization bottleneck induced by data silos across multiple schools through the utilization of dynamic weight aggregation and local knowledge distillation strategies. In cross-domain testing, it enhances the global evaluation accuracy by 12.5% and stringently controls the privacy leakage risk (ε) within 1.5, thereby achieving a balanced optimization of privacy protection and model performance.

This study pioneers the application of thermodynamic diffusion principles to education spatio-temporal modeling, culminating in the development of a lightweight evaluation system with independent intellectual property rights. This novel system facilitates real-time spatio-temporal analysis of 100,000 nodes, offering a comprehensive visualization of educational outcomes via a multi-scale visualization engine. When contrasted with traditional federated learning frameworks, our dynamic aggregation strategy enhances model training efficiency by approximately 40%, demonstrating stable convergence characteristics even under extreme data distribution scenarios. Furthermore, the privacy protection layer strategically combines Rényi differential privacy and gradient truncation technology. This ensures strict adherence to privacy budget constraints while maintaining an acceptable level of model utility loss.

From an operational standpoint, the implementation at Chengdu D School illustrates that the data-driven evaluation model can expedite the decision-making process from a traditionally experience-driven six months to a real-time response, with a system warning delay of less than two seconds and a strategy iteration cycle of seven days. Following the implementation of the Fed CL-STGDM system, a correlative improvement of 37% in evaluation accuracy was observed at Chengdu D School. While this substantial gain is temporally associated with the system’s deployment and aligns with its intended functionality, we acknowledge that the observational nature of this case study limits definitive causal attribution. To strengthen the validity of this finding, future work should employ controlled A/B testing. However, the initial resistance to change observed at Beijing University A underscores the necessity for a transitional framework that combines both data and experience in decision-making. This approach entails first fine-tuning the weights of experience-based metrics using data during the preliminary stages, and then gradually shifting towards fully data-driven decision-making through federated collaboration in subsequent phases. A pilot study conducted at Shijiazhuang University B using this hybrid model yielded promising results, with the model’s accuracy reaching 82.1%, marking a 19.5% improvement over purely experience-based models. It is important to address the methodological context of this real-world verification. The deployment of the Fed CL-STGDM system across the university alliance was a strategic decision, precluding the establishment of a randomized control group for a classical A/B test. Consequently, the performance comparisons presented here are primarily observational. To mitigate the inherent limitations of this design and bolster the claim of the system’s effectiveness, we pursued two strategies: First, we compared the trajectory of Chengdu D School against the static. experience-driven approach of Beijing A School, demonstrating a significant performance gap that emerged concurrently with our system’s adoption. Second, and more critically, the internal ablation studies and controlled laboratory experiments on the CSED−24 dataset provide robust, controlled evidence for the mechanistic superiority of the Fed CL-STGDM framework. The strong performance observed in the field study is consistent with these controlled experimental results, suggesting that the observed improvements are likely driven by the implemented system.

Despite the high technical complexity of STG-DM and FedCL framework, the system has effectively transformed from ‘technical indicators’ to ‘management insights’ through multi-level visualisation and semantic transformation mechanisms. For example, in Chengdu, School D, the system identified ‘2−4pm as an inefficient time for interaction’ and quickly adjusted the course schedule to increase student engagement by 18%. This shows that by providing an intuitive, actionable feedback interface, education administrators can make efficient decisions without having to deeply understand the mechanics of the model. In the future, we will further introduce interpretable AI techniques, such as feature importance attribution, to enhance the trust and acceptance of the model output on the management side.

Although the STG-DM with FedCL framework proposed in this study performs well in cross-school educational assessment, it still has several limitations. First, the model is highly dependent on high-quality multimodal data. In the data collection stage, if the video quality is low, the text sentiment labelling is inconsistent or the administrative records are missing, it will directly affect the accuracy of spatio-temporal alignment and feature fusion. For example, in some school districts with weak facilities, the insufficient video frame rate leads to a decrease in the confidence level of behaviour recognition, which in turn affects the computational stability of the hypergraph diffusion rate. Second, the model complexity is high and the deployment cost is significant. Both the fourth-order tensor convolution in STG-DM and the multi-round federation aggregation in FedCL place high demands on computational and communication resources. Although we reduce some of the overheads through Stiefel stream projection and attention compression, the real-time performance of the system may still be affected in resource-constrained environments (e.g., small and medium-sized institutions). Third, the quantification of cultural impedance factors still relies on the weighting of historical policy data, which fails to fully capture dynamic socio-cultural changes. For example, the adaptive ability of the model still lags behind in sudden policy adjustments or cross-regional cooperation. In addition, although the federal comparative learning mitigates some of the biases through knowledge distillation in the face of extreme non-independently identically distributed (non-IID) data, it still fails to fundamentally solve the problem of inconsistent model convergence. Finally, although the interpretability of the system is enhanced by heat maps and radar diagrams, there is still a ‘black box’ concern in the semantic transformation of high-dimensional spatial and temporal features to management decisions. Interpretable AI techniques (e.g., attention visualisation, feature attribution) will be introduced in the future to enhance decision transparency and user trust.

Conclusion

This paper proposes a cross-school educational evaluation system based on spatio-temporal graph diffusion models and federated contrastive learning. Its core contributions include: constructing an evaluation framework that balances data privacy and model performance, enabling cross-school collaboration under controllable privacy risks (ε < 1.5); Significantly enhancing predictive capability through dynamic spatio-temporal modelling, reducing prediction error by 18.7% and improving evaluation accuracy by 12.5% in heterogeneous data environments; Achieving lightweight system deployment with sub−2-second response latency, shortening decision cycles from months to near real-time. Moving forward, we shall pursue continuous optimisation across four dimensions: Enhancing cross-cultural adaptability by integrating social dynamics and meta-learning mechanisms; Deepening blockchain integration to establish traceable evaluation chains and smart contract incentive frameworks; Advancing model compression to achieve over 40% parameter reduction with no more than 3% performance degradation; Improving system interpretability by synthesising techniques such as SHAP and LIME to generate actionable management insights. These efforts will propel educational assessment towards greater security, efficiency, and transparency.