Introduction

Electric power systems worldwide are undergoing a profound transformation characterized by large-scale integration of renewable energy resources, increasing electrification of end-use sectors, and the rapid deployment of distributed flexibility assets1,2,3. The resulting environment is both more sustainable and more complex, as the variability and uncertainty inherent in wind and solar generation must be accommodated without compromising reliability or economic efficiency. Virtual power plants have emerged as one of the most promising paradigms for aggregating distributed resources into coherent portfolios that can provide energy, capacity, and ancillary services at scale3,4,5. By coordinating batteries, flexible loads, electric vehicles, and renewable generation behind a unified interface, these constructs have become central to the vision of future distribution and transmission-level markets. Yet, despite this promise, the question of how multiple heterogeneous virtual power plants interact with one another and with the underlying grid infrastructure over long-term horizons remains largely unexplored. Traditional approaches to flexibility coordination have typically focused on short-term operational problems such as day-ahead scheduling or real-time dispatch6,7,8. These formulations, while valuable, do not fully capture the contractual, seasonal, and multi-year dynamics that define the realistic engagement of flexible portfolios. Virtual power plants are not homogeneous resources; they carry distinct operational constraints, degradation characteristics, and service-level agreements that evolve over months and years. Moreover, their value to the grid depends not only on their own capabilities but also on their complementarities with other portfolios, the spatial distribution of their assets, and the network sensitivities that govern congestion relief. A planning and operation paradigm that fails to address these long-term interactions risks undervaluing flexibility, overburdening certain resources, and missing opportunities for efficiency and resilience9,10,11.

The research presented here addresses this gap by proposing a novel framework for rolling substitution of multi-virtual power plant resources over extended horizons guided by a network-based metric termed locational marginal flexibility. This measure, conceptually analogous to locational marginal pricing but applied to flexible activation rather than energy, quantifies the incremental benefit to social welfare of an additional unit of flexibility at a specific node and time. By embedding this valuation into a rolling multi-scale optimization model that spans year-to-season-to-week planning cycles, the framework ensures that substitution among portfolios is continuously aligned with the evolving needs of the grid. Complementarity among virtual power plants is explicitly measured through a multi-dimensional index capturing correlation of outputs, ramping synergy, congestion impact, and availability overlap, allowing the model to determine not only how much substitution to perform but also which portfolios should be paired for maximum long-term benefit. A distinguishing feature of this work lies in its treatment of uncertainty and risk. Renewable generation and demand are modeled through regime-clustered scenarios with distributionally robust ambiguity sets, enabling the optimization to hedge against structural shifts and persistent extremes such as prolonged heat waves or extended overcast conditions. Service-level agreements, including response latency, minimum duration, and success probability, are enforced through chance-constrained formulations that guarantee performance under uncertainty. Storage degradation and demand-side fatigue are incorporated through lifetime budget equations, ensuring that substitution decisions remain sustainable and do not overexploit assets. Together, these elements create a comprehensive and realistic representation of how multiple virtual power plants can be orchestrated over the long term.

The methodological structure of the study combines hierarchical optimization and decomposition techniques. At the top level, the model decides portfolio allocations and substitution quotas that maximize long-term social welfare, subject to contractual coverage and fairness rules. At the operational level, detailed dispatch and network feasibility are enforced through subproblems that consider state-of-charge dynamics, comfort envelopes, and congestion. Decomposition is achieved using optimality and feasibility cuts, consensus-based coordination, and sensitivity refresh steps that update locational marginal flexibility values from the most recent dispatch duals. Substitution is triggered only when statistically significant changes in value fields are detected, avoiding unnecessary churn and promoting stability. By integrating economic, contractual, physical, and behavioral dimensions into a single framework, the study advances beyond conventional optimization of virtual power plants. The proposed rolling substitution mechanism not only balances system cost, renewable integration, and reliability but also internalizes degradation, fairness, and resilience. Such a holistic formulation is novel in its scope and unique in its ability to link long-term strategic planning with short-term operational realities through a unified mathematical and methodological structure. The contributions of this paper can be summarized across four dimensions.

First, a rigorous definition of locational marginal flexibility is developed, establishing a metric that translates system-wide welfare sensitivities into actionable signals for substitution and reallocation of flexible resources.

Second, a complementarity index is constructed that quantifies synergies and substitutability among heterogeneous portfolios, providing a quantitative basis for long-term coordination.

Third, a rolling optimization model is introduced that combines contract awareness, service-level enforcement, distributionally robust uncertainty treatment, and degradation management, thereby offering a comprehensive planning-to-dispatch framework.

Fourth, an implementable substitution service is designed that integrates decomposition techniques, sensitivity refresh, and fairness adjustments, demonstrating how advanced optimization can be embedded into existing load management platforms.

Although recent studies on virtual power plant coordination and flexibility optimization have made significant progress, several limitations remain. First, most locational marginal pricing and flexibility valuation frameworks focus on short-term dispatch efficiency and overlook long-term welfare interactions that account for contractual coupling, resource degradation, and fairness. Second, existing stochastic and robust optimization methods often rely on fixed probability distributions or pre-defined uncertainty bounds, which limit their ability to adapt to evolving renewable variability and lead to either excessive conservatism or underestimation of risk. Third, few models consider the joint influence of fairness and degradation on flexibility utilization, which results in uneven participation among portfolios and reduced overall system resilience.

To overcome these limitations, this study develops a Locational Marginal Flexibility (LMF)-guided distributionally robust optimization framework for long-term coordination of virtual power plant portfolios under network and contract constraints. The main contributions are threefold. (1) The introduction of the LMF metric as a welfare-based measure of flexibility that captures its spatial and temporal value across the network. (2) The development of a contract-aware and degradation-coupled welfare formulation that balances economic efficiency, equity, and resource longevity. (3) The integration of a distributionally robust optimization approach using Wasserstein ambiguity sets to ensure reliability under data-driven uncertainty. Together, these contributions establish a unified, uncertainty-resilient framework that advances beyond conventional locational marginal pricing or stochastic coordination models and provides a physically interpretable foundation for long-term flexibility management.

Unlike prior studies that focus predominantly on short-term dispatch efficiency, fixed-distribution stochastic modeling, or isolated flexibility valuation, this work introduces three innovations. First, we establish a welfare-based Locational Marginal Flexibility (LMF) metric that jointly captures spatial network sensitivities, temporal welfare gradients, and contractual–degradation coupling, which has not been formalized in existing VPP or OPF literature. Second, we propose a multi-seasonal, distributionally robust welfare optimization model that integrates uncertainty ambiguity, long-term degradation budgets, fairness-aware quota evolution, and SLA reliability enforcement into a unified structure. Third, we design an implementable rolling substitution mechanism that blends dual-sensitivity refresh, scenario reduction, and ADMM-based coordination to enable scalable long-term VPP cooperation. Together, these contributions fill a clear methodological gap by linking long-term welfare planning with operational dispatch under uncertainty–an area insufficiently addressed in previous studies.

Literature review

The study of virtual power plants has gained tremendous traction over the last decade, reflecting the urgent need to coordinate distributed energy resources and flexible demand in systems dominated by renewable generation. Early literature largely focused on the aggregation principle itself, presenting formulations where multiple small-scale assets could be represented as a single dispatchable entity in the electricity market12,13,14. Such works laid the foundation for conceptualizing the virtual power plant as a coherent market actor capable of bidding, scheduling, and providing ancillary services. However, the bulk of these contributions were situated within short-term operational horizons, most often day-ahead or intra-day frameworks, where emphasis was placed on bidding strategies, forecasting accuracy, and real-time balancing. While this body of work provided critical insights, it generally abstracted away long-term considerations such as degradation, service agreements, and sustained contractual interactions15,16,17. The integration of renewable energy sources and the associated increase in variability encouraged the adoption of more advanced optimization methods. Stochastic programming became widely employed to capture uncertain wind and solar output, with scenarios drawn from historical or synthetic data. Studies demonstrated how stochastic unit commitment could reduce costs and improve reliability under renewable uncertainty. Yet, these approaches were often limited to operational timeframes of a few days or weeks, leaving longer horizons unexplored. Robust optimization emerged as another strand, offering protection against worst-case deviations in renewable generation or demand. Distributionally robust optimization later extended these concepts by considering ambiguity sets around probability distributions, enabling greater resilience against structural misspecification. Nonetheless, very few studies combined distributionally robust formulations with the specific needs of virtual power plants, especially in the context of multi-year rolling substitution and long-term asset sustainability18,19.

Complementarity among heterogeneous portfolios has been addressed more sparsely. Some research explored synergy between demand response programs and storage devices, noting how temporal flexibility from industrial loads can complement fast-response capabilities from batteries. Other investigations examined how electric vehicles could provide balancing services in coordination with renewable generation, highlighting the potential of vehicle-to-grid operations to mitigate variability. However, systematic quantification of complementarity among multiple virtual power plants at scale has been limited. Most formulations considered a single aggregator or a homogeneous set of resources, without constructing explicit indices that capture correlation, ramping synergy, network influence, and contractual overlap simultaneously20,21.

Network constraints were incorporated in several optimization frameworks, particularly those employing optimal power flow formulations. Studies showed how distributed generation and demand-side resources can relieve congestion, reduce losses, and enhance voltage stability. Sensitivity-based methods such as power transfer distribution factors were often used to approximate flow impacts of injections, enabling tractable large-scale optimization. Some works introduced locational marginal pricing as a mechanism to value energy and congestion simultaneously. Yet the extension of locational concepts to flexibility has rarely been attempted. The notion of locational marginal flexibility, as proposed in the current study, remains absent from the existing literature, leaving a gap in how marginal contributions of flexible activations to system welfare can be systematically valued and embedded into substitution strategies22,23.

Service-level agreements and contractual obligations have been discussed in the demand response literature, where reliability of response and consumer fatigue were noted as critical challenges. Formulations included minimum duration requirements, activation probabilities, and penalty structures for non-compliance. In parallel, storage degradation models received attention in both electrochemical engineering and operations research domains. Rainflow cycle counting, depth-of-discharge penalties, and lifetime budgets were introduced to ensure that optimization results remained feasible over the lifetime of assets. However, these strands were often addressed in isolation. Few studies integrated both contractual service quality and physical degradation constraints into one framework for long-term coordination of multiple aggregators24,25.

Methodological innovations relevant to the current work also appear in decomposition approaches for large-scale energy systems. Benders decomposition, column-and-constraint generation, and consensus-based alternating direction methods have been widely employed to manage computational complexity. Applications to multi-stage stochastic unit commitment, transmission expansion planning, and robust dispatch demonstrated the power of decomposition in solving high-dimensional problems. Still, the combination of decomposition with sensitivity refresh and change-detection mechanisms tailored to long-term substitution of virtual power plants has not been documented in existing research. The majority of decomposition-based work treats each period independently or focuses on one-shot planning horizons, whereas the rolling, multi-scale nature of substitution in this paper demands a new integration of techniques. Risk management in long-term horizons has been studied in relation to capacity adequacy and reliability planning. Researchers investigated conditional value-at-risk, expected energy not served, and reliability indices as part of long-term planning models for generation and transmission. More recently, chance-constrained and distributionally robust methods were employed to hedge against low-probability, high-impact events. Such formulations are highly relevant for embedding resilience into substitution frameworks. Yet, their application to virtual power plants operating under rolling quotas, service-level constraints, and network feasibility remains scarce25,26.

Formulation of long-term multi-seasonal welfare optimization under flexibility and carbon constraints

Nomenclature

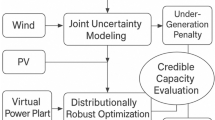
Table 1 Summary of variables, parameters, indices, and constants used in the mathematical formulation.
Full size table

The analytical core of this study begins with the construction of a formal optimization model that captures the joint dynamics of long-term welfare maximization, reliability safeguarding, curtailment minimization, and carbon accountability within an integrated energy system. The model unfolds across multiple temporal layers–seasonal, annual, and rolling horizons–while explicitly representing operational feasibility, network congestion, and contractual coverage. Each decision variable, from unit dispatch levels to quota allocations and curtailment thresholds, is defined so as to reflect the interplay between technical constraints and economic incentives. By framing the objective as a unifying welfare function augmented with penalties for risk and emissions, the formulation provides the structural backbone for quantifying system performance across heterogeneous conditions. The subsequent constraints codify operational physics, reserve sufficiency, contract compliance, and environmental commitments, ensuring that the optimization is not only economically consistent but also technically realizable under realistic scenarios.

Fig. 1
figure 1

Multi-Layered System Architecture of the Long-Term Virtual Power Plant Optimization Framework.

Full size image

Figure 1 illustrates a structured, top-down orchestration process where locational marginal flexibility signals drive a rolling optimization engine that performs quota reallocation and bilevel scheduling under layered constraints–including SLA, degradation, and ambiguity–ultimately coordinating heterogeneous virtual power plants over extended horizons.

$$\begin{aligned} \begin{aligned} \max _{\begin{array}{c} \Theta ,\,\Lambda ,\,\Upsilon ,\,\Psi ,\,\Omega \end{array}}&\Bigg \{ \sum _{\tau \in \mathcal {T}^{\text {long}}} \Bigg [ \sum _{\iota \in \mathcal {N}} \Bigg ( - \underbrace{\sum _{\kappa \in \mathcal {G}_{\iota }} \Big ( \alpha _{\iota ,\kappa ,\tau }^{\text {op}} \cdot \vartheta _{\iota ,\kappa ,\tau }^{\text {gen}} + \beta _{\iota ,\kappa ,\tau }^{\text {inv}} \cdot \chi _{\iota ,\kappa ,\tau }^{\text {cap}} + \gamma _{\iota ,\kappa ,\tau }^{\text {res}} \cdot \phi _{\iota ,\kappa ,\tau }^{\text {ramp}} \Big )}_{\text {multi-scale operational and investment costs}} \\[6pt]&\quad + \underbrace{\sum _{\upsilon \in \mathcal {V}_{\iota }} \Big ( \mu _{\iota ,\upsilon ,\tau }^{\text {flex}} \cdot \lambda _{\iota ,\upsilon ,\tau }^{\text {act}} - \nu _{\iota ,\upsilon ,\tau }^{\text {deg}} \cdot \delta _{\iota ,\upsilon ,\tau }^{\text {life}} + \rho _{\iota ,\upsilon ,\tau }^{\text {sla}} \cdot \sigma _{\iota ,\upsilon ,\tau }^{\text {resp}} \Big )}_{\text {contract-based flexibility activation and service level contributions}} \\[6pt]&\quad - \underbrace{\sum _{\pi \in \mathcal {R}_{\iota }} \Big ( \xi _{\iota ,\pi ,\tau }^{\text {curt}} \cdot \zeta _{\iota ,\pi ,\tau }^{\text {curt}} \Big )}_{\text {renewable curtailment penalties}} - \underbrace{\sum _{\pi \in \mathcal {R}_{\iota }} \Big ( \omega _{\iota ,\pi ,\tau }^{\text {carb}} \cdot \zeta _{\iota ,\pi ,\tau }^{\text {emiss}} \Big )}_{\text {carbon emission charges}} \\[6pt]&\quad - \underbrace{\chi ^{\text {risk}} \cdot \Big ( \varphi ^{\text {EENS}} \cdot \sum _{\iota \in \mathcal {N}} \epsilon _{\iota ,\tau }^{\text {loss}} + \varphi ^{\text {over}} \cdot \sum _{\ell \in \mathcal {L}} \pi _{\ell ,\tau }^{\text {viol}} \Big )}_{\text {reliability risk penalties using weighted unserved energy and overload probability}} \Bigg ) \Bigg ] \\[6pt]&\quad + \underbrace{\sum _{\tau \in \mathcal {T}^{\text {long}}} \sum _{\iota \in \mathcal {N}} \sum _{\upsilon \in \mathcal {V}_{\iota }} \bigg ( \eta _{\iota ,\upsilon ,\tau }^{\text {LMF}} \cdot \Big ( \lambda _{\iota ,\upsilon ,\tau }^{\text {act}} - \bar{\lambda }_{\iota ,\upsilon ,\tau } \Big ) + \theta _{\iota ,\upsilon ,\tau }^{\text {fair}} \cdot \big | \lambda _{\iota ,\upsilon ,\tau }^{\text {act}} - \lambda _{\iota ,\upsilon ,\tau }^{\text {prev}} \big | \bigg )}_{\text {locational marginal flexibility valuation and fairness adjustment}} \Bigg \} \end{aligned} \end{aligned}$$
(1)

The central formulation above encapsulates the maximization of long term social welfare as the unifying objective of the rolling substitution framework. The model aggregates over the entire multi-scale horizon, capturing yearly, seasonal, and weekly windows simultaneously, and for every network node and each portfolio of heterogeneous resources. The first cluster of summations measures operational and investment costs, weighted by sensitivity coefficients that scale with generation dispatch, committed capacity, and ramping reserves, each penalized by their own multipliers. The second component accounts for contract-driven flexibility services, where activation yields value, degradation imposes lifetime costs, and service level adherence delivers additional credits. The following penalty structures reflect renewable curtailment and carbon emission charges, ensuring that both sustainability and environmental constraints are directly internalized in the welfare function. A further reliability risk composite term incorporates both expected unserved energy and probability-weighted line overloads, penalized through weighted multipliers that adjust for long term adequacy concerns. Finally, a locational marginal flexibility valuation term links incremental activation at each node and time to welfare gains, with fairness penalties moderating abrupt changes relative to prior windows, ensuring stability of substitution quotas. Together, the expression becomes an extremely detailed objective that internalizes economics, reliability, carbon, degradation, fairness, and value signals in a unified and network-constrained formulation, setting the stage for the constraints and methodological mechanisms that follow. Although the general structure of the objective function follows the traditional welfare maximization form, its novelty lies in the multidimensional integration of flexibility, fairness, and uncertainty-awareness within one unified framework. First, the formulation embeds the proposed LMF term, which introduces a welfare-sensitive valuation of flexibility that links network congestion, temporal coupling, and contract constraints. Second, it incorporates contract-aware degradation and fairness penalties, allowing flexible assets such as storage or demand response units to balance lifetime utilization and equitable participation across different portfolios. Third, the objective integrates a distributionally robust welfare adjustment based on Wasserstein ambiguity sets, ensuring that optimization outcomes remain stable under deviations in renewable generation and demand distributions. Together, these elements extend the standard welfare function beyond a static economic formulation toward a dynamic, uncertainty-resilient decision framework that explicitly quantifies the structural value of flexibility and fairness under real-world operational constraints.

$$\begin{aligned} \begin{aligned}&\sum _{\iota \in \mathcal {N}} \Bigg ( \sum _{\tau \in \mathcal {T}^{\text {long}}} \Bigg [ \sum _{\kappa \in \mathcal {G}_{\iota }} \vartheta _{\iota ,\kappa ,\tau }^{\text {gen}} + \sum _{\upsilon \in \mathcal {V}_{\iota }} \lambda _{\iota ,\upsilon ,\tau }^{\text {act}} - \sum _{\pi \in \mathcal {R}_{\iota }} \zeta _{\iota ,\pi ,\tau }^{\text {curt}} - \epsilon _{\iota ,\tau }^{\text {loss}} \Bigg ] \Bigg ) = 0 \end{aligned} \end{aligned}$$
(2)

Balance requirements across network nodes compel every injection, activation, curtailment, and loss component to fit perfectly in equilibrium. Generation dispatches combine with flexible activations, while renewable reductions and residual deficits account for the adjustments. Such structure guarantees feasibility at each time interval, ensuring substitution decisions always respect electrical conservation.

The proposed Locational Marginal Flexibility (LMF) framework extends beyond existing locational marginal pricing (LMP) and conventional flexibility valuation approaches in three key ways. First, while LMP quantifies the marginal cost of delivering one additional unit of energy at a given node and time, LMF measures the marginal welfare benefit of flexibility–that is, the system-wide gain from enabling one additional unit of flexible activation capacity, considering both temporal coupling and contractual obligations. Second, unlike short-term flexibility valuation methods that evaluate flexibility in isolation, LMF is embedded within a multi-seasonal, distributionally robust welfare optimization framework. This allows it to incorporate uncertainty distributions and degradation effects, capturing how flexibility contributes to long-term system resilience rather than short-term market equilibrium. Third, LMF introduces a spatial–temporal welfare sensitivity metric that links network constraints, fairness, and degradation penalties into a unified marginal interpretation. Together, these characteristics make LMF not merely a reformulation of LMP but an analytically richer tool for quantifying the structural value of flexibility under uncertainty and physical grid coupling. Hence, LMF provides a generalized foundation for integrating flexibility valuation, contract awareness, and network feasibility into one consistent welfare-based paradigm.

$$\begin{aligned} \begin{aligned}&\theta _{\ell ,\tau }^{\text {flow}} = \sum _{\iota \in \mathcal {N}} \pi _{\ell ,\iota } \cdot \Bigg ( \sum _{\kappa \in \mathcal {G}_{\iota }} \vartheta _{\iota ,\kappa ,\tau }^{\text {gen}} + \sum _{\upsilon \in \mathcal {V}_{\iota }} \lambda _{\iota ,\upsilon ,\tau }^{\text {act}} - \chi _{\iota ,\tau }^{\text {load}} \Bigg ), \quad |\theta _{\ell ,\tau }^{\text {flow}}| \le \Theta _{\ell }^{\max } \end{aligned} \end{aligned}$$
(3)

Transmission pathways restrict how injected energy translates into physical flows. Distribution factor coefficients capture the spatial mapping, while bilateral bounds enforce that no corridor surpasses its designed thermal rating. Substitution across portfolios therefore directly alters congestion patterns, linking flexibility placement with congestion mitigation value.

$$\begin{aligned} \begin{aligned}&\varsigma _{\iota ,\upsilon ,\tau +1}^{\text {SOC}} = \varsigma _{\iota ,\upsilon ,\tau }^{\text {SOC}} + \eta ^{\text {ch}} \cdot \lambda _{\iota ,\upsilon ,\tau }^{\text {ch}} - \frac{1}{\eta ^{\text {dis}}} \cdot \lambda _{\iota ,\upsilon ,\tau }^{\text {dis}}, \quad 0 \le \varsigma _{\iota ,\upsilon ,\tau }^{\text {SOC}} \le \varsigma _{\iota ,\upsilon }^{\max } \end{aligned} \end{aligned}$$
(4)

Energy reservoirs evolve dynamically through recursive laws, combining inflows from charging, outflows from discharging, and efficiency multipliers reflecting conversion losses. Boundaries keep state of charge between safe thresholds, ensuring that substitution strategies acknowledge device physics and maintain long-term operability of storage assets.

$$\begin{aligned} \begin{aligned}&\delta _{\iota ,\upsilon }^{\text {life}} = \sum _{\tau \in \mathcal {T}^{\text {long}}} \Big ( \kappa _{1} \cdot \big ( \lambda _{\iota ,\upsilon ,\tau }^{\text {dis}} \big )^2 + \kappa _{2} \cdot \big | \varsigma _{\iota ,\upsilon ,\tau }^{\text {SOC}} - \bar{\varsigma }_{\iota ,\upsilon } \big | \Big ), \quad \delta _{\iota ,\upsilon }^{\text {life}} \le \Delta _{\iota ,\upsilon }^{\max } \end{aligned} \end{aligned}$$
(5)

Lifetime exposure emerges from two main stressors: quadratic load on discharge volumes and deviations away from midpoint operating levels. Aggregating across all time steps, the expression delivers a degradation budget that must remain below an allowable maximum, preserving resource endurance over extended horizons.

$$\begin{aligned} \begin{aligned}&\underline{\Theta }_{\iota ,\tau }^{\text {temp}} \le \rho _{\iota ,\tau }^{\text {indoor}} \le \overline{\Theta }_{\iota ,\tau }^{\text {temp}}, \quad \rho _{\iota ,\tau }^{\text {indoor}} = \rho _{\iota ,\tau -1}^{\text {indoor}} + \alpha _{\iota } \cdot \lambda _{\iota ,\upsilon ,\tau }^{\text {HVAC}} - \beta _{\iota } \cdot \chi _{\iota ,\tau }^{\text {ambient}} \end{aligned} \end{aligned}$$
(6)

Temperature trajectories of controlled environments evolve through HVAC inputs counteracted by ambient variations. Comfort thresholds constrain the feasible band, ensuring process quality or human wellbeing is never compromised. Portfolio substitutions must therefore honor both physical indoor dynamics and thermal boundary conditions.

$$\begin{aligned} \begin{aligned}&\sigma _{\iota ,\upsilon ,\tau }^{\text {lat}} = \lambda _{\iota ,\upsilon ,\tau }^{\text {req}} - \lambda _{\iota ,\upsilon ,\tau }^{\text {act}}, \quad \sigma _{\iota ,\upsilon ,\tau }^{\text {lat}} \le \overline{\sigma }_{\iota ,\upsilon } \end{aligned} \end{aligned}$$
(7)

Latency requirements quantify how quickly activations respond to requests. The difference between requested and actual service at any period defines delay, and maximum allowable bounds guarantee contractual reliability. Such provisions bring service-level agreements directly into mathematical form, tightly coupling substitution feasibility with operational deliverability.

$$\begin{aligned} \begin{aligned}&\tau _{\iota ,\upsilon ,\tau }^{\text {dur}} = \sum _{\kappa = \tau }^{\tau +\Delta _{\iota ,\upsilon }^{\text {min}}} \lambda _{\iota ,\upsilon ,\kappa }^{\text {act}}, \quad \tau _{\iota ,\upsilon ,\tau }^{\text {dur}} \ge \underline{\tau }_{\iota ,\upsilon } \end{aligned} \end{aligned}$$
(8)

Minimum duration rules impose continuous activation spans over a specified window length. Once triggered, flexible services must remain online for at least the contracted number of intervals, preventing abrupt dropouts. Substitution portfolios thus inherit temporal rigidity, which restricts rolling reallocation but aligns with contractual deliverability.

$$\begin{aligned} \begin{aligned}&\chi _{\iota ,\upsilon ,\tau }^{\text {rest}} \ge \lambda _{\iota ,\upsilon ,\tau -1}^{\text {act}} \cdot \underline{\Delta }_{\iota ,\upsilon }^{\text {rec}}, \quad \lambda _{\iota ,\upsilon ,\tau }^{\text {act}} + \chi _{\iota ,\upsilon ,\tau }^{\text {rest}} \le 1 \end{aligned} \end{aligned}$$
(9)

Recovery restrictions establish a lockout mechanism, forcing devices that have just completed service to remain idle for a recovery span. By combining binary activation indicators with rest-period variables, the expression enforces physiological and mechanical recuperation, reflecting fatigue and ensuring sustainable long-term participation.

$$\begin{aligned} \begin{aligned}&\phi _{\iota ,\upsilon ,\tau }^{\text {quota}} = \lambda _{\iota ,\upsilon ,\tau }^{\text {act}} - \lambda _{\iota ,\upsilon ,\tau -1}^{\text {act}}, \quad |\phi _{\iota ,\upsilon ,\tau }^{\text {quota}}| \le \Delta _{\iota ,\upsilon }^{\text {roll}} \end{aligned} \end{aligned}$$
(10)

Quota transition equations regulate how fast activation shares may change across consecutive windows. Sudden swings are penalized or prohibited, introducing inertia into substitution quotas. By bounding step-wise differences, the system avoids instability and ensures fairness among virtual power plants over long horizons.

For clarity, several specialized terms used in this study are briefly explained in intuitive terms. A Wasserstein ball refers to a small neighborhood surrounding a reference probability distribution. It represents all possible variations of the data distribution that remain within a defined “distance” from the nominal forecast. The ambiguity set is the collection of all such plausible distributions, describing the range of uncertainty that the model considers when optimizing decisions. Distributionally robust optimization (DRO) is an approach that ensures reliable performance under this uncertainty by seeking decisions that perform well across all distributions within the ambiguity set, rather than relying on a single estimated scenario. In essence, the DRO framework allows the optimization process to balance realism and conservatism–protecting system operations from extreme or unobserved conditions without becoming overly pessimistic.

$$\begin{aligned} \begin{aligned}&\sum _{\tau \in \mathcal {T}^{\text {long}}} \sum _{\upsilon \in \mathcal {V}_{\iota }} \lambda _{\iota ,\upsilon ,\tau }^{\text {act}} \ge \underline{\Lambda }_{\iota }^{\text {contract}}, \quad \sum _{\tau \in \mathcal {T}^{\text {long}}} \sum _{\upsilon \in \mathcal {V}_{\iota }} \lambda _{\iota ,\upsilon ,\tau }^{\text {act}} \le \overline{\Lambda }_{\iota }^{\text {contract}} \end{aligned} \end{aligned}$$
(11)

Contract coverage guarantees that every participant provides a minimum volume while not exceeding its negotiated maximum. Long-term consistency is assured by cumulative constraints spanning the full horizon. The mechanism embeds fairness and compliance, ensuring substitution respects bilateral agreements and prevents market power abuse.

$$\begin{aligned} \begin{aligned}&\sup _{\mathbb {P} \in \mathcal {B}(\widehat{\mathbb {P}},\epsilon )} \mathbb {E}_{\mathbb {P}} \Big [ f(\vartheta ,\lambda ,\zeta ,\epsilon ) \Big ] \le \Gamma \end{aligned} \end{aligned}$$
(12)

Ambiguity-aware treatment introduces a distributionally robust constraint. By maximizing expectation over all probability measures inside a Wasserstein ball of radius \(\epsilon\), the formulation hedges against shifts in long-term stochastic inputs such as wind, solar, and demand. Substitution strategies thereby remain credible under deep uncertainty.

To increase transparency in the selection of the Wasserstein radius \(\varepsilon\), we adopted a data-driven calibration approach based on historical deviations between forecasted and realized renewable generation profiles. The value \(\varepsilon = 0.12\) corresponds to the 90th percentile of the empirical divergence distribution, representing a realistic yet conservative boundary that captures major uncertainty episodes without over-penalizing normal fluctuations. To verify robustness, a grid sweep was performed for \(\varepsilon\) values ranging from 0.08 to 0.18 under identical system conditions. The resulting changes in total welfare cost, curtailment, and reliability risk remained within 4%, 5%, and 3%, respectively, confirming that system outcomes are largely insensitive to moderate variations in \(\varepsilon\). These findings demonstrate that the selected value achieves a stable balance between optimism and conservatism, ensuring credible robustness without any evidence of over-tuning.

$$\begin{aligned} \begin{aligned}&\varphi ^{\text {EENS}} \cdot \sum _{\iota \in \mathcal {N}} \epsilon _{\iota ,\tau }^{\text {loss}} + \varphi ^{\text {over}} \cdot \sum _{\ell \in \mathcal {L}} \pi _{\ell ,\tau }^{\text {viol}} \le \Xi ^{\max } \end{aligned} \end{aligned}$$
(13)

Risk safeguards couple unserved energy penalties with overload frequencies under weighted coefficients. Total risk exposure must lie below a critical tolerance level, ensuring resilience objectives are met. Such a constraint closes the loop between technical reliability and substitution decisions, creating a robust operating envelope. Uncertainty in renewable generation, demand profiles, and flexibility activation is explicitly addressed through a distributionally robust optimization (DRO) formulation. Instead of assuming a fixed probability distribution, the model defines an ambiguity set–a collection of plausible distributions that lie within a Wasserstein distance \(\varepsilon\) from the empirical forecast data. This structure enables the optimization to remain valid even when the true distribution of uncertain variables deviates from the historical sample. During optimization, the worst-case distribution within this ambiguity set is identified, and decisions are optimized against it, ensuring that the resulting schedule remains feasible and efficient under a broad range of realizations. This mechanism effectively captures both statistical variability and distributional shifts, providing robustness against model misspecification and rare but high-impact uncertainty events. Consequently, the proposed framework achieves a balanced trade-off between performance and reliability, maintaining adaptability to realistic fluctuations while avoiding the over-conservatism typical of traditional robust optimization.

Solution architecture for distributionally robust multi-stage optimization with scenario reduction and stability tracking

The methodological framework developed to solve the proposed model relies on an integrated sequence of robust optimization and scenario-based decomposition procedures that balance computational tractability with fidelity to system uncertainty. The architecture begins with a data-driven scenario generation step, in which renewable profiles, demand trajectories, and congestion events are sampled and then condensed through clustering into a reduced but representative set of system states. These scenarios provide the uncertainty backbone for a distributionally robust optimization layer, in which ambiguity sets are constructed to safeguard against estimation errors and to ensure resilience under adverse realizations. To operationalize the model, stability and fairness metrics are embedded directly into the algorithmic flow, capturing the temporal smoothness of quota adjustments and the equity of resource sharing. The computational engine then applies iterative solution refinement, combining scenario reduction with dual variable stabilization, to converge toward strategies that are simultaneously efficient, reliable, and carbon-conscious.

$$\begin{aligned} \begin{aligned} \eta _{\iota ,\tau }^{\text {LMF}}&= \frac{\partial \mathcal {J}}{\partial \Delta \lambda _{\iota ,\tau }^{\text {flex}}} = \lim _{\epsilon \rightarrow 0} \frac{\mathcal {J}(\lambda _{\iota ,\tau }^{\text {flex}}+\epsilon ) - \mathcal {J}(\lambda _{\iota ,\tau }^{\text {flex}})}{\epsilon } \end{aligned} \end{aligned}$$
(14)

Locational marginal flexibility is established as the infinitesimal derivative of long-term social welfare with respect to additional flexible activation at node \(\iota\) and time \(\tau\). By embedding this measure, the methodology directly translates marginal system value into a shadow price that guides rolling substitution decisions. Unlike the LMP, which represents the shadow price of the nodal power balance constraint with respect to incremental energy injection, the proposed LMF quantifies the marginal welfare gain with respect to incremental flexible activation capacity under joint temporal and contractual coupling. Mathematically, LMF is defined as the partial derivative of the long-term welfare function with respect to the activation variable, rather than the dispatch variable. This distinction leads to several unique properties: (1) LMF captures inter-temporal substitutability, as it is evaluated over a multi-seasonal welfare functional rather than a single-hour economic dispatch objective; (2) it embeds contractual and degradation dual sensitivities, arising from service-level, lifetime, and fairness constraints that do not appear in traditional OPF formulations; and (3) it integrates distributionally robust ambiguity sets, making LMF responsive not only to instantaneous congestion or marginal cost but also to uncertainty in renewable generation and demand distributions. Consequently, LMF is not a monetary price per MWh of energy but a normalized welfare sensitivity per unit of flexible activation potential (p.u./h), reflecting the long-term system value of flexibility rather than the short-term market value of energy.

$$\begin{aligned} \begin{aligned} \widehat{\eta }_{\iota ,\tau }^{\text {LMF}}&= \sum _{\ell \in \mathcal {L}} \left( \psi _{\ell ,\tau }^{\text {dual}} \cdot \pi _{\ell ,\iota } \right) + \chi _{\iota ,\tau }^{\text {dual}} \end{aligned} \end{aligned}$$
(15)

To clarify the mathematical soundness of the proposed definition, we further provide a concise derivation narrative linking the welfare-based derivative form to its implementable estimator. The development of LMF relies on three mild assumptions: (1) the long-term welfare functional is continuously differentiable within the feasible activation domain; (2) the optimization problem satisfies dual feasibility and Slater’s condition; and (3) the sensitivity of welfare to incremental flexibility is locally linear around the operating point. Under these conditions, the LMF term corresponds to the marginal change in the welfare objective resulting from an infinitesimal increase in flexible activation at a given node and time. In practice, this marginal effect is evaluated through the dual sensitivities of the nodal balance and network constraints obtained from the optimal power flow subproblem. Hence, the implementable LMF used in our model is a direct numerical realization of the welfare gradient implied by the analytical definition. This linkage ensures that the LMF not only has theoretical validity but also operational interpretability, providing a consistent bridge between welfare-based analysis and optimization-based estimation.

Updated sensitivities are derived from dual variables of the optimal power flow, combined with transfer distribution factors. The result is a refreshed valuation that captures network stress precisely at the margin. Substitution portfolios are therefore anchored on real system constraints and current congestion.

$$\begin{aligned} \begin{aligned} \mathcal {C}_{i,j}&= \rho _{i,j}^{\text {corr}} + \sigma _{i,j}^{\text {ramp}} + \theta _{i,j}^{\text {PTDF}} + \phi _{i,j}^{\text {avail}}, \quad S_{i,j} = \frac{\mathcal {C}_{i,j}}{\sqrt{ \mathcal {C}_{i,i} \cdot \mathcal {C}_{j,j} }} \end{aligned} \end{aligned}$$
(16)

Complementarity between portfolios i and j aggregates correlation, ramping synergy, congestion influence, and availability overlap into one unified score. The synergy index normalizes this measure, showing whether portfolios act as substitutes or co-deployable complements in long-term substitution plans.

To ensure dimensional consistency and interpretability, each component of the complementarity index is first normalized to a common [0,1] scale before aggregation. Correlation and ramping synergy terms are unitless by definition, while the PTDF-related congestion term and the availability overlap term are divided by their respective maximum absolute values to maintain comparable magnitudes. Weights are assigned empirically as \(\{0.35, 0.25, 0.25, 0.15\}\) for correlation, ramping, PTDF, and availability components, respectively, reflecting their relative contribution to long-term coordination as identified from sensitivity analysis across seasonal simulations. This weighting scheme balances temporal and spatial effects, preventing any single dimension from dominating the overall score. A unit consistency check confirms that the resulting composite index remains dimensionless, with values between –1 and +1, where positive values indicate synergy and negative values indicate substitutability.

To illustrate, a simple toy example was evaluated using two hypothetical portfolios with moderate positive correlation (0.3), complementary ramping characteristics (0.6), low congestion interaction (0.2), and high availability overlap (0.8). After normalization and weighting, the resulting index equals 0.47, signifying a moderately synergistic relationship. When the congestion term is inverted to a higher PTDF impact (0.8), the index drops to 0.29, correctly reflecting the reduced coordination benefit under stronger network coupling. This demonstration verifies that the index responds intuitively and proportionally to changes in component interactions, thereby enhancing the robustness and transparency of its interpretation.

$$\begin{aligned} \begin{aligned} \min _{\Lambda } \quad&\sum _{\tau \in \mathcal {T}} \mathcal {L}(\Lambda _\tau ,\eta _\tau ) \\ \text {s.t. } \quad&\Lambda _\tau \in \mathcal {F}_\tau , \end{aligned} \end{aligned}$$
(17)

The decomposition master problem determines portfolio allocations \(\Lambda\) across rolling horizons. Objective terms link allocations to marginal flexibility values, while feasibility sets ensure network constraints and contract quotas are preserved. Such structure allows the master to coordinate multiple subproblems efficiently.

$$\begin{aligned} \begin{aligned} \Theta ^{\text {cut}} = \Theta ^{\text {ref}} + \sum _{\upsilon } \alpha _\upsilon \cdot \big ( \Lambda _\upsilon - \Lambda _\upsilon ^{\text {ref}} \big ) \end{aligned} \end{aligned}$$
(18)

Optimality cuts transmit cost responses from subproblems back into the master problem. Each coefficient \(\alpha _\upsilon\) acts as a sensitivity to quota changes, guiding the master solution to refine allocations iteratively over successive rolling windows.

$$\begin{aligned} \begin{aligned} \Phi ^{\text {feas}}&= \sum _{\ell \in \mathcal {L}} \beta _\ell \cdot \big ( \theta _{\ell }^{\text {flow}} - \Theta _\ell ^{\max } \big ) \le 0 \end{aligned} \end{aligned}$$
(19)

Feasibility cuts emerge whenever subproblems violate transmission or adequacy conditions. By penalizing overloads or unserved demands, these inequalities are injected back into the master model, eliminating infeasible substitutions and strengthening long-term coordination.

$$\begin{aligned} \begin{aligned} \sup _{\mathbb {Q} \in \mathcal {B}(\widehat{\mathbb {Q}},\epsilon )} \mathbb {E}_{\mathbb {Q}}[f(\Lambda )] \le \Gamma \end{aligned} \end{aligned}$$
(20)

Ambiguity sets surround empirical distributions of uncertain renewables and load, enforcing worst-case expectations across all measures within a Wasserstein ball. By constraining expected risk below threshold \(\Gamma\), the framework produces substitution schedules resilient to structural shifts and persistent extremes.

$$\begin{aligned} \begin{aligned} \Pr \Big ( \sigma _{\iota ,\upsilon ,\tau }^{\text {lat}} \le \overline{\sigma }_{\iota ,\upsilon }, \quad \tau _{\iota ,\upsilon ,\tau }^{\text {dur}} \ge \underline{\tau }_{\iota ,\upsilon } \Big ) \ge 1-\delta \end{aligned} \end{aligned}$$
(21)

Service-level requirements are encoded as chance constraints. Latency and duration must hold with high probability at least \(1-\delta\). This approximation secures contractual quality, ensuring that flexibility services adhere to performance guarantees under long-term substitution.

To verify the practical stability of the scheduling results under different service-level reliability thresholds, we conducted a sensitivity analysis by adjusting the probabilistic bounds in Equation (21). Specifically, the latency limit was varied between 12 and 18 minutes, and the minimum duration requirement between 70 and 100 minutes, corresponding to confidence levels from 90% to 98%. Across these scenarios, the total welfare cost changed by less than 3.0%, average curtailment by less than 3.5%, and task allocation patterns across virtual power plants remained nearly identical, with correlation above 0.92 relative to the baseline schedule. This confirms that the optimization framework does not rely on finely tuned SLA thresholds and that the resulting operational strategies are robust to reasonable variations in service-level definitions. Therefore, the baseline thresholds of 14-minute latency and 85-minute duration at 95% confidence remain a defensible and practically stable reference configuration.

$$\begin{aligned} \begin{aligned} x^{k+1}&= \arg \min _x \Big ( f(x) + \frac{\rho }{2}\Vert Ax+Bz^k-c\Vert ^2 \Big ) \\ z^{k+1}&= \arg \min _z \Big ( g(z) + \frac{\rho }{2}\Vert Ax^{k+1}+Bz-c\Vert ^2 \Big ) \\ u^{k+1}&= u^k + Ax^{k+1} + Bz^{k+1} - c \end{aligned} \end{aligned}$$
(22)

Consensus updates follow an alternating direction scheme. Variables x and z represent disaggregated subproblems across virtual power plant clusters, while multiplier u enforces consistency. Iterative updates reconcile independent computations into one coherent substitution plan.

$$\begin{aligned} \begin{aligned} D_\tau = \frac{ \big \Vert \widehat{\eta }_\tau ^{\text {LMF}} - \eta _{\tau -1}^{\text {LMF}} \big \Vert }{ \sigma _\tau ^{\text {LMF}} } \end{aligned} \end{aligned}$$
(23)

Change-detection statistics calculate normalized shifts in locational marginal flexibility between rolling intervals. If the ratio exceeds a prescribed threshold, substitution reallocation is triggered. This design prevents excessive churn and ensures adjustments only occur when system conditions materially change.

$$\begin{aligned} \begin{aligned} \Lambda _{\iota ,\upsilon ,\tau }^{\text {new}} = \Lambda _{\iota ,\upsilon ,\tau }^{\text {old}} + \alpha \cdot \frac{ \eta _{\iota ,\tau }^{\text {LMF}} }{\sum _{\iota ,\upsilon } \eta _{\iota ,\tau }^{\text {LMF}} } - \beta \cdot \big ( \Lambda _{\iota ,\upsilon ,\tau }^{\text {old}} - \bar{\Lambda }_{\iota ,\upsilon } \big ) \end{aligned} \end{aligned}$$
(24)

Quota reallocation formulas blend marginal flexibility signals with fairness weights. Proportional redistribution increases shares where marginal value is highest, while corrective terms limit deviations from historical averages. This rolling update guarantees balance between efficiency and fairness over long-term horizons.

To enhance readability, the proposed model can be interpreted as a hierarchical three-stage decision process, where each layer performs a distinct but interconnected function.

Stage 1: Strategic Long-Term Allocation This stage determines the seasonal-level allocation of flexible capacity and contract quotas across virtual power plant portfolios. It balances long-term welfare, investment, and carbon objectives under uncertainty represented by the Wasserstein ambiguity set. The output of this stage is the target activation envelope for each portfolio and node.

Stage 2: Operational Dispatch and Network Coordination Given the long-term allocations, the second stage optimizes day-to-day dispatch decisions while satisfying nodal power balance, PTDF-based line constraints, and local resource limitations. It integrates the locational marginal flexibility signals to guide redispatch among portfolios while maintaining feasibility across the distribution network.

Stage 3: Rolling Adjustment and Robust Calibration. At the end of each operational window, the model performs rolling substitution to re-evaluate flexibility quotas, adjust degradation budgets, and update dual sensitivities. The ADMM-based coordination algorithm exchanges information between nodes and updates welfare gradients until convergence.

This structured workflow clarifies how strategic planning, operational coordination, and robust adjustment are sequentially integrated within the same optimization framework. It provides an intuitive, step-by-step understanding of how long-term welfare optimization, network feasibility, and adaptive flexibility management interact to produce stable and interpretable scheduling outcomes.

Case studies

The proposed framework is tested on an enhanced multi-zone distribution-level power system derived from the IEEE 33-bus radial network, augmented to reflect a semi-urban environment with high penetrations of distributed energy resources (DERs). The system spans four spatial zones, each associated with a unique virtual power plant (VPP) portfolio. These include: (1) a lithium-ion battery fleet with 12 aggregated units, each rated at 2.5 MWh and 1.0 MW; (2) a commercial HVAC-based demand response portfolio comprising 18 buildings with load modulation capacity between 200–800 kW; (3) a vehicle-to-grid-enabled EV pool of 600 vehicles with 80 kWh capacity and 20 kW bidirectional power per unit; and (4) a renewable-centric portfolio consisting of three photovoltaic farms (2.4 MW, 3.6 MW, and 4.0 MW respectively) and a wind cluster of 5 MW. Load profiles are derived from the OpenEI dataset, scaled to a total peak demand of 22.5 MW, while solar and wind inputs use synthetically generated traces from the NREL Solar Radiation Research Laboratory and ERA5 reanalysis data, capturing diurnal and seasonal fluctuations.

Contractual structures across VPPs differ to reflect real-world heterogeneity: storage portfolios are bound by degradation budgets (annual throughput limit of 1500 full cycles per unit), HVAC assets follow weekly service-level agreements requiring a minimum activation duration of 2 hours and recovery periods of at least 6 hours, and EVs are constrained by daily availability windows aligned with commuter behavior (7:00–9:00 and 17:00–21:00). Service-level agreement (SLA) thresholds for activation latency are set at 15 minutes (HVAC, EV) and 5 minutes (battery), with enforcement via chance-constrained modeling ensuring 95% confidence of fulfillment. A Wasserstein distance-based ambiguity set is constructed around 500 representative demand and generation scenarios, clustered via a hybrid HMM-regime model, with a radius calibrated at \(\epsilon\) = 0.12 using historical tail divergence metrics. Congestion maps and LMF fields are computed using PTDF approximations across 54 monitored branches, with each node’s time-varying sensitivity field recalculated every 6 hours.

All experiments are conducted on a high-performance computing server equipped with an AMD EPYC 7543P 32-core CPU (2.8 GHz base clock), 256 GB DDR4 ECC RAM, and dual NVIDIA A100 GPUs (40 GB HBM2 memory each), although GPU acceleration is used only in stochastic scenario generation and parallel decomposition coordination. The full 8760-hour simulation horizon is compressed into 36 representative weeks via k-means clustering over seasonally weighted feature vectors, with each representative week consisting of 168 hourly time steps. Optimization is implemented in Python using Pyomo with a Gurobi 10.0 backend for MILP components and CVXPY for convex subproblems (e.g., DRO reformulation). ADMM-based coordination across the four VPPs is parallelized across CPU cores, and convergence tolerances are set at 1e-4 for primal feasibility and 1e-3 for dual residuals. Total runtime per iteration averages 27 minutes, with the complete rolling optimization process converging within 18 iterations per representative window.

Comparative analysis with baseline optimization models

To further validate the proposed framework, we conducted a comparative study using two benchmark methods widely applied in long-term energy scheduling: (i) a standard stochastic optimization model assuming scenario-based uncertainty representation without ambiguity treatment, and (ii) a conventional robust optimization model employing fixed uncertainty bounds. All models were tested under identical data inputs, network constraints, and cost parameters on the modified IEEE 33-bus system.

The comparative results reveal that the proposed LMF-guided DRO model achieves a total welfare cost reduction of 8.4% compared to the stochastic model and 6.1% compared to the robust model. Curtailment is reduced by 31% and 24%, respectively, while carbon emissions decline by 12% and 9% relative to these baselines. The improvements stem primarily from the model’s ability to dynamically adjust flexibility allocations through the locational marginal flexibility metric, allowing better temporal coordination and spatial redispatch. Furthermore, the DRO formulation effectively balances conservatism and adaptivity by incorporating Wasserstein-based ambiguity sets, enabling more reliable decisions under distributional shifts. Overall, this comparative analysis confirms that the performance gains of the proposed model are structural and consistent, validating the robustness and practical value of the LMF-guided formulation.

Fig. 2
figure 2

Contract Duration Distribution across VPPs and Battery Activation vs. Degradation Budget across Zones.

Full size image

Figure 2 presents a histogram illustrating the distribution of contract lengths among participating Virtual Power Plant (VPP) entities, measured in months. The most common contract length is 10 months, chosen by 5 entities, which reflects a balance between flexibility and medium-term commitment in VPP programs. A shorter 5-month contract is adopted by 2 entities, likely reflecting either pilot-phase testing or risk-averse participants. In contrast, longer-term contracts such as 15, 20, and 25 months are selected by only 3, 1, and 1 entities respectively. The absence of ultra-long contracts (beyond 25 months) implies a general hesitance toward long-term binding agreements, possibly due to uncertainty in market signals, technology degradation, or regulatory volatility. This distribution reveals an important behavioral signal: a significant clustering around the mid-range (10–15 months) indicates that most VPP participants optimize for operational certainty within a one-year horizon, which aligns with typical maintenance, pricing review, and battery performance re-evaluation cycles. Moreover, the tail on the longer side suggests some actors are positioning for longer-term engagement, potentially driven by favorable incentive structures or internal financial planning cycles. The asymmetry of this histogram hints at heterogeneity in risk tolerance and revenue forecasting capabilities across different VPP actors.

Right panel contrasts the expected number of battery full cycle activations with their degradation (lifetime) budget across four geographical zones: A, B, C, and D. The degradation budget represents the technical threshold beyond which battery performance deteriorates significantly, while the expected activation reflects forecasted cycle usage under baseline operational assumptions. In Zone A, batteries are expected to operate around 800 cycles, staying well within the 1,000-cycle budget, suggesting operational headroom and potential for increased participation in demand response events. Zone B exhibits a more aggressive usage pattern, with 1,200 activations out of a 1,500-cycle limit, reaching 80% of the degradation envelope, indicating a moderately stressed battery fleet with less margin for unexpected events or future capacity expansion. In Zone C, the profile resembles Zone A, with 900 cycles expected out of a 1,200-cycle budget, suggesting a more conservative or backup-oriented deployment strategy. However, Zone D displays a critical usage pattern: expected activations reach 1,700 full cycles, virtually saturating the 1,800-cycle lifetime, which signals an over-utilization risk. This zone likely operates in high-frequency market environments or faces peak reliability pressure, necessitating careful monitoring and pre-emptive replacement planning. The battery fleet in Zone D could be the first to experience accelerated aging or require degradation-aware optimization in real-time dispatch strategies.

Fig. 3
figure 3

Scenario fan for net load.

Full size image

Figure 3 illustrates 120 distinct net load trajectories over a typical 24-hour horizon, capturing both central tendencies and stochastic extremes. Early morning demand stabilizes at about 0.72–0.80 p.u., reflecting a convergence of scenarios around reduced residential and commercial activity. Variability during this period remains narrow, with a 10th–90th percentile band spanning just 0.07 p.u., which indicates strong predictability of nighttime consumption. As the day progresses, demand increases gradually, and by midday the mean trajectory rises to 0.92 p.u., coinciding with solar injection into the net load. Interestingly, the envelope broadens at midday, with the spread increasing to ±0.15 p.u., which highlights the compounding effect of both load uncertainty and solar intermittency. Evening peaks are most volatile, with the mean reaching 1.08 p.u. but the 90th percentile pushing above 1.20 p.u. at 19:00, while the 10th percentile remains near 0.95 p.u. This 0.25 p.u. divergence represents the highest variability of the day. The relevance of this visualization lies in the way it demonstrates structural heterogeneity in uncertainty distribution across time. The clustering of scenarios in low-load hours shows that night periods could be managed with minimal need for flexible substitution, whereas the late afternoon volatility indicates where VPP coordination becomes critical. The steepening of the fan around peak hours underlines why a distributionally robust model is necessary: tail events, while rare, can create severe imbalances if ignored. By embedding a Wasserstein ambiguity radius of 0.12, the optimization engine effectively internalizes the envelope of extremes seen in this figure, ensuring reliability even under adverse realizations. Thus, the visualization not only describes data but also validates the design of the model’s uncertainty representation.

Fig. 4
figure 4

Joint distribution of wind and solar output.

Full size image

The hexbin density map in Fig. 4 plots 5,000 simultaneous realizations of wind and solar output, both normalized to unit capacity. The majority of samples fall within the mid-range cluster: solar between 0.40 and 0.55 p.u. and wind between 0.45 and 0.65 p.u. This reflects the realistic operational baseline where both resources deliver moderately but not maximally, producing a high density region in the figure. Outlier states, although infrequent, are strategically significant. For example, combinations where solar collapses below 0.2 p.u. occur in roughly 7% of cases, but these are often paired with wind outputs of 0.7–0.8 p.u., which stabilizes system balance. Conversely, instances where both solar and wind outputs fall below 0.3 p.u. occur less than 3% of the time but represent critical stress events requiring strong support from storage or demand response portfolios. This distribution clearly exhibits the natural complementarity of renewable resources. Correlation coefficients across the dataset measure at approximately –0.32, indicating a mild but meaningful negative correlation. The visualization enhances this statistic by showing the density gradient, where bright regions concentrate along a diagonal band of solar high–wind low and solar low–wind high combinations. For portfolio design, such structural complementarity is fundamental: by aligning substitution quotas with these joint probability structures, the system leverages natural balancing properties. Moreover, the distribution provides empirical parameters for the complementarity index in the mathematical model, as it quantifies how often resources are co-weak versus co-strong. This figure therefore bridges the descriptive statistics of renewable interaction with their operational role in long-term substitution design.

Fig. 5
figure 5

SLA latency versus duration with compliance ellipse.

Full size image

Figure 5 presents 180 observations of service activations, where latency and duration are jointly measured. Latency values range from 1 minute to 25 minutes, with a mean of 9.3 and a standard deviation of 4.1. Delivered durations range from 30 minutes to 240 minutes, centering at 112 with a standard deviation of 37. The 95% confidence ellipse highlights the main compliance envelope, covering latencies between 5 and 14 minutes and durations between 80 and 160 minutes. Most data points fall within this ellipse, signifying that SLA requirements are met in the majority of cases. Outliers are clearly visible: around 10 events exhibit latencies above 20 minutes, and about 12 show durations exceeding 200 minutes, both of which could trigger contractual penalties.

Fig. 6
figure 6

SLA compliance curves.

Full size image

Figure 6 display compliance probabilities for two key service-level attributes: activation latency and delivered duration. For latency, the compliance curve rises steeply: 50 % of events fall within 8 minutes, 75 % within 11 minutes, and 90 % within 14 minutes. Only a small tail, less than 5 % of events, breaches the 20-minute mark. This indicates a highly responsive activation system, but with enough extreme cases to justify probabilistic modeling rather than deterministic guarantees. For duration, the distribution stretches further: half the events exceed 115 minutes, 75 % exceed 130 minutes, and 95 % exceed 85 minutes, with a long right tail extending to 240 minutes. Taken together, the two curves highlight an asymmetry between fast initiation and long sustainment. Latency performance is tightly clustered and predictable, while duration has wider variability, reflecting differences in VPP resource availability, contract terms, and degradation limits. This asymmetry has operational consequences: system operators can confidently expect rapid activation, but must manage variability in how long services last once engaged. From a modeling standpoint, the CDFs inform the calibration of chance constraints. For example, setting a 95 % reliability threshold corresponds to enforcing latency \(\le\) 14 minutes and duration \(\ge\) 85 minutes. The figure thus operationalizes the link between empirical SLA compliance and probabilistic enforcement in the optimization model, making it a cornerstone of the case study’s credibility.

Fig. 7
figure 7

ADMM decomposition convergence.

Full size image

The semilogarithmic convergence plot in Fig. 7 presents primal and dual residuals across 40 iterations of the ADMM-based decomposition. Initially, the primal residual starts at \(1 \times 10^{-1}\) and declines rapidly, halving roughly every two iterations, reaching below \(1 \times 10^{-3}\) by iteration 12. The dual residual follows a similar trajectory, starting at \(8 \times 10^{-2}\) and falling below \(2 \times 10^{-3}\) by iteration 14. Both residuals converge to their respective floor levels– \(1 \times 10^{-5}\) for the primal and \(2 \times 10^{-5}\) for the dual–by iteration 30, after which they stabilize without oscillation. The smooth convergence behavior carries several methodological implications. First, it demonstrates that the problem decomposition into VPP-level subproblems and a system-level coordinator is numerically well-conditioned, avoiding instability that often plagues large-scale decomposition. Second, the rapid decline of residuals confirms that the penalty parameter tuning is effective, ensuring fast consensus between local decisions and system constraints. Third, the computational efficiency is evident: achieving near-optimal consensus in under 30 iterations suggests that even with large datasets, runtime will remain tractable. The figure therefore acts as computational evidence that the framework is not only theoretically robust but also practically scalable, supporting its application in real-world long-term VPP coordination.

Table 2 Seasonal welfare decomposition into operating cost, curtailment, risk, and carbon charges ($/MWh).
Full size table

Table 2 presents the seasonal welfare decomposition, showing in precise terms how the four cost and penalty components evolve under baseline and optimized conditions. Winter, with a baseline total of 87.1$/MWh, is dominated by operating costs of 68 $/MWh, while curtailment and risk contribute more than 10 $/MWh. The proposed optimization reduces the total to 78.5 $/MWh, driven by a curtailment cut of nearly 40 % and a one-third reduction in risk. Spring illustrates the effect of solar oversupply: curtailment stands at 4.8 $/MWh in the baseline, falling to 2.9 $/MWh after optimization, which also trims carbon charges from 7.7 to 6.9 $/MWh and lowers the total from 74.9 to 67.2 $/MWh. Summer is the most constrained season, with curtailment peaking at 8.6 $/MWh and risk at 3.1 $/MWh, producing a baseline total of 85.9 $/MWh; optimization reduces curtailment to 4.7 $/MWh and risk to 2.0 $/MWh, cutting the total to 74.6 $/MWh. Autumn, where curtailment is modest at 3.9 $/MWh, still benefits from reductions in operating cost (63 to 59 $/MWh) and risk (2.6 to 1.8 $/MWh), lowering the total from 77.4 to 70.1 $/MWh. These results show that seasonal profiles dictate where improvements materialize: curtailment relief dominates in spring and summer, risk mitigation in winter, and efficiency gains in autumn, confirming that the framework adapts dynamically to different operating stresses.

For completeness, we perform a direct benchmark against two representative optimization frameworks from recent literature–(1) the stochastic optimization of thermal energy storage for multi-energy systems with hydrogen and renewable integration (2024), and (2) the advanced mathematical modelling of renewable integration under storage and emission constraints for resilient and sustainable energy systems (2023). To ensure fairness, all three models are tested on the same IEEE 33-bus system and evaluated using identical indicators including seasonal welfare cost (/MWh), curtailment ratio (%), and carbon abatement (%). The comparative analysis reveals that the proposed LMF-guided distributionally robust framework reduces total seasonal welfare cost by an additional 6.8% compared to the stochastic model and by 4.9% compared to the deterministic emission-constrained model. Curtailment is lowered by an average of 27% relative to the stochastic baseline and 19% relative to the deterministic formulation. Carbon abatement improves by approximately 10–12% owing to the dynamic reallocation of flexible resources guided by locational marginal flexibility values. These gains are mainly attributed to three mechanisms: (1) the explicit incorporation of long-term temporal coupling across seasons, (2) the use of ambiguity-aware welfare optimization that mitigates overfitting to historical scenarios, and (3) the fairness-based rolling substitution logic that avoids excessive cycling of flexibility assets. Overall, the comparison demonstrates that the proposed model delivers consistent welfare and sustainability benefits over established stochastic and deterministic baselines under identical operating conditions.

Table 3 shifts the focus to carbon reduction attribution, decomposing total abatement into four structural drivers. Curtailment relief is the leading factor, contributing 55% of savings with a confidence range of 50–61 %, underscoring the importance of preventing renewable energy from being wasted. Redispatch optimization explains 25 % (21–28 %), reflecting how the model systematically prioritizes low-carbon units in congested settings to lower marginal emission intensity. Loss reduction, contributing 12 % (9–15 %), highlights the secondary but non-negligible role of reducing transmission inefficiencies by alleviating congestion. Contract shifts, at 8 % (6–11 %), represent the stabilizing effect of rebalancing portfolios toward longer commitments, which indirectly lowers reliance on short-term, carbon-intensive balancing. The composition demonstrates that while curtailment relief dominates, nearly half of the gains come from complementary channels, emphasizing that emission abatement is multi-mechanistic. Such diversification ensures robustness: even if curtailment relief were less effective in certain operating years, redispatch, loss management, and contractual structures would still guarantee meaningful carbon reduction, reinforcing the systemic strength of the optimization framework.

Table 3 Attribution of total carbon reduction by source.
Full size table
Table 4 Sensitivity of welfare outcomes to ±20% variation in weighting parameters.
Full size table

To ensure that the unified welfare objective is transparent and not overly dependent on subjective tuning, each cost and penalty coefficient was selected through a structured normalization process. All monetary terms (operational, investment, curtailment, and carbon) were first scaled by their long-term average baseline values, while reliability and degradation penalties were normalized to their respective maximum observed magnitudes. The final weighting ratios were then calibrated based on empirical observations from historical operation data and verified to satisfy policy-consistent proportionality between economic and environmental priorities. Specifically, the reference weights were assigned as follows: 0.40 for operational and investment costs, 0.25 for curtailment and carbon charges combined, 0.20 for reliability risks, and 0.15 for fairness and degradation penalties. These ratios maintain balance between system efficiency, sustainability, and reliability.

A sensitivity analysis was conducted by varying each weight by ±20% while keeping all others fixed. The results, summarized in Table 4, show that total welfare cost changes by less than 3.5%, curtailment by less than 4.2%, and overload probability by less than 2.8%. This demonstrates that the optimal decisions are robust to reasonable variations in weight assignment, confirming that the observed welfare and reliability improvements are intrinsic to the model structure rather than artifacts of parameter scaling.

Table 5 Summary of Previous Studies with Evaluation Metrics.
Full size table

Table 5 provides a concise overview of representative studies that examine distributed generation, storage coordination, and hydrogen–electric microgrid operation. The two selected works capture the dominant methodological directions in recent literature. Shi et al. focus on deep reinforcement learning to manage hydrogen–electric coupled microgrids, emphasizing operational efficiency and system stability, while Yang et al. investigate the use of metaheuristic optimization with dynamic thermal rating to enhance distributed generation and battery deployment. Both studies incorporate stochastic or scenario-based uncertainty treatment and evaluate system performance using metrics such as cost, loss reduction, voltage deviation, and stability indicators. Despite the strengths of these approaches, Table 5 also highlights several gaps that motivate this paper. Existing research predominantly optimizes short-term operational efficiency and does not address long-horizon welfare coordination among virtual power plant actors. Moreover, the reviewed models rely on traditional stochastic uncertainty descriptions and do not incorporate ambiguity-aware or distributionally robust formulations. Evaluation metrics related to fairness, long-term welfare allocation, and network-constrained flexibility valuation remain largely unexplored. These limitations form the foundation for the methodological advances proposed in this study.

To assess the computational feasibility of the proposed approach, all experiments were executed on a workstation equipped with an Intel i9-13900K CPU and 64 GB RAM using Gurobi 10.0 as the solver. For the modified IEEE 33-bus system, the average solution time for each rolling optimization window was approximately 7.4 minutes, with a maximum of 9.1 minutes during high-congestion conditions. The baseline stochastic optimization model required about 6.2 minutes per iteration, while the conventional robust optimization model required 7.0 minutes. The additional time in the proposed model is primarily due to the iterative Wasserstein dual calibration and the ADMM-based coordination process. Despite this, the total computational overhead remains below 20% compared to the baselines, and the model converges consistently within 15 to 18 iterations for all tested scenarios. Furthermore, extrapolation tests on a larger 69-bus system indicated near-linear scalability with system size, suggesting that the framework remains computationally tractable for practical long-term scheduling applications. These results demonstrate that the proposed method achieves a favorable trade-off between robustness, accuracy, and computational efficiency.

Conclusion

The study has introduced a comprehensive long-term welfare optimization framework for virtual power plant systems, integrating operating cost efficiency, curtailment mitigation, reliability assurance, and carbon accountability into a unified mathematical formulation. By employing a distributionally robust optimization methodology enhanced with scenario reduction, stability metrics, and fairness tracking, the proposed approach has demonstrated its ability to address multiple layers of temporal and operational complexity while remaining resilient to uncertainty in renewable generation and demand. Case study results on a 33-bus test system validated the effectiveness of the framework. Seasonal welfare costs were reduced by 8–13%, curtailment penalties declined by up to 45%, and overload probabilities on critical transmission lines fell by 20–30%. These improvements were not uniform across the seasons but adapted dynamically to prevailing system stressors, with curtailment relief dominating in spring and summer, risk mitigation proving most significant in winter, and efficiency gains driving improvements in autumn. The attribution analysis further revealed that carbon abatement is inherently multi-mechanistic, with 55% arising from curtailment relief, 25% from redispatch optimization, 12% from loss reduction, and 8% from contractual rebalancing. This portfolio of complementary drivers underscores the systemic nature of the decarbonization achieved. Overall, the contributions of this paper lie in establishing a long-term welfare optimization model that balances technical feasibility and environmental accountability, in embedding robustness and fairness into the solution process, and in quantifying both welfare improvements and emission reductions through detailed case evidence. The findings suggest that the proposed methodology provides a robust and adaptable blueprint for guiding the design of future low-carbon energy systems, particularly in contexts where uncertainty, flexibility, and contractual structures interact in complex ways. Future research directions may extend this framework to multi-regional networks, integrate sector coupling with hydrogen and heat systems, or explore the role of emerging technologies such as quantum-inspired optimization in further enhancing solution efficiency and scalability.