Introduction

Organizing proteins into families based on shared structure, function and catalytic mechanism, is a fundamental aspect of comparative and evolutionary genomics1. This classification, primarily derived from amino acid sequences, enables researchers to predict tertiary structures, identify catalytic residues, and elucidate enzymatic mechanisms for particular sequences within entire protein families2,3. Additionally, classifying enzyme sequences in protein families enables the inference of structure and function for uncharacterized sequences in organisms of interest by leveraging knowledge from well-studied proteins within the same family4,5. A critical step in managing and analyzing protein and enzyme families is the identification of representative sequences. This process involves reducing a large set of protein sequences into a small subset that effectively captures the diversity and essential characteristics of all sequences in the entire family. The selection of representative sequences aims to strike a balance between maintaining completeness (ensuring all significant variations within the family are represented) and curtailing redundancy (minimizing overrepresentation of highly similar sequences). Such sequence subsets are crucial for various applications in biological and biomedical research, such as aiding in modeling protein structures in structural biology, which is essential for understanding protein function and interactions, and facilitating drug design6; enabling the identification and quantification of proteins in complex samples using mass spectrometry7,8; or being used in enzyme engineering and synthetic biology to develop novel biological systems and enhance industrial applications9.

Representative sequences are particularly relevant in the context of specialized enzyme databases. Our group recently updated and renewed the ThYme (Thioester-active enzYmes) database, an open-access resource that categorizes thioesterase (TE) enzymes into 35 distinct families4. ThYme also includes sequences, classified into families, of other enzymes involved in the fatty acid synthesis cycle, and/or active with substrates that include thioesters such as acyl transferases5. We constructed each enzyme family in ThYme around a set of representative sequences, which we use as the foundation for populating the families. However, selecting the most appropriate representative sequences for each specific family presents a substantial challenge. For a dataset containing n sequences, one must theoretically evaluate all \(2^n\) possible subsets to find the optimal representation. This becomes computationally infeasible as n increases. Many existing approaches introduce a specific threshold (e.g. \(\%\) identity or similarity) to define sequence representation10,11,12,13,14,15,16,17. These approaches typically rely on heuristic algorithms to find the smallest subset of the ground set that represents all sequences. However, these methods have significant limitations: they often disregard all similarities below the predefined threshold, potentially overlooking important relationships, and there is no theoretical guarantee that these heuristic algorithms produce a subset close to the optimal representative set of sequences.

Researchers have proposed a framework using submodular optimization to address these challenges, an approach that has shown remarkable success in data summarization18,19. In a recent study, Libbrecht et al.20 demonstrated that this framework can yield a concise yet comprehensive representation of data, offering particular benefits in handling the redundancy common in sequence datasets. However, the scientific community has not adopted this approach for selecting representative sequences. Several factors contribute to this limited adoption: (i) the NP-hard complexity of subset selection; (ii) the non-trivial task of defining submodular functions for sequencing data and developing algorithms to use these functions; and iii) the lack of straightforward methods to test algorithm efficiency or validate the completeness and non-redundancy of results.

In this article, we present a ranking-based submodular optimization framework to select representative sequences for protein families in the ThYme database where sequences within each family share high sequence similarity, and sequences in different families have low similarity. We aim to demonstrate how submodular optimization can facilitate the creation of sequence subsets that maintain the integrity of protein and enzyme families. Our approach ensures the inclusion of all known sequences within an enzyme family (completeness) while correctly identifying sequences in their appropriate families (specificity). We explore how this optimization framework excels in distributing known sequences across different enzyme families, providing a more accurate and informative data representation. We apply our framework to enhance the selection process for representative sequences of thioesterase families in the ThYme database, which currently relies on an ad hoc procedure with expert curation. By implementing this methodology, we seek to improve the accuracy, efficiency, and robustness of representative sequence selection. We also applied the submodular algorithms to two protein families in the MEROPS (peptidases) and ESTHER (esterases) databases.

Methods

Representative protein sequences selection

The selection of representative sequences is critical in protein sequence analysis, with significant implications for molecular biology and bioinformatics. Researchers choose representative sequences for each protein family, defining them as a subset of sequences within that family. These carefully selected sequences serve multiple crucial functions: populating protein families in databases4, classifying newly discovered protein sequences21, categorizing 3D protein structures21, and guiding target selection in structural genomics initiatives22. The objective of selecting representative sequences is to identify the smallest subset that fulfills a predefined criterion, typically described as “maximum coverage with minimum redundancy”9 from a finite set of protein sequences, referred to as the “ground set”. Maximum coverage ensures that each sequence in the family is represented by at least one sequence in the representative set, while minimum redundancy guarantees that no two proteins in the representative set exceed a predefined sequence identity threshold.

The primary challenge in selecting a representative set from a large dataset lies in its combinatorial complexity. Even for a relatively small set of 100 sequences, evaluating all \(2^{100} \approx 10^{30}\) possible combinations to find the optimal subset is computationally infeasible. Hobohm et al.9 developed one of the earliest systematic approaches to construct a representative set of non-redundant protein sequences. This algorithm calculates similarity between sequences, using an alignment score or similar metrics, and sets a specific threshold (e.g. % similarity) to determine if two proteins are neighbors. Given a list of candidate proteins and a list of neighbors for each of the proteins, the algorithm removes one protein at a time until those remaining in the list have no neighbor. Subsequent algorithms, including CD-HIT23, PISCES24, MMSEQS25 and UCLUST26, have further developed this concept, typically sorting protein sequences by length and sequentially adding sequences to the representative set if no existing member exceeds a specified similarity threshold. However, these approaches have several limitations: (i) reliance on greedy strategies often leads to suboptimal solutions, (ii) ignoring all similarities below the specified cutoff may overlook important relationships, and iii) lack of control over the size of the representative set as it is possible to include all sequences or only one depending on the predefined threshold.

In this study, we apply classical submodular optimization to the challenge of selecting representative protein sequences. This approach has demonstrated remarkable success in diverse fields, including the selection of representative subsets in text document analysis18,19,27, speech recognition28,29,30, machine translation31, and image analysis32. However, its application in sequence analysis remains limited. A recent study by Libbrecht et al.20 applied this approach to choose non-redundant representative subsets of protein sequences, demonstrating that submodular optimization achieves the best possible results in polynomial time. In the following sections, we provide a detailed description of how submodular optimization can be effectively utilized for selecting representative protein sequences, exploring its potential to overcome the limitations of previous methods and enhance the accuracy and efficiency of protein sequence analysis.

Mathematical description of submodular optimization

Fig. 1
figure 1

Selecting representative sequences using submodular optimization. The objective is to identify a subset of sequences that effectively represent the diversity within a given protein family. While an exhaustive search would require evaluating \(2^n\) possible subsets (where n is the number of sequences), rendering the problem NP-hard, submodular optimization offers an efficient approach to find a near-optimal solution in polynomial time.

Full size image

Mathematical notations

Capital letters denote sets and lowercase letters to denote items in the sets (i.e., sequences).

  • \(\{a,b,c\}\) denotes a set with items a, b and c.

  • \(\emptyset\) is the empty set.

  • \(A \cup B\) is the union of A and B.

  • \(A \setminus B\) is the set of all items in A but not in B.

  • \(a \in A\) means a is an element of A.

  • \(A \subseteq B\) means A is a subset of B.

Submodular function

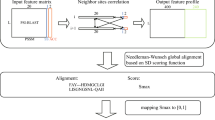
Figure 1 illustrates the application of submodular optimization in identifying a set of representative protein sequences. Let \(S=\{s_{1}, s_{2}, \dots , s_{n}\}\) denote a finite set of protein sequences, and \(f:2^S \rightarrow \mathbb {R}\) represent a function over subsets of S. The function f evaluates a set of elements and outputs a real value quantifying the quality of that set. We assume that f is monotonically increasing. For any subset \(X \subseteq S\), we define the marginal improvement of adding an element \(s \in S \setminus X\) to set X as \(f(X \cup \{s\}) - f(X)\). The function f is considered submodular and normalized if and only if it satisfies the following three conditions:

$$\begin{aligned}&f(\emptyset ) = 0\end{aligned}$$
(1)
$$\begin{aligned}&f(X \cup \{s\}) - f(X) \ge 0, \forall s \in S \setminus X, X \subseteq S\end{aligned}$$
(2)
$$\begin{aligned}&f(X \cup \{s\}) - f(X) \ge f(Y \cup \{s\}) - f(Y), \forall X \subseteq Y \subseteq S, s \not \in Y \end{aligned}$$
(3)

Equation (1) establishes that the function has a value of zero for an empty set. Equation (2) ensures the function is monotonically non-decreasing, meaning that adding a new sequence to the representative set can only maintain or increase its value. Equation (3) describes a crucial property of submodular functions: as we select more points from the ground set, the incremental gain decreases. In the context of selecting representative sequences, this property reflects that the benefit of adding a given protein sequence diminishes when the representative set already contains similar sequences. Our objective is to identify a subset \(R \subseteq S\) that maximizes the value of f, thereby obtaining an optimal set of representative sequences that efficiently captures the diversity within the protein family.

Submodular functions form a broad class of functions with applications across various domains. Notable examples include the weighted coverage function33, rank function of a matroid34, entropy35, mutual information36, and cut capacity37. In this study, we employ a classical submodular function known as the facility location function38 to select representative sequences for protein families. Facility location functions are versatile submodular functions that, when maximized, select examples that effectively represent the data space. These functions optimize the pairwise similarities between points in the dataset and their nearest neighbors, ensuring that the chosen subset accurately reflects the overall data distribution. The general form of the facility location function is:

$$\begin{aligned} f(R) = \frac{1}{|S|}\sum _{s \in S} \max _{r \in R}\phi (s,r) \end{aligned}$$
(4)

where f denotes the facility location function, S is the ground set of all protein sequences, \(R \subseteq S\) is the selected subset of representative sequences, s and r are individual sequences in the ground set, and \(\phi (s,r)\) represents the similarity measure between sequences.

This function satisfies all properties defined in Eqs. (1)–(3): (1) normalization: \(f(R) = 0\) when \(R = \emptyset\); (2) monotonicity: f is monotonically non-decreasing; and (3) submodularity: adding sequences similar to those already in R yields diminishing returns in the value of the function. In our context, maximizing this facility location function will select a subset of sequences that represents the entire protein family. These chosen sequences serve as query sequences for retrieving related proteins from the database, efficiently capturing the diversity within the family while minimizing redundancy.

Similarity function

The similarity function must be non-negative, with higher values indicating greater similarity between sequences. In this study, we define the similarity between a pair of sequences, \(\phi (s,r)\), as the fraction of matching residues. This metric, widely used in protein sequence analysis, can be efficiently calculated using BLAST (Basic Local Alignment Search Tool) tools. For our analysis, we employed BLAST with its default settings optimized for alignment tasks. These settings include: 1) an expect value for saving hits set at 0.05 (evalue), 2) retaining a maximum of 100 aligned sequences (max_target_seqs), 3) a word size of 3 (wordsize), and 4) the BLOSUM62 substitution matrix. We observed that modifying these parameters did not significantly affect the similarity measures returned by BLAST. In cases where BLAST does not report a similarity between a pair of sequences, we assign a similarity value of 0.

Optimization algorithms

Submodular functions arise in numerous applications, making the study of submodular optimization both natural and crucial. While extensive research has been conducted on minimizing submodular functions37,39, our focus lies on maximizing these functions in the context of representative sequence selection. Specifically, we aim to solve problems of the form:

$$\begin{aligned} \max {f(R)},\text { subject to some contraints in } R \subseteq S \end{aligned}$$
(5)

The simplest optimization approach involves cardinality constraints, where we require that \(|R| \le k\) for some positive integer k. In our application using the facility location function, this translates to finding the k best representative sequences for a given protein family. However, even this seemingly simple approach is computationally challenging and classified as NP-hard. Fortunately, efficient approximation algorithms for submodular functions exist, capable of finding solutions guaranteed to be close to the optimal33,40. These algorithms provide a balance between computational feasibility and solution quality. In this study, we employ two such algorithms, as described hereinafter.

The first algorithm we employ is the Greedy algorithm, which guarantees solutions that are at least \((1 - \frac{1}{e}) \approx 63.2\%\) of the optimal value41, where e is the base of natural logarithm. Algorithm 1 presents the pseudocode for this approach. The algorithm starts by initializing an empty representative set and then repeatedly identifies new representative sequences through the following steps. Particularly, for each sequence in the remaining set, the algorithm calculates the marginal improvement in the submodular function (Equation 4) when adding the sequence to the current representative set. Next, it selects the sequence that provides the largest improvement and adds it to the representative set. The algorithm then removes the selected sequence from the remaining set and eliminates other sequences in the remaining set that are identical to the selected sequence (above a 90% threshold). The algorithm repeats this process until no sequences remain in the set.

Algorithm 1
figure a

Pseudocode of the Greedy algorithm.

Full size image

The second algorithm we employ is the Bidirectional Greedy algorithm, which guarantees solutions that are at least \(\frac{1}{2}\) of the optimal value42. Algorithm 2 presents the pseudocode for this approach. Unlike the standard Greedy algorithm, this method introduces randomization and maintains two sets: a “growing set” initialized as empty, and a “shrinking set” initialized as the complete ground set. The algorithm iteratively considers each sequence, deciding whether to add it to the growing set or remove it from the shrinking set based on which action yields the greater gain in the objective function (Eq. 4). If adding the sequence provides a greater gain, the algorithm adds it to the growing set; otherwise, it removes the sequence from the shrinking set. The algorithm terminates when the growing and shrinking sets converge to identical sets, either of which represents the final solution.

Algorithm 2
figure b

Pseudocode of the bidirectional Greedy algorithm.

Full size image

We significantly enhance the performance of these algorithms by executing them multiple times to obtain the optimal set with the highest score. We propose a ranking strategy that combines the results from multiple runs of each algorithm to select the optimal set. For each run, we shuffle the ground set, generate a representative set, and assign ranks to the sequences based on their inclusion order (lower rank indicates a better sequence). We then iteratively select the sequences that appear most frequently and hold the lowest ranks, adding them to the final set. We continue this addition process until a BLAST search using the selected sequences as query sequences successfully retrieves all members of the ground set. We configure the BLAST parameters max_target_seqs and evalue with default values of 999999 and \(1e-07\), respectively.

Results

Protein sequences data

We evaluated our submodular optimization approach for selecting representative protein sequences using data from thioesterase (TE) enzyme families. We downloaded protein sequence data in FASTA format from the ThYme database that have been developed and maintained by our group (https://thyme.engr.unr.edu/v2.0/)4. In the ThYme database, we categorized TE enzymes into 35 families based on their structural similarity, function, and catalytic mechanism (Fig. 2). Enzymes with different structural folds catalyze thioesterase function. Most TEs have either a HotDog fold or an alpha/beta-Hydrolase fold; however, enzymes with the NagB, SGCH, Lactamase, Beta-hairpin/TIM barrel folds can also perform thioesterase function4. Enzymes families within each fold are more closely related to each other than to families with a different structural fold. Our recent review on TE enzymes, which describes in detail how the TE families were defined based on sequences similarity, shows phylogenetic trees of how the TE families within the HotDog and alpha/beta-Hydrolase folds are related to each other. The phylogenetic and structural diversity of the TEs ensures that the submodular optimization approach works for different enzymes/protein families (Fig. 3), which is a reason why TEs were chosen to develop the submodular optimization approach to identify representative sequences.

Each TE family is based on at least one experimentally verified sequence which serves as a representative sequence. Families are populated with protein BLAST using the catalytic domain of the representative sequences as a query. Families are verified to have nearly identical tertiary enzyme. This results in that ThYme families have approximately 15-30% sequence similarity, which corresponds to narrow subfamilies of larger protein families based on sequence profiles for example in the Pfam database43. Among different TEs, sequences come from different structural folds, so the TE families are very different to others, as shown in Fig. 3. Accordingly, to perform the representative sequences selection using submodular optimization, we created an initial ground set of sequences for each TE family, including only unique and experimentally characterized sequences. We identified these sequences using the “Evidence at Protein Level” indicator in UniProt, as clearly marked in the ThYme database. We excluded families (TE5, TE12, TE19, TE24, TE28, TE32, TE33, and TE35) with fewer than three sequences in their ground set from further analysis. In total, we obtained 737 sequences in the ground set across all selected families, with each family containing between four and one hundred sequences, as shown in Table 1.

The main goal of this article is to introduce the two greedy algorithms based on submodular optimization to replace the ad hoc procedure with submodular optimization in the ThYme database. We are optimistic that future algorithms based on submodular optimization can be developed for the purpose of finding representative sequences for many other protein families. To demonstrate the potential of this new direction, we evaluate the approach using sequence data from a carboxylesterase (CE) enzyme family and the peptidase family A1 (A1A). We retrieved 12,277 sequences of the CE family from the ESTHER database44 and 13,847 sequences of the A1A family from the MEROPS database45. Unlike TE families in which know the sequences that have been experimentally characterized, we used all sequences for the CE and A1A families as available in MEROPS and ESTHER. To facilitate reproducibility of our analysis results, we consolidated all ground sets for individual families into a single local database, which we provide as a .FASTA file (see Data availability).

Fig. 2
figure 2

Five superimposed enzymes in TE15: 5PVJ (Homo sapiens) - pink, 2W3X (Micromonospora echiospora - yellow), 2XEM (Micromonospora chersina - orange), 2XFL (Micromonospora chersina - green), and 4I4J (Streptomyces globisorus - blue) all have very similar tertiary structures even though they originate in different organisms.

Full size image
Fig. 3
figure 3

Sequence similarity among the TE families. We performed pairwise sequence alignments on experimentally verified sequences from 35 TE families using blastp, with percentage identity used as a measure of sequence similarity. For each pair of families, we calculated inter-family similarity by averaging the percentage identities of the pairs consisting of one sequence from each family. Among different TEs, sequences come from different structural folds, so the TE families are very different to others. Within each family, sequence similarity is high.

Full size image

Ad hoc procedure for identifying protein families

The TE enzyme families in the ThYme database are based from representative sequences that were chosen by an ad hoc procedure from a larger pool that includes all known TE sequences that have been experimentally verified2. The ad hoc method to identify enzyme families in ThYme prioritizes completeness to ensure the inclusion of all known sequences with a specific function, particularly those experimentally characterized or with known tertiary structures. We retrieved sequences with specific functions and experimental characterizations from the UniProt database46,47. We then used each retrieved sequence as a query in a Basic Local Alignment Search Tool (BLAST)48,49 search against all known protein sequences (nr database). We compared the BLAST results against each other to identify the representative sequence of a family: which is the query sequence with the BLAST results that ensure completeness. We then populated the families by subjecting the catalytic domain of the representative sequence of a family through BLAST again and verifying sequence and structural similarity with multiple sequence alignments and tertiary structure superimposition. After identifying representative sequences using this ad hoc method, we performed expert manual curation to further refine the set and ensure the inclusion of the correct sequences if needed. While this procedure ensures completeness, it remains labor-intensive, particularly in verifying the quality of the representative set, which currently hampers the update and maintenance processes of the ThYme database.

Evaluation workflow

Figure 4 illustrates our overall analysis workflow for method evaluation. In this analysis, we will apply submodular optimization using the Greedy and Bidirectional Greedy algorithms and compare their performance to two widely-used clustering methods for identifying representative protein sequences: CD-HIT23 and MMseqs225. For each family, after establishing the ground set, we used BLAST alignment tool (blastp) to compute the percentage identity for every pair of sequences within this set. This step produces a pairwise percentage identity matrix that captures the similarity relationships among the sequences, serving as input for our submodular function. For CD-HIT and MMseq2, we provided the required ground set .FASTA files as input and used the default settings for the evaluation analysis.

For TE families, we compared the representative sequences generated by these algorithms with those obtained through our ad hoc procedure, which includes manual curation as used in the current ThYme database. We focus our comparison on the correctly recognized protein sequences that are highly similar to these optimal sets of representative sequences. Additionally, we use two metrics, sensitivity and specificity, to assess the quality of the representative sets generated by the submodular optimization in terms of completeness (inclusion of all known sequences belonging to the family) and specificity (accurate family representation). To do this, we use the representative sequences generated by the submodular optimization algorithms as the query set for a BLAST search against a local database containing all experimentally characterized sequences from all families in the TE group. We define sensitivity for a specific family as the percentage of that family’s sequences (ground set) correctly identified in the BLAST search results. Specificity is calculated as one minus the proportion of sequences from other families that are incorrectly identified as belonging to the family in question when using its representative sequences as the query set.

We do not know how the MEROPS and ESTHER databases populate the CE and A1A families. Unlike the TE families in ThYme which are based on blastp results of experimentally-verified sequences, we cannot compare our results for the CE and A1A against representative sequences with experimental validation. Instead, we assess the performance of the algorithms by comparing the coverage of the entire family, using sensitivity as the primary metric. For the CE and A1A families, sensitivity reflects the proportion of sequences in the family that are correctly identified by the representative sets returned by the different algorithms, providing a measure of how well the returned sets cover the entire family.

Fig. 4
figure 4

For each protein family, we use BLAST to compute pairwise percentage identities within the ground set, generating an identity matrix that serves as input for the submodular function. For families from the ThYme database, we compare the representative sequences generated by submodular optimization algorithms with those from our ad hoc procedure as a benchmark. Our comparison focuses on correctly recognized protein IDs and residue identity. For all families, we evaluate the quality of the representative sets using sensitivity and/or specificity metrics. We perform a BLAST search against a local database of ground sets, using sensitivity to assess completeness (coverage) and specificity to measure accuracy.

Full size image
Fig. 5
figure 5

Distributions of sequence identity between the benchmark representative sequences of each family and the sets returned by four optimization methods: two submodular optimization algorithms (Greedy and Bidirectional), CD-HIT, and MMseqs2. Each family is represented by four box plots showing the results for the Greedy algorithm, Bidirectional Greedy algorithm, CD-HIT, and MMseqs2, arranged from left (high transparency) to right (low transparency). A box plot with a single dot indicates that the algorithm returned a set containing only one sequence; otherwise, the returned set contains multiple sequences. Overall, the Greedy algorithm demonstrates the best performance, producing a tight set with high similarity to the ground truth. CD-HIT also performs well, though its representative sets generally contain more sequences than those from the Greedy algorithm. The Bidirectional Greedy algorithm and MMseqs2 show similar performance, often returning larger sets of representative sequences for each family.

Full size image

Comparing the optimization approaches with the ad hoc procedure

Table 1 presents a comparative analysis of the representative sequence selection results across five different methods: the Greedy algorithm, the Bidirectional Greedy algorithm, CD-HIT, MMseqs2, and the ad hoc procedure (which includes manual curation) used in the ThYme database. The “Ground Set Size” column indicates the number of experimentally verified protein sequences within each TE family, serving as the ground set on which the algorithms operate. We considered the sets returned from the ad hoc procedure as the benchmark in the analysis for TE families. In general, all algorithms produce representative sequence sets that include most of the sequences identified by the ad hoc procedure for the majority of TE families. However, there are notable differences in the size of the representative sets generated by each algorithm. The Greedy algorithm, which focuses on selecting a minimal yet diverse set of representatives, performs similarly to the ad hoc procedure in 12 out of the 27 TE families. It produces smaller sets in 6 families (e.g. TE1, TE6) and larger sets in 9 families (e.g. TE2, TE4). In terms of redundancy, measured by the size of the representative set, the Greedy algorithm performs similarly to our ad hoc procedure in 12 out of 27 TE families. It returns smaller sets in 6 families and larger sets in 9 families compared to the benchmark. Conversely, we observe that the Bidirectional Greedy algorithm generally returns larger sets than the ad hoc procedure, with exceptions in TE27 (similar to ad hoc) and TE6 (smaller than ad hoc). CD-HIT returns a larger set compared to the benchmark for 19 TE families, sets with equal size for 6 TE families and did not return any result for 2 families (TE21 and TE34). Similarly, MMseqs2 also returns less tighter representative sets for most of the families, with exeptions for TE3, TE27, TE29 (equal size) and TE13 (smaller set). We conclude that the Greedy algorithm tends to select a smaller number of representative sequences compared to the other algorithms. This approach effectively captures the essential diversity within each family while minimizing unnecessary duplications, resulting in a more concise and efficient representation.

Table 1 Representative sets for TE families produced by Greedy algorithm, Bidirectional Greedy algorithm, CD-HIT, MMseqs2, and the ad hoc with manual curation currently used in the ThYme database.
Full size table

We further compared the sequence identity of the sets returned by four algorithms-Greedy, Bidirectional Greedy, CD-HIT, and MMseqs2- with the current set in our database, which we created using an ad hoc procedure with careful manual curation. Figure 5 presents the distributions of percentage identity between the sequences in the sets returned by the two algorithms and those in the optimal sets from our ad hoc procedure. The results reveal that the Greedy and Bidirectional Greedy algorithms achieve sequence sets with high similarity to the ad hoc procedure in many families, with a similarity exceeding 80% in TE1, TE8, TE18, TE21, TE22, TE29, and TE35. However, in families with a larger number of sequences, such as TE4, TE16, TE26, TE27, and TE30, the Greedy algorithm exhibits lower similarity, with percentage identities below 50%. The Bidirectional Greedy algorithm also returns sets with lower similarity in families such as TE4, TE17, and TE30. For CD-HIT and MMseqs2, the performance is more variable across TE families. CD-HIT tends to generate sets with high similarity to the ad hoc sets in several families, including TE7, TE18, TE29, and TE31, but struggles with lower similarity (below 50%) in families like TE4, TE6, TE26, and TE30. Similarly, MMseqs2 performs well for TE17, TE18, TE22, and TE34 but shows lower similarity in TE4, TE26, and TE30.

Overall, the Greedy algorithm tends to select fewer representative sequences compared to the Bidirectional Greedy algorithm, CD-HIT, and MMseqs2. This approach effectively captures the essential diversity within each TE family while minimizing redundancy, resulting in a more concise and efficient representation of the sequence space. The Bidirectional Greedy algorithm, although generally returning larger sets, also struggles with certain families. Both CD-HIT and MMseqs2 show mixed results, indicating that further refinement is needed to improve their performance, particularly in complex families with many sequences.

Sensitivity and specificity analysis

We assess the accuracy of both algorithms by using their returned representative sequences to populate their corresponding TE families. Figure 6 provides insights into the sensitivity of the Greedy and Bidirectional Greedy algorithms in selecting representative sequences for TE families. We observe robust performance from both algorithms, which achieve a sensitivity of \(100\%\) across all TE families when considering sequences with evidence at the protein level. The Greedy algorithm, on average, achieves an impressive \(80\%\) sensitivity with a representative set size of only 2 sequences. In contrast, the Bidirectional Greedy algorithm requires a larger representative set size of 4 sequences to reach a similar sensitivity level. This difference highlights the varying efficiency of the algorithms in capturing the diversity and coverage of sequences within each TE family. Furthermore, we find that both algorithms consistently produce representative sets that effectively retrieve all sequences from their respective TE families in BLAST searches, underscoring their utility in comprehensive sequence representation.

Fig. 6
figure 6

Comparison of the sensitivity of two algorithms, Greedy and Bidirectional Greedy, in optimizing submodular functions for identifying representative protein sequences. The sensitivity values are plotted against the number of selected representative sequences across protein families in the TE group. Both algorithm demonstrates high sensitivity, but Greedy algorithm performs better in reducing the redundancy than Bidirectional Greedy algorithm does.

Full size image

We assess the specificity of the representative sets generated by the Greedy and Bidirectional Greedy algorithms and show the results in Fig. 7. We observe a specificity of 1 across all TE families, indicating that both algorithms terminate without errors in sequence identification from other families. The maximum error rate, averaging around \(0.02\%\), signifies the high precision and accuracy of these representative sets in distinguishing sequences belonging exclusively to their respective families. Although both algorithms perform exceptionally well, we find that the Greedy algorithm exhibits a slightly superior specificity compared to the Bidirectional Greedy algorithm, showcasing its ability to minimize cross-family sequence identifications more effectively.

Fig. 7
figure 7

Comparison of the specificity of two algorithms, Greedy and Bidirectional Greedy, in optimizing submodular functions for identifying representative protein sequences. The specificity values are plotted against the number of selected representative sequences across various protein families (TE1 to TE35). Both algorithms exhibit high specificity, with the maximum error rate is around \(0.02\%\).

Full size image

We emphasize that the size of the representative set produced by these algorithms was not our primary focus in this application. We configure the Greedy algorithm to terminate based on a predefined threshold of sequence similarity, ensuring that the selected sequences adequately represent the diversity within each family. In contrast, we allow the Bidirectional Greedy algorithm to continue until it successfully identifies all sequences in the ground set via BLAST, potentially resulting in larger representative sets. Since the Bidirectional Greedy algorithm builds upon the Greedy algorithm, their sensitivity and specificity outcomes are generally comparable. This consistency in performance underscores the reliability of both algorithms in accurately identifying and representing sequences from their respective TE families.

Coverage analysis for carboxylesterase and peptidase families

Here we demonstrate that submodular functions can be applied to identify representative sequences of other protein families. Results show the potential of greedy algorithms in finding representative protein sequences of enzymes families with high sequence similarity; however, results are not complete without a thorough validation that greedy algorithms can identify representative sequences for any protein family. We applied the approach to two additional protein families, carboxylesterase (CE) enzyme family and the peptidase family A1 (A1A). We also compared the four methods (Greedy, Bidirectional Greedy, CD-HIT, MMseqs2) using the same data from CE and A1A families. For these two families, MMseqs2 returned many representative sequences. Specifically, MMseqs2 returned 2,323 representative sequences for the CE family and 1,701 for the A1A family. On the other hand, CD-HIT generated 10,564 representative sequences for the CE family and 8,774 for the A1A family. Note that CD-HIT and MMseqs2 are based on clustering, i.e., the methods group the sequences based on their similarity and then returns a representative sequence for each cluster50. There are two potential drawbacks of such approach: (1) it might return many clusters with many representative sequences, as shown above, and (2) it does not necessary provide high coverage because a cluster of sequences might not be covered 100% by a single representative sequence.

In contrast, the submodular optimization approaches offer more flexibility, allowing us to control the number of representative sequences returned Fig. 8 shows the coverage against on the number of representative sequences chosen by the two submodular algorithms. For CE family, both algorithms achieve 100% coverage with less than 10 representative sequences. For the A1A family, both algorithms achieve over 90% coverage with less than 10 representative sequences. The two algorithms achieve a 100% coverage with approximately 600 sequences, in which the Greedy algorithm has a slightly tighter set.

Fig. 8
figure 8

Comparison of the coverage of two algorithms, Greedy and Bidirectional Greedy, in optimizing submodular functions for identifying representative protein sequences. The coverage values are plotted against the number of selected representative sequences across protein families in the two protein families: the carboxylesterase (CE) enzyme family and the peptidase family A1 (A1A). Both algorithm demonstrates to return the representative set with high coverage, but Greedy algorithm performs better in reducing the redundancy than Bidirectional Greedy algorithm does.

Full size image

Discussion

In this study, we employed submodular optimization techniques to select representative sequences within thioesterase protein families in the ThYme database. This approach was motivated by the inherent redundancy in biological sequence datasets, which can obscure meaningful patterns and complicate genetic analysis. Our goal was to demonstrate the effectiveness of the facility location function, a widely used submodular function, in conjunction with optimization algorithms to enhance the selection of representative sequences. We specifically selected these algorithms because they minimize redundancy while ensuring high coverage of the protein family. Facility location functions have proven effective in modeling problems that involve selecting a representative subset from a larger set, particularly in clustering and summarization tasks. These functions balance the need to maximize coverage while minimizing redundancy, making them an ideal choice for selecting representative sequences from biological datasets. In contrast, information-theoretic functions like entropy or mutual information-though powerful-focus primarily on maximizing information gain. They are more suited to scenarios where capturing diverse information is essential, such as in cases involving uncertainty51,52, rather than focusing on physical proximity or sequence similarity. Since our primary objective was to select a set of sequences based on similarity and redundancy reduction, facility location functions were more directly applicable to our problem. However, information-theoretic approaches could be valuable for future extensions of this work.

Accordingly, we applied the approaches to real-world datasets to evaluate their performance. The results of our study highlight several key findings. Firstly, the submodular optimization approach consistently produced representative sets that effectively captured the entire spectrum of sequences within their respective families, achieving high sensitivity. This capability is crucial in ensuring that no significant sequence variations or genetic traits are overlooked during analysis. Furthermore, we meticulously evaluated the specificity of our approach. This involved assessing the extent to which sequences from unrelated families were mistakenly identified when using the representative sequences of a specific family as query sequences Our findings indicate that the representative sets generated through submodular optimization exhibited commendable specificity, minimizing the occurrence of false positive identifications and maintaining accurate family-level distinctions. In terms of optimization algorithm performance, the Greedy algorithm emerged as particularly effective in enhancing specificity and reducing redundancy compared to the Bidirectional Greedy algorithm. The Greedy algorithm systematically adds sequences based on their marginal contributions to the overall representation, thereby optimizing the balance between coverage and specificity, which explains its superior performance.

When applied to protein families with significant sequence similarity, our approach enables the selection of smaller, yet highly informative set of representative sequences compared to traditional clustering algorithms. It is important to note that representative subset selection differs fundamentally from clustering. While clustering results in groups of similar sequences, representative subset selection focuses on choosing individual sequences that best represent the entire dataset. Applying clustering methods to representative selection requires an additional step to identify an exemplar sequence for each cluster. In practice, clustering algorithms are rarely used for the purpose of selecting representative sequences from large datasets20. We note that when dealing with large datasets, unverified sequences are often present, and submodular optimization algorithms may frequently select these unverified sequences based solely on amino acid sequences, which can lead to inaccuracies. This means that these algorithms are not necessarily robust to errors occurring in generic-purpose databases, and are to be used for carefully curated datasets.

In summary, our study underscores the significant advantages of employing submodular optimization in the selection of representative sequences within protein families with significant sequence similarity in specialized, curated databases. By addressing redundancy and enhancing specificity, this methodology not only improves the accuracy of biological analyses but also contributes to a deeper understanding of genetic diversity and evolutionary relationships. These insights are pivotal for advancing research in various biological disciplines and informing strategies for precision medicine and biotechnological applications.