Research on credit risk of listed companies: a hybrid model based on TCN and DilateFormer

Abstract

The ability to assess and manage corporate credit risk enables financial institutions and investors to mitigate risk, enhance the precision of their decision-making, and adapt their strategies in a prompt and effective manner. The growing quantity of data and the increasing complexity of indicators have rendered traditional machine learning methods ineffective in enhancing the accuracy of credit risk assessment. Consequently, academics have begun to explore the potential of models based on deep learning. In this paper, we apply the concept of combining Transformer and CNN to the financial field, building on the traditional CNN-Transformer model’s capacity to effectively process local features, perform parallel processing, and handle long-distance dependencies. To enhance the model’s ability to capture financial data over extended periods and address the challenge of high-dimensional financial data, we propose a novel hybrid model, TCN-DilateFormer. This integration improves the accuracy of corporate credit risk assessment. The empirical study demonstrates that the model exhibits superior prediction accuracy compared to traditional machine learning assessment models, thereby offering a novel and efficacious tool for corporate credit risk assessment.

Introduction

Enterprise credit risk is not only a major concern in the financial sector but is also closely tied to societal development. Credit risk impacts the survival of banks, influencing the stability of both the country and society¹. To maintain national economic stability in the wave of globalization, it is essential to actively assess enterprise credit risk and implement effective risk assessment methods².

The evaluation of enterprise credit risk can also be regarded as a study of corporate financial distress, essentially a binary or multi-class classification problem³. With the continuous growth in data volume and complexity, the development of credit risk assessment methods has progressed through three stages: manual judgment based on experience, statistical discriminant analysis, and big data evaluation using machine learning techniques⁴. This evolution reflects a shift from qualitative to quantitative analysis and from indicator-based to model-based approaches⁵. Although traditional assessment methods have addressed corporate credit risk identification to some extent, the changing financial market environment and the explosive growth of data urgently call for more efficient and accurate evaluation models.

This study aims to develop a novel hybrid model to enhance the accuracy and reliability of credit risk prediction. Specifically, it proposes a hybrid model based on the CNN and Transformer framework but replaces the standard components with temporal convolutional network (TCN) and DilateFormer modules to optimize the extraction and modeling of time-series features. For publicly listed companies, default cases are a minority, leading to a significant imbalance between default and non-default data. To address this issue, a Gaussian noise-based data augmentation technique is employed during model training to improve the classification performance under imbalanced sample conditions. Additionally, this study modifies the attention mechanisms in both the TCN and DilateFormer modules, introducing optimizations in both the temporal and channel dimensions. These enhancements significantly improve the model’s feature extraction capability and prediction performance.

Based on the above analysis, this study establishes a hybrid model based on TCN-DilateFormer to evaluate the credit risk of publicly listed companies, utilizing real financial indicator data from the CSMAR Database covering the years 2012 to 2022. The model employs the TCN module to extract local features from raw financial data, while the DilateFormer module processes and integrates sequence features. Ultimately, the model outputs credit risk prediction labels for each company, enabling accurate judgment and prediction of corporate defaults.

The key innovations of this study are as follows: (1) A novel hybrid model based on CNN and Transformer is designed, enhancing the model’s capability in handling time-series classification tasks. (2) Gaussian noise is introduced into the default data to address the issue of data imbalance, thereby improving the model’s generalization ability and prediction accuracy. (3) The attention mechanism is refined to achieve joint optimization across the temporal and channel dimensions, significantly boosting the model’s feature extraction capability and prediction performance.

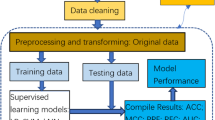
Our complete workflow, as illustrated in Fig. 1, comprises several key steps: data import and processing, model training and validation, parameter optimization, result analysis, and future outlook. The remainder of this paper is organized as follows: Sect “Related works” reviews related work on credit risk analysis. Sect “Theoretical explanation of CNN and Transformer” provides a theoretical overview of CNN, Transformer, and related models. Sect “Methodology” details the architecture and design of the TCN-DilateFormer model. Sect “Data” introduces the dataset and data processing methods. Sect “Empirical analysis” presents the experiments and provides a discussion of the results. Sect “Discussion” explores the future prospects of the proposed model. Sect “Conclusion” concludes the study with key findings.

Fig. 1

Overall framework diagram.

Related works

Manual discrimination methods

Early credit risk assessment primarily relied on expert judgment. Sowers and David (1942)⁶ developed personal credit risk evaluation metrics, using experience-based assessments and expert scoring to judge individual risks. Early methods included the 5 C factor analysis and the DuPont financial analysis. However, these methods heavily depended on subjective expert opinions, resulting in evaluation outcomes that were often unconvincing due to their significant subjectivity⁷.

Statistical discriminant analysis methods

Following Fisher’s pioneering work on credit rating using the least squares method⁸, researchers increasingly adopted rigorous statistical approaches. Statistical methods based on linear discrimination were widely utilized to address the limitations of manual judgment, integrating the concept of mathematical modeling into the field of credit risk assessment⁹. Among these, Altman’s multiple discriminant analysis model¹⁰ became a landmark, driving the development of statistical models in credit evaluation. Representative methods in this category include the Z-score model and Logistic regression¹¹, as well as multivariate statistical models such as multiple discriminant analysis and multivariate regression analysis. These models typically offer high accuracy, relying on only a few variables to effectively discriminate between samples. Their strong interpretability makes them particularly effective in low-dimensional data analysis tasks. However, these models impose strict assumptions, which real-world financial data often fail to fully satisfy, limiting their applicability. Additionally, their predictive capabilities have gradually been surpassed by subsequent machine learning methods¹².

Machine learning-based methods

With the advent of the era of big data, machine learning methods have demonstrated significant advantages in credit risk assessment. Compared to traditional statistical models, machine learning algorithms such as support vector machines (SVMs), neural networks, and random forests are better equipped to handle large-scale data and model complex nonlinear relationships. For instance, Xiaohong Yu¹³ achieved a 100% recognition rate for samples using a random forest-based P2P lending risk warning model. Similarly, Luo et al.¹⁴ applied a non-kernel surface SVM model to credit risk assessment and demonstrated its superior predictive performance compared to traditional classification models. These studies highlight the remarkable effectiveness and advantages of machine learning algorithms over traditional statistical methods in credit risk evaluation. However, machine learning methods face challenges in processing large-scale nonlinear data and are sensitive to data quality. Inaccurate or noisy data can negatively impact the performance of these models.

Deep learning-based methods

As a branch of machine learning, deep learning has gained wide application in credit risk assessment due to its advantages in automatically learning and extracting high-dimensional features from data¹⁵. Neural networks, one of the representative techniques of deep learning¹⁶, are commonly used for tasks such as classification and regression. Among these, convolutional neural networks (CNNs) are particularly notable for their robust ability to extract local features, significantly reducing computational complexity and the number of training parameters¹⁷. CNNs are widely used for image feature extraction and sequence feature mining. Existing studies have applied CNNs to the financial sector; for example, some researchers have constructed CNN-LSTM hybrid models for personal risk assessment, estimating customer default probabilities¹⁸. However, CNNs are more suited to handling data with local spatial structures, such as images or text, and struggle to capture long-term dependencies and global information in time-series data¹⁹, which are essential in credit risk analysis. Recently, Transformer models have achieved breakthrough advancements in artificial intelligence through self-supervised predictive encoding and have been widely applied to tasks such as natural language processing, computer vision, and time-series analysis²⁰. For example, Tian et al.²¹ employed Swin-MSP to train an image recognition model, incorporating spectral masking pretraining techniques and hierarchical architectures for layered modeling of hyperspectral data. Transformer models excel at extracting latent information from complex, high-dimensional datasets and effectively capturing time-series features and logical relationships, thereby offering more precise assessments in credit risk prediction. Existing research has applied Transformer models to corporate credit risk analysis. Stevenson et al. utilized a Transformer-based BERT model combined with textual data to predict the credit risk of micro-enterprises, achieving promising results; however, their study did not consider time-series data²². Similarly, Korangi et al. developed the Transformer-based TEP model to predict the credit risk of medium-sized listed companies, outperforming traditional models²³. Despite its strong ability to capture long-term dependencies, the TEP model still has room for improvement in local feature extraction.

Development of hybrid models

To overcome the limitations of single models, researchers have explored combining CNN and Transformer architectures, leveraging the local feature extraction capability of CNNs and the long-distance dependency modeling power of Transformers to improve the performance of credit risk prediction²⁴. However, traditional CNN and Transformer models both face limitations when handling time-series-based credit risk classification tasks, leaving their hybrid CNN-Transformer models room for further refinement. One key issue is that hybrid models heavily depend on the Transformer component for processing dynamic time-series data. Due to the structural limitations of CNNs, expanding the receptive field often requires adding more convolutional layers to enhance data reception. However, excessively deep networks may result in gradient explosion or vanishing problems, leading to information loss and reduced prediction accuracy. To address these challenges, some studies have introduced improved CNN-based modules, such as temporal convolutional networks (TCNs)²⁵, and incorporated DilateFormer modules in the Transformer component²⁶ to optimize the temporal analysis capability of these models.

In summary, while existing models have made significant progress in corporate credit risk assessment, numerous challenges remain. Developing effective hybrid models that integrate multiple techniques for classifying time-series financial data is a key direction for future research.

Theoretical explanation of CNN and Transformer

CNN and TCN architectures

CNN is a widely used and powerful deep learning architecture that mimics the human visual system to efficiently recognize and classify objects and features in images. Its local connectivity and weight-sharing features significantly reduce model parameters, making it suitable for large-scale data processing. The main components of CNN include four core modules: the convolutional layer, activation layer, pooling layer, and fully connected layer. The convolutional layer, a key component of CNN, operates by sliding a set of convolutional kernels over the input data to extract local features, generating a two-dimensional matrix called the feature map. The mathematical expression for the convolution operation is:

$$O\left( {m,n} \right) = \mathop \sum \limits_{i} \mathop \sum \limits_{j} I\left( {m + I,n + j} \right) \cdot K\left( {I,j} \right) + b$$

(1)

Where I is the input image data, K is the convolution kernel, O is the output feature map, (m, n) are the input image coordinates, (i, j) are the convolution kernel coordinates, and b is the bias term.

The pooling layer processes the feature maps generated by the convolutional layer to reduce their size, decrease computational load, and prevent overfitting. The pooling layer is typically located after the convolutional layer, with the two layers often alternating. Common pooling methods include average pooling and max pooling, which compute the average and maximum values, respectively.

Specifically:

$$O\left( {m,n} \right)=\hbox{max} {\left( {I,j} \right)_{ \in w}}I\left( {m\cdots+I,n\cdots+j} \right)$$

(2)

$$O\left( {m,n} \right)=\frac{1}{{\left| w \right|}}\sum {\left( {I,j} \right)_{ \in W}}I\left( {m\cdots+I,n\cdots+j} \right)$$

(3)

where W is the pooling window and s is the step size. The fully connected layer integrates the high-level features extracted by the convolutional and pooling layers, enabling classification and prediction. The convolutional and pooling layers handle feature extraction, while the fully connected layer performs classification.

Its mathematical formulation is as follows

$$O = w \cdot I + b$$

(4)

Where I is the input feature vector, W is the weight matrix, b is the bias vector and O is the output feature vector.

In nonlinear multi-classification tasks, activation functions are employed to introduce nonlinearity into the model, enabling the calculation of probabilities for a sample belonging to different categories based on the output vectors of fully connected layers. This enhances the model’s representational capability. In this model, the ReLU activation function is used in the TCN layers to introduce nonlinearity, while the GeLU activation function is utilized in the DilateFormer module.

Both ReLU and GeLU are advanced activation functions widely adopted in neural network architectures, particularly in fields like natural language processing and computer vision. GeLU, by incorporating the Gaussian distribution characteristics of the input, smoothly activates neurons. Compared to ReLU, GeLU provides a superior nonlinear transformation, making it especially effective in Transformer-based models.

Its mathematical expression is:

$$\begin{array}{*{20}{c}} {GeLU\left( x \right)=x \cdot \Phi \left( x \right)} \\ {\Phi \left( x \right)=\frac{1}{2}\left( {1+erf\left( {\frac{x}{{\sqrt 2 }}} \right)} \right)} \end{array}$$

(5)

CNN’s 2D convolution is highly effective for processing image and spatial data, but 1D convolution is typically employed for temporal data. However, CNN’s structure is not inherently designed for temporal data, making it challenging to achieve optimal results. CNN uses a fixed-size receptive field to capture local features but lacks temporal dependency, leading to weak contextual connections and potential loss of associated information, which limits its performance in temporal classification tasks. To better handle corporate annual financial report data, this paper introduces the temporal convolutional network (TCN), a CNN-based variant model.

TCN is a neural network architecture specifically designed for processing time-series data. It is optimized through a series of specialized designs and performs well in tasks requiring long-term dependencies. Unlike CNN, TCN primarily uses causal convolution, which differs from traditional bidirectional convolution. Causal convolution imposes one-way temporal constraints, ensuring the model relies solely on past information without accessing future data when making predictions. The output at time t is computed using only the inputs at time t and earlier.

The mathematical expression for this is:

$$y\left( t \right) = \mathop \sum \limits_{{k = 0}}^{{K - 1}} w\left( k \right) \cdot x\left( {t - k} \right)$$

(6)

where y(t) is the output at time t, w(k) is the weight k of the convolution kernel, x(t) is the input at time t, and K is the convolution kernel size.

Due to the limited size of the convolution kernel, causal convolution requires stacking additional layers to capture longer sequence information. To address this and capture longer time dependencies, TCN introduces dilated convolutions. By adjusting the dilation factor, dilated convolution expands the receptive field without significantly increasing computational burden. The dilation factor grows exponentially with network depth, enabling the network to cover a broader time span.

The mathematical expression for this is:

$$y\left( t \right) = \mathop \sum \limits_{{k = 0}}^{{K - 1}} w\left( k \right) \cdot x\left( {t - k \cdot d} \right)$$

(7)

where d is the expansion factor.

TCNs frequently incorporate residual connections to mitigate the issue of vanishing gradients during deep network training. Residual connections allow each layer to directly learn useful information from the previous layer and facilitate information flow across multiple layers, thereby enhancing the network’s learning capacity. The mathematical expression for this is:

$$y\left( t \right)=F\left( {x\left( t \right),W} \right)+x\left( t \right)$$

(8)

where y(t) is the residual module output, x(t) is the residual module input, F(x) is the convolution output and W is the convolution kernel weights.

Transformer and DilateFormer structure

Transformer is a deep learning model based on a self-attention mechanism designed for processing sequential data, such as text and time series. Key features of the Transformer include the self-attention mechanism, which enables the model to consider all other elements when processing each element in the sequence; the multi-head attention mechanism, which learns different aspects of the sequence through multiple “heads”; positional encoding, which provides information about the position of elements; and a feed-forward neural network and normalization layer, which, along with residual connections, enhances the training process. The strengths of the Transformer lie in its parallel processing capabilities and its effective handling of long-distance dependencies, enabling it to excel in a wide range of tasks.

To enhance the processing capability of Transformer, this paper introduces the DilateFormer module. DilateFormer is a variant that incorporates a dilation attention mechanism into graph neural networks, originally designed to process high-dimensional image features. It aims to improve the performance and efficiency of the Transformer when handling long sequence data. In time series tasks, DilateFormer expands the model’s receptive field using a sliding window dilation attention mechanism, thereby capturing longer-range dependencies while effectively controlling computational complexity. Additionally, DilateFormer increases the receptive field of each attention head by expanding the self-attention range and adjusts the dilation rate to more efficiently capture long-distance dependencies. This makes it particularly well-suited for time series analysis, text processing, and other tasks requiring an understanding of long-range context.

TCN-DilateFormer hybrid model based on CNN-Transformer

CNN excels at capturing local features but is limited by the size of the convolutional kernel, making it difficult to capture global information in long-term dependent time series data. In contrast, the Transformer has strong global feature extraction capabilities due to its global attention mechanism, but it is less effective than CNN in processing local features. The CNN-Transformer model combines the strengths of both CNN and Transformer, retaining CNN’s advantage in local feature extraction while leveraging Transformer’s global feature extraction capability, resulting in more comprehensive and efficient data processing.

TCN enhances time-series tasks by using a dilated convolution structure that ensures temporal coherence. Compared to CNN, TCN’s causal and dilated convolution is specifically designed to capture long-range time dependencies without incorporating future information. Since trends and patterns in financial cycles often require analysis over longer time scales, TCN’s structure effectively aligns with the characteristics of financial data. Additionally, the residual connections and dilated convolution layers in TCN effectively capture long-range dependencies, which are crucial for understanding and predicting credit risk based on historical financial performance.

Additionally, financial data often exhibit complex temporal dynamics and periodic patterns with long-term continuity in time series. Since DilateFormer is designed to enhance feature extraction in high-dimensional image tasks by effectively capturing long-distance relationships in high-pixel images, and given that high-dimensional financial data shares similar characteristics of high parameters and complexity, this paper abstracts the features of financial indicators into pixels and the years into channels, which aligns perfectly with DilateFormer’s input requirements.

Methodology

This section introduces the details of the TCN-DilateFormer model. In the first subsection, we provide an overview of the model’s overall structure, followed by a detailed explanation of the Channel Attention used in TCN and the Multi-scale Attention employed in DilateFormer in the second subsection.

Overall structure

The overall structure of the TCN-DilateFormer model is illustrated in Fig. 2. The model adopts a typical Encoder–Decoder architecture, consisting of three main components: the TCN layer, the DilateFormer layer, and the output mapping layer, which include modules such as the TCN Block and DilateFormer Block. Input data is processed through multiple modules, enabling the model to effectively extract multi-scale temporal features in different stages, thereby improving prediction accuracy.

First, the feature data is fed into the model. This data is time-series data obtained through sliding window and data augmentation processes, which will be explained in detail in subsequent sections. We define the input data as $\:X\in\:{\mathbb{R}}^{B\times\:C\times\:H}$, where B represents the batch size, C the dimensionality of the input features, and H the length of the time series. These feature data are first passed into the TCN Layer for local feature extraction.

The TCN Layer is composed of multiple stacked TCN Blocks. The number of stacks is determined by the parameter N₁, which is set to N₁ = 4 in this model. Unlike standard TCN, each TCN Block in this model includes not only a dilated convolution layer but also a Batch Normalization layer and a ReLU activation function to stabilize the training process. Additionally, a Dropout layer is incorporated to prevent overfitting. The output features from multiple stacked blocks are passed to the output via skip connections, mitigating the vanishing gradient problem and retaining low-level information from the input features. The output formula for the TCN Block is as follows:

$${X_{out}}=\operatorname{Re} LU\left( {BatcnNorm\left( {Conv1D\left( {{X_{in}}} \right)} \right)} \right)+{X_{in}}$$

(9)

Where $\:{X}_{in}$ is the input. The design of multiple stacked blocks efficiently captures the local dependencies between adjacent time steps while ensuring stable gradient flow throughout the network. At the end of the TCN Layer, an attention module approximating channel attention is included. This module generates attention weights using global average pooling, which are then used to reweight the feature channels. The details of this attention mechanism will be discussed in the next subsection.

Fig. 2

Model architecture diagram.

The DilateFormer layer is used to further process the features initially extracted by the TCN Layer, enabling multi-scale analysis and temporal modeling. It consists of three parts: the Encoder, Bottleneck, and Decoder, with the core module being the DilateFormer Block. The DilateFormer Block is capable of handling multi-scale temporal dependencies and capturing global information in long time series.It employs layer normalization to normalize the input features and utilizes multi-scale dilated attention for multi-scale attention computation. The multi-scale attention mechanism uses convolutions with different dilation rates to extract features at various temporal scales. Its calculation formula is expressed as follows:

$${X_d}=Conv1D\left( {X,~dilation=d} \right),\quad d \in \left\{ {1,2,4} \right\}.$$

(10)

Subsequently, the attention mechanism is used for fusion to capture dependencies across different time steps:

$$Q={X_{stacked}}{W_Q},\quad K={X_{stacked}}{W_K},\quad V={X_{stacked}}{W_V}$$

(11)

$$A=Soft\hbox{max} \left( {\frac{{Q{K^T}}}{{\sqrt {{d_k}} }}} \right) \cdot V$$

(12)

$${X_{out}}=Concat\left( {{A_1},{A_2},{A_4}} \right)$$

(13)

Where $\:{d}_{k}$ is represents the dimension of each head. The attention output is passed through a two-layer fully connected network (FFN) and undergoes nonlinear transformation using the GeLU activation function. Its formula is as follows:

$${X_{FFN}}=Linear\left( {\operatorname{Re} LU~\left( {Linear\left( X \right)} \right)} \right)$$

(14)

Residual connections are introduced within the multi-scale attention and FFN modules to ensure stable feature propagation and gradient flow. The Encoder consists of N₂ stacked DilateFormer Blocks, where N₂ is defined as 2 in this model. Each DilateFormer Block is followed by a Down Sample module, which uses stride-2 convolution to reduce the temporal length while increasing the number of channels:

$$X_{{down}} = BatcnNorm(Conv1D\left( X \right),X_{{down}} \in \mathbb{R}^{{B \times 2C \times \frac{H}{2}}}$$

(15)

Following the Encoder is the Bottleneck, which contains a single DilateFormer Block. Unlike the FFN in Transformer, which uses only linear mapping, the Bottleneck incorporates multi-scale dilated convolutions, enabling the simultaneous capture of both local and global features. The Decoder is composed of Up Sample Layers, Fusion Layers, and N₃ stacked DilateFormer Blocks, designed to restore the temporal resolution and integrate the multi-scale features from the Encoder output. The Up Sample Layers use ConvTranspose1D to expand the temporal length:

$$X_{{up}} = ConvTranspose1D\left( X \right),~X_{{up}} \in \mathbb{R}^{{B \times \frac{C}{2} \times 2H}}$$

(16)

Finally, the Fusion Layer combines the upsampled features from the Decoder with the corresponding features from the Encoder through concatenation and 1D convolution:

$${X_{fused}}=Conv1D\left( {\left[ {{X_{up}};{X_{encoder}}} \right]} \right)$$

(17)

The temporal features output by the DilateFormer are then passed to the fully connected layer for prediction. In the mapping layer, global average pooling is performed along the temporal dimension, and a linear transformation projects the global features into the target space:

$$Y=Linear\left( {{X_{global}}} \right)$$

(18)

This results in the final binary classification prediction, $\:Y\in\:{\mathbb{R}}^{B\times\:outputdim}$, completing the corporate default prediction task.

Channel attention

In time-series tasks, the importance of feature channels often varies. Inspired by the Squeeze-and-Excitation (SE) mechanism²⁷ from the image domain, which extracts global channel features through global pooling and generates attention weights using fully connected networks, we designed a modified channel attention mechanism tailored for time-series tasks within the TCN. This mechanism dynamically adjusts the weights of each feature channel by reweighting the channel dimension of the input features. As shown in the model architecture Fig. 3, for the input tensor $\:X\in\:{\mathbb{R}}^{B\times\:C\times\:H}$, global average pooling is first used to extract the global feature representation of each channel:

$$z=\frac{1}{H}\mathop \sum \limits_{{i=1}}^{H} X\left[ {:,:,i} \right],\quad z \in {{\mathbb{R}}^{B \times C}}$$

(19)

After that, a two-layer fully connected network is used to achieve weight adjustment:

$$a=\sigma \left( {{W_2} \cdot \operatorname{Re} LU\left( {{W_1} \cdot z} \right)} \right),\quad a \in {{\mathbb{R}}^{B \times C}}$$

(20)

Where $\:{W}_{1}$, $\:{W}_{2}$ are learnable weight matrices, σ is sigmoid. Compared with the general channel attention mechanism, such a design realizes the dynamic weighting of feature channels, and the lightweight architecture can efficiently handle large-scale time series tasks with relatively low computational costs.

Fig. 3

Channel attention.

Multi-scale dilated attention

In the DilateFormer, we designed the multi-scale dilated attention (MSDA) module, which combines the advantages of multi-scale dilated convolutions and self-attention mechanisms. This design efficiently captures both local and global dependencies in time series with relatively low computational complexity. As illustrated in Fig. 4, the module first employs three DilatedConv1D operations with different dilation rates to generate multi-scale feature maps. Feature stacking is then performed across these different feature maps, and Self-Attention is applied to compute Q, K, and V, capturing global temporal dependencies. The attention weights are calculated according to the previously mentioned formula, and the attention features from different scales are then fused through weighted summation, producing the final multi-scale feature representation. The computation processes for the dilated convolution and attention module can be expressed as follows:

$${X^{\left( i \right)}}_{{scale}}=DilatedConv\left( {X,~rate={r_i}} \right)$$

(21)

$$MSDA\left( X \right)=\mathop \sum \limits_{{i=1}}^{s} Attention\left( {{Q_i},{K_i}{V_i}} \right)$$

(22)

Where$\:{\:r}_{i}$ is the dilation rate of the i-th dilated convolution, and S is the number of scales. With this design, the Channel Attention mechanism allows the model to filter out important features and reduce interference from redundant information during the early stages of training. In the later stages, the multi-scale dilated attention mechanism captures long-range dependencies on a global scale, enhancing the model’s ability to understand complex patterns within the sequence. This design enables an effective division of labor between the two mechanisms.

Fig. 4

Multi-scale dilated attention.

The TCN-DilateFormer model processes corporate data by feeding it into the improved CNN structure, TCN, for time-series feature extraction, while leveraging the Transformer-based DilateFormer to capture long-range dependencies in the corporate feature data. This combination enables the model to effectively extract spatial features while simultaneously capturing dynamic temporal changes when handling data with both spatial and temporal dimensions. It offers a novel approach for processing time-series corporate credit data.

Data

Introduction to the dataset

Credit risk is closely tied to financial risk, and in the domestic stock exchange market, various methods are used to assess the financial risk of a listed company, with the most common being the application of the ST or *ST symbol. When a listed company incurs losses for three consecutive years, it is labeled as an ST company, indicating a risk of delisting. This label acts as an early warning to the company’s shareholders. Therefore, such a company can be considered high-risk in terms of credit risk, and studying these companies can provide insights into the credit risk of listed enterprises.

The data used in this study was sourced from the CSMAR Database, comprising annual data from 3762 publicly listed companies in the manufacturing and mining industries on the A-share market from 2012 to 2022. Category labels were constructed based on whether a company was classified as ST. If a company was designated as ST in a particular year, the label was set to 1, representing a positive sample; otherwise, the label was set to 0, representing a negative sample. If a company’s stock code in a given year was identified as ST or *ST, it was classified as a defaulting company for that year, and the corresponding data was considered default data. According to this criterion, out of the 3762 companies, 320 were identified as defaulting companies.

During data processing, a padding procedure is applied to fit the temporal convolutional network model. The time step for each enterprise sample is adjusted to a maximum of 11 years, with samples of fewer than 11 years padded with zero vectors. The processed data is then merged into a unified tensor for model input. This preprocessing method ensures data consistency and facilitates smooth model training.

Selection of indicators

This paper draws on the research of Tong Menghua and other scholars²⁸ and utilizes the existing indicator system in the CSMAR database to construct a financial indicator system encompassing six aspects: solvency, operating ability, profitability, development ability, ratio structure, and cash flow analysis. To ensure data quality, indicators with more than 20% missing values were excluded. Linear regression was used to fill in the missing values for the remaining indicators, and the raw data was standardized to eliminate the influence of scale. During the standardization process, the mean (µ) and standard deviation (σ) of the original features were first calculated. The mean (µ) was then subtracted from the original features and the result divided by the standard deviation (σ) to ensure the data conformed to a standard normal distribution with a mean of 0 and a variance of 1. The calculation process is shown in Eq. Ultimately, 32,246 data points from 3762 enterprises, covering 132 financial indicators were used. According to the previous definition, the dataset consists of 32,246 entries, including 672 default data entries, accounting for 2.08% of the total data. This represents a highly imbalanced sample. As shown in Table 1 below.

Table 1 Comparison of two labels.

$${X_{norm}}=\frac{{X - {X_{\hbox{min} }}}}{{X\hbox{max} - X\hbox{min} }}$$

(23)

where X_min is the minimum value of the data, X_max is the maximum value of the data, and X_norm is the normalized value.

Table 2 Coverage scope of indicators at various levels.

Data processing

Credit risk default data typically suffer from an imbalance where positive class samples significantly outnumber negative class samples, necessitating a sample balancing process to prevent model overfitting. In this study, the dataset comprises 31,574 non-default samples (class 0) and 672 default samples (class 1), resulting in a 50-fold difference between the two classes, indicating an extremely imbalanced dataset. It is commonly accepted that in binary classification tasks, maintaining a ratio between 1:1 and 1:10 for positive and negative samples optimizes model performance. The commonly used method to address this issue is the SMOTE algorithm, which oversamples minority class samples. However, some scholars have noted that SMOTE focuses solely on quantity and overlooks the distributional characteristics of neighboring samples, leading to potential randomness and redundancy in the newly generated data²⁹.This paper adopts a data training method from an algorithmic perspective to address the issue of sample imbalance.

The data processing methodology in this study is illustrated in the Fig. 5 below and primarily includes data loading and preprocessing, sliding window sampling, data augmentation, negative sample downsampling, and cross-validation splitting. In the original dataset, the stock code of each company is used as its ID. Each company has 11 years of data comprising 132 financial indicators and the corresponding annual category label (0 or 1). First, the data is grouped by company ID to create a time-series data list organized by enterprise ID:

$$D=\left\{ {{D_{id1}},~{D_{id2,~}} \ldots {D_{idn}}} \right\}$$

(24)

Where n is the number of enterprises. Subsequently, a sliding window with a length of K is applied to slice the time series of each company, ensuring the preservation of the temporal characteristics of the data. Specifically, starting from year t, data from K consecutive years is used as the sample features to predict the category label of the company for year K + 1:

$${X_t}=\left\{ {{D_{id}}\left[ t \right],{D_{id}}\left[ {t+1} \right], \ldots ,{D_{id}}\left[ {t+K - 1} \right],} \right\}$$

(25)

$${Y_t}={D_{id}}\left[ {t+K} \right]$$

(26)

Where t = 1,2,…,T-K. To evaluate the robustness of the model, we use Stratified K-Fold Cross-Validation to divide the samples. This ensures that the proportion of positive and negative samples in each fold’s training and validation sets is consistent with that of the original dataset, avoiding biases in sample distribution that could affect model evaluation. Specifically, the dataset is randomly split into k non-overlapping subsets in a stratified manner, maintaining the original ratio of classes. During each training iteration, one subset is used as the validation set, while the remaining k−1 subsets are used as the training set. In this study, the baseline model is configured with k = 5.

Fig. 5

Data processing flowchart.

To address the issue of sample imbalance between the two classes, during each round of cross-validation, we performed data augmentation on the default (label 1) samples when the subset was used as a training set, while leaving the validation set unchanged. Specifically, the default data with label 1 was subjected to n-fold repeated sampling. It is generally accepted that deep learning models, due to their strong generalization capabilities, can handle repeated sampling datasets with 5 to 10 times the original data. Considering the overall size of our dataset, we applied 5-fold repeated sampling to the default data. During the repetition process, Gaussian noise with a standard deviation of sigma was added. Assuming the feature value of a positive sample $\:{X}^{+}$ is $\:{x}_{i}$:

$$\widehat {{{x_i}}}=\hbox{max} \left( {{x_i}+\smallint ,0} \right)~,~~~~~\smallint \sim N\left( {0,~{\sigma ^2}} \right)$$

(27)

In this experiment,σis set to 0.05. Additionally, to align with the characteristics of financial indicators, only non-negative values are retained for the enhanced sample features. After this operation, the number of default samples in the training set is expanded to k + 1 times the original data.

To further balance the samples, we performed downsampling on the non-default data based on the expanded number of default samples. The non-default data was downsampled to twice the size of the enhanced default data to reduce the risk of model bias toward non-default data, while mitigating the data loss issue caused by downsampling.

$${\hat {X}^ - }=RandonSample\left( {{X^ - },\hbox{min} \left( {\left| {{X^ - }} \right|,1.5 \times \left| {{X^+}} \right|} \right)} \right)$$

(28)

By performing data augmentation on the training set, the issue of data imbalance was effectively mitigated, ensuring the model’s learning capability for minority class samples and the fairness of performance evaluation. Table 3 presents a comparison of the data volumes before and after augmentation.

Table 3 Comparison of the data volumes.

Evaluation criteria

Credit risk assessment models aim to quantitatively distinguish customers’ credit levels, requiring evaluation metrics to reflect the classification accuracy of the model. When there is a significant imbalance between the number of positive and negative samples, metrics such as precision, recall, and their composite measures (e.g., F1-score), as well as specificity, provide a more comprehensive evaluation of model performance. This study employs the following metrics to evaluate the accuracy of the model.

Recall measures the proportion of actual defaulting firms that the model correctly identifies. A high recall rate indicates that the model is effective at identifying defaulting firms. It is calculated using the following formula:

$$recall=~\frac{{TP}}{{TP+FN}}$$

(29)

Precision measures the proportion of firms predicted by the model as defaulting that actually do default. A high precision rate indicates that the model is more accurate in predicting defaulting firms, with a lower rate of false positives. It is calculated using the following formula:

$$\Pr ecision=\frac{{TP}}{{TP+FP}}$$

(30)

Where TP (true positive) refers to the number of samples that the model correctly predicted as positive, while FN (false negative) refers to the number of samples that the model incorrectly predicted as negative but were actually positive. FP (false positive) refers to the number of samples that the model incorrectly predicted as positive but were actually negative.

The F1 score is the harmonic mean of precision and recall, providing a comprehensive assessment of the model’s accuracy and recall. It is calculated using the following formula:

$$F1~score=2 \times \frac{{\Pr ecision \times \operatorname{Re} call}}{{\Pr ecision+\operatorname{Re} call}}$$

(31)

Specificity is an important metric for measuring the model’s ability to correctly classify the negative class. Compared to the aforementioned metrics, it focuses more on the model’s performance on negative samples. In highly imbalanced datasets, Specificity can effectively compensate for the limitations of Precision and Recall. Its calculation formula is:

$$Specificity=\frac{{TN}}{{TN+FP}}$$

(32)

Focal loss

In our task, the two classes are extremely imbalanced. Therefore, during training, we used the Focal Loss function, which is specifically designed to address imbalance issues. Unlike the traditional cross-entropy loss function, Focal Loss introduces a weighting factor that assigns higher weights to minority class samples, optimizing the classification of imbalanced categories. Its calculation formula is:

$${L_{focal}}\left( {{p_i}} \right)= - {a_t}{\left( {1 - {p_t}} \right)^\gamma }\log \left( {{p_t}} \right)$$

(33)

Where $\:{p}_{i}$ represents the predicted probability, $\:{a}_{t}$ is the balancing factor which is used to adjust the impact of positive and negative samples on the loss,γis the focusing factor which is employed to adjust the degree of weight decay for easily classified samples.

During model training, its calculation formula for the entire batch is as follows:

$$L=\frac{1}{N}\mathop \sum \limits_{{i=1}}^{N} {L_{focal}}\left( {{p_t}^{{\left( i \right)}}} \right)$$

(34)

Where N represents the number of samples in the current batch, $\:{L}_{focal}\left({{p}_{t}}^{\left(i\right)}\right)$ is the Focal Loss of the i-th sample.

Empirical analysis

In this section, we will provide a detailed explanation of the experimental setup, using the TCN-DilateFormer model to perform binary classification predictions on time-series financial data of listed companies to determine whether a company defaults. Subsequently, we conducted comparative experiments with other models and validated the robustness of the model through ablation experiments.

Default analysis of listed companies

The experiments were conducted on a workstation equipped with two NVIDIA GeForce RTX 3080 × 2 GPUs and an Intel(R) Xeon(R) Silver 4214R processor. The PyTorch 1.8.1 framework with CUDA 11.1 was used, and multi-GPU parallel acceleration was implemented using PyTorch’s DataParallel mode. Model parameters were initialized using a uniform distribution. During training, the dropout rate was set to 0.2, and the number of epochs was set to 100.

The TCN channel configuration was set to [64,128,256,512], and the Transformer hidden dimension was set to 64. Training was conducted with a batch size of 16, a maximum of 100 training epochs, and 1000 samples per epoch. The optimizer used was Adam with an initial learning rate of 0.0001. MultiStepLR scheduler was employed to adjust the learning rate, reducing it by a factor of 0.1 every 30 epochs. For Focal Loss, the settings were γ = 2.0 and α = 0.25.

We compared the TCN-DilateFormer model with classical models and two SOTA models, including CNN-LSTM, CNN-Transformer, and state-of-the-art models for time-series classification tasks: TimeMIL³⁰ and ConvTimeNet³¹. For all models, the optimal parameter settings from the respective literature were used. The Precision, Recall, F1 Score, and Specificity of the model with the minimum loss in each experiment were calculated. Each model was subjected to five-fold cross-validation, and the average results were reported. The results are presented in Table 4.

Table 4 Model results comparison.

All models demonstrated relatively high overall performance in terms of Precision, Recall, and F1 Score, with performance gradually improving from CNN-LSTM to TCN-DilateFormer. It can be observed that in the time-series binary classification task for credit risk analysis of listed companies, our model consistently achieved the best performance. Specifically, the Precision was 0.9681, Recall 0.8689, F1 Score 0.9157, and Specificity 0.9809. This further indicates that TCN-DilateFormer exhibits strong performance and has potential in binary classification tasks involving time-series financial data. Figure 6 provides a more intuitive visualization of the evaluation metrics for each model.

Fig. 6

Model performance comparison.

Parameter optimization experiment

In this section, we modify the dilation factors in the TCN Layer and the number of DilatedConv1D layers in the Multi-Scale Dilated Attention of the DilateFormer layer to identify the optimal parameter combination. In these experiments, all parameters remain consistent with the main experiment except for the adjusted ones. The average results of various performance metrics are computed through cross-validation.

First, parameter optimization experiments were conducted for the dilation factors. The original model’s dilation setting of [1,2,4,8] was used as the baseline. While keeping the number of TCN layers and channels unchanged, the dilation factors were modified to [1,1,2,2] and [1,2,8,16] for two additional experiments. The results of the three experiments are presented in the Table 5.

Table 5 Comparison of experimental results with different dilation factors.

As shown in the results, reducing the dilation factor leads to slight decreases in Precision, F1 Score, and Recall, while increasing the dilation factor does not achieve the expected improvement. Therefore [1,2,4,8], is considered the optimal combination.

Next, we modify the scales in the Multi-Scale Dilated Attention mechanism to observe the model’s performance. The baseline is the original model’s setting of [1,2,4]. We then modify it to [1,4] and [1,2,4,8] and repeat the experiments with these two parameter sets. The results are presented in Table 6.

Table 6 Comparison of experimental results with different scales.

From the results in the table, the performance differences across the groups are minimal. When using only [1,4], the model’s performance declines significantly. While increasing the scales to [1,2,4,8] results in a slight improvement in Recall, the overall performance difference remains small. To avoid the additional computational cost and potential overfitting caused by an overly complex model structure, we retain [1,2,4] as the parameter combination.

Parameter sensitivity & robustness analysis

In this section, we modify three parameters, learning rate, window size, and the standard deviation of Gaussian noise to observe changes in model performance. In each experiment, only the parameter being adjusted is modified, while all other settings remain unchanged. The performance metrics are then calculated and reported.

Using a learning rate of 0.0001 as the baseline, we adjust it to 0.0002 and 0.0005, repeating the experiments. The results are presented in Table 7.

Table 7 Comparison of experimental results with different learning rates.

The results in the table indicate that the model performs well when the learning rate is set to 0.0001 or 0.0002, but performance declines significantly when the learning rate is increased to 0.0005. This suggests that the model has a certain tolerance to changes in the learning rate, but as the learning rate increases, the model’s ability to converge stably decreases, leading to performance degradation. Therefore, a learning rate of 0.0001 is selected.

The size of the sliding window determines the amount of historical data the model can utilize for prediction. Considering that each company only has 11 years of data, we set the window size to 3, 5, and 10, respectively. The experiments are repeated with other parameters unchanged to observe changes in model performance. The results are shown in Table 8.

Table 8 Comparison of experimental results with different window sizes.

The results indicate that the model performs slightly better when the window size is set to 5. This may be because a smaller window size limits the model’s ability to capture temporal information, while a larger window size introduces information redundancy. However, overall, all metrics show consistently good performance.

In the data augmentation process, Gaussian noise was added to minority class samples to expand the dataset. Next, we modify the standard deviation of the Gaussian noise to observe the model’s sensitivity to noise intensity. In the main experiment, the standard deviation of the Gaussian noise was set to 0.05. We adjust it to 0.01 and 0.1, respectively, and conduct experiments for each setting.

According to the results in Table 9, when the noise is too small, the effectiveness of data augmentation decreases, leading to a decline in model performance. Conversely, when the noise is too large, the increase in spurious features also results in performance loss. Overall, the model shows low sensitivity to changes in the standard deviation of Gaussian noise, demonstrating a certain degree of robustness.

Table 9 Comparison of experimental results with different noises.

Statistical test

In this section, we perform a significance test comparing the F1 Scores from the K-fold cross-validation of TCN-DilateFormer, ConvTimeNet, and TimeMIL. F1 Score, being the harmonic mean of Recall and Precision, is a more representative metric.

The experiment uses five-fold cross-validation, and Table 10 presents the results of each cross-validation iteration for the three models:

Table 10 Five-fold cross-validation results of different models.

This study employs the Wilcoxon Signed-Rank Test, a non-parametric paired statistical test used to evaluate whether there is a statistically significant difference in results under two different conditions for the same set of samples. We perform the Wilcoxon test to compare TCN-DilateFormer with TimeMIL and ConvTimeNet, respectively. For each test, the F1 Scores from cross-validation are paired such that the i-th F1 Score of TCN-DilateFormer is compared with the i-th F1 Score of TimeMIL and ConvTimeNet.

Define the null hypothesis and alternative hypothesis as follows:

H₀ = There is no significant difference in the F1 Scores between the two models.

H₁ = The F1 Score of TCN-DilateFormer shows a significant difference compared to the control model.

Defineα = 0.05, When P<0.05, reject the null hypothesis, The results are shown in Table 11:

Table 11 Wilcoxon signed-rank test results.

It can be observed that both p-values are less than α = 0.05. Therefore, the null hypothesis is rejected, indicating that the performance of TCN-DilateFormer is significantly superior to that of the comparison models.

Discussion

The TCN-DilateFormer hybrid model developed in this study demonstrates excellent performance in corporate credit risk analysis tasks, showcasing significant application potential. TCN provides efficient local feature extraction for time-series data, enabling precise capture of short-term dynamic changes in corporate financial indicators. DilateFormer, through its Multi-Scale Dilated Attention mechanism, effectively captures long-range dependencies in financial time-series data. Additionally, the data augmentation methods employed during training significantly improve the model’s performance in handling imbalanced data, enhancing its robustness.

We note that there is still room for improvement in the model. First, the model relies heavily on the quality of input data, and the effectiveness of data preprocessing directly impacts predictive performance. Second, the issue of training data wastage caused by the downsampling strategy employed during the data processing stage requires further investigation.

Future research will focus on optimizing the network structure to reduce computational complexity while maintaining model performance and adopting more innovative data processing methods to address the sample imbalance issue. Additionally, beyond financial time-series data, we will explore the application of the model to unstructured data and macroeconomic data to further enhance the accuracy of credit risk prediction. Moreover, we aim to investigate the model’s potential in other time-series tasks, such as individual customer default risk prediction and supply chain risk management, to broaden its applicability and provide effective solutions for a wider range of fields.

Conclusion

In this paper, we focus on time-series financial data and consider the advantages of CNN in capturing local sequence features and the Transformer’s strong global feature extraction capability. We innovatively integrate TCN, an improved CNN module, and DilateFormer, an enhanced Transformer module, to construct a TCN-DilateFormer hybrid model. This model not only improves the performance of the traditional CNN-Transformer but also enhances the processing accuracy of time-series financial data, thereby improving the accuracy of enterprise credit risk assessment. TCN’s causal and dilated convolution designs allow the model to capture long-term trends and patterns in financial data. DilateFormer, through the extension of the attention mechanism, effectively enhances the model’s ability to handle long-range dependencies in high-dimensional financial data.

Experimental results show that the TCN-DilateFormer model outperforms traditional time-series classification models in terms of precision, recall, and F1 score. Therefore, this study concludes that the TCN-DilateFormer model is more effective in capturing local features and global dependencies in time-series data while maintaining high computational efficiency when handling large-scale data. In summary, this research provides an effective tool for corporate credit risk assessment and offers new insights for deep learning-based corporate credit risk studies.