Introduction

Natural Deep Eutectic Systems, abbreviated as NADES, are a subclass of Deep Eutectic Systems (DES), which can be described as mixtures of Lewis or Brønsted acids/bases natural organic compounds1,2. Fluctuations in the network of hydrogen bonds created between the components involved have been pointed out as one of the reasons behind the large (“deep”) depression in the melting point, which allows them to be liquid over a wide window of molar composition and temperature3,4. Unlike DES, which may contain one or more synthetic and/or semi-synthetic (e.g., choline chloride, urea, ethylene glycol, glycerol carbonate etc.) in the mixture, NADES are typically described as being solely composed of naturally occurring metabolites (e.g., glucose, malic acid, L-proline, etc.), which make them more biocompatible and eco-friendlier1,2,5,6. Despite much discussion in the literature about the correct use of the designation DES or NADES, it is also true that, fundamentally, the two are practically the same, which often makes it quite difficult to distinguish between them4,7. Meanwhile, when looking at their most common applications, it becomes evident that, in addition to the nature of the components, the use of thermology also depends on the scientific field in which the application is intended. For example, DES is a broadly used term, found especially in fields such as chemical synthesis or catalysis, electrochemistry, pharmaceutical and biomedical applications8,9,10,11,12,13; on the other hand, NADES are widely used in the extraction processes, food and cosmetical industries and pharmaceutical applications5,14,15,16,17.

Among the several remarkable characteristics and physicochemical properties of NADES (and DES), it is increasingly noticeable the interest of researchers for the good ability to dissolve and improve the solubility of a wide range of compounds, for example, curcumin18, phytochemicals19, rutin20, gluten1, and some non-steroidal anti-inflammatory drugs (e.g., ibuprofen, aspirin, acetaminophen, etc.)21,22. However, in order to leverage this property of NADES, it is fundamental to know what are the factors that may better explain such behaviour.

HSPs have been commonly used as a complementary tool in research involving solubility studies (e.g., the solubility of Active Pharmaceutical Ingredients (APIs)), due to their reasonable prediction of the affinity between different materials, allowing screening and select the best solvents for a given compound23,24,25,26,27. However, for solvents such as NADES, the experimental determination of the partial HSPs is a problematic and challenging task as it would require their vaporization, but due to their non-volatile nature, they undergo thermal degradation before they vaporize28. When heating these systems at very high temperatures, the intermolecular forces (especially the hydrogen bonds) that hold their structure together are disrupted29,30,31. Therefore, theoretical models, such as the one proposed by Hoftyzer-Van Krevelen32, are commonly used to predict the HSPs of NADES; however, since the majority of these models were developed using the typical molecular solvents (e.g., water, methanol, toluene, etc.), which intrinsically/fundamentally are and act very differently from NADES, the application of these models in these systems is certainly dubious. Furthermore, there are nowadays several different theoretical approaches to estimating the HSPs, but still with some restrictions that can make it difficult for their applications, not only in eutectic mixtures but also in other molecular solvents.

Thus, given the limitations in determining experimentally the solubility parameters, in this work, a set of theoretical approaches, empirical (EM) (based on the group-contribution methods) and semi-empirical models (SEM) (based on correlative equations), were tested in order to evaluate and comprehend their applicability in the eutectic mixture field, as well as identify models that shares the most similarity, which may allow to overcome some limitations presented by these theoretical models.

Materials and methods

Chemicals

The list of the chemical compounds used in this work, their abbreviation, CAS number, purity, and brand is shown in Table 1.

Table 1 Information about chemical compounds used in this work.
Full size table

Preparation of NADES

The preparation of these was carried out using the heating and stirring method33: The amount required for each component was weighted using an analytic balance KERN ABS 220-4N with an uncertainty of 0.0001 g and then mixed and stirred at a temperature ≤ 60 °C, until form a homogenous fluid. All the NADES here investigated are systems that were characterized physiochemically in a previous work34, therefore, except for surface tension, all the values presented in Table S.1 for the properties, namely, density, molar volume, refractive index, dielectric constant, dipole moment and water content, are those already reported. Additionally, Table S.1 lists also the physicochemical properties’ values for a set of conventional solvents. These data were only used for calculating the HSPs’ of these organic compounds and evaluating them, consequently, as will be further explained, the performance of each of the studied theoretical models tested in the NADES field.

Surface tension

The surface tension of NADES was obtained using an Ossila Contact Angle Goniometer (with a measurement accuracy of ± 1°), through the pendant drop method, with a metal hub needle (22-gauge, length of 51 mm ± 1 mm) from Hamilton®. All the tests were performed at room temperature (293.15 K), and the data listed in Table S.1 correspond to an average of at least three measurements. More details can also be seen in Table S.14, in SI.

Fourier transform infrared (FTIR) Spectroscopy

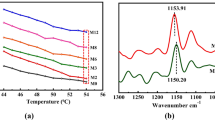
The FTIR spectrums of each NADES, as well as the components used in their formulation, were obtained using a PerkinElmer Spectrum Two equipment (Waltham, MA, USA) with attenuated total reflection (ATR) in the Transmittance mode and at a wavenumber range of 400–4000 cm−1 and a resolution of 4 cm−135 (see Supplementary information (Figs. S.3–S.21).

Theory

Prediction of physicochemical properties

Group contribution methods were used to estimate some of the physicochemical properties required for the determination of the surface tension and enthalpy of vaporization. For surface tension, the molar Parachor method36 (Sugden’s approach) was used (see more details in Table S.14 and from Tables S.17–S.40), while, the thermodynamic properties, namely critical points and acentric factor, were estimated using the group-contribution table of Valderrama et al.37 and applying the mixing rules proposed by Lee–Kesler38 and Knapp et al.39. These were then used to predict the enthalpy of vaporization of both NADES (See also Table S.15 and from Tables S.41–S.63).

Determination of Hansen solubility parameters

Theoretically, the model proposed by Hansen is an extension approach of the single solubility parameter’s theory introduced previously by Hildebrand and Scoot40,41 (Eq. 1), suggesting the division of the total energy of vaporization or cohesive energy (Ecoh), into three parts that represent the energetic contribution of nonpolar or dispersive forces (ED), the energetic contribution from dipolar forces (EP) and the energetic contribution from the hydrogen-bond interaction (EH), as shown in Eq. 242. The three Hansen solubility parameters (δd, δp and δh) emerged then by dividing each of these energetic contributions by the molar volume (Eq. 3) of the compound, hence it is often written as Eq. 4:

$$\delta_{{t\left( {Hil} \right)}} = \sqrt {C.E.D} = \sqrt {\frac{{E_{coh} }}{{V_{m} }}} = \sqrt {\frac{{\Delta H_{vap} - RT}}{{V_{m} }} }$$
(1)
$$E_{coh} = E_{D} + E_{P} + E_{H}$$
(2)
$$\delta_{d} = \left( {\frac{{E_{D} }}{{V_{m} }}} \right)^{\frac{1}{2}} ;\;\;\delta_{p} = \left( {\frac{{E_{P} }}{{V_{m} }}} \right)^{\frac{1}{2}} ;\;\;\delta_{h} = \left( {\frac{{E_{H} }}{{V_{m} }}} \right)^{\frac{1}{2}}$$
(3)
$$\delta_{{t\left( {Hans} \right)}}^{2} = \delta_{d}^{2} + \delta_{p}^{2} + \delta_{h}^{2}$$
(4)

where δt(Hil) is the total solubility parameter of Hildebrand (in (cal/cm3)1/2), C.E.D is the cohesive energy density (also called cohesive pressure, in cal cm−3)1/2, Ecoh is the cohesive energy or energy vaporization of the compound (in KJ mol−1) and Vm is the molar volume (in cm3/mol). ∆Hvap, R, and T are the latent heat of vaporization (also called enthalpy of vaporization (in KJ mol−1, universal gas constant (8.314 cm3 MPa K−1 mol−1), and the absolute temperature (in Kelvins, K), respectively. δd is the dispersion contribution to the solubility parameter, δp is the polar contribution to the solubility parameter, and δh is the hydrogen bonding contribution to the solubility parameter. δt(Hans) is the total solubility parameter of Hansen (in (cal/cm3)1/2)41. Knowing the HSPs of both solute and solvent, it is possible to calculate their dissimilarity factor (Ra), using the following equation (Eq. 5):

$$Ra = \sqrt {4\left( {\delta_{d}^{S1} - \delta_{d}^{S2} } \right)^{2} + \left( {\delta_{p}^{S1} - \delta_{p}^{S2} } \right)^{2} + \left( {\delta_{h}^{S1} - \delta_{h}^{S2} } \right)^{2} }$$
(5)

However, this equation is only valid for pure solvents. In the case of a mixture of compounds or solvents, Eq. 6, presented by Jaime Lara et al.43, is perhaps more suitable. Although this has been mainly used in the polymers field, such an approach has been also found to be applied in several studies related to the solubility of other compounds in solvent mixtures, including in eutectic ones and ionic liquids44,45,46,47,48,49.

$$Ra = \sqrt {4\left( {\delta_{d}^{S1} - \delta_{d}^{M} } \right)^{2} + \left( {\delta_{p}^{S1} - \delta_{p}^{M} } \right)^{2} + \left( {\delta_{h}^{S1} - \delta_{h}^{M} } \right)^{2} }$$
(6)

Knowing that by the mixture rule:

$$\delta_{d}^{M} = \mathop \sum \limits_{i} \varphi_{i} \delta_{d}^{i}$$
(7)
$$\delta_{p}^{M} = \mathop \sum \limits_{i} \varphi_{i} \delta_{p}^{i}$$
(8)
$$\delta_{h}^{M} = \mathop \sum \limits_{i} \varphi_{i} \delta_{h}^{i}$$
(9)

being,

$$\varphi_{i} = \frac{{x_{i} V_{i} }}{{x_{i} V_{i} + x_{j} V_{j} }}$$
(10)

Herein, the superscripts S1 and S2 denote solute and pure solvent, respectively, while M, corresponds to the mixture. φi, xi, and Vi are, in turn, the volume fraction, the molar fraction, and the molar volume of component i in a mixture with k components. Finally, xj and Vj are, respectively, the molar fraction and molar volume of component j, in a sum from component 1 to component k. As can be noted, the presented mixture rules are all based on volume fraction and not molar fraction. This is in fact a very common practice observed in the solubility parameters models. Some authors such as Charles Hansen and Flory–have even demonstrated that the best results are obtained when volume fraction is used40,41. Still, if considered that most of the components used in a eutectic mixture formulation are small molecules of similar size, the difference in using volume fraction or molar fraction might be negligible. However, if there is a big difference in their molecular size, volume fraction may be still the most appropriate as, theoretically, the interactions between components are rather facilitated by their occupied volume (due to the cohesive energy density (as shown in Eq. 1) and molecular packing) than their stoichiometric ratio. For HSPs that are focused mainly on solubility and intermolecular forces, the molar ratio solely may not be enough to explain the volume-dependent interactions41. Furthermore, as reported in the work of Bergua et al.50, the polar parameter (δp) is the only HSPs that may show a relatively high dependence on the molar fraction. Nevertheless, it is also important to mention that the used mixture rule equations (Eqs. 7–9) are based on the thermodynamic ideality principle, assuming that the internal energy (ΔU) is null44, which means that in practice these could not be applied in NADES (or DES) field. However, some current studies have been showing that the solubility parameter values estimated with these approaches are not so different from those that would be obtained using a more advanced tool such as Perturbed-Chain Statistical Associating Fluid Theory (PC-SAFT), showing both a good agreement with the experimental data, even in systems with non-ideal behaviour44,51. Therefore, these equations were tested in this work. To guarantee the effectiveness of all the semi-empirical models (SEM) used, as well as the empirical models (EM) under study, their applicability was first tested in a group of conventional solvents, namely, water, methanol, ethanol, ethylene glycol, glycerol, hexane, and cyclohexane. This methodology was used before the calculation of each one of NADES’ HSPs.

Semi-empirical models (SEM). In this study, the set of equations listed in Table 2 was used to calculate each of the partial solubility parameters. As can be noted, these approaches are mainly based on correlative equations between partial solubility parameters and some physicochemical properties, such as refractive index (nD), dipole moment (µ), dielectric constant (ε′) and molar volume (Vm).

Table 2 List of semi-empirical models (SEM) evaluated in this work.
Full size table

In addition to these parameters, it is very common to find semi-empirical models that correlate the solubility parameters with enthalpy of vaporization (ΔHv) and surface tension (σ). In fact, most of the SEM found in the literature are based on this approach52,56. Hence, the equations presented in the supplementary information (Table S.2) were also investigated.

Empirical models (EM). Various satisfactory models, widely recommended in the absence of experimental data, were evaluated in this work, namely, those proposed by Hansen and Beerbower41, Hoftyzer-Van Krevelen and their combination with Fedors (HK and HKF, respectively)32,57, Stefanis and Panayiotou (StP)58,59, Hoy60, and Yamamoto (Ymt)53,61. They are all based on the group contribution method (GCM), i.e., each functional group present in the molecular structure serves a purpose that is represented in each property (See more details in the Supplementary information, Table S.16 and from Tables S.64–S.86).

The differences between the calculated values of conventional solvents using theoretical models (cal) and the ones described in Hansen’s book41 (exp), as well as those between semi-empirical and empirical values of NADES were calculated using, respectively, the following absolute average relative deviation percentage (AARD%) equations (Eqs. 19 and 20):

$$AARD\% = \frac{100}{N}\mathop \sum \limits_{i}^{N} \left| {\frac{{\delta_{i, \exp } - \delta_{i, cal} }}{{\delta_{i, \exp } }}} \right|$$
(19)
$$ARD\% = \frac{100}{N}\mathop \sum \limits_{i}^{N} \left| {\frac{{\delta_{i,SEM} - \delta_{i,EM} }}{{\delta_{i, EM} }}} \right|$$
(20)

Results and discussion

Dispersion solubility parameter (δd)

In general, the δd parameter measures the extension of the Van der Walls interactions or, in other words, the energy density that arises from dispersion bonds between molecules53,62. Semi-empirically, it can be estimated using the refractive index, as shown in Table 2 (Eqs. 13 and 14). From a preliminary test using the conventional solvent list (Table S.3, in the supplementary information), it was possible to confirm that the empirical models (EM) such as Stefanis-Panayiotou (StP) and Yamamoto (Ymt) (AARD% of 2.13 and 2.40, respectively) and semi-empirical (SEM) ones such as of Koenhen and Smolders (KoS) and YAH (AARD% of 2.83 and 5.03, respectively) are those that showed lowest deviation from Hansen’s values41. Therefore, these can be indicated as the most appropriate to calculate δd. On the other hand, since the refractive indexes of the studied NADES are known, the same methodology was used to evaluate their dispersive parameter, and the results are listed in Table 3.

Table 3 The δd parameter values of NADES, predicted using Semi- (SEM) (KoS—Koenhen-Smolders (Eq. 13); YAH—Yamamoto-Hansen-Abbott (Eq. 14)) and Empirical Models (EM) (StP—Stefanis and Panayiotou; HK—Hoftyzer and Van Krevelen; HKF—Hoftyzer-Van Krevelen and Fedors; Ymt—Yamamoto).
Full size table

As can be observed, there are no significant differences between the δd calculated by the two theoretical approaches (SEM and EM). Additionally, when evaluating the AARD% between SEM and EM (Table S.4, in the supplementary information), it was found that the semi-empirical model KoS is the one that shares the most similarity with empirical ones, in particular, Ymt and StP.

Polar solubility parameter (δp)

The δp parameter is a measure of the energy/electrical attraction arising from dipolar intermolecular forces between molecules62,63. For most of the semi-empirical models, the quantification of the dipole’s permanent contribution (δp) of a given compound to the C.E.D., requires the knowledge of its dipole moment (µ). In the case of eutectic mixtures, a good method such as the one proposed by Onsager can be used to estimate the dipole moment of NADES and consequently their δp parameter34,64. This was first validated using the values of conventional solvents, where the AARD% results (Table S.5, in the supplementary information) proved once again that the empirical models are indeed much more efficient than the semi-empirical ones in predicting the δp parameter, in particular the model of Hoftyzer and Van Krevelen (HK), which has the lowest AARD% (4.39%). Among the semi-empirical models, Beerbower (Bb) was found to be the one with the lowest AARD% (11.20%). On the other hand, when these models were used to estimate the δp parameter of NADES, the results presented in Table 4 were obtained.

Table 4 The δp parameter values of NADES, predicted using Semi- (SEM) (Böt—Böttcher (Eq. 15); HB—Hansen and Beerbower (Eq. 16); Bb—Beerbower (Eq. 17); KoS′—Koenhen and Smolders (Eq. 18)) and Empirical models (EM) (StP—Stefanis and Panayiotou; HK—Hoftyzer and Van Krevelen; HKF—Hoftyzer-Van Krevelen and Fedors; Ymt—Yamamoto); µO—Onsager’s dipole moment (Table S.1, in the supplementary information).
Full size table

As can be noted, the major differences between the semi-empirical and empirical models were found in the δp values of the hydrophilic systems, which can be explained by the type of relationship, direct (δp versus µ) or indirectly proportional (δp versus Vm) that exists between the parameters (from Eqs. 15–18). In the case of hydrophobic NADES, most results appear to be in a very close range of values.

Given the fact that empirical models, more specifically the HK one, seem to be apparently, the most suitable approaches to estimate δp, the following step was then tracking SEM that shares the most similar behaviour to these theoretical models (EM). From these results (see Table S.6, in the supplementary information), it was possible to see that, unlike the estimation of the δd parameter, there is very little or no similarity between the two theoretical methods. Still, among all the presented SEM, Beerbower’s one (Bb, Eq. 17) stands out as one of the models that deviates relatively less from the empirical models (HK one), that is, if considering the conventional solvents (13.76%), general list (26.95%) and hydrophilic (25.32%) data set. On the other hand, in the evaluation using the hydrophobic data set, the model of Koenhen and Smolders (KoS′, Eq. 18) appears to be the most suitable model to be a possible substitute for the HK model (AARD% of 24.83).

Hydrogen-bond solubility parameter (δh)

The δh parameter measures the energy from hydrogen-bonds interaction between molecules42. The first method proposed by Hansen to quantify the hydrogen-bond contribution for the C.E.D. was using FTIR spectroscopy. In theory, it would be necessary the knowledge of the assignment of the OH···O bond (~ 5000 cal/mol), the number of OH (nOH) in the molecule as well as its molar volume (Vm) (see Eq. 17). Thus, in this work these methodologies were also tested, i.e., using the specific energy of vaporization of the OH···O bond (EOH) calculated from the FTIR data of each system (Hans-TW) (see Figure S.1 and S.2, and Table S.14, in the supplementary information) and the 5000 cal/mol constant assumed by Hansen (Hans). The results from the preliminary tests with the conventional solvents can be seen in Table S.7, in the supplementary information, where it was possible to confirm HK, once again, as the empirical model that generates values closer to those of Hansen (AARD% of 3.70). On the other hand, the results of the estimation of the δh parameter estimation of NADES are shown in Table 5.

Table 5 The δh parameter values of NADES, predicted using Semi- (SEM) (Hans—Hansen’s model (Eq. 17); ψHans-TW—same as Hans, but using the specific energies obtained from FTIR spectrum instead of the constant 5000 cal/mol proposed by Hansen (see more information in Table S.14 and Figure S.1 and S.2) and Empirical models (EM) (StP—Stefanis and Panayiotou; HK—Hoftyzer and Van Krevelen; HKF—Hoftyzer-Van Krevelen and Fedors; Ymt—Yamamoto).
Full size table

Here, as can be noted, the difference between the use of Hansen’s constant (Hans, Eq. 17) and the values obtained in this work (Hans-TW) is very small, which means that when the FTIR data of a given NADES is unknown, the constant (5000 cal/mol) can be used. However, if comparing these values with those obtained from the empirical models, it is possible to note a large difference between them, predominantly in the hydrophilic NADES case, where some values of Hans/Hans-TW are even more than five times higher than those from the EM (e.g., Bet:Suc:Pro:W (5:2:2:21), Fru:Glc:Suc:W (1:1:1:10), Glc:Pro:Gly:W (3:5:3:20), etc.). In fact, when evaluated in terms of AARD% it was possible to confirm such differences (Table S.8, in supplementary information). These results indicate that, unlike the semi-empirical models used to calculate δd and δp, these two methods proposed by Hansen to estimate δh are only applicable to molecular solvents. For complex structures such as NADES, they may not be the most suitable. Meanwhile, several factors can explain the found discrepancy between Hans/Hans-TW and the empirical model, in particular, in hydrophilic NADES, for example: their poly-alcoholic nature; low molar volume; or also the presence of water as a mixture’s component, which leads to a great increase in the δh values (when using Eq. 17). Actually, these characteristics of hydrophilic NADES are included in some of the limitations of Hans’s models42. Therefore, it may be necessary to use other approaches to assess the δh parameter.

Total solubility parameter (δt)

In addition to Eq. 17, Hansen has also proposed another method to estimate the hydrogen bond parameter, which consists of subtracting the total solubility parameter (δt) by the sum of dispersion and polar contribution (Eq. 18)42. Therefore, knowing the last missing parameter, δt, it is then possible to achieve δh. In practice, most of the theoretical methods used to δt, are based on either a correlation with the enthalpy of vaporization (ΔHv) or surface tension (σ), such as the set of semi-empirical models presented in Table S.2 (in the supplementary information (SI)). Hence, the models proposed by Reid, Prausnitz, and Poling (RPP, Eq. 21, in SI) and Kabo et al. (Kab, Eq. 22, in SI) were used to predict the enthalpy of vaporization of the studied solvents/systems, and then their δt (Table 6). Despite being models that use parameters estimated through the group contribution method, in other words, EM ones, here, these two models (RPP and Kab) were treated as SEM, so they can be compared with the commonly used EM and used further in the evaluation (see also Table S.15, in SI). Additionally, a set of semi-empirical models that correlate δt with the surface tension (σ) were also evaluated, namely those from Beerbower (Bb′, Eq. 23, in SI), Hildebrand-Scott-Lee collaboration (HSL, Eq. 24, in SI), Sheldon (She, Eq. 25, in SI), Jarray (Jar, Eq. 26, in SI) and Gordon (Gor, Eq. 27, in SI). The results are also listed in Table 6.

Table 6 The δt parameter values of NADES, predicted using Semi- (SEM) (RPP—Reid, Prausnitz and Poling (Eq. 21); Kab—Kabo (Eq. 22); Bb′—Beerbower (Eq. 23); HSL—Hildebrand-Scott-Lee collaboration (Eq. 24); She—Sheldon (Eq. 25); Jar—Jarray (Eq. 26); Gor—Gordon (Eq. 27)) and Empirical models (EM) (StP—Stefanis and Panayiotou; HK – Hoftyzer and Van Krevelen; HKF—Hoftyzer-Van Krevelen and Fedors; Ymt—Yamamoto).
Full size table

When it comes to conventional solvents, HK and HKF were found to be the approaches with the lowest deviation from Hansen’s values (AARD% of 2.86 and 5.78, respectively) (see Table S.9, in supplementary information). In fact, just by looking at the results presented in Table 6, it is possible to note that in the case of NADES, RPP is also the semi-empirical model with the most similar values to those of the two empirical models (HK and HKF). This was in fact confirmed by the AARD% evaluation shown in Table S.10 (in the supplementary information), in which, if considering data sets containing solely polar solvents, i.e., the “conventional solvents” and “hydrophilic list”, it can be observed that there is a good relationship between RPP and HKF (AARD% of 2.02 and 7.79, respectively). However, on the other hand, by introducing some hydrophobic solvents (“General list”) or evaluating, uniquely, a set of hydrophobic nature substances (hydrophilic list), it is possible to conclude that Bb′ is the SEM that shares the most resemblance with the EM (Bb′-HK and Bb′-HKF with AARD% of 8.07 and 2.37, respectively).

Estimation of the δh parameter using the SEM combinations

Throughout this research, various semi-empirical HSP prediction models were presented and used, and the values obtained were then compared in terms of similarity to those estimated using empirical models. However, unlike the EM, where the same model allows the prediction of all the 3 HSPs (δd, δp and δh) and consequently the δt, in the case of the SEM, it is necessary to use different models to determine each of the HSPs. However, this also means that several different combinations are possible, such as those shown in Fig. 1.

Fig. 1
figure 1

Possible combinations of semi-empirical HSPs that can be used to predict δh parameter, using the subtracting method.

Full size image

This could be a very interesting approach since it is possible to address these combinations in order to find the ones that are most similar to the EM. Thus, considering the SEM used to predict, respectively, the parameters δd (KoS (A1) and YAH (A2)), δp (Böt (B1), HB (B2), Bb (B3) and KoS′ (B4)), and δt parameter (RPP (C1), Kab (C2), Bb′ (C3), HSL (C4), She (C5), Jar (C6) and Gor (C7)), there is a total of 56 different combinations that could be used to estimate semi-empirically the δh parameter, using the “subtracting method” of Hansen (Eq. 18). These are presented in Table S.11 (in the supplementary information).

By comparing the results obtained from this method with those from the empirical model, in particular, HK and HKF, it was found that the combinations C1 to 7 + A1 + B3 (from D1.1.3 to D7.1.3) (highlighted in Table S.11) are those that generate the most similar values. Given a large amount of data, only the results from these combinations are presented in Table S.12 (in Supplementary information), along with the values obtained previously using Hans-TW and the empirical ones. The results showed that there is, in general, a good agreement between the δh values of the two theoretical models (SEM and EM), when the second approach Hansen is used (Eq. 18). In fact, compared to the results shown previously in Table 5, there is a substantial increase in the similarity degree between SEM and EM, as can be confirmed in Table S.13 (in the supplementary information). Additionally, based on the findings of Table S.13, it can be also inferred that the combinations D7.1.3 and D2.1.3 are the SEM, which share the most similarity with the empirical models HK/HKF (highlighted in grey), for the general/hydrophobic list (14.3% and 12.44%, respectively) and hydrophilic one (9.27%), respectively.

Despite this good similarity degree between SEM and EM, it is very important to emphasize, once again, that this combination method was only tested because of the large difference found initially between the two theoretical approaches. This, assuming that the empirical models, especially the widely used ones (HK/HKF), are those that could provide better results for NADES. Although there are no experimental data available to confirm the real effectiveness of such a method, it can still be considered a good alternative for the empirical models if future works prove their applicability.

It is well known that among the three HSPs, δh is undoubtedly the most controversial parameter and this was even pointed out by Stavroudis and Blank as a limitation of the HSPs since Hansen’s assumption did not explain the nature of all hydrogen bonding65. In other words, according to these authors, this single parameter does not dictate the character of a compound to act as a donor or an acceptor. Moreover, the scientific community does not generally support the concept of including all remaining intermolecular forces in δh58. That is why this parameter has been studied more extensively than the others. In addition, it is also true that when it comes to eutectic systems, hydrogen bonds are inevitably the most important intermolecular forces, as they are pointed out as the major contributors to the formation of NADES. Therefore, a correct measurement/estimation of the δh parameter may be a good starting point to understand better these unusual solvents or even how they interact with other compounds.

Advantages and disadvantages of the SEM and EM

So far, what this work provides is data on the HSPs for various types of NADES, estimated using a set of theoretical models, which may work as alternative for each other, taking into consideration their limitations. Although this study was mainly focused on testing such differences when empirical and semi-empirical models are applied in eutectic mixtures, it is undeniable that the thinking of using models developed and recommended mostly for simple molecules/solvents in multicomponent ones as eutectic mixture field can be indeed suspicious. That is why, it is not possible in this study to indicate the most suitable models. Meanwhile, since up to this point, there are no concrete studies evaluating these models, which somehow are still being used, what this study provides is an extensive database that may be useful in future work to evaluate, comprehend and even design new HPSs models, more appropriate for eutectic mixtures. Yet, after gathering all the information acquired in this work, it was then possible to draw some conclusions regarding some possible advantages/disadvantages of each of these approaches that may be important in further works, as well as a brief evaluation of their applicability in the NADES field. These are presented in Table 7.

Table 7 Some advantages and disadvantages of the theoretical models identified throughout this work.
Full size table

The listed considerations not only identify the characteristics, advantages and limitations of each one of the approaches that may make difficult the application of these theoretical models in the prediction of the HSPs of NADES but will also contribute significantly to orient other researchers in further similar works. Since all the investigated theoretical models were developed using training data, that certainly did not include uncommon solvents such as NADES, the found discrepancies may be at some point expected and understandable. Moreover, given the number of compounds and the number of possible combinations to form NADES, developing new models suitable for NADES would certainly be challenging. However, both the development of new models and the improvement of currently used models could significantly favour their applicability in the field of eutectic mixtures, leading to a more accurate estimation of the HSPs. On the other hand, there are also nowadays many other powerful tools that have been used to predict the HSPs with very good accuracy, such as COnductor like Screening MOdel for Real Solvents (COSMO-RS) and machine learning (ML)66,67,68,69. However, compared to EM and SEM, both methodologies (COSMO-RS and ML) can be very challenging to use, mainly for those who never worked on them, because of some factors such as the complexity barrier, training data and datasets required, interpretation, time-consuming and the cost.

Conclusions

Hansen Solubility parameters (HSPs) are one of the most common tools used in studies involving solubility between materials. However, their application in the field of eutectic systems is still limited and dubious due to the incompatibility of the conventional methodologies used in the experimental determination of parameters. Hence, the performance of a set of theoretical models, based on the group contribution methods (empirical models, EM) and correlations with some physicochemical properties (semi-empirical models, SEM), was investigated. Thus, the main objective of this work was to find empirical and semi-empirical models that reproduce the most similar values of HSPs, which may be important since this approach may allow us to overcome some limitations of these methods such as the complexity of the molecules (in the case of EM) or the absence of experimental data (SEM mostly).

To better understand the variations between the estimation of HSPs using an empirical or semi-empirical model, a preliminary evaluation using a set of conventional solvents, whose values are already well described in the literature, was conducted. The results show that there is a better agreement between the Hansen experimental values and those that are estimated empirically. Therefore, the next step was then identified, for each solubility parameter, the semi-empirical models that can be considered the most similar to empirical ones, in terms of estimating values. From the results, it was possible to conclude that in fact, in both cases, conventional solvents and eutectic mixtures, the values obtained by the two methods are very similar in the prediction of dispersive (δd), polar (δp) and total solubility parameters (δt). However, when it comes to the hydrogen-bond solubility parameter (δh), there is a big difference between the estimated values, even between the empirical models. This occurs mainly in solvents/systems with a highly polar nature. Therefore, different combinations of the semi-empirical models were tested, where it possible to find combinations that could generate more similar values to the empirical models.

In fact, up to this point, there is no experimental data available to validate the results obtained in this work, so it is not possible to confirm the real applicability of HSPs in the field of eutectic mixtures, as it was done with conventional solvents. However, when looking at the correlations between the empirical and semi-empirical models, it is clear that a similar behaviour was found, whether using a list with only conventional solvents or a list with only NADES. It is also very important to mention that this study was mainly focused on understating how different are the values HSPs of the studied list of NADES, when empirical and semi-empirical are used. Therefore, although there is clearly a slight tendency in the discussion to highlight empirical models as hypothetically the most appropriate for NADES, largely because of the results observed in conventional solvents, more studies are certainly necessary to prove this theory. However, what is also true, is that this work will contribute significantly to the future ones. For example, by using these estimated HSPs to calculate the affinity degrees and then correlate it with experimental data on the solubility of different solutes in NADES. Furthermore, in order to have a more comprehensive study, the selected solutes would have different natures (e.g., polar and nonpolar). This method would make it possible to validate more accurately the effectiveness of each model and help to understand the real of HSPs in the eutectic mixture.