A method for monitoring three dimensional surface deformation in mining areas combining SBAS-InSAR, GNSS and probability integral method

Abstract

In the process of mineral resource extraction, monitoring surface deformation is crucial for ensuring the safety of engineering and ground infrastructure. Monitoring complete three-dimensional surface deformation is particularly significant. Traditional synthetic aperture radar (InSAR) technology provides deformation components only along the line of sight (LOS) and often lacks sufficient effective data in vegetation-covered mining areas and mining subsidence centers. To address this, this study proposes a method (SBAS-PIM) that combines SBAS-InSAR with the probabilistic integral method (PIM). This method leverages high-coherence points in mining areas and GNSS data from vegetation-covered regions to invert the parameters required by PIM, thus obtaining three-dimensional surface deformation results. The proposed method allows for the acquisition of three-dimensional deformation data with fewer InSAR points and GNSS data, significantly reducing labor costs and addressing the gap in InSAR monitoring of three-dimensional surface deformation in densely vegetated areas. Additionally, it accounts for the mutual influence of multiple adjacent working faces. Finally, through the application to a mining area in Heze, China, the maximum displacements in the vertical, east–west, and north–south directions were obtained as −2011, −418, and − 281 mm, respectively. The correlation coefficients between the vertical and east–west directions and GNSS data were both greater than or equal to 0.9, indicating that this method can effectively monitor the three-dimensional surface deformation of the mining area.

Introduction

Coal, often referred to as the “grain of industry,” is closely related to economic development. Its extraction can significantly boost local economies, but it also creates numerous voids underground, leading to surface subsidence and other issues. These can result in severe hazards such as surface collapse, mine-induced earthquakes, and landslides, causing extensive damage to infrastructure, farmland, and posing serious threats to the safety of property and lives in mining areas^1,2.

Precise leveling and Global Navigation Satellite System (GNSS) measurements are commonly used methods for monitoring surface deformation in coal mining today. However, they face several challenges, such as large workload, long operational cycles, low spatiotemporal resolution, and the inability of leveling measurements to monitor horizontal deformations, which imposes significant limitations^3,4,5. In recent years, the development of Interferometric Synthetic Aperture Radar (InSAR) has greatly addressed these shortcomings with its high efficiency, low cost, high precision, and wide coverage, providing a new method for surface deformation monitoring^6,7,8,9. Nevertheless, InSAR still has unavoidable limitations, such as only measuring line-of-sight deformations and distortion in areas with large deformation magnitudes^10,11,12. Although methods proposed by researchers like Chang-Qiang offer ways to retrieve complete three-dimensional surface displacement components from two parallel orbit measurements, issues such as small applicable areas, distortion in large deformation regions, and difficulty in obtaining azimuthal deformations in mining areas remain¹³.

To address these issues, Liu Baochen and Liao Guohua proposed the Probability Integral Method (PIM), which is a subsidence prediction method based on random medium theory¹⁴. Fan HD was the first to propose a model combining InSAR and PIM for extracting large deformation mining subsidence¹⁵. In 2021, Chen Yang proposed combining InSAR with PIM to address deformation distortion issues in large deformation areas due to low coherence¹⁶, but it still could not decompose the three directional deformation values from the InSAR line-of-sight data. In 2016, Z. F. Yang and others used a combination of InSAR and PIM to detect three-dimensional deformation in mining areas, with results matching survey data, proving the method’s feasibility in mining measurement¹⁷. However, these methods only considered a simple working face and the DInSAR technology used could not meet the needs for long-term continuous monitoring, and had drawbacks like atmospheric delay and residual terrain phase removal. Subsequently, many scientists combined SBAS-InSAR with probabilistic integral methods to monitor surface deformation in mining areas. However, effective methods for deformation in vegetated mining areas have not been proposed, and the feasibility of combining SBAS-InSAR with probabilistic integral methods in such areas remains unverified^{18,19,20,21,22,23}.

This paper uses SBAS-InSAR technology to process 82 Sentinel-1 A images, obtaining LOS deformation for a mining area in Heze City, Shandong Province. By combining high-coherence points and a few GNSS points with PIM, we acquired three-dimensional deformation information for the mining area and validated it against GPS monitoring results to study the feasibility of this method in three-dimensional deformation monitoring.

Additionally, we considered the impact of complex working faces and their interactions. We either superimposed the deformation caused by multiple working faces or divided the complex working face into several rectangular working faces, calculating their deformation separately and then superimposing them.

Finally, we predicted the three-dimensional deformation of other local working faces and verified the prediction feasibility using leveling data.

Study area and data

Study area

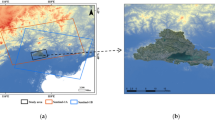
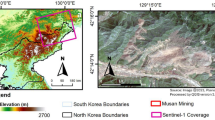
In this study, we focus on a coal mine located in Yuncheng County, Heze City, Shandong Province, Eastern China. The mine has proven reserves of 107,645.55 million tons and is situated near Yuncheng Station on the Jingjiu Railway and the county town of Yuncheng. The Jingjiu Railway runs through the western part of the mine, extending north to Beijing via Hebei and south through Henan, Anhui, Hubei, Jiangxi to Jiulong, providing very convenient transportation. The mine area and its surroundings contain numerous villages, with a significant presence of farmland, factories, residential buildings, and roads on the surface. Mining activities at the coal mine have severely impacted the buildings and farmland in the villages due to underground extraction.

The study area is covered by a large expanse of farmland, making it challenging to obtain a sufficient amount of effective data directly using InSAR monitoring. Additionally, multiple adjacent working faces interact with each other, complicating estimates using conventional Probability Integral Method.

Figure 1 marks the extent of the mine and the location of the study area (indicated by a pink rectangle), the specific locations of the working faces (outlined in red), and the positions of GPS points on two inclination observation lines and one strike observation line (marked by green circles)²⁴.

Fig. 1

The study area of this research. (a) represents the city where the coal mine in the study area is located, and (b) is the satellite optical image of the coal mine, with the image sourced from Google Earth.

Datasets used in this study

This study employs multi-temporal SBAS-InSAR technology, utilizing 82 Sentinel-1 A ascending SAR images with a 12-day interval throughout the working face operation. The images are acquired in the IW (Interferometric Wide) mode with VV (Vertical-Vertical) polarization. The specific acquisition dates are listed in (Table 1). Additionally, precise orbit data (POD) is used to correct the orbital accuracy of the SLC images for the corresponding acquisition dates. The terrain phase is removed using SRTM DEM data.

Table 1 Acquisition date for SAR images.

Methodology

SBAS-InSAR technique

Berardino et al. introduced the SBAS-InSAR technique, which overcomes many limitations of traditional InSAR and effectively improves the accuracy of surface deformation monitoring²¹.

SBAS-InSAR is a time-series InSAR method developed based on traditional InSAR technology, which maps surface deformation by minimizing the inherent spatiotemporal decorrelation and artifacts of InSAR. A network is organized using multiple master images, and SAR interferograms are generated using SAR images with small temporal and spatial baselines. Due to the short revisit cycle and excellent global coverage orbit control of the Sentinel-1 A/B satellites, the small baseline requirement is inherently met. Then, based on the coherence in the interferogram, pixels with sufficient coherence are selected for phase unwrapping. At this point, the phase sequence of the interferogram satisfies²⁵:

$$Av=\delta \phi$$

(1)

where, $\delta \phi$ represents the known phase of the interferogram, v is the deformation phase rate of change, and A is the coefficient matrix, which can be solved using the least squares (LS) or singular value decomposition (SVD) method to obtain parameters such as deformation amplitude and velocity²¹.

Probability integral method

Probability integral method, also known as the random medium theory method, is a forecasting technique based on the theory of random media. It was first applied by Polish researchers such as Litwiniszyn to study the movement of rock layers and the surface in discontinuous media²⁶, using the mechanics of particulate media. They suggested that the patterns of rock layer and surface movement caused by mining are similar on a macroscopic level to those described by the particulate media model as a random medium. Later, Chinese scholars such as Liu Baochen and Liao Guohua developed this into the probability integral method.

Based on the probability integral method, for a working face with a dip length of ${D_1}$ and a strike length of ${D_3}$, which can give the vertical displacement W(x, y) as well as the horizontal deformation U_N(x, y) and U_E(x, y) in both the North and East directions. Therefore, for the mining-induced ground subsidence at any point P(x, y), the calculation equation of real 3-D displacements can be described as:

$$\left\{ \begin{gathered} W\left( {x,y} \right)=\frac{1}{{{W_0}}}{W^0}(x){W^0}(y) \hfill \\ {U_N}(x,y)=\frac{1}{{{W_0}}}\left[ {{U^0}(x){W^0}(y)\cos {\varphi _E}+{U^0}(y){W^0}(x)\sin {\varphi _E}} \right] \hfill \\ {U_E}(x,y)=\frac{1}{{{W_0}}}\left[ {{U^0}(x){W^0}(y)\cos {\varphi _N}+{U^0}(y){W^0}(x)\sin {\varphi _N}} \right] \hfill \\ \end{gathered} \right.$$

(2)

with

$$\left\{ \begin{gathered} {W_0}=mq\cos \alpha \hfill \\ {W^0}(x)=\frac{{{W_0}}}{2}\left\{ {\left[ {erf\left( {\sqrt \pi \frac{x}{r}} \right) - erf\left[ {\sqrt \pi \frac{{(x - l)}}{r}} \right]} \right.} \right\} \hfill \\ {W^0}(y)=\frac{{{W_0}}}{2}\left\{ {\left[ {erf\left( {\sqrt \pi \frac{y}{{{r_1}}}} \right) - erf\left[ {\sqrt \pi \frac{{(x - L)}}{{{r_2}}}} \right]} \right.} \right\} \hfill \\ \end{gathered} \right.$$

(3)

$$\left\{ \begin{gathered} {U^0}(x)=b{W_0}\left[ {{e^{ - \pi \frac{{{x^2}}}{{{r^2}}}}} - {e^{ - \pi \frac{{{{(x - l)}^2}}}{{{r^2}}}}}} \right] \hfill \\ {U^0}(y)=b{W_0}\left[ {{e^{ - \pi \frac{{{y^2}}}{{{r_1}^{2}}}}} - {e^{ - \pi \frac{{{{(y - L)}^2}}}{{{r_2}^{2}}}}}} \right] \hfill \\ \end{gathered} \right.$$

(4)

$$\left\{ \begin{gathered} l={D_3} - {s_3} - {s_4} \hfill \\ L=\left( {{D_1} - {s_1} - {s_2}} \right)\frac{{\sin ({\theta _0}+\alpha )}}{{\sin {\theta _0}}} \hfill \\ \end{gathered} \right.$$

(5)

where ${W_0}$ stands for the maximum mining subsidence, ${W^0}(x)$,${W^0}(y)$ are the components of vertical deformation in both the strike and dip directions, and ${U^0}(x)$,${U^0}(y)$ are the components of horizontal deformation in both the strike and dip directions. r,${r_1}$,${r_2}$ are the expressions of major influence radius of subsidence, with $r=\frac{H}{{\tan \beta }}$,${r_1}=\frac{{{H_1}}}{{\tan {\beta _1}}}$,${r_2}=\frac{{{H_2}}}{{\tan {\beta _2}}}$, which H, H1, H2 $\beta$,${\beta _1}$,${\beta _2}$ are the mining depth and influence angle in three directions, that is, the directions along the strike, down-dip, and up-dip of the working panel, respectively. m is the thickness of the coal seam, q is the subsidence coefficient, and $\alpha$ is the dip angle of the coal bed. l, L are the computing length of the working face in the strike and dip direction, with ${\varphi _N}$,${\varphi _E}$ are the azimuth angles between the strike direction of the working face with North and East (clockwise). s1,s2,s3,and s4 are the offsets of inflection points along the strike left, strike right, down-dip, and up-dip directions of the working panel, respectively.

In which, m, $\alpha$,${D_1}$,${D_3}$, H, ${H_1}$,${H_2}$,${\varphi _N}$,${\varphi _E}$are known parameters, q,$\beta$,${\beta _1}$,${\beta _2}$,${s_1}$,${s_2}$,${s_3}$,${s_4}$,$\theta$, b are unknown parameters²².

The impact of adjacent multiple working faces on the PIM

In regions with multiple working faces or complex face shapes, the interactions between multiple working faces or different parts of a single face can challenge traditional probability integral methods, which are designed for simple rectangular faces. As shown in (Fig. 2):

where, ${D_1}$and $D_{1} ^{\prime }$ represent the strike lengths of working faces 1 and 2, respectively; ${D_3}$ and $D_{3} ^{\prime }$ represent the dip lengths of working faces 1 and 2, respectively.

Fig. 2

Diagram of mutual influences between adjacent working faces.

Due to the mutual interactions between multiple (n) working faces, the resulting deformations are cumulative:

$$\left\{ \begin{gathered} W\left( {x,y} \right)=\sum\limits_{{k=1}}^{n} {W{{\left( {x,y} \right)}_k}} \hfill \\ {U_N}(x,y)=\sum\limits_{{k=1}}^{n} {{U_N}{{(x,y)}_k}} \hfill \\ {U_E}(x,y)=\sum\limits_{{k=1}}^{n} {{U_E}{{(x,y)}_k}} \hfill \\ \end{gathered} \right.$$

(6)

where $W{(x,y)_k}$,${U_N}{(x,y)_k}$, and ${U_E}{(x,y)_k}$ represent the deformation values in the vertical, north-south, and east-west directions caused by working face (k), respectively.

Combining Eq. (2) to (5), the three-dimensional ground surface deformation field under the mutual influence of complex working faces or multiple working faces can be determined.

Overview of the SBAS-PIM method

In coal mining, surface deformation consists of vertical. east-west, and north–south components. The LOS (line of sight) deformation obtained from SBAS-InSAR is a combination of these three directional components, as shown in (Fig. 3).

Fig. 3

Relationship between LOS deformation and vertical, north–south, and east–west deformations.

The InSAR-derived deformation along the LOS ( d LOS ) direction is a composite of the vertical, east-west, and north-south displacement components, which can be expressed as :

$${d_{LOS}}=\left[ {\cos {\theta _I}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin {\theta _I}\sin {\alpha _H}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \sin {\theta _I}\cos {\alpha _H}} \right]\left[ \begin{gathered} W \hfill \\ {U_N} \hfill \\ {U_E} \hfill \\ \end{gathered} \right]$$

(7)

where $\theta$ denotes the incidence angle of the SAR sensor at the measurement point, $\alpha$denotes the azimuth of the satellite’s flight direction (positive clockwise from North), and W,${U_N}$, and ${U_E}$ are the displacement in the vertical, north–south and east-west directions, respectively.

From Sect. 3.2, W, ${U_N}$, ${U_E}$ is a function of q, $\beta$, ${\beta _1}$, ${\beta _2}$, ${s_1}$, ${s_2}$, ${s_3}$, ${s_4}$, $\theta$ and b. Let $B=[q,\beta ,{\beta _1},{\beta _2},{s_1},{s_2},{s_3},{s_4},\theta ,b]$, then $\left( {W,{U_N},{U_E}} \right)=f[(x,y),B]$. Combining with Eq. (7), the function relationship between ${d_{LOS}}$ and W, ${U_N}$ and ${U_E}$ is given by:

$${d_{LOS}}=g[(x,y),B]$$

(8)

In the SBAS-InSAR results, select 20–30 high-coherence points as known points, and choose 4–5 GPS points with significant deformation values at the subsidence center as known points. Use Eq. (6) to synthesize the LOS deformation, then apply the least squares method to obtain the optimal solution for the parameters in Eq. (8). Consequently, the 3D deformation of the mining area can be determined using Eqs. (2–5).

Results and discussion

In this study, SBAS InSAR was used to process 82 Sentinel-1 A SAR images, and high coherence points were extracted. Combined with the three-dimensional GNSS data of the subsidence center, the three-dimensional surface deformation of the working face was calculated by PIM, and compared, analyzed and verified with GNSS data.

SBAS-InSAR monitoring of surface deformation in mining areas

The SBAS-InSAR technology is used to process the 82 Sentinel-1 A data. Because it is affected by various noises, adaptive filtering is used to remove or weaken it, and the filtered differential interferogram and coherence coefficient map are obtained.

The platform used for this data processing is the commercial software GAMMA, developed by the world-renowned Swiss remote sensing company GAMMA, specifically for processing SAR data²⁷. First, the raw SAR data format was converted to the SLC data format and registered to form a common reference grid. Here, we selected the SAR image from November 30, 2019, as the reference image, with other images registered to this date’s SAR image as auxiliary images. In this process, the registration between the DEM and SAR images was also carried out. Once the registration was complete, interferometric processing was performed using the ISP module. It is important to note that, prior to this, an SBAS interferometric network needed to be established. We set the maximum time baseline to 24 days and the maximum vertical baseline to 200 m, resulting in a total of 161 interferometric pairs. The SRTM DEM was used as an external DEM to eliminate flat ground and topographic effects. Multi-looking is crucial for SBAS-InSAR as it helps suppress speckle noise. In this study, a 10-pixel multi-look ratio was applied in the range direction and a 2-pixel ratio in the azimuth direction. After generating the interferograms, filtering and phase unwrapping were performed iteratively. In this process, we used an adaptive filter and the minimum-cost flow (MCF) algorithm based on Delaunay triangulation for phase filtering and unwrapping, respectively. Then, using the estimated precise baseline, the process of “differential interferometric processing → filtering → differential interferogram unwrapping” was repeated. The unwrapped differential interferograms obtained from the second round were manually selected to remove those still affected by orbital and atmospheric delay errors, forming an optimal sequence of unwrapped differential interferograms. Finally, surface deformation inversion and normalization were performed to obtain the surface deformation time series for the study area. The obtained deformation results were interpolated using Kriging, and an overall correction was applied based on reference points to obtain the final deformation results, as shown in (Fig. 4).

Fig. 4

Cumulative deformation in the LOS direction from SBAS-InSAR monitoring in the study area between June 20, 2018, and April 5, 2021.

Because the working face is covered by a large amount of vegetation, the coherence in summer is low, resulting in less effective data. Therefore, the final deformation results are obtained by maskless method during unwrapping, and the feature points matched with GNSS points are selected to verify the accuracy of SBAS-InSAR results, as shown in (Fig. 5).

Fig. 5

Comparison of SBAS-InSAR monitoring results and GNSS data in the study area from June 20, 2018, to April 5, 2021.

It can be seen from Fig. 5 that the SBAS-InSAR results are not much different from the GNSS results in most areas with small deformation, but there is a large gap near the subsidence center with large deformation and some small deformation areas, which cannot be directly used as monitoring results. This is mainly caused by two reasons: 1 ) The large gradient deformation area will lead to decoherence and poor unwrapping results, which will lead to unsatisfactory monitoring results; 2 ) There are a large number of farmlands near the study area, and the radar band cannot pass through the vegetation to observe the ground, which ultimately affects the observation results.

Combining SBAS-InSAR with PIM to solve for 3D deformation

SBAS-InSAR is a rapid method for obtaining surface deformation in the Line of Sight (LOS) direction. However, due to the rapid subsidence rate and large subsidence gradients in mining areas, there is often poor coherence in these regions. As a result, accurate deformation information cannot be detected in subsidence centers and densely vegetated areas, which limits the application of SBAS-InSAR in mining regions. According to Chen Yang et al. (2021), reliable InSAR results can be obtained when coherence is greater than or equal to 0.3. By combining the advantages of SBAS-InSAR and PIM, accurate 3D deformation information in mining areas can be obtained. This experiment combines SBAS-InSAR with the probability integral method, and by using Eq. (6), three-dimensional deformation information for three adjacent working faces is obtained. The specific steps are as follows:

(1) According to ground subsidence measurement standards, SAR image coherence values greater than 0.3 are considered reliable. Set the unwrapping coherence threshold to 0.3. Through temporal accumulation, obtain cumulative deformation maps where all coherence values are above 0.3. Select 29 high-coherence feature points near the working faces as uniformly as possible, and extract their coordinates and LOS deformation values${d_{los}}(1\sim 29)$. Choose 9 GNSS feature points at the subsidence center and calculate their LOS deformation values ${d_{los}}(30\sim 38)$ using Eq. (7).The location information is shown in (Fig. 6).

Fig. 6

Location of feature points. The base map is derived from optical satellite imagery of Google Earth.

(2) Project the 38 SBAS-InSAR and GNSS feature points onto the working face coordinate system to obtain working face coordinates $(x,y)$. Assume the LOS deformation is ${d_{LOS}}(x,y)$. According to surface fitting methods, this can be represented as a function related to feature point coordinates $(x,y)$ and the probabilistic integral estimate parameter (B), as shown in Eq. (10). Let ${d_{LO{S_k}}}(k=1,2, \cdot \cdot \cdot ,n)$ represent the measured deformation at each feature point, and adjust the surface fitting value ${d_{LOS}}(x,y)$ to minimize the deviation between the fitted values and actual monitoring results, such that the sum of squared errors is minimized.

$$V{V^T}=\sum\limits_{{k=1}}^{n} {{{\left[ {{d_{LO{S_K}}} - {d_{LOS}}(x,y)} \right]}^2}} =\hbox{min}$$

(9)

where, V represents the deviation of the actual monitoring values of each feature point from the least squares fitting values. Thus, the inversion result for the probabilistic integral parameter in the mining area can be obtained as:

$$B=[q,\beta ,{\beta _1},{\beta _2},{s_1},{s_2},{s_3},{s_4},\theta ,b]$$

(10)

(3) Based on the inverted probabilistic integral parameters and using Eq. (4)~(7), a probabilistic integral subsidence model for the mining area was established. The subsidence results were then converted to the geographic coordinate system, yielding continuous probabilistic integral three-dimensional deformation results $W\left( {x,y} \right)$,${U_N}(x,y)$ and ${U_E}(x,y)$. The results are shown in (Figs. 7 and 8).

Analyzing Figs. 7 and 8, the maximum subsidence in the vertical direction is -2011 mm, located between the two working faces. The east-west deformation ranges from [−418, 238] (positive westward), with the extreme values on either side of the working face and smaller deformations in the middle, indicating a trend of movement towards the centerline on the east and west sides. The north-south deformation ranges from [-281, 213] (positive southward), with extreme values at the northern and southern ends of the working face and minimal deformation along the north-south centerline, suggesting that the working face moves towards the center from both the north and south sides.

In order to verify the feasibility of this method, the three-dimensional deformation results obtained by combining SBAS-InSAR with PIM are compared with the measured GNSS data, and the correlation coefficient R with the straight line y = x is calculated, as shown in (Fig. 8). Analysis of Fig. 9 shows that the correlation coefficient R in the vertical direction and the east–west direction is greater than or equal to 0.9, which can be considered to be highly correlated, and it is also highly consistent with the measured GNSS data. It can be considered that the accuracy is high and has the conditions for practical application. The correlation between Fig. 9c,f is high, but there is a serious deviation when the north deformation is large. Combined with the comparison with the measured GNSS data, it can also be seen that the north–south deformation obtained by this method is consistent with the measured GNSS data, but the size gap is large. The reason for the analysis may be due to the inconspicuous deformation of InSAR in the north-south direction. The specific reasons and improvement measures need to be further studied.

Fig. 7

Three-dimensional deformation results from the combination of SBAS-InSAR and PIM. (a) represents vertical deformation, (b) represents east–west deformation, and (c) represents north–south deformation.

Fig. 8

Three-dimensional deformation visualization. (a) represents the three-dimensional visualization of vertical deformation obtained by this method, and (b) represents the direction and contours of horizontal deformation, where the length of the arrows indicates the magnitude of deformation and the direction of the arrows indicates the direction of deformation.

Fig. 9

Compare the three-dimensional deformation obtained with this method to measured GNSS data: (a,d) show the vertical direction, (b,e) show the east-west direction, and (c,f) show the north-south direction.

Conclusion

We use the method proposed in this paper to obtain the three-dimensional surface deformation of a mining area in Heze City and verify it. The results show that the method can solve the problem of areas with dense vegetation in or around urban. and multi-working face interaction in the mining area. Compared with the existing methods, some characteristics of the method are summarized:

• (1) The method only needs some scattered SBAS-InSAR high coherence points at the edge of the working face, and similar high coherence points can be found in most mining areas, supplemented by a small number of measured GNSS points in the subsidence center.

• (2) The method takes into account the mutual influence factors between multiple working faces, and improves the algorithm to further broaden the scope of application of the method.

• (3) Most of the existing methods are combined with D-InSAR, but D-InSAR cannot meet the needs of long-term continuous monitoring, and there are defects such as atmospheric delay and residual terrain phase that are difficult to remove. In this paper, SBAS-InSAR technology is combined with probability integral method to meet the monitoring needs of long-term mining in mining areas.

• (4) It is undeniable that this method still does not solve the defect of the large difference between the north and south deformation values in InSAR monitoring, which needs further study.