State switch control of magnetically suspended flywheel energy storage system in uninterrupted power supply system

Abstract

The magnetically suspended flywheel energy storage system (MS-FESS) is an energy storage equipment that accomplishes the bidirectional transfer between electric energy and kinetic energy, and it is widely used as the power conversion unit in the uninterrupted power supply (UPS) system. First, the structure of the FESS-UPS system is introduced, and the working principles at different working states are described. Furthermore, the control strategy of the FESS-UPS is developed, and the switch oscillation of the FESS-UPS system between the charging and discharging states is analyzed. Then, the switch strategy using the angle compensation of the flux linkage is designed to control the FESS-UPS system among different working states, and the peak values of current and voltage at the switch moment are suppressed. Finally, the simulations and experiments are performed to validate the performances of the switch strategy used in the FESS-UPS system, and the results prove that the current/voltage peaks during the switching process are effectively mitigated, so the impact on the power converter caused by the state switch is suppressed. Therefore, the control performance of the UPS using the MS-FESS could be further improved, and the FESS-UPS could realize the fast and safe discharge/charge for the grid source and three-phase loads.

Introduction

The flywheel energy storage system (FESS), as an important energy conversion device, could accomplish the bidirectional conversion between the kinetic energy of the flywheel (FW) rotor and the electrical energy of the grid^1,2,3. Compared to other kinds of energy storage methods, the FESS has the advantages of fast conversion speed, high power density, and little environmental pollution. As illustrated in Table 1, the FESS is widely applied in the power conversion unit of the uninterrupted power supply (UPS) system^4,5,6, the braking energy recovery system of the rail transit^7,8, the peaking regulation system of the grid^9,10,11, the fast charging station of electric vehicles^12,13,14, and etc. Furthermore, the active magnetic bearings (AMBs)^15,16,17are used in the FESS to take the place of the mechanical bearings, and the FW rotor is suspended by the magnetic force such that the mechanical friction between the FW rotor and the stator is avoided. In addition, the tunable magnetic forces could actively suppress the vibration amplitudes of the stator part and FW rotor suffering the disturbance at a high rotational speed^18,19. Thus, the magnetically suspended FESS (MS-FESS) is promising for energy storage, considering the extremely low vibration and the active controllability.

Table 1 A summary of the FESS used in different applications.

At the charging stage, the MS-FESS works in the electric motor status, and the rotational speed is improved to realize the conversion from electric energy to kinetic energy^20,21. At the discharge stage, the MS-FESS could be changed to the generator state, and the rotational speed is slowed so the stored kinetic energy is converted to electric energy^22,23. Therefore, the switching process between the charging and discharging states could affect the operational stability of the MS-FESS and the power quality of the grid side. In reference²⁴, for the FESS-UPS system, the designed extended state observer improved the charging efficiency and the proposed sliding mode control method reduced the oscillation of the outputted DC-bus voltage, and the oscillation at the switch state from the charging to the discharging was not suppressed. To promote the quality of the DC-bus voltage outputted by the FESS system, a linear tracking differentiator energy control method was designed for the voltage control of a FESS²⁵, and the measurement results have proved the fast-tracking speed and foregoing robustness of the DC-bus voltage. However, the charging performance was not analyzed and upgraded, and the switch oscillation of the FESS system among different states was not considered. The double-loop proportional-integral (PI) control strategy was used in the grid-side control of the FESS based on an estimator model^26,27,28. The designed control strategy not only mitigated the frequency deviation of the microgrid, but also reduced the oscillation amplitude of the DC-bus voltage. The reinforcement learning method was proposed for controlling the DC-bus voltage outputted by the FESS²⁹, and the simulations were performed to prove the good abilities of voltage error and generation cost. Nevertheless, the switch control of the FESS among different states was not investigated, so the impact at the switching moment still affects the stability and security of the FESS. An adaptive PI control using the neural network was proposed to control the charging state of the FESS-battery system³⁰, and the charge efficiency was improved with a great charging current. In addition, the model predictive control method was used in the FESS system for the wind farm³¹, and the smooth power output was realized by regulating the discharging state. The compound control strategy based on the internal mode control and the active disturbance rejection control was applied to the discharge control of a high-speed FESS system³², and the smooth DC-bus voltage was outputted for industrial applications.

Based on the publications mentioned above, the charging and discharging characteristics of the FESS are investigated, and the charging and discharging states of the FESS-UPS system are controlled by regulating the rotating speed of the FW rotor. Nevertheless, the current/voltage oscillations at the switching moment of the FESS-UPS system are not analyzed, and then the switch strategy among different states was not investigated. Therefore, based on the position compensation model of the flux linkage, the switch strategy of the MS-FESS used in the UPS system is researched, and the fast and safe switch among different states of the FESS-UPS system is realized. Then, the results verified that the proposed switch strategy using the angle compensation of the flux linkage is applied in the FESS-UPS system to improve the switch stability and mitigate the voltage and current oscillations at the switch moment. This article is concentrated on two parts as follows,

• 1. The working states of the FESS-UPS are detailly introduced, and the current/voltage oscillations at the transient switching moment are analyzed.

• 2. The switch strategy of the FESS-UPS using the position compensation of the flux linkage is developed, and the transient peaks of the voltage/current are suppressed at the switching moment.

Compared to the mentioned method, the novel switch strategy using the compensation term of the rotor angle could better realize the transition between the charging and discharging state, and the switch oscillations of the DC-bus voltage and the current are mitigated by 11% and 30%. To accomplish accurate compensation, the angle information of the FW rotor at the charging and discharging state should be timely and precisely measured, so the requirements on the angle measurement system are high. The structure of this article is as follows, the UPS system using the MS-FESS is introduced in Sect. “Introduction”, and the three working states of the FESS-UPS system are analyzed. In Sect. "Switch strategy of FESS-UPS system", the switch control strategy between the charge and discharge states is investigated, and the switch oscillations are also analyzed. Furthermore, the simulations and experiments are conducted in Sects. "Numerical simulation of FESS-UPS system" and "Experimental verifications of FESS-UPS system". The conclusions are summarized in "Conclusion".

System configuration of FESS-UPS

Prototype introduction of MS-FESS

The FESS combining the magnetic bearings is illustrated in Fig. 1(a), and it consists of the mechanical body, the driving unit, and the suspension unit. The mechanical body includes the stator house, the flywheel rotor, and the rotor shaft. The stator parts of the magnetic suspension system and motor are mounted on the stator house, and the housing is also used to provide a vacuum environment to the motor. The flywheel rotor uses carbon fiber material that is fixed on the rotor shaft, and the rotating velocity is controlled by a permanent magnet synchronous motor (PMSM). Moreover, the PMSM, as the critical driving unit of the FESS, works as the motor to store the power energy as the kinetic energy at the charging state. It operates at the generator to release the kinetic energy at the discharging state. The suspension unit, including the radial AMB, the axial AMB and the backup bearing, is utilized to levitate the FW rotor such that mechanical friction is avoided.

Fig. 1

(a) The schematic diagram of the MS-FESS, (b) the force and displacement coordinates of the FW rotor.

With the control of the magnetic suspension system including the radial AMB and axial AMB, the multiple-DoFs force model and displacement coordinate of the FW rotor are shown in Fig. 1(b). In detail, the radial AMB units at the up-end and low-end generate magnetic forces to control two-DoF radial displacements [d_x, d_y], and two-DoF radial tilting angles [α, β] are also controlled by the resultant torques of radial magnetic forces. In addition, the axial AMB units at the up-end and low-end of the flywheel disc output magnetic forces based on the differential control method of the displacement, and then the axial displacement d_z is controlled by overcoming the gravity of the rotor units. Therefore, magnetic forces and torques of levitating the FW rotor are [f_x, f_y, f_z, M_α, M_β], and the controllable displacements of the suspension unit are defined as [d_x, d_y, d_z, α, β].

Structure introduction of FESS-UPS system

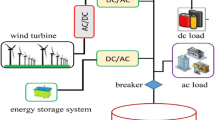
As shown in Fig. 2, the FESS-UPS system consists of the power input, the MS-FESS, the power device, and the load. In detail, the power input is provided by the grid source at the normal state, and supplied by the diesel generator at the emergency state. The three-phase AC power with the amplitude of 380 V is outputted to the power load. In general, the power input is offered by the grid, but it is transferred to the power source of the diesel generator in case of the grid’s failure. The flywheel battery includes the bidirectional converter (DC/AC and AC/DC) and the MS-FESS. The DC side of the converter is linked to the UPS’s power device, and the AC side is connected to the MS-FESS. In addition, the power device of the UPS system contains the static transfer switch (STS), the rectifier (AC/DC), the inverter (DC/AC), and the bypass device, and it is used to accomplish power conversion among the power input, the MS-FESS and the loads. The two independent power converter units are applied to realize the power device’s DC/AC inverting and AC/DC rectifying. The insulated gate bipolar transistor (IGBT) is used to realize the high-frequency inverting and the pulse width modulation (PWM) rectifying. However, the two independent converter structures could not fulfill a fast switch between the charging and discharging modes, and the hardware cost also improved. Therefore, the minimum power topology of the power device is illustrated in Fig. 3. The six IGBTs are formed into the power unit to realize the DC/AC inverting and AC/DC rectifying.

Fig. 2

The schematic diagram of the FESS-UPS system.

In detail, the source input of the grid could be outputted to the load through power devices, and also drive the MS-FESS to improve the rotating speed, so the electric energy of the grid is converted to the kinetic energy. The kinetic energy is released to electric energy for continuous supply and protection of the load when the power source of the grid is cut off, and the starting signal is sent to the STS and the diesel generator. Then, the power supply of the load is transferred to the generator, which simultaneously recharges the MS-FESS. The diesel generator is shut down and the power supply is switched to the grid, and then the MS-FESS restarts in the charging mode and protects the power loads.

As the critical protection unit of the FESS-UPS system, the MS-FESS would work in three modes (charging mode, holding mode, and discharging mode) according to the switch signals of the STS. According to the minimum power topology in Fig. 3, the three working modes are studied too.

Fig. 3

The minimum power topology diagram.

Under the charging mode, the MS-FESS is transferred to the motor state, and the inverter (DC/AC) starts working. The DC-bus voltage could charge the capacitors C₁, C₂ and C₃, and the equalizing resistances (R₁, R₂ and R₃) are used to equally distribute the voltages of the capacitors. When the DC-bus voltage V_DC is higher than the defined value, the control unit would ensure the IGBT units work at the high-frequency inverting state. Then, the current flows to the motor through the DC side, and the rotating speed is improved to the rated value, so the electric power is transferred to the kinetic energy. In the holding mode, the main control unit (MCU) can control the IGBT units at the high-frequency inverting state, and the minimum current is used to hold the rated speed. In the discharging mode, the MS-FESS is transferred from the motor state to the generator state, and the rectifier (AC/DC) begins to work. The control unit could detect that the DC-bus voltage V_DC is lower than the reference value, and the IGBT units could be switched to the high-frequency rectifier state. The current of the motor is quickly reversed and flows out to the DC-bus side, and the conversion from the kinetic energy to the electric power is realized.

The voltage functions of the motor/generator in the MS-FESS are

$${{\mathbf{u}}_s}={R_s}{{\mathbf{i}}_s}+{L_s}\frac{{d{{\mathbf{i}}_s}}}{{dt}}+\frac{{d{{\mathbf{\varphi }}_s}}}{{dt}}$$

(1)

where, u_s=[u_a, u_b, u_c] are the three-phase voltages, i_s=[i_a, i_b, i_c] are the three-phase currents, R_s is the stator resistance, L_s is stator inductance.

The stator flux linkages are written as

$${{\mathbf{\varphi }}_s}={\varphi _{pm}}\left[ \begin{gathered} \sin \left( {{\omega _r}t+{\theta _r}} \right) \hfill \\ \sin \left( {{\omega _r}t+{\theta _r}+{{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-0pt} 3}} \right) \hfill \\ \sin \left( {{\omega _r}t+{\theta _r}+{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0pt} 3}} \right) \hfill \\ \end{gathered} \right]$$

(2)

where φ_pm is the permanent magnet flux of the stator, ω_r and θ_r are the angle velocity and rotor angle, respectively.

The control voltages are divided into the excitation component and the effective torque component to realize the decoupling control of the motor/generator. Then, the voltage functions are written as

$$\left\{ \begin{gathered} {u_q}={R_s}{i_q}+{L_q}\frac{{d{i_q}}}{{dt}}+{\omega _r}{L_d}{i_d}+{\omega _r}{\varphi _{pm}} \hfill \\ {u_d}={R_s}{i_d}+{L_d}\frac{{d{i_d}}}{{dt}} - {\omega _r}{L_q}{i_q} \hfill \\ \end{gathered} \right.$$

(3)

where u_d and u_q are the d-axis voltage and q-axis voltage, respectively, i_d and i_q is the d-axis current and q-axis current, respectively.

The effective torque equation is

$${T_e}=p{\varphi _{pm}}{i_q}=\frac{J}{p}\frac{{d\omega {}_{r}}}{{dt}}+{T_d}$$

(4)

where p is the polar pair, J is the moment of inertia, and T_d is the disturbance torque.

Control strategy of FESS-UPS system

The state vector PWM (SVPWM) control diagram of the MS-FESS is shown in Fig. 4, the double-loop control diagram is used for the speed regulation of the motor/generator, so the transient switching between the charging mode and the discharging mode is accomplished.

In the charging mode, the double-loop control strategy, including the outer speed loop and the inner current loop, is used to control the speed of the MS-FESS at the motor state. In addition, the estimation model is designed to obtain the speed and position signals. The i_q could control the effective electromagnetic torque, and then control the excitation component in the current loop. To improve the control efficiency with a high-power factor, the d-axis current is defined as 0 A to maintain the low excitation component, and the stator current is used to control the rotating speed.

When the operation status is transferred to the discharging mode, the outer voltage loop and the inner current loop are formed into the voltage control strategy. The d-axis current is defined as i_{d_ref}=0, and the i_qref is achieved by the voltage compensator to hold the DC-bus voltage at a constant term. Thus, the working state of the MS-FESS is transferred from the motor to the generator.

Fig. 4

The charging/discharging control diagram.

Switch strategy of FESS-UPS system

Voltage/current oscillation at switching moment

At the charging and discharging modes, the phase voltage, the phase current and the back EMF of the MS-FESS are plotted in Fig. 5(a). In the charging mode, the phase voltage, the phase current, and the back EMF change in the same direction, and the amplitude of the phase voltage is greater than the back EMF, so the electric power flows from the DC-bus side into the motor. At the discharging mode, the varying direction of the phase current and the back EMF is opposite to the phase voltage, and then the electric power is flowed out from the motor to the DC bus side. At the transient state from the charging mode to the discharging mode, the phase current is quickly varied from the flow-in to the flow-out status, so the pumping-up process of the DC voltage is finished by the boost circuit of the back EMF and the stator inductance.

In the practical situation, the MS-FESS should realize the full power discharging within several milliseconds, and then the great current leads to the rapid reduction of the back-EMF considering the soft characteristics of the motor, so the current peak would occur during the voltage pumping-up process. Moreover, the current peak could be aggravated by the increasing load power, and the overcurrent protection of the inverter is possibly started. As shown in Fig. 5(b), the FW rotor turns at the rated speed when the current i_q is kept in a low current state, so the MS-FESS would be charged to the full power status. At the switching moment t₁, the MS-FESS is changed to the discharging mode, and the current i_q is increased to hold the DC-bus voltage. However, because the back-EMF is declined at the switching moment t₁, the peak values of current i_q and i_d would occur in Fig. 5(b) and (c).

Fig. 5

(a) The phase current, the phase voltage, and the back-EMF curves at the charging and discharging modes, (b) the current peak of i q at the charging and discharging modes, (c) the current peak of i d at the charging and discharging modes.

Switching method of MS-FESS

To realize the smooth switch between the charging mode and the discharging mode, the flux linkage position of the motor/generator is compensated to improve the control accuracy. Based on the actual value of the flux linkage position, the angle compensation information is achieved through the q-axis and d-axis voltages.

For the motor/generator used in the MS-FESS, the back-EMF³³ is expressed as

$$E=4.4 N\varphi {K_e}f$$

(5)

where N is the number of turns, φ is the flux, K_e is the back-EMF coefficient, and f is the current frequency.

To improve the efficiency of the stator magnetic field and avoid flux saturation, there is

$$\frac{E}{f}=4.4 N\varphi {K_e}={\text{constant}}$$

(6)

Thus, the stator voltage is improved by increasing the current frequency.

Based on the control strategy in Fig. 4, the Eq. (3) is simplified to

$$\left\{ \begin{gathered} {u_q}={R_s}{i_{qc}}+{\omega _r}{\varphi _{pm}} \hfill \\ {u_d}= - {\omega _r}{L_q}{i_q} \hfill \\ \end{gathered} \right.$$

(7)

where i_qc is the charging current.

At the rated value of the rotating speed, the moment voltage and the excitation voltage are

$$\left\{ \begin{gathered} {V_q}={V_{q0}}+\Delta {V_q} \hfill \\ {V_d}={V_{d0}}+\Delta {V_d} \hfill \\ {V_{q0}}={R_s}{i_{qc}},\Delta {V_q}=\Delta {\omega _r}{\varphi _f} \hfill \\ {V_{d0}}=0,\Delta {V_d}= - \Delta {\omega _r}{L_q}{i_{qc}} \hfill \\ \end{gathered} \right.$$

(8)

Then, the rotor flux is weakened when the back-EMF is suddenly reduced, so the rotor flux is mitigated at the charging mode. Furthermore, the variations of the moment voltage and the excitation voltage easily lead to the current peak at the switching moment.

The flux angle could be regulated to change the voltage V_d, and the magnetic field of the rotor would be improved to reduce the back-EMF. Furthermore, the current peak could be suppressed by holding the rotor voltage.

The compensation terms of the flux angle are designed as

$$\Delta {\theta _r}=\frac{\pi }{4} - \arctan \left( {\frac{{\left| {{V_{q1}}} \right|}}{{\left| {{V_{d1}}} \right|}}} \right)$$

(9)

The d-axis and the q-axis voltages are expressed as

$$\left\{ \begin{gathered} {V_{q1}}=\left| {{V_q}} \right| - \left| {{V_{q0}}} \right| \hfill \\ {V_{d1}}=\left| {{V_d}} \right| - \left| {{V_{d0}}} \right| \hfill \\ \end{gathered} \right.$$

(10)

where V_q0 and V_d0 are the initial values of the torque voltage and the excitation voltage.

To balance the positive and negative excitation magnetic fields, there are

$$\left\{ \begin{gathered} \left| {{V_{q1}}} \right|=\left| {{V_{d1}}} \right| \Rightarrow \Delta {\theta _r}=0 \hfill \\ \left| {{V_{q1}}} \right|<\left| {{V_{d1}}} \right| \Rightarrow \Delta {\theta _r}>0 \hfill \\ \left| {{V_{q1}}} \right|>\left| {{V_{d1}}} \right| \Rightarrow \Delta {\theta _r}<0 \hfill \\ \end{gathered} \right.$$

(11)

The compensation term of the flux angle is defined as Δθ_r > 0 to add the positive excitation magnetic field, and there is Δθ_r < 0 to add the negative excitation magnetic field.

Moreover, the threshold value of the voltage error ΔV is adopted to regulate the compensation term, and there are

$$\Delta {\theta _r}=\left\{ \begin{gathered} 0{\text{ ,}}\left| {\left| {{V_{q1}}} \right| - \left| {{V_{d1}}} \right|} \right| \leqslant \Delta V \\ \frac{\pi }{4} - \arctan \left( {\frac{{\left| {{V_{q1}}} \right|}}{{\left| {{V_{d1}}} \right|}}} \right),\left| {\left| {{V_{q1}}} \right| - \left| {{V_{d1}}} \right|} \right|>\Delta V \\ \end{gathered} \right.$$

(12)

Furthermore, the flux angle using the compensation term is

$${\theta _{rc}}={\theta _r}+\Delta {\theta _r}$$

(13)

Finally, the compensation methods could be referred to following steps.

1, Regulating initial values of the voltages V_q0 and V_d0. The rotating speed is improved to ω₀ (ω₀ > 500 rpm) using the charging methods, the torque voltage and the excitation voltage are defined as initial values.

2, Substituting initial voltages into Eq. (7), the real-time values (V_q and V_d) of the torque voltage and the excitation voltage are obtained, and the compensation terms of the voltages V_q1 and V_d1 are derived using Eq. (9).

3, The compensation term Δθ_r of the flux angle is achieved using the V_q1, V_d1 and Eq. (9).

4, Substituting Δθ_r into Eq. (13), and the θ_rc is finally got

The detailed operation can be referred to in the following flowchart in Fig. 6.

Fig. 6

 The phase compensation flowchart of rotor flux linkage.

Numerical simulation of FESS-UPS system

During the charging process of the FESS-UPS system, the DC-bus voltage is kept at 600 V. Then, the electric energy of the grid source is stored as kinetic energy so the rotational speed is improved and stabilized at the rated value. When the grid source is suddenly switched off, the FESS-UPS system can supply power to the three-phase load, and the DC-bus voltage is defined as 500 V. Thus, the DC-bus voltage of the load side is stabilized by the FESS-UPS system at the discharge state.

Simulation results of DC-bus voltage

First, the simulation results of the DC-bus voltage are tested at the discharging and charging modes, and the voltage curves are plotted in Fig. 7. The DC-bus voltage controlled by the normal switch strategy using the dual-loop PI method is plotted by the red line, and that controlled by the proposed switch strategy using the angle compensation is shown by the green line. For the normal switch strategy, the oscillation value of the DC-bus voltage reaches 136 V from the holding stage to the discharging stage. For the proposed switch strategy using the compensation model, the variation of the DC-bus voltage is reduced to 102 V during the switching process. In addition, during the switching process from the discharge state to the charge state, the proposed switch strategy could better respond to the charging command based on the flux linkage compensation, so the charging efficiency and stability of the FESS-UPS system are improved.

Fig. 7

The simulation results of the DC-bus voltage.

Simulation results of control current

Moreover, the d-axis and q-axis currents during the charge and discharge processes are illustrated in Fig. 8, and the control properties of different switching methods are analyzed. As shown in Fig. 8(a), the d-axis current is kept at a stable amplitude of 20 A during the charge and discharge processes. The q-axis current of the grid side would vary with the working states of the FESS-UPS system, and its amplitude could be rapidly increased to 350 A at the switch moment from the holding stage to the discharge stage. For the q-axis current of the grid side (marked by the red line) controlled by the normal switch method in Fig. 8(b), the oscillation value (peak-peak value) at the switch process approaches 580 A. The oscillation value of the q-axis current is reduced to 360 A by the proposed switch method using the angle compensation, and the q-axis current could also quickly respond to the charge command. Thus, the current oscillations during the discharge process are suppressed, and the tracking performance is improved, too, based on the flux linkage compensation.

Fig. 8

 The simulation results of the d -axis and q -axis currents.

Simulation result of control voltage

In the meanwhile, the ratios between the d-axis/q-axis voltage and the DC-bus voltage are also analyzed to evaluate the voltage performance, the ratio between the d-axis voltage and the DC-bus voltage is defined as V_d/V_dc, that between the q-axis voltage and the DC-bus voltage is V_q/V_dc. First, the curves of the ratio V_d/V_dc at the charge and discharge states are shown in Fig. 9(a). For the normal switch method, the amplitude of the term V_d/V_dc is kept at 0.58 during the charge process, and it is reduced to 0.05 at the discharge state. For the proposed switch strategy, the ratio V_d/V_dc is held at 0.61 at the charge state to stabilize the rotational speed. Moreover, the curves of the ratio V_q/V_dc are illustrated in Fig. 9(b). The amplitude of V_q/V_dc is about 0.63 at the charge state, and it varies with the switch command at the discharge state. For the normal switch method, the peak value of the V_q/V_dc reaches 0.31 from the holding stage to the discharge stage, and the steady value is 0.78. For the voltage ratio controlled by the proposed switch method, the peak value is mitigated to 0.23, and the steady-state term is 0.83 at the charge state. Thus, the value of the ratio V_d/V_dc approaches that of V_q/V_dc at the charge state, and the amplitude of V_d could be closer to the V_q using the angle compensation of the flux linkage.

Fig. 9

The simulation results of the d -axis and q -axis voltages.

Experimental verifications of FESS-UPS system

Experimental setup of FESS-UPS system

Fig. 10

The whole experimental setup of the FESS-UPS system.

The performances of the proposed switch strategy are verified in the UPS system in Fig. 10. The whole experiment system consists of the voltage transformer, the bidirectional converter, the MS-FESS, and the power load. The host computer could collect and display the system information to observe the operational state of the whole FESS-UPS system. In the experimental process, the MS-FESS is located downstairs and protected by energy-absorbing materials, and the pump could keep the housing of the MS-FESS at a low vacuum environment (1–5 Pa). The MS-FESS, as the storage conversion unit, could realize the mutual transfer between the kinetic energy and the electric energy by tuning the rotating speed. Moreover, the magnetic suspension system levitates rotor components to prevent friction and control the vibration. Then, to realize the active control of the MS-FESS system, the closed-loop displacement control of the FW rotor is realized by the MCU (based on the DSP chip and FPGA chip) based on displacement signals obtained by the displacement sensors³⁴. Considering the windage loss at the rated speed and the power consumption of the magnetic suspension system and motor, the energy loss of the whole MS-FESS system is about 5% of the stored energy.

Table 2 The parameters of the FESS-UPS system.

For the FESS-UPS system mounted on upstairs, the AC 380 V of the grid source could be converted to the DC 600 V by the rectifier of the UPS system, and the DC voltage is provided to the power load through the inverter and the bidirectional converter. At the charging state, the electric energy of the grid side is converted to the kinetic energy of the MS-FESS through the rectifier. When the grid source is suddenly switched off, the FESS-UPS system could work at the discharging process to supply power to the power load. The parameters of the FESS-UPS system in the experiment are shown in Table 2, and the control parameters of the switch method used in the charging/discharging processes are listed in Table 3.

Table 3 The control parameters used in the charging/discharging processes of the FESS-UPS.

Experimental results of DC-bus voltage

In the experiment, the DC-bus voltage of the FESS-UPS system is tested, and the voltage curves using different switch strategies are plotted in Fig. 11. For the DC-bus voltage controlled by the normal switch method, the peak-peak value at the switching moment from the holding state to the discharging state is 146 V, and the peak-peak value at the charging stage reaches 150 V. For the DC-bus voltage curve of the proposed switch strategy, the peak-peak value from the holding stage to the discharging stage approaches 130 V, and that at switch moment from the discharging state to the charging state is 116 V. Comparing oscillation values using the two different switch methods, the proposed switch method based on the flux linkage compensation has better performance on suppressing the peak-peak value of the DC-bus voltage.

Fig. 11

The experimental result of the DC-bus voltage.

Experimental results of control current

Moreover, the control currents in the experiment are tested, and the control current curves are shown in Fig. 12. For the q-axis currents using different switch methods in Fig. 12(a), the amplitude is increased to 350 A at the discharging stage. The peak-peak value of the q-axis current controlled by the normal switch method is 444 A from the holding stage to the discharging stage, but that of the proposed switch method is reduced to 310 A. Moreover, the d-axis currents at the charging and discharging states are illustrated in Fig. 12(b), and the amplitudes of the two switch methods are close to 20 A because the reference value is defined as 0 A. Thus, the proposed switch method using the angle compensation of the flux linkage could reduce the current peak at the charging and discharging states, and then the impact on the bidirectional converter could be mitigated.

Fig. 12

The experimental results of the d -axis and q -axis currents.

Experimental results of control voltage

Moreover, the ratios V_d/V_dc and V_q/V_dc are also measured to analyze the control voltages at the charging and discharging states. The ratio V_d/V_dc is illustrated in Fig. 13(a), and the amplitude of the V_d/V_dc using the normal switch method is about 0.53, and the amplitude of the proposed switch method is improved to 0.65. For the ratio V_q/V_dc in Fig. 13(b), the peak-peak value of the normal switch method from the holding stage to the discharging state is 0.56, and that of the proposed switch method is 0.26.

Fig. 13

The experimental results of the d -axis and q -axis voltages.

At the charging state of the FESS-UPS system, the d-axis voltage V_d is a negative value and the q-axis voltage V_q is a positive value to stabilize the rotating speed, which is consistent with the theoretical analysis result in (8). The V_d and the V_q are varied within a stable range, so the ratio V_q/V_dc also oscillates within the range from 0.6 to 0.8. Therefore, the results indicate that the amplitudes of the ratios V_d/V_dc and V_q/V_dc are close using the compensation method, and the amplitude of the V_q is greater than the V_d. Thus, the main flux linkage could be fully used to improve the efficiency at the charging state.

At the discharging state, the kinetic power is released to stabilize the DC-bus voltage, and the current of the stator windings is reversed and improved to stabilize the DC-bus voltage. The amplitude of V_q declines with the discharging period, but the amplitude of the V_d is increased. Moreover, the V_q is determined by the rotational speed and the load power, and the amplitude of V_d could be reduced when the rotational speed is low and the reverse current is enhanced. Using the angle compensation of the flux linkage, the V_d could be varied from the negative value to the positive value, and the amplitude could be improved with the decline of the rotational speed.

Experimental results of rotating speed

Finally, the rotational speed curves of the MS-FESS using different switch methods are shown in Fig. 14, and the rated speed at the charge and holding stages is 10,500 rpm, and the rated speed at the discharge stage is 8500 rpm. For the rotational speed using the normal switch method plotted by the red line, the oscillation value is 2400 rpm at the transition stage from the holding state to the discharge state, and that from the discharge state to the charge state is 400 rpm. For the rotational speed of the proposed switch method plotted by the green line, the variation is 2100 rpm when the working state is switched from the holding state to the discharge state, and the speed curve could better track the reference speed from the discharge state to the charge state. Therefore, the working states of the MS-FESS are smoothly changed by the proposed switch method using the angle compensation of the flux linkage.

Fig. 14

The experimental results of the speed regulation.

Conclusion

The MS-FESS could be used as the energy storage device in the UPS system to realize the charging and discharging, such that the high-efficiency conversion between the kinetic energy and the electric energy could be accomplished. However, the transient switching of the charging and discharging states leads to the current peak and the voltage peak, and the impact caused by the switching of the charging and discharging states could affect the security of the conversion unit in the FESS-UPS system. Based on the position compensation of the flux linkage in the MS-FESS, a transient switching strategy is proposed to realize a fast and safe transition between the charging and discharging state, so the impact on the power conversion unit is mitigated. The experimental results illustrate that the switch peak of the DC-bus voltage is mitigated by 11% and the the current peak is mitigated by 30%. Therefore, the proposed switch strategy could realize a smooth transition among different states of the FESS-UPS system, and the impact on the power conversion unit is mitigated. Moreover, the system stability of the FESS-UPS system is enhanced because the influences on the power conversion system caused by the current/voltage peaks is effectively mitigated.

In the current research, the switching oscillation of the DC-bus voltage is effectively suppressed by the proposed method, but an angle measurement system is needed to achieve the position information of the MS-FESS. Thus, to further improve the switching performance of the FESS-UPS system, the more advanced methods such as the model predictive control are worthy of being investigated. Moreover, the sensorless observation method should be studied to avoid the angle measurement system, and the control performance of the FESS-UPS system could be further improved.