Introduction

Motivation in this paper

The primary objective of the power grid is to efficiently, reliably, and securely deliver electricity to consumers in a cost-effective manner1. There has been considerable interest in investigating the stability of such systems, particularly concerning voltage stability and collapse2, due to their critical role in major blackouts, such as those experienced in Sweden, the US, and Japan, as documented in3. Voltage stability refers to the system’s inability to maintain acceptable steady-state voltages at all points during normal operations or after disturbances. This issue often arises due to a lack of reactive power generation and excessive system loading4. The main consequences of voltage instability include cascade disconnection of grid components triggered by protective mechanisms, load reduction, or even complete blackouts5. Amid escalating worries regarding atmospheric pollution in recent times, alternative energy sources have the potential to assume a more prominent and efficient position within electricity networks6,7. On the contrary, ensuring voltage stability is paramount when integrating the power system with microgrid systems, to optimize energy management. The power system’s dependence on the microgrid could exacerbate voltage instability if energy transactions between the grid and microgrid are injected or altered in a non-optimal manner for any reason. This issue can become a primary target for cyberattacks aimed at disrupting the power grid through false data injection in the transfer point. Hence, identifying such targeted cyber-attacks may be facilitated by implementing an adaptive defense strategy trained with the attack model. The concept of learning generative networks could effectively detect false data injection attacks within the microgrid-integrated power grid due to its ongoing interaction with the environment.

Literature review

Recently, microgrids have become the focus of research due to the increasing demand for areas far from the upstream grid. Regarding the use of various renewable energy sources (RES), Ref.8 proposed the energy management control problem of solar power generation system by using the data-driven method9. Similarly, the authors in10 suggested the power schedule of RESs using the Chaotic Self-Adaptive Sine Cosine Algorithm (CSASCA). Ref.11 examined a game theory-based problem-solving method without considering the control power of the microgrid. Reference12 presented a decentralized method to manage the hybrid energy structure. This approach considers a multilevel problem, including the location of the power transformer, DC microgrid, and AC microgrid, respectively. Inspired by the multi-objective problem concept, the paper13 effectively provided a combined framework for the operational objective functions of AC and DC microgrids. Also, the authors in14 suggested a multi-layer optimization framework for energy management in cooperative multi-microgrids. It incorporates demand response programs and integrates techno-economic-environmental objectives. The concept encourages microgrids to operate in unison and share resources as efficiently as possible. A closer look at electricity transmission15 in microgrids reveals some concerns about the uncertainties regarding renewable energy production16. The evidence discloses that numerous investigations were conducted to improve this problem. In this way, authors in17 neutrally eliminated the above concerns and proposed Taguchi’s orthogonal array-based absorption method aimed at modeling uncertainties. Additionally, power management considering uncertainty for AC/DC microgrids is described in18. In this study, as the authors considered the uncertainty, so did the relationship between the parameters. It is worth saying that the microgrid can handle uncertainty when operating in grid-connected mode. Then again, once the hybrid microgrid is connected to the upstream grid through the bus station19, the grid can be more controlled and more flexible to deal with unforeseen and emerging threats arising from the misuse of smart tools20. So to speak, as smart devices improve accuracy and control, cyber attacks can disrupt physical operations. The deficiency of a secure platform for the sake of utilizing smart devices will increase the risk of inaccessibility. Hence, the false data injection attack called FDI21 is introduced as the most dangerous in the electrical grid. Research on FDI attacks in many literatures generally includes three perspectives: 1- Theoretical research on the creation or creation of effective FDIA22,23,24,25, 2- Research on the overall impact of FDIA26,27,28,29, 3- Six Machine FDIA Maintain30,31,32. Reference33 published a review of the effects of incorrect injection data in modern electronic systems. Paper34 pointed out how the FDI attack can affect the energy exchange in the power grid35. The authors in36 attempted to provide a comprehensive review of FDI attacks. This attack may bring about unwise decision-making for the grid operation if it is undetected, as soon as possible. Based on this, Ref37. conducted a type of FDI attack and pointed out that corruption of information on monitoring equipment will hide the performance of the electricity grid38,39. first introduced a cyber attack called blind FDI attack, which is free from knowledge. Indeed, the authors presented an FDI attack for state estimation. In Reference40, cyber-attacks aiming to change the values of meters through smart devices were examined. In the literature, researchers have evaluated the cybersecurity of supervisory control and data acquisition (SCADA) state estimation in energy projects. Identifying these types of attacks has become an interesting topic for researchers in late literature on power systems. some investigations have been focused on providing detection algorithms41 for various fields including control, energy management, electrical vehicles, resiliency, and so forth. However, there is a markable gap in research regarding the effects of cyber-security on microgrid operations42. Hence, abnormal data detection techniques for energy management in the power system have been proposed to identify anomalies in measurement data. Reference43 also suggested an analysis method aimed at finding the error in state estimation once power supply SCADA systems inject latent misinformation. In recent years, using the different concepts of artificial intelligence in detection algorithms has emerged as an intriguing topic for researchers. Among all, machine learning methods44 can be well-suited in the development of the attack detection system due to their high accuracy. Regarding the learning methods in the literature45, the search method based on relational network (GAN) classification is also well known. As a special feature of the GAN protocol, it has been widely used in the smart industry since 198646. The system uses a set of identifiers (IDs) to place running data on smart devices. Unfortunately, the previous methods cannot guarantee the safety of the energy scheduling in the power system equipped with smart devices. So this can be a weak area and has become a major challenge for power systems in recent years. In the following, a brief comparison between references is proposed (see Table 1).

Contribution

The main contributions of this work considering literature works can be defined as follows:

  • Developing a well-balanced framework for the microgrid systems in preparation for employing the most generation resources with the various primary energies such as wind, solar, water current, and hydrogen.

  • Identifying the weakness of microgrid systems, especially operation in the grid-connected mode based on the cybersecurity concept and proposing an advanced attack model named the false transferred data injection (FTDI) derived from the change in the power transferred between the microgrid and the upstream grid.

  • Proposing the artificial intelligent defense strategy inspired by the generative adversarial network (GAN) concept aiming to learn the FTDI attack within the microgrid systems.

The rest of the paper is as follows: Section “Problem formulation” is referred to the problem formulation definition. Also, Sect. “Cyber attack model” shows the cyber attack models within the microgrid. The detection model is modeled in Sect. “Proposed detection model” and the results are concluded in Sect. “Simulation results”. All in all, Sect. “Conclusions” is related to the calculation.

Table 1 The comparison of contribution in literature.
Full size table

Problem formulation

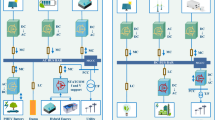
Recent studies have demonstrated that microgrid performance can assist in making the grid energy operation more flexible and controllable in the event of critical events, such as cyber-attacks37. Hence, this section attempts to propose an exceptional energy framework based on AC/DC microgrids with the goal of energy management for cyberattacks47. A cost-effective way to utilize both AC/DC sources within an eco-friendly framework is the hybrid microgrid. Figure 1 shows the created structure, which includes the wind turbine units, solar units, hydrogen-based fuel cell resources, and tidal turbine units for the successful realization of the suggested hybrid microgrid. This section presents the mathematical foundation of the suggested microgrid.

Renewable energy management for isolated/grid-connected modes

In technical terms, there are three types of microgrids based on the type of energy resource used: DC microgrids, AC microgrids, and integrated energy resource-based microgrids. The provision of an AC microgrid including the wind turbine (WT) unit and the tidal turbine system is the focus in the first place. It goes without saying that these renewable energy sources’ structures are a contentious justification for their inclusion in the AC microgrid class8. However, it is important to note that these resources are being used in DC microgrids because of the various electronic converters. There is a clear relationship between wind speed and WT output power, with changing wind speed due to weather conditions causing unsettling variations in output power. Similarly, the same explanation can be applied to the tidal turbine in relation to the output power and current speed. In summary, Eqs. (1)–(3) define the mathematical objective function, resources, and pertinent constraints.

$${C^m}=min\sum\limits_{{t \in {\Omega ^T}}} {W_{t}^{{WT}}PW_{t}+TI_{t}^{{tidal}}PT_{t}} $$
(1)
$$PW_{t}=\frac{1}{2}\rho Sl(V{e_t})^{3}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall t \in {\Omega ^T}$$
(2)
$$PT_{t}=\left\{ \begin{gathered} 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\,\, \leqslant \,{C_t}\, \leqslant {C_{rated}}\,\,\,\,\, \hfill \\ 0.5{H_p}{\rho _1}{S_1}C_{t}^{3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{C_{cutin}}\, \leqslant {C_t} \leqslant {C_{rated}} \hfill \\ P{T_{rated}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{C_{rated}}\,\, \leqslant {C_{t\,}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} \right.\;\forall t \in {\Omega ^T}$$
(3)

The WT and the tidal system are the two components of the objective function (1). As previously said, owners of renewable resources tend to have lower energy costs in relation to the hourly energy prices set by the energy market. Similarly, we use the minimization issue as the basis for the objective function. Equation (2) shows how to satisfy the WT’s output power given the wind speed. It makes a relationship with the wind speed cube, which is in need of the output power, as can be observed. According to (3), the power produced by the tidal unit is derived with a strong emphasis on the different values of the current speed. It is evident that the output power can be detached based on variations in the current speed. The DC microgrid system described in this work comprises DC renewable resources, like the fuel cell system based on hydrogen generation and the solar unit with the storage system. By using electronic converters, this type of microgrid may meet both DC and even AC demands. The performance of DC energy units is explained in the sections that follow. Of all the several kinds of fuel cell units described in the literature, the protein exchange membrane fuel cell (PEMFC) may be the best. Hydrogen H2 is the fuel that PEMFCs require in order to produce electricity. The hydrogen value required to meet the output power requirement is computed using Eqs. (6) and (7) where the generated hydrogen is derived from the total output power related to the fuel cell energy units and the hydrogen tanker’s limitations. Conversely, the storage unit assumes the responsibility of meeting needs in emergency situations. This indicates that the storage units are able to meet the dynamic swings in demand on an hourly basis. As a result, as shown in (4) the total power equals the sum of the fuel cell and storage powers. Additionally, by using (5)37, the output capacity limits can be determined.

$$P_{t}^{{Cell}}=P_{t}^{{FCell}}+P_{t}^{{Cell\_B}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall t \in {\Omega ^T}$$
(4)
$$P_{{Cell}}^{{\hbox{min} }} \leqslant P_{t}^{{FCell}}+P_{t}^{{Cell\_B}} \leqslant P_{{Cell}}^{{\hbox{max} }}\forall t \in {\Omega ^T}$$
(5)
$$0 \leqslant Hg_{2}^{t} \leqslant Hg_{2}^{{\hbox{max} }}\,\,\,\,\,\,\,\,\,\,\,\forall t \in {\Omega ^T}$$
(6)
$$Hg_{2}^{t}=(P_{t}^{{FCell}}+P_{t}^{{Cell\_B}}) \times \frac{{3.6{\raise0.7ex\hbox{${MJ}$} \!\mathord{\left/ {\vphantom {{MJ} {kWh}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${kWh}$}}}}{{119.96{\raise0.7ex\hbox{${MJ}$} \!\mathord{\left/ {\vphantom {{MJ} {Kg}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${Kg}$}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall t \in {\Omega ^T}$$
(7)

The other DC resources used in the DC microgrid are the PV units. In photovoltaic systems, the link between solar radiation and output power is a well-established fundamental interaction based on (8). It may be inferred that the PV unit’s power generation grows in tandem with solar radiation. It is obvious that neglecting the PV loss throughout the computation procedure could result in an abnormal generated power calculation. Additionally, by working together to meet shared demands, PV and storage units can counteract and assure output power swings brought on by unpredictability in solar radiation. The storage unit’s limitations are specified in compliance with (9)–(12). As can be seen in (9), the fuel cell unit’s power consumption as well as the charging and discharging power are taken into account when determining the output power of the storage unit. Every hour, the battery’s energy level is also measured using Eq. (10) to check the allowed level. As seen in (11) and (12), the storage unit is permitted to operate with a focus on the charging/discharging power constraints and the allowable energy level. Finality, the intended DC microgrid’s goal function is defined in (13).

$$PV_{t}^{{PV}}=\frac{{SA \times C_{t}^{{PV}}}}{g} \times (1 - P{V^{loss}})\,\,\,\,\,\,\,\,\,\,\,\,\forall t \in {\Omega ^T}$$
(8)
$$P_{{t}}^{{bat}}=P_{{t}}^{{bat\_ch}} - P_{{t}}^{{bat\_dis}}+P_{t}^{{Cell\_B}}\,\,\,\,\,\forall t \in {\Omega ^T}$$
(9)
$$Eg_{t}^{{Bat}}=Eg_{{t - 1}}^{{Bat}}+(P_{{t}}^{{bat\_ch}} - P_{{t}}^{{bat\_dis}}){\eta ^{Bat}}\,\,\,\,\,\,\,\forall t \in {\Omega ^T}$$
(10)
$$P_{{}}^{{\hbox{min} }} \leqslant P_{{t}}^{{bat\_ch}},P_{{t}}^{{bat\_dis}} \leqslant \,P_{{}}^{{\hbox{max} }}\,\,\,\,\,\,\,\,\forall t \in {\Omega ^T}$$
(11)
$$E_{{}}^{{\hbox{min} }} \leqslant Eg_{{n,t}}^{{Bat}} \leqslant \,E_{{}}^{{\hbox{max} }}\,\,\,\,\,\,\,\,\forall t \in {\Omega ^T},\forall b \in {\Omega ^b}$$
(12)
$${C^{total\_dc}}=min\sum\limits_{{t \in {\Omega ^T}}} {C_{t}^{{pv}}PV_{t}^{{pv}}+C_{t}^{{Cell}}P_{t}^{{Cell}}} +(P_{{t}}^{{bat\_ch}} - P_{{t}}^{{bat\_dis}}) \times C_{{_{t}}}^{b}$$
(13)
$$\begin{gathered} PW_{t}+PT_{t}+PV_{t}^{{PV}}+P_{t}^{{Cell}}+P_{{t}}^{{bat\_ch}} - P_{{t}}^{{bat\_dis}}+ \hfill \\ P_{t}^{{Microgrid}}=P_{t}^{{dc\_load}} \hfill \\ +P_{t}^{{ac\_load}}\,\,\forall t \in {\Omega ^T} \hfill \\ \end{gathered} $$
(14)
$${C^{total}}={C^{total\_dc}}+{C^{total\_ac}}\,$$
(15)

In order to reliably and optimally meet the AC/DC demands, the AC/DC microgrids can collaborate to create a cooperative energy framework. Also, the microgrids are capable of exchanging the surplus power with the upstream grid through the grid-connected mode. To do so, the hybrid energy structure’s generation units and loads are expressed in a power balance by Eq. (14). The output powers of all energy units that are intended to meet the AC and DC loads that are specified on the opposite hand are included in the right-hand term in this relationship. The variable \(\:{P}_{\:t\:}^{G-M}\) indicates the power exchange between the microgrids and the upstream grid. In conclusion, Eq. (15) defines the hybrid microgrid’s overall cost.

Definition of the upstream grid structure

As previously indicated, let us assume that the hybrid microgrid is intended to decrease uncertainty and is now in a grid-connected mode through the upstream grid. Therefore, it is necessary to present the basic formulation of the primary grid. It is clear that lines, loads, and fossil fuel-based generator units make up the electrical grid. In order to achieve energy-optimal scheduling, which minimizes the overall cost including the cost of starting and shutting down generators and their reactive and active power, the grid energy management must satisfy the loads (see Eq. (16)). Another responsibility for the operator to follow is maintaining all technical constraints including power generation limitations and power balance.

Therefore, the grid’s technical restrictions are introduced in equations (16) through (28). To bring about optimal power sustainability, a balanced power supply between the energy units and the load demands through lines is necessary to comply with the grid. Thus, by (21), and (22), we define the power balance here. The generation units commit to following the guidelines (17)–(18). Remember that ramping limits are constantly taken into account for generators to prevent any technical issues related to changes in load. As a result, the generator-related ramping power is restricted in (19)–(20). It goes without saying that the networking structure of the grid’s lines establishes the relationship between the generators and loads. Thus, we can understand the behavior of the grid and arrive at the best solution by modeling the flowing power of lines. Taking this into consideration, we here estimate the flowing power of lines (Eqs. (23), (24)) based on the angle difference and bus voltage that is limited by (25)–(26) and must maintain within the permitted bounds as shown in (27)–(28)34. In fact, the suggested hybrid microgrids may be helpful in reducing the grid variables through the use of power transactions in Eq. (21). This results in a notable reduction in the generators’ power as well as in the power flow and voltage values over Eqs. (23) and (24).

$${C^{grid}}=\hbox{min} \sum\limits_{t} {\sum\limits_{u} {\left[ \begin{gathered} C\left( {P_{{u,t}}^{{grid}}} \right)+U_{{u,t}}^{{grid}} \hfill \\ \_D_{{u,t}}^{{grid}} \hfill \\ \end{gathered} \right]} } $$
(16)
$$P_{u}^{{min}}{u_{u,,t}} \leqslant P_{{u,t}}^{{grid}} \leqslant P_{u}^{{max}}{u}_{{u,t}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall t \in {\Omega ^T}$$
(17)
$$Q_{u}^{{min}}{u}_{{u,t}} \leqslant Q_{{u,t}}^{{grid}} \leqslant Q_{u}^{{max}}{u}_{{u,t}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall t \in {\Omega ^T}$$
(18)
$$P_{{u,t}}^{{grid}} - P_{{u,t - 1}}^{{grid}} \leqslant R_{{grid}}^{+}{u}_{{u,t - 1}}\,\,\,\,\,\,\,\,\,\,\,\forall t \in {\Omega ^T}$$
(19)
$$P_{{u,t - 1}}^{{grid}} - P_{{u,t}}^{{grid}} \leqslant R_{{grid}}^{+}{u}_{{u,t}}\,\,\,\,\,\,\,\,\,\,\forall t \in {\Omega ^T}$$
(20)
$$\mathop \sum \limits_{{\forall u\left( n \right)}} \left( {P_{{u,t}}^{{grid}}} \right) - \mathop \sum \limits_{{\forall k\left( {n,m} \right)}} \left( {PL_{{l,t}}} \right)+P_{t}^{{Microgrid}}=Pl_{{b,t}}\,\,\,\,\,\forall t \in {\Omega ^T},\forall n \in {\Omega ^n}$$
(21)
$$\mathop \sum \limits_{{\forall u\left( n \right)}} Q_{{u,t}}^{{grid}}+\mathop \sum \limits_{{\forall k\left( {n,m} \right)}} \left( {QL_{{l,t}}} \right)=Q{l_{b,t}}\,\,\,\,\,\,\forall t \in {\Omega ^T},\forall n \in {\Omega ^n}$$
(22)
$$P{L_l}=\left( {d{V_n} - d{V_m}} \right)g{b_l} - b{g_l}{\delta _l}\,,\,\forall m \in {\Omega ^m},\forall n \in {\Omega ^n},\forall l \in {\Omega ^l}$$
(23)
$$\begin{gathered} Q{L_l}= - \left( {1+2d{V_n}} \right)b{g_{l0}} - \left( {d{V_n} - d{V_m}} \right)b{g_l} - g{b_l}{\delta _l}\,\,, \hfill \\ \forall m \in {\Omega ^m},\forall n \in {\Omega ^n},\forall l \in {\Omega ^l} \hfill \\ \end{gathered} $$
(24)
$$\delta _{l}^{{min}} \leqslant \delta _{{l,t}} \leqslant \delta _{l}^{{max}}\,\,\,\,\forall t \in {\Omega ^T},\forall l \in {\Omega ^l}$$
(25)
$$d{V_{min,n}} \leqslant dV_{{n,t}} \leqslant d{V_{max,n}}\,\,\forall t \in {\Omega ^T},\forall n \in {\Omega ^n}$$
(26)
$$ - PL_{l}^{{max}} \leqslant PL_{{l,t}} \leqslant PL_{l}^{{max}}\,\,\,\,\forall t \in {\Omega ^T},\forall l \in {\Omega ^l}$$
(27)
$$ - QL_{l}^{{max}} \leqslant QL_{{l,t}} \leqslant QL_{l}^{{max}}\,\,\forall t \in {\Omega ^T},\forall l \in {\Omega ^l}$$
(28)
Fig. 1
figure 1

The cyber energy microgrid framework.

Full size image

Cyber attack model

the most important duty in a problem to examine the various aspects of system security is modeling the cyber-attacks. The mathematical concept for stealthy cyberattacks in power systems is introduced in this part. Cyberattack models are typically developed and classified into several types, including attack trees, attack networks, and attack graphs28. The acyclic-directed graph is used to model the attack tree approach according to the network nodes. When an attack is launched in the network, the attack graph model can find solutions for hackers. The third technique, known as attack networks, is a reliable model that may mimic an attack in terms of a hacker’s malevolent choice. FDIA-type assaults classified as third-model are among the most devastating ones for the power cyber-physical systems. By altering data, a successful FDIA can have negative physical and economic repercussions on the power systems. As a result, the effects of FDIA on the power system are broadly divided into three areas: (1) The effects on the economy (2) Attacks using load redistribution (3) The deceivative onslaught of energy. For example, hackers may attack the energy transferred between two systems in an attempt to manipulate the power balancing so they can bring nefarious intentions.

To further explain the FDIA concept, let’s assume that the hacker can obtain the data by means of the pertinent system communications. In light of this, (29) designates the problem function, where X and S show the system’s data and objective function, respectively. An attacker can transform the problematic function of a system (S) into a new function (S), where the corrupted data is represented by \(\:{X}_{bad}\), as illustrated in (30). The residue norm for the fake function must be zero or exhibit a small mistake when compared to function one, as demonstrated in (31), in order for an FDIA to be successful.

$$S=h({X_t})$$
(29)
$${S_\lambda }=h({X_{bad,t}})$$
(30)
$$\left\| {{S_\lambda } - h({X_{bad,t}})} \right\|=\left\| {S - h({X_t})} \right\|$$
(31)

Additionally, a major criterion that is defined as follows can be used to verify the FDIA assessment:

$$\lambda =h({X_t}+{c_{t=\kappa }})\, - h({X_t})$$
(32)

where c is the malicious data that is injected at time , and also is defined based on the attack vector that allows the hacker to verify the necessary variation to enter a successful FDIA. The fake data is defined as follows in order to make a targeted attack:

$${X_{bad,t}}=\left\{ \begin{gathered} {X_t}+{c_t}\,\,\,\,if\,\,\,t \geqslant \kappa \hfill \\ {X_t}\,\,\,\,\,\,\,\,\,\,\,\,otherwise \hfill \\ \end{gathered} \right.$$
(34)

where the change time for introducing fake data into the system is denoted by index .

The advanced attack model

The understanding of a power system’s voltage stability is crucial for both grid operators and cyber attackers. For grid operators, preserving stability is essential to guaranteeing a consistent power supply. On the other hand, voltage stability is seen by attackers as a possible weakness that might be taken advantage of. Their goal is to do as much damage as possible with their evil deeds and as little work as possible. This means focusing on holes in the system and making sure their attacks are low-profile and economical. The microgrid systems can affect the local voltage in the upstream grid through the connection point once are operating in the grid-connected mode. Because of their complexity, such systems provide particular difficulties for voltage stability monitoring in the grid-connected mode. The conventional techniques employed in microgrids may require modifications, or new indices may need to be created. The fast voltage stability index, line stability index, and voltage stability index are a few of the widely used voltage stability monitoring indices. A dependable method for evaluating voltage stability at certain grid points, or buses, is the Voltage Stability Index. The voltage stability index takes into account the amount of power delivered into a certain bus, as demonstrated in Eq. (35) (see the original equation for mathematical details). Generally, values fall between 0 and 1, where 0 denotes a stable system and values nearer 1 indicate a higher chance of voltage breakdown.

$${I^{Stability}}=\frac{{2 \times P_{t}^{{Microgrid}} \times {X_{line}}(1+\sin {\delta _{bus,t}})}}{{V_{{bus,t}}^{2}}}$$
(35)

In order to particularly target vulnerabilities at the points of connection between the microgrid and the upstream grid, this article presents an enhanced attack model based on the false data injection in the voltage bus for the microgrids in the grid-connected mode. This attack named the false transferred data injection (FTDI) aims to manipulatively alter the power flowing from the microgrid to the upstream grid for raising voltage usability probability. Indeed, two crucial elements are involved in any power interaction between the grid and the microgrid: the amount of power and the direction of energy flow, which can either be from the grid to the microgrid or vice versa. Changes to either of these factors can significantly impact energy management. For instance, altering the direction of energy flow can disrupt the microgrid’s intended functionality and operations. Similarly, changes in power magnitude can affect the balance between supply and demand. Such shifts can lead to energy mismanagement, resource allocation errors, and even system instability, making this type of attack particularly relevant in contemporary grid systems.To influence the system and create maximum disruption while reducing the visibility of the attacker, the model makes use of the voltage stability index as a critical indicator. As demonstrated by Eq. (36), a connection point bus’s voltage stability is greatly impacted by power exchange. The aim of the proposed FTDI attack is to manipulate the amount and direction of power transfer between the microgrid and the upstream grid. Any alteration in the transferred power disrupts the power balance at the bus to which the microgrid is connected in the upstream network, leading to voltage fluctuations. These fluctuations at a single bus can propagate throughout the interconnected system, affecting the voltages of nearby buses and potentially resulting in widespread voltage instability. Instability in the power system can lead to voltage sags or surges, which negatively impacts power quality and reduces energy delivery efficiency. This fluctuation can also damage equipment. Additionally, as the interconnected system becomes more susceptible to malfunctions or outages, overall reliability decreases, particularly during periods of high demand or other critical operational conditions. To maintain system stability and ensure reliable operations, effective detection and mitigation techniques are essential. The voltage stability index is susceptible to manipulation by hostile actors, who could push its value closer to the crucial threshold of 1. The details of the advanced attack model are shown in Eqs. (36)–(38). This model takes into account the attacker’s goals as well as the microgrid’s operational behavior. The following goal is taken into consideration in the first step: 1) Eq. (37) is the main objective of the attack technique at the targeted connection point. This manipulation throws off the system’s voltage stability, which could result in blackouts and cascading failures. The associated equation for this goal is shown below.

$$F1=\hbox{max} (\frac{{2 \times P_{t}^{{Microgrid}} \times {X_{line}}(1+\sin {\delta _{bus,t}})}}{{V_{{bus,t}}^{2}}})$$
(36)

2) Reducing any discernible alterations in the system’s functioning is a crucial facet of the assault. This increases the attack’s impact by enabling the attacker to stay hidden for a longer amount of time.

$$F2=\hbox{min} (\beta \times P_{t}^{{Microgrid}})$$
(37)
$$ - \alpha \times P_{t}^{{Microgrid}} \leqslant \Delta P_{t}^{{Microgrid}} \leqslant \alpha \times P_{t}^{{Microgrid}}$$
(38)

3) Because this attack model is sophisticated, operator behavior is examined in the second stage. Here, the attacker’s manipulation of the voltage is used by the model to answer an equation. The first stage receives the consequent change in the \(\:{I}^{Stability}\). This feedback loop aids in determining the attacker’s ideal harmful alteration value.

$${\text{Solving }}\;{\text{Eqs}}.\;\;\left( {{\text{18}}} \right)$$
(39)
$${\text{Subject }}\;{\text{to}}:{\text{ Solving}}\;{\text{ Eqs}}.\;\;\left( {{{1}}0} \right) - \left( {{\text{17}}} \right)$$
(40)

This approach provides an insightful viewpoint on how attackers could take advantage of security holes in microgrids. Operators can greatly increase the system’s resilience against such targeted assaults by identifying these weaknesses and putting strong defense methods in place, such as increased cybersecurity and monitoring at connection points of the microgrid.

Proposed detection model

This section addresses the removal of the false transferred power using an attack detection model inspired by the deep learning technique. It is significant to say that the power transaction between the microgrid and the upstream grid is in the wide range of the bilateral exchange at any time. In other words, regarding the FTDI attack, not only is the value of transferred power important for the detection system, but the power direction in the microgrid. Hence, the false data detector has to simultaneously identify the changes in both the value and direction of power once the microgrid is operating in the grid-connected mode.

GAN-based detection model

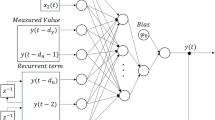
This paper provides a generative network model to identify the maliciously targeted change in the probability values, which is based on the generative adversarial network (GAN) model. The primary goal of current cybersecurity policies for microgrids is to safeguard essential infrastructure, including control systems, energy assets, and communication networks. Traditional security measures such as intrusion detection systems (IDS), Man-in-the-Middle (MITM) attacks48, firewalls, encryption, and authentication are crucial strategies in this effort. These protocols aim to protect microgrids from threats like FTDI, unauthorized access, and data manipulation. Additionally, advanced threat detection often relies on anomaly detection models, rule-based systems, and machine learning algorithms that analyze patterns of both normal and malicious network activity. However, conventional methods often struggle to identify complex threats, such as FTDI attacks, which exploit vulnerabilities in microgrid control systems. These attacks pose serious threats to the stability and security of the grid because they can alter system settings and disrupt operations without triggering conventional alarm thresholds. The proposed GAN-based framework significantly enhances these protocols by employing Generative Adversarial Networks (GANs) to learn complex patterns in both normal and attack-related data. This approach improves the framework’s ability to detect subtle anomalies indicative of FTDI attacks. During training, the GAN can generate artificial attack scenarios, which helps it generalize across a wider range of potential threats. Moreover, the framework boosts detection capabilities by identifying both known and previously unknown attack methods. It provides real-time monitoring, makes more accurate predictions, and reduces false positives. As a result, microgrid systems are better protected against evolving cyber threats due to this advanced detection capability. As was previously indicated, the microgrid may exchange its plus/needy power with the upstream grid through the connection point. Because the connection point is susceptible to cyberattacks, the GAN model is thought to provide a secure communication channel for the microgrid. In actuality, the GAN model protects the power exchange from cyberattacks that try to destabilize the voltage stability. In order to achieve this, the GAN algorithm is used to examine each power produced at each hour to identify any modifications that are prohibited. Stated differently, the GAN model uses the values of \(\:{P}_{t}^{Microgrid}\)as inputs. When the GAN algorithm yields a value of 1, it indicates that the \(\:{P}_{t}^{Microgrid}\) can be utilized in the decision-making center. If not, the GAN algorithm’s resultant value of 0 indicates that changes to the values of \(\:{P}_{t}^{Microgrid}\) are not permitted. In theory, this model consists of two primary brain components: (1) The generating part (G) and (2) The discriminator part (D). This approach is implemented using an adversarial game, where each part (G/D) can be learned by focusing on the opposing player’s answer. To be sure, the discriminator component is being checked by the noise sample that is created by the generator part. Conversely, the second part (D) moves in the direction of enhancing the learning process as soon as the fictitious data starts to deviate from the real data. Figure 2 is an illustration of the GAN structure. It is evident that the D can ascertain the input signal’s false probability within the interval of 0 to 1. The noise signal vector, G (N), takes the probability of \(\:{P}_{G}\left(N\right)\) into consideration. This signal is used in the D section to verify that the actual data \(\:{P}_{R}\left(x\right)\) is correct. Following that, in response to the checking feedback for the G/D portions, an error signal is created. During this game session. To track the D part, the G component attempts to implement the bogus data while taking into account the genuine data x. In a similar manner, this process continues until \(\:{P}_{G}\left(N\right)\) and \(\:{P}_{R}\left(x\right)\). Based on46, the loss function associated with the discriminator is computed given the parameter of D denoted by \(\:{\theta\:}^{D}\).

$$\:V\left(D,{\theta\:}^{\left(D\right)}\right)=-{E}_{x\sim{P}_{R}\left(x\right)}\left[log\:D\left(x\right)\right]-{E}_{N\sim{P}_{g}\left(N\right)}\left[\text{l}\text{o}\text{g}\left(1-D\left(G\left(N\right)\right)\right)\right]$$
(41)

Similar to D, the G portion takes into account the parameter \(\:{\theta\:}^{G}\) would accept the following relative loss24:

$$\:V\left(G,{\theta\:}^{\left(G\right)}\right)={E}_{N\sim{P}_{g}\left(N\right)}\left[\text{l}\text{o}\text{g}\left(1-D\left(G\left(N\right)\right)\right)\right]$$
(42)

Examining Eqs. (24) and (25), each component takes into account an owned objective function that needs to be optimized. In fact, if the variables of \(\:V\left(D,{\theta\:}^{\left(D\right)}\right)\), \(\:V\left(G,{\theta\:}^{\left(G\right)}\right)\:\)are minimized in order to train \(\:{\theta\:}^{\left(G\right)}\) upon receiving the fixed value for \(\:{\theta\:}^{\left(D\right)}\) and vice versa, the training process becomes essentially undefined. A new min-max function of loss is taken into consideration as follows in order to follow both of the aforementioned objective functions in the same way:

$$\:\underset{G}{\text{min}}\underset{D}{\text{max}}V\left(D,G\right)={E}_{x\sim{P}_{R}\left(x\right)}\left[log\:D\left(x\right)\right]+{E}_{N\sim{P}_{g}\left(N\right)}\left[\text{l}\text{o}\text{g}\left(1-D\left(G\left(N\right)\right)\right)\right]$$
(43)

The max operator is indicated by the first term in (26), while the min operator is shown by the second term. Once the G/D portions converge into a Nash equilibrium point, the min-max process keeps going.

Fig. 2
figure 2

Illustration of the GAN model.

Full size image

Simulation results

In this section, the authors focus on the defense strategy evaluation of microgrids against cyberattacks, particularly when operating in grid-connected mode. To do so, this paper first introduces an advanced attack model based on the FTDI concept for the microgrid. Conversely, this paper also proposes an efficient defense strategy inspired by the GAN model, aiming to detect the advanced FTDI attack in the energy synergy between the microgrid and the upstream grid. To put it in fuller terms, this strategy is able to prevent the probable voltage instability in the upstream grid that is aimed at the FTDI attack. Hence, a studied microgrid including two WT units, a PV unit, a tidal unit, a storage unit, and a fuel cell unit was performed. This microgrid is connected to a 24-bus test - IEEE system as an upstream grid. Detailed information about renewable energy units and the tested IEEE system was derived from8. It is important that the 24-bus system is a widely recognized benchmark for evaluating the behavior and performance of energy systems and is extensively used in power system research. This system serves as a realistic, scaled-down representation of actual power networks, making it effective for simulation and analysis while still retaining key features of larger systems. With its balanced complexity, the 24-bus system allows for the assessment of energy management and power flow techniques, particularly in the context of microgrids interacting with the upstream grid. Its manageable size enables meaningful reflections of real-world conditions without being overly complicated or computationally intensive. The system can be utilized to test the proposed FTDI attack and evaluate its impact on overall performance. It is capable of modeling the interactions between distributed generators, energy storage, and various control mechanisms. The data for the 24-bus system, including network topology, generation capacities, and typical load profiles, is widely accessible. This availability facilitates realistic simulations and enables the model to be validated with real-world data, increasing its credibility. Furthermore, this framework allows for a clear demonstration of the interactions between the microgrid and the main grid, providing a comprehensive analysis of how the FTDI attack affects security protocols and energy management. Considering all factors, the 24-bus IEEE grid is a practical choice for model validation. It strikes a good balance between complexity, data availability, and relevance for modeling interactions between microgrids and larger, interconnected power systems. This ensures that the model can be applied to real-world scenarios and provides a manageable platform for initial testing and refinement. In this case, the studied microgrid can transfer surplus energy itself to the upstream grid through bus 1 in grid-connected mode. Following this, the proposed advanced FTDI attack was launched in the studied case. The relative results were compared with the traditional attack model in the literature. Also, the GAN-based defense strategy was carried out in the studied microgrid under the FTDI attack, and the strategy’s effectiveness was analyzed individually. To elaborate on the proposed framework, the following case studies are provided where the first one is relevant to the analysis of microgrid performance and the other two cases will discuss cybersecurity.

Case I: The energy synergy analysis of the microgrid in connection with the upstream grid.

Case II: The advanced FTDI attack model.

Case III: The evaluation of the GAN-based defense strategy.

Case I: the energy synergy analysis of the microgrid in connection with the upstream grid

As previously indicated, the microgrid system’s central energy management uses a variety of renewable energy sources, such as fuel cells, tidal turbines, PV, WT, and energy storage units, to attempt to meet load demands hourly. Additionally, the microgrid system is connected to the upstream grid by the transformer unit for exchanging the required or surplus energy with the aim of decreasing the energy cost. However, the microgrid may operate in island mode based only on renewable energy units. Consequently, the energy resource scheduling of the microgrid would be changeable regarding the island/grid-connected modes. Indeed, the operator makes the appropriate decisions based on the load profile and the cost decrease in real-time. To keep this in mind, the microgrid’s energy management was carried out based on the technical limitations of renewable energy units under both the island and grid-connected modes. The relative results of energy management were plotted in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19. Figure 3 illustrates the load demands satisfied by the microgrid for 24 h. The storage unit is used to control the generation ramp related to the renewable energy units, the outputs of which are uncertain due to the unpredictable input parameters. The operator can choose the charging and discharging statuses for the storage unit according to their needs. Hence, Figs. 4 and 5 show the charging and discharging powers of the storage units in island mode for a 24-hour horizon. As can be seen, the storage unit was arrested in the discharge status in hours 1 to 5 and 19 to 21 because the power output of the PV unit was 0 at the same time. Also, the storage unit was often in the charging status for hours 8 to 17, in which most generation units were online. The power scheduling of the fuel cell unit in the microgrid’s energy management was plotted in Fig. 6. Looking over this figure, when the generated power was decreased by the WT and PV units owing to the lack of wind speed and solar radiation, the required power was covered by the fuel cell unit in hours 1 to 5, 16–24. Given the weather conditions, the PV and WT units could generate the required power in only hours 6 to 15, as shown in Figs. (7) and (8). The tidal turbine unit generates output power based on the water’s current speed, which is limited most of the time. On the basis of this, the operator could utilize the tidal turbine unit to generate the required power when energy management was particularly problematic for satisfying the microgrid load. Figure 9 shows the power output of the tidal turbine unit during a 24-hour horizon. The contribution of power generated by renewable energy units once the microgrid is in island mode is plotted in Fig. 10. As can be seen, the fuel cell unit contributed 43% of the total generated power due to the high capacity of hydrogen and its availability most of the time. The microgrid operation in the grid-connected mode is different from the other mode because of the transformer unit. So to speak, the microgrid in this mode is capable of utilizing the surplus power capacity of the upstream grid to facilitate load satisfaction in low-cost conditions. In light of this fact, the energy scheduling of the microgrid was performed in grid-connected mode, and the relative results are plotted in Figs. 11, 12, 13, 14, 15, 16, 17, 18 and 19.

Fig. 3
figure 3

Microgrid load.

Full size image
Fig. 4
figure 4

The charging status of battery in the island mode.

Full size image
Fig. 5
figure 5

The discharging status of battery in the island mode.

Full size image
Fig. 6
figure 6

The output of fuel cell in the island mode.

Full size image
Fig. 7
figure 7

The output of PV in the island mode.

Full size image
Fig. 8
figure 8

The output of WT in the island mode.

Full size image
Fig. 9
figure 9

The output of tidal turbine in the island mode.

Full size image
Fig. 10
figure 10

The microgrid contribution in the island mode.

Full size image

Figures 11 and 12 demonstrate the charging and discharging statuses of the storage unit in grid-connected mode. The number of charge states took a markable decrease of 12 to 9 compared to mode one. Also, the discharge power of storage units was 24 kW on average for a 24-hour horizon, while it was 34.5 kW in island mode. This means that the power ramp of renewable energy units has decreased due to the power received from the upstream grid. On the other hand, the power generation of PV, WT, and tidal turbine units took an ascending range of 3%, 3%, and 4% compared to the island mode. Figures 13, 14 and 15 indicate the power output of PV, WT, and tidal turbine units in the grid-connected mode. As can be seen in Fig. 16, the contribution of the fuel cell unit to the balancing load has decreased from 43 to 18% due to the use of the transformer unit during load peak time.

Fig. 11
figure 11

The charging status of battery in the grid-connected mode.

Full size image
Fig. 12
figure 12

The discharging status of battery in the grid-connected mode.

Full size image
Fig. 13
figure 13

The output of PV in the grid-connected mode.

Full size image
Fig. 14
figure 14

the output of tidal turbine in the grid-connected mode.

Full size image
Fig. 15
figure 15

The output of WT in the grid-connected mode.

Full size image
Fig. 16
figure 16

The output of fuel cell in the grid-connected mode.

Full size image
Fig. 17
figure 17

The output of grid energy exchange.

Full size image
Fig. 18
figure 18

The microgrid contribution in the grid-connected mode.

Full size image

Based on Figs. 17 and 18, the power exchange contributed 21.6% of the total load when the microgrid was in the grid-connected mode. All in all, the operator tried to use the energy capacity of the fuel cell unit in the island mode to optimally balance the load demand. While, in the grid-connected mode, the operator has injected the surplus generations into the upstream grid with the use of increasing the output power related to the renewable energy units. The comparative result of the microgrid in both the island and grid-connected modes was plotted in Fig. 19.

Fig. 19
figure 19

The compare resutls in the grid-connected/island modes.

Full size image

Case II: the advanced FTDI attack model

In this paper, a unique advanced FTDI attack that targets a hybrid microgrid, in particular, is proposed. Because of their intrinsic complexity, these hybrid systems are more susceptible to cyberattacks. The connection point between the microgrid and the upstream grid is the main target of the suggested attack, which takes advantage of this weakness. It is worth to say that the 24-bus IEEE system was chosen as the model for the upstream grid due to its relevance and effectiveness in simulating the interaction between a microgrid and the larger grid. A microgrid can operate in either islanded mode or grid-connected mode, as illustrated in Figs. 19 and 20. This dual mode of operation directly influences the energy management of the microgrid. The upstream grid plays a significant role in determining the generation capacity, power flow, and operational status of the microgrid’s distributed resources, making its presence essential for formulating the microgrid’s energy management strategy. The connection point of the microgrid to the upstream grid—specifically, the bus it connects to—significantly affects the flow of electricity between the two systems. The balance at specific buses in the 24-bus system greatly influences how power is delivered from the microgrid to the upstream grid and vice versa. Variations in load and generation at each bus can alter the direction and magnitude of power flows, impacting the microgrid’s energy management efficiency and its vulnerability to potential attacks. Additionally, the placement of the buses plays a crucial role in determining the microgrid’s level of susceptibility to possible threats. This is particularly important in light of the proposed FTDI attack, as understanding the structure of the 24-bus system is key to comprehending the effects of power transfers between the grid and the microgrid.To effectively detect and mitigate hazards arising from the interactions between the grid and microgrid, the proposed detection framework must account for variations in power transfer at different connection points. The 24-bus system provides a controlled environment for simulating and testing these interactions, ensuring that the detection framework is scalable and resilient in real-world applications. The assault method manipulates exchange power to cause disruptions in voltage stability within the upstream grid. By taking into account the defined index \(\:{I}^{Stability}\), the attack’s effectiveness was evaluated in Fig. 20. Compared to normal operation, the accelerated FTDI attack significantly increased\(\:{I}^{Stability}\) by 50.7% on average, as shown in Fig. 20. This means that, in the advanced attack scenario, there will be a far higher level of voltage instability. On the other hand, the typical attack had very little effect on \(\:{I}^{Stability}\), increasing by a total of only 25.29% in a 24-hour period.

Fig. 20
figure 20

the compare resutls of the attack models.

Full size image

Case III: the evaluation of the GAN-based defense strategy

The microgrid would be vulnerable to cyberattacks through the connection point with the upstream grid. As shown in the previous section, the FTDI attack could affect the voltage stability of the upstream grid In a high-risk area with the use of altering the transferred power within the microgrid. To overcome this problem, the GAN-based detection model is able to identify the false data in the energy scheduling of the microgrid which is generated for any reason. By doing so, the verification of the detection model under the FTDI attacks is necessary from the viewpoint of the cyberattack. To this end, the confusion matrix tabulates the discrepancies between the forecasts and the actual ground truth to categorize the model’s predictions into four outcomes:

True positives (TP)

Situations where the model correctly predicts a positive class (Hit Rate).

True negatives (TN)

When a negative class is accurately predicted by the model, these are known as TN (C.R. Rate).

False positives (FP)

Situations in which the model predicts a positive class but makes a (F.A. Rate).

False negatives (FN)

Situations where the model predicts a negative class incorrectly (Miss Rate).

This matrix can be used to produce a number of performance metrics that show how successfully the model identifies cyberattacks. Accuracy, precision, recall (sensitivity), specificity, F1-score, and other metrics are among them. Hence, the detection model was performed on the energy scheduling of the microgrid and provided the results related to the confusion matrix in Figs. 21 and 22. As previously stated, the GAN technique uses a generator that aims to deceive the discriminator network by generating false data, and a discriminator that filters out samples that are disqualified, leaving valid samples for more precise attack detection. The output value of the discriminator system in relation to the dataset (real and false) is displayed in Fig. 21. This figure demonstrates how the discriminator network in the GAN technique may most likely identify genuine data. After 500 episodes, the Hit rate, C.R. rate, F.A. rate, and Miss rate took 0.95%, 0.92%, 0.7%, and 10%, respectively. As can be seen in Fig. 22, how accurate and efficient this method is.

Fig. 21
figure 21

the data sample for discriminator part.

Full size image
Fig. 22
figure 22

the compare resutls of the attack models.

Full size image

Conclusions

The current paper explored the vulnerability area of microgrid systems from the viewpoint of cybersecurity, especially once operating in grid-connected mode. Indeed, an attacker can cybernetically affect the energy scheduling of the upstream grid through the change in the power transferred from the microgrid. Hence, this paper introduced an advanced attack model developed on the false transferred data injection (FTDI) attack for microgrid systems in the grid-connected mode. In other words, to increase the likelihood that the voltage would be unstable, the false transferred data injection, or FTDI, attempts to artificially change the power coming from the microgrid to the upstream grid. Conversely, this paper also proposed a learning detection model inspired by the GAN approach to cope with the FTDI attack on the microgrid. To clarify the effectiveness of the proposed framework, a microgrid, considering the various renewable energy units along with the 24-bus IEEE system as the upstream grid was implemented in GAMS and MATLAB software. the results indicated that the fuel cell unit contributed more rage 43% of energy scheduling in the microgrid in the island mode. While the microgrid had a markable energy exchanging contribution of 21% in the grid-connected mode. This means that the transferred power can considerably affect the energy management of microgrid systems. In this way, the FTDI attack was carried out in the microgrid. On the basis of comparative results, the average rise in the accelerated FTDI attack was 50.7% higher than that of regular operations. This indicates that there would be much more voltage instability in the advanced attack scenario. Conversely, the average attack had only a negligible impact, rising by a total of 25.29%. Additionally, the proposed detection model was evaluated on 500 trials, and the relative results were calculated based on the confusion matrix. The detection model could obtain an average range of 94% for true decisions and 8.5% for false decisions. This proves the effectiveness of the detection strategy against the FTDI attack for microgrids. As future work, enhancing the grid’s performance after an attack requires advancements in algorithms, including more robust fault detection systems, real-time decision-making capabilities, and better integration of security protocols to mitigate the impact of future attacks.