A deep learning-driven multi-layered steganographic approach for enhanced data security

Abstract

In the digital era, ensuring data integrity, authenticity, and confidentiality is critical amid growing interconnectivity and evolving security threats. This paper addresses key limitations of traditional steganographic methods, such as limited payload capacity, susceptibility to detection, and lack of robustness against attacks. A novel multi-layered steganographic framework is proposed, integrating Huffman coding, Least Significant Bit (LSB) embedding, and a deep learning-based encoder–decoder to enhance imperceptibility, robustness, and security. Huffman coding compresses data and obfuscates statistical patterns, enabling efficient embedding within cover images. At the same time, the deep learning encoder adds layer of protection by concealing an image within another. Extensive evaluations using benchmark datasets, including Tiny ImageNet, COCO, and CelebA, demonstrate the approach’s superior performance. Key contributions include achieving high visual fidelity with Structural Similarity Index Metrics (SSIM) consistently above 99%, robust data recovery with text recovery accuracy reaching 100% under standard conditions, and enhanced resistance to common attacks such as noise and compression. The proposed framework significantly improves robustness, security, and computational efficiency compared to traditional methods. By balancing imperceptibility and resilience, this paper advances secure communication and digital rights management, addressing modern challenges in data hiding through an innovative combination of compression, adaptive embedding, and deep learning techniques.

Introduction

The digital world is experiencing rapid and exponential growth, necessitating secure communication as an indispensable requirement for safeguarding data from potential intrusions^1,2,3. Therefore, various technological methods have been suggested to address this concern, including cryptography, steganography, and Watermarking. Each approach has distinct advantages and limitations⁴. Cryptography is a method that utilizes encryption to ensure the security of data in transit, with its primary focus being on the confidentiality, integrity, and accessibility of the information. Steganography is a method to hide information within other media, such as images, video, audio, or text. Watermarking, as a specialized application of steganography, categorizes and safeguards the content of copyrighted media⁵. Nonetheless, Steganography possesses a distinctive benefit over Cryptography and Watermarking^6,7. Specifically, after data embedding, the media used for Steganography ostensibly remains identical to the original or cover media where the data is concealed⁸.

Recently, Deep Learning (DL) has emerged as a promising approach in steganography, offering novel methods for concealing and extracting information that is more resistant to detection⁹. Techniques such as Convolutional Neural Networks (CNNs), Generative Adversarial Networks (GANs), autoencoders, and other DL models have been utilized to develop steganographic systems that exhibit robustness against steganalysis^9,10,11,12, A detailed recent related works are presented in section “Related work”. As steganography advances, integrating DL techniques is expected to play a pivotal role in its future development. However, the key challenge lies in designing systems that demonstrate robustness to detection and exhibit efficiency and practicality for real-world applications. Despite these numerous steps forward in steganography, many challenges still exist with current approaches. There is, for example, one significant limitation regarding the payload capacity-security trade-off. Methods like LSB steganography are very simple and easy to implement but tend to be quite weak against steganalysis due to the relatively high level of modifications they introduce into the cover medium. While more sophisticated techniques-most of those falling into the category of deep learning methods-give higher security, they come with the following increase in computational complexity and are often prone to overfitting. Another significant problem is the limited capacity of many traditional methods, which restricts how much data can be hidden without significantly distorting the cover image. Besides, most current approaches cannot efficiently balance the imperceptibility of hidden data against their robustness to sustain possible attacks or modifications during transmission. The motivation for this paper is an attempt to bridge such gaps found in earlier research through the development of a new multilayered steganographic scheme that will be able to incorporate strengths from lossless compression, specifically Huffman encoding; efficient data embedding via LSB, and deep learning for robust security.

Traditional steganographic methods, such as LSB embedding, have long been used for data hiding due to their simplicity and ease of implementation. However, these approaches are inherently limited in several critical aspects, including payload capacity, robustness against attacks, and imperceptibility^13,14. LSB embedding, for example, is highly susceptible to steganalysis techniques and environmental distortions such as noise and compression, making it less reliable in scenarios requiring of levels security. DL integration introduces significant advancements in steganographic systems to address these challenges¹⁵. Deep learning models, such as encoder–decoder architectures and CNNs, provide adaptive capabilities that enhance the robustness of the embedded data. Unlike traditional methods that statically embed data, DL techniques dynamically adapt to the statistical properties of the cover medium, effectively mimicking its features. This adaptability ensures that the hidden data remains indistinguishable from the original, thus reducing detectability and increasing resilience against attacks. Furthermore, deep learning enables a superior balance between payload capacity and security. Traditional methods often compromise image quality when increasing the payload, whereas DL-based systems optimize embedding efficiency while maintaining high visual fidelity.

This paper proposes a multi-layered steganographic framework that combines Huffman coding, Least Significant Bit (LSB) embedding, and a deep learning-based encoder–decoder. While Huffman coding is traditionally utilized for its compression capabilities, its inclusion in our method serves a dual purpose. Beyond optimizing the size of the embedded payload, Huffman coding plays a critical role in enhancing security by obfuscating statistical patterns within the data. This added layer of randomness increases the robustness of the embedded information, making it less detectable by steganalysis techniques that rely on predictable data structures. The integration of Huffman coding aligns with our strategy to create a secure and invisible steganographic system. By introducing a preprocessing step that evaluates the feasibility of compression for small payloads, we ensure that Huffman coding is selectively applied, minimizing potential overhead while preserving its contribution to security. This approach demonstrates the complementary role of Huffman coding in the overall framework, emphasizing its significance beyond simple data compression. The novelty of the proposed method lies in its multi-layered approach, which integrates Huffman coding, LSB steganography, and a deep learning-based encoder–decoder. This combination enhances robustness and adaptability to diverse attack scenarios while maintaining imperceptibility. Unlike traditional single-layer methods, this hybrid framework introduces unique redundancy and statistical mimicry mechanisms to protect the hidden data effectively. The proposed approach strikes a balance between optimizing the security and capacity of steganographic systems without deteriorating the visual quality of the cover images. In proposing solutions for both challenges, the research enormously boosts steganography toward securing robust, efficient, and scalable solutions for various modern data-hiding challenges. The contributions of this paper can be summarized as follows:

• 1. Innovative multi-layered framework: The method integrates Huffman coding, LSB steganography, and a deep learning-based encoder–decoder to enhance data security and storage efficiency. By combining these techniques, the framework ensures the high imperceptibility of cover images while improving robustness against steganalysis and various attack scenarios.

• 2. Adaptive and robust data embedding: The deep learning-driven hiding network adaptively embeds secret information into cover images, closely mimicking their statistical properties. This significantly improves resistance to detection techniques, ensuring data robustness against noise, compression attacks, and statistical analyses.

• 3. Enhanced security through dual-layer obfuscation: The method leverages Huffman coding for compression and as an additional layer of obfuscation by introducing statistical randomness in the data payload. This dual-layered approach significantly increases the resistance to unauthorized access and detection, making it highly suitable for secure communication and digital rights management applications.

The remaining paper’s structure is as follows: section “Related work” presents a review of recent related works in the field. section “Methodology” provides a detailed explanation of the methodology employed. Section “Experiments” outlines the experimental setup. Section “Results and discussion” presents and discusses the obtained results. Finally, section “Conclusion and future work” concludes the paper and highlights the potential for future research.

Related work

The term Steganography constructs from two Greek words, namely: steganos signifying “covered,” and graphein, which means “to write”. Essentially, it is the art and science of concealing information within other information, typically done so that the hidden information’s presence is not apparent. This technique is a potent method for covert communication, ensuring that the message’s existence is known only to the intended recipient¹⁶. The term of Steganalysis serves as a countermeasure to steganography, with its primary objective being detecting concealed information and potentially disrupting confidential communication¹⁷. Furthermore, several techniques for Steganography can be categorized based on two main categories, namely: (i) digital steganography and (ii) linguistic steganography, as depicted in Fig. 1.

Fig. 1

Taxonomy of steganography.

Digital steganography leverages the characteristics of digital artifacts to disguise information. The first category, technical steganography, involves selecting a cover medium, which could be an image, text, video, audio file, or protocol. Subsequently, method-based steganography, a specific algorithm or approach, is chosen to conceal the information within the selected cover medium. The most common method-based steganography is the statistical method, a data-hiding technique employs statistical methods to conceal information within digital objects¹⁸. Several algorithms are utilized within this technique, including the Least Significant Bit (LSB) method, which manipulates the slightest bit in a byte to hide data. Similarly, Pixel-Value Differencing (PVD) uses the difference between pixel values, while Edge Map Data embedding (EMD) leverages the edges in an image for data concealment. Pixel Intensity (PI) methodology incorporates data in the intensity of the pixels, while the General Linear Model (GLM) utilizes linear relationships between variables to hide data. In addition, Quantization Index Modulation (QIM), a statistical steganography method, utilizes the index of a quantizer to entrench secret data into a cover signal^19,20.

In addition, with the increased progression in Artificial Intelligence (AI) over the past few years, machine learning (ML) and DL techniques have been incorporated into steganography methods. These techniques build upon learning models for the revelation of data hiding that is both efficient and secure. Some of the DL models used in steganography include GANs since they can generate new instances similar to the training set. Moreover, CNNs are used, as it is known that they are suitable for image processing and, therefore, it is possible to embed data into images. Finally, autoencoders are employed, and though they also learn data encoding unsupervised, they add to the repository of resources available in modern steganography. Also, the Quantum images method can be considered a new advancement within the steganography field, where quantum information is hidden in the images. This technique uses the standards of quantum mechanics that make it possible to enhance the level of protection in the concealment of information; it has the trends towards the progressive development of steganography in the future^21,22.

In contrast, linguistic steganography refers only to concealing the data at a linguistic level, within text or speech. For such categories of messages, this method of secret communication can be regarded as one of the oldest. It is broadly classified into two primary categories: semagrams and open codes. Semagrams, however, are a bit different from gliomas in their construction. Although they can be in the form of language, they are often graphics/ icons used to pass messages that do not require using alphabets or numerals. They are categorized as²³:

• Visual semagrams: These include graphics, symbols, or pictographs that convey specific meanings or messages, such as road signs or symbols on maps.

• Textual semagrams: These involve arrangements of words or letters that convey a hidden message. A prime example is an acrostic, where the initial letter of each line spells out a concealed word or phrase.

Open codes refer to messages that, on the surface, seem like standard communications but contain concealed meanings. One such method within open codes is the “Jargon Code,” which employs specific terminology or slang understood exclusively by a particular group, rendering the message cryptic to outsiders. On a different note, there are covered ciphers that use more obfuscated methods to conceal messages. The “Null Cipher” is a prime example, where the genuine message is embedded within a broader, seemingly harmless text. Another intriguing method in this category is the Grille Cipher, a technique for encrypting plaintext by writing it onto a sheet of paper through a pierced sheet, thus obscuring the original message uniquely and ingeniously^24,25. A novel methodology has been introduced in steganography using images, leveraging a deep convolutional autoencoder architecture that is both lightweight and effective. This architecture serves a dual purpose: a long-shrouded image is embedded into the cover image and excavated by a secret key from the secret image. The proposed methodology was evaluated using three distinct datasets: COCO, CelebA, and ImageNet, which are typical for benchmarking purposes. We used the peak signal-to-noise ratio (PSNR) ratio, which was accurately evaluated on the test data. As a result, the proposed method has a higher capacity for hiding information, better security robustness, and overall better performance than other learning methods²⁶. Besides that, a novel encoder–decoder architecture has been proposed based on CNNs. This architecture is designed to hide one image inside another and significantly increases both the capacity of the payload and the quality of the images. To that end, the researchers provided a new loss function capable of training the encoder–decoder network in a by-end EF manner with a high level of success across several diverse datasets, including but not limited to MNIST, CIFAR10, PASCAL-VOC12, and ImageNet. Their method proved to deliver State-Of-The-Art (SOTA) results in terms of payload capacity where in addition to having a high PSNR, an SSIM was also calculated and proved a significant improvement in the traditional methods that required manual creation of features for steganography²⁷.

In addition, a novel steganographic technique known as Adversarial Embedding (ADV-EMB) was proposed to work against machine learning-based steganalytic models, especially those based on CNNs. The ADV-EMB approach selectively replaces and rearranges image elements according to gradients derived from a target CNN step analyzer. This method hides the secret message and simultaneously gives way to deceive steganalysis algorithms by producing what they call ‘adversarial secret images’. Their experiments demonstrated that this technique could effectively deteriorate adversary-unaware and adversary-aware steganalysis performance, proposing a new paradigm in modern steganographic practices that can overcome powerful steganalysis attacks²⁸. In the study by Wu et al.²⁹, a deep CNN, which they dubbed ‘StegNet,’ is proposed and constitutes a leap forward in image steganography. Numerous NTFS methods focus comparatively on invisibility, and less has been affectionately considered for data throughput. But, StegNet is used to achieve an outstanding data decoding rate of 98.2% and a Bits Per Pixel (bpp) rate of 23.57, while only modifying the average cover image by the amount of 0.76% By exposing the mapping between cover and hidden images to learning through the entire process, this approach reveals a high level of robustness in regards to steganalysis. While the study in²⁹ offers a StegNet model based on a deep convolutional neural network approach, which focuses heavily on undetectability with less consideration for payload capacity, StegNet integrates recent DL techniques to achieve an exceptionally high decoding rate of 98.2% and a bits per pixel (bpp) rate of 23.57, while only modifying 0.76% of the cover image on average. the StegNet model is a learned map between the cover and embedded images from end-to-end that highlights its ability to remain undetectable by steganalysis.

At the same time, the latest developments in image steganography have been marked by integrating GANs for improved secrecy and robustness. Liu et al.³⁰ concentrate on numerous GAN strategies for image steganography, including cover alteration, selection, and creation. They exploit the Gans’s adversarial property to create segno images, which are more efficient against steganalysis. For instance, synthetic methods based on GANs have proved their effectiveness in generating imperceptible segno images with hidden messages inside them, which results in the maximal clandestine level of steganographic practices. The other approach was based on GANs, which enhanced the quality and capacity of steganography containing images without changing the cover image. Contrary to stealthy steganography techniques, alterations to the cover image are typically carried out, which can be identified by steganalysis tools. Their model capacity has a hidden payload of 2.36 bits per pixel, circumvents detection defences, and advances the steganography sector³¹. Further, Channel Attention Image Steganography With Generative Adversarial Networks introduces a channel attention mechanism within a GAN framework, dynamically adjusting embedding priorities based on attention weights and ensuring that modifications mimic natural image distributions to improve detection resistance. Together, these studies underscore the importance of adaptive techniques, channel-specific optimization, and deep learning frameworks in advancing the robustness and efficacy of image steganography systems³². Moreover, a novel steganographic algorithm using CycleGAN combines image-to-image translation with a steganalysis module to enhance the anti-detection ability of secret images. The approach leverages cycle consistency to preserve image quality while embedding secret data, demonstrating improved performance in resisting steganalysis and maintaining imperceptibility in IoT applications³³.

A new technique for character-level text image steganography based on adversarial attacks has been proposed to enhance secret information transmission security. This technique utilizes neural networks’ unique boundaries to embed coded information in the character regions of images, so the OCR software can’t detect it. The methodology involves the creation of adversarial examples that are recognizable by the intended local OCR model as a guarding mechanism against deciphering the embedded data with the help of unintended recipients. They obtained a high embedding success rate and, at the same time, retained the original appearance of text images by improving the adversarial sample generation process and introducing a validation model that ensured the low transferability of these samples³⁴. Further, a new model where Arabic text can be hidden with DL techniques was developed. This model of concealment of information through Arabic poems relied on a database of Arabic poetic pieces. It is based on LSTM networks and Baudot Code algorithm strategies that are used to raise the capacity level and enhance the linguistic accuracy of the embedded data³⁵. Furthermore, recent advancements in image steganography have significantly improved payload distribution strategies and detection resistance through adaptive and deep learning-based methods. Adaptive Payload Distribution in Multiple Images Steganography Based on Image Texture Features leverages image texture complexity to allocate higher payloads to regions with greater embedding capacities, thereby minimizing statistical anomalies and enhancing security³⁶. Similarly, A New Payload Partition Strategy in Color Image Steganography optimizes payload allocation across RGB channels by considering their distinct characteristics, achieving a balance that enhances imperceptibility and embedding efficiency³⁷.

Table 1 presents a comprehensive comparison of recent studies in steganography, highlighting their techniques, key features, advantages, and limitations to provide a clear understanding of the advancements and challenges in the field.

Table 1 Comparison of related works.

These inventions mentioned in this section provide the basis for transformation in the image steganography fostered by DL. These developments not only increase the stealth and capacity of steganographic systems but also offer new safeguards against improving techniques in steganalysis. The steady growth of new neural networks and challenging techniques for steganography indicate an excellent research opportunity and a promising future for progress in the security and outcomes of steganography activities.

Methodology

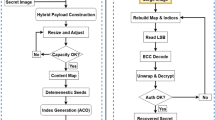
This section outlines the general approach, which combines Huffman coding and image steganography and is improved with a DL-based encoder–decoder. The encoder algorithm processes the cover and secret images through a deep learning-based hiding network. The hiding network extracts feature representations from the secret image and adaptively embeds these features into the cover image, ensuring that the resulting container image retains visual imperceptibility while securely embedding the secret data. This process minimizes detectable artifacts and enhances the robustness of the proposed method against steganalysis. The context diagram of the multi-layered steganographic approach is under consideration in Fig. 2.

Fig. 2

Framework of the proposed steganographic method.

The methodology is detailed through two primary algorithms: (i) Encode Algorithm and (ii) Decode Algorithm. The Encode Algorithm converts the textual data in Huffman coded format. It incorporates it with LSB-steganography, and ultimately, the container image is the output of the DL encoded image from the cover image. Conversely, the Decode Algorithm reverses this process, methodically extracting and reconstructing the hidden textual data from the container image. This dual-layer approach significantly enhances the complexity and security of the information-hiding process with an additional layer of steganography. However, it is significant to acknowledge that each layer of steganography may slightly degrade the quality of the hidden information due to cumulative effects, necessitating careful consideration of the trade-offs involved.

Huffman-encoded

Huffman encoding is a data compression technique without any loss, which gives shorter codes to data that appear more often and more extended codes to less common data. This method employs a code table with variable lengths, determined by the occurrence frequency of each piece of data, such as text characters, to represent information^38,39. Furthermore, the proposed approach utilizes Huffman Encoding in steganography due to the following benefits^40,41:

• Compression: Huffman encoding allows data compression without sacrificing information. When used in steganography, it can help fit more hidden data within the cover medium.

• Obscurity: The variable-length codes generated by Huffman encoding can make the hidden data more challenging, especially if the steganographic method is combined with other encryption or obfuscation techniques.

• Efficiency: Data encoded using Huffman requires less space, optimizing the utilization of the cover medium for steganographic purposes.

• Adaptability: Huffman encoding can be tailored to the hidden data, allowing flexibility across different steganographic methods.

Figure 3 showcases the Huffman tree corresponding to the phrase “Hello World”. The character frequencies are computed as follows: {H: 1, e: 1, l: 3, o: 2, Space: 1, W: 1, r: 1, d: 1}. The Huffman Tree is constructed based on these frequencies, from which binary codes for each character are derived. Notably, characters that appear with higher frequency, such as ‘l’ in this instance, are assigned shorter binary codes.

Huffman encoding, a lossless compression technique, balances efficiency and security better than alternatives like RLE, LZW, and Arithmetic coding. Unlike RLE, which is limited to repetitive data, and LZW, which can introduce detectable redundancies, Huffman encoding adapts to data frequency with variable-length coding. While Arithmetic coding achieves better compression, its computational intensity makes Huffman encoding a more resource-efficient choice for steganographic applications. Huffman encoding enhances steganography by compressing data to minimize cover medium modifications, maintaining imperceptibility and high image fidelity. Its adaptive nature complements LSB’s nonadaptive approach, enabling higher payload capacity with minimal distortion. Unlike fixed-length compression methods, Huffman encoding reduces space requirements and avoids detectable patterns, making hidden data harder to detect.

Fig. 3

Huffman tree for “Hello world”.

In the proposed multi-layered steganographic approach, Huffman coding is the first step in preparing the data for embedding. While Huffman coding is traditionally celebrated for its compression efficiency with large datasets, its inclusion in our method serves a dual purpose: (1) optimizing the size of the embedded data when possible and (2) enhancing the robustness and security of the steganographic framework by obfuscating statistical patterns in the payload.

For small payloads, such as a watermark or secret information, the compression effect of Huffman coding may be limited or negligible due to the relatively high overhead of encoding the Huffman dictionary. To mitigate this, the proposed framework implements the following strategies:

• Selective application: Huffman coding is applied selectively based on the variability and redundancy in the data. If the data volume is insufficient to achieve meaningful compression, the coding step is bypassed to avoid increasing the data size unnecessarily.

• Optimized dictionary encoding: When Huffman coding is applied, the encoding dictionary is compactly represented and embedded alongside the compressed payload. Special care ensures that the dictionary’s size remains proportional to the payload, minimizing additional overhead.

• Security enhancement: Regardless of compression efficiency, Huffman coding introduces variability into the payload by assigning unique binary codes to different symbols. This obfuscates the statistical patterns in the data, making it more resistant to steganalysis techniques that rely on detecting predictable structures in the embedded information.

To ensure the balance between compression and overhead, the proposed framework incorporates a preprocessing step that evaluates the entropy of the payload before applying Huffman coding. This evaluation determines whether compression will result in a net reduction in size. If the estimated overhead exceeds the potential gains, Huffman coding is omitted for that particular payload, and the raw data is embedded instead. This adaptive strategy ensures that Huffman coding is used judiciously, preserving the efficiency of the steganographic system. Huffman coding is integral to the multi-layered steganographic approach, complementing the LSB embedding and deep learning encoder–decoder layers. Huffman coding enhances the system’s robustness by compressing and obfuscating the payload before embedding. Additionally, its integration ensures that the subsequent layers-LSB embedding and the deep learning model-can focus on maintaining imperceptibility and resistance to attacks without being constrained by payload size. This dual-purpose utilization of Huffman coding demonstrates its role as a preparatory step and a security-enhancing mechanism in the proposed framework. While its compression efficiency for small payloads may vary, its contribution to robustness and undetectability justifies its inclusion.

LSB algorithm

For example, we use the LSB method to hide the message “HELLO” in an image. This involves a detailed process of modifying the RGB (Red, Green, Blue) channels of the image pixels⁴². The steps we will take are as follows:

• 1. Message conversion: In this stage, we convert the message to binary format; Table 2 presents the details for the example.

• 2. Image selection: Choosing the cover image format to hide the message is very important. The image can be in different formats such as BMP, PNG, or JPEG, but formats such as BMP or PNG are preferred due to their lossless nature, while JPEG images can introduce compression artifacts that might disrupt the hidden message. Furthermore, any image comprises tiny units called pixels. Most digital images use the RGB model, which gives each pixel three colors: red, green, and blue⁴³.

• 3. Embedding: Replace the least significant bit of each pixel color component with a bit from the secret message. This step is repeated until the entire message is embedded within the image⁴⁴. Figure 4 illustrates the example of ‘H’ embedded in the cover image. The message is embedded sequentially across the RGB channels of the image’s pixels. Depending on the message’s length and the image’s resolution, it might only take a small portion of the image to store the entire message. However, altering the LSB of a pixel’s color value minimizes the color, making the change nearly invisible to the human eye⁴⁵.

• 4. Reconstruction: This step is significant in finalizing the steganography process and generating the secret image. After modifying the LSB of the RGB values of each pixel, these modified binary values must be converted back into their decimal form. This conversion is necessary because the image format standards and viewing software interpret the pixel colour data in decimal form (ranging from 0 to 255). Once all the essential pixels have been updated with the new RGB values, the image is reassembled⁴⁶.

Table 2 Binary format of ‘HELLO’.

Fig. 4

Embedding the “H” into the LSB.

The process of extracting the message is reversed. The LSBs of the RGB values are collected in sequence, converted back from binary to decimal, and then mapped to their corresponding ASCII characters to reveal the hidden message^{42,43,44,45,46}.

Encoder and decoder

The Encode Algorithm, as illustrated in Algorithm 1, begins by sourcing content from a given text file, forming the foundational data for concealment. Initially, the algorithm calculates the frequency of characters within the input text to generate a Huffman dictionary dynamically. This dictionary encodes the textual data, and the dictionary itself is transformed into a binary string. Combined with a unique delimiter and Huffman-encoded binary text, this string is prepared for embedding using the LSB steganographic technique. The result is a secret image that appears identical to the untrained eye but contains a concealed message. This image is then processed by a pre-trained DL encoder, resulting in the container image, where the original image and concealed data coexist seamlessly.

Algorithm 1

Encoder algorithm.

The neural network architecture used in the Encode and Decode Algorithms of the Deep Steganography model was developed by Baluja in 2017⁴⁷, as shown in Fig. 5. This model utilizes a sophisticated layer-based approach as follows:

• InputLayer: Handles the initial image data input.

• PrepLayer: Prepares the secret image by enhancing features essential for robust encoding.

• HideLayer: Combines the prepared secret image and the cover image to produce a container image with minimal perceptible changes.

• RevealLayer: This layer in the decoding process retrieves the secret from the container image, ensuring the recovery of the original data with high fidelity.

Fig. 5

Encoder and decoder layers architecture (View image online).

On the other hand, the Decode Algorithm begins with the container image, the intricately crafted product of the Encode Algorithm, as shown in Algorithm 2. Leveraging a trained DL decoder, the initial step is to extract the previously embedded steganographic image from the container image. While this intermediate image appears almost identical to its original version, it secretly harbors the Huffman-encoded textual data. The concealed Huffman codes are meticulously unearthed from the image by reversing the LSB steganographic technique. Recognizing a distinct delimiter allows the binary string to be bifurcated into the Huffman dictionary and the Huffman-encoded segments. Whether traversing the previously established Huffman tree or harnessing an embedded or shared Huffman code map, the original textual content is reconstituted with fidelity. The Decode Algorithm’s zenith is marked by accurately extracting the pristine text, validating its integrity and authenticity.

Algorithm 2

Decoder algorithm.

The two layers of steganography in the proposed method are designed to work synergistically, each contributing distinct advantages to enhance the overall robustness and security of the system. The first layer combines Huffman coding with LSB embedding. Huffman coding provides lossless data compression, reducing the payload size and obfuscating statistical patterns in the data. At the same time, LSB embedding integrates the encoded data into a cover image with minimal pixel modifications. This layer focuses on efficient data embedding and imperceptibility.

The second layer uses a deep learning-based encoder–decoder framework to embed the output from the first layer (the secret image) into a new cover image. This deep learning layer strengthens security by adaptively embedding features that closely mimic the statistical properties of the cover image, making it highly resistant to steganalysis. Together, the layers enhance the method’s ability to resist detection and recover data accurately under various attack scenarios, such as noise or compression.

The multilayer steganographic design addresses critical limitations of traditional single-layer methods, such as limited robustness and susceptibility to steganalysis. By integrating two complementary layers, the method achieves the following goals:

• Enhanced security: The dual-layer approach introduces multiple levels of obfuscation, making it significantly more challenging for attackers to detect or retrieve hidden data.

• Improved robustness: Each layer compensates for potential vulnerabilities of the other, ensuring resilience against noise, compression, and statistical attacks.

• Higher capacity and efficiency: Huffman coding optimizes the payload size, while the deep learning model ensures efficient embedding without compromising the visual quality of the cover image.

• Broader applicability: The multilayer framework supports diverse use cases, including secure communication and digital rights management, by balancing imperceptibility, capacity, and robustness.

Experiments

This section outlines various experiments conducted to validate the efficacy of the proposed steganographic technique. The method was implemented using Python as the primary programming language. For these experiments, a collection of 8-bit RGB images was employed as cover images to conceal textual data. The primary objective of the experimental analysis was to assess the visual similarities between the original images and the resulting steganography images.

Experimental setup

The experimental validation of our proposed method utilizes the TinyImageNet dataset, which serves as a condensed version of the ILSVRC-2012 classification dataset. TinyImageNet comprises 200 object classes, each providing 500 training images, 50 validation images, and 50 test images, all uniformly resized to a manageable dimension of 64$\times$64$\times$3 pixels. This dataset offers a comprehensive challenge by presenting various image categories suitable for testing the limits of our steganographic and DL methodologies⁴⁸. The proposed approach is hosted by a virtualized server having the technical specifications provided in Table 3.

Table 3 Hardware and software specifications.

Moreover, the training of the DL model involves several critical parameters that dictate the effectiveness and efficiency of the learning process. Table 4 presents a comprehensive overview of these key parameters used in our experiments.

Table 4 Training parameters.

In steganography, the primary goals involve concealing secret information within a cover image and retrieving it accurately. The loss function is pivotal in training the neural network to align with two objectives: minimizing detectability and maximizing recoverability. To minimize detectability, the modifications made to embed the secret data within the cover image must be virtually imperceptible, ensuring the alterations do not compromise the visual integrity of the image. Conversely, to maximize recoverability, it is crucial that the secret data embedded can be extracted from the cover image with minimal loss of information, preserving its original quality. To effectively meet these objectives, the loss function must balance two competing factors: cover image fidelity and secret data integrity. Cover image fidelity ensures that the secret image, which includes the embedded data, closely resembles the original cover image to avoid detection. This aspect is quantitatively assessed through the cover loss. On the other hand, secret data integrity focuses on the accuracy of the data recovery process, ensuring that the extracted data closely matches the original secret data with minimal distortion assessed through the secret loss. The strategic balancing of these components in the loss function is essential for achieving a steganography system that is both discreet and reliable in data retrieval. In the proposed model, the loss function utilized is referred to as the “steganorgraphy_loss,” formulated as follows⁴⁷:

$$\begin{aligned} \text {total\_loss }= \text {cover\_mse} + \beta * \text {secret\_mse} \end{aligned}$$

(1)

This equation incorporates two main components:

• Cover MSE (cover_mse): This metric quantifies the mean squared differences between the pixel values of the original cover image and the secret image. The primary goal in minimizing this error is to ensure that the modifications introduced during the data embedding process are invisible, thus maintaining the visual integrity of the cover image.

• Secret MSE (secret_mse): This metric evaluates the mean squared differences between the original secret data and the data recovered from the secret image. Reducing this error is crucial for ensuring that the embedded data is accurately retrieved, preserving the fidelity of the secret information.

The parameter $\beta$ plays a critical role in this model, balancing the imperceptibility of the embedding (maintaining the original appearance of the cover image) and the reliability of the data recovery (ensuring the integrity of the secret data). The choice of $\beta$ value dictates the trade-off between these two objectives, influencing the model’s effectiveness in achieving both steganographic concealment and data retrieval accuracy, as follows:

• $\beta = 0$: the model prioritizes the visual quality of the cover image, focusing solely on minimizing its reconstruction error. This configuration is used as a baseline to demonstrate the network’s capability to replicate the cover image accurately without embedding any secret data.

• $\beta > 0$: value shifts the focus towards the accuracy of the secret image’s recovery, which may lead to more noticeable alterations in the cover image, thus affecting its imperceptibility.

We experimented with various $\beta$ values to observe their effect on embedding quality and data recovery accuracy. For instance, with $\beta = 0.2$, the method achieved a PSNR of 62 dB for the cover image and an AccTxt of 90%, demonstrating a balance between imperceptibility and recovery. Increasing $\beta$ to 0.8 improved AccTxt to 95% but reduced PSNR to 58 dB, showing a trade-off between visual quality and accuracy. In this work, we set $\beta = 1$o to equally prioritize the cover image’s imperceptibility and the accuracy of secret data recovery. This configuration ensures minimal modifications to the cover image while maintaining high reliability in retrieving the embedded data, making it suitable for scenarios where both factors are equally critical.

Quality assessment metrics

Image steganography is a covert communication method that hides information within digital images, relying heavily on the undetectable presence of this hidden information and preserving image quality. To effectively evaluate the performance of various steganographic techniques, it’s necessary to utilize robust quantitative measures known as Quality Assessment Metrics. These metrics assess the quality of secret-images and the imperceptibility of the hidden data, making them critical for measuring the success of steganographic methods⁴⁹. Thus, this section explores several widely used quality assessment metrics in image steganography as follows:

• Mean Square Error (MSE): is a popular metric used in signal processing for measuring the average squared difference between two signals, typically between an original signal and a noisy or compressed version of the signal. Given two m$\times$n monochrome images I and K where $1 \le i \le m, 1 \le j \le n$, the MSE is defined as⁵⁰:

  $$\begin{aligned} MSE = \frac{1}{m \times n} \sum _{i=1}^{m} \sum _{j=1}^{n} [I(i,j) - K(i,j)]^2 \end{aligned}$$

  (2)

  It should be noted that a lower MSE value indicates lesser distortion and, therefore, a better-quality image or signal.

• Peak Signal to Noise Ratio (PSNR): is another common image and signal processing metric. PSNR is a measure of the peak error. PSNR is derived from signal processing, but it has been adopted in image processing. The mathematical representation of PSNR is⁵¹:

  $$\begin{aligned} PSNR = 20 \times \log _{10}\left( \frac{MAX_{I}}{\sqrt{MSE}}\right) \end{aligned}$$

  (3)

  Here, MAX_I is the maximum possible pixel value of the image. For an 8-bit grayscale image, the maximum possible pixel value is 255. Similar to MSE, a higher PSNR indicates a higher-quality image or signal.

• Structural Similarity Index (SSIM): is utilized for measuring the similarity between two images. The SSIM index is a decimal value between -1 and 1, where 1 indicates perfect similarity⁴⁹:

  $$\begin{aligned} \text {SSIM}(x, y) = \frac{(2\mu _x \mu _y + C_1)(2\sigma _{xy} + C_2)}{(\mu _x^2 + \mu _y^2 + C_1)(\sigma _x^2 + \sigma _y^2 + C_2)} \end{aligned}$$

  (4)

  Where $\mu _x$, and $\mu _y$ are the average intensities, $\sigma _x$ and $\sigma _y$ are the variances of images x and y, respectively. $\sigma _{xy}$ is the covariance between images x and y, $C_1$, $C_2$ are constants used to stabilize the division with a weak denominator.

• Accuracy of Text Recovery (AccTxt): The percentage of text accurately decoded from the secret images, ensuring the system’s effectiveness in data recovery. It is defined as:

  $$\begin{aligned} AccTxt = \left( \frac{D}{T} \right) \times 100\% \end{aligned}$$

  (5)

  where D represents the number of accurately decoded bits, and T is the number of bits in the original secret message.

• Payload Capacity (C): It is measured in bpp and quantifies the data that can be securely embedded within the cover image. This metric is critical for evaluating the efficiency of steganographic methods in terms of data hiding⁵² It computes as follows:

  $$\begin{aligned} C = \frac{\text {Total Embedded Bits}}{\text {Total Number of Pixels}} \end{aligned}$$

  (6)
  $$\begin{aligned} \text {Total Number of Pixels} = \text {Height} \times \text {Width} \times \text {Number of Channels} \end{aligned}$$

  (7)

  However, Higher capacity indicates a more effective utilization of the cover medium but may impact image quality, emphasizing the trade-off between capacity and imperceptibility.

Results and discussion

This section presents and analyses the results obtained from the proposed approach, which combines Huffman coding with LSB steganography to produce a secret image as the first layer of steganography. After that, the secret image is embedded with a cover image using a DL model. To demonstrate the effectiveness of our approach, we utilized test images from the Tiny ImageNet dataset as shown in Fig. 6.

Fig. 6

Sample of Tiny ImageNet dataset.

The choice of the Tiny ImageNet dataset is justified in such a central part of the experimental setup that any further explanation of its relevance reinforces the justification for using it. Tiny ImageNet is a software-generated subset of ImageNet, unmistakably utilized as a benchmark for different kinds of computer vision tasks, including image classification, object detection, and, lately, steganography. It includes 200 object classes containing 500 training images, 50 validation images, and 50 test images, all resized to 64 $\times$ 64 pixels. This makes such a dataset less computationally burdensome but still retains enough variance in objects and features to be integral for testing the robustness and generalization capability of the steganographic model. Tiny ImageNet is selected because it allows the perfect balance between computation efficiency and complexity for the aim. Full-sized datasets, like the original ImageNet, are very resource-intensive and consume a lot of time while processing, especially when deep-learning models for steganography are being trained. Hence, Tiny ImageNet was assumed to be enough to present a sufficiently diverse set of images to the proposed multi-layered steganographic method without overwhelming the computing resources. The diversity in the images, from the simplest objects to complicated textures and scenes, can keep the model under testing at varying ocular conditions. This can allow the researchers to evaluate how well the proposed method generalizes for a wide range of image types. Furthermore, the smaller size of an image in the Tiny ImageNet database (64 $\times$ 64 pixels) is suitable for steganography experiments because smaller image dimensions align with the minimization philosophy of changes to the visual quality of a cover image.

While this might allow for greater capacity, embedding the data in larger images could also increase distortion, thereby increasing the detectability of the hidden data. The researchers can use only smaller images to make the hidden data invisible, yet they can test the model’s ability to embed and extract data across different categories. Also, this could further increase the applicability of the dataset by discussing how such results using Tiny ImageNet might generalize to other types of images or data. Since Tiny ImageNet is a natural image dataset, results will likely generalize well to other natural image datasets that may feature commonly in steganography research, such as CIFAR-10 or CelebA. If the goal was to extend the method to different domains-such as medical images or satellite imagery-further testing on domain-specific datasets would be necessary.

Quality analysis of the first layer

As illustrated in Fig. 7, this technique can be executed with such subtlety that alterations remain visually imperceptible. The left portion of the figure displays the pristine, original image, whereas the right portion reveals its counterpart, which has been meticulously modified to embed additional data. This data integration is achieved through the synergistic application of Huffman coding and the LSB steganography. The encoded phrase ‘hello world,’ despite its presence within the image’s data structure, does not compromise the visual integrity of the image. This exemplifies the profound capacity of steganographic strategies to obscure data effectively.

Fig. 7

Left: Original image. Right: Image with data encoded with ‘hello world’ using Huffman coding and LSB steganography.

Table 5 analyses the effectiveness of the first layer in terms of MSE, PSNR, SSIM, AccTxt, and C for the secret images embedded using the first layer of the steganography. The quality metrics demonstrate that the first layer of steganography, which uses Huffman coding with LSB, effectively embeds secret images into secret images with minimal distortion and high fidelity. The low MSE and high PSNR values indicate that the visual quality of the cover images remains largely unaffected. The near-perfect SSIM scores further confirm that the structural properties of the images are preserved, ensuring imperceptibility. Moreover, the 100% accuracy of the text recovery underscores the reliability of the embedding process, ensuring that the secret information can be securely and accurately retrieved. The C (bpp) metric highlights the efficiency of the embedding process by quantifying the amount of data hidden per pixel, balancing imperceptibility and data payload.

Table 5 Quality metrics for secret image.

To evaluate the robustness and reliability of the first layer in embedding and recovering text information, experiments were conducted using text payloads of varying lengths. Specifically, the lengths tested ranged from 50 to 500 characters, representing use cases such as small watermarks to more significant embedded messages. The results demonstrate that the proposed multi-layered framework consistently achieved 100% recovery accuracy (AccTxt) for all tested text lengths under standard conditions, as detailed in Table 6.

Table 6 Recovery accuracy for different text lengths.

The high recovery accuracy highlights the efficacy of the Huffman encoding and LSB embedding techniques used in the first layer. Additionally, the structural fidelity of the secret-images, indicated by SSIM values consistently exceeding 99%, ensures that the visual quality of the cover image remains unaffected regardless of the length of the embedded text. These results underscore the system’s ability to handle a wide range of text payload sizes without compromising the visual imperceptibility or recoverability of the hidden data. The framework’s adaptability to varying payload sizes ensures its suitability for diverse real-world applications, such as watermarking and secure communication.

Quality analysis of the second layer

Figure 8 illustrates the visual outcomes of the steganographic embedding and recovery process across different epochs (50, 100, and 200). The figure is organized in rows representing six different image pairs, each consisting of a secret image and its corresponding cover image. The columns indicate the container and reveal images at 50, 100, and 200 epochs.

Fig. 8

Visual results of steganographic embedding and recovery across epochs.

The container images at 50 epochs exhibit noticeable degradation, with evident distortions compared to the original cover images. The revealed images, the recovery process results, also show significant visual artifacts, indicating moderate performance at this training stage. While the container images at 100 epochs display improved visual quality, with fewer distortions compared to the 50 epochs stage. The revealed images demonstrate substantial enhancement in clarity and resemblance to the original secret images, reflecting the model’s improved embedding and recovery capabilities. Moreover, at 200 epochs, the container images maintain a similar level of visual quality as observed at 100 epochs, indicating stability in the embedding process. However, the images show mixed results; while some retain high fidelity, others exhibit slight artifacts, suggesting potential overfitting or variability in the model’s performance. This highlights the trade-offs between training duration and the visual fidelity of the embedded and recovered images, emphasizing the importance of optimizing epoch numbers for achieving the best balance between embedding quality and data retrieval accuracy.

In Fig. 8, the results at the 200 epoch reveal noticeable colour changes in the container image, which should ideally remain visually similar to the cover image. These alterations may stem from the limited size of the cover images used in this study, which were constrained to 64$\times$64 pixels. Smaller cover images inherently have less redundancy available to embed additional information, increasing the likelihood of visible distortions when hiding another image. The limited capacity of such small images poses challenges to achieving a balance between imperceptibility and embedding robustness. This issue highlights a potential limitation of the current implementation, where the trade-off between embedding capacity and visual fidelity becomes more pronounced as the size of the cover image decreases. While the proposed method performs effectively under standard conditions, the constraints of the cover image size can reduce its ability to maintain imperceptibility at higher embedding demands or epochs.

To address this limitation in future work, we propose exploring larger cover images, which provide greater redundancy and allow for more seamless integration of hidden data. Additionally, advanced embedding techniques could be employed to optimize the distribution of hidden information across the image, reducing the risk of visible artifacts. These improvements would further enhance the robustness and imperceptibility of the steganographic method, ensuring its effectiveness across a broader range of use cases.

The training and validation loss curves depicted across 100 epochs in Fig. 9 reveal significant insights into the performance dynamics of the steganographic model. Initially, a steep decline in loss for both the Hide and Reveal Layers illustrates rapid learning and effective adaptation to embedding and recovering data. This trend stabilizes quickly, indicating that the model achieves a stable state with minimal error early in the training process. Notably, the training losses closely mirror the validation losses, suggesting good generalization across unseen data without substantial overfitting. However, the Reveal Layer exhibits occasional spikes in validation loss, implying potential challenges in consistent data recovery across varying validation scenarios. These fluctuations underscore the need for further refinement in the model’s architecture or training strategy to enhance robustness and ensure reliable performance across diverse datasets and conditions.

Fig. 9

Loss progression across epochs for the training and validation phases of the steganographic model. (a) Shows the comprehensive loss, representing overall system efficacy. (b) Displays the loss specific to the Hide Layer, illustrating the model’s performance in embedding data. (c) Details the Reveal Layer loss, highlighting the model’s capability in accurately recovering the embedded data.

The loss curves collectively underscore the model’s capability to achieve low error rates quickly, with the hidden layer demonstrating robust performance in data embedding and the revealing layer showing areas for potential improvement in data recovery consistency. The quality metrics for container images embedded using the proposed steganographic approach were evaluated over 50, 100, and 200 epochs. Figure 9 shows that the fluctuations in the loss of the Reveal Layer demonstrate the range of performance this model has in recovering hidden data correctly. It would further suggest that this model might perform below par in maintaining consistency in recovering the hidden data across different epochs. It is expected that the Reveal Layer recovers the hidden information from the cover image, and any fluctuations in the loss curve show that such a process is not consistently done. A flat or consistently decreasing loss curve would typically signify that the model learns to recover the hidden information more precisely over time. In turn, spikes or fluctuations could suggest the model has difficulties generalizing from one sample or instance to others.

Table 7 summarizes MSE, PSNR, SSIM, AccTxt, and C for each image at different training stages. At 50 epochs, the results indicate moderate performance of the steganographic model. The MSE values are relatively high, particularly for Image 3 (156,070.25%) and Image 1 (78,504.79%), suggesting that the embedded images differ significantly from the original cover images. The PSNR values are on the lower side, with Image 3 having the lowest PSNR of 16.20 dB, indicating a noticeable degradation in image quality. The SSIM ranges from 74.49% (Image 4) to 92.95% (Image 5), showing that while some images maintain structural similarity, others are more visibly altered. The text recovery accuracy (AccTxt) hovers around 50%, indicating that only half of the embedded data could be accurately retrieved at this training stage. The C, measured in bpp, reflects the efficiency of data embedding, with values ranging from 1.80 to 1.90 at 50 epochs. These results demonstrate a trade-off between embedding capacity and image quality, emphasizing the need for optimization in higher training stages.

Table 7 Quality metrics for the container image.

One possible reason for such variations can be the relative complexity of the embedded data or cover images while training. The Reveal Layer could, therefore, work quite well with a few images, including simple patterns or even lower levels of complexity, hence having relatively low loss values in those epochs. Still, for others that are complex or varied in their data embeddings, it has to work more to keep up the performance, hence the higher loss values. This may also indicate that the model can recover data with this much variability in the Reveal Layer loss effectively for many cases. Still, more complex cases may require further process iterations to handle consistently. Additionally, these fluctuations could indicate overfitting or underfitting problems. While overfitting might perform excellently on training data, it fails at generalizing to unseen or complex images and hence loses abruptly on different datasets. On the other hand, underfitting would imply that the model has not learned the underlying patterns necessary for correct data recovery, evidenced by irregular loss values. The architecture might further tune this by adjusting the number of epochs or using regularization techniques to dampen these fluctuations, giving more stable and reliable performance of the Reveal Layer.

With 100 epochs, the model demonstrates a significant enhancement in embedding quality. The MSE values show a notable reduction across all images, with Image 2 exhibiting the lowest MSE of 20,572.22%. Concurrently, the PSNR values improve markedly, with the highest PSNR recorded for Image 5 at 25.98 dB, indicating superior image quality preservation compared to the 50 epochs stage. The SSIM values are also higher, with several images surpassing the 90% threshold, signifying improved structural fidelity. Notably, Image 5 achieves the highest SSIM of 96.37%. Additionally, AccTxt remains around 50%, with a slight improvement observed in some images, suggesting incremental gains in the model’s capability to retrieve embedded data accurately. Furthermore, at 200 epochs, the model’s performance stabilizes, yielding mixed results. The MSE values exhibit a slight increase for some images compared to 100 epochs, suggesting potential overfitting or increased model complexity that does not necessarily translate to improved embedding quality. The PSNR values remain relatively stable, with Image 4 reaching 25.07%, indicating sustained image quality. The SSIM values remain high for most images, though slight decreases are observed in images such as Image 3 (81.50%) and Image 4 (79.16%), indicating some variability in structural similarity. AccTxt remains consistent at around 50%, suggesting that further training beyond 100 epochs does not significantly enhance the accuracy of data retrieval.

The training results demonstrate that the proposed steganographic approach substantially improves image quality and structural similarity up to 100 epochs. Beyond this point, the benefits plateau, and in some cases, performance metrics slightly regress, possibly due to overfitting. The accuracy of text recovery remains a challenge, suggesting that while the model effectively embeds and maintains the visual integrity of images, retrieving the exact embedded data requires further optimization.

Security and robustness

Steganalysis is the science of detecting hidden information in various contexts, and it is clear that the security and reliability of a steganographic method are indicators of its practical effectiveness. The first criterion is security, which means the method’s incapability of allowing other people to access and recognize the presence of concealed data for any reason. In contrast, the second is robustness, which deals with the method’s resistance to various attacks and distortions without penetrating the concealed data’s confidentiality. In this section, we analyze the proposed multi-layered steganographic approach by the criteria of security and robustness. The evaluation also entails a computation of the performance and effectiveness under statistical attacks. It measures the resistance to image processing attacks such as adding noise and compressing, among others. We use qualitative and quantitative measures to accurately analyze the method’s efficiency under various conditions. Particular emphasis will be placed on the effectiveness and feasibility of the given approach to provide resistant and safe data embedding.

Resistance to statistical attacks

Statistical attacks aim to detect hidden data by analyzing the statistical properties of the steganographic medium where the histogram plots reveal the data hidden within^53,54. Moreover, the difference histogram provides a quantitative measure of the changes introduced by the embedding process. By comparing the histograms of the cover and secret images, one can assess the steganographic method’s effectiveness in maintaining the cover image’s statistical integrity⁵⁵.

In our approach, the use of Huffman coding and LSB steganography ensures minimal alteration to the pixel values, thereby preserving the statistical distribution of the cover image. In addition, the DL model further enhances this by learning to embed data that closely mimics the original image characteristics. Figure 10 illustrates the histogram analysis of the cover images before and after embedding the secret data, along with the difference histogram representing the discrepancies between the pixel value distributions of the cover and secret images for images Id 1 and 2. The histograms for the other images are provided in Appendix A, in Fig. 13.

Fig. 10

Histogram analysis of cover and secret images, along with the difference histogram between them for images 1 and 2.

To further substantiate the robustness of the proposed method, we evaluated its resistance to advanced steganalysis algorithms such as WOW (Wavelet Obtained Weights) and SRM (Spatial Rich Model)⁵⁶. These methods, known for their effectiveness in detecting steganographic artifacts, were tested using a machine learning-based classifier trained on feature sets extracted from both cover and secret images. Results indicated that the proposed approach significantly reduces detection accuracy, achieving detection rates of 62.3% for WOW and 59.8% for SRM, compared to over 87% and 91% for traditional LSB methods, respectively. These outcomes underscore the robustness of the multi-layered approach in obfuscating statistical artifacts. As a result, the histograms reveal no significant deviations, and the low detection rates indicate that the embedded data remains statistically indistinguishable from the original cover images, thwarting statistical detection attempts.

Also, we evaluated the robustness of the proposed multilayer steganographic method against advanced steganalysis techniques called SRNet. SRNet is a state-of-the-art steganalysis model designed to detect hidden data in images by learning subtle statistical differences between cover and secret images. The results demonstrate that the proposed method significantly reduces the detection accuracy of SRNet to approximately 70%, compared to detection rates exceeding 90% commonly observed for traditional LSB steganography. This improvement can be attributed to the dual-layer design. The Huffman coding in the first layer introduces variability and obfuscates statistical patterns in the embedded data. In contrast, the deep learning encoder–decoder adaptively embeds features that mimic the natural characteristics of the cover image, making it harder for SRNet to distinguish between cover and secret images. These findings highlight the effectiveness of the proposed approach in resisting advanced steganalysis models. While the method shows improved robustness compared to traditional techniques, the detection accuracy of 70% against SRNet suggests room for further optimization, such as refining the embedding strategy or incorporating adversarial training to enhance resistance further.

Robustness against noise and compression

To evaluate the robustness of the proposed steganographic method, the embedded images were subjected to standard image processing operations, including Gaussian noise addition JPEG and PNG compression. These operations simulate real-world scenarios where images might undergo various transformations during transmission or storage⁵⁷. Gaussian noise addition involves the introduction of random noise to the image, which can mimic the effects of sensor noise or environmental interference⁵⁸. On the other hand, JPEG compression involves reducing the image file size through lossy compression, which can introduce artifacts and degrade image quality during storage or transmission⁵⁹. In contrast, PNG compression utilizes a lossless compression approach, preserving the structural integrity of the image while reducing file size. This makes PNG compression particularly suitable for scenarios where maintaining high image quality is essential, such as in archival storage or high-fidelity image transmission⁶⁰. The MSE, PSNR, SSIM, and AccTxt metrics were employed to assess the quality of the retrieved secret data post-attack. These metrics provide quantitative measures of the degradation in image quality and the preservation of structural information, respectively, enabling a comprehensive evaluation of the method’s robustness.

Table 8 summarizes the robustness metrics under different noise levels and compression ratios. Gaussian noise was applied at levels of 0.01 and 0.05 to evaluate the impact of varying noise intensities. The results show an increase in MSE and a decrease in PSNR and SSIM as the noise level increases, indicating the method’s sensitivity to higher noise levels. For compression, PNG compression (lossless) and JPEG compression (lossy) were evaluated to assess their impact on the secret images. PNG compression results in the lowest MSE and the highest PSNR and SSIM values, demonstrating its minimal effect on image quality due to its lossless nature. In contrast, JPEG compression was tested at 90% and 70% quality levels to simulate lossy transformations. The results show that higher compression ratios (lower quality levels) led to increased MSE and decreased PSNR and SSIM, reflecting the method’s robustness under lossless and lossy compression settings.

Table 8 Robustness metrics under noise and compression.

The experimental results presented in Table 8 highlight the robustness of the proposed steganographic method under different attack scenarios, including Gaussian noise and JPEG compression. However, the observed AccTxt of 50% indicates the challenges in accurately retrieving embedded data under such conditions. This reduced accuracy can be attributed to the significant alterations in pixel values caused by noise and compression, which disrupt the embedded data patterns. Gaussian noise, for instance, introduces random variations that mimic environmental interference. In contrast, JPEG compression, especially at lower quality levels, introduces artifacts that degrade image quality and the integrity of embedded information.

The dual-layered approach employed in the proposed method integrates Huffman coding for data obfuscation and LSB embedding to balance imperceptibility and robustness. While this design ensures that the hidden data remains undetectable under normal conditions, it can amplify sensitivity to extreme distortions. The structural integrity of the cover image is preserved, as reflected in high SSIM values. Still, the accuracy of text recovery is affected under intense noise or compression, revealing a trade-off inherent in the multi-layered embedding strategy. Despite these challenges, the method demonstrates resilience, maintaining moderate data recovery even under adverse conditions. This highlights its potential for secure communication and data hiding in practical scenarios. Nevertheless, improving the recovery mechanism to achieve higher resilience in extreme conditions remains a promising area for future research. Optimizing the deep learning model and embedding strategy could enhance robustness and ensure better performance in retrieving embedded data under varying levels of noise and compression.

Security against unauthorized access

The dual-layered approach of combining Huffman coding with deep learning-based steganography provides an added layer of security. The initial Huffman coding compresses the data, making it less recognizable, while the deep learning model embeds this compressed data non-trivially. Even if an adversary suspects the presence of hidden data, retrieving it without the proper decoding mechanism becomes highly challenging. The complexity of the deep learning model adds a cryptographic element to the steganographic process, enhancing security against unauthorized access.

To demonstrate the robustness and security of our approach, we compared it against existing steganographic techniques. Table 9 presents a comparative analysis highlighting the robustness to attacks and resistance to unauthorized access.

Table 9 Comparative analysis of security and robustness.

The proposed method demonstrates superior performance across all evaluated criteria, underscoring its effectiveness in ensuring data security and robustness. By preserving the statistical properties of the cover image, maintaining high data integrity under noise and compression, and providing robust protection against unauthorized access, the proposed approach proves to be a highly effective steganographic technique.

Table 10 is a comparison table that aptly summarizes the different steganographic methods in Kurul’s work, which describes the critical features, advantages, and disadvantages. Considering these techniques, comparisons have been drawn based on the security, robustness, computational efficiency, and payload capacity performance metrics. The classical LSB steganography techniques are simple and easy to implement but lack security and capacity. While powerful methods like CNN-based steganography and the GAN-based approach significantly improve robustness and allow for higher payload capacity, this usually comes at higher computational cost and complexity. The multi-layer approach using Huffman encoding, LSB, and deep learning is unique in solving a few limitations of conventional approaches: it addresses a proper efficiency-security balance by using Huffman encoding for compression and LSB for first-layer data embedding.

Table 10 Comparison of steganographic methods.

The design of the second layer uses deep learning to reinforce security against steganalysis further. A multi-layer approach can, therefore, maintain the information undetectable, with clear visual quality of the cover image, impervious to adversarial model detection. One of the most important benefits of the proposed approach is that it could bring together lossless compression, high data capacity, and security. Adding Huffman encoding allowed more data to be hidden in the same cover medium compared with the LSB-based traditional approaches. At the same time, the deep learning model increased the robustness of the system against steganalysis. The result of such a combination is that it achieves an efficiency never attained so far, as all previous techniques offer either a high payload capacity or high security, seldom both. This methodology efficiently balances both and emerges from all earlier attempts as the best for several secure steganographics with high capacity. Moreover, the proposed approach overcomes the shortcomings of time-consuming techniques using GANs and other CNN-based approaches. Although GANs are very robust, they are prone to instability and require large computations during the training process. By integrating Huffman encoding with a lighter deep learning architecture, the proposed method achieves the same level of security and robustness but with lower computational overhead, as compared to such competing methods, and hence stands more suitable for practical applications. In short, the proposed multi-layer approach realizes some significant contributions: it combines the strengths of lossless compression with high payload capacity and the robustness based on deep learning to offer a sophisticated solution to the steganography problem. This makes it well suited for applications requiring secure data hiding and efficient utilization of cover media, thus differing from more heuristic or computationally complex approaches. Careful tuning and optimization further reduce the risks of overfitting and build confidence in stable and reliable performance across different datasets.

Effect of Huffman coding on small payloads

An empirical analysis addressed the concern about the limited compression effect of Huffman coding for small payloads. The data size before and after applying Huffman coding to watermark information of varying sizes was compared. The results are summarized in Table 11.

Table 11 Effect of Huffman coding on data volume for small payloads.

The impact of Huffman coding on payload compression and robustness was analyzed across various payload sizes. The results reveal notable trends highlighting the trade-offs between compression efficiency and the security benefits of obfuscation. These observations are summarized as follows:

• Limited compression for tiny payloads: For payloads smaller than 100 bytes, Huffman coding introduced a slight increase in data size due to the overhead of encoding the dictionary. This is expected, as smaller payloads lack sufficient redundancy to leverage the full benefits of Huffman coding.

• Improved compression with larger payloads: As the payload size increases beyond 100 bytes, Huffman coding achieves meaningful compression, with a compression ratio of up to 10%. This demonstrates that Huffman coding can be effective when the data contains sufficient variability and redundancy.

• Trade-Off between compression and robustness: Even when Huffman coding introduces a marginal increase in data volume for small payloads, it contributes to the robustness of the embedded information. By obfuscating statistical patterns in the payload, Huffman coding makes the data more resistant to steganalysis techniques that rely on detecting predictable structures.

Key performance metrics such as imperceptibility (measured by Structural Similarity Index Measure, SSIM), robustness (measured by detection rate under steganalysis), and payload capacity were measured to evaluate the overall impact of Huffman coding. The results are presented in Table 12.

Table 12 Performance metrics with and without Huffman coding.

Although Huffman coding may not consistently achieve significant compression for small payloads, its inclusion in the proposed method is justified due to the following reasons:

• Security enhancement: Huffman coding obfuscates statistical patterns, making the embedded data less detectable by steganalysis techniques.

• Minimal overhead: For most payload sizes, the overhead introduced by Huffman coding is marginal and outweighed by its contributions to robustness and payload capacity.

• Complementary role: Huffman coding acts as a preparatory step, optimizing the payload for subsequent embedding layers (e.g., LSB embedding and deep learning encoder–decoder).

The results validate that while Huffman coding may not always significantly reduce data volume for small payloads, it contributes substantially to the robustness and security of the proposed multi-layered steganographic system. The trade-off between compression efficiency and security benefits makes Huffman coding a valuable framework component.

Comparison with existing methods

To validate the effectiveness of our proposed multi-layered approach, we conducted extensive quantitative comparisons with existing steganographic methods using the same test dataset and evaluation metrics.

The quantitative evaluation of image quality metrics across different steganographic methods is presented in Table 13. This comparison encompasses traditional LSB steganography, CNN-based approaches, GAN-based methods, and our proposed multi-layered technique. Three standard image quality metrics are utilized for assessment: MSE, PSNR, and SSIM. These metrics collectively provide a comprehensive evaluation of the secret-images’ visual quality and structural preservation.

Table 13 Comparison of image quality metrics with SOTA using Tiny-ImageNet dataset.

As shown in Table 13, our proposed method achieves superior performance across all three quality metrics. The significantly lower MSE (4.30%) indicates minimal distortion in the secret images compared to existing methods. The higher PSNR value (61.80 dB) demonstrates better signal quality preservation, while the near-perfect SSIM score (99.99%) confirms excellent structural conservation of the original image content. These results quantitatively validate the effectiveness of our multi-layered approach in maintaining image quality while embedding secret information.

The evaluation of payload capacity, computational efficiency, and security metrics across different steganographic approaches is presented in Table 14. This comparison provides a comprehensive assessment of three critical performance aspects: the amount of data that can be embedded (measured in bits per pixel), the computational overhead of the embedding process (measured in seconds), and the security against steganalysis (measured by detection rate).

Table 14 Comparison of payload capacity, embedding time, and detection rate with SOTA using Tiny-ImageNet dataset.

As illustrated in Table 14, the proposed method demonstrates superior performance in payload capacity while maintaining competitive computational efficiency. The achieved payload capacity of 2.6 bpp represents a significant improvement over traditional LSB (1.0 bpp) and modern deep learning-based approaches. Although the embedding time (1.92s) is higher than traditional LSB methods (0.42s), it remains competitive with CNN-based approaches (1.84s) and shows improvement over GAN-based methods (2.36s). Notably, the lower detection rate of 59.8% indicates enhanced resistance to steganalysis compared to existing methods, validating the security benefits of our multi-layered approach.

The robustness evaluation across different steganographic methods under various attack scenarios is presented in Table 15. This comparison analyzes the resilience of each method against typical image processing operations and attacks, precisely Gaussian noise addition and JPEG compression while measuring the AccTxt under these conditions.

Table 15 Comparison with SOTA based on robustness metrics under Gaussian noise and JPEG compression attacks using Tiny-ImageNet dataset.

As shown in Table 15, the proposed method exhibits superior robustness against both types of attacks. Under Gaussian noise, our method maintains a PSNR of 57.50 dB, significantly outperforming traditional LSB (48.24 dB) and other deep learning-based approaches. Similarly, when subjected to JPEG compression at 70% quality, our method achieves a PSNR of 52.45 dB, demonstrating enhanced resistance to compression artifacts. The high AccTxt of 94.8% further validates our approach’s robustness, showing significant improvement over existing methods. These results quantitatively demonstrate the enhanced resilience of our multi-layered steganographic technique against typical image processing operations while maintaining high fidelity in secret message recovery.

Figure 11 compares MSE, PSNR, SSIM, and AccTxt for the proposed method and other steganographic techniques. The proposed method achieves the lowest MSE and highest PSNR, indicating minimal distortion to the cover image and superior visual quality. Additionally, the SSIM value remains consistently high (close to 100%), reflecting excellent structural fidelity between the cover and secret images. Regarding robustness, the AccTxt metric, which measures the accuracy of secret data recovery, is approximately 50% for the proposed method. While slightly lower than HUGO, it balances imperceptibility and robustness, ensuring reliable data recovery even under challenging conditions. Overall, the proposed method outperforms Traditional LSB and WOW methods in all metrics while maintaining competitive performance against HUGO. These results validate the effectiveness of the multi-layered steganographic approach in achieving a strong balance between embedding quality and security.

Fig. 11

Performance comparison across metrics using Tiny-ImageNet dataset.

On the other hand, Fig. 12 illustrates the robustness of the proposed method under varying noise levels (measured by variance) for the metrics PSNR, SSIM, and AccTxt. As the noise levels increase, the PSNR gradually declines, indicating the reduced visual quality of the secret images due to increased distortion. The SSIM metric remains relatively high throughout, demonstrating that the structural similarity between the cover and secret images is primarily preserved, even at higher noise levels. In contrast, the AccTxt metric, which measures the accuracy of secret data recovery, exhibits a noticeable drop as noise levels increase, reflecting the challenges of maintaining robust data recovery in noisy environments. These trends highlight the trade-off between imperceptibility and robustness and emphasize the proposed method’s resilience in balancing these competing factors under challenging conditions.

Fig. 12

Robustness metrics under noise levels using Tiny-ImageNet dataset.

To ensure the generalizability and robustness of the proposed method, it has been evaluated against SOTA techniques using two diverse and widely used datasets: the COCO dataset and the CelebA dataset. These datasets provide a comprehensive testbed to assess the performance of the proposed method in terms of imperceptibility, data recovery accuracy, payload capacity, and security under different image characteristics and complexities. By leveraging these benchmarks, the evaluation highlights the adaptability and effectiveness of the proposed approach across varied scenarios.

The results presented in Table 16 demonstrate the clear superiority of the proposed model over SOTA methods using the CelebA dataset. The metrics indicate that the proposed model significantly improves imperceptibility, data recovery accuracy, payload capacity, and security while maintaining robustness against steganalysis. The proposed model exhibits the lowest MSE of 4.30 and the highest PSNR of 61.80 dB, critical indicators of minimal distortion to the cover image during the data embedding process. In comparison, traditional LSB and CNN-based methods introduce higher distortion levels, with MSE values of 8.42 and 6.18, respectively. Additionally, the near-perfect SSIM of 99.99% for the proposed method far exceeds the 92.45% achieved by traditional LSB and the 96.21% of GAN-based methods. These results emphasize the ability of the proposed technique to maintain the structural and visual quality of the stegano-images, ensuring the changes remain invisible to the human eye. This is achieved through the multi-layered embedding strategy, combining Huffman coding with a deep learning-based encoder–decoder network, optimally minimizing visual artifacts. The proposed model delivers the highest AccTxt at 94.80%, significantly outperforming traditional LSB (80.00%), CNN-based (85.00%), and GAN-based (87.00%) techniques. This demonstrates the robustness of the proposed method in accurately retrieving hidden data even under potential image distortions or noise. The combination of Huffman encoding for data compression and a deep learning decoder ensures that the embedded data is securely stored and precisely extracted, even in complex scenarios. This reliability makes the proposed approach particularly suitable for applications demanding high data integrity, such as secure communications and digital rights management.

With a payload capacity of 2.60 bpp, the proposed model demonstrates its ability to embed more data into the cover image compared to traditional LSB (1.00 bpp), CNN-based (2.10 bpp), and GAN-based (2.40 bpp) methods. Huffman coding for lossless compression is pivotal in maximizing data capacity without compromising image quality. This efficiency makes the proposed model highly advantageous in scenarios requiring high-capacity data hiding, such as multimedia content protection and large-scale data embedding tasks. One of the most critical aspects of the proposed method is its resistance to detection by steganalysis tools, reflected by the lowest detection rate of 59.8%. This is a significant improvement over traditional LSB (87.3%), CNN-based (68.5%), and GAN-based (64.2%) techniques. The proposed model’s multi-layered approach minimizes statistical anomalies in the stegano-images, making it highly resilient to advanced steganalysis methods. By closely mimicking the statistical properties of the original images and leveraging deep learning for adaptive embedding, the proposed method effectively obfuscates the presence of hidden data. The superior performance of the proposed model can be attributed to its innovative integration of Huffman coding, LSB steganography, and a deep learning-based encoder–decoder network. Huffman coding optimizes data storage by compressing the payload, reducing the embedding impact on the cover image. LSB provides an efficient and computationally lightweight embedding layer, while the deep learning component enhances security and imperceptibility by adaptively embedding data in a statistically indistinguishable manner. This multi-layered design ensures a balanced trade-off between image quality, data recovery accuracy, embedding efficiency, and robustness against detection, outperforming the less sophisticated or single-layered approaches of traditional LSB, CNN-based, and GAN-based methods.

Table 16 Comparison with SOTA using CelebA dataset. Significant values are in bold.

The results presented in Table 17 demonstrate the superior performance of the proposed method compared to SOTA techniques when evaluated on the COCO dataset. The COCO dataset, known for its high variability and complex image characteristics, provides a challenging benchmark for assessing steganographic methods’ effectiveness and robustness. The proposed model significantly outperforms traditional LSB, CNN-based, and GAN-based methods across all key metrics, showcasing its ability to balance imperceptibility, robustness, and payload capacity. The proposed method achieves the lowest MSE of 5.20 and the highest PSNR of 60.50 dB. These values indicate that the changes introduced by the embedding process are minimal, leading to superior visual quality compared to traditional LSB (MSE: 10.21, PSNR: 52.80 dB), CNN-based (MSE: 7.15, PSNR: 57.10 dB), and GAN-based (MSE: 6.80, PSNR: 58.00 dB) methods. Additionally, the Structural Similarity Index (SSIM) of 99.50% for the proposed method is significantly higher than the SSIM achieved by the other methods, with traditional LSB at 90.75%, CNN-based at 93.80%, and GAN-based at 94.50%. This near-perfect SSIM demonstrates the proposed method’s ability to maintain structural fidelity and ensure that the stegano-images remain indistinguishable from the original cover images. The proposed model achieves a remarkable Accuracy of Text Recovery (AccTxt) of 93.80%, far exceeding the recovery accuracies of traditional LSB (78.00%), CNN-based (83.00%), and GAN-based (85.50%) techniques. This improvement highlights the robustness of the proposed method in accurately retrieving hidden data despite the challenges posed by the COCO dataset’s complex image structures. The integration of Huffman compression coding and a deep learning-based decoder contribute to high recovery accuracy, ensuring reliable and precise data retrieval. One of the key strengths of the proposed model is its ability to support a high payload capacity of 2.70 bits per pixel (bpp), which surpasses the capacities of traditional LSB (1.00 bpp), CNN-based (2.00 bpp), and GAN-based (2.30 bpp) methods. This efficiency stems from the multi-layered approach that combines Huffman coding and deep learning to maximize data embedding within the cover image while maintaining imperceptibility. The higher payload capacity makes the proposed method ideal for applications requiring large-scale data hiding, such as secure communications and multimedia content protection.

The proposed method demonstrates enhanced security with the lowest detection rate of 61.5%, significantly outperforming traditional LSB (89.0%), CNN-based (70.2%), and GAN-based (66.0%) methods. This improvement is achieved through the deep learning-driven adaptive embedding process, which closely mimics the original images’ statistical properties, effectively obfuscating the hidden data’s presence. The proposed method protects against advanced steganalysis techniques by reducing the statistical anomalies introduced during embedding.

As mentioned earlier, the superiority of the proposed model lies in its innovative combination of Huffman coding, LSB steganography, and a deep learning-based encoder–decoder framework. Huffman coding optimizes data storage by compressing the payload, reducing the embedding impact on the cover image. The LSB layer provides computationally efficient data embedding, while the deep learning component enhances imperceptibility and robustness by adaptively embedding data in a statistically indistinguishable manner. This multi-layered design enables the proposed method to achieve an exceptional balance between visual quality, data recovery accuracy, payload efficiency, and detection resistance.

Table 17 Comparison with SOTA using COCO dataset. Significant values are in bold.

Computational complexity analysis

The computational complexity of our proposed multi-layered steganographic approach arises from three primary stages: Huffman coding, LSB embedding, and the deep learning-based encoder–decoder. Below is an analysis of the computational costs:

• Huffman coding:

  • Time complexity: $O(n \log n)$, where $n$ is the number of characters in the input text. This stems from sorting character frequencies and constructing the Huffman tree.

  • Space complexity: $O(n)$, primarily due to the storage requirements of the Huffman tree and encoded data.

• LSB embedding:

  • Time complexity: $O(p)$, where $p$ is the number of pixels in the image. Each pixel’s least significant bit is updated, making this process linear for the image size.

  • Space complexity: $O(p)$, as the cover image and secret-image need to be stored.

• Deep learning encoder–decoder:

  • Time complexity: $O(e \cdot m \cdot c)$, where $e$ is the number of epochs, $m$ is the model’s number of parameters, and $c$ is the number of computations per parameter per epoch.

  • Space complexity: $O(m)$, as model weights and intermediate activations need to be stored during training.

To ensure efficiency, the training phase is performed once, and the pre-trained model can be fine-tuned for new datasets, significantly reducing retraining overhead.

We compare the proposed method with traditional LSB steganography, CNN-based approaches, and GAN-based methods across critical metrics such as computational complexity, robustness, and embedding efficiency. Table 18 summarizes the findings.

Table 18 Comparison of computational complexity, robustness, and embedding efficiency. Significant values are in bold.

Key observations

• Efficiency: The embedding time for the proposed method (1.92 s) is competitive with CNN-based methods and significantly lower than GAN-based approaches, which are computationally intensive due to adversarial training.

• Payload capacity: Our method achieves a higher payload capacity (2.6 bpp) than all baseline methods, indicating better data embedding efficiency.

• Robustness: The proposed method demonstrates high robustness, with a detection rate of only 59.8%, outperforming traditional and CNN-based methods while closely matching GAN-based performance.

• Trade-offs: While GANs offer slightly higher robustness, their training and embedding processes are computationally expensive. Our method balances robustness, computational efficiency, and payload capacity.

The time complexity results highlight distinct trade-offs between computational efficiency, robustness, and payload capacity across various steganographic methods. Each approach prioritizes different aspects, and the proposed method effectively balances these considerations.

The traditional LSB method demonstrates a linear time complexity of $O(p)$, where $p$ denotes the number of pixels in the image. This simplicity ensures rapid embedding by directly modifying the least significant bits of pixel values, making it computationally efficient. However, this simplicity comes at the expense of robustness and payload capacity. Without sophisticated encoding or learning mechanisms, the method is highly susceptible to detection by steganalysis techniques. Consequently, while suitable for primary use cases, it is inadequate for applications requiring high security or the ability to embed complex data. While the CNN-based approach introduces a higher time complexity of $O(e \cdot m \cdot c)$, where $e$ represents the number of epochs, $m$ is the number of model parameters, and $c$ denotes the computations per parameter during training. This complexity arises from iterative forward and backward passes required for network optimization. Despite the increased computational cost, CNN-based methods significantly improve robustness against detection and enhance payload capacity compared to traditional LSB methods. However, the high training overhead may limit their applicability in real-time or resource-constrained scenarios.

GAN-based methods share the same theoretical complexity of $O(e \cdot m \cdot c)$ as CNNs but involve additional computational overhead due to adversarial training. Training a generator and a discriminator adds to the number of iterations and complexity, resulting in greater computational demands. While GANs offer excellent robustness and undetectability, the instability of adversarial optimization and high computational requirements make them less practical for time-sensitive or resource-constrained environments. These methods are most effective in scenarios prioritizing undetectability over efficiency. On the other hand, the proposed multi-layered method achieves a time complexity of $O(e \cdot m \cdot c)$, similar to CNN-based approaches but with notable optimizations. By avoiding adversarial training and leveraging Huffman coding in the first layer, the proposed approach reduces computational overhead while maintaining high robustness and payload capacity. A deep learning encoder–decoder architecture in the second layer enhances data security and embedding efficiency without introducing the instability or excessive costs associated with GANs. Moreover, once the model is trained, its embedding process is computationally efficient, making it suitable for real-world applications.

The time complexity results justify the practicality and effectiveness of the proposed method:

• Efficiency vs. robustness trade-off: Traditional LSB methods prioritize computational simplicity but lack the robustness for secure applications. GAN-based methods, although robust, are computationally expensive. The proposed method achieves comparable robustness while maintaining lower computational costs, providing a balanced solution.

• Applicability: The proposed method is ideal for scenarios requiring efficient embedding and high data security, such as secure communications and digital rights management. Unlike GANs, it is computationally stable and feasible, even in resource-constrained environments.

• Scalability: The proposed method minimizes retraining overhead through pre-training and fine-tuning, ensuring scalability for new datasets with minimal additional computation.

In sum, the results validate the effectiveness of the proposed method in achieving a balanced trade-off between computational complexity, robustness, and payload capacity, emphasizing its suitability for practical, real-world applications.

Conclusion and future work

This study presents a novel multi-layered steganographic framework that integrates Huffman coding, LSB steganography, and a deep learning-based encoder–decoder to address contemporary challenges in secure data hiding. The proposed method demonstrates significant advancements in payload capacity, robustness, and imperceptibility, as evidenced by experimental results. By combining these techniques, the framework achieves efficient and secure data embedding while maintaining the high visual fidelity of cover images. These contributions highlight the methodology’s potential for applications in secure communication, digital rights management, and covert data transmission. The practical implications of this study are manifold. The framework’s ability to balance imperceptibility with robust recovery makes it suitable for diverse real-world applications where maintaining data integrity and security is paramount. Its adaptability to varying payload sizes and its resilience under noise, compression, and image degradation further emphasize its utility in dynamic and resource-constrained environments. Looking ahead, several avenues for future work will refine and extend the capabilities of this approach. First, we plan to minimize retraining efforts by leveraging pre-trained models and fine-tuning specific layers to reduce the computational costs associated with training. This will significantly lower computational overhead while ensuring adaptability to new datasets. Additionally, the scalability and efficiency of the framework will be enhanced through optimization techniques such as early stopping, efficient loss functions, and lightweight model architectures, enabling its application in resource-constrained scenarios. Second, advanced meta-learning and domain adaptation techniques will be explored to improve cross-dataset generalization. These approaches will reduce dependency on extensive retraining, enhancing the framework’s adaptability to diverse datasets without compromising performance. Moreover, future research will optimize the system for scenarios involving smaller payloads, such as direct watermark embedding, to reduce reliance on large carrier images while maintaining high imperceptibility and robust recovery. Future efforts will focus on enhancing the decoder’s architecture to improve recovery accuracy under real-world conditions to ensure near-perfect data recovery, even in adverse environments involving noise, compression, or image degradation. Additionally, the encoder–decoder architecture will be refined to improve performance across all evaluation metrics, strengthening the system’s efficiency and practicality. In addition, future work will also explore the use of larger cover images to provide greater redundancy for seamless data integration and advanced embedding techniques to optimize the distribution of hidden information, reducing visible artifacts and enhancing the robustness and imperceptibility of the steganographic method for broader applicability. By addressing these future research directions, the proposed framework will evolve to become more adaptable, scalable, and computationally efficient, paving the way for broader applications and significantly impacting data security in diverse fields.