Phase-free traffic signal control for balanced flow in sensor-limited environments

Abstract

This paper introduces a phase-free traffic signal control system designed to improve both efficiency and equity in sensor-limited environments. While traditional Adaptive Traffic Signal Control (ATSC) effectively reduces delays, it often results in inequitable green time allocation, particularly under oversaturated conditions. To address this issue, this study proposes a Cell Transmission Model (CTM)-based approach for estimating queue lengths beyond the detection zones of point sensors in congested conditions. By exchanging traffic information between adjacent intersections in distributed environments, the proposed approach estimates real-time queue lengths and waiting times for each traffic movement. The phase-free system dynamically allocates green time to balance these estimates, ensuring more equitable and efficient traffic management. The system was evaluated through numerical experiments on a two-intersection network and a 3 × 3 grid network, where it achieved a 15% reduction in average control delay and small deviations in the level of service between movements compared to traditional control systems. The results demonstrate the system’s potential for real-world applications, particularly in urban areas with uneven traffic flows and limited sensor coverage. By addressing the dual objectives of maximizing throughput and ensuring equitable treatment of all traffic movements, the proposed control system provides a scalable solution for modern urban traffic networks.

Introduction

Traffic signal control systems are critical for managing urban mobility, safety, and environmental impact. Adaptive Traffic Signal Control (ATSC), including prominent examples like SCOOT, SCATS, OPAC, and RHODES^1,2,3,4, was developed to dynamically adjust signal timings based on real-time data. These systems aim to optimize traffic throughput and reduce delays, thus playing a significant role in handling fluctuating traffic demand. However, despite their widespread use, these systems face challenges in highly congested and oversaturated conditions, where the reliance on fixed cycle lengths and predefined phase sequences can result in inefficiencies, especially on side streets and for lower-priority movements.

ATSC systems often optimize green time allocation for major traffic flows while minimizing total delays. However, they still rely on predefined timing plans, phase sequences, and fixed cycle lengths. OPAC, for example, incorporates phase-skipping to minimize delay but still requires a fixed cycle length⁵. Such rigidity results in imbalanced signal timing, especially in oversaturated conditions where high-demand movements receive excessive priority, leaving side streets and turning movements with disproportionately longer delays. This limitation has driven research toward distributed control strategies, which aim to provide more adaptive and flexible traffic management by avoiding rigid cycles and responding dynamically to real-time traffic demand⁶.

Phase-free control offers a potential solution to these challenges by eliminating predefined phase sequences and allowing the allocation of green time to be fully responsive to real-time traffic demand. This approach can more effectively handle dynamic demand patterns and reduce overall delay. Phase-free control research has primarily focused on two approaches: throughput maximization and queue minimization. Hajbabaie’s group^7,8 developed phase-free methods aimed at maximizing throughput, demonstrating superior intersection capacity compared to traditional signal control methods. The queue minimization approach focuses on alleviating congestion by allocating green time to waiting vehicles. Abelghaffar and Rakha^9,10 validated the effectiveness of minimizing and balancing queues at individual intersections under undersaturated conditions. At the network level, max-pressure control methods have been proposed, selecting phases with the highest pressure, calculated as the difference between upstream demand and downstream supply capacity^11,12,13. These methods have proven to be effective, particularly under oversaturated conditions.

One of the critical challenges in both traditional and phase-free traffic control systems is the inequitable distribution of green time. Throughput maximization and queue minimization approaches prioritize high-demand movements, resulting in longer delays for side streets and turning movements. This imbalance becomes more severe under oversaturated conditions, where major traffic movements dominate green time allocations^14,15,16. To address this issue, Liang et al.¹⁷ proposed an equitable control scheme for phase-free systems, using maximum delay thresholds to ensure fairer distribution of green time. By setting limits on the maximum allowable delay for low-demand movements, the system aims to minimize inequities while maintaining efficiency. However, although this approach prevents extreme delays for low-demand movements, it can still increase their delay up to the maximum threshold, which hinders balance across traffic movements.

In a phase-free system to ensure equity among traffic movements, real-time data collection is necessary to identify the traffic conditions for each movement. This requirement can be effectively addressed in Connected Vehicle (CV) environments. In fully CV environments, systems like those proposed by^9,10,18 have shown that phase-free control can optimize traffic flows by leveraging comprehensive real-time vehicle data. However, in mixed CV environments, where data availability is more limited, challenges remain. Feng et al.¹⁹ and Islam et al.²⁰ have explored adaptive control in mixed CV settings, demonstrating some effectiveness, but further development is needed to handle incomplete data effectively.

In many urban environments, point sensors such as video detectors and inductive loops are commonly used to collect traffic data. In undersaturated conditions, phase-free systems can be operated efficiently by utilizing information from these sensors, as queues are formed within the detection range. However, under oversaturated conditions, queues for several traffic movements may extend beyond the detection zones^21,22. This creates a challenge for phase-free systems, as determining which movements should be prioritized for green time allocation becomes difficult when traffic states in undetectable areas are unknown.

To overcome this limitation, methods based on the Cell Transmission Model (CTM), initially proposed by Daganzo^23,24, have been adopted to estimate traffic states in undetected areas by leveraging upstream traffic information^25,26. CTM simulates traffic flow propagation by dividing roadways into discrete cells, where traffic conditions are updated at each time step based on inflows and outflows. However, accurate estimation of traffic states requires precise calibration of key CTM parameters, including free-flow speed, maximum allowable inflow, and backward shockwave speed^27,28. Proper calibration ensures that CTM can reliably represent vehicle dynamics at a macroscopic level and provide essential information for phase-free systems operating in sensor-limited environments. Building on this CTM-based approach, Hajbabaie’s group’s phase-free systems^7,8 employed CTM to simulate traffic dynamics in undetectable areas within distributed environments, where intersections operate independently but exchange traffic information with adjacent intersections. By utilizing inductive loops installed at upstream intersections, these systems track the number of vehicles released from upstream intersections.

Despite advancements in phase-free control, most studies prioritize efficiency for high-demand movements, often overlooking equity for side streets and lower-priority flows. In addition, reliance on fully CV environments limits the practical applicability of phase-free control in urban networks, where sensor-limited environments with point detectors are prevalent. To address these gaps, this study proposes a CTM-based traffic state estimation model in distributed environments. The proposed model estimates the number of vehicles in undetectable areas using departure volumes from upstream intersections, which enables the calculation of queue lengths and waiting times for each traffic movement. By balancing these factors, the proposed phase-free system ensures a more equitable distribution of green time across all movements, prioritizing main movements while applying penalties to mitigate excessive delays for lower-priority movements.

This study makes several key contributions to the field of traffic signal control, specifically within the context of phase-free control and balanced traffic management:

• Incorporation of Balance into Signal Control: Unlike traditional phase-free systems that focus on maximizing throughput or queue minimization, this study integrates both queue length and waiting time into the decision-making process. This ensures that all traffic movements, including those on side streets or low-volume lanes, receive more balanced treatment, reducing the imbalance often seen in oversaturated conditions.

• Development of a Phase-Free Control System for Sensor-Limited Environments: This study introduces a phase-free control system that leverages CTM-based queue length estimation to address the challenges of sensor-limited environments. In distributed environments, by combining real-time data from point sensors (e.g., video detectors) and inflow information from adjacent intersections, the system accurately estimates traffic conditions, including vehicle counts in both detected and undetected areas.

The rest of the paper is organized as follows. Section II defines the problem, focusing on the limitations of previous traffic signal control systems and the need for a more balanced phase-free control system. Section III outlines the proposed methods, including a cell-based traffic state prediction model and the phase-free optimal action decision framework. Section IV presents the results of the numerical experiments conducted to evaluate the system’s performance in three case study scenarios: two signalized intersections and a 3 × 3 grid network. Section V concludes the paper by summarizing the key findings and contributions and discussing potential directions for future research.

Problem Statement

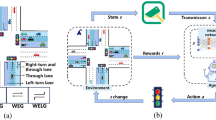
This study aims to explore the effect on individual traffic movements when equity is considered in phase-free traffic signal control with a focus on maximizing throughput. In this context, phase-free traffic signal control refers to the process of assigning the green time to specific traffic movements at each time step. As shown in Fig. 1, when both left-turn and through movements are present at the signalized intersection, the problem addressed is to determine the optimal phase for the next time step, considering both traffic efficiency and equity.

In this study, balance is defined as the difference in delay levels between traffic movements. The proposed method prioritizes high-demand traffic movements. For instance, in Fig. 1, traffic movements 1 and 6 are allocated the green time during the current time step due to their higher demand. However, this increases the delay for traffic movements 4 and 8, which have lower demand. To balance the delay across all movements, the proposed method selects the phase with traffic movements 4 and 8 as optimal for the next time step.

To address the different delay levels between movements, traffic state information at the movement level is required. With the installation of video cameras at stop lines to monitor signalized intersections, it is now possible to estimate the state of each traffic movement. However, due to the limited sensing range of cameras, undetectable areas still exist. To overcome this, the study targets the distributed environment where adjacent intersections can share traffic information, allowing for the estimation of the number of vehicles in undetectable areas.

This study aims to develop a phase-free traffic signal control method that balances delay levels across traffic movements in sensor-limited environments. Building on DISCO^25,26 and DC^7,8, which focus on maximizing efficiency in CV environments, this study extends their applicability to limited sensing coverage and addresses delays for low-priority movements. The proposed method incorporates CTM-based queue length estimation in point sensor environments to calculate waiting time at the traffic movement level. This waiting time is integrated into the objective function to enable a more equitable allocation of green time. By addressing these challenges, this study seeks to achieve both efficiency and equity in vehicle passage through signalized intersections, supporting its application in sensor-limited urban networks.

Fig. 1

Illustration of balanced phase-free traffic signal control at a signalized intersection.

Methods

This study proposes the phase-free traffic signal control model in a camera-based detection environment. The framework of the proposed model is illustrated in Fig. 2. To estimate the current state of the target signalized intersection, this paper focuses on the distributed approach where the target intersection can receive traffic information, such as the departure volume from upstream intersections.

The proposed traffic signal control model consists of two stages. The first stage involves cell-based traffic state prediction, which generates input data for traffic signal control. Based on estimated information from both detectable and undetectable areas, the number of vehicles at the next time point is predicted for each phase. In the second stage, the optimal phase for the next time step is determined. To account for varying delay levels for each traffic movement, the average waiting time per movement is applied as the parameter in the objective function.

Fig. 2

Framework for the proposed model.

A. Cell-based Traffic State Prediction

The section-based traffic state for signal control is predicted using data collected from video camera detectors. To model traffic dynamics at the signalized intersection, the CTM is employed, representing the traffic state as the number of vehicles in each cell. Each section is organized by movement, which is divided into homogeneous cells.

Figure 3 illustrates the process for estimating and predicting the number of vehicles in cells. Each section is composed of both detectable and undetectable areas to account for the limitations of the detection range of video camera detectors. In the estimation level, the number of vehicles in cells within the detectable area is calculated using actual sensing data. Conversely, the number of vehicles in cells within the undetectable area is estimated by leveraging the predicted number of vehicles in cells at the previous time point and the inflow data from the upstream intersections. In the prediction level, based on the estimated current state, the number of vehicles in cells at the next time point is predicted for each action, which refers to the phase assigned the green time.

Table 1 summarizes the notation for all sets, decision variables, and parameters used in the proposed model. $\:{n}_{i,\:j}\left(t\right)$ is introduced to indicate the number of vehicles in cell $\:j\in\:{J}_{\left(i\right)}$ at the current time point $\:t$. The following Eqs. (1) and (2) represent $\:{n}_{i,\:j}\left(t\right)$ within the undetectable area, where $\:{n}_{i,j}^{{\prime\:}}\left(t\right)$ is the number of vehicles predicted at the previous time point; $\:{f}_{i,1}\left(t-\varDelta\:t\right)$ is the inflow from upstream intersection to cell 1 for movement $\:i\in\:I$ during previous time step:

$$\:{n}_{i,1}\left(t\right)={n}_{i,\:\:1}^{{\prime\:}}\left(t\right)+{f}_{i,1}\left(t-\varDelta\:t\right)\:\forall\:i\in\:I$$

(1)

$$\:{n}_{i,j}\left(t\right)={n}_{i,\:j}^{{\prime\:}}\left(t\right)\:\forall\:i\in\:I,\:\forall\:j\in\:{U}_{\left(i\right)}$$

(2)

At the prediction level, prior research models, DISCO^25,26 and DC^7,8, are used to calculate the number of vehicles at the next time point according to each action. Traffic dynamics based on CTM are expressed through DISCO. Equation (3) updates the number of vehicles $\:{n}_{i,\:\:j}^{{\prime\:}}\left(t+\varDelta\:t\right)$ at the next time point $\:t+\varDelta\:t$. This update is based on the number of vehicles $\:{n}_{i,\:j}\left(t\right)$ at the current time point $\:t$, plus the inflow $\:{f}_{i,\:j}\left(t\right),$ minus the outflow $\:{f}_{i,\:j+1}\left(t\right)$.

$$\:{n}_{i,\:\:j}^{{\prime\:}}\left(t+\varDelta\:t\right)={n}_{i,j}\left(t\right)+{f}_{i,j}\left(t\right)-{f}_{i,j+1}\left(t\right)\:\:\forall\:i\in\:I,\:\forall\:j\in\:{J}_{\left(i\right)}$$

(3)

Fig. 3

Cell-based traffic state estimation and prediction process.

Equation (4) restricts the flow $\:{f}_{i,\:j}\left(t\right)$ from cell $\:(j-1)$ to cell $\:j$ based on the number of vehicles $\:{n}_{i,\:j-1}\left(t\right)$ in cell $\:(j-1)$ at time point $\:t$, the inflow capacity $\:{Q}_{i,j}\left(t\right)$, and the available space $\:{\frac{w}{v}[N}_{i,j}\left(t\right)-{n}_{i,j}\left(t\right)]\:$for movement $\:i$ in cell $\:j$ at time point $\:t$.

$$\:{f}_{i,\:j}\left(t\right)=min\left\{{n}_{i,j-1}\left(t\right),\:{Q}_{i,j}\left(t\right),{\frac{w}{v}[N}_{i,j}\left(t\right)-{n}_{i,j}\left(t\right)]\:\right\}\:\forall\:i\in\:I,\:\forall\:j\in\:{J}_{\left(i\right)}$$

(4)

Conflict

ing traffic movements and start-up lost time are constrained based on DC. Equations (5)-(7) represent the number of green signals and their continuous allocation. Equations (5) and (6) limit the signal for conflicting movements of movement. Equation (7), designed in this study, imposes an upper limit on the queue length for movement to ensure that the queue length is maintained below a predefined threshold. The maximum queue length for movement is restricted by the maximum number of consecutive green signals, which prevents the extension of green signals beyond the threshold.

$$\:\sum\:_{i}{g}_{i}\left(t\right)=\:2\:\forall\:i\in\:I$$

(5)

$$\:{g}_{i}\left(t\right)\:+{g}_{k}\left(t\right)\le\:1\:\:\:\forall\:i\in\:I,\:\forall\:k\in\:{K}_{\left(i\right)}$$

(6)

$$\:{g}_{i}\left(t\right)\le\:{m}_{i}-{c}_{i}\left(t\right)\:\forall\:i\in\:I$$

(7)

Equations (8)-(10) address the inflow capacity for each cell type. To reflect the influence on start-up lost time, a signalized cell is introduced, which is located at the stop line. Equations (8) and (9) restrict the inflow capacity in downstream cell of signalized cell $\:j\in\:{C}_{\left(i\right)}$ by factoring in the saturation headway $\:{h}_{s}$ and the signal. Equation (8) facilitates vehicle progression based on the ideal saturation flow rate when the green times are continuously assigned. Equation (9) accounts for the reduction in inflow capacity of downstream cell of signalized cell during transitions from red to green by considering the start-up lost time as the parameter $\:r$. For other cells, Eq. (10) limits the inflow capacity to the ideal saturation flow.

$$\:{Q}_{i,j+1}\left(t\right)\le\:\frac{\varDelta\:t}{{h}_{s}}{g}_{i}\left(t\right)\:\forall\:i\in\:I,\:\forall\:j\in\:{C}_{\left(i\right)}$$

(8)

$$\:{Q}_{i,j+1}\left(t\right)\le\:\frac{\varDelta\:t}{{h}_{s}}\:-r\left(\frac{\varDelta\:t}{{h}_{s}}\right)\left({g}_{i}\right(t)-{g}_{i}\left(t-\varDelta\:t\right))\:\:\forall\:i\in\:I,\:\:\:\forall\:j\in\:{C}_{\left(i\right)}$$

(9)

$$\:{Q}_{i,j}\left(t\right)=\frac{\varDelta\:t}{{h}_{s}}\:\forall\:i\in\:I,\:\forall\:j\in\:{J}_{\left(i\right)},\:\forall\:j\notin\:{C}_{\left(i\right)}$$

(10)

Equations (11) and (12) ensure non-negativity and that the signal is a binary variable.

$$\:{n}_{i,\:j}\left(t\right),\:{Q}_{i,\:j}\left(t\right),\:{f}_{i,\:j}\left(t\right)\ge\:0\:\forall\:i\in\:I,\:\forall\:j\in\:{J}_{\left(i\right)}$$

(11)

$$\:{g}_{i}\left(t\right)\in\:\left\{\text{0,1}\right\}\:\forall\:i\in\:I$$

(12)

The proposed traffic state prediction model calculates the number of vehicles at the next time point for each action using mixed-integer linear programming. However, Eq. (4) contains nonlinearity due to embedded minimization. Therefore, Eq. (4) is decomposed into linear equations based on DISCO’s approach. The predicted traffic state for each action is used as input data for phase-free traffic signal control.

Table 1 Notation used for the proposed model.

B. Phase-free based optimal action decision

This section explains the process for selecting the optimal phase to assign the green time for the next time step. A phase-free traffic signal control approach determines the optimum based on the predicted traffic state.

The optimal phase is defined as maximizing throughput while imposing penalties for deviations in delays between individual traffic movements. Although the approach of maximizing throughput reduces the number of residual vehicles in the signalized intersection, it has limitations in considering the state of each traffic movement. To address this, the study reflects the waiting time for each movement as the parameter in the objective function.

The waiting time is computed using the estimated number of vehicles in the cells as described in Section III-A. The calculation involves a two-step process. First, the queue length is estimated based on cell occupancy. By introducing a queue cell to distinguish between driving and stopped vehicles, the cell in the jam density state is identified as the queue cell. The queue length is then found by summing the number of vehicles in the queue cells. Second, the waiting time is computed using the estimated queue length. Equation (13) indicates the total delay for movement $\:i\in\:\:I$ up to the current time step $\:t\in\:T$, given as the product of the sum of the number of vehicles in the queue cell $\:j\in\:{S}_{\left(i\right)}$ and the time step $\:\varDelta\:t$.

$$\:{\sum\:}_{t}{\sum\:}_{j}{n}_{i,j}\left(t\right)\varDelta\:t\:\:\:\:\forall\:i\in\:I,\:\:\:\:\forall\:j\in\:{S}_{\left(i\right)},\:\:\forall\:t\in\:T$$

(13)

The cumulative number of vehicles departing from the signalized cell $\:j\in\:{C}_{\left(i\right)}$ for movement $\:i\in\:I$ is given in Eq. (14).

$$\:{\sum\:}_{t}{\sum\:}_{j}{f}_{i,j+1}\left(t-\varDelta\:t\right)\:\forall\:i\in\:I,\:\forall\:j\in\:{C}_{\left(i\right)},\:\:\forall\:t\in\:T$$

(14)

The waiting time for each movement is obtained by dividing (13) by (14):

$$\:{d}_{i}\left(t\right)={\sum\:}_{t}{\sum\:}_{j}\frac{{n}_{i,j}\left(t\right)\varDelta\:t}{{f}_{i,c+1}\left(t-\varDelta\:t\right)}\:\:\forall\:i\in\:I,\:\:\forall\:j\in\:{S}_{\left(i\right)},\:\forall\:c\in\:{C}_{\left(i\right)},\:\forall\:t\in\:T$$

(15)

The weighting factor $\:{\phi\:}_{i}\left(t\right)$ for movement $\:i\in\:I$ is determined as the ratio of its waiting time to the sum of waiting time for all movements in the intersection:

$$\:{\phi\:}_{i}\left(t\right)=\frac{{d}_{i}\left(t\right)}{{\sum\:}_{i}{d}_{i}\left(t\right)}\:\forall\:i\in\:I$$

(16)

Based on the predicted traffic state for each action and the weighting factor, the optimal phase to allocate the green time is determined, as described in Eq. (17). This phase minimizes the number of vehicles in cells while equalizing delays for individual movements for the next time step.

$$\:min{\sum\:}_{i}{\sum\:}_{j}\left\{{n}_{ij}\left(t\right)-{f}_{ij+1}\left(t\right)\right\}{\phi\:}_{i}\left(t\right)$$

(17)

The process of traffic state prediction and optimal phase decision is repeated at each time step. The predicted number of vehicles in cells within undetectable areas at the current time point is used to estimate the undetectable areas at the next time point.

Results

A. Experimental setup

To evaluate the effectiveness of the proposed model, three case study networks were selected, as illustrated in Fig. 4.

The first network consists of two signalized intersections, while the second is a 3 × 3 grid network with nine intersections. All roadways in both networks are two-way, with one lane per direction for left-turn and through movements, and the same turning ratio was applied. The third network introduces more realistic conditions by designating two lanes for the eastbound and westbound through movements, with the turning ratio of 1:4 for left-turn and through movements. Traffic demand patterns were tested under free-flow, saturated, and oversaturated conditions.

The proposed model was compared with two phase-free traffic signal control models, DISCO and DC, in the first and second case studies. DISCO follows a maximizing throughput approach and divides each lane into homogeneous cells. Originally, DISCO was a cycle-based traffic signal control model, so it was transformed into a phase-free method by relaxing its constraints. DC, on the other hand, sets each lane as one cell and also uses the maximizing throughput approach. To assess the proposed model against DISCO and DC, all cells in the signalized intersections in the first case study were set as undetectable areas. This was because DC uses only one cell per traffic movement, thereby preventing the differentiation between undetectable and detectable areas. In the second case study, both DISCO and the proposed model were employed, allowing for the consideration of both undetectable and detectable areas. In the third case study, the proposed model was compared with a pressure-based phase-free traffic signal control (PTSC) model. PTSC allocates green time to the movement with the highest pressure, defined as the deviation between arrival and departure volumes, aligning with the queue minimization approach. All four control models include the process for estimating traffic states at every time point. The primary distinction between the proposed model and the compared models lies in the inclusion of a weighting factor.

Fig. 4

Case study layouts: (a) two signalized intersections (free flow/saturated/oversaturated conditions), (b) 3 × 3 grid network with symmetrical lanes (free flow/saturated conditions), and (c) 3 × 3 grid network with asymmetrical lanes (free flow/saturated conditions).

Simulations were conducted in VISSIM. To accurately represent undetected areas, the CTM parameters were set based on VISSIM settings, including free-flow speed, time headway, and standstill distance. The calibrated parameters included a free-flow speed of 50 km/h, a jam density of 166 vehicles/km, an optimal density of 36 vehicles/km, a saturation flow of 1,800 vehicles/h, and a backward shockwave speed of 14 km/h. The time step was set to 4 s, with a start-up lost time of 2 s, and the saturation flow during the transition from red to green signals was reduced by 50%. The cell length was defined as 54 m, covering the detectable range of 108 m, equivalent to two cells. Each cell accommodates up to 9 vehicles per single lane and 18 vehicles per two lanes.

To validate the similarity between the calibrated CTM and VISSIM, a comparison was performed using the flow-density data generated by the calibrated CTM and those collected from a signalized cell in VISSIM. As shown in Fig. 5, the fundamental diagram formed by the calibrated CTM closely matches the observed flow-density relationship. A more detailed validation was conducted by comparing the temporal variations of flow and density from both models over a one-hour period. The comparison, based on the first undetected cell of the eastbound through movement at Intersection 1 in Case Study 2, demonstrated close agreement, as illustrated in Fig. 6. Additionally, total travel times obtained from VISSIM were used for further validation, following the method in^{27] and [28}. The results showed errors of 6.5% under free-flow conditions and 8.9% under saturated conditions, confirming the reliability of the calibrated CTM in representing traffic states.

For Case Studies 2 and 3, a calibrated backward shockwave speed of 14 km/h was applied to both models. In Case Study 1, however, the originally assumed speed of 50 km/h was maintained to match the DC model’s assumptions. For each demand scenario, traffic movements were assumed to enter the network at a constant rate. The effect analysis was performed from 600 to 3,600 s into the simulation, after vehicles entered the network. Python was used for mixed-integer linear programming to determine the optimal phase. The effectiveness of each model was evaluated using metrics calculated through VISSIM and COM interfaces.

Fig. 5

Fundamental diagram from signalized cell at Intersection 1 in Case Study 2.

Fig. 6

Measured and estimated flow and density at the first undetected area cell for the eastbound through movement at Intersection 1.

B. Case Study 1: two Signalized intersections

In this section, the effectiveness of the proposed model is compared with previous models, DISCO and DC, at two signalized intersections. All lanes are considered as undetectable areas. The east-west bounds function as main streets, while the north-south bounds serve as side streets.

Table 2 Performance comparison for different control models (case study 1).

Table 2 presents the average stopped delay and control delay of the three models under different traffic demand levels. In the free-flow conditions, where demand across all movements is low, the three models exhibited similar stopped delays. However, as traffic demand approached saturation and oversaturation, the models produced different outcomes. The proposed model showed the highest average stopped delay due to its strategy of continuously allocating green time until delay levels between movements became balanced. As a result, movements with lower delays waited while congestion in higher-delay movements was alleviated. In contrast, DISCO and DC prioritized high-demand movements, leading to reduced stopped delays for eastbound and westbound through movements, as shown in Table 3. However, this prioritization significantly increased delays for other movements. By contrast, the proposed model substantially reduced delays for low-demand movements by penalizing delay deviation across movements, thereby improving equity.

Table 3 Average stopped delay (s/veh) for individual movements at intersection 1.

Figure 7(a) and (b) show that the westbound through movement at Intersection 1 experienced minimal delay under DISCO and DC. In contrast, the northbound through movement, due to its low demand, received less green time, resulting in longer queues and increased delays, as illustrated in Fig. 7(d) and (e). While the proposed model also aims to maximize throughput, it incorporates penalties to balance delay levels across movements. As a result, the northbound through movement passed through the intersection without substantial delay, as shown in Fig. 7(f). The westbound through movement experienced some delay due to green time allocation for side-street movements; however, queues were cleared during the green phase, as shown in Fig. 7(c). Although the proposed model appears to deteriorate traffic efficiency due to increased stopped delay, it ultimately improved overall performance by mitigating acceleration and deceleration delay caused by frequent phase switching in DISCO and DC. By consecutively assigning green time until delay levels across movements became balanced, the proposed model reduced control delay by 15.1–43.9% under congested conditions compared to the previous models.

Fig. 7

Input–output analysis in oversaturated conditions: (a) westbound through (DISCO), (b) westbound through (DC), (c) westbound through (proposed model), (d) northbound through (DISCO), (e) northbound through (DC), and (f) northbound through (proposed model).

C. Case Study 2: 3 × 3 Grid Network with symmetrical lanes

This section discusses the proposed model and DISCO in the 3 × 3 grid network. Each lane contains both detectable and undetectable areas due to the sensing range limitations of point detectors. The two models differ in their application of the weighting factor and start-up lost time.

Table 4 summarizes the average stopped delay, average control delay, average number of stops, CO emissions, and number of completed trips for DISCO and the proposed model. Both models show similar outcomes under free flow conditions. However, under saturated conditions, all measures except for the stopped delay were improved in the proposed model.

Table 4 Performance comparison for different control models (case study 2).

Figure 8 depicts the level of service for each movement based on the control delay, following the Korea Highway Capacity Manual²⁹. DISCO shows 81% of all movements in Level of Service (LOS) A to D, which is 1.1 times higher than the proposed model. However, some traffic movements experienced LOS FF to FFF. In contrast, the proposed model equalized the levels of control delay, with no traffic movements showing LOS FF. These observations indicate that the proposed model did not result in substantial delays for specific movements under saturated conditions.

When DISCO is operated, although the eastbound through movements at Intersections 1, 4, and 7 and the westbound through movements at Intersections 3, 6, and 9 indicate the highest demand levels, these movements showed LOS levels from F to FFF. This is due to the small deviation of demand levels between movements on main and side streets. As shown in Table 5, traffic demand on the main street at Intersection 1 in Case Study 1 is 63% of the total, while it is 52% in Case Study 2.

Fig. 8

Average control delay under saturated conditions for network 2: (a) DISCO, and (b) proposed model.

Table 5 Traffic demand in the DISCO model at intersection 1.

Both DISCO and the proposed model allocate the most green time to the eastbound through movement at Intersection 1, which has the highest traffic demand, as shown in Fig. 9. Since DISCO performs the throughput-maximizing approach without considering start-up lost time, it offers green time to two movements to maximize departure volumes per time step. As a result, the eastbound through movement experienced substantial delay due to start-up lost time resulting from frequent phase changes. In contrast, the proposed model allocates the green time continuously until the delay levels of each traffic movement are similar. Owing to the continuous allocation of green time, vehicles underwent fewer stops and had lower emissions compared to DISCO. Consequently, in the saturated conditions, 6,281 vehicles completed their routes, which was 15.4% more than with DISCO.

Fig. 9

Green time distribution at Intersection 1 under saturated conditions in network 2: (a) DISCO, and (b) proposed model.

D. Case Study 3: 3 × 3 Grid Network with asymmetrical lanes

This section compares the proposed model with PTSC in the 3 × 3 grid network, where the eastbound and westbound through movements are the main movements. PTSC prioritizes movements with high-demand movements, while the proposed model minimizes deviations in delay across all movements.

Table 6 summarizes the average stopped delay and control delay for both models under free-flow and saturated conditions. The proposed model achieved lower stopped delay than PTSC. This is attributed to PTSC’s prioritization of movements with high-demand movements, leading to longer stopped delay for low-demand movements.

Table 6 Performance comparison for different control models (case study 3).

Figure 10(a) and (b) illustrate the LOS for each traffic movement under free-flow conditions. The proposed model maintained LOS A to D for all movements, while PTSC resulted in LOS E for the southbound left movement at Intersection 3. This outcome arises from the interaction between the traffic movement and its compatible movements.

Fig. 10

Average control delay for network 3: (a) PTSC (free flow conditions), (b) proposed model (free flow conditions), (c) PTSC (saturated conditions), and (d) proposed model (saturated conditions).

As detailed in Table 7, although the traffic demand for the southbound left movement is 4.3 times higher than the westbound left movement, it received only 1.4 times more green time. This difference is due to the traffic demand of their compatible movements. The westbound through and eastbound left movements, compatible with the westbound left, comprise 29.6% of the total traffic demand. In contrast, the southbound through and northbound left movements, compatible with the southbound left, account for only 9.9% of the total traffic demand. These findings indicate that, even under free-flow conditions, PTSC may fail to allocate green time to movements such as the southbound left when their compatible movements also have low traffic demand.

Table 7 Green time ratios in the PTSC model under free flow conditions at intersection 3.

Under saturated conditions, the LOS for some traffic movement deteriorated, as shown in Fig. 10(c) and (d). PTSC improved the LOS for main movements but caused LOS FF to FFF for low-demand movements. In contrast, the proposed model ensured that all movements maintained above LOS FF.

Table 8 summarizes the green time ratios and average control delay at Intersection 7. PTSC prioritized high-demand movements, allocating 1.2 times more green time to the eastbound and westbound through movements compared to the proposed model. However, this approach led to LOS F to FFF for the northbound left, westbound left, and southbound through movements. The proposed model mitigated the delay for the northbound left movement by assigning 1.1 times more green time. Although PTSC allocated green time to the westbound left and southbound through movements similarly to the proposed model, it caused worse delays. This is due to frequent phase transitions, as maximum pressure changed sensitively in response to traffic volume fluctuations. In contrast, the proposed model continuously allocated green time until delays between movements were balanced, achieving a 27.4% reduction in control delay compared to PTSC.

Table 8 Green time ratios and control delay under saturated conditions at intersection 7.

Conclusions

This study introduces the equitable phase-free traffic signal control model to balance delay levels across individual traffic movements. The proposed model addresses which phase will operate during the next time step through a two-step process. First, the current number of vehicles in each cell, divided into homogeneous lengths, is estimated using data from video cameras installed at upstream and target signalized intersections. Based on the estimated state, CTM is applied to predict the number of vehicles for each phase at the next time point, serving as input for optimizing traffic signal control. Subsequently, the optimal phase is selected. To ensure that traffic movements with low demand receive the green time, the average waiting time per movement is incorporated into the objective function. The function is formulated to maximize throughput while penalizing deviations in delay levels between movements.

The effectiveness of the proposed model was demonstrated through simulations and compared with previous phase-free signal control models that employ throughput-maximization and queue-minimization approaches. Results from microscopic simulations on three different networks highlight the advantages of the proposed model. In free-flow situations at two signalized intersections, the proposed model yielded outcomes similar to previous models. However, in saturated conditions, previous models deteriorated the performance of traffic movements with low demand as the main traffic movement was frequently allocated the green time. Despite the prioritization of the main movement, the proposed model improved the delays of low-demand traffic movement by considering delay deviations between movements. In the 3 × 3 grid network, the proposed model maintained network conditions without traffic movements showing LOS FF or FFF. Moreover, average stops, CO emissions, and completed trips improved by continuously assigning the green time until the delay levels of all movements were similar. These results emphasize the importance of considering individual traffic movements as well as the overall efficiency of signalized intersections in phase-free traffic signal control.

Future work includes incorporating individual vehicle data and conducting real-world demonstrations. The current work estimated the traffic state per movement using aggregated data collected by video camera detectors. Since phase-free signal control aims to allow vehicles to pass through intersections smoothly, the proposed model could be extended to reflect the state of each individual vehicle. The model was designed for practical use at signalized intersections. Therefore, real-world applications should be conducted to demonstrate the effectiveness of the model.