Introduction

The most popular part of research in prediction methods, in the field of software engineering, is Software Defect Prediction (SDP)1. The effective forecast of deficiencies in software is actually an essential activity of the software expansion process, which can greatly contribute to the improvement and accuracy of defect prediction2. Therefore, software failure prediction is an important research topic in software engineering3. By finding the optimal models for predicting software defects, a number of distributed defects are often analyzed4. Software defect prediction methods use previous software metrics and defect data to predict defect-prone modules in future software versions5. If an error is reported during or after the testing process, the error data for the module will be 1, otherwise it will be 06. For predictive modeling, software metrics are used as independent variables and defect data is used as dependent variable7. Therefore, we need a version control system to store the source code, a change management system to log defects, and a tool to collect product metrics from the system version control8. The parameters of the prediction model are calculated using previous software metrics and defect data9. These models identify fault-prone modules before the testing phase10.

Problem statement

Recently, quality of software has been rapidly rising, which influences the reliability and cost of the software. However, the existence of deficiencies in the software reduces the quality in linear way and raises the finished price of the software product. Software defect prediction is one that makes a categorizer and forecasts areas of code that potentially include deficiencies11.

The results of the categorizer (for example, the programming part containing defects) can provide clues for code reviewers to make efforts to correct defects. Software defect prediction is an important part of analysis of software quality, which is analyzed through competence engineering Software reliability12. In engineering of software, early prediction of flawed sections of a software system is able to assist engineers and developers in appropriately using constrained resources in the maintenance and testing stages of software expansion.

Gap of the study

Recently, deep learning is widely utilized in different settings of machine learning. In the meantime, various methods have been presented for using this technique for software defect prediction. We deal with software defect prediction as it has become key in software development since it helps developers detect and fix defects earlier, which leads to cost efficiency and better-quality products. Despite the need for an automated and intelligent defect prediction solution, traditional manual testing procedures are inefficient and labor-intensive. More formally, the problem that concerns us is the construction of a valid and sufficiently effective model that can predict software defects from source code.

Objective and contributions

Several defect prediction models already exist in the literature, but little effort has been done in combining deep learning techniques with optimization algorithms for defect prediction. This study introduces a new defect prediction model, assess its performance and explore its possibilities to enhance software quality. This study makes the following contributions:

  • A new Residual/Shuffle (RS) Networks-based defect prediction model combined with an enhanced variant of Fish Migration Optimization (UFMO) algorithm.

  • Assessment of the suggested model on several open-source projects to show its practicality

  • Role of the proposed model in enhancing software quality and development practices. The paper is structured to include background and motivation, the proposed defect prediction model, the performance evaluation of the proposed metric, and discussion of the results, limitations, and conclusions.

The organization of the paper is continued as follows. Section "Related works" explains about the literature review about works in this field. Section "Conception" represents conception of the work about the bugs and errors and their detection. Section "Residual/Shuffle network" defines a general definition about the Residual-Shuffle Network. Section "Upgraded Fish migration optimization (UFMO) algorithm" describes about the proposed method for providing the upgraded Fish Migration Optimization (UFMO) Algorithm. Section "Methodology" explains about methodology of the work. Section "Simulation results" shows the simulations and experiments applied to analyze the method, and the paper is concluded in Section "Conclusions".

Related works

Qiao et al.4 suggested a new method that utilized deep learning approaches to forecast the quantity of deficiencies within software system. Firstly, a publicly accessible dataset was preprocessed, which involved data normalization and log transformation. Secondly, data modeling was carried out to prepare the input of data for the deep learning approach. Thirdly, the modeled data was input into a particularly developed deep neural network model for predicting the quantity of deficiencies. Additionally, the proposed approach was evaluated using two famous datasets. The assessment outcomes indicated that the suggested method was accurate and could outperform existing strategies. The proposed method led to a significant reduction in mean square error by 14% and an increase in the squared correlation coefficient by 8%.

Zheng et al.13 suggested an approach relevant to software flaw forecasting, which was on the basis of the Transformer model. Moreover, it entirely depended on self-attention approach. The code semantics of the end-to-end learning software could embed important details. To begin with, the module of software was transformed into an abstract syntax tree, which extracted the word series. Next, by considering the input, the layer of self-attention was utilized to conduct semantic attribute embedding. Ultimately, the Softmax NN was employed to forecast the software deficiency. Experimental findings demonstrated that the software deficiency forecasting method using the Transformer model yielded superior deficiency forecasting outcomes, with an average improvement of 3.2% compared to the optimal model based on CNN (Convolutional Neural Network).

Farid et al.14 recommended a hybrid model that was named CBIL, which could forecast the flawed zones of source code. First, the semantics of AST tokens were extracted by a CNN. Next, a Bi-LSTM (Bidirectional Long Short-Term Memory) was used to retain important features and disregard others, thereby improving the accuracy of software defect prediction. The outcomes indicated that the model of CBIL enhanced the mean F-measure by 25% in comparison with CNN. Additionally, regarding average AUC, the CBIL model demonstrated an 18% improvement in comparison with the RNN (Recurrent Neural Network), which achieved the highest efficacy among the baseline models.

Nevendra and Singh15 offered a method for identifying the modules that have deficiencies within software employing enhanced CNNs. The article’s objective was to detect faulty samples employing an improved deep learning approach. The trials revolved around WPDP (Within Project Defect Prediction) and involved K-fold cross-validation. The experimental findings demonstrated that the suggested method outperformed the standard ML and Li’s CNN model. Furthermore, the Scott-Knot ESD exam was conducted that confirmed the efficacy of the suggested technique. It was illustrated by the results that the suggested model could achieve the average values of 0.775, 0.782, and 0.786 for accuracy, precision, and F1-accuracy.

Khleel and Nehéz16 suggested sampling approach to overcome the imbalance issue of the class and enhance the efficacy of the ML within SDP. The suggested network was on the basis of CNN (Convolutional Neural Network) and GRU (Gated Recurrent Unit) integrated with the Tomek link (SMOTE Tomek) and synthetic minority oversampling approach. The findings of the study revealed that the suggested network forecasted the deficiencies of software more efficiently using the balanced dataset. There was 19% enhancement in CNN and 24% enhancement in GRU model regarding AUC. The results displayed the suggested network could highly outperform the other SDP techniques on numerous datasets. Table 1 reviews the related state-of-the-art methods in software defect prediction:

Table 1 The related state-of-the-art methods in software defect prediction.
Full size table

It is important to recognize that the advantages and disadvantages outlined are not comprehensive and may differ based on the particular implementation and dataset employed.

Conception

Software defects, often called bugs or errors, arise as the unintended results of human errors during the complex software development process, which can be subtle and complex, leading to discrepancies in the expected behavior of the code and ultimately causing the software to fail when are executed It is not possible to encounter software that is completely free of defects17. In reality, most applications have multiple defects that can range from major issues that require immediate attention to minor bugs that are considered to be of low impact18.

These defects can have far-reaching consequences and affect the performance, security and overall user experience of the software. Software defect prediction has emerged as a preventive measure to predict and address specific problems. Using analytical methods, historical data, and code metrics, developers can create predictive models that highlight potential areas of future versions with defects. This predictive strategy allows developers to allocate resources more effectively, improve software quality, and reduce problems related to defect resolution. Reliable fault prediction models are very important to ensure the reliability and resilience of software applications. The importance of Software Defect Prediction (SDP) is further emphasized by the possible consequences of undetected defects. Severe defects can lead to catastrophic system failures, data corruption, or even risks to user safety. Although minor defects may seem insignificant, they can gradually reduce user satisfaction, hinder productivity, and damage the credibility of the software and the development team.

Hence, effective defect prediction and subsequent resolution is critical to ensuring the overall success and longevity of a software program. In the presented table, we provide illustrative examples of clean code without defects and defective code containing possible problems. By scrutinizing and comparing these cases, valuable insights can be gained into patterns, best practices, and common problems that contribute to software defects. This analytical process forms a platform for developing robust defect prediction models and refining software development methods19. The SDP has seen significant advances characterized by the integration of sophisticated machine learning and deep learning techniques. These advanced models have the ability to independently detect patterns and complex relationships in the code and thus increase the accuracy of the prediction. In addition, the synergistic collaboration between development tools and SDP SDP, complemented by continuous integration methods, facilitates rapid defect detection and proactive prevention, ultimately increasing the quality of the software. Table 2 shows a sample of two examples of clean and defective code.

Table 2 A sample of two examples of clean and defective code.
Full size table

We have two types of software defect prediction models. Within-Project Defect Prediction Model (WPDP) and Cross-Project Defect Prediction Model (CPDP). The WPDP model uses data derived from historical versions in a single project, with training and testing datasets from the same project. In contrast, the CPDP model consists of two separate projects, where the model is trained using the data set from one project and evaluated with the data set from the other project. This study evaluates the performance of a hybrid deep model in the context of WPDP and CPDP.

The aim of this study is to present an advanced deep learning model to scrutinize the way that deep learning models carry out with flaw forecast datasets. The suggested model uses state-of-the-art convolutional neural networks to predict defect-containing samples from historical datasets. The proposed method includes two steps: model building and forecast. Within the model establishment stage, we initially choose relevant features employing techniques of feature selection and then use them to make the network through advanced convolutional neural network approaches. When, the network has been established, we proceed to forecast software defects in the next step. To assess the proposed technique, we use key machine learning evaluation criteria.

Residual/shuffle network

The Residual-Shuffle Network has been specifically created for SDP and is an effective CNN. Its central component incorporates a streamlined shuffle unit that has a residual skip link20. To enable the model to learn local characteristics rather than global ones, multiple convolutions are utilized within the structure.

The current model’s framework is derived from the fundamental version of ShuffleNet V2. However, the initial single outlet has been split into two channels. One outlet undergoes convolution operation while the other operates as a feed-forward element. Overall, the model consists of 3 network flows: bottom, middle, and top modules21. In the subsequent description, the Residual-Shuffle-Net module has been depicted, and the size of input image has been shown as 256 × 256 pixels.

$$RS = M_{1} \times M_{2} \times M_{3} \times I$$
(1)

where, \({M}_{1}\) the bottom module includes an entry model that will produce difficult features by employing two layers of convolution \(C\) and the maximum operators of down-pooling. The present model uses Leaky ReLU activation function and batch normalization for all convolution operations. In the initial part of the model, small filter sizes are utilized to keep the quantity of variables minimal. The bottom structure contains 16 and 8 channels for the two convolution operations.

$$M_{1} = C_{1} .P_{1} .C_{2} .P_{2}$$
(2)

The main RSU has been involved within the \(M_{2}\) (middle module). Four consecutive RSU networks exist here that \(P\) with the purpose decreasing the scope of feature map; however, element four is not included.

$$M_{2} = (\mathop \prod \limits_{i = 0}^{3} RSU_{i} \times P_{i} ) \times RSU_{4}$$
(3)

The primary feature map scope in the current model is \(64 \times 64\) pixels, and the feature map scope at the output of the model is \(8 \times 8\) pixels. Therefore, the variation in feature map scope is minimal to maintain the suggested network’s lightweight design. Convolutional operators will be present at all stages. The network uses a bottleneck approach for convolution operations, with the middle convolutional operator having fewer filters compared to the third and initial operators.

The residual skip connection’s input layer is based on the output of the first convolution and will be combined with the output of the third convolution22. Within the second convolution operation, shuffling and grouping operations have been performed, using a simple channel splitting process to divide the feature maps into two equal groups. Additionally, the integrated result will be combined again using a combination operator. The inclusion of group and shuffle operations forces the network to learn from diverse sets of features rather than overall characteristics.

The consecutive RSU framework allow the network to learn diverse local features instead of global features within each layer of convolution. The framework of the suggested model has been demonstrated in Fig. 1.

Fig. 1
figure 1

The framework of the residual-shuffle unit.

Full size image

\({M}_{3}\) (eventual module) utilizes a Spatial Pyramid Pooling (SPP) element that is created through a combination of average pooling and dense connections. This study focused on a three-class issue, so a softmax activation function with three output classes is used to determine the likelihood of an image belonging to each class23. The incorporation of the SPP component aims to improve the capability of network to extract multi-scale features from sports images. In this study, the dataset is used to demonstrate that the model’s effectiveness encompasses various levels of the problem complexity.

The problem exhibits various scopes of air pockets, which makes it difficult to distinguish them with the naked eye. In order to handle this issue, three identical down-pooling operations were carried out to extract the multi-scale characteristics, which will be resized and recombined later. Down-pooling using 2 by 2, 4 by 4, and 6 by 6 kernels was performed to create similarly spaced scales, as the input feature map’s size is 8 × 8 pixels. The spatial pyramid pooling unit’s framework is illustrated in Fig. 2.

Fig. 2
figure 2

The framework of the SPP unit.

Full size image

Following this, a standard global average pooling operator \(G\) is used to sample the most detailed multiscale features before being processed by a dense feedforward layer24. The dense connection layer is indicated by \(D\) and has three output categories. To categorize the model with 1,988,558 parameters, the SoftMax activation function is utilized.

$$M_{3} = SPP \times G \times D$$
(4)

It is possible to improve the Residual-Shuffle Network (RSE) by using metaheuristics. Metaheuristics are optimization techniques that can effectively explore complex search spaces to find nearly optimum solutions. They can be essential in optimizing various aspects of the RSE network, such as its structure, hyperparameters, weights, and control signals. This paper introduces a novel approach for optimizing the model called the city game optimizer.

Upgraded fish migration optimization (UFMO) algorithm

Every fish serves a distinct purpose as it moves through the water. The grayling method enhances the optimization of fish migration. The “M1” to “M4” values represent the quantity of fish capable of survival, while “R2” to “R4” indicate the efficiency of fish returning to their place of origin. Young fish are signified by ‘0 + ’. Throughout this life phase, they remain close to their birthplace in search of food since they cannot migrate. Each grayling moves and search for nutrition in farther regions when they grow up.

Once these animals get to phase ‘ + 4’, they have to move back to their place of birth. The graylings have been found to be endangered via enemies in nature, and some of them are eaten each year.

Initialization

The process of optimizing starts by randomly selecting the location of the fish in five different categories of age. The distribution of grayling numbers is in the following way: 1: 1: 1: 0.64: 0.64. Fish are capable of migrating based on their energy level, denoted as \({y}_{eng}\) in the proposed approach. It is believed that each grayling begins at a 2 percent rate.

Evolution

The Graylings commence migration when they are at phase ‘2’. The capacity of fish in moving has been influenced by its energy. This procedure has been computed in the following formula:

$$Y_{eng\left( j \right)} = Y_{eng\left( j \right)} - \frac{{f_{j} }}{{\mathop \sum \nolimits_{j = 1}^{n} f_{j} }}$$
(5)

here, the quantity of these animals has been displayed via \(n\), the individuals have been demonstrated by \(j\), and the value of benchmark function is depicted via \(f_{j}\).

As the individuals grow up, their energy level decreases. Whereas, considering the current approach, the energy level of these candidates progresses when a superior solution is found.

$$Y_{eng\left( j \right)} = Y_{eng\left( j \right)} + r_{1} {*}Y\_eng\left( {j,init} \right)$$
(6)

The initial energy of individual \(j\) has been represented by \(Y_{eng} \left( {j, init} \right)\), and a stochastic number has been provided by \(r_{1}\), ranging from 0 to 1.

Fertility

The entire quantity of these individuals changes after a while, because some of these candidates get eaten. The whole procedure can be computed subsequently:

$$Y_{{number\left( {t + 1} \right)}} = Y_{number\left( t \right)} {*}state\left( t \right)$$
(7)

where, the quantity of these candidates within iteration \(\left( {t + 1} \right)\) has been demonstrated via \(Z\), the ratio of survival has been depicted by \(state\), and the value of ratio from the initial stage to the last one (fourth) has been 1, 0.92, 0.90, 0.85, and 0.64. A proportion of these candidates has been eaten in stage ‘0 + ’, and most of them have been eaten in stage ‘4 + ’25.

The objective is to prevent getting stuck in exploitation employing this optimizer and increase the chance for exploration. The algorithmic stages involve the young fish altering the deceased individual, which is the most effective method for determining the migration paths of the remaining individuals.

$$temp = r_{2} {*}(Y_{s} - gb_{pos} )$$
(8)
$$Y_{s} = temp + gb_{pos}$$
(9)

where, the optimum global situation has been demonstrated by \(gb\_pos\), \(r_{2}\) has been found to be a number ranging from 0 to 1, and the survived individuals have been indicated by \(Y_{s}\).

Movement

Once each individual grows up well, the commence migrating and travelling. This behavior has been mathematically calculated in the subsequent manner:

$$ori_{speed} = \left\{ {\begin{array}{*{20}l} {Y\left( j \right) - Y_{pre} \left( j \right)} \hfill & {if\quad \left( {r_{3} \ge 0.5} \right)} \hfill \\ {Y_{pre} \left( j \right) - Y\left( j \right)} \hfill & {\quad \quad else} \hfill \\ \end{array} } \right.$$
(10)
$$Y\left( j \right) = ori_{speed} {*}consumption + Y_{{eng\left( {j,init} \right)}} {*}r_{4} {*}\left( {gb_{pos} - Y\left( j \right)} \right)$$
(11)
$$consumption = \left\{ {\begin{array}{*{20}l} {Y_{eng} \left( {i,init} \right)*r_{4} } \hfill & { if\quad (Y_{eng} \left( j \right) \ge Y_{eng} \left( {j,int} \right)} \hfill \\ {Y_{eng} \left( j \right)*r_{6} } \hfill & {\quad \quad else} \hfill \\ \end{array} } \right.$$
(12)

where, the variables \(r_{6}\), \(r_{5}\), \(r_{4}\), and \(r_{3}\) range from 0 to 1, the initial situation of the individuals has been displayed via \(Y\_pre\), and the movement energy for travelling has been depicted by \(Y\_eng\).

Equation (7) determines the situation renewal within stages “ + 4”, “ + 1”, and “ + 0”. Moreover, the situation renewal in steps “ + 3” and “ + 2” have been determined via Eq. (9).

Upgraded fish migration optimization (UFMO) algorithm

This part of the paper presents an improved version of the Fish Migration Optimization (FMO) algorithm with the aim of increasing its performance and efficiency. A significant change is made to the wandering hunting phase to improve step size adjustment. Instead of providing a random factor, we use an adaptive factor that changes the step size according to the fitness value of the current solution and the best solution identified to date. This adaptive approach helps to avoid local optima trapping and improves the exploration capabilities of the algorithm.

$$\zeta_{j} = \frac{{f\left( {Y_{eng} \left( j \right)} \right) - f\left( {Y_{best} \left( j \right)} \right)}}{{f\left( {Y_{best} \left( j \right)} \right) + \epsilon }}$$
(13)

where, and \(\epsilon\) is set to be a small positive constant for avoiding division via zero, \(f\left( {Y_{eng} \left( j \right)} \right)\) represents the fitness value of the candidate at iteration \(j\), \(f\left( {Y_{best} \left( j \right)} \right)\) describes the fitness value of the best candidate at iteration \(j\). The situation of the GKS is updated as:

$$Y_{eng\left( j \right)} = Y_{eng\left( j \right)} + \zeta_{\left( j \right)} {*}Y_{eng} \left( {j,init} \right)$$
(14)

Proposed residual/shuffle/UFMO (RSH/UFMO)

The UFMO is capable of optimizing the variables and framework of RSE; moreover, it can determine the most appropriate permutation function for all RSUs.

It has been previously debated that an RSU works as the major element of the suggested network, which comprises two Beneš blocks and a residual connection. The Beneš blocks, a switches network, that can perform input’s permutation in stages of \(O(log n)\), and the length of sequence has been displayed via \(n\). a switch, which has been considered a fundamental element, is capable of passing through or swapping its inputs on the basis of signal of a binary control. The model can acquire the switches’ control signals via training.

For optimization of the present framework, the fitness function of the suggested network is calculated in the following manner:

$$L\left( {\theta ,\lambda } \right) = \mathop \sum \limits_{i = 1}^{N} l\left( {y_{i} ,\hat{y}_{i} } \right) + R\left( {\theta ,\lambda } \right)$$
(15)
$$\hat{y}_{i} = f\left( {x_{i} ,\theta } \right)$$
(16)

here, the variables of the network have been depicted via \(\theta\), the hyperparameters have been represented via \(\lambda\), the samples of training have been indicated via \(N\), the forecasted output has been demonstrated via \(\hat{y}_{i}\), the input has been illustrated via \(x_{i}\), the function performed via RSE has been signified via \(f\), the loss function has been represented via \(l\), the real output has been displayed via \(y_{i}\), and the term of regularization has been shown by \(R\left( {\theta ,\lambda } \right)\), which has been affected by choosing regularization variables and optimizer. The aforementioned elements have been computed subsequently:

$$l\left( {y_{i} ,\hat{y}_{i} } \right) = \frac{1}{2}(y_{i} - \hat{y}_{i} )^{2}$$
(17)
$$R\left( {\theta ,\lambda } \right) = \frac{\lambda }{2}\mathop \sum \limits_{w \in \theta } w^{2}$$
(18)

where, weight has been represented by \(w\), and its L2-norm has been demonstrated by \(R\) that has been determined via \(\lambda\).

The best values for the decision variables are \(x\) and \(y\) that are equal to 5, indicating that the rectangle ought to be a square with each side should be 5. The optimum outcome of the fitness function is \(Z\) which equals 25, signifying that the best zone of the rectangle has been found to be 25. The current solution has been confirmed by replacing the values of \(y\) and \(x\) with the fitness function and the limitation.

Methodology

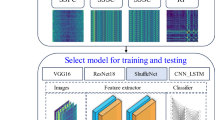
This section introduces our proposed Residual/Shuffle/UFMO (RSH/UFMO) arrangement, designed to enhance software defect prediction accuracy through the automated extraction of semantic and structural features from source code. Complementing these novel features, RSH/UFMO incorporates traditional defect prediction metrics for a comprehensive approach. The general outline is displayed in Fig. 3.

Fig. 3
figure 3

The general outline of the prosed system.

Full size image

As can be observed from Fig. 3, the RSH/UFMO model includes four main stages. At first, training and test datasets source code files endure parsing to generate Abstract Syntax Trees (ASTs). ASTs serve as a foundational representation of code structure, capturing syntactic relationships between code elements. To transform these ASTs into a machine-processable format, representative nodes have been chosen and converted into token vectors. This process encodes the source files as a sequence of tokens.

In the next stage, the token vectors have been encoded. To simplify the transition from textual to numerical representations, a correspondence has been established between tokens and integers. These integer representations are transformed into dense numerical vectors using word embedding techniques, that compass both semantic and syntactic information. These enhanced vectors serve as the input for the subsequent Convolutional Neural Network (CNN) layer.

The CNN layer is important in the automatic extraction of high-level semantic and structural features from the encoded source code. With implementing filters into the input vectors, the CNN separates patterns and relationships within the code. The features learned through this process create a comprehensive feature set in conjunction with traditional defect prediction metrics. A detailed representation of the feature selection process is displayed in Fig. 4.

Fig. 4
figure 4

A detailed representation of the feature selection process.

Full size image

In the final stage, a Logistic Regression classifier has been trained on the integrated feature set. This classifier evaluates the new code files, conveying a probability that specifies its potential to contain defects. The model effectively differentiates between defective and clean code by fine-tuning the weights and biases within both the CNN and Logistic Regression components.

Source code parsing

Preprocessing

Preprocessing is the first stage in preparing source code for the RSH/UFMO model. Preprocessing cleans and normalizes the code to enhance the consequent analysis. This study uses four methods for preprocessing the data:

  • Comment removal Eliminating comments from the code as they typically do not contribute to the code’s functionality or structure.

  • Whitespace normalization Consistent formatting of whitespace (spaces, tabs, newlines) to improve readability and prevent unintended tokenization issues.

  • Language-specific cleaning Removing language-specific constructs or elements that might interfere with the parsing process. For example, in Python, removing docstrings or shebang lines.

  • Code style normalization Applying consistent code style conventions (e.g., using specific indentation styles, naming conventions) to reduce variations in the codebase.

Abstract syntax tree (AST) generation

An Abstract Syntax Tree (AST) is a step-by-step syntactic structure representation of a program which indicates the interconnections among different code components and offering an organized perspective of the code. The main steps of the AST are given below:

  • Lexical analysis in this stage, the code has been segmented into tokens (like keywords, identifiers, operators, and literals). This is done based on the specific rules of the programming language.

  • Parsing Based on grammatical framework identification using a parser, an AST has been constructed which contains applying the step-by-step relationships among tokens and forming corresponding nodes by the AST.

  • AST construction In this stage, the nodes have been generated by different syntactic components (like functions, classes, statements, and expressions). There is a specific code for the nodes with their children as sub-components.

ASTs provide significant impact in code analysis by providing a structured format which provide in the extraction of both semantic and structural information. A comprehensive understanding of the syntactic structure of the code enables the model to more effectively recognize patterns and relationships among code elements.

Tokenization

Tokenization divides the AST into individual tokens as essential units for the next processing. There are multiple tokenization schemes: word-based tokenization treats entire words or identifiers as tokens, suitable for languages with strong lexical structure; character-based tokenization splits code into individual characters, capturing fine-grained information but potentially leading to a larger vocabulary; and subtokenization, a hybrid approach using subword units (e.g., Byte Pair Encoding), balances the strengths of both methods. The optimal tokenization scheme depends on the language’s characteristics and the desired level of analysis granularity.

Token selection

Token selection is important for improving the efficiency and focus of model that contains the careful curation of a token subset from the AST. A significant criteria for selection is codebase token frequency, while their informativeness for defect prediction (e.g., prioritizing error handling or control flow keywords), and the reduction of computational complexity through dimensionality reduction. By leading to improved performance and strategically selecting representative tokens, the model can prioritize relevant information.

Here, three specific categories of nodes within AST have been observed for tokens:

  1. A.

    Nodes that signify method requests and the class instances creation have been recognized by their corresponding method or class names.

  2. B.

    Declaration nodes that contain method declarations, type declarations, and enum declarations, as the source from which we derive values to create our tokens.

  3. C.

    Control-flow nodes (like IfStatement, WhileStatement, ForStatement, ThrowStatement, and CatchClause) are documented exclusively by their types.

In this study, some specific categories of AST nodes like Assignment nodes that regularly knotted to specific methods or classes and do not possess consistent relevance throughout the entire project have been exclude.

Figure 5 shows the selected AST nodes for this study.

Fig. 5
figure 5

The selected AST nodes for this study.

Full size image

This enables us to convert the source files into a vector of tokens.

Tokens encoding and imbalance handling

In this section, the tokens transformation, like the potential issue of class imbalance has been addressed into a numerical illustration suitable for machine learning models. Token embedding techniques, (here Word2Vec) are used to convert tokens into dense numerical vectors, capturing both semantic and syntactic information. These embeddings are then integrated through a process called vectorization to form numerical representations for entire source code files. However, software defect prediction datasets often suffer from class imbalance, where non-defective instances far more than defective ones, which can negatively impact model performance. To mitigate this issue, various techniques can be employed, including oversampling the minority class, undersampling the majority class, or using class weighting to assign different weights to each class, thereby balancing the dataset and improving model accuracy.

Predicting defects

This section focuses on the final stage of the RSH/UFMO model, where the model makes predictions about code defects. The main idea is to be covered include the choice of Logistic Regression as the classifier, which should be explained along with the rationale for using this model.

Also, the training process should be described in detail, including the optimization algorithms, loss functions, and hyperparameter tuning used. The evaluation metrics used to assess the model’s performance, along with how the model is evaluated on both training and testing datasets. Finally, if applicable, techniques for interpreting the model’s predictions, such as feature importance analysis, should be explored to provide a deeper understanding of the model’s decision-making process.

Simulation results

The results of this study are compared with various models specifically designed for predicting software defects. The experimental configuration employed MatlabR2019b on a system featuring an Intel Xeon Gold 5218 CPU, which has 24 cores operating at a clock speed of 3.4 GHz, complemented by 128 GB of RAM and an Nvidia Quadro RTX 6000 GPU, providing 4608 CUDA cores and 24 GB of graphics memory.

Dataset description

This section uses PROMISE dataset for analyzing our model. The dataset is based on 7 projects of open-source Java. The PROMISE dataset has been found to be a publicly accessible repository frequently used for tasks related to software defect prediction. The selected projects represent a wide array of applications, including an XML parser, adapters of data transport, and a library of text search engine. Figure 6 represents comprehensive details of the projects.

Fig. 6
figure 6

Comprehensive details of the projects.

Full size image

Where, the total files are [1.4, 1.6], [4.0, 4.1], [2.0, 2.2], [2.5, 3.0], [1.1, 1.2], [2.5, 2.6], and [1.2, 1.3] for Camel, Jedit, Lucene, Poi, Synapse, Xalan, and Xerces, respectively.

For the suggested RSH/UFMO model, the embedding dimension is set 20, enabling the representation of each token within a 20-dimensional framework. Also, the length of the AST vector is set to 1500 to encapsulate the structural features of the code. In the dense layer, the sigmoid activation function is used to generate the output values ranging from 0 to 1, which is especially advantageous for binary classification tasks. The parameters are uniformly applied based on a batch size of 32 and an epoch count of 40 to ensure consistent processing and training of the model.

Validation of upgraded fish migration optimization (UFMO) algorithm

Evaluating the effectiveness of optimization algorithms often involves rigorous testing against a suite of well-known mathematical functions with known global optima, a process commonly referred to as global optimization or real-valued parameter optimization. This practice has become prevalent in the optimization community due to the abundance of proposed techniques and the need for standardized comparisons. Synthetic functions, such as the "CEC-BC-2017 test suite," serve as benchmarks to assess the performance of metaheuristics algorithms.

In this study, the proposed UFMO algorithm was put to the test against ten randomly selected cost functions from the CEC-BC-2017 test suite. To ensure impartial scrutiny, strict parameters were set: search boundaries between -100 and 100, a maximum iteration count of 200, and a population size of 50. The performance of UFMO was then compared against five established optimization algorithms: Teamwork Optimization Algorithm (TOA)26, Harris Hawks Optimization (HHO)27, Supply–Demand-Based Optimization (SDO)28, Dwarf Mongoose Optimization Algorithm (DMOA)29, and Growth Optimizer (GO)30. Table 3 indicates the parameter set value for the studied algorithms.

Table 3 Parameter set value for the studied algorithms.
Full size table

We have evaluated the algorithms for 10 times for each function to provide a fair analysis. Table 3 indicates the algorithm analysis based on average value (Avg) and standard deviation value (StD) compared with the aforementioned algorithms.

As can be seen, UFMO outperforms all other algorithms across the evaluated functions as indicated by its lower mean for the objective function. Based on the results, UFMO has consistently outperformed other algorithms in terms of average performance in all evaluated functions, indicating its robustness and efficiency in identifying near-optimal solutions. In many cases, UFMO also exhibits a lower standard deviation compared to its counterparts, indicating that it is less prone to random variation during the search process and produces more reliable results.

Measurement indicators

The evaluation of the RSH/UFMO model’s performance have been addressed by a range of standard and widely used metrics in software defect detection. These indicators include Precision, recall, F-measure, and AUC. The mathematical formulation for these indicators is defined below:

$$Precision = \frac{TP}{{TP + FP}}$$
(19)
$$Recall = \frac{TP}{{TP + FN}}$$
(20)
$$F - measure = \frac{2 \times Precision \times Recall}{{Precision + Recall}}$$
(21)

where, TP (True Positive), TN (True Negative), FP (False Positive), and FN (False Negative) represent the accurate predictions of vulnerable instances, the accurate predictions of non-vulnerable instances, the erroneous predictions where non-vulnerable instances are identified as vulnerable, and the erroneous predictions where vulnerable instances are identified as non-vulnerable, respectively.

Also, the Area Under the Curve (AUC) is used as another indicator which defines the efficacy of binary classification models. The AUC definitely affects to the area beneath the Receiver Operating Characteristic (ROC) curve as a term that determines the connection between the True Positive Rate (TPR) and the False Positive Rate (FPR) through different classification thresholds.

The ROC curve visually depicts the trade-offs in performance between TPR and FPR. Each classification threshold produces a coordinate pair (FPR, TPR), and the combination of these points constitutes the ROC curve. The AUC value quantifies the area beneath this curve, yielding a singular scalar value that encapsulates the model’s performance across all potential classification thresholds. AUC values range from 0 to 1, with higher values signifying superior model performance.

Comparison analysis

This section outlines the findings of the proposed RSH/UFMO model and addresses the research questions. The experiments were performed using the PROMISE dataset and were compared against some other models, including RSH, RSH/FMO, CNN, and RNN with the results detailed in Table 4. A total of 10 experiments were conducted, each with different learning rates.

Table 4 Algorithm analysis of the UFMO compared with some other state-of-the-art algorithms.
Full size table

The findings illustrated in Fig. 7 highlight the efficacy of the proposed RSH/UFMO model in software defect prediction, surpassing the performance of alternative models such as RSH, RSH/FMO, CNN, and RNN across seven distinct projects: Camel, Lucene, Jedit, Synapse, Poi, Xerces, and Xalan. The RSH/UFMO model consistently achieves the highest accuracy across all projects, with an impressive average accuracy of 0.93.

Fig. 7
figure 7

The comparison results of the analysis.

Full size image

This indicates that the combination of the Upgraded Fish Migration Optimization (UFMO) algorithm with the Residual/Shuffle (RSH) Network significantly enhances the model’s overall performance. The model demonstrates reliable performance across all projects, with accuracy metrics ranging from 0.78 to 0.99, thereby outperforming the other models, which exhibit lower average accuracy figures.

Furthermore, the RSH/UFMO model shows marked improvement over both the RSH and RSH/FMO models, underscoring the critical role of the UFMO algorithm in boosting the model’s effectiveness. A detailed project-wise analysis reveals that the RSH/UFMO model attains high accuracy levels across all projects, achieving a peak accuracy of 0.99 in the Xerces project. The result of the measurement indicators has been illustrated in Table 5.

Table 5 The result of the measurement indicators.
Full size table

As can be observed from Table 5, there is a comprehensive overview of the RSH/UFMO model’s performance across various software projects, utilizing key measurement indicators. Each indicator provides valuable insights into the model’s effectiveness in defect prediction. Precision, for instance, shows the model’s accuracy in identifying true defects, with values ranging from 0.73 to 0.98, minimizing false positives. Recall, on the other hand, measures the model’s ability to identify true defects out of all actual defects, and the RSH/UFMO model excels in this regard, achieving values between 0.71 and 0.98, reducing the risk of missing critical issues.

The F-measure, a balanced assessment considering both precision and recall, consistently yields high values, indicating the model’s overall effectiveness. AUC, or Area Under the Curve, underscores the model’s discrimination capability, with excellent values ranging from 0.78 to 0.99, highlighting its ability to effectively separate defective and non-defective instances. The results in Table 5 further emphasize the model’s consistent performance across different software projects, notably achieving peak accuracy in the Xerces project with a precision of 0.98, recall of 0.98, F-measure of 0.96, and AUC of 0.99.

The high precision and recall values obtained by the RSH/UFMO model validate its accuracy in identifying true defects while minimizing false positives and false negatives, ensuring that developers can focus their efforts on addressing genuine issues. Overall, the measurement indicators in Table 5 demonstrate the RSH/UFMO model’s strong performance and adaptability in software defect prediction, enhancing its potential to improve software quality and testing efficiency.

Conclusions

The software defects prediction is a significant process for ensuring the reliability of software applications. Conventional manual testing methods show limitations in efficiency, necessitating the exploration of the new solutions. In this study, an optimized deep learning methodology was introduced that meaningfully improved the processes involved in software defect prediction. By integrating the capabilities of Residual/Shuffle (RS) Networks with an upgraded version of Fish Migration Optimization (UFMO), the model’s efficiency in learning both semantic and structural features from software code was enhanced. The RS/UFMO model proved its effectiveness through extensive evaluations across various open-source projects, consistently uncovering potential defects and offering valuable insights to developers. The approach delivered an automated and intelligent solution for bug prediction, enhancing accuracy while preserving important resources. Through the application of deep learning and optimization algorithms, notable advancements were made in the capabilities of software defect prediction. The outcomes show an increase in the precision (78–98%), recall (71–98%), F-measure (72–96%) and Area Under the Curve (AUC)(78–99%). The exceptional performance of the RS/UFMO model highlighted the transformative potential of artificial intelligence in software development practices. The research illustrated how AI could be effectively utilized to resolve complex software challenges, ultimately resulting in higher-quality and more dependable software applications. However, the study has some limitations, including the reliance on a specific dataset. Also, the proposed method may not perform well on highly imbalanced datasets or datasets with a large number of features. This study donated to the ongoing progress in the field, equipping developers with improved tools and methodologies to enhance software quality and user satisfaction. Future research may focus on investigating deep learning architectures and optimization techniques to further enhance defect prediction accuracy and broaden its applicability across various software domains.