Nuclei discovered new practical insights via optimized soliton-like pulse analysis in a space fractional-time beta-derivatives equations

Abstract

Nerve signal conduction, and particularly in myelinated nerve fibers, is a highly dynamic phenomenon that is affected by various biological and physical factors. The propagation of such moving electric signals may seemingly help elucidate the mechanisms underlying normal and abnormal functioning. This work aims to derive the exact physical wave solutions of the nonlinear partial differential equations with fractional beta-derivatives for the cases of transmission of nerve impulses in coupled nerves. To this end, the research uses a polynomial expansion approach to convert the problems of modeling nerve impulses into a second order elliptic nonlinear ordinary differential equation containing fractional beta-derivatives. Such transformation permits the study of solitary waves and their perturbation responses in the case of nerve fibers. The other direction of this study is applying the fixed-point theory to analyze the system dynamics and obtaining the Jacobian matrix to peruse the stability. Modulation instability regions are visualized, and nerve impulse waveforms are shown in three and two dimensions. The investigation depicts how impulse transmission amplitude and velocity are influenced by changing nerve fiber diameter and varying order physiological parameters. Soliton-like kink, anti-kink, and rogue wave solutions are revealed to explain nerve impulse propagation thoroughly. The analysis provides significant regions of equilibrium and modulational instability showing that the behavior of the nerve fibers is more dynamic than appreciated by most authors. Additionally, the authors suggest a refined mathematical formulation of the nerve impulse conduction with particular emphasis on the effect of fractional beta-derivatives on the transmission of waves. The obtained solutions and the graphs support their usefulness in various medical and biological industries, specifically the research on myelinated nerve fibers. The findings provide additional insights into the processes of nerve conduction which may be useful in the treatment of various diseases of the nervous system.

Introduction

Prior to advancing with the current review, it is pertinent to recognize the numerous parallels between the architecture of nerve fibers and that of electrical conductors^{1,2,3,4,5,6,7,8,9,10}. The researchers Hodgkin and Huxley conducted a study in 1952 focused on the neuroelectric nerve impulse in the dorsal or temporal aspect of ameristatid purse-shaped giant axons⁶. As advancements in scientific research continue, numerous analytical studies on arterial behavior have been reported. The documents in question pertain to the behavior of these fibers, which are described by partial differential equations of nonsmoothed type, categorized as either fractional-order or integer-order^{4,5,11,12,13,14,15,16,17,18,19,20}. Signal conduction along the nerve fiber is a manifold process involving numerous interconnected mechanisms, similar to other biological activities. A multitude of efforts has been undertaken to scrutinize this dynamic; however, various experimental and theoretical methods converge in each of the approaches according to the application fields. Theoretical studies have focused on modeling and in vitro simulation of biological systems, population dynamics, and the mathematics of viral spread and control. Excitation along the nerve fiber represents a critical biological function within living systems. Subsequently, due to the aforementioned reasons, a thorough evaluation of nerve conduction is warranted, and several research studies were led^{21,22,23,24,25}. The characterization of nerve fibers involves the application of nonlinear partial differential equations, specifically the nonlinear reaction-diffusion equations within fractional derivatives operators. Multiple nerve fibers are indeed composed of periodic active structures that consist of branching nerve segments surrounded by myelin. The dynamics of impulse transmission in myelinated axons can be mathematically modeled using nonlinear difference-differential equations (NDDE), nonlinear partial differential equations (NPDEs), or a fractional-order of these NPDEs (FNPDEs)^26,27,28. The equations formulated in this study belong to anatomical and physiological parameters related to the features of nerve units. Furthermore, it has been proved that myelinated nerves facilitate a more rapid conduction of nerve impulses compared to alternative conduction methods, and this phenomenon becomes increasingly evident as the diameter of the nerve fiber decreases. Furthermore, myelination offers an additional benefit in the conduction of nerve impulses: a significant reduction in the energy expenditure involved. The phenomenon referred to as ‘saltatory’ conduction has garnered significant attention from anatomical physiologists studying myelinated nerve models, leading to the identification of two crucial qualitative changes^{9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25}. One of the factors previously noted is the increased speeds of conduction; additionally, another factor is the potential for failure when the distance (or resistance) between the active nodes exceeds a certain threshold. This study demonstrates that both phenomena are influenced by ephaptic coupling, which is linked to fractional-order derivatives, specifically space-time fractional beta-derivatives of coupled nerve fibers.

Regarding the myelinated nerve models, initial considerations must focus on the physical/physiological properties of nerve fibers, which impact the evolution of the modeling approaches. The NPDEs, have undergone extensive research in modeling various electrical and nonlinear complex phenomena, regardless of the relevance of these phenomena to their applicability. In this context, numerous documents are pertinent concerning fluid mechanics, plasma physics, solid state physics, optical fibers, geochemistry, chemical kinetics, chemical physics, and electrophysiology^{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35}. In greater detail, the biology involves a comprehensive approach beyond merely seeking solutions to NPDEs derived from nonlinear dynamics modeling of biological systems, which is a specialized domain of their expertise^{1,2,3,29,30,31,32,33,34,35,36}. Mathematics involving fractional calculus and analysis will be familiarized with non-classical NPDEs or NDDE, referred to as a new category of non-linear difference equation structures. Subsequently, numerous researchers across various scientific disciplines, including pure and applied mathematics, nonlinear physics, nonlinear optics, engineering, biology, and physiology/electrophysiology, investigated diverse classifications of fractional nonlinear evolution equations (FNEEs), many of which have been analyzed in both discrete and continuous formats. The computation steps’ of FNEEs, FNPDEs, and fractional nonlinear differential-difference equations (FNDDEs) currently display significant challenges due to the substantial impact of memory effects during the modeling process. In mathematical modeling, it is essential to recognize that conventional mechanical models, which utilize integer derivatives, fail to adequately account for the potential existence of memory effects^{37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52}. Other studies have demonstrated that fractional-order derivatives, which differ from integer derivatives and serve as a promising operator, allow for a more in-depth exploration of memory effects. Similarly, numerous methodologies utilizing fractional order calculus have been established, encompassing modified Riemann-Liouville derivatives, Caputo derivatives, conformable derivatives, M-truncated derivatives, and beta-derivatives. The beta-derivatives operators fulfill the chain rules properties and tackle some discrepancies reveal by others fractional derivatives operators⁴². The methodologies for computation enabled the simulation of physical systems and the effective resolution of applied problems with notable precision. Moreover, employing numerical approximations of biosystems through fractional order operators serves as a highly effective method for accurately characterizing the properties of systems exhibiting memory and the natural phenomena that arise within them. This study develops foundational models utilizing fractional calculus techniques to enhance the understanding of the dynamics involved in nervous impulse conduction with improved accuracy. Of course, regardless the researcher’s competences either mathematicians or physicists, pursue exact solutions of NPDEs can be led to well catching the dynamics involving in studied models, or to make available improved information on physical problems and possible applications. Meanwhile, fractional-order derivatives fascinated several researchers, some pioneers probed that, it is an accurate and efficient tool for fulfilling mimic real-world problems. Indeed, while the memory effect (control theory, signal processing, systems identification) or the features of hereditary properties (rheology, biology) play a main role or are highlighted inside a model, the fractional calculus suitable provide the way to faithfully describe the nature phenomena’s. In addition, there are some advantages and disadvantages to use fractional-order derivatives in various studies^{42,43,44,45,46,47,48,49,50,51,52,53}. Consistent with the findings of experiments performed by Westerlund, the electric current passing through the nonlinear capacitor conforms to the empirical law of Curie from 1889⁵². Jonscher had also shown that it is not possible to realize the ideal capacitor using only conventional methods involving natural system components with an integer-order of the Ohm law’s as known. Therefore, the physical applications of the studied model are related to retrieving signal processing, theory control analysis of nerve impulse through the coupled nerve fibers.

This study aims to develop an innovative signal processing method using a direct and uncomplicated approach, specifically designed to effectively delve physiological structures, particularly myelinated coupled nerve fibers^1,2,3,4. Nonetheless, the current proposed method presents a more direct procedure compared to alternatives that utilize sine-cosine and sinh-cosh techniques for modeling thin films, which may yield both rational and irrational solutions. Furthermore, the insights of this approach are: easy, can be replicable to any NPDE. However, it is denoted that, some solutions are included in one the most general technique; named the F-expansion method⁵². This solution encompasses various categories, including hyperbolic, elliptic, and trigonometric solutions. This situation is intricate regarding how specific solution types are influenced by the parameter values of the physiological system, which can be categorized as either rational or irrational. This biological model has been further examined subsequently, although not in relation to the beta-derivatives through polynomial expansion techniques. We emphasize the critical need for effective communication of the established methods and findings to the appropriate medical professionals, focusing on the underlying causes of neurological diseases and their treatment strategies. The distinguishing aspect of the current research compared to earlier studies is the implementation of linear stability analysis, which encompasses the identification of modulational instability, alongside the application of fixed points theory and the scrutiny of the Jacobian matrix. Particularly, specific threshold physiological parameters have been recognized that signify the occurrence of noteworthy and significant nonlinear complex phenomena (NCP) in the context of modulational instability (MI). During this research, we implemented an alternative strategy to generate a particular type of neural signal within the model of interconnected nerve fibers under investigation. The nonlinear partial differential equations have been addressed using various techniques, regardless of their fractional nature. Some notable methods include: the $\:\left(G^{\prime\:}\left(\xi\:\right)/G\left(\xi\:\right)\right)$–expansion mapping method including the generalized Riccati Eqs^8,37,45, the $\:exp\left(-\psi\:\left(\xi\:\right)\right)$–expansion function method, the extended $\:\left(G^{\prime\:}\left(\xi\:\right)/{G}^{2}\left(\xi\:\right)\right)$–expansion method^8,38,39, modified extended Tanh method, modified $\:\left(G^{\prime\:}\left(\xi\:\right)/{G}^{2}\left(\xi\:\right)\right)$–expansion method^8,53. Consequently, through the implementation of a fractional complex transform (FCT), we advance the model equation and reconfigure it into a second-order elliptical nonlinear ordinary differential equation (NODE)^{54,55,56,57,58,59,60}. To elucidate the rationale and gene regulatory mechanisms in physiology and impulse intricate dynamics, we present a comprehensive and detailed explanation of the mathematical theories, meticulously outlining each step. The results obtained yield significant findings and potential applications: the study focuses on examining modulational instability regions, equilibrium points, soliton solutions, and the influence of optical fiber and biological components on the velocity and intensity of nerve impulses. The objective is to delve the impact of alterations (anomalies) in the properties of nerve fibers on signal conduction, taking into account age-related factors and degenerative conditions.

The structure of this document is organized as follows: “An equational model of a circuit based on coupled nerve fibers” provides a comprehensive overview of the physical model governing the system of interconnected nerve fibers, along with the corresponding circuit equations elaborated in detail. In “Unstable modulation, stationary points and the Jacobian matrix”, we conduct an analysis of modulational instability, including the delving of fixed points and the Jacobian matrix. “Beta-derivatives and their properties: a preliminary look” holds fundamental details regarding beta-derivatives and their characteristics. “Evaluation of the method and its application to the space-time fractional beta-derivative coupled nerve fibers equations by means of mathematics” presents a concise overview of the methodology, accompanied by an illustrative example pertaining to the equations that describe space-time fractional beta-derivative coupled nerve fibers. “Analysis of the data using physical means and visual representation of those findings” focuses on the visual representation and validation of the operational outcomes. Finally, “Conclusions” reports a comprehensive overview of our efforts and the resulting outcomes.

An equational model of a circuit based on coupled nerve fibers

The electrical modeling of myelinated nerves is based on specific foundational postulates derived from the structural and functional framework, encompassing the biological aspects and the signal propagation within those models. In the scenario involving the juxtaposition of myelinated nerve fibers, the arrangement of the active nodes holds significant importance. The analysis of a fiber can be likened to the description of an electrical cable in terms of its structural components as depicted below. The matrix comprises a conductive component, the cellular protoplasm, encased within a fibrous sheath. The filaments in a bundle are coordinated by a synapse, which serves as an electric junction connecting the ends of other fibers. This study addresses the problem through a sophisticated model of nerve fibers, which comprises two interconnected systems of a chain of active Fitz Hugh-Nagumo circuits, as illustrated in Fig. 1⁴. The electric equivalent circuit of coupled nerve fibers is illustrated using a circuit diagram featuring two partially overlapping axons such as exhibited on Fig. 1. The diagram illustrates the configuration of internal and external resistors $\:\left({R}_{i},\:{R}_{o}\right)$, along with a capacitor $\:\left(C\right)$, interconnected through the conductance $\:\left(G\right)$.

Fig. 1

(a): A diagram illustrating the ephaptic coupling of two myelinated nerves; (b): An electrical circuit representing the coupling of the myelinated nerves.

In the provided electrical circuit in Fig. 1, $\:{V}_{n}^{\left(j\right)}$ represents the voltages across the active nodes, such as $\:j=\text{1,2}$, which correspond to specific fibers. Similarly, the network currents $\:{I}_{n}^{\left(j\right)}$, refer to the magnitudes and directions of currents in a network. The currents are calculated using Kirchhoff’s voltage laws and are treated as independent variables in this analysis. Subsequently, applying Kirchhoff’s voltage laws as illustrated in Fig. 1 yields the following set of Eq. 4:

$$\:\left\{\begin{array}{c}\begin{array}{c}{V}_{n}^{\left(1\right)}-{V}_{n+1}^{\left(1\right)}-\left({R}_{i}+{R}_{o}\right){I}_{n}^{\left(1\right)}-{R}_{o}\left(A{I}_{n}^{\left(2\right)}+\left(1-A\right){I}_{n-1}^{\left(2\right)}\right)=0,\\\:{V}_{n}^{\left(2\right)}-{V}_{n+1}^{\left(2\right)}-\left({R}_{i}+{R}_{o}\right){I}_{n}^{\left(2\right)}-{R}_{o}\left(A{I}_{n}^{\left(1\right)}+\left(1-A\right){I}_{n-1}^{\left(1\right)}\right)=0,\end{array}\\\:\begin{array}{c}\begin{array}{cc}{I}_{n-1}^{\left(j\right)}-{I}_{n}^{\left(j\right)}={I}_{c,n}^{\left(j\right)}+{I}_{ion,n}^{\left(j\right)},&\:j=\text{1,2},\end{array}\\\:{I}_{n}^{\left(j\right)}=\left(\frac{G}{{V}_{b}\left({V}_{b}-{V}_{a}\right)}\right){V}_{n}^{\left(j\right)}\left({V}_{n}^{\left(j\right)}-{V}_{a}\right)\left({V}_{n}^{\left(j\right)}-{V}_{b}\right).\end{array}\end{array}\right.$$

(1)

The variable $\:n$ denotes the index that represents the sequence of active nodes. The current $\:{I}_{n}^{\left(j\right)}$ is propagating longitudinally through the fiber from node$\:\:n$ to node $\:\:n+1$. The current$\:{I}_{c,n}^{\left(j\right)}$ at active node $\:n$ provides its capacity. The ionic current, consisting of sodium and potassium components, is represented as $\:{I}_{ion,n}^{\left(j\right)}$. Several prior studies^1,2,3,4 have documented the importance of an alignment parameter in the theoretical analysis of these categories. For instance, the notion of nodal alignment degrees is introduced to precisely define the alignment of nodes. In the case of fiber optic communication $\:A=1$, the active nodes on the two fibers are precisely aligned, while they are uniformly spaced for optimal performance$\:\:A=0.5$. In the final term of Eq. (1), $\:{V}_{a}$ represents the threshold voltage for sodium current entering an active node. The Nernst potential $\:{V}_{b}$ characterizes the electrical potential at which there is an equilibrium state, resulting in no net ion movement across the membrane. The overall ionic conductance pertains to the capacity of all ions to facilitate the flow of electric current in a given area. Additionally, several publications, along with theoretical and numerical analyses, elucidate certain specific assumptions that led us to establish the following values: $\:{v}_{n}^{\left(j\right)}=\frac{{V}_{n}^{\left(j\right)}}{{V}_{b}}$,$\:\:{i}_{n}^{\left(j\right)}=\frac{{R}_{f}{I}_{n}^{\left(j\right)}}{{V}_{b}}$, $\:a=\frac{{V}_{a}}{{V}_{b}}$, $\:R={R}_{i}+{R}_{o}$, $\:\eta\:=\frac{{R}_{o}}{R}$, $\:M=\frac{{R}_{f}}{R}$, $\:\beta\:=\frac{{R}_{f}G}{\left(1-a\right)}$. The mathematical expression for the electric current through the capacitor can be derived under specific assumptions:

$$\:{I}_{c,n}^{\left(j\right)}=C\frac{d{V}_{n}^{\left(j\right)}}{dt}.$$

(2)

The Eq. (1) becomes:

$$\:\left\{\begin{array}{c}\begin{array}{c}M\left({v}_{n}^{\left(1\right)}-{v}_{n+1}^{\left(1\right)}\right)={i}_{n}^{\left(1\right)}+\eta\:\left(A{i}_{n}^{\left(2\right)}+\left(1-A\right){i}_{n-1}^{\left(2\right)}\right),\\\:M\left({v}_{n}^{\left(2\right)}-{v}_{n+1}^{\left(2\right)}\right)={i}_{n}^{\left(2\right)}+\eta\:\left(A{i}_{n}^{\left(1\right)}+\left(1-A\right){i}_{n-1}^{\left(1\right)}\right),\end{array}\\\:\begin{array}{c}\begin{array}{cc}{i}_{n-1}^{\left(j\right)}-{i}_{n}^{\left(j\right)}={R}_{f}C\frac{d{V}_{n}^{\left(j\right)}}{dt}+{i}_{ion,n}^{\left(j\right)},&\:j=\text{1,2},\end{array}\\\:{i}_{ion,n}^{\left(j\right)}=\beta\:{v}_{n}^{\left(j\right)}\left({v}_{n}^{\left(j\right)}-a\right)\left({v}_{n}^{\left(j\right)}-1\right).\end{array}\end{array}\right.$$

(3)

Where $\:\eta\:$ denotes the linear coupling parameter of the two fibers, indicating that, they are evenly aligned while $\:A=1$. Afterwards, by assigning values to variables $\:{u}_{n}={v}_{n}^{\left(1\right)}$, $\:{v}_{n}={v}_{n}^{\left(2\right)}$, we obtain the following form through a series of mathematical calculus steps:

$$\:\left\{\begin{array}{c}\begin{array}{c}M\left(\left(1-\eta\:\right)\left({u}_{n+1}-2{u}_{n}+{u}_{n-1}\right)-\eta\:\left({v}_{n+1}-2{v}_{n}+{v}_{n-1}\right)\right)\\\:-{R}_{f}C\frac{d{u}_{n}}{dt}-\beta\:{u}_{n}\left({u}_{n}-a\right)\left({u}_{n}-1\right)=0,\end{array}\\\:\begin{array}{c}M\left(\left(1-\eta\:\right)\left({v}_{n+1}-2{v}_{n}+{v}_{n-1}\right)-\eta\:\left({u}_{n+1}-2{u}_{n}+{u}_{n-1}\right)\right)\\\:-{R}_{f}C\frac{d{v}_{n}}{dt}-\beta\:{v}_{n}\left({v}_{n}-a\right)\left({v}_{n}-1\right)=0.\end{array}\end{array}\right.$$

(4)

Considering the continuum limit in the context of a small internodal spacing $\:\delta\:$, we obtain a system of nonlinear coupled partial differential equations (NCPDEs) by taking $\:\delta\:n\to\:x$, $\:{u}_{n}=u\left(x,t\right)$, $\:{v}_{n}=v\left(x,t\right)$:

$$\:\left\{\begin{array}{c}M\left(\left(1-\eta\:\right){\delta\:}^{2}\frac{{d}^{2}u}{d{x}^{2}}-\eta\:{\delta\:}^{2}\frac{{d}^{2}v}{d{x}^{2}}\right)-{R}_{f}C\frac{du}{dt}-\beta\:u\left(u-a\right)\left(u-1\right)=0,\\\:M\left(\left(1-\eta\:\right){\delta\:}^{2}\frac{{d}^{2}v}{d{x}^{2}}-\eta\:{\delta\:}^{2}\frac{{d}^{2}u}{d{x}^{2}}\right)-{R}_{f}C\frac{dv}{dt}-\beta\:v\left(v-a\right)\left(v-1\right)=0.\end{array}\right.$$

(5)

The motion equation for the nerve fiber systems presented earlier (5) delineates the dynamics of the ephaptically coupled nerve fibers. The prior studies recorded in the scientific literature highlighted the following: identifying the conditions necessary for the formation of modulated waves in two ephaptically coupled nerve fibers⁵, assessing the maximum excitation levels and the temporal changes of pulses within the coupled nerve fibers^1,2, estimating behavior using the fundamental model of myelinated fibers, and deriving precise solutions through innovative modeling techniques for interacting nerve fibers^3,4, among other features. The current study examines the modulation instability within the system and its dynamic model, analyzing the fixed points of the vector field and the Jacobian to explore and comprehend novel complex behaviors and intriguing nontrivial aspects related to the propagation of excitation in two interconnected nerve cells. According to the current scientific literature, there have been no recent developments regarding the analysis of linear stability, the dynamics of fixed points, or the Jacobian matrix. A novel methodology utilizing polynomial expansion has been formulated to derive soliton solutions exhibiting various configurations. In addition, simulations have been performed using MATLAB R2016b (The MathWorks, Inc.), available at https://www.mathworks.com/products/matlab.html.

Unstable modulation, stationary points and the Jacobian matrix

This paragraph specifically aims to justify and elucidate the dynamic theory analysis of Eq. (5), which characterizes the behavior of interconnected models of nerve fibers through methodologies including Modulational Instability (MI), fixed points (FPs), and the Jacobian matrix (JM), among others. The analysis of bundles of nerve fibers highlights the critical inquiry into the fusion of the fibers. The interactions of muscles examined in this theoretical context focus on understanding the interconnections of nerve fiber clusters, a characteristic of the nervous systems of higher mammals, while also aiming to generate concepts for empirical research. Additionally, they provide both qualitative and quantitative approaches for the design of electrode and stimulus prototypes utilized in functional electrical stimulation, a process that involves transmitting signals, information, and pulses through two interconnected nerve fibers.

Unstable modulation

An electrical cable model can serve as a precise representation of the nerve fibers within the nervous system that facilitate the transmission of excitation pulses. The waveguide model, recognized in existing literature, effectively describes the propagation of nonlinear excitation during its transit in these systems. The generation and transmission of a nerve impulse depend on variations in the electrical conductivity of the local fiber tissue. Consequently, specific pathological processes, such as self-modulation instability (SMI), arise when typical nonlinearities, presumed to be weak, validate the application of averaged equations in the context of nonlinearly amplified propagation. The amplification process leads to the generation of additional, side-by-side waves, ultimately resulting in the disruption of the original waveform into a series of high waves. An electrical cable model can serve as a precise representation of the nerve fibers within the nervous system that facilitate the transmission of excitation pulses. The waveguide model, extensively documented in existing literature, effectively elucidates the behavior of nonlinear excitation during propagation in these systems. The generation and conduction of a nerve impulse relies on the localized changes in the electric conductivity of the fiber-tissue. Consequently, specific pathological processes, including self-modulation instability (SMI), occur when a sinusoidal wave exhibits nonlinearity and can be amplified via periodic feedback mechanisms. The amplification process leads to the emergence of extra spectral sidebands, ultimately causing the waveform to break down into a sequence of pulses rather than maintaining a continuous signal wave:

$$\:\left\{\begin{array}{c}u\left(x,t\right)=\left(\sqrt{{P}_{0}}+h\psi\:\left(x,t\right)\right),\\\:v\left(x,t\right)=\left(\sigma\:\sqrt{{P}_{0}}+h\phi\:\left(x,t\right)\right).\end{array}\right.$$

(6)

In the context of anti-symmetry, the value is represented as$\:\:\sigma\:=-1$. In the context of symmetry, the value is represented by the symbol$\:\:\sigma\:=1$. The term$\:\sqrt{{P}_{0}}$ stands for incident power, while $\:h$ is the smallest perturbation parameter. Moreover, the symbols$\:\:\psi\:\left(x,t\right)$, $\:\:\phi\:\left(x,t\right)$ represent the perturbation terms. The substitution of Eq. (6) into Eq. (5) is followed by the execution of analytical calculus operations. Using the linearizing principle, we obtain the following equations for the perturbed solutions $\:\psi\:\left(x,t\right)$, $\:\phi\:\left(x,t\right)$.

$$\:\left\{\begin{array}{c}\begin{array}{c}{R}_{f}C\frac{\partial\:\psi\:}{\partial\:t}+\beta\:\sqrt{{P}_{0}}\left(\sqrt{{P}_{0}}-a\right)\psi\:+\beta\:\left(\sqrt{{P}_{0}}-1\right)\left(2\sqrt{{P}_{0}}-a\right)\psi\:\\\:-M\left(\left(1-\eta\:\right){\delta\:}^{2}\frac{{\partial\:}^{2}\psi\:}{\partial\:{x}^{2}}-\eta\:{\delta\:}^{2}\frac{{\partial\:}^{2}\phi\:}{\partial\:{x}^{2}}\right)=0,\end{array}\\\:\begin{array}{c}{R}_{f}C\frac{\partial\:\phi\:}{\partial\:t}+\beta\:\sqrt{{P}_{0}}\left(\sqrt{{P}_{0}}-a\right)\phi\:+\beta\:\left(\sqrt{{P}_{0}}-1\right)\left(2\sqrt{{P}_{0}}-a\right)\phi\:\\\:-M\left(\left(1-\eta\:\right){\delta\:}^{2}\frac{{\partial\:}^{2}\phi\:}{\partial\:{x}^{2}}-\eta\:{\delta\:}^{2}\frac{{\partial\:}^{2}\psi\:}{\partial\:{x}^{2}}\right)=0,\end{array}\end{array}\right.$$

(7)

Let us acknowledge that these sought perturbed solutions, denoted as $\:\psi\:\left(x,t\right)$, $\:\phi\:\left(x,t\right)$, have the following form^61,62:

$$\:\left\{\begin{array}{c}\psi\:\left(x,t\right)={P}_{11}{e}^{i\left(qx-{\Omega\:}t\right)}+{P}_{12}{e}^{-i\left(qx-{\varOmega\:}^{*}t\right)},\\\:\phi\:\left(x,t\right)={P}_{21}{e}^{i\left(qx-\varOmega\:t\right)}+{P}_{22}{e}^{-i\left(qx-{\varOmega\:}^{*}t\right)}.\end{array}\right.$$

(8)

The symbols $\:q$ and $\:\varOmega\:$ represent the normalized wave number and the frequency of the perturbation, respectively. By performing substitution of Eq. (8) into Eq. (7) and isolating the coefficients in terms of$\:{e}^{i\left(qx-{\Omega\:}t\right)}$ and $\:{e}^{-i\left(qx-{\varOmega\:}^{*}t\right)}$, it leads to the formation of the following system of homogeneous equations:

$$\:\left\{\begin{array}{c}\begin{array}{c}\left[M{\delta\:}^{2}{q}^{2}\left(1-\eta\:\right)+3\beta\:{P}_{0}+a\beta\:\left(1-2\sqrt{{P}_{0}}\right)-2\beta\:\sqrt{{P}_{0}}+i{R}_{f}C\varOmega\:\right]{P}_{11}-M\eta\:{\delta\:}^{2}{q}^{2}{P}_{21}=0,\\\:\left[M{\delta\:}^{2}{q}^{2}\left(1-\eta\:\right)+3\beta\:{P}_{0}+a\beta\:\left(1-2\sqrt{{P}_{0}}\right)-2\beta\:\sqrt{{P}_{0}}+i{R}_{f}C\varOmega\:\right]{P}_{12}-M\eta\:{\delta\:}^{2}{q}^{2}{P}_{22}=0,\end{array}\\\:\begin{array}{c}\left[M{\delta\:}^{2}{q}^{2}\left(1-\eta\:\right)+3\beta\:{\sigma\:}^{2}{P}_{0}+a\beta\:\left(1-2\sigma\:\sqrt{{P}_{0}}\right)-2\beta\:\sigma\:\sqrt{{P}_{0}}+i{R}_{f}C\varOmega\:\right]{P}_{21}-M\eta\:{\delta\:}^{2}{q}^{2}{P}_{11}=0,\\\:\left[M{\delta\:}^{2}{q}^{2}\left(1-\eta\:\right)+3\beta\:{\sigma\:}^{2}{P}_{0}+a\beta\:\left(1-2\sigma\:\sqrt{{P}_{0}}\right)-2\beta\:\sigma\:\sqrt{{P}_{0}}+i{R}_{f}C\varOmega\:\right]{P}_{22}-M\eta\:{\delta\:}^{2}{q}^{2}{P}_{12}=0.\end{array}\end{array}\right.$$

(9)

To obtain the nontrivial solution of the system of equations developed within the context of Eq. (9), it is essential to compute the determinant formed by the matrix of coefficients derived from (9). The desired solutions are obtained by solving the relevant polynomial equation $\:\varOmega\:=\varOmega\:\left(q\right)$ represented by:

$$\:{m}_{4}{\varOmega\:}^{4}+{m}_{3}{\varOmega\:}^{3}+{m}_{2}{\varOmega\:}^{2}+{m}_{1}\varOmega\:+{m}_{0}=0,$$

(10)

with$\:\gamma\:={R}_{f}C$, $\:b=-M{\delta\:}^{2}{q}^{2}$, $\:A=b+M{\delta\:}^{2}{q}^{2}-2\beta\:\sqrt{{P}_{0}}\left(1+a\right)+a\beta\:+3\beta\:{P}_{0}$, $\:{m}_{4}={\gamma\:}^{4}$, $\:{m}_{3}=-2i{\gamma\:}^{3}\left(A+B\right)$, $\:B=b+M{\delta\:}^{2}{q}^{2}-2\beta\:\sigma\:\sqrt{{P}_{0}}\left(1+a\right)+a\beta\:+3\beta\:{\sigma\:}^{2}{P}_{0}$, $\:{m}_{2}=-\left({\left(A+B\right)}^{2}+2AB-b+{b}^{2}\right)$, $\:{m}_{1}=-i\gamma\:\left(\left(A+B\right)\left(2AB-b-{b}^{2}\right)\right)$, $\:{m}_{0}={A}^{2}{B}^{2}-AB\left(b+{b}^{2}\right)+{b}^{4}$. Analytically solving Eq. (10) can be quite labor-intensive and require significant time investment. The subsequent steps involve numerical computations utilizing MATLAB software, which serves as an efficient platform for these mathematical applications. The linear equation presented above (10) illustrates the linear stability analysis of the steady-state solution, which is consistent with physical principles. The modulational instability domain encompasses a specific range of instability that exists under certain conditions. A steady-state is considered stable when $\:\varOmega\:$ is a real number. Conversely, the presence of an imaginary $\:\:\varOmega\:$ indicates a perturbation in the steady state solution, characterized by the exponential growth of disturbances. The gain spectrum associated with modulational instability is analyzed:

$$\:g\left(q\right)=2Im\left(\varOmega\:\left(q\right)\right).$$

(11)

In this scenario, it is evident that the solution $\:\varOmega\:$ is defined by Eq. (10). This section outlines several significant inter-information dependencies identified in specific experiments and subjected to thorough analysis.

Symmetric case: $\:\sigma\:=1$

Fig. 2

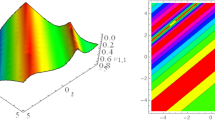
These panels display the MI plots under conditions $\:{P}_{0}=1$, $\:\delta\:=1$, $\:\gamma\:=5.{10}^{-4}$, such as for top row: $\:M>0$ panel (a) $\:a=0.25$, $\:\beta\:>0$; panel (b) $\:a=0.75$, $\:\beta\:>0$; panel (c) $\:a=0.99$, $\:\beta\:>0$ $\:\left(a=1.01,\:\beta\:<0\right)$; for bottom row: $\:M<0$ panel (d) $\:a=0.25$, $\:\beta\:>0$; panel (e) $\:a=0.75$, $\:\beta\:>0$; panel (f) $\:a=0.99$, $\:\beta\:>0$ $\:\left(a=1.01,\:\beta\:<0\right)$.

The defined parameters for obtaining the MI graphs are reasonable and invite debates about certain physiological mechanisms. In fact, we carry out a deep examination to the mutual information graphs shown in the panels of Figs. 2 and 3. In fact, with certain constraints on the parameters of the nervous system, a zone of MI is obtained with a positive gain. In the given scenario where$\:\:\sigma\:=1$ (denotes symmetry), $\:a=0.25$ ($\:a$ less than 1) and $\:M=0.5$ ($\:M$ less than 1), we notice the presence of a zone of MI as Binczak et al. have suggested³. From³, we have also noticed a jump like threshold that could be interpreted as a blockage of the impulse current (which actually can be a bad feature of real nerves), to this effect see Fig. 2a. In addition, sometimes at the same premises which were indicated above, when the value of $\:a$ was equal to 0.75, one can see a stability region for $\:g\left(q\right)=0$ as $\:q$ approaches 0.75 or – 0.75 in Fig. 2b. Instead the gain $\:g\left(q\right)$ is also reduced. As a result, when $\:a=0.99$ (or $\:a=1.01$) $\:M$ is lower than 1 $\:\left(M=0.5\right)$ and MI lobes are clearly visible. And in Fig. 2c this occurrence happens when $\:\eta\:<0$ considering a narrower band of disturbance of wave number $\:q$ which is $\:-0.25<q<0.25$. Likewise, on Fig. 2c, in the case of $\:-0.75<q<-0.25$ $\:\left(0.25<q<0.75\right)$, the $\:\eta\:$ value is negative giving stable nervous impulse as. Also, for any value of the increased $\:\eta\:$ or any value of $\:q$ in the range $\:q\in\:\left[-0.75,\:0.75\right]$, it is apparent from the physiological point of view that the operating parameters of the currently available range of the nervous system is the safety net for the system as seen in Fig. 2c. For complex phenomena, when the value of $\:M$ is negative (regressive propagating impulse) two symmetric patterns of MI will occur for a value of $\:a=0.25$ at which $\:\eta\:$ is greater than 0 and $\:q$ in the range − 2 to 2. When the value of $\:\eta\:$ becomes negative, the gain $\:g\left(q\right)$ takes on the value of zero. This means, the stability condition is still maintained even in the absence of MI area (as we can see in panels Fig. 2d–f). Additionally, when the value of the parameter $\:a$ sticks at 0.75, the lobe of MI and the distance between these two lobes is said to go up. Usage of parameter $\:a\to\:1$ also suggests that there exists a Brillouin’s zone, which corresponds to the stability with $\:g\left(q\right)=0$, lying in between the two MI zones. There emerges a threshold value of the parameter above which the Brillouin’s zone corresponds to one of the MI zones. See Fig. 2 (e), (f) for this. We consider MI for such abnormal states of nerve fibers $\:\left(M<0,\:\eta\:>0.5\right)$ and show that there is no risk of any injury of nerve impulses even under such conditions.

Anti-symmetric case: $\:\sigma\:=-1$

Fig. 3

These panels exhibit the MI plots under conditions $\:{P}_{0}=1$, $\:\delta\:=1$, $\:\gamma\:=5.{10}^{-4}$, such as for top row: $\:M>0$ panel (a) $\:a=0.25$, $\:\beta\:>0$; panel (b) $\:a=0.75$, $\:\beta\:>0$; panel (c) $\:a=0.99$, $\:\beta\:>0$ $\:\left(a=1.01,\:\beta\:<0\right)$; for bottom row: $\:M<0$ panel (d) $\:a=0.25$, $\:\beta\:>0$; panel (e) $\:a=0.75$, $\:\beta\:>0$; panel (f) $\:a=0.99$, $\:\beta\:>0$ $\:\left(a=1.01,\:\beta\:<0\right)$.

For example, in the case of anti-symmetry, when denoted by the would-be $\:\sigma\:=-1$, and when $\:M$ is greater than 0, the panels in Fig. 3a and b show that MI domains exist inside the Brillouin’s zone displays by$\:-0.75<q<0.75$. It can be noticed that the observed domains are positively proportional to the amplitude of gain that the parameter $\:a$ will take. But, while the parameter $\:a$ comes close to 1, there is active interest in the range where $\:q$ is limited from − 0.75 to 0.75, regardless of the $\:\eta\:$ parameter value (which can be positive or negative), Fig. 3c will be referred to for further details. In addition, when the value of $\:\eta\:$ is greater than $\:0.5$ it is found out that the interconnected nerve fibers transmit nervous impulses through the assisting nerve fibers, without the help of amplification devices regardless of the value of $\:q$ mentioned in the range of – 2 to 2. While $\:M$ is less than 0, the MI zones drop down together with the amplitude of the gain which is lower in value of 0.25. As the value of $\:a$ turns out to be bigger (for instance $\:a=0.75$ so does the amplitude of the gain. This feature could be treated as a somatic mechanism for transmitting more complex signals (for example, signal integration) among axons and between hemispheres of the brain. Also, for$\:\:0<\eta\:<2$ and$\:-2\le\:q\le\:2$ signal transmitted through the two, inter-connecting nerve fibers does not diverge from steady state as $\:g\left(q\right)=0$ validate. For$\:\:\eta\:>2$, the condition that the Modulational Instability plot in Fig. 3f indicates two regions of instability which are surrounded by one stable area for all $\:q$ values lying within $\:\left[-0.75,\:0.75\right]$. With increase in the parameter $\:a$ the area of instability decreases hence the maximum gain attained as displayed in Fig. 3c when compared with Fig. 3d and e. The limit of amplification region constricts however extend stability region tends that increasing the values of $\:q$ that cluster on size-extreme interactively moderate area dilation or depletes the region, while values of $\:q$ that clustering pose on the stability region sails, however. The MI analysis has as its principal purpose the act of verifying the model under study with respect to the existence of soliton-like solutions. In this, we have demonstrated that, under realistic circumstances, the MI zones are quite large, providing enough scope for the physiological system to generate solitonic impulses over a wide range of $\:M$, $\:\eta\:$, and $\:q$ values. They have hitherto been seen in both symmetric and asymmetric cases, $\:\sigma\:=1$ and $\:\sigma\:=-1$ respectively, showing the presence of MI zones. They are caused by non-very normal values of $\:M$ and $\:\eta\:$, and possibly, in relation to anatomical, medical, and neurological diseases. In addition to these, we also offer some form of experimental evidence supporting the notion of MI lobes as being discernible, within particular limited parameter regimes of $\:M$, $\:\eta\:$, and $\:q$. It confirms that, solitonic impulses can indeed be triggered towards the very specific parameters at which MI zones come into being. Hence, the pathological physiology of the nerve fibers gives rise to a different form of solitonic impulse.

Jacobian matrix and fixed points theory

Equation (5), as defined by the applicable mathematical model, allows for the determination of equilibrium points and the requisite Jacobian matrix, which aids in the analysis of the linear stability of the two interacting components governed by the system. From a mathematical perspective, conducting numerical experiments related to Eq. (5) or its transformed variants aids in establishing and understanding the existence of various useful solutions. In this context, we will examine the wave transformation characterized by the variables$\:\:\zeta\:=k\left(x-\lambda\:t\right)$,$\:\:u\left(x,t\right)=U\left(\zeta\:\right)$, $\:v\left(x,t\right)=V\left(\zeta\:\right)$. The provided expressions generate a comparable autonomous dynamical system in the specified format:

$$\:\left\{\begin{array}{c}\begin{array}{c}\frac{dU}{d\zeta\:}={U}^{{\prime\:}}=Y,\\\:\frac{dY}{d\zeta\:}=\frac{1}{\left(1-\eta\:\right){k}^{2}{\delta\:}^{2}}\left(\eta\:{k}^{2}{\delta\:}^{2}\frac{dU}{d\zeta\:}-\frac{1}{M}\left({R}_{f}Ck\lambda\:Y-\beta\:U\left(U-a\right)\left(U-1\right)\right)\right),\end{array}\\\:\begin{array}{c}\frac{dV}{d\zeta\:}={V}^{{\prime\:}}=Z,\\\:\frac{dZ}{d\zeta\:}=\frac{1}{\left(1-\eta\:\right){k}^{2}{\delta\:}^{2}}\left(\eta\:{k}^{2}{\delta\:}^{2}\frac{dY}{d\zeta\:}-\frac{1}{M}\left({R}_{f}Ck\lambda\:Z-\beta\:V\left(V-a\right)\left(V-1\right)\right)\right).\end{array}\end{array}\right.$$

(12)

By setting$\:\frac{dU}{d\zeta\:}=0$,$\:\:\frac{dY}{d\zeta\:}=0$,$\:\:\frac{dV}{d\zeta\:}=0$ and $\:\frac{dZ}{d\zeta\:}=0$ within the framework of Eq. (12), The solutions of (12) identify the equilibrium points, which are also referred to as fixed points. Upon successfully solving Eq. (12), the resulting fixed points $\:{X}_{i}\left(i=\text{1,2},3,.,6\right)$ can be articulated as follows:

$$\:\begin{array}{ccc}\left(0,\:0,\:0,\:0\right),&\:\left(1,\:0,\:1,\:0\right),&\:\left(a,\:0,\:a,\:0\right),\\\:\left(0,\:0,\:1,\:0\right),&\:\left(0,\:0,a,\:0\right),&\:\left(a,\:0,\:1,\:0\right).\end{array}$$

(13)

All fixed points collected are real and do not bear any peculiar conditions. Nevertheless, it is possible to use the determinant of the Jacobian matrix to determine the stability of the obtained fixed points. The study described in this paper is a linear stability analysis, and the mode of solution employs the usage of the Jacobian matrix $\:\left({M}_{J}\right)$. This suggests that positive values for the determinant of the Jacobian matrix pertaining to any fixed point $\:{X}_{i}$ would continue to positively support that fixed point irrespective of the movement of the system being considered. In case the determinant of the Jacobian matrix $\:\left({\left|{M}_{J}\right|}_{{X}_{i}}\right)$ pertaining to this particular point is negative then, that particular point or the fixed point $\:{X}_{i}$ is said to be unstable. The parameters of the equilibrium state represented in Eq. (12) can be restated in the following form:

$$\:\left\{\begin{array}{c}\begin{array}{c}\frac{dU}{d\zeta\:}=Y\equiv\:{F}_{1},\\\:\frac{dY}{d\zeta\:}=\frac{1}{\left(1-2\eta\:\right)M{k}^{2}{\delta\:}^{2}}\left(\begin{array}{c}{-R}_{f}Ck\lambda\:\left(\left(1-\eta\:\right)Y-\eta\:Z\right)-\beta\:\eta\:V\left(V-a\right)\left(V-1\right)\\\:+\left(1-\eta\:\right)U\left(U-a\right)\left(U-1\right)\end{array}\right)\equiv\:{F}_{2},\end{array}\\\:\begin{array}{c}\frac{dV}{d\zeta\:}=Z\equiv\:{F}_{3},\\\:\frac{dZ}{d\zeta\:}=\frac{1}{\left(1-2\eta\:\right)M{k}^{2}{\delta\:}^{2}}\left(\begin{array}{c}{-R}_{f}Ck\lambda\:\left(\eta\:Y-\left(1-\eta\:\right)Z\right)+\beta\:\eta\:U\left(U-a\right)\left(U-1\right)\\\:-\left(1-\eta\:\right)V\left(V-a\right)\left(V-1\right)\end{array}\right)\equiv\:{F}_{4}.\end{array}\end{array}\right.$$

(14)

The Jacobian matrix serves as a mathematical instrument commonly utilized to analyze the dynamics of autonomous systems, exemplified by the system represented in Eq. (14):

$$\:{M}_{J}=\left[\begin{array}{ccc}\begin{array}{cc}\frac{\partial\:{F}_{1}}{\partial\:{X}_{1}}&\:\frac{\partial\:{F}_{1}}{\partial\:{X}_{2}}\\\:\frac{\partial\:{F}_{2}}{\partial\:{X}_{1}}&\:\frac{\partial\:{F}_{2}}{\partial\:{X}_{2}}\end{array}&\:\cdots\:&\:\begin{array}{c}\frac{\partial\:{F}_{1}}{\partial\:{X}_{n}}\\\:\frac{\partial\:{F}_{2}}{\partial\:{X}_{n}}\end{array}\\\:\vdots&\:\ddots\:&\:\vdots\\\:\begin{array}{cc}\frac{\partial\:{F}_{n}}{\partial\:{X}_{1}}&\:\frac{\partial\:{F}_{n}}{\partial\:{X}_{2}}\end{array}&\:\cdots\:&\:\frac{\partial\:{F}_{n}}{\partial\:{X}_{n}}\end{array}\right].$$

(15)

According to the results of the current study, it has been noted:

$$\:{M}_{J}=\left[\begin{array}{cc}\begin{array}{cc}\frac{\partial\:{F}_{1}}{\partial\:U}&\:\frac{\partial\:{F}_{1}}{\partial\:Y}\\\:\frac{\partial\:{F}_{2}}{\partial\:U}&\:\frac{\partial\:{F}_{2}}{\partial\:Y}\end{array}&\:\begin{array}{cc}\frac{\partial\:{F}_{1}}{\partial\:V}&\:\frac{\partial\:{F}_{1}}{\partial\:Z}\\\:\frac{\partial\:{F}_{2}}{\partial\:V}&\:\frac{\partial\:{F}_{2}}{\partial\:Z}\end{array}\\\:\begin{array}{cc}\frac{\partial\:{F}_{3}}{\partial\:U}&\:\frac{\partial\:{F}_{3}}{\partial\:Y}\\\:\frac{\partial\:{F}_{4}}{\partial\:U}&\:\frac{\partial\:{F}_{4}}{\partial\:Y}\end{array}&\:\begin{array}{cc}\frac{\partial\:{F}_{3}}{\partial\:V}&\:\frac{\partial\:{F}_{3}}{\partial\:Z}\\\:\frac{\partial\:{F}_{4}}{\partial\:V}&\:\frac{\partial\:{F}_{4}}{\partial\:Z}\end{array}\end{array}\right].$$

(16)

With $\:\frac{\partial\:{F}_{1}}{\partial\:U}=0$, $\:\frac{\partial\:{F}_{1}}{\partial\:Y}=1$, $\:\frac{\partial\:{F}_{1}}{\partial\:V}=0$, $\:\frac{\partial\:{F}_{1}}{\partial\:Z}=0$, $\:\frac{\partial\:{F}_{2}}{\partial\:U}=\frac{\left(1-\eta\:\right)\beta\:\left(\left(U-a\right)\left(U-1\right)+U\left(U-1\right)+U\left(U-a\right)\right)}{\left(1-2\eta\:\right)M{k}^{2}{\delta\:}^{2}}$, $\:\frac{\partial\:{F}_{2}}{\partial\:Y}=\frac{{-R}_{f}Ck\lambda\:\left(1-\eta\:\right)}{\left(1-2\eta\:\right)M{k}^{2}{\delta\:}^{2}}$,$\:\:\frac{\partial\:{F}_{2}}{\partial\:V}=\frac{-\eta\:\beta\:\left(\left(V-a\right)\left(V-1\right)+V\left(V-1\right)+V\left(V-a\right)\right)}{\left(1-2\eta\:\right)M{k}^{2}{\delta\:}^{2}}$, $\:\frac{\partial\:{F}_{2}}{\partial\:Z}=\frac{{R}_{f}Ck\lambda\:\eta\:}{\left(1-2\eta\:\right)M{k}^{2}{\delta\:}^{2}}$, $\:\frac{\partial\:{F}_{3}}{\partial\:U}=0$, $\:\frac{\partial\:{F}_{3}}{\partial\:Y}=0$, $\:\frac{\partial\:{F}_{3}}{\partial\:V}=0$, $\:\frac{\partial\:{F}_{3}}{\partial\:Z}=1$,$\:\:\frac{\partial\:{F}_{4}}{\partial\:U}=\frac{\eta\:\beta\:\left(\left(U-a\right)\left(U-1\right)+U\left(U-1\right)+U\left(U-a\right)\right)}{\left(1-2\eta\:\right)M{k}^{2}{\delta\:}^{2}}$, $\:\:\frac{\partial\:{F}_{4}}{\partial\:Y}=\frac{{-R}_{f}Ck\lambda\:\eta\:}{\left(1-2\eta\:\right)M{k}^{2}{\delta\:}^{2}}$, $\:\frac{\partial\:{F}_{4}}{\partial\:V}=\frac{-\left(1-\eta\:\right)\beta\:\left(\left(V-a\right)\left(V-1\right)+V\left(V-1\right)+V\left(V-a\right)\right)}{\left(1-2\eta\:\right)M{k}^{2}{\delta\:}^{2}}$, $\:\frac{\partial\:{F}_{4}}{\partial\:Z}=\frac{{R}_{f}Ck\lambda\:\left(1-\eta\:\right)}{\left(1-2\eta\:\right)M{k}^{2}{\delta\:}^{2}}$. By evaluating the determinant of the Jacobian matrix $\:{M}_{J}$, it yields:

$$\:\left|{M}_{J}\right|=\frac{{\beta}^{2}\left(a\left(2U-1\right)+U\left(2-3U\right)\right)\left(a\left(2V-1\right)+V\left(2-3V\right)\right)}{\left(2\eta-1\right){M}^{2}{k}^{4}{\delta\:}^{4}}.$$

(17)

In the context of analyzing the behavior of interconnected neural fibers and their fixed-point structures, the establishment of equilibrium points can be achieved through the application of directional matrix methods, which involve determining the sign of the Jacobian matrix’s determinant at each invariant point. In this framework, calculating the determinant of a Jacobian matrix is crucial as it elucidates the stability of each of the analytical conditions established. The determinant of the Jacobian matrix in each iteration addresses the constraints imposed by the injection of $\:2\eta\:-1$ and a$\:-1$, thereby establishing the values of specific parameters within the nervous system, namely $\:\eta\:$ and $\:a$. As an example,

Case 1

η < 0.5 (2η - 1 < 0). According to the value of, a (a < 1, a > 1), |M_J|_Xi(i=1,2,3)<0, then, the related fixed points are overall unstable, whereas, |M_J|_X6 > 0 makes up X₆ a stable fixed point. In addition, for a < 1, |M_J|_X4 < 0, so X₄ is an unsteadyequilibrium point, while, |M_J|_X5 > 0 and consequently, X₅ is a stable fixed point.Unlike, if a > 1, |M_J|_X4 > 0, thus X₄ is a steady fixed point, however, |M_J|_X5 < 0therefore, X₅ is an unstable fixed point.

Case 2

η > 0.5 (2η – 1 > 0). Whatever the value of a (a < 1, a > 1), |M_J|_Xi(i=1,2,3) > 0,thus,, the linked fixed points are overall stable, whereas, |M_J|_X6 < 0, X₆ stands anunsteady equilibrium point. Furthermore, if a < 1, |M_J|_X4 > 0, so X₄ is a steadyequilibrium point, whereas, |M_J|_X5 < 0 and accordingly, X₅ is an unstable fixed point.However, for a > 1, |M_J|_X4 < 0, then, X₄ is an unsteady fixed point, whereas, X₅ is astable fixed point because |M_J|_X5 > 0.

Beta-derivatives and their properties: a preliminary look

Recently, numerous definitions of fractional derivatives have been proposed by various researchers, including Riemann Liouville, modified Riemann Liouville, Caputo, Caputo-Fabrizio, conformable fractional, and Atangana-Baleanu derivatives^{37,38,39,40,43,44,45,46,47,48,49,52,63,64,65}. The fractional definitions outlined previously possess certain advantages; however, they also exhibit incompatibilities that depend on the characteristics of the physical system or functions, such as differentiability and continuity. An important observation in this context is that many Fractional Orders in use lack some of the more advanced characteristics of classical calculus, such as the chain rule, the Leibnitz theorem, and the treatment of zero when differentiating a constant. A novel type of fractional derivative, referred to as the beta derivative, has been introduced by Atangana et al. The derivatives arise from the fundamental principles of classical calculus⁴².

Definition

Let consider, a function and therefore, the beta derivative of order with respect to which is defined as ensues:

$$\:{D}_{x}^{\alpha\:}\left(\psi\:\left(x\right)\right)=\underset{\epsilon\:\to\:0}{\text{lim}}\frac{\psi\:\left({x+\epsilon\:\left(x+\frac{1}{{\Gamma\:}\left(\alpha\:\right)}\right)}^{1-\alpha\:}\right)-\psi\:\left(x\right)}{\epsilon\:} \quad {\text { for all }} \:x\ge\:0 \text{ and }\:\psi\:\left(x\right)0<\alpha\:\le\:1,$$

(18)

with $\:{\Gamma\:}$ is the gamma function and $\:{D}_{x}^{\alpha\:}\left(\psi\:\left(x\right)\right)=\frac{d\psi\:\left(x\right)}{dx}$ for $\:\alpha\:=1$.

Properties

We assume that for all, and are -order differentiable,, two real parameters. Then, this fractional-order derivative type (named beta-derivative) involves the following crucial properties⁴².

• 1. $\:{D}_{x}^{\alpha\:}\left({\gamma\:}_{1}\psi\:\left(x\right)+{\gamma\:}_{2}u\left(x\right)\right)={\gamma\:}_{1}{D}_{x}^{\alpha\:}\left(\psi\:\left(x\right)\right)+{\gamma\:}_{2}{D}_{x}^{\alpha\:}\left(u\left(x\right)\right)$

• 2. $\:{D}_{x}^{\alpha\:}\left(k\right)=0$, such as $\:k$ stands an arbitrary constant.

• 3. $\:{D}_{x}^{\alpha\:}\left(\psi\:\left(x\right)u\left(x\right)\right)=u\left(x\right){D}_{x}^{\alpha\:}\left(\psi\:\left(x\right)\right)+\left(\psi\:\left(x\right)\right){D}_{x}^{\alpha\:}\left(u\left(x\right)\right)$

• 4. $\:{D}_{x}^{\alpha\:}\left(\frac{\psi\:\left(x\right)}{u\left(x\right)}\right)=\frac{u\left(x\right){D}_{x}^{\alpha\:}\left(\psi\:\left(x\right)\right)-\left(\psi\:\left(x\right)\right){D}_{x}^{\alpha\:}\left(u\left(x\right)\right)}{{\left(u\left(x\right)\right)}^{2}}$

• 5. $\:{D}_{x}^{\alpha\:}\left(\left(\psi\:\circ\:u\right)\left(x\right)\right)={D}_{x}^{\alpha\:}\left(\psi\:\left(u\left(x\right)\right)\right)u{\prime\:}\left(x\right)$

• 6. $\:{D}_{x}^{\alpha\:}\left(\frac{1}{\psi\:\left(x\right)}\right)=\frac{-{D}_{x}^{\alpha\:}\left(\psi\:\left(x\right)\right)}{{\left(\psi\:\left(x\right)\right)}^{2}}$

• 7. $\:{D}_{x}^{\alpha\:}\left(\psi\:\left(x\right)\right)=\left({x+\left(\frac{t}{\varGamma\:\left(\alpha\:\right)}\right)}^{1-\alpha\:}\right)\frac{d\psi\:\left(x\right)}{dx}$

Leveraging the characteristics of the beta-derivatives is especially beneficial for converting a fractional nonlinear partial differential equation FNPDE into the structure of NODE. The advanced formulation introduced by Atangana et al.⁴² has yet to reveal any limitations to date. Furthermore, it outlines the characteristics of interconnected integer-order derivatives. However, it does not apply this to the derivative of its constant functions. The beta derivative functions as a mathematical operator, facilitating the capture of the general characteristics of functions and aiding in the identification of their singularity points. Additionally, the beta derivative demonstrates greater appeal compared to earlier versions, highlighting the necessity for its application in a wider range of simulations addressing practical issues across various research domains, as supported by numerous scientific reports and studies. Investigation can be conducted on nonlinear dispersive electrical transmission networks and electrochemical systems, along with the modeling of complex geometries for electromagnetic waves in dielectric media and applications in cancer treatment^37,66,67,68. The aforementioned applications concerning beta-derivatives lead us to consider it as a logical extension of the Caputo and Riemann-Liouville types of derivatives. The fractional beta derivative is a mathematical tool that enhances flexibility and accuracy in the computation of NCS modeling. Furthermore, the distinct advantages outlined regarding this specific fractional derivative provide greater benefits due to its broad applicability compared to other fractional derivatives within similar domains.

Evaluation of the method and its application to the space-time fractional beta-derivative coupled nerve fibers equations by means of mathematics

A mathematical description of the procedure for expanding polynomials

Let us consider a given physical model where the dynamics of a complex function $\:\psi\:\left(t,x\right)$ are governed by:

$$\:P\left(\psi\:,{D}_{t}^{\alpha\:}\psi\:,{D}_{x}^{\alpha\:}\psi\:,{D}_{tt}^{2\alpha\:}\psi\:,{D}_{xx}^{2\alpha\:}\psi\:,{\psi\:}^{2},{\psi\:}^{3},{{\psi\:}^{2}D}_{t}^{\alpha\:}\psi\:,{{\psi\:}^{3}D}_{t}^{\alpha\:}\psi\:,\dots\:\right)=0.$$

(19)

The notation $\:P$ represents a polynomial in a complex variable that encompasses both linear and nonlinear monomials, along with their partial derivatives, including the beta variant of fractional order. In the following sections, we will delineate the fundamental algorithmic procedures of the method referred to as polynomial expansion, utilized for examining the solutions$\:\:\psi\:\left(t,x\right)$ of the complex function within the Eq. (19) presented in a less clear format.

Step 1: We execute a variable transformation as specified by

$$\:\begin{array}{cc}\psi\:\left(t,x\right)=\phi\:\left(\xi\:\right),&\:\xi\:=k\left({x-\frac{\lambda\:}{\alpha\:}\left(t+\frac{1}{\varGamma\:\left(\alpha\:\right)}\right)}^{\alpha\:}\right),\end{array}$$

(20)

with the arbitrary constants $\:k$ and $\:\lambda\:$, one can utilize Eq. (20). This allows for the transformation of the nondimensional fractional linear partial differential Eq. (19) into a nonlinear ordinary differential equation (NODE) concerning the varble$\:\:x$. The execution of this operation yields outcomes of:

$$\:Q\left(\phi\:,{D}_{\xi\:}^{1}\phi\:,{D}_{\xi\:}^{2}\phi\:,{\phi\:}^{2},{\phi\:}^{3},{\phi\:}^{2}{D}_{\xi\:}^{1}\phi\:,{\phi\:}^{3}{D}_{\xi\:}^{1}\phi\:,\dots\:\right)=0,$$

(21)

such as $\:{D}_{\xi\:}^{1}\left(\phi\:\right)=\frac{d\phi\:}{d\xi\:}=\phi\:{\prime\:}$, $\:{D}_{\xi\:}^{2}\left(\phi\:\right)=\frac{{d}^{2}\phi\:}{d{\xi\:}^{2}}=\phi\:{\prime\:}{\prime\:}$,…

Step 2: We hypothesize that the solutions to Eq. (21) exhibit a specific pattern:

$$\:\phi\:\left(\xi\:\right)=\sum_{i=1}^{N}{a}_{i}{\left(\varphi\:\left(\xi\:\right)\right)}^{i}+\sum_{i=1}^{N}{b}_{i}{\left(\varphi\:\left(\xi\:\right)\right)}^{-i}+{a}_{0}.$$

(22)

Where $\:{a}_{i}$, $\:{b}_{i}$, stand the unknown variables and $\:\varphi\:\left(\xi\:\right)$ fulfils the following newly polynomial auxiliary equation in the form

$$\:{\varphi\:}^{{\prime\:}}\left(\xi\:\right)={F}_{0}+{F}_{1}\varphi\:+{\varphi\:}^{2}.$$

(23)

The current methodology has been documented in the established scientific literature. Consequently, multiple sets of solutions that fulfill the Eq. (23)^69,70,71 can be provided. It is essential to highlight that solutions addressing the author’s evaluation align with the cases discussed more broadly in the literature, while ensuring a balance between the highest order of the linear context of the derivative term and the highest order of the non-linear term structure of Eq. (21). We aim to present multiple solution examples within a single document.

Case I: For $\:{F}_{0}=0$, $\:{F}_{1}=0$, the sought solution reads

$$\:\varphi\:\left(\xi\:\right)=\frac{1}{\xi\:}.$$

(Equ24)

Case II: For $\:{F}_{0}=0$, $\:{F}_{1}\ne\:0$, the sought solution reads

$$\:\varphi\:\left(\xi\:\right)=\frac{-\xi\:}{{B}_{0}{e}^{-{F}_{1}\xi\:}-1},$$

(25)

with$\:{B}_{0}$ an arbitrary constant.

Case III: While $\:{F}_{0}<0$, $\:{F}_{1}=0$, the solutions of Eq. (23) are

$$\:\begin{array}{c}\varphi\:\left(\xi\:\right)=\sqrt{-{F}_{0}}tanh\left(\sqrt{-{F}_{0}}\xi\:\right),\\\:\varphi\:\left(\xi\:\right)=-\sqrt{-{F}_{0}}coth\left(\sqrt{-{F}_{0}}\xi\:\right).\end{array}$$

(26)

Case IV: While $\:{F}_{0}>0$, $\:{F}_{1}=0$, the solutions of Eq. (23) are

$$\:\begin{array}{c}\varphi\:\left(\xi\:\right)=\sqrt{{F}_{0}}tan\left(\sqrt{{F}_{0}}\xi\:\right),\\\:\varphi\:\left(\xi\:\right)=-\sqrt{{F}_{0}}cot\left(\sqrt{{F}_{0}}\xi\:\right).\end{array}$$

(27)

Case V: For $\:{F}_{0}\ne\:0$, $\:{F}_{1}\ne\:0$, the solutions of Eq. (23) are

$$\:\varphi\:\left(\xi\:\right)=\frac{{A}_{1}-{A}_{2}{B}_{1}{e}^{\left({A}_{1}-{A}_{2}\right)\xi\:}}{1-{B}_{1}{e}^{\left({A}_{1}-{A}_{2}\right)\xi\:}}.$$

(28)

$\:{B}_{1}$ a constant, $\:{A}_{1}$ and $\:{A}_{2}$ are the roots of $\:{A}^{2}+{F}_{1}A+{F}_{0}$ and their expressions are given by

$$\:\begin{array}{cc}{A}_{1}=\frac{-{F}_{1}-\sqrt{{F}_{1}^{2}-4{F}_{0}}}{2},&\:{A}_{2}=\frac{-{F}_{1}+\sqrt{{F}_{1}^{2}-4{F}_{0}}}{2}.\end{array}$$

(29)

Step 3: After obtaining $\:N$, we substitute the expression of $\:\varphi\:\left(\xi\:\right)$ given at the second step which satisfies Eq. (23). We compute and collect all the same power terms in $\:\varphi\:\left(\xi\:\right)$ into the polynomial derived from Eq. (21) and equal them to zero. Subsequently, we reach an algebraic set of equations with $\:{a}_{0}$,$\:\:{a}_{i}\left(i=1,\dots\:,N\right)$,$\:\:{b}_{i}\left(i=\text{1,2},\dots\:,N\right)$, $\:k$, $\:\lambda\:$ the unknown parameters to deduce.

We would like to point out that the current study has not yet been undertaken regarding the coupling of beta-derivative fractional space-time equations with nerve fibers. The aim of this research is to focus on more soliton like forms so as to process signals in the nervous systems of higher order organisms, which are quite distinct and tend to deviate from the regular forms.

Euler equations for space-time fractional beta-derivative coupled nerve fibers obtained by the procedure detailed

The purpose of this section is to apply the method described in the previous one, which has more specific procedures. Now that we have come to the agreement to have the assumption confirmed, let us do a little self-review: Some authors have noted that the fractional-order derivative is more appropriate and accurate to model actual cases rather than using classical derivatives^{43,44,45,46,47,48,49,52}. There is a current work being done on the dynamical characteristics of soliton-like pulses propagating in nerve fibers with couplings, space-time fractional beta-derivatives. Linear stability analysis forms part of this research work. Explaining the motivation for the use of fractional derivatives such as beta-derivatives is worth emphasizing once again. Another interesting aspect of the system is that the subject of this work is a functional subsystem of the system which is responsible for the encoding and decoding of complex messages. Nonlinear complex phenomena headquarters (NCPH) is probably one way to define and focus on this particular subject. The studied electrical circuit was actually the right choice for this purpose, regarding the nonlinear excitation of this circuit, mainly the transfer of stimulation pulses through it. The authors state that the microwave integrated waveguides allow modelling systems of different kinds; for instance, the one mimicking the nervous system can be built with electrical elements like capacitors and resistors. Two nonlinear partial differential equations (NPDEs) arise from the fact that Kirchhoff’s laws are applied to the particularized electrical model of nerve fibers: coupled nerve fibers. These equations arise from mesh and node analysis of the circuit’s construction involving its electrical elements (the resistor and the capacitor). This has been taken a step further with recent research on the modeling of problems that are usually given in terms of integer NPDE as integer NDDE. Consistent with the findings of experiments carried out by Westerlund, the electric current passing through the nonlinear capacitor conforms to the empirical law of Curie from 1889^52,72. Jonscher had also shown that it is not possible to realize the ideal capacitor using only conventional methods using natural system components⁷³. The response of dielectric materials can be explained with the help of fractional order equations. Preassigned in⁶⁴⁷⁴⁷⁵ is the complex impedance of the internal electrode of the capacitor:

$$\:\begin{array}{cc}{Z}_{C}=\frac{1}{C{\left(j\omega\:\right)}^{\alpha\:}},&\:0<\alpha\:\le\:1.\end{array}$$

(30)

Thus, the value of the Ohm’s law for the capacitor is:

$$\:\begin{array}{cc}{I}_{c,n}^{\left(j\right)}=C\frac{{d}^{\alpha\:}{V}_{n}^{\left(j\right)}}{d{t}^{\alpha\:}},&\:0<\alpha\:\le\:1.\end{array}$$

(31)

It is feasible to derive the fractional order variant of Eq. (4) by incorporating the principles outlined in Kirchhoff’s laws and Curie’s laws, which represent the fractional Ohm laws applicable to electrical components, as detailed in Eq. (30) using the aforementioned calculus methodologies.

$$\:\left\{\begin{array}{c}\begin{array}{c}-M\left(\left(1-\eta\:\right)\left({u}_{n+1}-2{u}_{n}+{u}_{n-1}\right)-\eta\:\left({v}_{n+1}-2{v}_{n}+{v}_{n-1}\right)\right)\\\:+{R}_{f}C\frac{{d}^{\alpha\:}{u}_{n}}{{dt}^{\alpha\:}}+\beta\:{u}_{n}\left({u}_{n}-a\right)\left({u}_{n}-1\right)=0,\end{array}\\\:\begin{array}{c}-M\left(\left(1-\eta\:\right)\left({v}_{n+1}-2{v}_{n}+{v}_{n-1}\right)-\eta\:\left({u}_{n+1}-2{u}_{n}+{u}_{n-1}\right)\right)\\\:+{R}_{f}C\frac{{d}^{\alpha\:}{v}_{n}}{{dt}^{\alpha\:}}+\beta\:{v}_{n}\left({v}_{n}-a\right)\left({v}_{n}-1\right)=0.\end{array}\end{array}\right.$$

(32)

The continuous version is obtained through contouring, that is, modeling the medium as a continuous mass with the internodal distance being assumed to be small enough. This results in the creation of a set of fractional nonlinear coupled partial differential equations (FNCPDEs) provided certain conditions are satisfied $\:\delta\:n\to\:x$, $\:{u}_{n}=u\left(x,t\right)$, $\:{v}_{n}=v\left(x,t\right).$

$$\:\left\{\begin{array}{c}{R}_{f}C\frac{{d}^{\alpha\:}u}{{dt}^{\alpha\:}}+\beta\:u\left(u-a\right)\left(u-1\right)-M\left(\left(1-\eta\:\right){\delta\:}^{2}\frac{{d}^{2}u}{d{x}^{2}}-\eta\:{\delta\:}^{2}\frac{{d}^{2}v}{d{x}^{2}}\right)=0,\\\:{R}_{f}C\frac{{d}^{\alpha\:}v}{{dt}^{\alpha\:}}+\beta\:v\left(v-a\right)\left(v-1\right)-M\left(\left(1-\eta\:\right){\delta\:}^{2}\frac{{d}^{2}v}{d{x}^{2}}-\eta\:{\delta\:}^{2}\frac{{d}^{2}u}{d{x}^{2}}\right)=0.\end{array}\right.$$

(33)

Having examined the properties of the beta-derivatives outlined before, let us apply now the wave transformation and use the ansatz of the following manner:

$$\:\begin{array}{c}\xi\:=k\left({x-\frac{\lambda\:}{\alpha\:}\left(t+\frac{1}{\varGamma\:\left(\alpha\:\right)}\right)}^{\alpha\:}\right),\\\:u\left(t,x\right)=U\left(\xi\:\right),\\\:v\left(t,x\right)=V\left(\xi\:\right).\end{array}$$

(34)

Let $\:k$ and$\:\:\lambda\:$ denote the wave number and the velocity of the new wave transformation respectively. Therefore, let us rewrite Eq. (33) concerning the equations for the nerve fibers that are coupled with the space-time fractional beta-derivative and which are represented with a fractional coupled nonlinear partial differential equation (FNPDE) into a coupled nonlinear ordinary differential equation (NODE)

$$\:\left\{\begin{array}{c}-{R}_{f}Ck\lambda\:\frac{dU}{d\xi\:}+\beta\:U\left(U-a\right)\left(U-1\right)-M\left(\left(1-\eta\:\right){\delta\:}^{2}{k}^{2}\frac{{d}^{2}U}{d{\xi\:}^{2}}-\eta\:{\delta\:}^{2}{k}^{2}\frac{{d}^{2}V}{d{\xi\:}^{2}}\right)=0,\\\:-{R}_{f}Ck\lambda\:\frac{dV}{d\xi\:}+\beta\:V\left(V-a\right)\left(V-1\right)-M\left(\left(1-\eta\:\right){\delta\:}^{2}{k}^{2}\frac{{d}^{2}V}{d{\xi\:}^{2}}-\eta\:{\delta\:}^{2}{k}^{2}\frac{{d}^{2}U}{d{\xi\:}^{2}}\right)=0.\end{array}\right.$$

(35)

Using the previously established balance principle and the Eq. (34), we describe the borderline conditions necessary for the use of the Eq. (22). To obtain N, we implement the homogeneous balance principle between the higher nonlinearity order term (the higher nonlinearity of term $\:U\left(U-a\right)\left(U-1\right)$ is $\:{U}^{3}$) and the higher linear derivatives order$\:\:\left(\frac{{d}^{2}U}{d{\xi\:}^{2}}\right)$. Then, for the current study by applying the homogeneous balance principle, for $\:\left[U\right]=N$, $\:\text{w}\text{e}\:\text{g}\text{e}\text{t}$ (respectively, we proceed for $\:V$ as we do for $\:U$)

$$\:\left[{U}^{3}\right]=\left[\frac{{d}^{2}U}{d{\xi\:}^{2}}\right]\:\:\:\:\: \Rightarrow \:\:\:\:3N=N+2.$$

Then, $\:N=1$, we make use of the ansatz structured as follows:

$$\:\left\{\begin{array}{c}U\left(\xi\:\right)={a}_{10}+{a}_{11}\left(\varphi\:\left(\xi\:\right)\right)+{a}_{12}{\left(\varphi\:\right(\xi\:\left)\right)}^{-1},\\\:V\left(\xi\:\right)={b}_{10}+{b}_{11}\left(\varphi\:\left(\xi\:\right)\right)+{b}_{12}{\left(\varphi\:\right(\xi\:\left)\right)}^{-1}.\end{array}\right.$$

(36)

Where $\:\:\varphi\:\left(\xi\:\right)$satisfies the polynomial auxiliary Eq. (23), $\:\:{a}_{10}$, $\:{a}_{11}$, $\:{a}_{12}$, $\:{b}_{10}$, $\:{b}_{11}$, $\:{b}_{12}$, $\:k$ and$\:\:\lambda\:$ are the unknown parameters to seek. By substituting Eq. (36) inside Eq. (35) and throughout some analytical tedious calculus aiding by the software Maple, we find a coupled set of polynomial function equation in power of $\:{\left(\varphi\:\right(\xi\:\left)\right)}^{i}$ such as $\:{\left(\varphi\:\right(\xi\:\left)\right)}^{-1}i=\text{0,1},2,\dots\:,6$ (for each polynomial function equation in $\:\varphi\:\left(\xi\:\right)$). We perform the recommended enhanced methodology and incorporate it into the NODE (35) obtained from the equations of coupled nerve fibers with space-time fractional beta-derivatives. To generate a report on the desired solutions for families, we set $\:{{\Delta\:}}_{1}=-{F}_{1}^{2}+4{F}_{0}$, $\:{{\Delta\:}}_{2}=\sqrt{\frac{1}{{F}_{1}^{2}-4{F}_{0}}}$ and it yields:

Set 1: for $\:{a}_{11}=0$, $\:{b}_{11}=0$ with the restrictions $\:2a-1\ne\:0,\:\:2\eta\:-1\ne\:0,\:{\varDelta\:}_{1}\ne\:0,\:{\varDelta\:}_{2}\ne\:0$

Family 1:

$$\:\begin{array}{ccc}{a}_{10}=\frac{{\varDelta\:}_{1}{\varDelta\:}_{2}-{F}_{1}}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:1}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{12}={\varDelta\:}_{2}{F}_{0},&\:{b}_{12}={a}_{12},&\:\lambda\:=\frac{\left(2a-1\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(37)

Family 2:

$$\:\begin{array}{ccc}{a}_{10}=\frac{a\left({\varDelta\:}_{1}{\varDelta\:}_{2}-{F}_{1}\right)}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:a}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{12}={a\varDelta\:}_{2}{F}_{0},&\:{b}_{12}={a}_{12},&\:\lambda\:=\frac{-a\left(a-2\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(38)

Family 3:

$$\:\begin{array}{ccc}{a}_{10}=\frac{{\varDelta\:}_{1}{\varDelta\:}_{2}\left(1+a\right)+{F}_{1}\left(1-a\right)}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:\left(a-1\right)}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{12}=\left(a-1\right){\varDelta\:}_{2}{F}_{0},&\:{b}_{12}={a}_{12},&\:\lambda\:=\frac{-\left(a-1\right)\left(a+1\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(39)

Family 4:

$$\:\begin{array}{ccc}{a}_{10}=\frac{{\varDelta\:}_{1}{\varDelta\:}_{2}+{F}_{1}}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:1}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{12}=-{\varDelta\:}_{2}{F}_{0},&\:{b}_{12}={a}_{12},&\:\lambda\:=\frac{-\left(2a-1\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(40)

Family 5:

$$\:\begin{array}{ccc}{a}_{10}=\frac{a\left({\varDelta\:}_{1}{\varDelta\:}_{2}+{F}_{1}\right)}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:a}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{12}=-{a\varDelta\:}_{2}{F}_{0},&\:{b}_{12}={a}_{12},&\:\lambda\:=\frac{a\left(a-2\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(41)

Family 6:

$$\:\begin{array}{ccc}{a}_{10}=\frac{{\varDelta\:}_{1}{\varDelta\:}_{2}\left(1+a\right)-{F}_{1}\left(1-a\right)}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:\left(a-1\right)}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{12}=-\left(a-1\right){\varDelta\:}_{2}{F}_{0},&\:{b}_{12}={a}_{12},&\:\lambda\:=\frac{\left(a-1\right)\left(a+1\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(42)

Set 2: for $\:{a}_{12}=0$, $\:{b}_{12}=0$ under the restrictions $\:2a-1\ne\:0,\:\:2\eta\:-1\ne\:0,\:{\varDelta\:}_{1}\ne\:0,\:{\varDelta\:}_{2}\ne\:0$

Family 1:

$$\:\begin{array}{ccc}{a}_{10}=\frac{{\varDelta\:}_{1}{\varDelta\:}_{2}-{F}_{1}}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:1}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{11}={\varDelta\:}_{2},&\:{b}_{11}={a}_{11},&\:\lambda\:=\frac{-\left(2a-1\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(43)

Family 2:

$$\:\begin{array}{ccc}{a}_{10}=\frac{a\left({\varDelta\:}_{1}{\varDelta\:}_{2}-{F}_{1}\right)}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:a}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{11}={a\varDelta\:}_{2},&\:{b}_{11}={a}_{11},&\:\lambda\:=\frac{a\left(a-2\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(44)

Family 3:

$$\:\begin{array}{ccc}{a}_{10}=\frac{{\varDelta\:}_{1}{\varDelta\:}_{2}\left(1+a\right)+{F}_{1}\left(1-a\right)}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:\left(a-1\right)}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{11}=\left(a-1\right){\varDelta\:}_{2},&\:{b}_{11}={a}_{11},&\:\lambda\:=\frac{\left(a-1\right)\left(a+1\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(45)

Family 4:

$$\:\begin{array}{ccc}{a}_{10}=\frac{{\varDelta\:}_{1}{\varDelta\:}_{2}+{F}_{1}}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:1}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{11}={-\varDelta\:}_{2},&\:{b}_{11}={a}_{11},&\:\lambda\:=\frac{\left(2a-1\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(46)

Family 5:

$$\:\begin{array}{ccc}{a}_{10}=\frac{a\left({\varDelta\:}_{1}{\varDelta\:}_{2}+{F}_{1}\right)}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:a}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{11}={-a\varDelta\:}_{2},&\:{b}_{11}={a}_{11},&\:\lambda\:=\frac{-a\left(a-2\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(47)

Family 6:

$$\:\begin{array}{ccc}{a}_{10}=\frac{{\varDelta\:}_{1}{\varDelta\:}_{2}\left(1+a\right)-{F}_{1}\left(1-a\right)}{2{\varDelta\:}_{1}{\varDelta\:}_{2}},&\:{b}_{10}={a}_{10},&\:k=\frac{\pm\:\left(a-1\right)}{\delta\:}\sqrt{\frac{\beta\:}{2M{\varDelta\:}_{1}\left(2\eta\:-1\right)}},\\\:{a}_{11}=-\left(a-1\right){\varDelta\:}_{2},&\:{b}_{11}={a}_{11},&\:\lambda\:=\frac{-\left(a-1\right)\left(a+1\right)\beta\:{\varDelta\:}_{2}}{{R}_{f}Ck}\end{array}$$

(48)

Global sets one and two, as designated above, are the further advancements made by us. Solution families mentioned above rational, rational exponential, hyperbolic and trigonometric solitary waves are represented by Eqs. (24)–(28). After that we will also show several other solution profiles that will be useful for constructing these solutions.

Analysis of the data using physical means and visual representation of those findings

The results obtained are presented graphically through informative representations such as 2D and 3D graphs, as relevant, to effectively illustrate the solutions derived in a physical context with the restrictions $\:2a-1\ne\:0,\:\:2\eta\:-1\ne\:0,\:{\varDelta\:}_{1}\ne\:0,\:{\varDelta\:}_{2}\ne\:0$. An overarching analysis indicates that the solutions within each set lack the physical characteristics of solitary waves in both case I and case II, particularly in families 1 to 6 of set 1. Analysis reveals that case I from set 2 does not exhibit solitary waves across any of the solution families outlined (from family 1 to 6). The graphical representations of the set 1 where $\:{a}_{11}=0$,$\:\:{b}_{11}=0$, show that the families 1 to 6 do not display any profiles in the cases I ($\:{F}_{0}=0$,$\:\:{F}_{1}=0$ see Eq. (24)) and II ($\:{F}_{0}=0$,$\:\:{F}_{1}\ne\:0$ see Eq. (25)). Therefore, for this first set, we can plot the cases III, IV and V for any retrieved solutions families from families 1 to 6. Indeed, while $\:{F}_{0}=0$,$\:\:{F}_{1}=0$, the cases I, II display a constant signal due to the fact $\:{a}_{11}\ne\:0$,$\:\:{b}_{11}\ne\:0$, $\:{a}_{12}=0$,$\:\:{b}_{12}=0$. Thus, we depict on the below graph the families 1 and 2 of the case I in the set 2.

Fig. 4

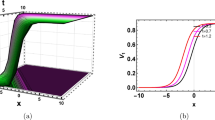
These panels exhibit families Eqs. (37) and (38) for $\:\delta\:={10}^{-3}$, $\:a=0.25$, $\:\eta\:=0.25$, $\:\beta\:=0.5$, $\:{B}_{0}=4$, $\:{B}_{1}=1.5$, $\:M=0.5$, $\:{R}_{f}C=4.{10}^{-4}$: case I (a)–(b) family 1 $\:\alpha\:=1$, $\:\alpha\:=0.75$ respectively; (c)–(d) family 2 $\:\alpha\:=1$, $\:\alpha\:=0.75$ respectively; (e) 2D graphs for the case I family 1; (f) 2D graphs for the case II family 1.

Fig. 5

These panels display the set 1 for $\:\delta\:={10}^{-3}$, $\:a=0.25$, $\:\eta\:=0.25$, $\:\beta\:=0.5$, $\:{B}_{0}=4$, $\:{B}_{1}=0.5$, $\:M=0.5$, $\:{R}_{f}C=4.{10}^{-4}$: case III.1 (a)-(b) with $\:{F}_{0}=-2$, $\:{F}_{1}=0$, family 1 $\:\alpha\:=1$, $\:\alpha\:=0.75$ respectively; case IV.1 (c)-(d) with $\:{F}_{0}=2$, $\:{F}_{1}=0$, family 1 $\:\alpha\:=1$, $\:\alpha\:=0.75$ respectively; (e) 2D graphs for the case III.1 family 1; (f) 2D graphs for the case IV.1 family 3.

The provided graphs concern outputs of families 3 and 4 from set 1. We move forward with the third and fourth families of the second set. Our results include the visual representation of the family 5 of the sets 1 (top row) and II (bottom row). We have obtained a range of new geometrical shapes with the possible categories being kink rogue waves and kink pulse solitary waves. The several of these are variations of the desired solutions which are presented as pulses (further details are in Fig. 4), as kinks (certain figures are as follows: Figs. 5a, b, e,  6a, b, e), as anti-kinks (Figs. 5c, d, f, 6c, d, f), as kink-rogue waves, and anti-kink rogue waves (see Figs. 5 and 6). The fractional-order (FO) operator not only changes the degree of the signal and also changes the rate of propagation of the signal. In particular, when the value of α is less than one (such as, $\:\alpha\:=0.75$ or $\:0.5$), all solitary waves are obtained and regardless of their appearance, are propagated at a higher rate than if $\:\alpha\:=1$. All these findings have been pinpointed and pointed out by the authors of the various papers where these different physical systems were studied, such as electrical circuits/networks or optical fibers, amongst others. Still, however, these findings have not as yet been recorded or reported on the nonlinear coupled nerve fibers consisting of the beta-derivative.

Fig. 6

These panels display the set 2 for $\:\delta\:={10}^{-3}$, $\:a=0.25$, $\:\eta\:=0.25$, $\:\beta\:=0.5$, $\:{B}_{0}=4$, $\:{B}_{1}=0.5$, $\:M=0.5$, $\:{R}_{f}C=4.{10}^{-4}$: case III.1 (a)-(b) with $\:{F}_{0}=-2$, $\:{F}_{1}=0$, family 1 $\:\alpha\:=1$, $\:\alpha\:=0.75$ respectively; case IV.1 (c)-(d) with $\:{F}_{0}=2$, $\:{F}_{1}=0$, family 1 $\:\alpha\:=1$, $\:\alpha\:=0.75$ respectively; (e) 2D graphs for the case III.1 family 1; (f) 2D graphs for the case IV.1 family 3.

Most limits (in comparison with those in previous investigations) of the classical theory for nonlinear coupled nerve fibers are: changing solitary wave speed, fluctuation in amplitude and including new solitary wave types forming such as kink-rogue and anti-kink-rogue. Using physiological parameters and employing non-integer order derivatives we are able to use these findings to justify the complex phenomena present in the current model described by conventional derivatives. It has been shown that the introduction of the FO derivative allows us to characterize the memory effect, incapability of periodicity and genetic characteristics of complex systems. In other instances, pre-existing investigations relying on the integer-order (IO) derivatives have, in certain instances, been silent to the existence of these phenomena. As a result, the memory phenomenon can be used to clarify some previously unexplained observations related to the propagation of impulses through myelinated fibers. Effects caused by ephaptic coupling, exact value of the FO parameter, and the distance between the active nodes affect also the ultra-significant amplitude change and increased speed of impulse conduction. Hence, while seeking to understand these phenomena as observed from the findings above, we are able to integrate the intricate mechanisms involved in phenomena like as the regulation and coordination of various anatomical structures of the body. Practically speaking, the recent mathematical concepts are linked with possible electro-physiological activities such as the propagation of action potentials in neurons and the changes of such physiological activity in some diseases. Further, these observations also offer us the chance to engage in discussions about the potentials on the applications and even in the ways on how the diagnostic techniques and treatment strategies for the neurological diseases can be improved.

Conclusions

The objective of this study was to search for new solitary waves given by the equation which is a beta differential-difference equation. The present equations containing the space fractional-time beta-derivative expanded the understanding of the physics of saltatory conduction in a network of axon fibers. We have revealed the regions of stability and instability of the model including modulation instability based on the linear stability analysis of the model. In addition, we have also set the equilibrium points and assessed the Jacobian matrix using dynamical theory analysis. After concerning the values and other indicators of some physiological parameters, we were able to visualize the three-dimensional modulational instability regions. The seen areas provide experimental validation for the existence of solitonic impulses in a wide band of (η, q) or in some narrow bands of (η, q) representative space. Additional, we have argued such areas in connection with neurological diseases when disordered propagation of nerve signals may cause complex pathological conditions such as epilepsy or neuropathic pain. We have carried out the study of the model equation by applying the new technique of polynomial expansion scheme. Certainly, it can be reported that we have introduced a superior wave transformation technique, the fractional complex transform. In this process, a certain value of a fractional beta-derivative is introduced and it is constructed employing a semi-discrete approach. Then, the equation describing the action of the nerve fiber was transformed into a complex of reduced ordinary differential elliptic equations. This system consists of two independent parameters. The algorithms of polynomial expansion in this case used two parameters from the related auxiliary equation. The limitation of the two auxiliary equation parameters, made it possible to find several families of sets. Being dependent on the magnitude and/or sign of these parameters, we have classified those solutions as rational, exponential, hyperbolic or trigonometric solutions. We have shown in 3D and 2D solution graphs, Kink/anti-kink solitary waves and their singular forms, short pulse waves and kink-rogue solitary waves with physiological as well as sustained stability and efficiency. There have been examples where graphs have been used to show a fractional-order effect seen in some nonlinear electronic transmission networks, specifically that of the physical bundles. The phenomenon relates to the change in the amplitude and the change in the speed of the nerve impulse. Changes resulting from the above can be traced thanks to such parameters as the nerve fiber’s diameter and the application of the fractional order means. Utilizing the set of plotted graphs, we were able to demonstrate visually the presence of a fractional-order effect that is observed in some nonlinear electrical communication networks, in particular, that of physical bundle configurations. This in turn involves the change in both the intensity or the rate of transmission of a nerve impulse. Changes resulting from the above can be traced thanks to such parameters as the nerve fiber’s diameter and the application of the fractional order methods.