Introduction

As a global concern, waste management is one of the key issues that need to be moved across the globe towards sustainability1. Heavy metal contamination is created in wastewater from various industrial operations, including mining and plating various metals. Heavy metals, including Cr, Hg, Cu, Pb, Cd, Zn, and Ni, are ecologically dangerous since they do not dissolve and can gather in organisms2,3. Adsorption is commonly regarded as an economical and efficient approach to treatment for wastewater and toxic pollutant removal4. Clay minerals have recently gained a lot of interest as adsorbents for several harmful chemicals and heavy metals5. Clay minerals as an adsorbent have various advantages over other materials, including fair, easy access, low price, non-toxic nature, significant specific surface area, and high efficiency in cationic exchange6. Bentonite is mostly made up of the mineral montmorillonite, calcite, feldspar, and quartz. Several scholars have examined the use of bentonite for heavy metal adsorption throughout the recent decade7,8,9,10,11. One approach to removing heavy metals is to include bentonite in materials like concrete mixtures. Bentonite plastic concrete (BPC) blends bentonite and typical concrete12. When exposed to water, bentonite may absorb it and expand in size. As a result of the bentonite’s water absorption potential, plastic concrete has a desirable low permeability level13. Abbaslou et al.14 investigated BPC’s capacity to remove dissolved cadmium components from water. Plastic concrete physical parameters were improved and modified, resulting in fewer cracks and a longer working life for various engineering constructions. Despite these advantages, the effective prediction of BPC’s mechanical properties, including slump, tensile strength, and elastic modulus, remains challenging due to experimental methods’ laborious and costly nature.

BPC is commonly used to build cut-off walls to decrease dam seepage. Dam water seepage reduces internal friction and causes the dam to slide or collapse15. BPC is gaining popularity due to its advantageous attributes, including its elastic-plastic features, low permeation, and uniformity16. Plastic concrete should tolerate strain between the wall and nearby soil to reduce the risk of excessive wall strain and facilitate displacement without separation. BPC should have great workability and homogeneity for easier filling of trenches and deep walls. However, the technical challenges of ensuring consistent mix design and predicting mechanical properties efficiently have limited its broader application. Addressing these gaps through computational methodologies is critical.

Previous studies on computational techniques for predicting BPC properties can be divided into three categories. The first group includes studies utilizing single machine learning (ML) models like artificial neural networks (ANN), M5 Tree, and Multivariate Adaptive Regression Splines (MARS)17,18,19. These models are more precise and robust than traditional regression methods in predicting green concrete characteristics20. ML techniques allow for accurate predictions of material properties, such as compressive strength and fracture toughness, without extensive experimentation21,22,23. Tavana Amlashi et al.19 demonstrated that ANN outperforms M5 Tree and MARS in predicting BPC slump, elastic modulus, and compressive strength. Ghanizadeh et al.24 employed SVM and ANN to forecast BPC compressive strength, identifying cement as the most influential factor. Tavana Amlashi et al.25 combined SVM, ANN, and Adaptive Neuro-Fuzzy Inference System (ANFIS) with Particle Swarm Optimization (PSO) to predict compressive and splitting tensile strength, with ANN-PSO achieving an R² of 0.95, outperforming other methods. In another study, Tavana Amlashi et al.26 used four computational techniques—Response Surface Methodology (RSM), Multigene Genetic Programming (MGGP), Group Method of Data Handling (GMDH), and SVM—to predict the compressive strength of BPC, based on parameters like water, silty clay, sand, gravel, cement, and bentonite.

The second group focuses on ensemble learning (EL) models, like Gradient Boosting Regression Trees (GBRT), Random Forests (RF), and Extreme Gradient Boosting (XGB). Alishvandi et al.27 applied six computational methods—GBRT, Decision Tree (DT), RF, XGB, k-Nearest Neighbors (KNN), and SVM—for predicting the compressive strength of plastic concrete using factors like temperature, bentonite, cement, sand, water, and water-to-cement ratio. Model performance was evaluated using R², RMSE, MAE, and MAPE. EL methods outperform individual ML algorithms28 in predicting the mechanical properties of various concrete types, including high-performance concrete (HPC)29,30,31,32,33,34,35, recycled aggregate concrete (RAC)36,37,38,39, lightweight foamed concrete (LFC)40, geopolymer concrete (GPC)41,42, self-compacting concrete (SCC)43, and concrete with rice husk ash (CCRHA)44,45,46,47. EL methods are categorized into stacking, boosting, and bagging techniques. Boosting models such as Adaptive Boosting (ADB), GBRT, and XGB are widely used29. Li and Song46 demonstrated that stacking EL models, with XGB as a base learner and linear regression as the second layer, enhances model precision by integrating base learners’ outputs. ADB assigns weights to training samples based on regression difficulty, creating a meta-learning model suitable for simple and complex data48. GBRT, a boosting method employing an additive model and residual reduction, uses CART to fit negative gradients of loss functions during training49,50. Bagging methods, such as RF, have also shown superior performance. Amin et al.45 reported that RF outperformed DT and ADB in compressive strength estimation of CCRHA. According to Iftikhar et al.47, an improved RF model using EL increased compressive strength prediction accuracy by 1.62% compared to standalone RF models.

The third group of models incorporates optimization techniques like Particle Swarm Optimization (PSO) and forensic-based investigation optimization (FBIO) to fine-tune hyperparameters in boosting and bagging algorithms, thereby improving accuracy and efficiency. Tuning meta-parameters is critical for developing ensemble learning (EL) systems51. However, the abundance of meta-parameters complicates the process, requiring a thorough understanding of their impacts on model outcomes52. This task is time-intensive and computationally demanding. Researchers have introduced various methods to simplify the development of EL models, aiming to reduce manual effort while enhancing performance within limited timeframes53,54,55,56,57. This research utilizes the FBIO method to optimize global meta-parameters for boosting and bagging algorithms48. FBIO ensures optimal performance by automating parameter tuning, alleviating manual selection challenges, and expediting EL model improvement58.

In this study, we address the challenges of predicting BPC’s mechanical properties by employing a novel approach that combines ensemble learning with FBIO for hyperparameter optimization. Using large laboratory datasets, we develop robust models capable of accurately estimating slump, tensile strength, and elastic modulus. Furthermore, to overcome the black-box nature of machine learning methods, we design an online, user-friendly application to facilitate the implementation of the suggested model by engineers on-field. This study aims to bridge the gap between theoretical advancements in ML and practical applications in BPC design, providing engineers with reliable tools to improve project efficiency and sustainability.

Methodology

ADB

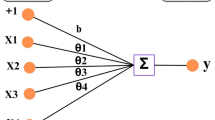
Schapire introduced the boosting method in 1990, which involves combining multiple weak learners in a series59. Equation 1 illustrates that the entire tree is replaced upon introducing a new tree model to the system, retaining only the strongest one. The iterative nature of computations leads to cumulative improvements in the overall model performance over time. The ADB approach continuously improves data categorization skills by training inside a suboptimal classification framework. This method assigns various weights to the input data to enhance classification accuracy60. This model focuses more on improving the classification of the incorrectly categorized samples61. Despite being a weak learner, ADB encompasses all machine learning regression techniques. Notably, DT regression and ANN are widely used within this framework. Decision Trees are preferred due to their extensive application across technical domains and the ease of model training. Various sources provide a comprehensive intellectual foundation for Decision Trees62. Figure 1 provides an overview of the ADB model. Training results differed because each training data set was unified, and the results were finally merged.

$${\text{F}}_{{\text{n}}} {\text{(x)}} = {\text{F}}_{{{\text{n - 1}}}} {\text{(x)}} + \mathop {\text{argmin} _{h} }\limits_{{}} \sum\limits_{{{\text{i}} = {\text{1}}}}^{{\text{n}}} {{\text{L(y}}_{{\text{i}}} ),} {\text{ F}}_{{{\text{n - 1}}}} {\text{(x}}_{{\text{i}}} ) + h(x_{i} )$$
(1)
Fig. 1
figure 1

The sequence of steps in the ADB modeling process.

Full size image

In this context, the comprehensive model is denoted as Fn(x) , where “n” represents the current cycle, and the model from the preceding cycle is represented as Fn-1(x). Furthermore, h(xi) refers to the recently added tree, and yi signifies the anticipated result of the i-th tree.

GBRT

Breiman et al.63 presented the CART method. CARTs could be applied to classification and regression methods64,65,66. Recursive techniques are employed to construct binary trees, which are the decision trees utilized in regression and classification methods. This study primarily focuses on the GBRT model developed by He et al.67, which combines the Gradient Boosting and CART methods. The CART is acknowledged for its higher forecasting precision than other artificial intelligence methods. The CART method generates regression trees serving as weak learners, as the GBRT model transforms these weak learners into more effective ones. The algorithm incorporates poor learners to refine previously obtained predictions, aiming to reduce forecasting errors and enhance overall reliability.

The associated leaf node region of the mth regression tree in the updated algorithm, denoted as Fm(x), or Rm, j, where j = 1, 2,. . ., Jm, is determined by Eq. 2:

$${\text{F}}_{{\text{m}}} {\text{(x)}} = {\text{F}}_{{{\text{m - 1}}}} {\text{(x)}} + \sum\limits_{{j = 1}}^{{J_{m} }} {{\text{c}}_{{{\text{m,j}}}} {\text{I(}}x \in {\text{R}}_{{{\text{m,j}}}} {\text{)}}}$$
(2)

I is around 1 if \({x} \in {R}_{m,j}\) and 0 otherwise68. The leaf node number in the mth regression tree is either denoted by Jm. The model is updated accordinglyFig. e 2 provides an overview of the GBRT model.

Fig. 2
figure 2

The basic process of GBRT.

Full size image

XGB

Chen and He69 are credited with developing the XGB methodology. XGB effectively addresses both regression and classification tasks by constructing boosted trees. This serves as the foundation of the XGB algorithm and is analogous to various optimization models. XGB offers a dependable and quick simulation model like the GBRT decision tree. The XGB algorithm is defined by (Fig. 3).

Fig. 3
figure 3

A flowchart depicting the structure of XGB trees.

Full size image

The objective function of XGB is reduced to optimize the ensemble tree and minimize errors Eq. 3

$$L^{{(t)}} = \sum\limits_{{i = 1}}^{n} {l(y_{{i,}} \hat{y}_{i}^{{(t - 1)}} + f_{t} (x_{i} )) + \Omega (f_{t} )}$$
(3)

Assuming ŷi is the predicted value, and yi is the observed value, l is a convex function applied to measure the discrepancy between observed and predicted outcomes. To minimize errors, iteration numbers (t) are applied, and the regularization term for the framework of the regression tree is defined as Eq. 4.

$$\Omega (f_{k} ) = \gamma T + \frac{1}{2}\lambda \left\| w \right\|^{2}$$
(4)

RF

Svetnik introduced the random forest regression model as an enhanced regression approach with classification capabilities70,71. The algorithm generates multiple decision trees by randomly sampling data points to construct its predictions. These decision trees are trained using distinct combinations of features and data subsets, culminating in a diverse ensemble of models. When integrated, this ensemble delivers precise predictions. By employing this ensemble learning approach, the algorithm minimizes the risk of overfitting and enhances its generalization capabilities. In RF regression, predictions are generated by constructing multiple decision trees, and the final output is determined by calculating the mean of the individual tree predictions. Figure 4 presents an overview of the RF algorithm’s framework. The regression equation utilized to analyze the RF method is summarized below (Eq. 5)72:

$$~M(x) = \frac{1}{N}\mathop \sum \limits_{{i = 1}}^{n} (y_{i} (x,\theta _{n} )$$
(5)
Fig. 4
figure 4

The schematic flowchart of RF.

Full size image

FBIO

Machine learning methods have been combined with metaheuristic optimization techniques to predict various factors, such as the Whale Optimization Algorithm, genetic algorithm, and particle swarm optimization73,74. The FBIO method distinguishes itself from other ways by eliminating the need to set internal factors. Instead, the optimization process is executed by adjusting iteration values and population sizes75.

Therefore, the FBIO method can be a new approach to building an accurate model to estimate plastic concrete characteristics. It was originally introduced by Chou and Nguyen76 as a mathematical problem-solving technique inspired by the simulation of police forces’ forensic investigation activities. In this model, the search area represents the extent of the officer’s query, and the term “culprit” denotes an optimal reply. The number of cooperating authorities determines the size of the community under examination. The level of complexity determines how much can be invested. Soon after the crime evidence is turned over to the FBIO base, the optimization process starts and stops when the culprit is taken to arrest. The FBI strategy is split into two phases: Stage P shows the track team’s operations with the police. At the same time, Stage I analyzes the event and directs the inspection team (Fig. 5).

Fig. 5
figure 5

The general process of FBIO.

Full size image

The application process

Specifics of data gathering

The database employed in this study comprises 115, 158, and 119 datasets for tensile strength, elastic module, and slump12,14,19,26,70,77,78,79,80,81,82,83,84.

Elwell and Fu85 proposed UNESCO conversion factors to homogenize cylindrical and cubic values. As effective variables for BPC properties, this research examined the following variables: contents of gravel, bentonite, silty clay, curing time, sand, cement, and water. As shown Fig. 6, the intended graph distribution is not uniform, so the developed models apply to a wide range of target data86. A lower correlation is observed between negative and positive values in the overall model variables, as shown Fig. 7. In addition, according to the correlation heat map analysis, water, gravel, and curing time have a greater positive impact on the S, TS, and E of BPC, respectively.

Fig. 6
figure 6

Frequency histogram of output targets.

Full size image
Fig. 7
figure 7

Pearson correlation Coefficients for S, TS, and E.

Full size image

Before modeling, the data were randomly split into testing (30%) and training (70%) parts. Tables 1, 2 and 3 display the statistical characteristics of the output and input variables for the testing and training data for S–BPC, TS–BPC, and E–BPC. A logical and technical range can be developed for each input variable by considering the highest value of the minimums and the lowest value of the maximums for each of the four data sets. In particular, these ranges are 295 to 875 kg/m3 for gravel, 524 to 1305 kg/m3 for sand, 0 to 260 kg/m3 for silty clay, 80 to 252 kg/m3 for cement, 18 to 100 kg/m3 for bentonite; 260 to 500 kg/m3 for water; and 7 to 180 days for curing time. Tables 1, 2 and 3 allow you to identify extreme data points (maximum and minimum), data centers (mean and median), data spread (standard deviation and variance), and distribution shapes (skewness and kurtosis)86. Moreover, the diversity among databases and the ability of models developed on them to generalize are illustrated by the diverse alterations observed in each of the outputs17.

Table 1 Comprehensive statistics for both testing and training data related to S-BPC.
Full size table
Table 2 Comprehensive statistics for both testing and training data related to TS-BPC.
Full size table
Table 3 Comprehensive statistics for both testing and training data related to E-BPC.
Full size table

Model efficiency assessment specifications

Several error metrics were employed to assess the accuracy of the models (Eqs. (6–11)). These variables are R2, MAE, RMSE, MAPE, a20-index, and OBJ18. These statistical metrics are summarized as follows:

$$R^{2} = \left[ {\frac{{\sum\limits_{{i = 1}}^{N} {(Y_{{obs}} - \overline{Y} _{{obs}} )(Y_{{pre}} - \overline{Y} _{{pre}} )} }}{{\sqrt {\sum\limits_{{i = 1}}^{N} {(Y_{{obs}} - \overline{Y} _{{obs}} )^{2} } \sum\limits_{{i = 1}}^{N} {(Y_{{pre}} - \overline{Y} _{{pre}} )^{2} } } }}} \right]^{2}$$
(6)
$$MAE = \frac{{\sum\nolimits_{{i = 1}}^{N} {\left| {Y_{{pre}} - Y_{{obs}} } \right|} }}{N}$$
(7)
$$MAPE = \frac{{\sum\nolimits_{{i = 1}}^{N} {\left| {Y_{{pre}} - Y_{{obs}} } \right|} }}{{\sum\nolimits_{{i = 1}}^{N} {Y_{{obs}} } }} \times 100$$
(8)
$$RMSE = \sqrt {\frac{1}{N}\sum\limits_{{i = 1}}^{N} {(Y_{{pre}} - Y_{{obs}} } )^{2} }$$
(9)
$$OBJ = (\frac{{N_{{tr}} }}{{N_{{all}} }}.\frac{{RMSE_{{tr}} + MAE_{{tr}} }}{{R_{{tr}}^{2} + 1}}) + (\frac{{N_{{tst}} }}{{N_{{all}} }}.\frac{{RMSE_{{tst}} + MAE_{{tst}} }}{{R_{{tst}}^{2} + 1}})$$
(10)
$$a20 - index = \frac{{m20}}{N}$$
(11)

When N is the number of records, Ypre and Yobs show the predicted and actual values, and the bar items over the parameters indicate the average rate; The variable m20 shows the quantity of the records where the Yobs /Ypre ratio ranges from 0.80 to 1.20; the terms “tst” applied for testing and “tr” applied for training data, accordingly.

Algorithms for hybrid ensemble learners

The FBIO was used in this study to determine the ideal values using the given criteria to set the first random values (Table 4). After these statistics were entered into EL approaches and the EL algorithms were trained using the training dataset, the objective function was determined to be the average RMSE of both data (test and train). Figure 8 provides a summary of the various EL- FBIO approaches. Tables 5, 6 and 7 present the multiple meta-parameter values optimized for the S-PC, TS-PC, and E-BPC models.

Fig. 8
figure 8

An overview of the modeling process in this study.

Full size image
Table 4 Different meta-parameter ranges used in the optimization process.
Full size table
Table 5 Optimized parameter values for S-BPC.
Full size table
Table 6 Optimized parameter values for TS-BPC.
Full size table
Table 7 Optimized parameter values for E-BPC.
Full size table

Model prediction accuracy study

Because of a higher R2-value and fewer scattered spots, the GBRT-FBIO approach outperforms conventional E-BPC models in both phases of testing and training, as shown in Fig. 9. Furthermore, with just a minor deviation from GBRT-FBIO, the given low values of RMSE and MAE in XGB-FBIO model demonstrate the excellent accuracy and dependability in the procedures of TS-BPC (Fig. 10). A20-index is a new significant engineering parameter that determines how many specimens have expected values at most 20% off from observed values87. With an a20-index of 0.916 during the testing step and 1.00 during training, XGB- FBIO is the most accurate predictor of S-BPC. Furthermore, with an a20-index of 0.833 and 0.963 throughout the testing and training step, the RF- FBIO had the lowest desire to perform well for S-BPC (Fig. 11).

Fig. 9
figure 9

Measured versus expected scattering dots in the E-BPC phases.

Full size image
Fig. 10
figure 10

Measured versus expected scattering dots in the TS-BPC phases.

Full size image
Fig. 11
figure 11

Measured versus expected scattering dots in the S-BPC phases.

Full size image

Different statistical indicators were evaluated for training and testing datasets to assess the precision of the proposed forecasting models. Table 8 shows the results for different statistical parameters. In the S-BPC training phase, ADB is 0.32, 0.02, and 0.76 cm lower than GBRT, XGB, and RF in terms of RMSE, while in the testing phase, XGB outperformed ADB, GBRT, and RF by 0.05, 0.07, and 0.53 cm of difference in RMSE, respectively. In addition, XGB surpasses other TS-BPC models with MAPE values of 0.3 and 0.12%, respectively, for the training and testing stages. A comparison of R2 values for E-BPC models reveals that GBRT (99.9% for train and 97.2% for test) and RF (94.1% for train and 87% for test) models exhibit the highest and lowest prediction accuracy, respectively.

Table 8 The precision and effectiveness of each EL-FBIO model.
Full size table

The OBJ enables the combination of numerous statistical indicators for testing and training data to assess the model’s generalizability88. The OBJ high values imply that a method performs badly compared to other ways89. The best efficiency for the GBRT method for E-BPC is presented in Fig. 12, with an OBJ of 0.275 and 0.097%. Furthermore, the RF method performs the worst S, TS, E -BPC given the OBJ quantities of 0.912%, 0.058%, and 0.369%, respectively.

Fig. 12
figure 12

OBJ values of different implemented FBIO models.

Full size image

The Nash-Sutcliffe efficiency (NSE) and the scatter index (SI) coefficient were used as supplementary validation tests for the models by Eqs. (12)-(13).

$$SI = \frac{{RMSE}}{{\overline{Y} _{{obs}} }}$$
(12)
$$NSE = 1 - \frac{{\sum\limits_{{i = 1}}^{N} {(Y_{{pre}} - Y_{{obs}} )^{2} } }}{{\sum\limits_{{i = 1}}^{N} {(Y_{{obs}} - \overline{Y} _{{obs}} )^{2} } }}$$
(13)

In which the bar items over the associated digits represent the average of each value, N represents the records number, and Yobs refer to the observed and Ypre represent anticipated quantities. A model’s predictive accuracy is regarded as excellent if NSE is more than 0.75 or SI is less than 0.1 or good if NSE is between 0.65 and 0.75 or SI is between 0.1 and 0.2. However, it is fair if the NSE value is between 0.5 and 0.65 or the SI is between 0.2 and 0.318. As seen in Fig. 13, all methods have SI rates less than 0.2, indicating that they are excellent or good predictors of plastic concrete. The results also show that all methods had NSE rates greater than 0.75, indicating the EL-FBIO models’ “excellent” accuracy in forecasting output values (Fig. 14).

Fig. 13
figure 13

Calculated SI values for FBIO models.

Full size image
Fig. 14
figure 14

Calculated NSE values for FBIO models.

Full size image

The effectiveness of each design was evaluated using Taylor’s diagram presented in Fig. 15. To compare the anticipated outcomes with the actual values, three statistical measures (RMSE, STD, and R2) were used. The standard deviation is shown through a circle connecting the plot’s horizontal and vertical axes; the horizontal green dots indicate RMSE, and the blue line shows the values of R2. As a result, among all techniques for S, TS, and E-BPC, the GBRT-FBIO and XGB methods have the top performance.

Fig. 15
figure 15

Taylor graphs of several EL-FBIO models and traditional approaches.

Full size image

ML and EL models can accurately predict BPC strength and workability properties, as reported by several studies19,26. According to the R2 comparison, the GBRT method for E and XGB methods for TS and Slump outperformed all existing models during the testing and training levels (Table 9). As a result, EL methods are more practical and more effective in generalizing BPC characteristics, thus saving time and resources.

Table 9 Comparing proposed EL models to those in the literature.
Full size table

Important features using shapley values

SHAP is a game-theoretic approach designed to describe the result of machine-learning methods90. SHAP presents the feature’s contribution to the model’s output, offering a more interpretable and transparent understanding of the model’s decision-making process. In the ensuing sections, we thoroughly analyze the outcomes in the proposed predicting structure, designed to interpret and comprehend the results of the probabilistic predicting model. Our initial focus is point forecasts, specifically examining how the developed model utilizes various features to make predictions. The SHAP method is employed for explanations, covering S, TS, and E. Figure 16 illustrates the average contribution of each feature, with each bar plot representing the importance of a specific property. Cement and water play significant roles in TS models, contributing more substantially. The primary contributors for E are curing time and cement, with mean SHAP values of + 0.18 and + 0.12, respectively. Water (+ 0.11) and sand (+ 0.09) make more notable contributions in the slump model. Silt (for E and S) and bentonite (for TS) exhibit minimal impact on the output of the models.

Fig. 16
figure 16

Feature significance of the input variables.

Full size image

Each dot in Fig. 17 represents a distinct forecasting, and its location along the x-axis signifies that attribute’s impact on the model’s output. Furthermore, each dot’s color corresponds to a feature value (varies from blue to red), emphasizing the relative contributions of different feature values to the final result. The long tails show highly significant characteristics. The dots’ vertical distribution suggests more findings with comparable effects. These SHAP summary graphs in such a setting include details on the number of reports with those qualities and the size and direction of each feature’s effect.

Fig. 17
figure 17

Summary plot of the point predicting model.

Full size image

A heatmap of SHAP values across all input variables is shown in Fig. 18. Slump, TS, and E were shown on top as functions of all variables. The ranges of SHAP values, which show the impact on each model target, are depicted in various colors ranging from blue to red. For this heatmap, arbitrary sample pools equal to training data sets were chosen. For S-BPC samples below 15, on the left of the heatmap, the highest prediction (highest in f(x)) corresponds to an absolute red color for water, indicating that it has contributed most to the slump. Considering the intense 77 on the right side of the TS-BPC heatmap, water again appears to be one key input parameter. However, curing time and cement with a strong red color on the left side are essential factors when predicting E-BPC.

Fig. 18
figure 18

SHAP values and function variations of each target.

Full size image

Online application of proposed BPC models

Models developed using EL-FBIO methods differ from classical regression methods as they do not simply relate inputs and outputs91. In this regard, implementing an online application makes it possible for researchers and practicing engineers, the end users of the proposed BPC models, to easily estimate values of mechanical and workability properties. In the past, several researchers have developed software using MATLAB Graphical User Interface (GUI) to predict the properties of different types of concrete92,93. There are several advantages to the developed online application: (i) results are available more quickly, and it provides a standard for an in-depth investigation of mix designs; (ii) reducing production costs while ensuring the safety of concrete designs and quality concerns as well, it allows to determine if a mix design is reasonable; and (iii) in addition to being easy to use, it will reduce human errors in calculations94. Free online access is also provided95. This application enables engineers and researchers to obtain a relatively accurate prediction of the strength and workability parameters of BPC at their project site in simple steps.

Limitations and future perspectives

The proposed ensemble learning models hybridized with Forensic-Based Investigation Optimization (FBIO) demonstrated high predictive accuracy, but certain limitations must be addressed. The relatively small dataset sizes of 158, 115, and 119 records for slump, tensile strength, and elastic modulus, respectively, may restrict the generalizability of the models to broader scenarios and diverse environmental conditions. Despite the application of SHAP analysis to provide insights into feature importance, the complexity of ensemble models may hinder their interpretability for non-specialist users. Additionally, the computational costs associated with FBIO-enhanced ensemble models for hyperparameter tuning and optimization may limit scalability for real-time applications or larger datasets. The reliance on datasets compiled from literature introduces potential biases that could impact the robustness of the models when applied to new or unseen data. To address these limitations, future studies should focus on expanding datasets to include more diverse material properties, environmental conditions, and testing protocols to enhance model robustness and generalizability. Simplifying models or integrating surrogate modeling techniques could improve interpretability without compromising accuracy. Advanced learning techniques such as deep neural networks (DNNs) and transfer learning could improve predictive performance and adaptability. Incorporating uncertainty quantification methods would enhance understanding of prediction reliability, especially for critical engineering applications. Finally, improving computational efficiency through optimization techniques like Bayesian optimization or genetic algorithms would facilitate real-time model implementation, enabling practical use in broader applications. Addressing these limitations and pursuing these potential improvements will significantly enhance the usability, accuracy, and efficiency of predictive models for BPC.

Conclusion

This study significantly advances the understanding and prediction of BPC properties by developing hybridized ensemble learning models enhanced with FBIO. Using datasets containing 158, 115, and 119 records for S, TS, and E, respectively, the proposed models achieved superior predictive accuracy, reducing the need for labor-intensive and costly experimental testing. A summary of the findings is provided below:

  1. 1.

    The study successfully introduced hybrid ensemble learning models, specifically GBRT, XGB, ADB, and RF, optimized with FBIO, which outperformed traditional approaches in predicting BPC properties.

  2. 2.

    Among the models, GBRT-FBIO achieved an R² value of 97.2% for elastic modulus predictions. XGB-FBIO attained an R² value of 97.7% and 96.6% for tensile strength and slump predictions, respectively.

  3. 3.

    GBRT-FBIO significantly reduced RMSE to 0.278 for elastic modulus predictions.

  4. 4.

    The study introduced new performance indicators, such as the a20-index, which revealed that XGB-FBIO achieved a20-indices of 91.6% for slump predictions, highlighting its high accuracy and reliability.

  5. 5.

    The models demonstrated scalability for real-world applications. XGB-FBIO and GBRT-FBIO achieved OBJ values of 0.012 and 0.097 for tensile strength and elastic modulus predictions, validating their reliability across diverse scenarios.

  6. 6.

    SHAP analysis revealed water as the most critical factor for slump, contributing a mean impact of + 0.11, while curing time was the primary determinant for tensile strength and elastic modulus, with mean contributions of + 0.18 and + 0.12, respectively.

  7. 7.

    The study developed an online user-friendly platform for predicting BPC properties, which reduces reliance on costly experimental tests and enables faster mix design evaluations directly at project sites.