Introduction

Wireless communication in the modern world has changed the way people interact, communicate, and access information, providing portability, ease, scalability, and flexibility1,2. A wideband spectrum is used in hospitals, smart homes, and smart environments due to its extensive coverage3,4. However, mutual interference in the ultra-wideband (UWB) spectrum caused by nearby users does not provide better spectrum management, direct wireless signal, or data security5,6. The frequency selective surface (FSS) is made up of an array of subwavelength-sized metallic patches or grids printed on a dielectric substrate to reduce interference7,8. In many cases, the UWB FSS can be combined with the UWB antenna to increase its gain9. Designing an FSS on a single-layer, single-sided substrate with a small footprint to prevent UWB without changing the polarisation and angular stability for an incoming wave of ϕ and θ is challenging.

Recently, several wideband FSS structures have been designed in10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31. In order to achieve a miniaturized size, 2.5D FSS with vias connecting the top and bottom layers is reported in10,11,12. The FSS is constructed in a 2D framework to reduce cost and make fabrication easier. Multilayer arrangements with multiple substrate and conductive layers are reported in13,14,15,16,17,29. A mesh grid with a dimension of 0.07λ0 is sandwiched between a square loop with interdigitated bends13. A circular loop is embedded on the top and bottom layers in14, while a square grid is developed in the centre layer to achieve miniaturization of 0.07λ0.

A stacked FSS structure with parallel strip lines with a size of 0.07λ0 is presented in15. In16, incorporating three conductive layers with square and cross-parasitic patches on two dielectric substrates with a unit cell size of 0.093λ0 can reject frequencies between 3.49 GHz and 12.13 GHz. Even though multi-layer FSS provide more bandwidth, they make the profile bulkier, therefore a single-layer FSS is created. A combined swastika-shaped and circular loop17, cross-shaped convoluted arms18, and a cross pattern enclosed in a circle19 are etched on the top and bottom layers of the substrate, resulting in a relatively larger profile thickness. In20, a wide band-stop FSS is designed using a modified Greek cross fractal element. The fractal technique offers a higher bandwidth of 13.69 GHz and a wider profile of 0.2λ0. The band-stop FSS at 3.5 GHz is designed using the interdigital topology, which has a larger footprint of 0.1λ032. Furthermore, the wide band-stop FSS in20,23,24,25,33,35 uses the FR4 substrate, making the structure unsuitable for conformal applications. The technique reported for wideband shielding in34,38 has a miniaturized form factor, the operating frequency is limited to 2 GHz and 3.5 GHz, respectively. The angular stability of the FSS refers to its ability to generate a stable frequency response for incoming theta (θ) electromagnetic waves. Polarization insensitivity indicates that the band-stop response remains constant regardless of the incident EM waves’ angles of phi (φ). In electromagnetic mitigation, where the FSS is mounted on the room’s walls, higher angular stability and polarization insensitivity are preferred, allowing the FSS to produce a stable frequency response when electromagnetic waves arrive from different directions with different polarization states. In addition to a lack of structural specifications, the two-fold symmetrical geometry of FSS prevents it from providing high angular stability17,18,21,28,36,37 and polarization insensitivity27. In the above-mentioned literature, some major issues are the larger size of the FSS unit cell, lack of polarization-insensitivity and conformability, low angular stability, multi-layer configuration, and the high profile of the FSS.

This paper presents a simple low-cost technique for obtaining single-layer, single-sided miniaturized FSS to address the aforementioned issues. The presented FSS has a periodicity of 0.041λ0 and is embedded on the top layer of the flexible polyester substrate. The proposed FSS has a UWB band stop response from 3.1 GHz to 10.6 GHz, with angular stability up to 75º. Its symmetric structure is polarization-insensitive for both TE and TM modes.

Design of the FSS unit cell

Design procedure

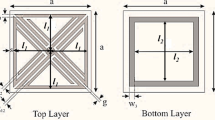
In Fig. 1a, a perfect electric conductor (PEC) of (h) 35 μm is printed on a flexible polyester substrate of (t) 50 μm with dimensions of 4 mm × 4 mm. The substrate, with a low dielectric constant and loss tangent (K) of 2.8 and 0.0045, respectively, helps to increase bandwidth, thereby improving FSS performance. The FSS is formed using the stepped impedance technique, which consists of metallic arms and slots with varying lengths and widths. A modified star slot is added between the simple swastika arm to limit its width, reducing the coupling effect and achieving the wide bandwidth. The modified star swastika (MSS) FSS unit cell has a miniaturised footprint of 0.041λ0 × 0.041λ0, where λ0 represents the lowest operating frequency. The side view of the proposed FSS unit cell is depicted in Fig. 1b. When electromagnetic waves with frequencies ranging from 3.1 GHz to 10.6 GHz are incident on the proposed FSS unit cell, they are reflected as shown in Fig. 1c. At resonance, the inductance and capacitance as indicated in the equivalent circuit model become short-circuited, resulting in the rejection of the incident waves.

Fig. 1
figure 1

(a) Design of the proposed FSS unit cell (U = 4 mm, U1 = 2.23 mm, U2 = 3.23 mm, U3 = 0.43. mm, U4 = 2.54 mm, U5 = 0.885 mm, U6 = 0.4 mm, U7 = 1.74 mm, U8 = 4.764 mm, V = 4 mm, V1 = 0.734 mm, V2 = 0.49 mm, V3 = 0.734 mm, V4 = 1.8 mm, V5 = 0.254 mm, (b) Side view, (c) Behaviour of incident electromagnetic waves on the proposed band-stop FSS.

Full size image

Transition of transmission coefficients at different stages

Figure 2a depicts the design process, which includes the step-by-step construction of metallic strips on a flexible polyester substrate. The first step is to add a PEC to a 0.041λ0 substrate. In Stage I, an L-Slot with a width (U1) of 0.3 mm is etched within the unit cell, resulting a band stop response ranging from 5.7 GHz to 13.05 GHz, as shown in Fig. 2b. The band stop response has a significant fractional bandwidth of 78.4%, with the resonant frequency centred at 8.9 GHz.

In Stage II, a modified star-shaped slot made up of two modified square slots is etched in the center of the substrate to achieve an operating frequency of 3.9 GHz to 11.1 GHz with a fractional bandwidth of 96% and good impedance match. Stage III aims to achieve a fractional bandwidth of 109.4% and frequency coverage from 3.1 GHz to 10.6 GHz, with attenuation below −10 dB using a modified L-slot.

Fig. 2
figure 2

(a) Evolution stages of the FSS unit cell, (b) S-parameters at each evolution stage.

Full size image

Behaviour of surface current pattern and ECM analysis

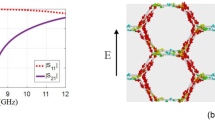
The MSS FSS is analyzed using the surface current distribution in TE and TM modes at 3.1 GHz and 10.6 GHz, as shown in Fig. 3. The largest width (U4) of the modified swastika arm allows the MSS FSS to achieve a wide bandwidth. The slot width (U1) of 0.3 mm, which has a capacitive effect, helps to minimize coupling between adjacent metallic arms. The strong flow of current between L-slots results in the highest operating frequency of 10.6 GHz. The strong current distributed along the swastika arm offers 3.1 GHz in both TE and TM modes.

Theoretically, the total electrical length for the lowest operating frequency is obtained as,

$$\:L=\frac{C}{4f\sqrt{\frac{{\epsilon\:}_{r\:}+\:1}{2}}}$$
(1)

Practically, the total length of the metallic strip is calculated as L = U1 + U2 + U3 + U4 + U5 + U6 + U7 + U8 + V1 = 16.953 mm. By substituting, the operating frequency is obtained as 3.2 GHz, which corresponds to 3.1 GHz. The following formula can be used to calculate the bandwidth (BW),

$$\:BW=\frac{K}{W}\:$$
(2)

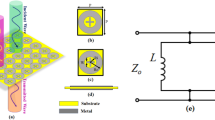
where K (= 0.0045) is the material property of the substrate and W is the width of the metallic resonator. Using Eq. (2), the bandwidth is calculated as 7.48 GHz, which is approximately 7.5 GHz. The equivalent circuit model (ECM) using Advanced Design System (ADS) software is illustrated in Fig. 4a.

Fig. 3
figure 3

(a) Surface current distribution on the resonator in TE mode at 3.1 GHz, (b) Surface current distribution on the resonator in TE mode at 10.6 GHz, (c) Surface current distribution on the resonator in TM mode at 3.1 GHz (d) Surface current distribution on the resonator in TM mode at 10.6 GHz.

Full size image

The inductor (L) and capacitor (C1) are connected in series to create an effective short circuit configuration, forming transmission nulls with term 1 and term 2 set to 377 Ω. The dielectric substrate is modelled as a transmission line with an impedance of Zd and height (t). The inductance (L) determines the electrical length of the metallic resonance, whereas the capacitances (C1, C2) define the gap (U1, U2) between adjacent metallic resonators. The addition of capacitor C2 in parallel with the series combination results in a wide bandwidth at the resonating frequency of 7.1 GHz. The total impedance of the ECM circuit is calculated and shown in Fig. 4a.

$$\:Z=\frac{\left(j\omega\:L\:+\:\frac{1}{j\omega\:C1}\right)\:\times\:\:\left(\frac{1}{j\omega\:C2}\right)}{j\omega\:L\:+\:\frac{1}{j\omega\:C1}\:+\:\frac{1}{j\omega\:C2}}$$
(3)

By solving Eq. (4) and equating the transmission poles and zeroes,

$$\:{\omega\:}^{2}=\frac{1}{C1L}$$
(4)
$$\:C2=\frac{C1}{{\omega\:}^{2}LC1\:-\:1}$$
(5)

The values of L, C1, and C2 are calculated using Eqs. (5) and (6). The ECM circuit provides an effective band-stop response for the UWB spectrum, covering frequencies ranging from 3.1 GHz to 10.6 GHz, with attenuation levels below −10 dB, as shown in Fig. 4b. To verify the practical simulation values, the operating frequency is calculated using Eq. (6) as,

$$\:f=\frac{1}{2\pi\:\sqrt{L{C}_{eq}}}$$
(6)

where Ceq = C1 + C2. By substituting the values for L, C1, and C2, the frequency (f) is evaluated as 7.04 GHz (using Eq. (3)), which represents the peak shielding of the band-stop response29.

Parametric analysis

The parametric analysis begins by increasing the width of the conducting arms (U4), and results in a significantly wide bandwidth, as shown in Fig. 5. Initially, the width of the conducting arm is set to 0.42 mm, resulting in a bandwidth of 6.134 GHz. In order to increase the bandwidth even further, the width of the P-shaped conducting arm is increased by 0.3 mm, resulting in a broadening of the bandwidth to 6.7 GHz.

An additional 0.3 mm addition in metallic arm width allows for rejection of an even wider band from 3.1 GHz to 10.6 GHz with a bandwidth of 7.5 GHz. Consequently, fractional bandwidth increases to 99.46%, 103.87%, and 109.48% at each stage. The direct relationship between the width of the metallic arms and bandwidth indicates that increasing the arm width (U4) naturally contributes to a significant increase in bandwidth range.

Results and discussion

In an experimental prototype, a periodic array of 51 × 58 elements made of a perfect electric conductor (PEC) is embedded in a 50 μm thick polyester with dimensions of 25.4 cm × 22.3 cm. The MSS FSS prototype is positioned between two identical horn antennas that are one meter apart. The experiment is carried out in an anechoic chamber with a vector network analyser (N9951A), as shown in Fig. 6, to evaluate the fabricated FSS performance in terms of transmission properties. The angular stability is measured by changing the incident angle of electromagnetic waves by precisely rotating the transmitting antenna from 0° to 75°. Figure 7 depicts the simulated and fabricated S-parameters of the FSS. Simulations were performed with a cylindrical bending radius (R) of 35 mm along the x and y axes to evaluate the conformal nature of the MSS FSS26. The bending radius that produces the bending angle (θ) in degrees is obtained through the radius (R) and length of the array (La = 51(U)) as45

$$\:\theta\:\left(\text{d}\text{e}\text{g}\right)=\frac{180\text{*}{L}_{a}}{\pi\:\text{*}R}$$
(7)

Notably, the performance of the FSS remains consistent with minimum shift regardless of the bending direction, demonstrating its remarkable ability in conformal applications. The shielding effectiveness (SE) of an FSS refers to its ability to block specific frequencies of electromagnetic waves while allowing others through. The shielding effectiveness25 is computed between the incident (Ei) and transmitted (Et) electric fields as,

$$\:SE\left(dB\right)=-20\left(\frac{{E}_{t}}{{E}_{i}}\right)$$
(8)

The frequency response under different incident angles (θ) and physical form factor (U) is given by24.

$$\:U<\frac{{\lambda\:}_{0}}{1\:+\text{\:sin}\theta\:}$$
(9)

For a resonating frequency of 7.1 GHz, the FSS size is calculated to be 21.11 mm with a maximum incident angle of 90°. The MSS FSS has a physical form factor of less than 21.475 mm, ensuring stability up to 75° as shown in Fig. 824. The value of U is constrained by this limitation. These tests demonstrate the ability of the FSS to maintain stable transmission properties across a wide range of incident angles and polarized electromagnetic waves.

Fig. 4
figure 4

(a) Circuit model, (b) Simulated |S21| from ADS and CST (L = 1 nH, C1 = 0.23 pF, C2 = 0.28 pF).

Full size image
Fig. 5
figure 5

Parametric analysis for different widths of metallic resonators.

Full size image
Fig. 6
figure 6

(a) Fabricated Prototype, (b) Measurement setup, (c) Schematic view of the measurement setup.

Full size image
Fig. 7
figure 7

Comparison of simulated and measured S-parameters with and without bending.

Full size image
Fig. 8
figure 8

Comparison of simulated and measured SE for (a) TE polarization, (b) TM polarization.

Full size image

Table 1 compares the proposed FSS to similar existing designs. The proposed UWB-shielded FSS unit cell has the following notable features:

  1. (a)

    The proposed UWB shielding FSS has a miniaturized physical form factor of 0.041λ0 × 0.041λ0 and covers a frequency range of 3.1–10.6 GHz. In comparison to existing literature10,16,17,18,19,21,24,29, the designed FSS achieves impressive size reductions of 65%, 80%, 86.1%, 84%, 94%, 61%, and 69.5%, respectively.

  2. (b)

    The miniaturized 2D UWB band-stop FSS presented is more cost-effective than10 due to the absence of a conducting hole.

  3. (c)

    The MSS FSS has a lower profile by incorporating the metallic resonator on the top surface of the polyester, while the FSS in10,16,17,18,29 consists of multiple substrate layers (SL) and conductive layers (CL).

  4. (d)

    Unlike FSSs in18,24 that have rigid substrates, the proposed MSS FSS is embedded on a conformal polyester substrate, covering the entire UWB range for conformal applications.

  5. (e)

    The proposed FSS, unlike10,16,17,18,19,21,29, maintains angular stability up to 75° due to its miniaturized footprint design.

  6. (f)

    Unlike27, the current art provides polarization insensitivity for oblique angles of phi up to 90° due to its fourfold symmetry.

  7. (g)

    The proposed FSS unit cell achieves a 10 dB peak shielding of 67.9 dB when compared to10,16,17,18,21,22,24,29.

Table 1 Performance comparison of the proposed FSS with similar existing designs.
Full size table

Mitigation of interference is critical to maintain reliable performance, as wideband systems operate over a wide frequency spectrum that overlaps with other wireless systems39. In multi-user UWB scenarios, metamaterial-based surfaces can isolate signals from different users by reflecting or absorbing unwanted frequencies in overlapping regions40,41. In the future, the metamaterial-based layers/surfaces could be embedded in antennas to suppress out-of-band interference and improving signal-to-noise ratio (SNR)42. Also, metamaterial-based panels can be used to shield wideband systems from interference in high-density wireless environments, such as offices or industrial setups43,44.

Conclusion

A single-layer miniaturized FSS designed on a flexible polyester substrate is presented. The FSS has a band-stop response across a large frequency range, effectively spanning from 3.1 to 10.6 GHz, with attenuation below −10 dB. Furthermore, its physical form factor of 4 mm ensures angular stability up to 75° for both TE and TM modes. The agreement between simulated and measured results, combined with bending analysis, further validates the performance of FSS. Hence, the designed FSS could be effectively used in antennas, radomes, and electromagnetic shielding to improve radiation performance by filtering out unwanted signals, selectively allowing certain frequencies for radar systems, or improving shielding in sensitive electronic environments.