An experimental case on dual mode coupling energy management strategy for islanded AC/DC hybrid microgrid

Abstract

The limited adjustable margin of the islanded AC/DC hybrid microgrid makes it difficult to both balance economic and stability. Therefore, an energy management strategy that can effectively harmonize economic and stability is highly desirable. In view of the issues, this paper proposes a novel dual mode coupling energy management strategy for islanded AC/DC hybrid microgrid. The strategy sets two modes for energy management of islanded AC/DC hybrid microgrid: economic mode and emergency mode. A two-stage stochastic predictive control (SPC) dispatch model is carried out for economic operation in economic mode. Furthermore, the economic mode can be switched to emergency mode according to the SOC (state of charge) of the V/F(voltage/frequency) control unit to ensure the stability of the microgrid. The economic mode is designed to guarantee the economic efficiency during normal operation. In contrast, the emergency mode serves to ensure the stability of the microgrid when the adjustable margin is inadequate. The two operation modes are coupled and closely coordinated. Finally, the strategy is applied in an existent AC/DC hybrid microgrid for experiments. According to the experimental results, this energy management strategy can achieve normal economic operation and short-term risk management of AC/DC hybrid microgrid. Moreover, unlike simulation research, this paper employs actual microgrids for strategy verification. The results demonstrate that the proposed strategy is a comprehensive optimal energy management strategy that can be directly applied to actual islanded AC/DC hybrid microgrid. This represents another major highlight of this paper, alongside the novel strategy itself.

Introduction

The AC/DC hybrid microgrid can operate in the grid-connected mode or island mode¹. Due to the loss of backup capacity provided by the main grid, island mode requires internal power source to maintain the voltage and frequency for stable operation^2,3,4. However, unlike the main grid, the internal power supply capacity is limited and lacks the ability to offer adequate adjustable margins. Therefore, taking into account the economy and stability of microgrid operation under a restricted adjustable margin has emerged as an urgent problem awaiting solution. In view of the issues, an energy management strategy that can effectively harmonize economic and stability is highly desirable^5,6,7.

In recent years, a significant amount of research work has been conducted to investigate microgrid energy management by the researchers. The research work has mainly focused on the island energy management strategy of traditional AC microgrid⁸. The primary objective of the strategy is to ensure the safe and stable operation as well as reliable power source of the microgrid during island operation^9,10,11. The power balance and voltage frequency stability during islanded operation of grid-connected microgrid have been studied in the existing literature. Reference¹² established an energy management strategy for islanded microgrid based on multi-time scale coordinated control for independent microgrids. The strategy comprehensively considers the demand side load responses and provides the start/ stop state and output power reference value of each distributed power source from two-time scales of day-ahead and intraday. Reference¹³ proposes a real-time optimal energy dispatch of standalone microgrid, which can not only realize the reliable and economical operation of microgrid, but also reduce the capacity configuration requirements of energy storage devices. Reference¹⁴ proposes an independent microgrid optimal scheduling method based on opportunity constrained programming by establishing an uncertainty model of rotating standby energy storage with probability constraints. Reference¹⁵ proposed a real-time energy management scheduling strategy that included two operation modes for the independent microgrid system used for seawater desalination, and determined the specific operation mode according to the ultra-short-term wind speed forecast. Reference¹⁶ proposed an islanded microgrid energy management method based on load classification scheduling by introducing demand side management. Reference¹⁷ proposed a flexible interconnected multi-microgrid multi-layer coordinated control strategy in order to improve the power source reliability and new energy consumption ability of multi-microgrid island operation. This strategy enables the multi-microgrid island operation to have fast and adaptive dynamic power mutual assistance ability. Reference¹⁸ proposes an optimal scheduling strategy for plug-in electric vehicles connected to the microgrid. The strategy includes both grid-connected mode and island mode, considering the grid constraints and the cost expectation of EV users. Reference¹⁹ proposes a coordinated control scheme for a vehicle to grid three-phase four-leg inverter. The scheme achieves grid-connected mode or standalone mode operation capability as well as fulfilling smooth transition between operation modes.

The above literature mainly considers economic dispatch during the stable operation or the low-frequency load cutting strategy under the condition of real-time power imbalance. However, the economy and stability of islanded microgrid are often difficult to balance^20,21. The previous research mostly only addressed one aspect of the problem. In addition, compared with the traditional AC microgrid, AC/DC hybrid microgrid has complex characteristics such as zoning of AC/DC operation, diversification of source and load, coupling of energy exchange, and diversification of operation modes. In the AC/DC hybrid microgrid dispatch, it is not only necessary to consider the uncertainty of renewable energy and load, but also the dynamic relationship between the two sides of the operation state should be considered, which makes the AC/DC hybrid microgrid dispatch present the characteristics of multiple uncertainties. In the past, the energy management strategy of AC/DC hybrid microgrid were usually only focused on the grid-connected operation status, while the island energy management strategies of AC/DC hybrid microgrids were rarely involved.

In response to the above issues, this paper proposes a dual mode coupling energy management strategy for islanded AC/DC hybrid microgrid. The main contributions are as follows:

• (1) This strategy sets two energy management operation modes for the islanded AC/DC hybrid microgrid: economic mode and emergency mode. The operation mode can be switched between each other according to the SOC of the V/F control unit to ensure the stability of the microgrid. The two operation modes are coupled and closely coordinated to achieve normal economic operation and short-term risk management of AC/DC hybrid microgrid.

• (2) The economic model is established based on a two-stage SPC strategy. This strategy adopts multi-scenario technology to characterize the intraday randomness of wind turbine (WT), photovoltaic (PV) and AC/DC loads in the control horizon. Based on tracking day-ahead schedules, the economy of day-ahead schedules is fully considered by rolling optimization for lower cost and more accurate tracking effect of day-ahead schedules.

• (3) The energy management strategy presented in this paper is a comprehensive approach designed to guide comprehensive engineering applications, rather than serving innovation under specific operation objectives or constraints. Furthermore, distinct from simulation studies, this paper employs experimental research to thoroughly verify the effectiveness of the proposed strategy in practical islanded AC/DC hybrid microgrids, which represents another major highlight of this paper, alongside the novel strategy itself.

The remainder of this paper is organized as follows. Section II describes the structure of AC/DC hybrid microgrid. Section III introduces the DCE model of BC. Section IV illustrates the operation cost models of microgrid components. Section V presents the temporally coordinated energy management strategy for AC/DC hybrid microgrid. Case studies are conducted in Section VI. The conclusions are drawn in Section VII.

Islanded AC/DC hybrid microgrid

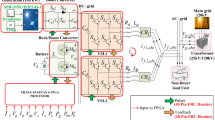
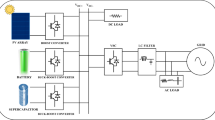
The islanded AC/DC hybrid microgrid structure studied in this paper is shown in Fig. 1. The AC bus is connected to lithium battery, WT and AC load. The DC bus is connected to fuel cell, PV, lithium battery and DC load. Since both AC and DC buses are connected to lithium batteries, in order to distinguish them, the lithium battery connected to DC bus is named lithium battery 1, and the lithium battery connected to AC bus is named lithium battery 2. AC bus and DC bus are connected through bidirectional AC/DC power converter (BC) to exchange power.

Fig. 1

Structure of islanded AC/DC hybrid microgrid.

Unlike the grid-connected mode, the islanded AC/DC hybrid microgrid requires an internal micro power source to maintain the voltage and frequency for stable operation. The micro power source is usually called V/F control unit. The unit adopts constant voltage-frequency control (V-F control), which can automatically stabilize the unbalanced power in the microgrid and ensure the stability of AC bus, which naturally ensures the stability of DC bus through a bidirectional AC/DC power converter. In this paper, lithium battery 2 is selected as the V/F control unit.

Dual mode coupled energy management strategy framework

The dual mode coupling energy management strategy of islanded AC/DC hybrid microgrid proposed in this paper is formulated according to the operation state of V/F control unit. As the V/F control unit of microgrid, the dispatch mode is divided according to the three critical SOC values of lithium battery 2. The critical value is taken as the minimum value SOC_2min, the set value SOC_2set and the maximum value SOC_2max, which meet the following relationship: SOC_2min < SOC_2set < SOC_2max. Two dispatch modes are set based on this: economic mode and emergency mode. The emergency mode is further divided into emergency mode 1 and emergency mode 2. According to the above settings, the main program of dual mode coupling energy management strategy of islanded AC/DC hybrid microgrid is shown in Fig. 2.

Fig. 2

Main program of dual mode coupling energy management for islanded AC/DC hybrid microgrid.

Islanded AC/DC hybrid microgrid operates in economic mode most of the time. In this mode, lithium battery 2 does not participate in the scheduling, but only acts as a V/F control unit to stabilize the instantaneous power fluctuation. The other equipment operates according to the schedules determined by the two-stage SPC strategy proposed in this paper to ensure the economy and robustness of microgrid operation. When the lithium battery 2 exceeds the range set in the economic mode, the microgrid enters the emergency mode. The emergency mode is divided into two types according to the SOC of lithium battery 2. When the value exceeds SOC_2max, emergency mode 1 should be activated. Emergency mode 2 should be triggered when the value falls below SOC_2min. The corresponding expert strategies are developed for the two emergency modes. In the emergency mode, when the SOC of the lithium battery 2 is restored to SOC_2set according to the expert strategy, the main program is returned and the economic mode operation is re-entered. The two energy management operation modes are coupled and closely coordinated with each other, which can achieve normal economic operation and short-term risk control. The strategy can effectively ensure the stability and security of the microgrid operation, while the operation economy and robustness are guaranteed.

Economic mode

There are multiple uncertainties in the operation of islanded AC/DC hybrid microgrid. Aiming at this issue, this paper proposes a two-stage SPC dispatch strategy in the economic mode, which includes two stages: day-ahead economic dispatch and intraday SPC. The framework of the scheduling strategy is shown in Fig. 3.

Fig. 3

Dispatch framework of two-stage SPC.

In the day-ahead economic dispatch stage, a day-ahead hourly schedule is determined to minimize the daily operation cost based on the day-ahead forecast data of WT, PV and AC/DC loads in the AC/DC hybrid microgrid. The operation cost and characteristics of distributed micro sources, energy storage and converters in the microgrid are comprehensively considered in this stage.

In the intraday SPC stage, based on the day-ahead schedules and intraday ultra-short-term power forecast data of WT, PV and AC and DC loads, the SPC is carried out for rolling optimization. The time scale of the stage is 5 min and the control horizon is 1 h (covers 12 intervals). At each time step, schedules for each interval in the control horizon are developed. But only the first 5 min-interval schedule is executed. Then, at the next time step, the control horizon moves forward by 5 min. The above process will be repeated 288 times in one day. Through continuous rolling optimization, the impact of day-ahead forecast error on the intraday optimal scheduling can be effectively reduced while ensuring the effectiveness of the day-ahead schedules.

• A. Day-ahead economic dispatch.

The objective of the day-ahead optimal dispatch of islanded AC/DC hybrid microgrid is to minimize the daily operation cost. Therefore, the objective function of the day-ahead optimal dispatch can be expressed as:

$$\min C_{{{\text{DA}}}} = \sum\limits_{{t = 1}}^{T} {\left( {C_{{{\text{FC}},t}} + C_{{li1,t}} + C_{{{\text{BC}},t}} } \right)}$$

(1)

s.t.

$$C_{{{\text{FC}},t}} = K_{{{\text{FCOM}}}} P_{{{\text{FC}},t}} \Delta t$$

(2)

$$C_{{li1,t}} = \left( {j_{1} \left( {P_{{{\text{ch}},t}} + P_{{{\text{dis}},t}} } \right)^{2} + j_{2} \left( {P_{{{\text{ch}},t}} + P_{{{\text{dis}},t}} } \right) + j_{3} } \right)\Delta t$$

(3)

$$C_{{{\text{BC}},t}} = \left( {K_{{{\text{BCOM}}}} + K_{L} \left( {1 - \eta _{{{\text{BC}}}} } \right)} \right)\left( {P_{{{\text{BC}},t}}^{{AC}} + P_{{{\text{BC}},t}}^{{DC}} } \right)\Delta t$$

(4)

The scheduling cost C_DA is composed of the day-ahead cost of fuel cell, lithium battery and the bidirectional AC/DC power converter, t is scheduling period. Where C_FC,t and P_FC,t are the cost and power of fuel cell, and K_FCOM is the operation and maintenance cost coefficient of fuel cell. Equation (3) is the cost of lithium battery 1, where P_ch,t and P_dis,t are the charging and discharging power of lithium battery 1, and J₁, J₂ and J₃ are the parameters related to the operation of lithium battery 1²². Equation (4) is the operation and maintenance cost and power loss cost of bidirectional AC/DC power converter, where K_BCOM is the operation and maintenance cost coefficient of converter, K_L is the loss cost coefficient of converter, PAC BC,t and PDC BC,t are the power injected into converter at AC side and DC side, η_BC is the conversion efficiency of the converter.

Considering the operation mode of islanded AC/DC hybrid microgrid and the operation characteristics of distributed micro generators, energy storage and converters, the following constraints need to be met for the current optimal dispatch:

$$\begin{gathered} P_{{{\text{PV}},t}} + P_{{{\text{WT}},t}} + P_{{{\text{FC}},t}} + P_{{{\text{dis}},t}} - P_{{{\text{ch}},t}} = P_{{{\text{Lac}},t}} \hfill \\ + P_{{{\text{Ldc}},t}} + \left( {1 - \eta _{{{\text{BC}}}} } \right)\left( {P_{{{\text{BC}},t}}^{{AC}} + P_{{{\text{BC}},t}}^{{DC}} } \right) \hfill \\ \end{gathered}$$

(5)

$$P_{{{\text{WT}},t}} = P_{{{\text{Lac}},t}} + P_{{{\text{BC}},t}}^{{AC}} - \eta _{{{\text{BC}}}} P_{{{\text{BC}},t}}^{{DC}}$$

(6)

$$P_{{{\text{PV}},t}} + P_{{{\text{FC}},t}} + P_{{{\text{dis}},t}} - P_{{{\text{ch}},t}} = P_{{{\text{Ldc}},t}} + P_{{{\text{BC}},t}}^{{DC}} - \eta _{{{\text{BC}}}} P_{{{\text{BC}},t}}^{{AC}}$$

(7)

$$P_{{{\text{FCmin}}}} \le P_{{{\text{FC}},t}} \le P_{{{\text{FCmax}}}}$$

(8)

$$0 \le P_{{{\text{ch}},t}} \le I_{{{\text{ch}},t}} P_{{{\text{li1max}}}} {\text{, }}0 \le P_{{dis,t}} \le I_{{dis,t}} P_{{{\text{li1max}}}}$$

(9)

$$I_{{{\text{ch}},t}} + I_{{dis,t}} \le 1,P_{{li1,t}} = P_{{dis,t}} - P_{{{\text{ch}},t}}$$

(10)

$$SOC_{{{\text{1min}}}} \le SOC_{{1t}} \le SOC_{{{\text{1max}}}} {\text{ , }}SOC_{{1t}} = {{E_{{{\text{1r}},t}} } \mathord{\left/ {\vphantom {{E_{{{\text{1r}},t}} } {E_{{{\text{1rc}}}} }}} \right. \kern-\nulldelimiterspace} {E_{{{\text{1rc}}}} }}$$

(11)

$$E_{{1r,t}} = E_{{1r,t - 1}} + \eta _{{{\text{li1}}}} P_{{{\text{ch}},t}} - {{P_{{{\text{dis}},t}} } \mathord{\left/ {\vphantom {{P_{{{\text{dis}},t}} } {\eta _{{{\text{li1}}}} }}} \right. \kern-\nulldelimiterspace} {\eta _{{{\text{li1}}}} }},E_{{{\text{1r}},0}} = E_{{{\text{1r}},T}}$$

(12)

$$0 \le P_{{{\text{BC}},t}}^{{AC}} \le I_{{{\text{BC}},t}}^{{AC}} P_{{{\text{BCmax}}}} {\text{ , }}0 \le P_{{{\text{BC}},t}}^{{DC}} \le I_{{{\text{BC}},t}}^{{DC}} P_{{{\text{BCmax}}}}$$

(13)

$$I_{{{\text{BC}},t}}^{{AC}} + I_{{{\text{BC}},t}}^{{DC}} \le 1{\text{ , }}P_{{BC,t}} = P_{{{\text{BC}},t}}^{{DC}} - P_{{{\text{BC}},t}}^{{AC}}$$

(14)

P_PV,t and P_WT,t, t are the power of PV and WT, P_Lac,t and P_Ldc,t are AC load and DC load of microgrid. P_FCmin and P_FCmax are the minimum and maximum output power of fuel cell. P_li1max is the maximum charge and discharge power of lithium battery 1. I_ch,t and I_dis,t are the indication marks of the charge and discharge state. They are binary variables. 1 represents that lithium battery 1 is in the charge or discharge state, respectively. P_li1,t is the power of lithium battery. It is specified that the discharge is positive and the charge is negative. SOC_1t is the charge state of lithium battery 1, SOC_1min and SOC_1max are the minimum and maximum state of charge values of lithium battery 1. E_1r,t is the remaining capacity of lithium battery 1, η_li1 is the charge-discharge efficiency of lithium battery 1, E_1r,0 and E_1r,t respectively represent the initial and final residual capacity of lithium battery 1. P_BCmax is the maximum transmission power of bidirectional AC/DC power converter; IAC BC,t and IDC BC,t are the indication marks of the transmission power flow direction. They are binary variables, “IAC BC,t = 1” represents that the transmission power from the AC side to the DC side, whereas “IDC BC,t = 1” is the opposite. P_BC,t is the injection converter power. It is specified that the injection at DC side is positive and the injection at AC side is negative.

• B. Intraday stochastic predictive control

The intraday dispatch of islanded AC/DC hybrid microgrid has the characteristics of multiple uncertainties and small adjustable power margin. According to the characteristic, this paper proposes an intraday SPC strategy. The strategy employs multi-scenario analysis technology to simulate the uncertainty of WT, PV and AC/DC loads, and makes full use of the control ability of the controllable micro power source through rolling optimization. It can effectively eliminate the influence of the day-ahead forecast error on the intraday dispatch based on tracking the day-ahead schedules. The intraday SPC strategy includes two parts: intraday stochastic multi-scenario modeling and optimization problem modeling.

• 1. Intraday stochastic multi-scenario modeling.

WT power, PV power and AC/DC loads have strong intraday randomness. According to the demand of intraday random control, this paper models and analyzes the randomness of WT, PV and AC/DC loads in the control horizon based on multi-scenario technology. The modes are as follows:

$$P_{{{\text{j}},t,s}}^{{\text{H}}} = P_{{{\text{j}},t}}^{{{\text{ID}}}} \left[ {1{\text{ + }}\xi _{{\text{j}}} {\text{\% }} \cdot \left( {R_{{{\text{j}},t}} {\text{ - }}\gamma } \right)} \right]$$

(15)

PH j,t, s is the intraday power of the intraday scenario in the control horizon H, PID j,t is the ultra-short-term power forecast data, ξ_j% is the percentage of forecast error threshold, R_j,t is a random number subject to a certain distribution, γ Is the random distribution correction factor, j can be WT, PV and AC/DC loads.

Relevant literature shows that the PV and AC/DC loads power forecast errors generally obey the normal distribution, while the WT power forecast error is more suitable to be characterized by beta distribution^23,24. The probability distribution is as follows:

$$f\left( {R_{{{\text{j}},t}} } \right){\text{ = }}\frac{1}{{\sigma \sqrt {2\pi } }}{\text{e}}^{{ - \frac{{\left( {R_{{{\text{j}},t}} - \mu } \right)^{2} }}{{2\sigma ^{2} }}}}$$

(16)

$$f\left( {R_{{{\text{j}},t}} } \right){\text{ = }}R_{{{\text{j}},t}}^{{\alpha - 1}} \cdot (1 - R_{{{\text{j}},t}} )^{{\beta - 1}} \cdot N_{{\text{d}}}$$

(17)

Where µ and σ Expectation and variance of normal distribution; α and β The shape and scale parameters of beta distribution; N_d is the normalization factor.

Based on the above forecast mode, this paper uses Latin hypercube sampling technology for multi-scenario generation, and then uses synchronous back substitution method for scenario reduction. The reduced typical scenario set can well reflect the probability distribution of the original scenario set. The typical scenarios of WT, PV and AC/DC loads are n_WT, n_PV, n_Lac and n_Ldc, respectively. Finally, the number of typical scenarios is the product of four

$$n_{s} = n_{{{\text{WT}}}} n_{{{\text{PV}}}} n_{{{\text{Lac}}}} n_{{{\text{Ldc}}}}$$

(18)

Corresponding combination typical scenario probability λ_S is

$$\lambda _{s} = \lambda _{{{\text{WT}}}} \lambda _{{{\text{PV}}}} \lambda _{{{\text{Lac}}}} \lambda _{{{\text{Ldc}}}} ,s = 1,2,...,n_{s}$$

(19)

Where λ_WT, λ_PV, λ_Lac and λ_Ldc is the probability corresponding to WT, PV and AC/DC loads scenarios, respectively.

• 2. Optimization problem modeling.

The objective function of intraday SPC in the control horizon is

$$\left\{ \begin{gathered} \min f = C_{{{\text{HS}}}} {\text{ + }}\left\| {{\mathbf{Y}} - {\mathbf{Y}}_{{{\text{ref}}}} } \right\|_{{\mathbf{G}}}^{2} \hfill \\ G = diag[G_{{BC}}^{1} ,G_{{SOC}}^{1} ,...,G_{{BC}}^{m} ,G_{{SOC}}^{m} ] \hfill \\ \end{gathered} \right.$$

(20)

s.t.

$$C_{{{\text{HS}}}} {\text{ = }}\sum\limits_{{s = 1}}^{{n_{s} }} {\lambda _{s} \sum\limits_{{k = 1}}^{{\text{m}}} {(C_{{{\text{FC}},t + k\Delta t,s}} + C_{{{\text{li1}},t + k\Delta t,s}} } } + C_{{{\text{BC}},t + k\Delta t,s}} )$$

(21)

$$C_{{{\text{FC}},t + k\Delta t,s}} = K_{{{\text{FCOM}}}} P_{{{\text{FC}},t + k\Delta t,s}} \Delta t$$

(22)

$$C_{{{\text{li1}},t + k\Delta t,s}} = \left( {j_{1} P_{{li1,t + k\Delta t,s}}^{2} + j_{2} P_{{li1,t + k\Delta t,s}} + j_{3} } \right)\Delta t$$

(23)

$$\begin{gathered} C_{{{\text{BC}},t + k\Delta t,s}} = \left( {K_{{{\text{BCOM}}}} + K_{L} \left( {1 - \eta _{{{\text{BC}}}} } \right)} \right) \hfill \\ \cdot \left( {P_{{{\text{BC}},t + k\Delta t,s}}^{{AC}} + P_{{{\text{BC}},t + k\Delta t,s}}^{{DC}} } \right)\Delta t \hfill \\ \end{gathered}$$

(24)

$$\begin{gathered} {\mathbf{Y}} = [P_{{{\text{BC}}}} (\left. {t + \Delta t} \right|t),SOC_{1} (\left. {t + \Delta t} \right|t), \ldots ,P_{{{\text{BC}}}} (\left. {t + m\Delta t} \right|t) \hfill \\ ,SOC_{1} (\left. {t + m\Delta t} \right|t)] \hfill \\ \end{gathered}$$

(25)

$${\mathbf{Y}}_{{{\text{ref}}}} = [P_{{{\text{BC,}}t + \Delta t}}^{{{\text{ref}}}} ,SOC_{{1t + \Delta }}^{{{\text{ref}}}} , \ldots ,P_{{{\text{BC,}}t + m\Delta t}}^{{{\text{ref}}}} ,SOC_{{1t + m\Delta t}}^{{{\text{ref}}}} ]$$

(26)

C_HS is the sum of the expected cost in the control horizon under each typical scenario; ||·||² represents two-norm arithmetic operator. Y and Y_ref are output vector and target vector, G is the penalty factor of target difference, which is a diagonal matrix. Subscript s represents the s-th intraday typical scenario in the control horizon, subscript t + kΔt represents the k-th scheduling period in the control horizon, such as P_{li1,t+kΔt, s} is the power of lithium battery 1 in the k-th scheduling period under the s-th typical scenario in the control horizon. Other physical quantities refer to Eqs. (2–4), which will not be repeated. x(t + kΔt|t) is the forecast data of t + kΔt at time t (k = 1,2,…, m), m is the number of periods in the control horizon. x can be the power and power change of each unit, the exchange power of BC and the SOC value of lithium battery 1. yref is dispatch objective, given by the day-ahead schedules, y can be BC exchange power and lithium battery 1 SOC.

The purpose of the objective function is to make the exchange power of the BC and the SOC of the lithium battery as close as possible to the day-ahead schedules, while minimizing the sum of expected cost in the control horizon in various typical scenarios. In addition to the power balance constraints specified in Eqs. (5–7), the intraday SPC should also meet the following constraints:

$$\begin{gathered} P_{{{\text{FCmin}}}} \le P_{{{\text{FC}}}} (\left. {t + k\Delta t} \right|t) \le P_{{{\text{FCmax}}}} \hfill \\ \Delta P_{{{\text{FCmin}}}} \le \Delta P_{{{\text{FC}}}} (\left. {t + k\Delta t} \right|t) \le \Delta P_{{{\text{FCmax}}}} \hfill \\ \end{gathered}$$

(27)

$$\begin{gathered} P_{{{\text{li1min}}}} \le P_{{{\text{li1}}}} (\left. {t + k\Delta t} \right|t) \le P_{{{\text{li1max}}}} \hfill \\ \Delta P_{{{\text{li1min}}}} \le \Delta P_{{{\text{li1}}}} (\left. {t + k\Delta t} \right|t) \le \Delta P_{{{\text{li1max}}}} \hfill \\ \end{gathered}$$

(28)

$$\begin{gathered} P_{{{\text{BCmin}}}} \le P_{{{\text{BC}}}} (\left. {t + k\Delta t} \right|t) \le P_{{{\text{BCmax}}}} \hfill \\ SOC_{{{\text{1min}}}} \le SOC_{1} (\left. {t + k\Delta t} \right|t) \le SOC_{{{\text{1max}}}} \hfill \\ \end{gathered}$$

(29)

$$\begin{gathered} P_{{{\text{PV}},t + k\Delta t,s}} + P_{{{\text{WT}},t + k\Delta t,s}} + P_{{{\text{FC}},t + k\Delta t,s}} + P_{{li1,t + k\Delta t,s}} \hfill \\ {\text{ = }}P_{{{\text{Lac}},t + k\Delta t,s}} + P_{{{\text{Ldc}},t + k\Delta t,s}} + \left( {1 - \eta _{{{\text{BC}}}} } \right)\left( {P_{{{\text{BC}},t + k\Delta t,s}}^{{AC}} + P_{{{\text{BC}},t + k\Delta t,s}}^{{DC}} } \right) \hfill \\ \end{gathered}$$

(30)

$$P_{{{\text{WT}},t + k\Delta t,s}} = P_{{{\text{Lac}},t + k\Delta t,s}} + P_{{{\text{BC}},t + k\Delta t,s}}^{{AC}} - \eta _{{{\text{BC}}}} P_{{{\text{BC}},t + k\Delta t,s}}^{{DC}}$$

(31)

$$\begin{gathered} P_{{{\text{PV}},t + k\Delta t,s}} + P_{{{\text{FC}},t + k\Delta t,s}} + P_{{li1,t + k\Delta t,s}} = P_{{{\text{Ldc}},t + k\Delta t,s}} \hfill \\ + P_{{{\text{BC}},t + k\Delta t,s}}^{{DC}} - \eta _{{{\text{BC}}}} P_{{{\text{BC}},t + k\Delta t,s}}^{{AC}} \hfill \\ \end{gathered}$$

(32)

$$\begin{gathered} P_{{{\text{FCmin}}}} \le P_{{{\text{FC}},t + k\Delta t,s}} \le P_{{{\text{FCmax}}}} \hfill \\ - P_{{{\text{li1max}}}} \le P_{{li1,t + k\Delta t,s}} \le P_{{{\text{li1max}}}}\hfill \\ \end{gathered}$$

(33)

$$- P_{{{\text{BCmax}}}} \le P_{{{\text{BC}},t + k\Delta t,s}}^{{AC}} ,P_{{{\text{BC}},t + k\Delta t,s}}^{{DC}} \le P_{{{\text{BCmax}}}}$$

(34)

$$P_{{{\text{BC}}}} (\left. {t + k\Delta t} \right|t){\text{ = }}P_{{{\text{BC}}}}^{{DC}} (\left. {t + k\Delta t} \right|t){\text{ - }}P_{{{\text{BC}}}}^{{AC}} (\left. {t + k\Delta t} \right|t)$$

(35)

$$\begin{gathered} P_{{{\text{FC}},t + k\Delta t,s}} = P_{{{\text{FC}}}} (\left. {t + k\Delta t} \right|t) + \Delta P_{{FC,t + k\Delta t,s}} \hfill \\ P_{{li1,t + k\Delta t,s}} = P_{{{\text{li1}}}} (\left. {t + k\Delta t} \right|t) + \Delta P_{{li1,t + k\Delta t,s}} \hfill \\ P_{{{\text{BC}},t + k\Delta t,s}}^{{{\text{AC}}}} = P_{{{\text{BC}}}}^{{{\text{AC}}}} (\left. {t + k\Delta t} \right|t) + \Delta P_{{{\text{BC}},t + k\Delta t,s}}^{{{\text{AC}}}} \hfill \\ P_{{{\text{BC}},t + k\Delta t,s}}^{{{\text{DC}}}} = P_{{{\text{BC}}}}^{{{\text{DC}}}} (\left. {t + k\Delta t} \right|t) + \Delta P_{{{\text{BC}},t + k\Delta t,s}}^{{{\text{DC}}}} \hfill \\ \end{gathered}$$

(36)

In the above constraints, ΔP_FCmin and ΔP_FCmaxis the minimum and maximum value of the change of fuel cell output power. ΔP_li1min and ΔP_li1max is the minimum and maximum value of output power variation of lithium battery 1. In Eq. (36) ΔP_{z,t+kΔt, s} is the power increment of the unit in the k-th scheduling period under the s-th typical scenario in the control horizon. Z can be the injection power of fuel cell, lithium battery 1 and AC side or DC side of BC.

The flow chart of intraday SPC is shown in Fig. 4. The specific steps are as follows:

• (1) Read the ultra-short-term power forecast data of WT, PV and AC/DC loads in the control horizon H and the day-ahead schedules.

• (2) According to the probability distribution function of WT, PV and AC/DC loads, the scenarios are generated and reduced to obtain the typical scenario set.

• (3) The intraday stochastic control mode constructed according to Eq. (20) and corresponding constraints solves the control vector in the control horizon.

• (4) Send the first control variable of the control vector to the microgrid controllable unit for execution.

• (5) Return to step 1 for a new round of rolling optimization, and repeat the above steps until the end of the scheduling cycle.

Fig. 4

Flow chart of intraday SPC.

Emergency mode

Compared with the AC/DC hybrid grid-connected to the grid, the islanded AC/DC hybrid microgrid does not provide sufficient regulation margin for the upper grid, and the V/F control unit is required to provide stable voltage and frequency support for the microgrid. However, due to the limited capacity of the V/F control unit, to prevent the instantaneous unplanned power fluctuation from endangering the stability and safety of the microgrid, an emergency mode needs to be set to deal with this situation.

The emergency mode of dual mode coupling energy management strategy of islanded AC/DC hybrid microgrid proposed in this paper formulates the corresponding expert strategy according to the operation state of V/F control unit. As the V/F control unit of microgrid, the emergency mode is divided into two types according to the charge state of lithium battery 2. When the value exceeds SOC_2max, emergency mode 1 should be activated. Emergency mode 2 should be triggered when the value falls below SOC_2min. The flow charts of expert strategies of the two emergency modes are shown in Figs. 5 and 6.

P_net in the figure represents the net load power of islanded AC/DC hybrid microgrid, which is defined as follows

$$P_{{{\text{net}}}} {\text{ = }}P_{{{\text{Ldc}},t}} - P_{{{\text{PV}},t}} + \eta _{{{\text{BC}}}} \left( {P_{{{\text{Lac}},t}} - P_{{{\text{WT}},t}} } \right)$$

(37)

Fig. 5

Expert strategy flow chart of emergency mode 1.

Fig. 6

Expert strategy flow chart of emergency mode 2.

The general idea of emergency mode is that when the SOC₂ of lithium battery 2 exceeds the upper limit SOC_2max, discharge until the set value SOC_2set is reached. When the of lithium battery 2 is lower than the lower limit SOC_2min, charge until the set value SOC_2set is reached.

The expert strategy for emergency mode 1 is to first decommission fuel cell and lithium battery 1. Then judge according to the net load power P_net: when P_net is greater than or equal to 0, it means that the power generation of new energy is less than the load demand, and the lithium battery 2 will be in the discharge state; On the contrary, it is necessary to cut off the PV and WT to make the lithium battery 2 supply the loads alone. Until SOC₂ is less than the SOC_2set, exit emergency mode 1 and return to the main program.

The expert strategy for emergency mode 2 is to first deactivate lithium battery (1) Then judge according to the net load power P_net: when P_net is less than 0, it means that the power generation of new energy is greater than the load demand. At this time, the fuel cell is out of operation, and the lithium battery 2 can still be in the charging mode. Make full use of the abundant new energy power to charge the lithium battery (2) When P_net is greater than or equal to 0, it means that the new energy power generation is less than the load demand. At this time, the fuel cell will operate at the maximum power. At this time, make a difference between P_net and fuel cell power. If the difference is less than 0, lithium battery 2 will be in a charged state. When SOC₂ is greater than SOC_2set, exit emergency mode 2 and return to the main program. If the difference is greater than or equal to 0, it means that the load demand exceeds the bearing range of the microgrid, and the load removal strategy needs to be implemented. It should be noted that the load cutting strategy can be implemented according to the demand response strategy or the load can be divided into primary load and secondary load. Since there are many relevant literature studies on this strategy, it will not be discussed²⁵.

Case studies

This section studies the effectiveness of the proposed dual mode coupling energy management strategy for islanded AC/DC hybrid microgrid based on an existent experimental AC/DC hybrid microgrid in China. The structure of islanded AC/DC hybrid microgrid is shown in Fig. 1, in which the maximum power of PV and WT is 300 kW and 50 kW, respectively. Figure 7 shows the actual experimental setup, including the experimental AC/DC hybrid microgrid and physical drawings of the devices. Devices include PV, WT, fuel cell, lithium batteries, AC and DC loads. The AC and DC loads are both programmed resistance load boxes with a maximum power of 200 kW. Lithium battery 1 and lithium battery 2 adopt lithium batteries with the same specifications and parameters, and the parameters are shown in Table 1.

Fig. 7

The actual experimental setup

Table 1 Operation parameters of microgrid.

In this paper, the actual engineering data of a typical day is selected as an example. Among them, the intraday forecast data and intraday ultra-short-term power forecast data of PV, WT and AC/DC loads are shown in Figs. 8 and 9. The errors of intraday ultra-short-term forecast and day-ahead day forecast are 26.3%, 31.4%, 16.8% and 15.7%, respectively.

Fig. 8

Day-ahead forecast data.

Fig. 9

Intraday ultra-short-term power forecast data.

In this example, Matlab / yalmip is used to model the optimization problem, and CPLEX solver is called to solve the problem. Intel Core (TM) i7-8700 CPU @ 3.2ghz and 64 bit computer with 16GB memory are used for calculation.

• A. Analysis of economic operation mode.

According to the day-ahead optimal dispatch mode in the economic mode in this paper, the day-ahead optimal dispatch results of islanded island AC/DC hybrid microgrid are shown in Fig. 10.

Fig. 10

Day-ahead dispatch of islanded AC/DC hybrid microgrid.

The cost of the day-ahead optimal dispatch of the islanded AC/DC hybrid microgrid is 592.31¥. As can be seen from Fig. 10, due to the large PV power on the DC side, the power of BC flows from DC side to AC side in the whole scheduling process. During the period from 00:00 to 9:00, the PV power is low, lithium battery 1 is in the discharge state, and the SOC of lithium battery 1 gradually decreases. During the period from 9:00 to 14:00, the PV power gradually reaches the intraday peak, and the lithium battery 1 enters the charging state and gradually reaches the intraday peak. Then as the PV power decreases, the lithium battery 1 discharges again, and the SOC value finally returns to the state where the scheduling starts. In the whole dispatch process, lithium battery 1 plays the role of “peak clipping/valley filling”, and fully ensures the economy of dispatch. Moreover, the SOC of the beginning and end are equal, so that the scheduling has periodicity.

Intraday SPC first needs to adopts scenario generation and reduction to generate the typical scenarios in the control horizon. Figures 11, 12 and 13 shows typical scenarios of WT, PV and AC/DC loads by taking the period of 14:00–15:00 as a single control horizon as an example. Based on the intraday ultra-short-term power forecast data of PV, WT and AC/DC loads, the random scenario in the control horizon is generated according to Eqs. (15–17) and Latin hypercube sampling technology. The values of µ and σ are 0.5 and 0.33, respectively, α and β both values are 2.5, γ is 0.5. According to the historical forecast accuracy of the microgrid, the intraday ultra-short-term power forecast errors of PV and WT are set to 20% and 30%, respectively, and the intraday ultra-short-term power forecast errors of AC and DC loads are 15%. After the random scenarios are reduced by the synchronous back substitution method, the number of intraday typical scenarios PV and WT is 5, the number of intraday typical scenarios of AC and DC loads is 2, and the final number of combined typical scenarios is 100.

Fig. 11

Representative scenarios of PV.

Fig. 12

Representative scenarios of WT.

Fig. 13

Representative scenarios of AC and DC loads.

To verify the economy and robustness of the intraday SPC proposed in this paper, the intraday model predictive control (MPC) is used for comparative analysis. Figures 14 and 15 show the intraday dispatch results of SPC and MPC.

Fig. 14

Intraday SPC dispatch results.

Fig. 15

Intraday MPC dispatch results.

Table 2 shows the intraday operation cost and the solution time of a single control horizon of both modes.

Table 2 Comparison of different intraday optimal dispatch strategy.

It can be seen from Table 2 that the intraday operation cost of SPC is lower than MPC, with a difference of 4.5%. However, SPC needs scenario generation and reduction in the control horizon. After generating a typical scenario, there are more variables involved in the calculation, so the solution time is much longer than MPC. Obviously, SPC achieves the reduction of scheduling cost by sacrificing solution time. As can be seen from Table 2, the single control horizon solution time of SPC is over 9 times that of MPC. However, considering that the time interval of control horizon rolling is 5 min, the intraday SPC still meets the dispatch time demand.

As shown in Figs. 14 and 15, the intraday SPC strategy and MPC strategy are compensated by adjusting the intraday power of lithium battery and fuel cell due to the intraday fluctuation of PV, WT and AC and DC loads. Thus, the impact of day-ahead forecast error on the intraday optimal scheduling can be effectively reduced while ensuring the effectiveness of the day-ahead schedules. However, by comparing the two figures, it can be found that in the schedules with SPC, the power fluctuation of lithium battery 1 is smaller, and the SOC control effect is better than MPC. To clearly reveal the effect of the two intraday dispatch strategies on tracking the day-ahead schedule of lithium battery 1 SOC, a comparison diagram of the tracking effect is given in Fig. 16.

Fig. 16

Comparison of intraday tracking effect.

As shown in Fig. 16, the tracking effects of the two strategies are quite different between 9:00 and 14:00. This is because, during this period, due to the sharp increase of PV power, the fuel cell stops operating, leaving only lithium battery 1 available for system dispatch. Although the MPC is similar to the SPC in the scheduling framework, it only employs intraday ultra-short-term power forecast data to optimize the operation. Moreover, the intraday scheduling target fails to consider the intraday economy and only keeps track of the day-ahead schedules. This makes the SOC tracking error of the lithium battery 1 accumulate gradually in this period, resulting in poor tracking effect. On the contrary, SPC makes the schedules based on typical scenarios and fully considers the economy of intraday scheduling. Thus, excessive dependence on the day-ahead schedules of lithium battery 1 is avoided, and better economy and robustness are achieved.

• B. Results of emergency operation mode.

To prevent the transient unplanned intraday power fluctuation from endangering the stability and safety of microgrid, the dual mode coupling energy management strategy of islanded AC/DC hybrid microgrid sets up an emergency mode to deal with this situation. Since the lithium battery 2 mainly suppresses the instantaneous unplanned power fluctuation, it may exceed the set SOC range of lithium battery 2 at any time. This section assumes that the upper limit SOC_2max of lithium battery 2 is exceeded at 14:00 in the schedules shown in Fig. 14. The reason for this setting is that at this time, the lithium battery 1 SOC just reaches the peak value, and the SOC of two lithium batteries in the microgrid both reach the upper limit peak value. There is no power consumption unit, which is an extreme scenario. If the emergency mode can effectively deal with this scenario, the mode can effectively ensure the stability and safety operation of islanded AC/DC hybrid microgrid.

In case of the above conditions, the intraday dispatch results of islanded AC/DC hybrid microgrid are shown in Fig. 17. Due to the SOC of lithium battery 2 exceeding the upper limit SOC_2max at 14:00, according to the dual mode coupling energy management strategy of islanded AC/DC hybrid microgrid, emergency mode 1 is triggered. Then, the lithium battery 1 and the fuel cell stop operating. Lithium battery 2 activates the discharge state until SOC₂ returns to the set value, and the microgrid returns to the economic operation mode again. Figure 18 further shows the operation of islanded AC/DC hybrid microgrid in emergency mode 1.

Fig. 17

Intraday dispatch results in case of emergency mode.

Fig. 18

Dispatch results under emergency mode.

In Fig. 18, according to the dispatch strategy of emergency mode 1, when the net load power is negative, PV and WT will stop operating, and lithium battery 2 will supply the load independently. In these periods, the discharge power of lithium battery 2 is large, the SOC decreases rapidly, and the BC exchange power flows from AC side to DC side. When the net load power is positive, the PV and WT are put into operation, and the lithium battery 2 is still in the discharge state. Since the discharge power is reduced, the rate of decline in the charge state is slowed down. The BC exchange power flows from the DC side to the AC side. Throughout the dispatch process, the SOC of lithium battery 2 has been consistently declining until lower than the set value, then the microgrid exits emergency mode 1 after 17:10. Table 3 shows the V/F control unit operation cost comparison between out of limit state and normal state in microgrid. It can be observed that the total intraday operation cost in the out-of-limit state is 11.6% lower than that of the operation without exceeding the limit. In case of out of the limit state, since the lithium battery 2 is in the discharge state in emergency mode and supplies the load, the operation cost of lithium battery 1 and fuel cell is reduced during this period. Therefore, although the emergency mode increases intraday additional costs, the total intraday operation cost is lower than the operation cost without exceeding the limit.

Table 3 Operation costs of AC/DC hybrid microgrid in different situations.

In conclusion, when the SOC of lithium battery 2 as the V/F control unit exceeds the limit, the dual mode coupling energy management strategy of islanded AC/DC hybrid microgrid quickly triggers the emergency mode. After a period of time, the SOC of lithium battery 2 returns to the set value, and the microgrid returns to the economic operation mode. This shows that the dual mode coupling energy management strategy of islanded AC/DC hybrid microgrid can not only ensure the economy and robustness of microgrid operation, but also guarantee the stability and security of intraday operation.

Conclusion

This paper proposes a dual mode coupling energy management strategy for islanded AC/DC hybrid microgrid. The strategy sets two operation modes: economic mode and emergency mode. The two energy management operation modes are coupled and closely coordinated with each other to achieve normal economic operation and short-term risk control. The proposed strategy is verified based on an experimental AC/DC hybrid microgrid in various case studies.

In two-stage SPC strategy based economic mode, multi-scenario technology is employed to characterize the intraday randomness of WT, PV and AC/DC loads in the control horizon. The economy of intraday dispatch is fully considered while tracking day-ahead schedules by rolling optimization. Compared with MPC, it achieves 4.5% lower operation cost and more accurate tracking effect of day-ahead schedules, reflecting better economy and robustness. Although the single control horizon solution time of SPC is over 9 times that of MPC., it still meets the needs of intraday dispatch time.

This paper selects an extreme scenario to verify the effectiveness of the emergency mode. The results indicate that the emergency mode can restore the V/F control unit to the set value and return to the economic mode after its SOC exceeds the limit. Thus, the intraday operation stability and safety can be guaranteed. Moreover, the total intraday operation cost in the out-of-limit state is 11.6% lower than that of the operation without exceeding the limit. In this process, the two energy management operation modes are coupled with each other, closely coordinated and smoothly connected, which reasonably balances the operation economy and security of islanded AC/DC hybrid microgrid.