Probabilistic analysis of active earth pressures in spatially variable soils using machine learning and confidence intervals

Abstract

This study introduces a probabilistic framework for assessing active earth pressures in soils exhibiting spatial variability in friction angles and unit weight. These properties are modeled using random fields with log-normal distributions and spatial correlation lengths. Monte Carlo simulations (MCS) are integrated with finite element limit analysis (FELA) to evaluate the failure probability under different design safety factors. To improve computational efficiency and prediction accuracy, machine learning models, such as Multivariate Adaptive Regression Splines (MARS), are utilized to predict failure probabilities based on key spatial variability parameters. A two-phase optimization approach, combining Random Search and Adaptive Sampling, is employed to refine the hyperparameters of the machine learning model. Confidence intervals are incorporated to quantify prediction reliability, providing engineers with robust decision-making tools under uncertainty. Furthermore, adaptive finite element meshes are applied to capture irregular stochastic failure mechanisms, offering deeper insights into the impact of spatial variability. The study produces parametric results in the form of practical contour design charts, aiding engineers in optimizing safety margins while accounting for soil variability. By combining computational methods, machine learning, and uncertainty quantification, this research enhances geotechnical design practices, ensuring more reliable and cost-effective solutions.

Introduction

Accurate estimation of active earth pressures is essential for the design and stability assessment of retaining walls. Classical methods, such as Rankine’s¹ and Coulomb’s² theories, have long served as the foundation for geotechnical analysis, providing simplicity and computational efficiency based on assumptions of homogeneous soil properties, linear pressure distributions, and smooth failure surfaces. More recent approaches, such as the rigorous solutions proposed by Nguyen³, Nguyen et al.⁴ have enhanced analytical precision. However, these methods often rely on key simplifications that do not fully account for real-world complexities, including spatial variability in soil properties, depth-dependent behaviors, and irregular failure mechanisms. Soils, shaped by processes such as weathering, deposition, and stress history, are inherently heterogeneous. Ignoring this variability can lead to designs that are either overly conservative or insufficiently robust, ultimately compromising the structural integrity of retaining walls⁵.

Spatial variability in soil parameters, such as unit weight and internal friction angle, plays a significant role in geotechnical performance^6,7,8. Early studies by Fenton et al.⁹ demonstrated how random fields influence active pressure distributions and failure mechanisms, emphasizing the need for probabilistic models to address these uncertainties. Similarly, Phoon and Kulhawy¹⁰ highlighted the importance of quantifying geotechnical variability to enhance design reliability. Building on this foundation, Soubra and Macuh¹¹ utilized kinematic limit analysis to derive active and passive pressure coefficients, while Al-Bittar and Soubra¹² applied sparse polynomial chaos expansions (SPCE) to assess strip footings on spatially random soils. These studies underline the crucial role of advanced probabilistic approaches in capturing the effects of spatial heterogeneity.

Recent advancements have further refined the understanding of variability effects. Qian et al.¹³ highlighted the limitations of linear models in capturing irregular failure surfaces and active pressure distributions in non-homogeneous soils. Building on this, Li and Yang¹⁴ incorporated soil cohesion and tensile strength cut-offs into three-dimensional (3D) retaining wall analyses, demonstrating that 3D effects provide more accurate stability predictions compared to two-dimensional models. Pan and Dias¹⁵ showcased the efficiency of sparse polynomial chaos expansions (SPCE) in high-dimensional probabilistic evaluations, illustrating its ability to reduce computational demands without sacrificing accuracy.

Despite these advancements, significant gaps remain in understanding active earth pressures under spatially variable and heterogeneous conditions. While research by Yang and Li¹⁶ investigated 3D seismic active earth pressures using kinematic limit analysis, few studies have systematically integrated spatial variability¹⁷, depth-dependent soil behaviors¹⁸, and machine learning-based frameworks into probabilistic design¹⁹. Additionally, practical tools that provide actionable insights, such as uncertainty quantification, confidence intervals, sensitivity analyses, and design charts, are still lacking, leaving engineers with limited means to address these challenges in real-world applications. These gaps collectively emphasize the increasing reliance on probabilistic frameworks to model geotechnical systems under uncertainty.

Monte Carlo Simulations (MCS) remain the cornerstone of probabilistic geotechnics, providing a reliable method for quantifying failure probabilities and safety factors^20,21. However, their computational intensity limits their practical application, especially when coupled with detailed finite element analyses. To address this challenge, surrogate modeling techniques and machine learning approaches, such as Multivariate Adaptive Regression Splines (MARS), have emerged as powerful tools for improving efficiency and accuracy in probabilistic analysis²². Machine learning has been increasingly employed for various geotechnical applications, including tunnel lining crack detection using deep learning-based models²³, geostress classification through automatic machine learning frameworks²⁴, and prediction of aftershock ground motions using generative adversarial networks²⁵. In addition, recent advancements in neural networks have demonstrated significant improvements in site response analysis based on large-scale seismic databases²⁶, underground seismic intensity measure predictions using conditional generative adversarial networks²⁷, and spectral acceleration prediction of aftershocks with deep learning methods²⁸. These advancements highlight the growing role of data-driven techniques in geotechnical engineering, demonstrating their potential to enhance efficiency, accuracy, and reliability in probabilistic modeling.

Among these data-driven techniques, MARS has emerged as a particularly effective surrogate model for probabilistic geotechnical analysis, offering both computational efficiency and interpretability. MARS excels in capturing complex, nonlinear relationships among variables while maintaining interpretability, which is an essential requirement for practical geotechnical applications. To enhance its performance, this study employs an optimization method for tuning the hyperparameters of the MARS model, including the maximum number of terms and maximum polynomial degree. A two-phase strategy combining Random Search and an Adaptive Sampling approach is implemented²⁹, ensuring an effective balance between exploration and exploitation of the hyperparameter space to identify optimal configurations.

In summary, this study seeks to address these gaps by developing a comprehensive probabilistic framework for assessing active earth pressures in spatially random frictional soils. The research combines Finite Element Limit Analysis (FELA)³⁰ with Monte Carlo Simulations (MCS) to evaluate failure probabilities under varying safety factors. To improve computational efficiency and interpretability, Multivariate Adaptive Regression Splines (MARS) are utilized as a surrogate model, with hyperparameters optimized through a two-phase strategy that integrates Random Search and Adaptive Sampling.

The study further introduces confidence intervals to quantify prediction reliability^31,32, providing engineers with a robust measure for decision-making under uncertainty - an aspect often overlooked in traditional geotechnical probabilistic models. In addition, advanced sensitivity analysis tools, including Partial Dependence Plots (PDPs) and feature importance assessments, are employed to provide a more interpretable, data-driven understanding of the influence of key geotechnical parameters such as the Factor of Safety (FoS), Coefficient of Variation (COV), and Spatial Correlation Length Ratio (SCLR). Unlike previous studies that primarily focus on probabilistic failure prediction, this research systematically integrates machine learning with FELA-based probabilistic modeling to improve computational efficiency while preserving interpretability. A novel two-phase optimization strategy combining Random Search and Adaptive Sampling is proposed to enhance the accuracy and generalizability of MARS-based surrogate models. Furthermore, this study develops comprehensive probabilistic design charts, bridging the gap between theoretical probabilistic modeling and practical engineering applications by offering actionable tools that correlate safety factors with failure probabilities. By addressing the limitations of traditional deterministic approaches, this research significantly advances reliability-based geotechnical design, enabling more efficient and robust engineering solutions under spatially variable soil conditions.

Problem statement

Finite element limit analysis

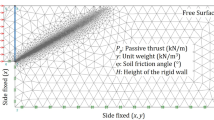
Figure 1 presents a representative example of an adaptive mesh used in the analysis of active earth pressure. The mesh is densely refined near the failure region to capture stress localization and soil deformation with higher accuracy while maintaining computational efficiency. In this case, a rigid wall is subjected to a normal velocity to induce active failure, with the resulting normal tensile pressure (P_A) exerted by the soil on the rigid wall being evaluated.

The wall-soil interface is assumed to be perfectly smooth (R = 0), and the wall height is indicated by (H). The backfilled sand is modeled as a Mohr-Coulomb material, defined by its unit weight (γ) and internal friction angle (ϕ). Standard boundary conditions are applied: the lateral edges of the domain are fixed in the horizontal direction (x), while the bottom boundary is constrained in both horizontal (x) and vertical (y) directions.

Fig. 1

A typical adaptive FELA mesh used for deterministic active earth pressure analysis under a smooth rigid wall assumption (ϕ = 30°, γ = 18 kN/m³).

The study considers a coefficient of variation (COV) ranging from 5 to 30%, allowing the internal friction angle (ϕ) and unit weight (γ) of the soil to fluctuate around their average values (ϕ = 30°, γ = 18 kN/m³). While a 30% COV does not encompass all real-world cases, it ensures a sufficiently comprehensive dataset for analysis while balancing computational efficiency and feasibility. While a 30% COV does not encompass all real-world cases, it ensures a sufficiently comprehensive dataset for analysis while balancing computational efficiency and feasibility. Thus, the selected conditions maintain a practical yet rigorous scope³³.

The ultimate load for various scenarios, accounting for factors such as cohesion, internal friction angle, and unit weight, is determined using Terzaghi’s bearing capacity³⁴ equation combined with the principle of superposition. For the case of active failure, detailed calculations are presented in Eq. (1), following the methodology employed by Nguyen and Shiau³⁵.

$${p_a}= - c{F_c}+{\sigma _s}{F_s}+\gamma H{F_\gamma }$$

(1)

For the sandy soil backfills considered in this study, it is assumed that the cohesion factor is zero and no surface load is applied. This approach simplifies the analysis and reduces Eq. (1) to (2), allowing the investigation to concentrate on the effects of other parameters such as the internal soil friction angle.

$${N_\gamma }={F_\gamma }=\frac{{{P_a}}}{{\gamma H}}$$

(2)

Where ${F_\gamma }$ is the soil unit weight factor that is equal to the stability factor,${N_\gamma }$, as defined in this paper. P_a is the active earth pressure exerted on the rigid wall under a critical active failure state. This value is to be determined by using the adaptive finite element limit analysis in this paper.

Random field analysis

In geotechnical engineering, the lognormal distribution is widely used in random field analysis to represent the spatial variability of sand properties, especially the soil friction angle. This distribution is preferred because it ensures that all values are positive, which is a critical requirement for parameters like the soil friction angle that cannot take negative values. Using a normal distribution in such cases could lead to unrealistic negative values, which are not physically meaningful (refer to Eq. (3)).

The assumption of a lognormal distribution for soil properties is widely used in geotechnical engineering, as it ensures strictly positive values for parameters such as unit weight (γ) and friction angle (ϕ), which are inherently non-negative. This assumption is supported by previous studies^36,37, which have demonstrated its suitability for modeling soil variability. However, we acknowledge that real-world soil data may sometimes deviate from a strict lognormal distribution due to site-specific heterogeneity and measurement uncertainties.

The lognormal distribution is characterized by two parameters: the mean (µ) and the standard deviation (σ), which describe the central tendency and variability of the data, respectively. It is derived from applying an exponential transformation to a normal distribution, ensuring the positivity of the data. This transformation introduces skewness to the distribution, making it more suitable for modeling parameters that naturally exhibit non-symmetric variability. The lognormal distribution is derived through an exponential transformation applied to a normal distribution, with its probability density function (PDF) defined in Eq. (4). This equation provides a quantitative representation of the distribution, enabling its use in probabilistic and statistical analyses for modeling soil properties.

$$f\left( x \right)=\frac{1}{{\sigma \sqrt {2\pi } }}\exp \left[ { - \frac{1}{2}{{\left( {\frac{{x - \mu }}{\sigma }} \right)}^2}} \right], {\text{for x }} \ge 0 {\text{ and x }} < 0$$

(3)

$$f\left( x \right)=\frac{1}{{x{\sigma _{\ln x}}\sqrt {2\pi } }}\exp \left[ { - \frac{1}{2}{{\left( {\frac{{\ln x - {\mu _{\ln x}}}}{{\sigma _{{\ln x}}^{{}}}}} \right)}^2}} \right], for x > 0$$

(4)

where,

$${\mu _{\ln x}}\,=\,\ln {\mu _x} - \frac{1}{2}{\sigma ^2}\ln x$$

(5)

$${\sigma _{\ln x}}\,=\,\sqrt {\ln \left( {1+CO{V^2}} \right)}$$

(6)

Equations (5) and (6) define the mean and standard deviation of the soil’s internal friction angle, with the coefficient of variation (COV) providing a practical measure of soil variability as the ratio of standard deviation to mean. The cumulative distribution function (CDF), derived by integrating the probability density function (Eq. 4) and expressed in Eq. (7) using the complementary error function, offers an alternative way to quantify probabilities^38,39.

$$f\left( x \right)=\frac{1}{2}erfc\left( { - \frac{{\ln x - {\mu _{\ln x}}}}{{{\sigma _{\ln x}}\sqrt 2 }}} \right)$$

(7)

Beyond the mean and coefficient of variation (COV), spatial variability is a key factor in accurately characterizing soil properties. This variability is particularly important in capturing the inherent heterogeneity of geotechnical materials, which directly impacts their mechanical behavior. The scale of fluctuation (Ѳ) is a widely used parameter in the implementation of random fields, particularly in two-dimensional analyses. It quantifies the spatial extent over which soil properties exhibit significant correlation within a given region. However, a key limitation of Ѳ is that its interpretation depends on the chosen autocorrelation model, making direct comparisons between studies difficult. Additionally, in anisotropic soils, defining Ѳ separately for different directions can be challenging, as the transition between correlation lengths is not always well-defined⁴⁰.

To address these challenges, spatial correlation lengths (SCL), denoted as SCL_x and SCL_y, provide a more flexible and intuitive measure of spatial variability⁴¹. These parameters explicitly define the degree of correlation between soil properties at two distinct points along the horizontal and vertical directions, respectively, allowing for a more accurate representation of anisotropic variability. A high spatial correlation indicates that soil properties at nearby points are strongly related, whereas low correlation suggests greater variability over short distances. In other words, small values of SCL_x or SCL_y​ correspond to a highly variable random field, where individual points exhibit minimal spatial dependence.

By using SCL instead of Ѳ, stochastic soil models can incorporate various autocorrelation structures without being restricted to a specific model, improving their adaptability in different geotechnical scenarios. This makes SCL a more practical and robust choice, particularly for cases where vertical and horizontal correlation lengths differ significantly, as is commonly observed in natural soil deposits. These correlations are essential for generating realistic random fields that can accurately model the complex behavior of soils under various loading conditions. Equation (8) defines the random field, incorporating the absolute horizontal and vertical distances between discrete points i and j.

$$\rho ({\tau _{xij}},{\tau _{yij}})=exp\left( { - \frac{{{\tau _{xij}}}}{{SC{L_x}}} - \frac{{{\tau _{yij}}}}{{SC{L_y}}}} \right)$$

(8)

In the present study on active earth pressures, it is assumed that the spatial correlation lengths in the horizontal (SCL_x​) and vertical (SCL_y​) directions are equal. This simplification allows the correlation length to be represented by a single parameter. The correlation length is further expressed as a dimensionless ratio, termed the Spatial Correlation Length Ratio (SCLR), which is defined in Eq. (9). This ratio is normalized by the height of the rigid wall (H), as depicted in Fig. 1. By normalizing the correlation length, the analysis accounts for the relative influence of spatial variability in soil properties with respect to the geometry of the problem, enabling a more scalable and consistent interpretation of the results.

$$SCLR=\frac{{SC{L_x}}}{H}=\frac{{SC{L_y}}}{H}$$

(9)

Random field analysis relies on three essential parameters: the mean value, the standard deviation, and the spatial correlation lengths in both the horizontal and vertical directions. These parameters collectively define the statistical and spatial characteristics of the soil properties being analyzed. To simulate random fields effectively for stability analysis, the Karhunen-Loève (KL) expansion method is utilized^42,43. The KL method is a powerful mathematical tool that calculates the covariance between random variables within the field. By doing so, it facilitates the generation of thousands of random field realizations, ensuring that the variability and correlation of soil properties are accurately captured.

Moreover, the KL method computes the eigenvalues and eigenvectors of the covariance function, which serve as a basis for approximating the random field. This decomposition enables the representation of complex spatial variability with a reduced number of terms, making the analysis computationally efficient while retaining accuracy. For a detailed discussion of the theoretical and computational aspects of the KL method, readers are referred to Adhikari and Friswell⁴⁴, Betz et al.⁴⁵, and Zheng et al.⁴⁶, which provide comprehensive insights into its application and implementation in random field analysis.

In recent years, geotechnical engineers have placed greater emphasis on integrating probability of failure assessments into design practices by utilizing specific Factors of Safety (FoS)⁴⁷. This approach enhances reliability and risk management in geotechnical designs⁴⁸. In the present study, active failure is defined as the condition when the computed stability factor for unit weight (${N_\gamma }$, see Eq. (2)​) in each Monte Carlo Simulation (MCS) is less than the deterministic value (N_rd) corresponding to a selected FoS. This probabilistic criterion ensures that the analysis accounts for uncertainties in soil properties and loading conditions. Equation (10) formalizes this definition, providing a clear mathematical framework for evaluating the probability of active failure. This approach enables systematic assessment of failure likelihood, offering insights that can guide safer and more efficient design decisions.

$$\:Active\:failure\:is\:identified\:when\:{N}_{c}<\:({N}_{cd}/FoS)for\:1000\:MCs$$

(10)

$$PF=P\left[ {{N_c}<\left( {{{{N_{cd}}} \mathord{\left/ {\vphantom {{{N_{cd}}} {FoS}}} \right. \kern-0pt} {FoS}}} \right)} \right]\,{\text{for 1}}000{\text{ MCs}}$$

(11)

Using Eq. (10), the probability of failure for a given “designed” Factor of Safety (FoS) is determined by counting the number of instances that meet the failure criterion defined in the equation and dividing this count by the total number of Monte Carlo Simulations (MCS). In this study, 1000 simulations were performed to ensure statistical reliability^33,49, and the detailed calculation procedure is provided in Eq. (11).

This probabilistic interpretation, as outlined in Eq. (11), facilitates a systematic analysis of how random field design parameters, such as the coefficient of variation (COV), the scale of fluctuation ratio (SCLR), and the selected FoS, affect the likelihood of failure. By considering the inherent variability and spatial correlations in soil properties, this approach provides a more realistic assessment of geotechnical risks compared to traditional deterministic methods.

However, it is important to note that this probabilistic framework demands significantly higher computational resources, approximately 1000 times more than a single deterministic analysis. Despite the increased computational cost, this methodology offers critical insights into the influence of uncertainty on design performance, enabling more informed decision-making in geotechnical engineering designs.

Fig. 2

A typical scatter plot for (COV = 15%, SCLR = 0.6).

Figure 2 provides a detailed visualization of the variability in results obtained through Monte Carlo Simulations (MCS) for a soil configuration characterized by a coefficient of variation (COV) of 15% and a spatial correlation length ratio (SCLR) of 0.6. Each point in the scatter plot corresponds to a single realization of the random field, showcasing the variability inherent in the stochastic modeling of soil properties.

The data reveals a significant spread of results, highlighting the influence of spatial variability, even when COV and SCLR values are fixed. The scatter plot also exhibits clustering around a central trend, representing the mean behaviour of the system. For the chosen SCLR of 0.6, which represents moderate spatial correlation among soil properties, the observed spread aligns with expected behavior where localized variability significantly influences the outcomes. The lack of outliers in the scatter plot suggests that the MCS model is robust, effectively capturing variability without producing unrealistic results, further validating the computational approach used.

This variability illustrates the importance of accounting for the stochastic nature of soil properties in geotechnical analysis. It challenges the assumptions made in deterministic approaches, which often assume uniform soil characteristics. Practically, this highlights the need for probabilistic methods to account for variability, as deterministic models often overlook such effects. Engineers can use these insights to refine safety factors and design decisions. Future analyses incorporating statistical metrics or varying COV and SCLR values could further enhance understanding of spatial variability’s influence on geotechnical stability.

Figure 3 presents the distribution of Factor of Safety (FoS) values derived from Monte Carlo Simulations (MCS) for a coefficient of variation (COV) of 15% and a spatial correlation length ratio (SCLR) of 0.6. The histogram shows a slightly skewed distribution, with the majority of values concentrated around the mean and a noticeable tail extending toward lower FoS values. This tail highlights the importance of considering these lower FoS values in risk assessment.

The Probability Density Function (PDF) smooths the variations observed in the histogram, providing a continuous representation of the distribution. This smooth curve enables a clearer understanding of the likelihood of different FoS outcomes. Meanwhile, the Cumulative Distribution Function (CDF) further enhances the analysis by indicating the probability of achieving specific FoS thresholds, offering a useful tool for assessing the reliability of soil stability design under varying conditions.

Fig. 3

A typical histogram for (COV = 15%, SCL = 0.6).

In summary, this representation emphasizes the probabilistic nature of soil stability and its critical implications for design reliability. The histogram, along with the Probability Density Function (PDF) and Cumulative Distribution Function (CDF), provides engineers with a clearer understanding of the variability in stability outcomes, reinforcing the need for probabilistic analyses.

In the following sections, further analysis of the distributions across varying coefficient of variation (COV) and spatial correlation length ratio (SCLR) values is presented. This additional analysis will help deepen the understanding of how spatial variability influences stability results, providing valuable insights for refining design practices and decision making using a traditional FoS design approach.

Results and discussion

Comparison of results

Figure 4 presents a comparative analysis of deterministic solutions for the soil unit weight factor ${F_\gamma }$ (as defined in Eq. (1), the stability factor (${F_\gamma }$) obtained using three different methods: adaptive meshing, uniform meshing, and the results from random field modeling with 1000 Monte Carlo Simulations (MCS) with SCLR = 2 and various seed values. These results are benchmarked against the Finite Element Limit Analysis (FELA) method by Nguyen and Shiau³⁵ and the analytical solution proposed by Lancellotta⁵⁰.

Fig. 4

Comparison of deterministic solutions obtained by adaptive, uniform meshing, random field 1000MCs of present solution, Nguyen and Shiau³⁵ FELA approach, and Lancellotta⁵⁰ analytical solution.

To assess variability in computed stability factors, Fig. 4 includes multiple realizations of the random field with different seed values (Seed = 1, 55, 111, 250, 500, 1000) under a coefficient of variation (COV) of 30% and SCLR of 2. The results show a wider spread compared to deterministic solutions from uniform and adaptive FELA meshes, highlighting the impact of soil heterogeneity on stability predictions. While deterministic solutions remain within the probabilistic range, the variability underscores the need for stochastic analyses in geotechnical design, as relying solely on deterministic values may overlook risks associated with spatially random soil properties.

The mean values from the 1000 Monte Carlo simulations closely align with deterministic predictions, confirming the robustness of the probabilistic approach. The agreement between the random field-based mean response and established solutions further validates the Monte Carlo framework.

Moreover, adaptive meshing outperforms uniform meshing in computational precision and convergence efficiency, yielding solutions that better match reference benchmarks. The incorporation of spatial variability through random field modeling provides a more realistic representation of soil heterogeneity, which is crucial for geotechnical stability analysis.

This comparison highlights the importance of selecting appropriate modeling approaches, particularly where spatial variability and uncertainty are significant. By integrating deterministic and probabilistic methods, this study enhances the reliability of geotechnical design, balancing computational efficiency with predictive accuracy.

Normalized mean critical stability number (N _{c, m}/N _{c, d})

Figure 5 illustrates the relationship between the normalized mean critical stability number (_,/_,) and the spatial correlation length ratio (SCLR) for various coefficients of variation (COV). The normalized stability number allows a direct comparison between probabilistic results (_,) and their deterministic counterpart (_,), highlighting the effects of spatial variability.

As SCLR increases, the normalized mean critical stability number decreases for all COV values, showing that longer spatial correlations lead to reduced stability due to more pronounced soil heterogeneities. The effect of spatial variability is especially pronounced at higher COV values, where deviations from deterministic predictions become more significant. For small SCLR values, the normalized stability numbers converge toward deterministic results, particularly at lower COVs, reflecting the limited influence of variability when soil properties are highly localized.

The figure also suggests that the impact of SCLR diminishes beyond a certain threshold, as the stability number approaches an asymptotic value. This indicates that, while spatial correlation significantly influences stability, its effect becomes less critical for very large correlation lengths. These findings demonstrate how probabilistic results deviate from deterministic predictions, emphasize the limitations of deterministic models in capturing the effects of spatial variability.

Fig. 5

Normalized mean critical stability number (N_{c, m}/N_{c, d}) vs. the spatial correlation length ratio (SLR) for various COV.

Figure 6 illustrates the relationship between the normalized mean critical stability number (_,/_,) and spatial correlation length ratios (SCLR) for various coefficients of variation (COV). This plot provides valuable insights into how spatial variability and correlation length impact the stability of geotechnical systems. The plot reveals that as SCLR increases, the normalized stability number consistently decreases for all COV values, signifying that greater spatial correlation in soil properties generally reduces stability. This effect is particularly pronounced at higher COV values, where the variability of soil properties has a more significant impact on stability outcomes.

Fig. 6

Normalized mean critical stability number (N_{c, m}/N_{c, d}) vs. COV % for various spatial correlation length ratios (SCLR).

For larger SCLR values, the rate of decline in the stability number with increasing COV becomes slower. This trend suggests that more globally correlated soil properties (i.e. higher SCLR) moderate the effects of variability. This behavior aligns with the expectation that spatial correlation length moderates the effects of random variability, with larger SCLR values distributing heterogeneities more evenly over the domain. The convergence of the normalized stability number for low COV values across all SCLR reinforces the reliability of deterministic models when soil variability is minimal. In such cases, deterministic approaches provide predictions close to those of probabilistic models, reducing the need for complex stochastic analyses.

From a practical perspective, Fig. 6 highlights the importance of accounting for both COV and SCLR in stability assessments. For soils with high variability (e.g. COV > 20%) and small correlation lengths, relying on deterministic stability predictions could lead to overestimation of safety. The trends observed in the figure provide engineers with a clear framework for understanding how variability impacts stability, helping to refine probabilistic methods and improve design reliability.

Probability of failure (PF)

Figure 7 demonstrates the relationship between the Probability of Failure (PF) and the Coefficient of Variation (COV) for various Factors of Safety (FoS), with SCLR held constant at 0.2. The results highlight distinct behaviors for different FoS values. For a low FoS of 0.5, the PF remains consistently at 1.0 across all COV values. This indicates a highly unstable system where failure is certain, irrespective of variability in COV values. Conversely, for high FoS values of 2.0 and 2.5, the PF is uniformly zero, reflecting a robust design where failure is essentially impossible regardless of COV fluctuations. These results are expected, as extreme FoS values inherently dominate the system’s response, rendering the effect of COV negligible.

Fig. 7

PF vs. COV for various FoS (SCLR = 0.2).

Of particular interest is the case of a design FoS of 1.0. Here, the PF starts at 50% when COV is minimal, aligning with the probabilistic interpretation of safety margins. As COV increases, the PF exhibits a slight decline, suggesting that higher variability in input parameters introduces some measure of statistical balance that marginally reduces the likelihood of failure. For intermediate FoS values (e.g., 1.25, 1.5, or 1.75), the PF shows a gentle but noticeable upward trend as COV increases. Overall, these patterns emphasize the interrelationship between FoS and COV in influencing system reliability, providing valuable insights for risk assessment and design optimization.

Fig. 8

PF vs. FoS for various SCL (COV = 30%).

Figure 8 explores the relationship between the Probability of Failure (PF) and the Factor of Safety (FoS) for different Spatial Correlation Length Ratios (SCLR) at a fixed Coefficient of Variation (COV) of 30%. The results show a consistent inverse relationship between PF and FoS, with PF decreasing sharply as FoS increases. For the chosen study of high COV value, PF is less sensitive to changes in SCLR. As FoS increases beyond 1.5, PF converges across all SCLR values, with negligible failure probability at FoS ≥ 2.0. The results highlight the non-linear interaction between FoS and SCLR, with SCLR playing a more critical role in designs with lower safety margins.

Figure 8 suggests that increasing the safety factor effectively reduces the influence of spatial correlation, making the system more robust to variability. From a practical perspective. It further highlights the importance of considering spatial correlation in geotechnical design, particularly for scenarios with low FoS and high COV. Understanding how SCLR and FoS affects PF allows engineers to better anticipate risks and make informed decisions about design safety margins.

Demonstration of random field vs. failure mechanism

Figure 9 demonstrates the spatial variability of the soil friction angle (ϕ) through two typical plots. Figure 9a demonstrates how random distributions of ϕ vary across different spatial correlation length ratios (SCLR) under fixed parameters (COV = 20% and SCLR = 1), while Fig. 9b highlights how the spatial distribution of ϕ changes with varying seed numbers for the same COV and simulation seed.

Figure 9a illustrates the influence of SCLR on the spatial distribution of ϕ. At lower SCLR values (e.g., 0.2), the distribution exhibits sharp transitions, reflecting highly localized variability. As SCLR increases (e.g., 1.0 or 2.0), the spatial variations become more gradual, with smoother transitions across the domain. Figure 9b highlights the stochastic nature of random field modeling. Each seed generates a unique realization of ϕ, revealing distinct spatial patterns while preserving overall statistical characteristics such as mean, variability, and correlation length. This variability fulfills the necessity of running multiple simulations in Monte Carlo analyses to capture a wide range of potential outcomes.

Fig. 9

(a) Demonstration of random distribution of ϕ for various SCLR (Seed = 1, COV = 20%); (b) Material (ϕ) plot for various seed numbers of ϕ (COV = 20, SCLR = 1).

Figure 10 demonstrates how spatial variability affects strain localization in soils. It is divided into two parts: subfigure 10a examines the effect of varying SCLR under fixed randomness (Seed = 555, COV = 30%), while subfigure 10b explores how the potential slip curve changes with varying seed numbers for a constant SCLR (SCLR = 0.6, COV = 30%).

In Fig. 10a, the results show that strain localization is very sensitive to changes in SCLR. When SCLR is small (e.g., 0.2), the strain differences are tightly focused, forming small zones of intense deformation. As SCLR increases (e.g., 1.0 or 2.0), the strain spreads out more evenly across larger areas. This means that shorter spatial correlations lead to concentrated instability, while longer correlations result in more uniform deformation. These insights are important for understanding how failures happen, as localized strains often trigger failure zones, which can greatly affect stability.

On the other note, Fig. 10b illustrates how using different random seeds affects strain distribution, even when the spatial variability parameters are the same. While the overall slip patterns look similar, the exact locations and intensities of strain zones differ. This highlights how randomness influences failure behavior, even if the soil’s statistical properties stay unchanged. It also emphasizes the importance of running multiple simulations to capture a full range of possible outcomes and better account for uncertainty in geotechnical studies.

Fig. 10

(a) Contour plot of principal strain difference for various SCLR of ϕ (Seed = 555, COV = 30%); (b) Contour plot of principal strain difference for various seed numbers (COV = 30%, SCLR = 0.6).

Design charts

Fig. 11

PF design chart for various FoS: (a) FoS = 1.0; (b) FoS = 1.25; (c) FoS = 1.5; (d) FoS = 2.0; (e) FoS = 2.5.

Figure 11 presents a series of design charts for determining the probability of failure (PF) as a function of the coefficient of variation (COV) and spatial correlation length ratio (SCLR) for different Factors of Safety (FoS). Subfigures (a) through (e) correspond to FoS values ranging from 1.0 to 2.5, providing a detailed view of how soil variability and safety margins interact to influence PF.

For lower safety factors, such as FoS = 1.0 in subfigure (a), PF is consistently high across a broad range of COV and SCLR values. This indicates that designs with minimal safety margins are highly sensitive to variability, particularly for soils with high COV (> 20%) and short SCLR (< 0.6). As FoS increases, seen in subfigures (b) through (e), PF decreases significantly. For example, at FoS = 2.0, PF is negligible for most combinations of COV and SCLR, demonstrating that higher safety factors effectively mitigate the risks posed by spatial variability.

The role of SCLR is particularly notable at lower FoS values. For designs with FoS = 1.0 or 1.25, shorter correlation lengths amplify failure risks due to localized variability, resulting in higher PF values. Conversely, longer SCLR values reduce PF by spreading variability more evenly across the domain. However, as FoS increases to 2.0 or 2.5, the influence of SCLR diminishes, with PF becoming uniformly low across all SCLR values. This convergence highlights that higher safety margins can effectively reduce the effects of spatial correlation.

These design charts offer practical insights for geotechnical engineers. They emphasize the importance of selecting appropriate safety factors based on site-specific soil variability. For scenarios involving highly variable soils and short correlation lengths, increasing FoS is essential to achieve acceptable reliability. In contrast, for soils with moderate variability and longer correlation lengths, designs with lower FoS may still perform reliably, offering opportunities to optimize costs without compromising safety. These charts bridge the gap between probabilistic analysis and practical decision-making, reinforcing the manuscript’s emphasis on modern, variability-aware design practices.

Soft computing approach

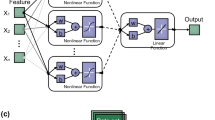
A major challenge in applying machine learning to geotechnical engineering is the trade-off between interpretability and model complexity. Traditional regression models (e.g., multiple linear regression) are easy to interpret but lack the flexibility to capture nonlinear relationships and spatial dependencies inherent in geotechnical data. Complex models such as decision trees, random forests, or deep learning models can capture intricate dependencies but are often considered “black box” models, making it difficult to derive explicit mathematical relationships. In this study, we offer a middle ground. Multivariate Adaptive Regression Splines (MARS) is employed as a surrogate model to predict the Probability of Failure (PF) based on key geotechnical parameters exhibiting spatial variability. MARS is a nonlinear regression technique that automatically partitions the input space into multiple regions and fits piecewise linear regression functions. One of its key advantages is its ability to balance model interpretability and predictive complexity, making it a suitable choice for geotechnical engineering applications where understanding model behavior is as important as achieving high accuracy.

By utilizing input parameters such as the coefficient of variation (COV), safety-critical load ratio (SCLR), and factor of safety (FoS), and training on datasets generated through Monte Carlo Simulations (MCS) combined with Finite Element Limit Analysis (FELA), the method effectively captures complex non-linear relationships. This approach not only ensures accurate predictions but also facilitates the creation of practical and interpretable tools for geotechnical design applications.

Theory of multivariate adaptive regression splines (MARS)

Multivariate Adaptive Regression Splines (MARS) is a machine learning technique designed to model complex, non-linear relationships through the use of piecewise linear models. The method employs basis functions, known as hinge functions, which are expressed mathematically as:

$$h(x) = max\,(0,\,x - t)\,or\,h(x) = max\,(0,\,t - x)$$

(12)

where t is a knot that defines intervals of the predictor variable. These hinge functions enable MARS to adapt dynamically to changes in the relationship between variables by partitioning the data space into segments and fitting a linear model within each segment⁵¹. The model construction involves two stages:

• 1. Forward Pass: Basis functions are incrementally added to minimize residual error.

• 2. Backward Pass: The model is pruned using generalized cross-validation (GCV) to balance complexity and accuracy.

MARS automatically picks the most important features, captures non-linear patterns, and finds interactions between variables, making it easy to understand and flexible to use. In this study, MARS is used to predict geotechnical parameters, providing a simple yet reliable way to model complex relationships.

Optimizers

The optimization method used to tune the hyperparameters max_terms and max_degree of the Multivariate Adaptive Regression Splines (MARS) model follows a two-phase strategy²⁹. This strategy combines Random Search with an Adaptive Sampling (RSAS) approach to efficiently determine suitable hyperparameters for predicting Probability of Failure (PF) in geotechnical systems. A critical aspect of this approach is its ability to balance computational cost and optimization efficiency compared to Grid Search and Metaheuristic Optimization. Grid Search exhaustively evaluates all hyperparameter combinations, ensuring the global optimum but at a high computational cost (assuming a sufficiently dense grid). Metaheuristic algorithms, such as GA and PSO, explore search spaces more efficiently but introduce additional computational overhead and require tuning their own hyperparameters. In contrast, RSAS adaptively refines the search space, reducing unnecessary evaluations while maintaining the accuracy of the MARS model, making it a more simple and efficient approach.

The performance of Multivariate Adaptive Regression Splines (MARS) depends significantly on the choice of max_terms (the maximum number of basis functions) and max_degree (the maximum order of interaction terms). The initial ranges for max_terms and max_degree are defined as:

$$\:max\_terms\in\:\left[1,\:30\right],\:\:max\_degree\in\:\left[1,\:10\right],$$

(13)

It should be noted that these ranges are not universally applicable to all MARS models. The appropriate hyperparameter range should be determined based on the nonlinear complexity of each problem, as different datasets may require different levels of model flexibility. If an optimal solution is found at the boundary of a search range, the range should be expanded to verify the true optimum. However, in this study, the optimized hyperparameters were located within the middle of the initial range, indicating that the selected range was appropriate.

A set of 20 initial samples is randomly generated within the specified ranges for max_terms and max_degree. For each sampled pair, the MARS model is trained using the training data, and its performance is evaluated on the test set. The evaluation uses the Mean Squared Error (MSE) metric with the k-fold cross-validation technique to ensure reliability (Eq. (14)).

$${\text{MSE}}=\frac{1}{n}\sum\limits_{{i=1}}^{n} {{{({y_i} - {{\hat {y}}_i})}^2}}$$

(14)

The sampled configurations are ranked in ascending order based on their MSE values. The top 5 configurations with the lowest MSE are selected to define a promising region in the hyperparameter space for further tuning and refinement.

Once the top-performing configurations are identified, the search focuses on the potential region, which is defined by the ranges of max_terms and max_degree from the top 5 configurations. This step refines the search by narrowing down the hyperparameter space (Eqs. (15 and (16)). The new search ranges are dynamically set based on the minimum and maximum values of max_terms and max_degree from the top 5 configurations.

$$\:\text{m}\text{a}\text{x}\_\text{t}\text{e}\text{r}\text{m}\text{s}\_\text{r}\text{a}\text{n}\text{g}\text{e}=\left[\text{m}\text{i}\text{n}\left(top\_\text{m}\text{a}\text{x}\_terms\right),\text{max}\left(top\_\text{m}\text{a}\text{x}\_terms\right)\right]$$

(15)

$$\:\text{m}\text{a}\text{x}\_\text{d}\text{e}\text{g}\text{r}\text{e}\text{e}\_\text{r}\text{a}\text{n}\text{g}\text{e}=\left[\text{m}\text{i}\text{n}\left(top\_\text{m}\text{a}\text{x}\_\text{d}\text{e}\text{g}\text{r}\text{e}\text{e}\right),\text{max}\left(top\_\text{m}\text{a}\text{x}\_\text{d}\text{e}\text{g}\text{r}\text{e}\text{e}\right)\right]$$

(16)

A larger set of 30 adaptive samples is generated within the refined ranges. The model is retrained and evaluated for each new sample, and the results are added to the ranking of configurations. The top 5 configurations are updated after each sampling round, further narrowing the search region. The optimization process concludes with the configuration that achieves the lowest MSE among all sampled combinations, which is considered the optimal choice for the hyperparameters.

The proposed optimization method is particularly advantageous for hyperparameter tuning in MARS models, where the number of hyperparameters is relatively low. By combining Random Search and Adaptive Sampling, the method achieves an effective balance between exploration and exploitation, enabling a comprehensive search of the hyperparameter space while focusing on refining the search around promising configurations. The dynamic adjustment of search ranges, guided by top-performing configurations, ensures targeted and efficient exploration. Unlike grid search, which becomes computationally expensive even for a modest number of hyperparameters, this approach significantly reduces computational cost and is much faster while maintaining robustness in finding optimal configurations. This efficiency is critical for MARS models, as it ensures effective hyperparameter tuning, leading to accurate predictions and minimized generalization errors.

Dataset properties

The performance and generalization ability of the MARS model depend on an effective training-test split strategy. In this study, the dataset is divided into 80% for training and 20% for testing, ensuring that the model learns from a sufficiently large portion of the data while maintaining an independent evaluation set. To preserve the statistical distribution of key geotechnical parameters, random sampling is used. Figures 12 and 13 provide an in-depth view of the dataset’s properties, illustrating the relationships between key input variables and the target variable, Probability of Failure (PF). Together, these figures highlight the dataset’s structure, variability, and its potential for predictive modeling in geotechnical engineering.

Fig. 12

Pairwise relationships between input parameters (COV, SCLR, FoS) and Probability of Failure (PF), illustrating parameter distributions and trends such as the inverse correlation between FoS and PF.

Figure 12 focuses on pairwise relationships between the primary input parameters, namely Coefficient of Variation (COV), Spatial Correlation Length Ratio (SCLR), and Factor of Safety (FoS), and their impact on the Probability of Failure (PF). The scatter plots reveal clear trends: PF decreases sharply as FoS increases, highlighting the strong mitigating effect of higher safety margins. COV shows a positive correlation with PF, indicating that higher variability in soil properties raises the likelihood of failure. The impact of SCLR is more complex, with shorter correlation lengths (lower SCLR values) linked to greater variability in PF. Color-coded PF values (ranging from blue for low to red for high) emphasize these relationships, while density plots along the diagonal show the distributions of individual variables. For example, COV is skewed toward lower values, reflecting typical geotechnical conditions, and FoS forms distinct clusters, aligned with standard engineering practices.

Fig. 13

Histograms and density plots of (a) FoS, (b) COV, (c) SCLR, and (d) PF, showing their frequency distributions and variability.

Figure 13 complements these findings by illustrating the frequency distributions of the key variables through histograms and density plots. The PF histogram reveals a concentration of lower failure probabilities, which aligns with scenarios designed for higher safety margins. The distributions of COV and SCLR emphasize the realistic variability captured in the dataset, ensuring it reflects practical geotechnical conditions. Similarly, the clustered nature of FoS values corresponds to commonly used safety margins, indicating that the dataset aligns well with real-world engineering standards.

In summary, the insights from Figs. 12 and 13 demonstrate the dataset’s robustness and its ability to capture complex interactions between the input parameters and PF. The variability and trends observed across the dataset ensure that the machine learning models can effectively learn and predict failure probabilities under diverse conditions. These figures highlight how well the dataset represents real-world scenarios and its potential for supporting accurate, data-driven geotechnical design.

Model’s optimization

Fig. 14

Hyperparameter optimization trajectory showing the search through maximum degree and maximum terms, with the black dot as the starting point and the green dot indicating the optimized value.

Figure 14 illustrates the iterative trajectory from initial to optimal parameters, refining the number of basis functions and maximum degree to minimize Mean Squared Error (MSE) and maximizing coefficient of determination (R²). The systematic search ensured broad exploration early on, followed by focused adjustments for precision.

The combined insights from Fig. 14 (RSAS approach) and Table 1 (manual search) demonstrate the effectiveness of our hyperparameter optimization strategy, emphasizing the balance between model complexity, accuracy, and generalizability. In Table 1, a manual grid search approach evaluates discrete increments of 5, 10, 15, 20, 25, 30 basis functions, observing that performance substantially improves with increasing complexity. For instance, the testing R² increases from 0.699 at 5 basis functions (degree 1) to nearly 1.000 at 30 basis functions (degree 7 or 8), while the MSE decreases from 0.0476 to 0.00004. However, beyond 30 basis functions and degree 7, performance gains begin to plateau, indicating that further complexity offers marginal benefits. By contrast, the RSAS approach (Fig. 14) identifies an optimal configuration at 27 basis functions and degree 7, closely matching the near-ideal performance found by the manual search yet avoiding the unnecessary increase to 30 basis functions. The minimal performance difference between 27 and 30 basis functions indicates that the additional complexity does not yield significant improvements-highlighting the RSAS method’s strength in converging to a parsimonious yet highly accurate solution. Moreover, the tight alignment between training and testing metrics in both approaches underscore the robustness of the final model. These results collectively confirm that the proposed optimization process effectively navigates the trade-off between complexity and predictive power, ultimately yielding a generalizable, high-performing MARS model for geotechnical failure probability analyses.

Table 1 Model performance across hyperparameter configurations by search manual.

Model’s performance

Figures 15 and 16 provide a comprehensive evaluation of the machine learning models’ performance, highlighting their predictive accuracy and generalizability. These figures collectively demonstrate the effectiveness of different modeling approaches for predicting the Probability of Failure (PF) in geotechnical systems.

Figure 15 presents a comparison between the predicted PF values and the exact values for both the training and testing datasets. The near-perfect alignment of data points along the 45-degree diagonal line reflects exceptional predictive performance. The model achieves an R² value of 1.000 for both training and testing datasets, indicating that it has captured the underlying relationships in the data with remarkable precision. Moreover, the close clustering of points around the diagonal, coupled with minimal Mean Absolute Error (MAE) and Mean Squared Error (MSE), confirms that the model is not only highly accurate but also generalizes well to unseen data. This robustness is critical in geotechnical engineering, where model reliability across diverse conditions is essential due to the inherent variability of soil properties.

Fig. 15

Predicted versus exact probability of failure (PF) for training data (left) and testing data (right).

In Fig. 16, the performance of four machine learning models, i.e., Multivariate Adaptive Regression Splines (MARS), Multilayer Perceptron (MLP), Support Vector Machines (SVM), and Decision Trees (DT), is compared using MAE as the primary metric. The results reveal that MARS and DT outperform the other models, achieving the lowest MAE values for the dataset. MARS demonstrates superior accuracy by effectively capturing non-linear interactions and automatically selecting significant input features, making it particularly suited for complex geotechnical datasets. Similarly, DT performs well by hierarchically segmenting the data based on the most influential variables, providing accurate and interpretable predictions.

Conversely, MLP and SVM exhibit relatively higher errors, suggesting that these methods may require additional optimization to handle the unique characteristics of the dataset. This performance gap underscores the importance of model selection and tuning when addressing specific geotechnical problems. The ability of MARS and DT to achieve high accuracy with moderate complexity makes them particularly appealing for practical applications where interpretability and computational efficiency are valued.

Fig. 16

Boxplots of MAE (left) and MSE (right) for different methods (MARS, MLP, SVM, DT), highlighting MARS and DT as the most accurate based on lower error values.

The findings presented in Figs. 15 and 16 highlight key aspects of model performance. Figure 15 demonstrates that the chosen model achieves exceptional accuracy and generalizability, with consistent results across training and testing datasets. Figure 16 emphasizes the variability in performance across models, with MARS and DT emerging as the most effective predictors due to their ability to balance flexibility, accuracy, and computational efficiency. These results underline the importance of selecting machine learning architectures that align with the characteristics of the dataset and the objectives of the analysis.

Importance-based sensitivity analysis

Feature importance analysis

Figures 17 and 18 offer valuable insights into the physical interpretation of the machine learning model’s predictions. Through sensitivity analysis and feature importance evaluation, they quantify the impact of input variables of Factor of Safety (FoS), Coefficient of Variation (COV), and Spatial Correlation Length Ratio (SCLR) on the output Probability of Failure (PF). These analyses connect data-driven predictions with geotechnical design principles, providing both validation and a deeper understanding of the model.

Fig. 17

Feature importance analysis showing the reduction in model performance (negative MSE) when each feature (FoS, COV, SCLR) is excluded.

Figure 17 highlights the relative importance of each input feature by measuring the increase in prediction error for MSE (negative Mean Squared Error) when a feature is excluded from the model. Among the features, FoS emerges as the most critical, with its removal causing a significant drop in model performance. This finding aligns with physical intuition, as FoS directly governs the safety margin in geotechnical design and thus exerts the most substantial influence on PF.

COV ranks second in importance, underscoring the critical role of variability in soil properties in determining stability. Higher variability introduces greater uncertainty in the system, leading to elevated PF values. The parameter SCLR, while contributing less than FoS and COV, plays a supporting role by influencing the spatial distribution of variability.

Fig. 18

SHAP value analysis showing the contribution of features (FoS, COV, SCLR) to the prediction of PF.

SHAP analysis eliminates the complex relationships between features and PF, offering a complementary perspective to Fig. 17. In Fig. 18, we provide a detailed breakdown of feature contributions to individual PF predictions using SHAP (SHapley Additive exPlanations) values. FoS exhibits a strong inverse relationship with PF. This trend is consistent with geotechnical theory, where larger safety factors reduce the likelihood of failure. COV shows a positive relationship with PF, with higher SHAP values indicating an increase in failure probability as soil variability intensifies. This result highlights the critical impact of uncertainty in soil properties on stability. The influence of SCLR is more subtle and indirect, affecting PF mainly through its interaction with COV and FoS, rather than acting as a dominant factor on its own. Its role in modifying the spatial distribution of variability reinforces its importance in specific geotechnical scenarios, particularly in heterogeneous or anisotropic soils.

Fig. 19

Local explanations in individual samples.

Figure 19 illustrates local explanations for individual data samples, providing insight into how each input feature (FoS, COV, SCLR) contributes to the predicted Probability of Failure (PF). Unlike global interpretations, which average contributions across the entire dataset, these local explanations reveal sample-specific interactions and highlight why certain points yield higher or lower failure probabilities. Figure 20 illustrates how the SHAP contribution of a primary feature Fos to the predicted Probability of Failure (PF) changes as its value varies along the horizontal axis. Each point represents an individual sample in the dataset, with its position on the x-axis indicating the actual value of the feature in question, and its position on the y-axis indicating the magnitude of that feature’s SHAP value (i.e., its contribution to PF). The color scale encodes another feature (COV and SCLR), allowing for the visualization of feature interactions.

Fig. 20

SHAP dependence plots.

Partial dependence plots (PDPs)

Figures 21 and 22 provide valuable insights into the relationships between input features FoS, COV, and SCLR and the output feature Probability of Failure (PF). By isolating the effects of individual features (Fig. 21) and feature pairs (Fig. 22), the Partial Dependence Plots (PDPs) offer a deeper understanding of how these variables influence failure probability.

Figure 21 illustrates the independent effects of each feature on PF. The relationship between PF and FoS is clear and intuitive: PF decreases sharply as FoS increases. This trend is particularly steep for FoS values below 1.5, where small increases in safety margins result in significant reductions in PF. Beyond a threshold (approximately FoS = 2.0), PF approaches zero, indicating that the likelihood of failure becomes negligible under conservative design conditions. This aligns with fundamental geotechnical principles, where safety margins are critical for ensuring stability.

Fig. 21

Partial dependence plots (PDPs) showing the relationship of PF with COV, SCLR, and FoS.

Fig. 22

Partial dependence plots (PDPs) showing the interaction effects of PF with pairs of features: (1) COV and SCLR, (2) COV and FoS, and (3) SCLR and FoS.

The relationship between PF and COV is equally significant. PF increases monotonically with higher COV, reflecting the direct impact of soil variability on failure likelihood. The effect becomes more pronounced at higher COV values, highlighting the importance of addressing variability in probabilistic geotechnical analyses. In contrast, the relationship between PF and SCLR is more complex. At lower SCLR values, PF is relatively high due to localized variability that intensifies failure mechanisms. As SCLR increases, PF decreases gradually, indicating that spatial correlation moderates the effects of variability by spreading it more uniformly across the domain. However, this effect diminishes beyond a certain SCLR value, where further increases have a limited impact on reducing PF.

Figure 22 extends the analysis by examining the combined effects of feature pairs on PF. The interaction between COV and SCLR reveals that high PF values are concentrated in regions where COV is large, and SCLR is small. This indicates that localized variability combined with high uncertainty amplifies failure risks. As SCLR increases, the impact of high COV on PF diminishes, confirming that spatial correlation can mitigate the effects of variability.

The interplay between COV and FoS shows that increasing FoS significantly reduces PF, even at high levels of variability. However, the rate of PF reduction is more pronounced for lower COV values, meaning that higher variability requires much larger safety margins to achieve similar stability.

Finally, the interaction between SCLR and FoS demonstrates that while PF decreases with increasing FoS across all SCLR values, the effect is less pronounced at low SCLR due to the dominant influence of localized variability. Higher SCLR values enhance the effectiveness of FoS in reducing PF, reinforcing the importance of spatial correlation in design considerations.

Design formula and confidence intervals

MARS based design formula

Equation (17) presents design formula that integrates key parameters, such as FoS, COV, and SCLR and PF into a detailed framework for evaluating active earth pressures. The formula’s higher-order terms highlight the need to account for nonlinearities when analyzing spatially variable soils, as simplistic linear models may overlook the combined influence of these parameters. These detailed relationships allow for a systematic understanding of how variability and spatial correlations impact active earth pressures under different safety factor conditions.

By capturing the complexity of soil behavior, this formula provides engineers with a robust tool for probabilistic analysis. It highlights the necessity of computational tools to facilitate its application, ensuring the accurate assessment of failure probabilities and enabling optimized design solutions for retaining wall stability.

$$\begin{gathered} - 0.00307390374599276*Co{V^2}*Fo{S^5}+0.0233251259352408*Co{V^2}*Fo{S^4} - … \hfill \\ 0.0669313645778268*Co{V^2}*Fo{S^3}+0.0896896089370779*Co{V^2}*Fo{S^2} - … \hfill \\ 0.0551402339095862*Co{V^2}*FoS+0.0121628833841137*Co{V^2}+… \hfill \\ 0.00117632363446029*CoV*SCL{R^4} - 0.00300604833431339*CoV*SCL{R^3}+… \hfill \\ 5.73547700836679e - 5*CoV*SCL{R^2}*Fo{S^3}+0.0275378569955602*CoV*SCLR*Fo{S^5} - … \hfill \\ 0.21309472588499*CoV*SCLR*Fo{S^4}+0.628022646338683*CoV*SCLR*Fo{S^3} - … \hfill \\ 0.873011971052842*CoV*SCLR*Fo{S^2}+0.562079574127308*CoV*SCLR*FoS - … \hfill \\ 0.125902653850613*CoV*SCLR - 0.000829974636127525*CoV*Fo{S^5}+… \hfill \\ 0.00289629501966047*CoV*Fo{S^4} - 0.00528207076076614*CoV*Fo{S^2}+… \hfill \\ 4.75996575453427*Fo{S^5} - 36.373459953245*Fo{S^4}+… \hfill \\ 105.216179869232*Fo{S^3} - 141.916468133753*Fo{S^2}+… \hfill \\ 86.7619764651043*FoS - 17.9288699929336; \hfill \\ \end{gathered}$$

(17)

Confidence intervals as a key to reliable predictions

To test the confidence intervals, where input noise is limited to 5% in Fig. 23, the model demonstrates strong performance. The predicted mean values closely follow the true values for most sample indices. The confidence intervals, especially the 80% and 95% bands, stay relatively narrow, showing low uncertainty and high confidence in the model’s predictions. While small deviations appear at sharp peaks and troughs (around sample indices 11, 21, and 31), the overall alignment between predicted and true values confirms the model’s robustness under low-noise conditions.

Fig. 23

Predicted mean values with 80% and 95% confidence intervals compared to true values, illustrating model performance under 5% input noise.

In Fig. 24, with noise input increased to 10%, the model’s predictive accuracy declines, shown by more frequent and larger deviations from the true values. The uncertainty bands widen significantly compared to Fig. 23, especially around peaks and sharp transitions, such as near sample indices 11, 17, and 23. This widening of the confidence intervals reflects the model’s increased difficulty in maintaining reliable predictions as input variability rises. While the general trend is still captured, higher noise introduces noticeable discrepancies, particularly in areas with rapid changes. Figure 24 predicted mean values with 80% and 95% confidence intervals compared to true values, showing model performance under 10% input noise.

Fig. 24

Predicted mean values with 80% and 95% confidence intervals compared to true values, illustrating model performance under 10% input noise.

In summary, the comparison between the two figures highlights the sensitivity of the model to input noise. At 5%, the narrow confidence intervals and consistent predictions demonstrate the model’s ability to maintain accuracy and reliability under low-noise conditions. However, at 10% noise, the broader uncertainty bands and larger deviations emphasize the trade-off between input noise and prediction performance. The widening confidence intervals serve as a useful measure of prediction uncertainty, providing a clearer understanding of the model’s limitations and highlighting the need for careful consideration of noise effects in practical applications.

Conclusion

This study has presented a comprehensive probabilistic framework for evaluating active earth pressures in geotechnical systems with spatially variable soil properties. By integrating advanced computational methods, including Finite Element Limit Analysis (FELA) and Monte Carlo Simulations (MCS), with machine learning techniques, the research effectively addressed the complexities of soil behavior variability and uncertainty. The proposed approach captured the stochastic nature of soil properties and provided valuable tools and insights into failure mechanisms.

The contributions of this study are as follows: (i) Development of a probabilistic framework integrating FELA and MCS to evaluate active earth pressures under spatial variability; (ii) Application of MARS to improve prediction accuracy, computational efficiency, and interpretability in probabilistic analysis; (iii) Implementation of a two-phase optimization strategy combining Random Search and Adaptive Sampling to tune MARS hyperparameters; (iv) Introduction of confidence intervals to quantify prediction reliability and support decision-making under uncertainty; (v) Employment of sensitivity analysis tools, such as PDPs, to provide insights into the relationships between key parameters and failure mechanisms; (vi) Creation of probabilistic design charts that serve as practical tools for engineers to optimize safety margins and manage soil variability effectively.

Key findings highlight the crucial role of the Factor of Safety (FoS) in reducing the Probability of Failure (PF), with machine learning models consistently identifying FoS as the most influential parameter. The Coefficient of Variation (COV) is a significant driver of uncertainty, increasing variability in failure probabilities. In contrast, the Spatial Correlation Length Ratio (SCLR) acts as a moderate factor, influencing the spatial distribution of soil properties. Rather than acting as a dominant factor on its own, the influence of SCLR on PF is more subtle and indirect, primarily occurring through its interaction with COV and FoS. The machine learning framework demonstrates strong predictive performance, achieving near-perfect accuracy (R² close to 1) and low error metrics across both training and testing datasets. Feature importance analyses, supported by SHAP evaluations and Partial Dependence Plots (PDPs), confirm the robustness and interpretability of the predictions, while confidence intervals provide quantifiable measures of reliability.

From a practical standpoint, the study contributes to geotechnical design by introducing probabilistic design charts and uncertainty quantifications. These tools allow engineers to optimize safety margins, manage variability effectively, and overcome the limitations of deterministic approaches. By bridging the gap between theoretical probabilistic models and real-world applications, the research provides great insights to develop safer and more resilient infrastructure.

Looking forward, future research could extend this probabilistic framework to more complex soil conditions, such as stratified or anisotropic soils, where spatial variability exhibits directional dependence⁵². Further studies could also explore its applicability to unsaturated or multi-layered soils, enhancing the model’s real-world relevance. Additionally, integrating dynamic or cyclic loading conditions - particularly for seismic risk assessments - could improve the framework’s utility in earthquake-prone regions. To enhance computational efficiency, future work may leverage machine learning-based surrogate models to reduce the cost of large-scale Monte Carlo simulations while preserving accuracy. These advancements would further refine probabilistic geotechnical analysis, strengthening its role in optimizing engineering design under uncertainty.