Comparison of machine learning models for rock UCS prediction using measurement while drilling data

Abstract

Accurately determining the uniaxial compressive strength (UCS) of rocks is crucial for various rock engineering applications. However, traditional methods of obtaining UCS are often time-consuming, labor-intensive, and unsuitable for fractured rock sections. In recent years, using Measurement-while-drilling data to identify UCS has gained traction as an alternative approach. To develop a method that can rapidly, efficiently, and economically estimate UCS across different rock types and engineering conditions based on while-drilling tests, this study compiles a comprehensive dataset from existing literature. The dataset includes drilling parameters and their corresponding UCS values, collected under varying lithologies, strength levels, drill bit types, and drilling conditions. Five machine learning models—multilayer perceptron (MLP), support vector regression (SVR), convolutional neural networks (CNN), random trees (RT), and long short-term memory networks (LSTM)—were trained and evaluated. Among these, RT demonstrated superior predictive performance, achieving a root mean square error (RMSE) of 15.851, a mean absolute error (MAE) of 4.449, a standard deviation of residuals (SDR) of 15.292, and an R² value of 0.959 on the test set. SVR also performed well, with an RMSE of 21.905, an MAE of 17.962, an SDR of 21.144, and an R² value of 0.922. While CNN and LSTM exhibited slightly higher errors, they showed better generalization capabilities across validation and test datasets. Furthermore, the models were validated on an unseen independent dataset, where RT achieved the best results, followed by SVR, while the other methods performed relatively poorly. This study indicates that RT and SVR demonstrate superior suitability for UCS prediction.

Introduction

The accurate identification of UCS of rocks is of great significance in civil engineering. Precisely determining the UCS of rocks plays a crucial role in the stability assessment of slopes and underground caverns, mine excavation, and energy storage sectors^1,2,3,4. Currently, laboratory testing is the primary method for obtaining rock UCS, and many researchers have studied and determined UCS through laboratory experiments⁵. However, this method involves a series of complex processes, such as field drilling, core sampling, transportation, sample preparation, and testing, which are not only time-consuming and labor-intensive but also impose high demands on core quality, making it particularly challenging to obtain the strength parameters of fractured rock masses⁶. Since core drilling is an unavoidable step in engineering, if the drilling parameters of rotary drilling rigs can be used to rapidly assess UCS, it would not only enable the acquisition of UCS for in situ and fractured rock zones but also significantly reduce costs and enhance economic benefits.

Measurement While Drilling (MWD) technology is an innovative in situ testing method that involves installing multiple sensors on the drilling rig to record operational parameters in real time. This technology enables the monitoring of various operational parameters during drilling, providing a solid foundation for analyzing the interaction between the drill bit and the rock⁷. It offers notable advantages in terms of convenience, cost-effectiveness, and speed. By establishing a relationship model between rock strength parameters and drilling parameters based on MWD data, the strength parameters of rocks can be rapidly estimated during drilling⁸. This allows for the quick and accurate acquisition of in situ strength parameters, significantly improving data acquisition efficiency while reducing economic costs. MWD has thus emerged as a novel method for in situ identification of rock mechanical parameters.

Current methods for identifying the UCS of rocks based on MWD technology largely rely on theoretical models or empirical formulas. The development of theoretical models typically involves first analyzing the rock-breaking mechanism of the drill bit and proposing reasonable assumptions. Based on these assumptions and the rock-breaking characteristics of the drill bit, corresponding mechanical models are constructed for analysis. Finally, by combining the results of mechanical analysis with the distribution of drill teeth, a relationship model is established between rock strength parameters and drilling speed, rotational speed, thrust force, torque, and drill bit geometry. Researchers such as Cheng⁹, Gao¹⁰, and Detourunay¹¹ have developed related models based on theoretical analysis. However, due to the significant differences in rock-breaking mechanisms between different types of drills and drill bits, creating a unified model is challenging. Consequently, scholars usually build models based on specific types of drill bits. Moreover, theoretical models often include empirical coefficients, which limit their applicability in practice.

In contrast, empirical formulas are mainly established through statistical methods such as regression fitting. For example, Mostofi et al.¹², based on the drilling speed prediction formula proposed by Warren¹³, developed an empirical model that correlates MWD parameters with UCS for rotary drilling rigs. Wang et al.¹⁴constructed a relationship model between drilling speed and UCS using statistical regression methods by monitoring the drilling parameters of rotary core drills. Feng et al.¹⁵ discovered during field monitoring that for rocks of the same strength, the ratio of drilling speed to thrust in rotary drilling rigs remains constant, and this ratio can be used to characterize the UCS of rocks. Cheng et al.,¹⁶ using the energy principle, derived a new specific energy index that accounts for abrasion dissipation energy and developed a model for the identification of UCS during drilling. However, empirical formulas are limited by specific engineering experience and expertise, and they are applicable to specific rock types and engineering conditions, with poor applicability in complex formations. Additionally, statistical methods require large datasets and impose high demands on data quality and distribution, leading to limitations and uncertainties in practical applications.

In recent years, the rapid advancement of computer science has accelerated the widespread application of artificial intelligence (AI) technologies, and the field of geotechnical engineering is no exception. Machine learning, as a crucial component of AI, is a powerful tool dedicated to developing systems that can learn from data and continuously improve performance. Its core objective is to create intelligent algorithms that enable computers to autonomously learn from experience and enhance their predictive or decision-making capabilities when confronted with new data. Unlike traditional programming, machine learning does not rely on explicit programming instructions; rather, it predicts or makes decisions by identifying patterns within the data. In the field of MWD identification, machine learning techniques have been widely applied to solve complex geotechnical engineering problems. For instance, Labelle et al.¹⁷ employed a multilayer feedforward neural network to identify rock layer categories using laboratory MWD data, achieving an accuracy of 95.5%. Ameur-Zaimeche et al.¹⁸ used MWD data from oil and gas drilling to predict rock porosity through methods such as multilayer perceptron (MLP), extreme learning machine (ELM), generalized regression network (GRNN), and support vector regression (SVR), with ELM yielding the best results. Kadkhodaie-Ilkhchi et al.¹⁹ applied fuzzy logic (FL), while Klyuchnikov et al.²⁰ and Romanenkova et al.²¹ employed ensemble optimal decision trees (EODT). Fang Yuwei et al.²² used the backpropagation algorithm (BP) to conduct machine learning studies based on a large amount of noisy MWD data, successfully identifying lithology. These studies highlight the immense potential and wide-ranging applications of machine learning in geotechnical engineering.

In the context of UCS identification using MWD data, Wang Qi et al.²³ utilized laboratory MWD data and applied support vector machines (SVM) to establish a relationship model between the drilling parameters of polycrystalline diamond compact (PDC) bits and the UCS of rocks, achieving a goodness of fit as high as 0.977. He et al.²⁴ employed a convolutional neural network (CNN) to predict the uniaxial compressive strength (UCS) of a slope using drilling data, achieving a prediction error of less than 10%. Zhao et al.²⁵ employed a deep feedforward neural network to predict the UCS using while-drilling test data from the Xiangjiawan Tunnel, achieving an R² value of 0.6616. Davoodi et al.²⁶ utilized various machine learning models, including the MELM-COA algorithm, to predict the UCS using drilling and petrophysical data from the Rag-e-Safid oil field, achieving a root mean squared error (RMSE) of 4.6945 MPa and a R² of 0.9873. Hany et al.²⁷applied artificial intelligence (AI) techniques, including random forest (RF) based on principal component analysis (PCA) and functional network (FN), to predict UCS in real-time using drilling parameters. The PCA-based RF model achieved a R² of 0.99 and an average absolute percentage error (AAPE) of 4.3%, outperforming the FN model, which attained an R² of 0.97 and an AAPE of 8.5%. However, current machine learning studies are predominantly based on digital drilling results under specific conditions, and their general applicability remains to be validated. Additionally, the predictive performance of different machine learning methods for this problem still requires further evaluation.

Therefore, to address the challenge of accurately, efficiently, and economically identifying UCS without dependence on practical engineering experience or expertise, and to ensure adaptability across diverse rock types and engineering conditions, this study collects extensive MWD data from rotary drilling rigs. The data is preprocessed to create a comprehensive dataset, which is then used to train and evaluate the performance of various machine learning algorithms, including classical models such as MLP, SVR, convolutional neural networks (CNN), decision trees, and long short-term memory (LSTM) networks. This study primarily aims to explore the applicability and robustness of classical machine learning models in predicting UCS under varying lithological conditions, strength levels, geological backgrounds, and drilling parameters. By systematically assessing the feasibility and effectiveness of these algorithms, this study seeks to provide a scientific foundation for practical engineering applications and to highlight the comparative advantages and limitations of different approaches in addressing the complexities of UCS prediction.

Dataset establishment and preprocessing

Dataset source

Accurate, detailed, and precise data are crucial for model training and performance evaluation. Several scholars have developed high-precision MWD platforms that can accurately control drilling parameters during rock drilling, thereby providing robust support for building reliable models. In this study, the collected and organized data established a dataset that forms a solid foundation for model construction and objective, accurate performance evaluation of different models. A total of 197 experimental data sets were collected, covering rock samples including granite, limestone, sandstone, coal, mudstone, and concrete mortar. The drilling parameters include thrust force, torque, drilling speed, and rotational speed, while the strength parameter is the UCS of the rocks (see Table 1). The typical variation of certain drilling parameters is depicted in Fig. 1, while the statistical analysis results of the dataset are provided in Table 2. Additionally, the dataset partitioning and training process are illustrated in Fig. 2, and the grid search method was employed for hyperparameter tuning.

Among these data, 54 sets were derived from Liang et al.²⁸, with rock samples of intact sandstone, granite, and limestone, having a UCS range of 22.34–46.01 MPa. Another 22 sets of data were sourced from Sun et al.,²⁹ involving different grades of cast concrete mortar, including M5, M7.5, M10, M15, M20, M25, and M30, with a UCS range of 2.20–20.80 MPa. Wang et al.³⁰ contributed 7 data sets, where rock samples included granite layers, limestone layers, siltstone layers, intact sandstone layers, fractured sandstone layers, and grouted sandstone layers, with UCS ranging from 9.4 to 81.9 MPa. Gao et al.³¹provided 36 data sets, involving cast concrete mortar of different grades (M5, M7.5, M10, M15, M20, M25, M30) and sandstone, with a UCS range of 1.90–61.91 MPa. Niu et al.³² provided 32 data sets, covering sandstone, mudstone, coal, and sandy mudstone, with UCS ranging from 5.13 to 57.61 MPa. Additionally, He et al.³³contributed 17 data sets, with UCS ranging from 1.98 to 116.09 MPa. Finally, Jiang et al.³⁴provided 30 data sets, involving cement mortar of various grades (M5, M10, M15, M20), with UCS ranging from 1.90 to 61.91 MPa.

Table 1 Major parameters.

Table 2 Data set sample parameter statistics.

Fig. 1

Typical variation of some drilling parameters.

Fig. 2

Workflow.

Standardization

In the actual drilling process, the collected drilling parameters, such as drilling speed, thrust force, impact energy, rotational speed, and torque, may vary significantly in magnitude due to their different dimensional units. In machine learning training, it is often assumed that all parameters have the same order of variance. If one parameter’s magnitude is much larger than others, its weight during the learning process will be disproportionately increased, leading to biased results. To mitigate the discrepancy in weights caused by differences in magnitude and to balance the contribution of each parameter in the model, these parameters must undergo standardization. The goal of standardization is to convert parameters with different dimensions into a common scale, ensuring they have similar variance in model training and preventing certain parameters with larger magnitudes from dominating the learning process. Therefore, the Min-Max normalization method is applied to scale the various parameters into the [0, 1] range. The specific formula for this normalization is shown in Eq. 1.

$$\:\begin{array}{c}{X}_{m}=\frac{{x}_{i}-{x}_{min}}{{x}_{max}-{x}_{min}}\:\end{array}$$

(1)

Where, $\:{X}_{m}$represents the normalized value, $\:{x}_{i}$ refers to the value of the i-th parameter, $\:{x}_{max}$ denotes the maximum value of the parameter, and $\:{x}_{min}$ represents the minimum value of the parameter.

Method

Multilayer perceptron

The Multilayer Perceptron is a typical and widely used feedforward artificial neural network, often applied to handle complex nonlinear problems³⁵. MLP consists of at least three layers of neurons: the input layer, hidden layers, and the output layer. It is an extension of the single-layer perceptron, and due to the presence of multiple hidden layers, it is referred to as a “multilayer perceptron.” Its structure is shown in Fig. 3. Each layer of neurons is fully connected to the neurons in the preceding and subsequent layers and undergoes transformation via a nonlinear activation function, enabling the model to address complex nonlinear issues. MLP computes outputs through forward propagation and adjusts weights and biases using the backpropagation algorithm, minimizing the loss function to optimize the model. Due to its strong nonlinear mapping capabilities, MLP is well-suited for predicting and identifying rock UCS based on MWD data. The calculation process is shown below.

The forward propagation process is as follows:

Output from input layer to hidden layer:

$$\:\begin{array}{c}{z}^{\left(1\right)}={W}^{\left(1\right)}x+{b}^{\left(1\right)}\:\end{array}$$

(2)

Where $\:x$ is the input vector, $\:{W}^{\left(1\right)}$ is the weight matrix between the input layer and the first hidden layer, $\:{b}^{\left(1\right)}$ is the bias vector of the hidden layer, and $\:{z}^{\left(1\right)}$ is the linear combination output of the first hidden layer.

Through activation function:

$$\:\begin{array}{c}{a}^{\left(1\right)}=\sigma\:\left({z}^{\left(1\right)}\right)\:\end{array}$$

(3)

Where $\:\sigma\:,{a}^{\left(1\right)}$ is the activation output of the first hidden layer.

Hidden layer to output layer calculation:

$$\:\begin{array}{c}{z}^{\left(2\right)}={W}^{\left(2\right)}{a}^{\left(1\right)}+{b}^{\left(2\right)}\:\end{array}$$

(4)

$$\:\begin{array}{c}{a}^{\left(2\right)}=\sigma\:\left({z}^{\left(2\right)}\right)\:\end{array}$$

(5)

The final output layer result:

$$\:\begin{array}{c}\widehat{y}={W}^{\left(L\right)}{a}^{\left(L-1\right)}+{b}^{\left(L\right)}\end{array}$$

(6)

Where $\:\widehat{y}$ is the output prediction result, L is the total number of layers, $\:{W}^{\left(L\right)}$and $\:{b}^{\left(L\right)}$ are the weight and bias of the last layer, respectively.

The backward propagation process is as follows:

The gradients are calculated through backpropagation, and the weights and biases are updated using the gradient descent method. The update formulas for the weights and biases for each layer are as follows:

$$\:\begin{array}{c}{W}^{\left(l\right)}={W}^{\left(l\right)}-\alpha\:\frac{\partial\:\varPhi\:}{\partial\:{W}^{\left(l\right)}}\:\end{array}$$

(7)

$$\:\begin{array}{c}{b}^{\left(l\right)}={b}^{\left(l\right)}-\alpha\:\frac{\partial\:\varPhi\:}{\partial\:{b}^{\left(l\right)}}\:\end{array}$$

(8)

Where $\:\alpha\:$ is the learning rate, $\:l$ represents layer $\:l$, and $\:\frac{\partial\:\varPhi\:}{\partial\:{W}^{\left(l\right)}}$ is the gradient of the loss function to the weight.

The loss function is the mean square error (MSE):

$$\:\begin{array}{c}\varPhi\:=\frac{1}{n}\sum\:_{i=1}^{n}{\left({y}_{i}-\widehat{{y}_{i}}\right)}^{2}\:\end{array}$$

(9)

Where, $\:{y}_{i}$ is the actual value, $\:\widehat{{y}_{i}}$ is the predicted value, and n is the total number of samples.

Fig. 3

MLP structure.

Support vector regression

Support Vector Regression is an extension of the classic supervised learning algorithm¹⁸, Support Vector Machine, and is primarily used for regression tasks. It is based on a solid mathematical foundation, with a schematic diagram shown in Fig. 4. The goal of SVR is to ensure that the deviation between the predicted values and the actual values does not exceed a given threshold while keeping the model complexity as low as possible. SVR maximizes the margin between the regression line and the data points, allowing for a certain range of error to achieve better generalization performance.

For a given training dataset $\:\left\{\left({x}_{1},{y}_{1}\right)\left({x}_{2},{y}_{2}\right)\dots\:({x}_{i},{y}_{i})({x}_{n},{y}_{n})\right\}$, where $\:{x}_{i}$ represents the input features and $\:{y}_{i}$ represents the actual values, SVR seeks a regression function of the form: $\:f\left(x\right)={w}^{T}x+b$, where is the weight vector and b is the bias, the objective is to minimize the norm of the weight vector while ensuring that the error between the predicted and actual values does not exceed a margin ϵ. This can be formulated as the following optimization problem:

$$\:\begin{array}{c}{\text{m}\text{i}\text{n}}_{w,b}\frac{1}{2} \left\| w \right\|^{2} \end{array}$$

(10)

The constraint is that the difference between the predicted value and the actual value within the ε range will not incur a penalty, expressed as:

$$\:\begin{array}{c}\left|{y}_{i}-({w}^{T}{x}_{i}+b)\right|\le\:\epsilon\end{array}$$

(11)

SVR allows a certain degree of flexibility, meaning it tolerates some data points exceeding the ε-tube. To account for this, SVR introduces slack variables $\:{\xi\:}_{i}$ and $\:{\xi\:}_{i}^{\text{*}}$, which represent the deviations of the predicted values exceeding the upper and lower limits of ε, respectively. The optimization problem is then formulated as:

$$\:\begin{array}{c}{\text{m}\text{i}\text{n}}_{w,b{\xi\:}_{i},{\xi\:}_{i}^{*}}\frac{1}{2} \left\| w \right\|^{2} +C\sum\:_{i=1}^{n}{(\xi\:}_{i}+{\xi\:}_{i}^{*})\end{array}$$

(12)

The constraint conditions are:

$$\:\begin{array}{c}{y}_{i}-\left({w}^{T}{x}_{i}+b\right)\le\:\epsilon+{\xi\:}_{i}\:\end{array}$$

(13)

$$\:\begin{array}{c}\left({w}^{T}{x}_{i}+b\right)-{y}_{i}\le\:\epsilon+{\xi\:}_{i}^{*}\:\end{array}$$

(14)

$$\:\begin{array}{c}{\xi\:}_{i},{\xi\:}_{i}^{*}\ge\:0\:\end{array}$$

(15)

Where C is the penalty coefficient, which controls the tolerance of the model to error.

SVR can also employ kernel functions (such as linear kernels, radial basis functions, or polynomial kernels) to map input data into a high-dimensional space, allowing for the handling of nonlinear regression problems. By introducing the kernel function $\:K({x}_{i},{x}_{j})$, the regression function can be expressed as:

$$\:\begin{array}{c}f\left(x\right)=\sum\:_{i=1}^{n}{(\alpha\:}_{i}+{\alpha\:}_{i}^{*})\:K\left({x}_{i},{x}_{j}\right)+b\end{array}$$

(16)

Where $\:{\alpha\:}_{i}$ and $\:{\alpha\:}_{i}^{\text{*}}$ are Lagrange multipliers, and the kernel function $\:K\left({x}_{i},{x}_{j}\right)$ is used to calculate the similarity between samples.

The loss function used is the epsilon-insensitive loss function, which means that no loss is calculated for data points with errors smaller than ϵ, while the loss for the portion exceeding ϵ is calculated according to Eq. (17). The advantage of this loss function is that it ensures small deviations do not affect the model, while the slack variables handle the errors that exceed the ϵ range.

$$\:\begin{array}{c}\varPhi\:(y,f\left(x\right))=max(0,\left|y-f\left(x\right)\right|-\epsilon)\end{array}$$

(17)

Since SVR is a powerful regression model capable of handling complex regression tasks while maintaining model simplicity, it is well-suited for predicting UCS of rocks based on MWD data.

Fig. 4

SVR structure.

Convolutional neural networks

Convolutional Neural Network is a specialized deep learning model²⁴. Compared to traditional fully connected neural networks, CNN reduces the number of parameters through local connections and weight sharing, making it more effective at capturing spatial or temporal features in data. As shown in Fig. 5, its structure is composed of a convolutional layer, an activation function, a pooling layer, and a fully connected layer.

The convolutional layer is the most critical component, responsible for extracting local features from the input data. It performs a sliding window operation on the input data using a convolutional filter (also referred to as a filter or kernel) to compute the features of local regions. The calculation formula is as follows:

$$\:\begin{array}{c}{h}_{i,j}={\left(W*X\right)}_{i,j}+b=\sum\:_{m}\sum\:_{n}{W}_{m,n}{X}_{i+m,j+n}+b\end{array}$$

(18)

Where $\:{h}_{i,j}$ is the output value at position (i, j), $\:X$ is the input matrix, $\:W$ is the convolution kernel matrix, b is the bias, m is the row index of the convolution kernel, n is the column index of the convolution kernel, and * represents the convolution operation.

The activation function and fully connected layer are consistent with those in the MLP, as shown in Eqs. (3), (1,2), and (5), and will not be elaborated further here. The pooling layer is used to perform dimensionality reduction on the features, reducing both the data volume and computational complexity while retaining important features. The most common pooling operations are Max Pooling and Average Pooling. In this case, Max Pooling is chosen, as shown in the following equation:

$$\:\begin{array}{c}{h}_{i,j}^{pool}=max{X}_{i+m,j+n}\end{array}$$

(19)

CNN is among the most influential models in the field of deep learning. Through the combination of convolutional, activation, pooling, and fully connected layers, CNN can extract both local and global features of the input data layer by layer, ultimately achieving accurate regression tasks.

Fig. 5

CNN structure.

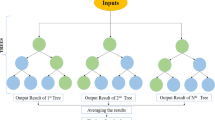
Random forest

Random Forest is an ensemble learning algorithm widely used for regression tasks³⁶. It improves model accuracy and stability by constructing multiple decision trees and integrating their results. Random Forest generates individual trees by randomly selecting samples and features, which reduces the risk of overfitting and enhances the model’s generalization ability.

As an ensemble model based on decision trees, Random Forest consists of many weak learners (individual decision trees). Each decision tree makes predictions on the input data, and the final prediction for regression tasks is obtained by averaging these predictions. A technique known as Bootstrap Sampling is employed when constructing the Random Forest. For each decision tree, a subset of the original training data is randomly sampled with replacement for training. As a result, some data points may be used multiple times, while others may be excluded. This sampling method increases the diversity of the model.

Additionally, when splitting nodes during the construction of each decision tree, not all features are considered. Instead, a random subset of features is chosen for each split. This strategy further increases the diversity among decision trees, making the model more robust and preventing any individual feature from having an excessive influence on the overall model.

The construction of a Random Forest, as illustrated in Fig. 6, can be divided into the following steps:

• 1. From the training set, randomly select n samples using Bootstrap sampling to construct multiple different training sets. Each training set is used to train a separate decision tree.

• 2. At each node of the decision tree, a random subset of features is selected, and the best feature from this subset is used to split the node.

• 3. Each decision tree is trained independently until it reaches the maximum depth or meets other stopping criteria.

• 4. For regression tasks, during prediction, the final prediction result is the average of the outputs from all decision trees, as shown in Eq. (20).

$$\:\begin{array}{c}\widehat{y}=\frac{1}{B}\sum\:_{b=1}^{B}\widehat{y}b\:\end{array}$$

(20)

Where $\:\widehat{y}$ is the final predicted value, B is the total number of trees in the ensemble, $\:\widehat{y}b$ represents the prediction made by the b-th tree, and $\:\sum\:_{b=1}^{B}\widehat{y}b$ denotes the summation of predictions from all trees, while $\:\frac{1}{B}$ represents the averaging operation across all trees.

Fig. 6

Random forest structure.

LSTM

Long Short-Term Memory is a specialized type of Recurrent Neural Network (RNN)³⁷, and its structure is shown in Fig. 7. Compared to traditional RNNs, LSTM is more complex, as it introduces three gates: the input gate, the forget gate, and the output gate, along with a cell state, which controls the flow and updating of information.

The input gate determines how the new information at the current time step updates the cell state. The forget gate decides which information from the previous cell state should be discarded. The cell state is then updated by combining the outputs of the forget and input gates. The output gate determines the hidden state and output of the current time step based on the updated cell state.

Through these mechanisms, LSTM effectively manages which information to retain and which to discard, ensuring that the network can remember long-term dependencies.

$$\:\text{I}\text{n}\text{p}\text{u}\text{t}\text{s}\:{Z}_{t}=\text{tanh}\left({W}_{z}\left[{h}_{t-1},{x}_{t}\right]+{b}_{z}\right)\:\:\:\:$$

(21)

$${\text{Input gates}} \:{i}_{t}={\upsigma\:}\left({W}_{i}\left[{h}_{t-1},{x}_{t}\right]+{b}_{i}\:\right)\:\:\:\:$$

(22)

$$\:\text{F}\text{o}\text{r}\text{g}\text{e}\text{t}\:\text{g}\text{a}\text{t}\text{e}\text{s}\:\:{f}_{t}={\upsigma\:}\left({W}_{f}\left[{h}_{t-1},{x}_{t}\right]+{b}_{f}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(23)

$$\:\text{C}\text{e}\text{l}\text{l}\:\text{s}\text{t}\text{a}\text{t}\text{e}\:\:{C}_{t}={f}_{t}\cdot\:{C}_{t-1}+{i}_{t}\cdot\:{Z}_{t}\:\:\:\:\:\:\:\:\:\:\:\:$$

(24)

$$\:\text{O}\text{u}\text{t}\text{p}\text{u}\text{t}\:\text{g}\text{a}\text{t}\text{e}\text{s}\:{O}_{t}={\upsigma\:}\left({W}_{o}\left[{h}_{t-1},{x}_{t}\right]+{b}_{o\:}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(25)

$$\:\text{O}\text{u}\text{t}\text{p}\text{u}\text{t}\text{s}\:{h}_{t}={O}_{t}\cdot\:\text{t}\text{a}\text{n}\text{h}\:\cdot\:{C}_{t}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(26)

Where $\:{Z}_{t}$ represents the candidate cell state, $\:{W}_{z}$ is the weight matrix associated with it, $\:{b}_{z}$ is the bias term, and $\:\text{t}\text{a}\text{n}\text{h}$ denotes the hyperbolic tangent activation function. $\:{i}_{t}$ is the input gate, controlled by the weight matrix $\:{W}_{i}$ and bias $\:{b}_{i}$, with $\:{\upsigma\:}$ representing the sigmoid activation function. $\:{f}_{t}$ is the forget gate, regulated by $\:{W}_{f}$ and $\:{b}_{f}$, also using the sigmoid function. $\:{C}_{t}$ is the current cell state, updated based on the previous cell state $\:{C}_{t-1}$, the forget gate $\:{f}_{t}$, the input gate $\:{i}_{t}$, and the candidate cell state $\:{Z}_{t}$. $\:{O}_{t}$ is the output gate, determined by $\:{W}_{o}$ and $\:{b}_{o\:}$ using a sigmoid activation. Finally, $\:{h}_{t}$ is the hidden state output, obtained by applying the output gate $\:{O}_{t}$ to the hyperbolic tangent of the cell state $\:{C}_{t}$.

Fig. 7

LSTM structure.

Evaluation metrics

Selecting appropriate evaluation metrics is crucial for model training and performance assessment. In this study, Root Mean Square Error (RMSE), Coefficient of Determination (R²), Mean Absolute Error (MAE) and the Standard Deviation of Residuals (SDR) are used as combined evaluation metrics to measure model performance from multiple perspectives, allowing for a more comprehensive and in-depth evaluation of the model’s capabilities.

RMSE is a metric that measures the difference between the predicted and actual values. By taking the square root of the mean of squared errors, RMSE effectively reflects the overall magnitude of errors, and it is particularly sensitive to larger errors. A smaller RMSE indicates better predictive performance of the model. The calculation formula is provided in Eq. (27):

$$\:\begin{array}{c}RMSE=\sqrt{\frac{1}{n}\sum\:_{i=1}^{n}{\left({y}_{i}-\widehat{{y}_{i}}\right)}^{2}}\:\end{array}$$

(27)

Where n is the number of samples; $\:{y}_{i}$ is the actual value; $\:\widehat{{y}_{i}}$ is the predicted value.

R², also known as the coefficient of determination, is a metric used to evaluate the goodness of fit of a model. It measures the explanatory power of the independent variables in relation to the dependent variable’s variation. The value of R² ranges from 0 to 1, with values closer to 1 indicating better model fit and higher explanatory power of the independent variables over the dependent variable. If R² equals 0, it signifies that the model has no explanatory power. The calculation formula is provided in Eq. (28):

$$\:\begin{array}{c}{R}^{2}=1-\frac{\sum\:_{i=1}^{n}{\left({y}_{i}-\widehat{{y}_{i}}\right)}^{2}}{\sum\:_{i=1}^{n}{\left({y}_{i}-\stackrel{-}{y}\right)}^{2}}\:\end{array}$$

(28)

Where n is the number of samples, $\:{y}_{i}$ is the actual value, $\:\widehat{{y}_{i}}$ is the predicted value, $\:\stackrel{-}{y}$ is the mean value of the actual value.

MAE is another metric for measuring the difference between predicted and actual values. Unlike RMSE, MAE directly takes the absolute value of the errors, making it less sensitive to large errors. A smaller MAE indicates better predictive performance of the model. The calculation formula is provided in Eq. (29):

$$\:\begin{array}{c}MAE=\frac{1}{n}\sum\:_{i=1}^{n}\left|{y}_{i}-\widehat{{y}_{i}}\right|\end{array}$$

(29)

Where n is the number of samples, $\:{y}_{i}$ is the actual value; $\:\widehat{{y}_{i}}$ is the predicted value.

SDR is a metric used to assess the variability of the errors between predicted and actual values. It quantifies the spread of residuals around their mean and provides insight into the consistency of the model’s predictions. Residual Error (RE) is calculated according to Eq. (30). A smaller standard deviation of residuals indicates better predictive performance of the model. The calculation formula is provided in Eq. (31):

$$\:\begin{array}{c}RE={y}_{i}-\widehat{{y}_{i}}\end{array}$$

(30)

$$\:\begin{array}{c}{\sigma\:}_{RE}=\sqrt{\frac{1}{n-1}\sum\:_{i=1}^{n}{({RE}_{i}-\stackrel{-}{RE})}^{2}}\end{array}$$

(31)

Where n is the number of samples, $\:{RE}_{i}$ is the residual error for the i-th sample, $\:\stackrel{-}{RE}$ is the mean of the residuals.

Evaluation

The dataset was divided into training, validation, and test sets in proportions of 70%, 15%, and 15%, resulting in 137 groups for the training set, 30 groups for the validation set, and 30 groups for the test set, as illustrated in Fig. 8. Subsequently, the MLP, SVR, CNN, DT, and LSTM models were trained, and, as mentioned earlier, the grid search method was utilized for hyperparameter tuning to improve model performance. The tuning process was guided by R² as the optimization criterion, while the model predictions were comprehensively evaluated using RMSE, R², MAE and SDR metrics. The specific results are presented in Table 3, and the comparison of predicted and actual values for both the training and test sets is shown in Figs. 9, 10, 11, 12 and 13.

Fig. 8

Distribution of dataset.

Table 3 Results of training set and test set.

Fig. 9

Comparison of Predicted and Actual Values in Training, Validation, and Test Sets for MLP.

Fig. 10

Comparison of Predicted and Actual Values in Training, Validation, and Test Sets for SVR.

Fig. 11

Comparison of Predicted and Actual Values in Training, Validation, and Test Sets for CNN.

Fig. 12

Comparison of Predicted and Actual Values in Training, Validation, and Test Sets for RT.

Fig. 13

Comparison of Predicted and Actual Values in Training, Validation, and Test Sets for LSTM.

As shown in Table 3; Figs. 9, 10, 11, 12 and 13, for the training set, the MLP model has an RMSE of 24.869, R² of 0.869, MAE of 18.372 and SDR of 24.821, demonstrating relatively high accuracy. However, compared to the other models, its errors are slightly higher. The SVR model performed exceptionally well on the training set, with an RMSE of 19.776, R² as high as 0.917, MAE of 16.480, and SDR of 19.007 indicating strong performance. CNN’s RMSE was 24.583, R² was 0.872, MAE was 18.048, and SDR of 23.655 outperforming MLP but slightly lagging behind SVR. The RT model exhibited an outstanding performance on the training set, with an RMSE of 0.301, R² of 1.000, MAE of 0.036, and SDR of 0.301 indicating that the model perfectly fits the training data but might be at risk of overfitting. LSTM had the highest error on the training set, with an RMSE of 26.488, R² of 0.852, MAE of 19.757, and SDR of 26.25 showing the weakest performance.

For the test set, MLP’s RMSE increased significantly to 30.946, R² decreased to 0.844, MAE rose to 23.887, and SDR rose to 30.941 suggesting limited generalization ability. SVR performed well on the test set, with an RMSE of 21.905, R² of 0.922, MAE of 17.962, and SDR of 21.144, demonstrating strong generalization capability and stability. CNN had an RMSE of 32.899, R² of 0.832, MAE of 24.066, and SDR of 29.595 showing relatively weak generalization ability, although slightly better than MLP. RT’s test set RMSE was 15.851, R² was 0.959, MAE was 4.449, and SDR of 15.292, indicating that despite potential overfitting in the training set, the model still performed well on the test set. LSTM, on the other hand, had the worst performance on the test set, with an RMSE of 34.155, R² of 0.810, MAE of 26.622, and SDR of 33.671, highlighting poor generalization ability.

Overall, the RT model perfectly fit the training data and still performed well on the test set, making it a top choice, though it may require fine-tuning in practical applications to avoid overfitting. SVR demonstrated stable performance on both the training and test sets, with good generalization ability, making it a strong candidate. CNN and MLP showed similar performance, both suffering from weaker generalization, with higher errors on the test set. LSTM exhibited the highest errors on both the training and test sets, particularly in terms of generalization, making it the least suitable model for this task. In conclusion, for predicting UCS based on MWD data, SVR and RT outperformed the other models in balancing fitting ability and generalization.

Prediction

To further explore the generalization capability of the model, specifically its performance on unseen datasets, an independent dataset was constructed based on the data presented in Cheng et al.‘s study¹⁶. This dataset comprises 18 contributed data entries, including rock samples of sandstone, granite, and limestone, with UCS values ranging from 45.96 MPa to 241.07 MPa. The trained models, including MLP, SVR, CNN, RT, and LSTM, were applied to predict the target values for this dataset. Their performance was evaluated using the metrics outlined in Sect. 3.6. The results are presented in Table 4; Fig. 14.

Fig. 14

Comparison of Predicted and Actual Values in independent dataset for all models.

Table 4 Results of prediction.

As evidenced by the results in Table 4; Fig. 14, the RT method demonstrates the best performance among all approaches, achieving the highest R² value of 0.887. Additionally, it exhibits the lowest error metrics, with an RMSE of 24.716, MAE of 20.105, and SDR of 24.659, indicating its superior predictive capability. The second-best performer is the SVR method, which achieves an R² value of 0.823. Although slightly lower than that of RT, it still demonstrates strong predictive performance with an RMSE of 33.748, MAE of 26.669, and SDR of 32.856.

In contrast, the remaining three methods exhibit relatively poorer performance. Among them, CNN achieves an R² value of 0.693, which is slightly higher than those of MLP and LSTM. However, its RMSE (43.503), MAE (38.422), and SDR (41.953) are considerably higher than those of RT and SVR, reflecting its limitations in predictive accuracy. The MLP method records an R² value of only 0.574, while LSTM performs marginally better with an R² value of 0.596. Both methods show significantly higher error metrics, including RMSE, MAE, and SDR, compared to RT and SVR. Overall, RT and SVR exhibit superior performance, while CNN outperforms MLP and LSTM but remains suboptimal.

Additionally, it is noteworthy that the predictive performance of all models significantly declines when applied to the independent dataset compared to their performance on the training, validation, and test datasets. However, the ranking of their performance on the independent dataset aligns closely with their rankings on the training, validation, and test datasets. RT and SVR consistently demonstrate the best results across all datasets, further affirming their robustness and generalization capability.

Discussion

In recent years, many scholars have employed fitting methods to establish models relating drilling parameters to UCS for predictive purposes. This approach offers convenience and speed, and under specific drilling rig and bit conditions, it can achieve a high level of accuracy within a certain area. However, to explore whether it is feasible to develop a more broadly applicable empirical model with fewer constraints under varying drilling rigs, different rock types, and diverse drilling conditions, this section discusses the issue from the perspective of correlation analysis. Using Kendall’s correlation analysis, experimental data from multiple researchers were evaluated, with the results presented in a heatmap, as shown in Fig. 15. In the heatmap, values close to 1 indicate a strong positive correlation, values near − 1 represent a strong negative correlation, and values around 0 suggest no significant correlation between the variables.

The analysis shows that the correlation coefficient between drilling speed and UCS is -0.36, indicating a moderate negative correlation, meaning that as drilling speed increases, UCS tends to decrease, which is consistent with previous studies. The correlation coefficient between rotation speed and UCS is 0.35, indicating a moderate positive correlation, suggesting that higher rotation speeds may be associated with higher UCS. The correlation coefficient between thrust and UCS is 0.27, suggesting that greater thrust corresponds to higher UCS. This can be interpreted as the need to apply greater thrust when drilling into harder rocks to penetrate the surface, implying a certain positive correlation between thrust and UCS, although the correlation is not strong. The correlation coefficient between torque and UCS is only − 0.07, suggesting no significant relationship between the two. The size of the torque may be more influenced by factors such as the type of drilling equipment or the geometry of the drill bit, rather than the compressive strength of the rock.

In summary, it is difficult to identify a single drilling parameter that has a strong correlation with UCS, indicating that constructing a broadly applicable empirical model through simple fitting methods presents significant challenges. Therefore, machine learning-based intelligent recognition methods may be more effective in establishing widely applicable models, further highlighting the potential advantages and importance of machine learning in UCS prediction during drilling.

Fig. 15

Heatmap of Kendall correlation.

Conclusions

The study successfully constructed a dataset suitable for machine learning model training by collecting a large amount of while-drilling test data from rotary drilling machines and systematically preprocessing the data. Subsequently, five models—MLP, SVR, CNN, RT, and LSTM—were trained and tested on the dataset. The models’ performance was evaluated using three metrics: RMSE, R², and MAE. Additionally, the models were further validated on an unseen independent dataset to evaluate their generalization capability. These analyses provided valuable insights, leading to the following conclusions:

• 1. SVR and RT models demonstrated strong generalization capabilities. Although the RT model showed a tendency to overfit on the training set (with an R² of 1.000 and an RMSE of only 0.301), it still performed exceptionally well on the test set, with an RMSE of 15.851, MAE of 4.449, SDR of 15.292, and R² of 0.959, indicating robust predictive ability in practical applications. The SVR model exhibited balanced performance on both the training and test sets, achieving an RMSE of 21.905, MAE of 17.962, SDR of 21.144, and an R² of 0.922 on the test set, demonstrating good adaptability and stability.

• 2. In contrast, MLP and CNN showed relatively weaker generalization ability. MLP’s RMSE increased from 24.869 on the training set to 30.946 on the test set, with the R² dropping to 0.844, indicating significant errors when handling unseen data. Similarly, CNN performed adequately on the training set (with an RMSE of 24.583 and R² of 0.872), but its test set error increased substantially, with an RMSE of 32.899, MAE of 24.066, SDR of 29.595, and R² dropping to 0.832, suggesting that its predictive performance on complex tasks was inferior to SVR and DT.

• 3. The LSTM model performed the worst. Its RMSE on the training set was 26.488, and this further increased to 34.155 on the test set, with an MAE of 26.622, SDR of 33.671 and R² of only 0.810. The LSTM model exhibited poor generalization ability in this study, with significantly higher prediction errors compared to other models, indicating limited effectiveness in this task and difficulty in providing accurate predictions in practical engineering applications.

• 4. The models were further evaluated on an unseen independent dataset to assess their generalization capability. Consistent with the findings from the training and test sets, the RT method demonstrated the best performance, followed by the SVR method.

• 5. The primary limitation of this study lies in the dataset. Due to the relatively small sample size, the generalizability of the findings may be restricted. Future work will focus on expanding the dataset through additional sample collection. Additionally, the absence of independent dataset validation is a limitation. In subsequent studies, the proposed models will be applied to engineering practices to further verify their reliability and effectiveness under real-world conditions.

In conclusion, this study demonstrates that SVR and RT models performed the best in predicting the UCS of rocks, offering the potential for efficient, economical, and accurate identification of UCS. These two models not only performed well on the training set but also exhibited strong generalization capabilities on the test set, providing scientific support for rapid and accurate prediction across different rock types and engineering conditions. However, it is worth noting that the RT model showed a tendency toward overfitting on the training set, indicating the need for careful hyperparameter tuning and validation to ensure its robustness in practical applications. These findings provide important theoretical foundations and technical support for the future development of automated, intelligent identification of UCS without relying on engineering experience or domain expertise. Future work could further incorporate additional features and advanced model optimization techniques to enhance the generalization capabilities and applicability of the algorithms, providing more reliable scientific references for practical engineering applications.