Enhanced novelty approaches for resource allocation model for multi-cloud environment in vehicular Ad-Hoc networks

Abstract

As the number of service requests for applications continues increasing due to various conditions, the limitations on the number of resources provide a barrier in providing the applications with the appropriate Quality of Service (QoS) assurances. As a result, an efficient scheduling mechanism is required to determine the order of handling application requests, as well as the appropriate use of a broadcast media and data transfer. In this paper an innovative approach, incorporating the Crossover and Mutation (CM)-centered Marine Predator Algorithm (MPA) is introduced for an effective resource allocation. This strategic resource allocation optimally schedules resources within the Vehicular Edge computing (VEC) network, ensuring the most efficient utilization. The proposed method begins by the meticulous feature extraction from the Vehicular network model, with attributes such as mobility patterns, transmission medium, bandwidth, storage capacity, and packet delivery ratio. For further analysis the Elephant Herding Lion Optimizer (EHLO) algorithm is employed to pinpoint the most critical attributes. Subsequently the Modified Fuzzy C-Means (MFCM) algorithm is used for efficient vehicle clustering centred on selected attributes. These clustered vehicle characteristics are then transferred and stored within the cloud server infrastructure. The performance of the proposed methodology is evaluated using MATLAB software using simulation method. This study offers a comprehensive solution to the resource allocation challenge in Vehicular Cloud Networks, addresses the burgeoning demands of modern applications while ensuring QoS assurances and signifies a significant advancement in the field of VEC.

Introduction

The goal of Vehicular Cloud Computing (VCC) is to improve the capabilities of automobiles in a networked world via the creative combination of cloud computing and vehicular networking¹. Through the integration of cloud infrastructure and vehicular ad hoc networks (VANETs), Vehicle-Computer-Chat (VCC) enables automobiles to function as mobile computing platforms that can process, store, and share data in real-time². This paradigm optimises computer processes, improves driving safety, and allows cars to access cloud resources on demand via dynamic resource allocation. Vehicle-to-vehicle cooperation (VCC) enables applications including data exchange for better traffic control and platooning for fuel economy^3,4. Furthermore, edge computing integration facilitates data caching for effective retrieval and guarantees low-latency answers for crucial applications like collision avoidance⁵. Notwithstanding its promise, VCC encounters obstacles like as privacy issues, communication during high-mobility situations, and uninterrupted network maintenance. In the long run, VCC hopes to transform transportation networks by bringing in car diagnostics, improved navigation, and personalised services. The potential for a unified ecosystem that improves driving experiences, road safety, and the state of mobility overall exists due to the convergence of cloud and vehicular networks^6,7.

For Vehicular Cloud Computing (VCC) to reach its full potential, a number of implementation-related obstacles must be overcome⁸. Securing sensitive data transferred between cars and cloud resources is the biggest problem, requiring strong privacy safeguards and defence against cyberattacks. Furthermore, since VCC is dynamic and highly mobile, it presents communication challenges because of changing network topologies, necessitating seamless connection solutions⁹. While integrating edge computing might help lower latency, careful resource management is necessary to maximise cloud-edge interactions. For widespread deployment, smooth compatibility across several vehicle communication protocols is essential^10,11. Establishing a robust vehicular communication infrastructure, placing cloud data centres strategically, and positioning edge computing nodes are necessary for the effective implementation of VCC. To ensure data security, advanced encryption, authentication methods, and cooperative key management protocols must be used. To develop standardised communication protocols and regulatory frameworks, industry players must collaborate closely together on this endeavour^12,13. VCC has the potential to completely transform transportation by providing increased safety, efficiency, and a seamless, connected driving experience by tackling these technological, security, and interoperability issues from an integrated perspective¹⁴.

Numerous studies have been conducted to overcome the difficulties inherent in vehicular cloud computing (VCC), producing creative approaches and solutions^15,16. Investigations into secure data aggregation, homomorphic encryption, and blockchain-based techniques improve data security and privacy while protecting private vehicle data and facilitating insightful analysis¹⁷. In order to effectively handle communication issues and provide continuous connection in the face of changing topologies and mobility, researchers have investigated dynamic routing methods, spectrum allocation, and vehicular network clustering¹⁸. In order to reduce latency and improve computation, research on workload offloading, resource management, and node location optimisation have been spurred by the efficient integration of edge computing. Research on cross-domain architectures and standardised communication protocols promotes interoperability; C-V2X technology is one example of such an endeavour¹⁹. Intelligent vehicle communication infrastructures and optimised cloud data centre networks have been suggested as necessary for the effective deployment of VCC, supporting resource responsiveness and availability. Intrusion detection systems and privacy-preserving techniques are examples of security advances that support safer and more private automotive settings. The advancement of VCC is fueled by these joint research initiatives, bringing in an era of connected, safe, and effective transportation²⁰.

The main contributions in this paper are:

The work presented in this paper makes several significant contributions to the field of Vehicular Edge Computing (VEC) and resource allocation in Vehicular Ad Hoc Networks (VANETs):

• An innovative approach to resource allocation within Vehicular Edge Computing (VEC) networks is introduced which presents a novel method to address the growing challenges associated with allocating resources effectively²¹.

• The study recognizes the surge in service requests driven by varying conditions and emphasizes the need for a strategic resource allocation mechanism. This mechanism aims to ensure the efficient delivery of applications while maintaining the desired Quality of Service (QoS) assurances.

• The work incorporates the Crossover and Mutation (CM)-centered Marine Predator Algorithm (MPA), which is a novel algorithm designed to optimize resource scheduling and utilization within VEC networks. This integration provides a unique solution to the resource allocation problem.

• The research utilizes the Elephant Herding Lion Optimizer (EHLO) algorithm to pinpoint critical attributes and employs the modified Fuzzy c-means (MFCM) algorithm for efficient vehicle clustering based on selected attributes. These algorithms enhance the precision and efficiency of the resource allocation system.

• The effectiveness of the suggested technique was assessed using performance metrics including energy consumption, throughput, latency, and packet delivery ratio. Software called MATLAB was used to complete the implementation.

The remains of the article are structured as follows. Related work is included in “Literature review”. The proposed work’s technique is presented in “Proposed methodology”. The performance of the proposed approach is outlined in “Results and discussion”. The intended work is concluded in “Conclusion and future scope”.

Literature review

To ensure the efficient communication in the VANETs, constructing the cloud of RSUs and (or) the hybrid cloud are the typical ways for achieving the generality of the entire network. In this section, lots of existing work on the various clouds in the VANETs shall be briefly reviewed.

Qun et al.²² presented an energy-aware technique for load balancing in fog-based VANETs. They employed the ACO-ABC approach, which combines artificial bee colonies with ant colony optimization. The results of the Network Simulator 2 simulation indicated that the VANET’s energy usage increased as the number of nodes increased. Furthermore, when the number of jobs rose, the suggested method improved load balancing.

Gai et al.²³ examined the Swarm Optimized Non-Dominated Sorting Genetic Algorithm (SONG) for optimizing delay and energy-aware facility placement in vehicular fog networks. SONG combines the Non-dominated Sorting Genetic Algorithm (NSGA-II) and the Speed-constrained Particle Swarm Optimization (SMPSO), two popular Evolutionary Multi-Objective (EMO) techniques. The bounds of the delay-energy solutions and the related layout design were initially demonstrated by solving an example problem using the SONG approach. The performance of the SONG algorithm’s development was then assessed using real vehicle traces and three quality indicators: Inverted Generational Distance (IGD), Hyper-Volume (HV), and CPU delay gap.

In order to maximize the effectiveness of IoT task processing, Hameed et al.²⁴ presented a dynamic cluster-enabled capacity-based load-balancing technique for energy- and performance-aware vehicular fog distributed computing. This method creates clusters that act as pools of computer resources based on the position, speed, and direction of the vehicles. By detecting departure timings from clusters, the article also suggests a method for predicting a vehicle’s future position inside the dynamic network.

A multi-objective method based on deep learning algorithms and differential evolution has been described by Taha et al.²⁵ for VANETs. Here, the cluster algorithm uses the Kubernetes container-base to choose different cars that meet the requirements of the algorithm. As a result, we are able to carry out difficult operations for data owner automobiles. Our method uses a deep learning model to determine the fit complexity of sub-tasks, and the cars’ information is accessible on the master vehicle (data owner vehicle) when the vehicle enters the cluster. The MOTD-DE that has been suggested divides up subtasks among groups of cars in order to minimize task execution time and the number of vehicles required to complete it. Additionally, we take the subtasks to be autonomous.

Li et al.²⁶ have presented a nature-inspired fuzzy-based resource allocation technique for automotive cloud computing called the Cuckoo Search Algorithm. Landlords may rent these resources, or cars can share them, for a variety of uses, including supplying the hardware required by automobile network services and apps. It is feasible to provide the automobile network’s expanding resource needs. The results demonstrated how the suggested approach performs better than other algorithms in terms of makespan, latency, and execution time. A resource allocation method for VANETS that draws inspiration from the banker’s algorithm has been introduced by Balzano et al.²⁷. By using this approach, handle cars as processes that make requests and the roads as resources that need to be distributed. Then provide an algorithm to control the distribution of vehicles along the available pathways in order to lessen traffic congestion.

Vakili, Asrin’s²¹ study, titled “A new service composition method in the cloud-based Internet of Things environment using a grey wolf optimization algorithm and MapReduce framework,” presents an innovative approach to service composition within the IoT domain. The research leverages the Grey Wolf Optimization (GWO) algorithm alongside the MapReduce framework to address challenges in the cloud-based IoT environment, particularly in managing the complexity and efficiency of service composition. The method focuses on optimizing service performance, ensuring scalability, and reducing computational overhead, which are critical for handling the dynamic nature of IoT ecosystems. By integrating GWO and MapReduce, the study offers a robust solution to enhance resource utilization, minimize latency, and improve the overall efficiency of service delivery in cloud-based IoT systems. This research contributes significantly to the development of advanced methodologies for IoT service management, paving the way for more efficient and scalable systems in the rapidly growing IoT landscape.

Heidari et al.^28,29 conducted a comprehensive study on the reliability and availability of WSNs in industrial environments, addressing key challenges such as permanent faults, network resilience, and fault-tolerant mechanisms. Their research introduced a hybrid fault-tolerant model that integrates redundancy strategies, adaptive routing protocols, and predictive maintenance techniques to enhance the robustness of sensor networks.

Heidari, Arash^30,31, and colleagues have made significant contributions to deepfake detection through two key studies in 2024. The first, “Deepfake detection using deep learning methods: A systematic and comprehensive review” (Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery), offers an extensive analysis of current deep learning techniques used for detecting deepfakes, reviewing their effectiveness and limitations. The second study, “A Novel Blockchain-Based Deepfake Detection Method Using Federated and Deep Learning Models” (Cognitive Computation), presents an innovative solution by combining blockchain technology with federated learning and deep learning models to ensure secure, privacy-preserving deepfake detection in decentralized systems. These works collectively advance the field of deepfake detection by proposing new methods for improved accuracy, security, and real-time performance, addressing critical challenges in media verification, cybersecurity, and ethical AI applications.

Heidari et al.³² introduced a cloud-based framework for non-destructive characterization, leveraging cloud computing, artificial intelligence (AI), and machine learning algorithms to improve material evaluation processes. Their study highlights the advantages of remote data processing and real-time analysis, allowing industries to perform large-scale material assessments without physical intervention.

Heidari, Arash³³, and colleagues in their 2024 paper, “A reliable method for data aggregation on the industrial internet of things using a hybrid optimization algorithm and density correlation degree,” published in Cluster Computing, present a novel approach for optimizing data aggregation in Industrial Internet of Things (IIoT) environments. The proposed method leverages a hybrid optimization algorithm, which combines multiple techniques to enhance the efficiency and reliability of data aggregation. Additionally, the concept of density correlation degree is incorporated to improve the accuracy and relevance of the collected data. This approach is designed to address the challenges of large-scale data handling, sensor network reliability, and real-time data processing in IIoT applications, ultimately contributing to better decision-making and system performance. The work offers valuable insights into optimizing IIoT data management, making it more scalable and robust for industrial applications.

Heidari, Navimipour, and Unal³⁴ proposed a secure intrusion detection platform by integrating blockchain technology and Radial Basis Function Neural Networks (RBFNNs) in their 2023 study published in IEEE Internet of Things Journal. Their research highlights the advantages of blockchain’s decentralized, tamper-proof ledger combined with AI-driven anomaly detection for securing drone networks. The authors emphasize that blockchain ensures data integrity, while RBFNNs enhance real-time intrusion detection with high accuracy and low false-positive rates.

Zanbouri et al.³⁵ focuses on leveraging Glowworm Swarm Optimization (GSO) to balance key performance parameters such as latency, throughput, and energy consumption in IIoT networks. By utilizing blockchain technology, their approach enhances data security, decentralization, and fault tolerance, making it a robust solution for industrial automation.

Heidari et al.³⁶, provide a comprehensive overview of ChatGPT’s architecture, functionalities, and potential use cases. Their research explores the core components of ChatGPT, including its natural language processing capabilities, training methodologies, and contextual adaptability.

Amiri et al.³⁷ provides a comprehensive overview of artificial intelligence techniques for climate change mitigation, highlighting the role of machine learning, deep learning, and optimization models in addressing climate adaptation, energy efficiency, and carbon footprint reduction. The study explores how AI can optimize renewable energy sources, improve smart grid performance, and develop predictive models for climate impact assessment.

Asadi et al.³⁸ provide a comprehensive survey on evolving botnet threats and defense strategies, the latest advancements in botnet structures, including peer-to-peer (P2P) botnets, IoT-based botnets, and stealth malware techniques. By analyzing emerging attack methodologies, the authors highlight new trends in cyber threats that target critical infrastructure, cloud environments, and smart devices.

Heidari et al.³⁹ propose a fuzzy logic-based multicriteria decision-making approach to mitigate broadcast storms in vehicular ad hoc networks (VANETs). This addresses the challenges of excessive message dissemination, which can lead to network congestion and increased latency. By leveraging fuzzy logic, the model dynamically evaluates multiple criteria, such as vehicle density, distance, and message priority, to optimize data dissemination and reduce broadcast redundancy. The proposed method enhances network performance by improving packet delivery rates and minimizing collision probability in high-density traffic scenarios.

Heidari et al.⁴⁰ explore the enhancement of solar convection analysis using multi-core processors and GPUs to accelerate computational simulations. It focuses on improving the efficiency and accuracy of numerical models by leveraging parallel processing techniques to handle complex fluid dynamics and heat transfer computations. The proposed approach significantly reduces computation time while maintaining high precision, making it well-suited for large-scale solar energy applications. The results demonstrate that GPU-based solutions outperform traditional CPU-based methods, providing a scalable framework for real-time solar convection analysis.

The reviewed research on resource allocation in vehicular ad hoc networks (VANETs) have multiple drawbacks when applied to multi-cloud systems. These techniques frequently have problems with scalability because they cannot properly handle the large-scale nature of multi-cloud systems with various vehicles and resources. Real-time performance is another issue, as many approaches fail to meet the stringent latency requirements of automotive applications such as autonomous driving. Security and privacy problems are also not sufficiently addressed, particularly in floating multi-cloud systems where inter-cloud connectivity introduces risks. Furthermore, complicated optimization algorithms might result in significant computing overhead, making them unsuitable for dynamic, real-time networks. These differences emphasize the need for more adaptable, efficient, and secure methods of resource allocation for VANETs in multi-cloud contexts.

Proposed methodology

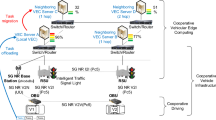
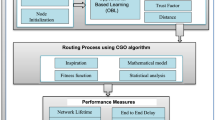
The VEC optimization model is a multi-objective optimization model that aims to minimize service delay and energy consumption in Vehicular Edge Computing (VEC) networks, while also optimizing resource allocation in the cloud. It takes into account several factors, including the location and capacity of edge nodes, traffic demand between edge nodes and Personal Devices (PDs), communication costs between edge nodes, the energy consumption of edge nodes, and the availability of resources in the cloud.The model uses the adaptive Elephant Herding Lion Optimizer (EHLO) algorithm to select the most important features. EHLO is a swarm intelligence algorithm that combines clans and lion score information to identify the best path and reduce travel time. The modified Fuzzy c-means (MFCM) algorithm is then used to cluster vehicles into groups based on their residual energy and signal strength. This grouping helps connect vehicles with similar energy levels and communication capabilities, ultimately reducing service delay and energy consumption. Finally, the optimal facility locations in VEC networks and the optimal resource allocation in the cloud are determined using the Crossover and Mutation (CM)-cantered Marine Predator Algorithm (MPA) algorithm. Figure 1 shows a block diagram of the proposed technique.

Fig. 1

Overview of proposed methodology.

Network model

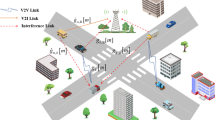
Along the straight road are M Road Side Units (RSUs), each of which is linked to a MEC server. Vehicles may only reach an RSU inside the area in which it is situated. Each RSU covers a single region. The vehicle has the ability to transmit and receive information via communication with nearby cars or RSUs. P request vehicles with a Poisson distribution are deployed, as shown in Fig. 2, and are stated as$Vl\left( {x \in \left\{ {1,2,.,P} \right\}} \right)$. V-UEs are served by each RSU${S_y}\left( {y \in \left\{ {1,2,\ldots ,Q} \right\}} \right)$. In order to multiplex spectrum, we assume that there is interference between RSUs because numerous RSUs share a same spectral resource. There are several channels K inside the bandwidth$Bw$. In the orthogonal frequency-division multiple access (OFDMA) mode, which allows V-UEs to connect to RSUs, each V-UE channel inside an RSU is orthogonal to all other V-UE channels. The quantity of the calculation input data${t_{x,y}}$, ${u_{x,y}}$which indicates the total number of CPU cycles needed to finish the computation job, and the maximum latency that the V-UE can withstand are $T_{{x,y}}^{{Max}}$all indicative of the y compute-intensive task ${F_{x,y}}=\left\{ {{t_{x,y}},{u_{x,y}},T_{{x,y}}^{{Max}}} \right\}$that has to be done ${t_{x,y}}$in this network’s$V - U{E_x}$ RSU⁴¹. Each V-UE has the option of carrying out its work locally on the device or remotely via computation offloading on the VEC server. Assume${r_{x,y}}$ that RSU y decides to unload$V - U{E_x}$. If $V - U{E_y}$the RSU y transfers its workload to the VEC server, ${r_{x,y}}=1$and ${r_{x,y}}=0$in the event that it does not.

Fig. 2

Model of network.

Local computing

Define ${\aleph _{x,L}}$as the V-UEs’ computing power, measured in CPU cycles per second. The calculation execution time is stated as $Et_{{x,y}}^{L}$follows when the job ${F_{x,y}}$is performed locally:

$$Et_{{x,y}}^{L}=\frac{{{u_{x,y}}}}{{{\aleph _{x,L}}}}$$

(1)

The V-UE’s related energy usage for local execution may be found using,

$$Ec_{{x,y}}^{L}=\omega {\left( {{\aleph _{x,L}}} \right)^2}{u_{x,y}}$$

(2)

In this case, $\omega ={10^{ - 26}}$is a chip architecture-dependent coefficient.

Vehicular Edge Computing

Through a wireless link between users and cars, the ${x^{th}}$UE may transfer the calculation work $C{t_x}$to the VEC for the VES computing technique. The job will then be computed for the UEs by the VES. As a result, communication time and calculation time are included in the overall time cost of doing the activity. The calculation input data size $U{E_x}$and the data rate provided by VEC ${R_{VEC,x}}$determine the communication time expenses$T_{{x,com}}^{{VEC}}$; as a result, we have

$$T_{{x,com}}^{{VEC}}=\frac{{Sc{d_x}}}{{R_{{_{{VEC,x}}}}^{i}}}$$

(3)

$Sc{d_x}$indicates the amount of calculation data in this case. Let $C{r_{VEC,x}}$be the VES compute resource that is allocated to$U{E_x}$. Afterwards, the task’s computation time costs may be computed as$T{c_x}$,

$$T_{{x,comp}}^{{VEC}}=\frac{{{\Re _x}}}{{Cr_{{_{{VEC,x}}}}^{i}}}$$

(4)

As a result, the overall time required for the work$U{E_x}$ to be completed by VEC is provided by,

$$T_{x}^{{VEC}}=T_{{x,com}}^{{VEC}}+T_{{t,comp}}^{{VEC}}$$

(5)

Feature extraction of vehicles

Feature extraction in this context would typically involve identifying and capturing relevant information or characteristics from vehicles and the network to enhance the resource allocation model. While the specific features for extraction may depend on the details of the work, here are selected features that could be considered for extraction in vehicular edge computing:

Location data

Gathering GPS coordinates and vehicle positions to enable location-based edge resource allocation and service optimization.

Network latency

Measuring the latency between vehicles and edge servers to ensure low-latency communication for time-sensitive applications.

Edge server workload

Monitoring the workload and resource utilization of edge servers to allocate tasks efficiently.

Vehicle speed and acceleration

Extracting data on vehicle speed and acceleration to assess mobility patterns and optimize edge resource allocation accordingly.

Data rate and throughput

Capturing data transfer rates and throughput between vehicles and edge servers to ensure efficient data processing.

Service request queue

Analyzing the queue of service requests from vehicles to prioritize and allocate edge resources effectively.

Edge server availability

Tracking the availability and health status of edge servers to make resource allocation decisions based on reliability.

Power and energy consumption

Monitoring power usage and energy consumption of both vehicles and edge servers to optimize energy-efficient computing.

Weather conditions

Considering weather data (e.g., temperature, precipitation) to adapt resource allocation based on environmental factors.

These extracted features are essential for optimizing vehicular edge computing systems, ensuring efficient resource allocation, and meeting the specific requirements of applications and services running on vehicles.

Feature selection in vehicular edge computing using elephant herding Lion optimizer (EHLO)

Here, the future selection is selected from the vehicular edge computing-based feature extraction using Elephant Herding Lion Optimizer (EHLO). The elephant herding optimization algorithm is developed based on herding behaviour of elephants. Due to the gregarious character of the elephant, there are several factions of female elephants in the group, each of which is carrying a calf. Each group’s movement is influenced by its matriarch or leader elephant. But, it has the local optimum problem for complex data which may increase the poor searching capability. To solve that problem, this research methodology updates the position by using the Lion optimization process. The proposed algorithm provides a global search with quick convergence rate. The proposed method has a high EHO search efficiency and a dynamic LOA capability that extends the life of vehicular edge nodes. Here, vehicular nodes of each cluster are considered as the elephant. The first step of the elephant optimization algorithm is to randomly generate population over the solution space. Every solution is represented by:

$$I_{p}=e_1, e_2, \ldots \ldots , e_n$$

(6)

Where, e_n specifies the dimensional space. Then, the fitness is evaluated for the proposed research methodology which considers the minimum amount power consumption energy$\left( {{P_V}} \right)$, minimum amount of delay $\left( D \right)$and throughput. The fitness function (f_t)is mathematically defined as follows,

$${F_t}=Min\left( {{t_p}} \right),Min\left( {{P_V},D} \right)$$

(7)

Following that, each clan includes elephants, and the best and worst possibilities for every elephant in every family in this third stage are included in the status of every elephant P, except the matriarch C_i and a male elephant⁴². The elephant i = 1, 2, ...P is a sign of jth clan j = 1, 2, ...C and position L_i,j. The position of the elephant as of right now ith is shown as,

$${L_{new,c_{i,j}}}=L_{c_{i,j}}+\alpha (L_{best, c_{i,j}}-L_{c_{i,j}})\times r$$

(8)

Here ${L_{new,c_{i,j}}} \to$ updated position, ${L_{c_{i,j}}} \to$ old position, ${L_{best,c_{i,j}}} \to$ Position of best in the clan. $\alpha$ and $r \in 0 \,to\, 1$.

The ideal posture that represents the matriarch cannot be changed by using the aforementioned techniques. The most fitting clan member’s position update is given by,

$${L_{new,c_{i,j}}}=\beta\times L_{center, c_j} \text{ and } L_{center, c_j}= \sum \limits_{i=1}^{n}L_{c_{i,j}}/n_l$$

(9)

Here, $n_l to$ the total number of elephants in each clan and $\beta \in [0\, 1]$

Various objectives, such as energy maximisation and delay reduction, may be achieved using the proposed approach, contingent on the intra- and inter-distances between vehicles and nodes. The proposed technique combines the EHO and LOA searching behaviour, as was previously discussed. Stated differently, the proposed approach may eliminate negative searchability while using enhanced searchability for convergence. Thus, the new role of a female lion may be explained as follows:

$$FL^{\prime}=FL+2G\times \eta_d \{{S_1}\} + w(-1,1)\times \tan (\theta) \times G\times \{{S_2}\}$$

(10)

Where, $FL^{\prime}$ represents the new position of the female lion, $FL$ specifies the female lion, G shows the distance between the female lion’s position and the selected point chosen by tournament selection among the pride’s territory, $\{{S_1}\}$ is a vector which its start point is the previous location of the female lion, and its direction is toward the selected position, and $\{{S_1}\}$ which is perpendicular to $\{{S_1}\}$. Then, the nomad lions are also hunting the prey⁴³. The nomad lions are generated as follows,

$$N_{d} (O_{{ij}} ) = \left\{ {\begin{array}{*{20}c} {O_{{ij}} } \\ {(\eta _{d} )_{j} } \\ \end{array} } \right.\begin{array}{*{20}c} {if(\eta _{d} )_{j}> (p_{b} )_{i} } \\ {otherwise} \\ \end{array}$$

(11)

Where, $N_{d} (O_{{ij}} )$is the current position of ithnomad lion, j is the dimension, $(\eta _{{d}} )_{j}$is a uniform random number within [0, 1], and $(p _{{b}} )_{i}$is a probability that is calculated for each nomad lion independently. Then, mating process is carried out. Mating is an essential process that assures the lions’ survival, as well as providing an opportunity for information exchange among members. The mating operator is a linear combination of parents for producing two new offspring. For the mating process two offspring process is derived which is given as follows,

$$og_{j}^{1} = \tau * FL_{j} + \sum {\frac{{1 - \tau }}{{Z_{i} }}*ML_{j} *Z_{i} }$$

(12)

$$og_{j}^{2} = (1 - \tau ) * FL_{j} + \sum {\frac{\tau }{{Z_{i} }}*ML_{j} *Z_{i} }$$

(13)

Where, j is the dimension, Z_i equals 1 if Lions are selected for mating, otherwise it equals 0, $ML_{j}$ indicates the male lion and $\tau$ is a randomly generated number with a normal distribution with mean value 0.5 and standard deviation 0.1. Finally, male elephants or the worst elephants would be taken away from their family groupings the lowest ranking changed to,

$$L_{{worst,c_{{i,j}} }} = L_{{\min }} + (L_{{\max }} - L_{{\min }} + 1) \times r$$

(14)

Where $L_{{worst,c_{{i,j}} }} \to$ the clan’s worst male elephants, $L_{{\max }} \;and\;L_{{\min }} \to$are, as well as the elephants’ permitted maximum and lowest range. The pseudocode for the proposed EHLO is given as follows,

These selected features can help enhance the efficiency, performance, and responsiveness of vehicular edge computing systems by tailoring resource allocation and decision-making to the unique characteristics and requirements of the vehicles and the edge computing environment.

Vehicle clustering in vehicular edge computing using MFCM

After network formation, the cluster is formed by using the Modified Fuzzy C-Means Clustering (MFCM). FCM is an unsupervised clustering algorithm. The clusters are formed according to the distance between data points and the cluster centres are formed for each cluster. The main reason for choosing FCM is it gives flexibility. The work in the task set arecategorised using the MFCM clustering method, and the computing tasks of the on board unit (OBU) are separated into three categories: computing, storage, and network bandwidth demand types. But it has random centroid selection which may provide an inaccurate clustering output and it uses the Euclidean distance which is not support for the large amount of data. So, here the centroid is selected by calculating modified deviation between each data point and maximum deviated input node is considered as the centroid and this research uses the Manhattan distance instead of Euclidean distance. The purpose of the cluster formation in this cluster head node is to minimize the following objective function (F_o):

$$F_{o} = \sum {\sum {D_{{uv}}^{l} T_{{uv}} } }$$

(15)

Where, $D_{{uv}}^{l}$ is node v’s degree of belonging to cluster u, l is the any real number greater and $T_{{uv}}$is the job and each cluster centre, and the closest cluster centre was given the work assignment. First, the centroid point is selected by calculating standard deviation between nodes which expressed as follows,

$$G_{i} = \sqrt {\frac{{\alpha _{s} - \mu }}{{\alpha _{n} }}}$$

(16)

Where µ denotes the mean value and G_isignifies the cluster centre. Following the centre vector computation, the distance matrix is computed using the Manhattan distance calculation, and the result is as follows:

$$T_{{uv}} = \left| {G_{{i + 1}} - G_{i} } \right| + \left| {\alpha _{{i + 1}} - \alpha _{i} } \right|$$

(17)

Then, update the partition matrix for the jth step is derived as follows,

$$D_{{uv}}^{l} = \left( {1/\sum {(T_{{uv}} /T_{{sv}} )^{{2/l - 1}} } } \right)$$

(18)

Where, s denotes the iteration step. The MFCM process is repeated until it converges. In this way the cluster is formed. The formed cluster is denoted as,

$$H_{s} = \left\{ {h_{1} ,h_{2} ,h_{3} , \ldots h_{n} } \right\}\,({\text{or}})\,H_{s} = h_{i} ,\quad i = 1,2, \ldots ,n$$

(19)

Where, H_s indicates the formed cluster sets and h_n defines the n-number of clusters.

Finally, the obtained cluster heads are expressed as in Eq. (20):

$$L_{D} = \left\{ {l_{1} ,l_{2} , \ldots ,l_{d} } \right\}\;({\text{Or}})\;L_{D} = l_{j}$$

(20)

Where, L_D defines the obtained cluster head set, and l_d denotes the d-number of cluster heads.

Resource allocation in vehicular cloud using CM-centered marine predator algorithm

The CM-centered Marine Predator Algorithm (CM-MPA) is a hybrid heuristic optimization algorithm that combines various crossover and mutation techniques to explore a wide solution space effectively. It was specifically designed to optimize resource allocation in vehicular clouds, where the goal is to improve resource utilization, reduce latency, and enhance overall system performance while adapting to the ever-changing conditions and requirements of vehicular networks.Because it can adjust to the constantly changing circumstances and demands of vehicular networks, the CM-MPA is a good fit for optimising resource allocation in vehicular clouds. Because it employs a dynamic fitness function that considers the vehicular network’s present condition, the CM-MPA is able to do this. Furthermore, the CM-MPA employs a range of search techniques, enabling it to locate answers fast and effectively. The primary fitness function is calculated by dividing the total delay time of all computing tasks by the degree of matching between each task and the scheduled cell. Here, the jobs assigned to each computing unit and their computing order are represented by a task list split into L blocks.

Assign tasks to natural numbers one through N in a random order first, and then choose the numbers starting at the zeroth place in the series. The tasks are scheduled to M computer units sequentially based on the resource limits of the computing unit and the task’s time constraints. The work is sent to the next computer unit if the current one is unable to complete it within the given restrictions⁴⁴. Following the aforementioned procedures, a CM is ultimately encoded, resulting in the first step towards solving the task scheduling issue. To create an initial population with an individual size of $X, X - 1$ repeat the aforementioned procedure steps a number of times.

A fitness function that represents the accomplishment of all goals should be created in order to evaluate the chromosomes’ quality. Equation (21) is $\Re$definition of the fitness function.

$$\left\{ {\begin{array}{*{20}{c}} {{\Re _i}\left( x \right)=\left( {\frac{1}{{f{f_i}\left( x \right)}}} \right)} \\ {\Re \left( x \right)=\sum\limits_{{i=1}}^{n} {{\Re _i}\left( x \right)} } \end{array}} \right.$$

(21)

where n is the quantity of target functions. $\Re \left( x \right)$ is both the value of individual x’s objective function i and its fitness$f{f_i}\left( x \right)$. A random selection of two chromosomes is made from the mating pool. It generates a random integer between 0 and 1. The gene location is arbitrarily chosen as the crossover point if the random number is less than the crossover probability. Equation (22) is the crossover probability function that we created based on the fitness of the individuals. A higher fitness level is correlated with a lower crossover probability setting.

$${C_P}=\left\{ {\begin{array}{*{20}{c}} {\frac{{{u_1}\left( {1 - \sum\nolimits_{{i=1}}^{n} {{\mu _i}\frac{{{\Re _i}\left( x \right)}}{{\Re _{i}^{{Max}}}}} } \right)}}{{1 - \sum\nolimits_{{i=1}}^{n} {{\mu _i}\frac{{\Re _{i}^{{avg}}}}{{\Re _{i}^{{Max}}}}} }},\,{\Re _i}\left( x \right) \geqslant \Re _{i}^{{avg}}\left( {i=1,2,\ldots n} \right)\,} \\ {{u_2},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Re {v_i}\left( x \right)<\Re _{i}^{{avg}}\left( {i=1,2,\ldots n} \right)\,} \\ {\frac{{{L_n}}}{n}{u_2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,else} \end{array}} \right.$$

(22)

Here, ${\mu _i}$ is the weight coefficient, and is the ith fitness, ${\mu _1},\ldots \ldots .,{\mu _i},\ldots .,{\mu _n}$which corresponds to the objective function i of individual x. $\Re _{i}^{{avg}}$is the average of the ith fitness, and $\Re _{i}^{{Max}}$ is the maximum of the xth fitness. The parameters in the crossover probability function, ${u_1}$and ${u_2}$, have values set as constants between 0 and 1. ${L_n}$is the quantity of goal functions where the associated fitness values fall short of the mean fitness value. A high crossover probability is established if every fitness value for individual x is lower than the associated averages. A little crossover chance is established if each of individual I’s fitness values is higher than the associated averages. Furthermore, a lower setting of the crossover probability is associated with increased fitness. If not, the number of objective functions that result in matching fitness values that are less than the average fitness value is used to determine the crossover probability. This kind of crossover probability setting protects exceptional people from moving into the following generation.

$${G_{CM}}=\sum\limits_{{i=1}}^{n} {{u_i}} \left[ {\frac{1}{{n{P_s}}}\sum\limits_{{x=1}}^{{n{P_s}}} {{{\left( {\frac{{F{F_i}\left( x \right)}}{{FF_{i}^{{Max}}}} - \frac{{FF_{i}^{{avg}}}}{{FF_{i}^{{Max}}}}} \right)}^2}} } \right]$$

(23)

Where ${G_{CM}}$ the values of the goal function diverge. $n{P_s}$ is the number of population. The value of the specified mutation location${G_{CM}}$ is changed to one of the other available values if the resulting number is less than the mutation probability. A substantial mutation probability is established when there is little variation between the individuals’ objective function values. If not, a low chance of mutation is established. Equation (23) defines the difference between the values of the goal function. This way of adjusting the mutation probability prevents the creation of a local optimum.

The selection of the MPA.

Every chromosome in the population is chosen by the MPA’s selection operation procedure, which chooses the chromosome with the highest fitness value²¹. The MPA optimisation procedure is broken down into three primary stages that each represent a particular velocity ratio and a day in the lives of a predator and prey:

• when the predator is going faster than the prey;

• when the predator and prey are travelling at almost the same speed; in low velocity ratio when the predator is moving faster than the prey.

• There is a predefined and allocated iteration duration for every defined phase.

These actions are designed to resemble how predators and prey move in the wild by adhering to the regulations governing that behaviour. Among these three stages are:

Phase 1

When there is a large speed ratio $\left( {Hs>10} \right)$, the predator travels more slowly than its prey, and its optimum foraging tactic is to move very little at all. This stage is in charge of investigating algorithms, and the corresponding mathematical formula is as follows

$$While\,\,I<\frac{1}{3} * Max\_I$$

(24)

$$\overrightarrow {Stepsize{\,_x}} ={\vec {\Omega }_y} \otimes \left( {\overrightarrow {{E_x}} - {{\vec {\Omega }}_y} \otimes \overrightarrow {{P_x}} } \right),\,\,x=1,2,\ldots n$$

(25)

$$\overrightarrow {{p_x}} =\overrightarrow {{P_x}} +P * \vec {\Omega } \otimes \overrightarrow {Stepsiz{e_x}}$$

(26)

where $Max\_I$ is the maximum number of iterations and I is the number of iterations that are currently in use. is a vector that depicts ${\vec {\Omega }_y}$ Brownian motion and is made up of a sequence of randomly generated integers based on a normal distribution. $\otimes$ symbolises entry-wise multiplications, $\overrightarrow {Stepsize{\,_x}}$ while the step size vector denotes the predator’s xth move. $P=0.5$ remains constant. $\vec {\Omega }$ is a vector of randomly generated numbers in the interval 0 to 1.

Phase 2

The prey and the predator travel at the same speed in the unit velocity ratio, and exploration eventually gives way to exploitation. The following is the formula.

$$While\,\,\frac{1}{3} * Max\_I<I<\frac{2}{3} * Max\_I$$

(27)

Regarding the first 50% of the population (Exploration)

$$\overrightarrow {Stepsize{\,_x}} ={\vec {\Omega }_Q} \otimes \left( {\overrightarrow {{E_x}} - {{\vec {\Omega }}_Q} \otimes \overrightarrow {{P_x}} } \right),\,\,x=1,2,\ldots \frac{n}{2}$$

(28)

$$\overrightarrow {{p_x}} =\overrightarrow {{P_x}} +P * \vec {\Omega } \otimes \overrightarrow {Stepsiz{e_x}}$$

(29)

Regarding the latter half of the populace (exploitation)

$$\overrightarrow {Stepsize{\,_x}} ={\vec {\Omega }_y} \otimes \left( {{{\vec {\Omega }}_y} \otimes \overrightarrow {{E_x}} - \overrightarrow {\,{P_x}} } \right),\,\,x=\frac{n}{2},\ldots .,n$$

(30)

$$\overrightarrow {{p_x}} =\overrightarrow {{E_x}} +P * cf. \otimes \overrightarrow {Stepsiz{e_x}}$$

(31)

where${\vec {\Omega }_y}$ is a Levy distribution-based random number vector that symbolises Levy movement. $cf$ is an adaptive parameter that regulates the predator’s stride size. The following formula is used to calculate it:

$$cf={\left( {1 - \frac{I}{{Max\_I}}} \right)^{\left( {2 * \frac{I}{{Max\_I}}} \right)}}$$

(32)

Currently, half of the population moves in two ways: half moves in a Brownian step (exploration) while the other half goes in a Levy step (exploitation). Make the shift from exploration to development by combining Levy and Brownian tactics.

Phase 3

When there is a low velocity ratio$\left( {Hs=0.1} \right)$, exploration gives way to exploitation because the predator travels more quickly than the prey. A predator’s Levy movement is its ideal foraging approach, and the formula is as follows

$$While\,\,I>\frac{2}{3} * Max\_I$$

(33)

$$\overrightarrow {Stepsize{\,_x}} ={\vec {\Omega }_Q} \otimes \left( {{{\vec {\Omega }}_Q} \otimes \overrightarrow {{E_x}} - \overrightarrow {\,{P_x}} } \right),\,\,x=1,2,\ldots .,n$$

(34)

$$\overrightarrow {{p_x}} =\overrightarrow {{E_x}} +P * cf. \otimes \overrightarrow {Stepsiz{e_x}}$$

(35)

In the natural world, fish gathering devices (FADs) and eddy current creation may have an impact on marine predator behaviour. The FADs effect is regarded in MPA as local optimum traps, and the following is the definition of its mathematical model:

$$\overrightarrow {{p_x}} =\left\{ {\begin{array}{l} {\overrightarrow {{p_x}} +cf\left[ {{{\vec {M}}_{\hbox{min} }}+\vec {\Omega } \otimes \left( {{{\vec {M}}_{\hbox{max} }} - {{\vec {M}}_{\hbox{min} }}} \right)} \right] \otimes \vec {R} \quad \,if\,rand \leqslant fad} \\ {\overrightarrow {{p_x}} +cf\left[ {fad\left( {1 - rand} \right)+rand} \right] \otimes \left( {\overrightarrow {{p_{rand1}}} - \overrightarrow {{p_{rand2}}} } \right)\quad \,if\,rand \geqslant fad} \end{array}} \right.$$

(36)

where the likelihood that FADs will have an impact on the optimisation process is expressed as fad = 0.2. and ${\vec {M}_{\hbox{min} }}$ are vectors that represent the dimension’s upper and lower boundaries. A randomly generated number between 0 and 1 is denoted by $rand$. $\vec {R}$ is a binary vector that has two random elements that make up the Prey matrix$\overrightarrow {{p_{rand1}}}$ and $\overrightarrow {{p_{rand2}}}$. Its array is set to 0 when the value is more than 0.2 and to 1 when $rand$ it is less than 0.2. $\vec {\Omega }$is a vector of random numbers made up of the produced numbers from 0 to 1. Because of their excellent memory, marine predators are able to recall the exact location of every successful kill. Storage in the cloud’s optimum resource allocation allows for the accomplishment of this operation. The effectiveness of the suggested research approach is examined in the next section.

Results and discussion

The MATALB software now includes the hybrid optimisation model that has been proposed for the multi-cloud resource allocation method. In order to simulate the suggested method RU-VMM, we build a virtual environment using MATLAB R2022b (version 9.2) on a computer system with Intel(R) core (TM) i7-4790 CPU@3.60 GHz 3.60 GHz, 8 GB RAM, and 64-bit Windows 10 operating system. The suggested approach can be evaluated using performance measures including throughput, delay, energy, SNR, and throughput. Every cloud is taken to have a distinct resource capacity, and each cloud’s physical host is also supposed to be distinct, in order to mimic the actual multi-cloud situation. The suggested hybrid EHLO model is contrasted with the traditional Drawer Algorithm (DA), Coati Optimisation Algorithm (COA), Particle Swarm Optimisation (PSO), and Genetic Algorithm (GA) models in order to evaluate the efficacy of the multi-cloud resource allocation model that was just provided.

Fig. 3

Comparative analysis of (a) SNR and (b) delivery ratio.

A study of the SNR output in the suggested and current VEC approaches is shown in Fig. 3a. In this regard, the suggested method advances the idea of VEC centroid localization by giving weights to the coordinates of each surrounding vehicle based on SNR values and distances. When compared to the suggested research technique, the GA, COA, PSO, and GA achieve lower values, but the SNR value of the suggested method is over 1.94*10⁵. because the superior ideal positioning function with the VEC is used in the suggested study technique. Figure 3b displays the delivery ratio findings for parcels with varying automobile speeds and density. A connection failure brought on by rising speed had an impact on the packet delivery ratio because the transmitters were unable to send the packets to the nearby vehicular unit. As a result, there is a link with rising network density and the connection breaks. Performance was significantly impacted by the connection disruption in terms of the packet loss stimulus rate. Vehicle packet collisions led to higher packet loss rates and higher vehicle densities, which in turn reduced overhead network functionality. According to the simulation findings, the suggested CM-MPA was more feasible to implement than DA, COA, PSO, and GA.

Fig. 4

Comparative analysis of (a) energy efficiency and (b) throughput.

The total energy received multiplied by the number of nodes and the energy transferred is known as energy efficiency. As a result, Fig. 4a displays the energy efficiency of the suggested and current study approach. Energy efficiency has somewhat improved for the amount of nodes, but it is still quite low when compared to the current approaches. This energy usage should be at its highest to improve communication and prevent the node from failing the network. When compared to the current methods, the suggested method achieves a greater energy efficiency. Figure 4b shows the outcomes of the data with various data rates. The network density and vehicle speeds affect the data rates differently. Due to the simulation, the vehicle travelled on both straight and curved areas of the road at the lowest possible speed and throughput, resulting in the highest output at the boundaries of the roadways. When compared to other techniques that use the best possible vehicle selection for road segments, the suggested CM-MPA also improved network performance. A drop in throughput was seen in DA, COA, PSO, and GA. The optimum selection decreased the packet loss rate, and the selection of the ideally neighbouring vehicle hops effectively allows vehicles to be employed for connection determination and hence strictly prohibit energy waste by connecting dependability.

Fig. 5

Comparative analysis of (a) coefficient of variance and (b) energy savings.

A comparison of the energy savings and coefficient of variation (CV) in vehicle energy control (VEC) is shown in Fig. 5. The CV simulation models are shown in Fig. 5a. The data showed little changes since the arrival rate is Poisson. Still, there is a noticeable difference between the analytical results and the simulation results. Compared to other approaches now in use, such DA, COA, PSO, and GA, the suggested method has a lower CV. The best way to allocate VEC resources in order to consistently save 100% of the energy consumption using the suggested method is shown in Fig. 5b. On the other hand, when the number of automobiles rises, the savings for DA, COA, PSO, and GA decrease.

Fig. 6

Comparative analysis of (a) execution time and (b) negative balance.

The task execution time as a function of the resources allotted to it is shown in Fig. 6a. The suggested approach may distribute resources in a manner that minimises task execution time while still achieving the desired results. The job execution time utilising the suggested strategy is shown by the blue curve on the graph. When using a classic resource allocation technique like DA, COA, PSO, or GA, the task execution time is represented by the red, orange, violet, and green curves. The suggested approach may provide greater results with the same number of resources, as the picture illustrates. This is a result of the suggested method’s consideration of task execution time when allocating resources. The comparative study of a VEC system’s negative balance output as a function of the system’s vehicle count is shown in Fig. 6b. The suggested approach can achieve the production requirements while allocating resources to vehicles in a manner that minimises the output of the negative balance. Using the suggested approach, the VEC system’s negative balance output is maximised at 98% for 100 to 500 cars. When 100 to 500 cars are involved, the negative balance output of the VEC system is minimised at 97%, 96.5%, 96%, and 95%, respectively, when utilising conventional resource allocation techniques as DA, COA, PSO, or GA. Based on the aforementioned findings, we can say that, in comparison to other current approaches, the suggested strategy performs better than optimum resource allocation for VEC to cloud servers.

The proposed resource allocation method is little bit hard when it goes with more vehicular data sets, but compromising to the level expected as the proposed model integrates the Crossover and Mutation (CM)-centered Marine Predator Algorithm (MPA), Elephant Herding Lion Optimizer (EHLO), and modified Fuzzy C-means (MFCM) clustering. It is mainly designed to handle the problems in view of adding more vehicular data sets. The MFCM-based clustering process confirms the efficient vehicle adding by dynamically adapting to the adding more vehicular data sets. CM-MPA minimizes the resource utility across more edge servers, by minimizes the latency to low level. Add on lightweight communication protocols and distributed processing architecture manages add on vehicular data sets. The simulations validate the systems’ ability to level the energy, low latency and high throughput when adding more vehicular data sets. Hence, these will help to maintain the scalability of this system to handle more vehicular data sets and more edge servers.

Conclusion and future scope

Conclusion

In this paper presented an innovative solution to address resource allocation challenges in Vehicular Edge Computing (VEC) networks. The increasing volume of service requests under various conditions necessitates a strategic resource allocation mechanism to ensure efficient application delivery while maintaining Quality of Service (QoS) standards. The proposed method, incorporating the Crossover and Mutation (CM)-centered Marine Predator Algorithm (MPA), focuses on optimizing resource scheduling and utilization within VEC networks. Key features of the Vehicular network model, including mobility patterns, transmission medium, bandwidth, storage capacity, and packet delivery ratio, are extracted and refined using the Elephant Herding Lion Optimizer (EHLO) and modified Fuzzy c-means (MFCM) algorithms. These refined attributes are stored within a cloud server infrastructure to create an agile resource allocation system. Extensive MATLAB simulations demonstrate the effectiveness of our approach in addressing resource allocation challenges, meeting modern application demands and ensuring QoS. In an increasingly interconnected world reliant on real-time data processing, this research offers potential to enhance VEC network performance and reliability for a more efficient and connected future.

Future scope

The suggested CM-MPA model for resource allocation in Vehicular Edge Computing (VEC) networks provides numerous opportunities for further investigation and enhancement. Scalability testing on large-scale vehicular networks with varying densities and traffic conditions can demonstrate its usefulness in real-world situations. Integrating the model with new technologies like 5G/6G networks, IoT-enabled cars, and smart city infrastructure might help to improve communication efficiency and support latency-sensitive applications. Its robustness will be enhanced by its capacity to react dynamically to unanticipated mobility patterns and changing network topologies. Optimization for energy efficiency, such as the use of renewable energy sources for edge servers, can help to increase sustainability. Expanding the approach to allow for cross-cloud interoperability will result in seamless resource management across many cloud platforms The suggested CM-MPA model for resource distribution at the vehicular edge enhances decision-making skills. Real-world deployment in actual vehicular networks and smart transportation systems will provide valuable insights while maintaining the model’s scalability and operational success.