Introduction

Each passing day witness’s faster evolution in technology in the field of engineering. Optimization techniques are proving to be the preferred technique in an incredibly diverse range of fields1,2. Optimization techniques are being increasingly used in diverse fields ranging from mechanical and electrical to civil and aerospace fields because these methods can result in greater efficiency, cost-effectiveness, and improved performance in overall systems3,4. Accelerating urbanization requires a careful articulation of building geometric parameters at least in reference to stability and performance levels5,6,7. However, China, as an earthquake-prone country, urban seismicity is the main disaster center when earthquakes occur8. Therefore, improving the seismic performance (SP) of high-rise buildings to safeguard people’s lives and properties has become an important research topic in the field of structural engineering9,10,11. During an earthquake, building structures (BSs) need to convert seismic energy (SE) into other forms of energy for dissipation12,13. Conventional seismic structures of buildings consume SE mainly through the walls, columns, beams, and other components in the main body of the building. These components are damaged to varying degrees during earthquakes, thus counteracting the SE. Therefore, traditional seismic design (SD) methods often rely on increasing structural stiffness and strength, but this brings limitations in the form of increased cost of construction and increased weight of the BS14. The viscous damper (VD), as an efficient energy dissipation device, is gradually being used in the design of seismic-damped structures15. A building damper is a device installed in the structural system of a building to mitigate the structural response to external actions such as earthquakes and wind16. They usually achieve energy dissipation through friction, viscous or elastic materials. Vibration control systems show great promise for effective vibration control17,18. They also contribute significantly to increasing structural stability under dynamic loading19,20,21. The VD is capable of generating damping forces by displacing relative velocities, which effectively reduces the response of the structure under seismic action and improves the SP and comfort of the structure20,22. To improve the SP of the BSs and to offer assistance and a point of reference for the design of innovative and effective seismic-resistant structures, the study, in this context, analyzes the parametric properties of VD in BSs using the energy method and modifies the arrangement position of VD based on the displacement. Rheological optimization, akin to 3D concrete printing, can enhance damper placement, while methods like Neural ODEs and Neural Networks optimize system dynamics and parameter estimation23,24,25. Therefore, applying multi-objective optimization techniques to the optimal placement of viscous dampers with the view of enhancing seismic performance without extra cost and with a minimized structural weight is the most novel aspect of this study. Besides bridging the gap in traditional methods, the findings lay a very good foundation for next-level seismic design. The research contains four main parts. The second part is to carry out a review of the current status of research on seismic strengthening of BSs and VD at home and abroad. The third part carries out the design of VD damping structures. Research on the displacement-based restoring force (RF) model of VD and the design of seismic-damped structures is shown in the first section. Research on the design and analysis approach of seismic-damped VD structures based on multi-objective optimization is presented in the second section. The fourth part validates the design of displacement-based VD damping structures.

The paper provides an original methodology to optimize seismic performance in building frames by optimizing placement of viscous dampers in displacement-based design. As compared to traditional methods where structural strength and stiffness is targeted to mitigate seismic response, this paper provides an original multi-objective optimality technique to optimally place viscous dampers to absorb energy better while ensuring structural stability without contributing to building cost or weight. Additionally, displacement-based damping design is an original technique to mitigate interstory displacement angles, acceleration, and storey displacement during earthquakes. This technique provides an efficient better seismic damping method, particularly in seismic-prone locations where high rise buildings have been constructed. This paper bridges the gap between traditional seismic design practices and advanced optimality practices by providing an efficient technique to mitigate earthquake-induced damage while ensuring building stability.

Related works

Numerous academics have stressed the importance of seismic strengthening for BSs, and numerous specialists and scholars have conducted extensive research and produced numerous findings. To predict the seismic limit state capacity of BSs under earthquakes, Kazemi F and other researchers proposed to utilize machine learning techniques in combination with the development of data-driven techniques to design a machine learning-based model for predicting the flexural seismic response of reinforced concrete (RC). The model utilized an extreme gradient enhancement algorithm to improve the artificial neural network architecture. The results revealed that the model effectively reduces the analytical effort and computational cost of prediction with high effectiveness26. Leyva H et al. proposed to design the optimal seismic structure of the BS using 3D RC technique combined with non-dominated sorting genetic algorithm. The method designed a 3D frame structure based on supporting frames such as beams and columns, and used this to establish two objective functions that constrain the building cost in one and SP in the other. The outcomes suggested that the method effectively reduces the total structural cost while guaranteeing the SP of the building27. Mele A and other researchers, in order to predict building structural changes under earthquake and landslide disasters, proposed to construct a building structural deformation detection model by using differential synthesis technique combined with aperture radar interferometry deformation data. The model utilized a code-based seismic safety assessment method to implement a nonlinear static analysis procedure to judge the deformed structure. The results indicated that the method can timely predict and warn the building deformation structure under earthquake and landslide disasters28. Tarque N’s research team proposed a seismic reinforcement construction method in an attempt to improve the SP of single-story adobe houses. The method utilized nylon ropes to control the reinforcement of the adobe wall and constructed a rope mesh reinforcement system outside the adobe wall to prevent wall displacement. The test results demonstrated that the reinforcing approach may successfully lower seismic risk and preserve structural integrity in the face of powerful earthquakes29. To improve the SP of RC bridges, the research team of Khedmatgozar Dolati S S proposed to utilize plate rubber bearings in conjunction with VD for the structural design of bridges. The plate rubber bearings acted as fuses to partially isolate the substructure of the abutment from the superstructure and the VD acted as a passive energy dissipation device to dissipate the SE. The design can effectively reduce residual displacement following an earthquake to almost nil, according to the results30.

The VD has been widely used in the fields of construction engineering and machinery due to its advantages such as simple structure, stable performance and long life. To deduct the economic cost of improving the SP of BSs, Karami M and other scholars developed a method to enhance the SP of BSs by improving the control device. The method proposed the application of fluid viscous damper (FVD) and the use of genetic algorithm to achieve the minimum life cycle cost of the key design parameters along with nonlinear analysis using endurance time method. The results revealed that the FVD with nonlinear structure reduced the total seismic loss by 40% compared to the damper with linear structure31. To analyze the action of different VD as an energy dissipation device on BSs under earthquake, Kookalani S et al. proposed to analyze a seven-story steel framed structure equipped with FVD using various parameters. The installation of longitudinal nonlinear FVD can considerably lessen the seismic response, according to the outcomes32. Bhandari et al. (2017) studied response of base-isolated structures to both near-field earthquakes and far-field earthquakes and confirmed that in near-field earthquakes, especially in fling-step earthquakes, base isolation is not as effective. Their work depicts that inelastic response can be produced by base isolation in design-level earthquakes33. Bhandari et al. (2018) compared capacity spectrum method (CSM) in seismic demand prediction in design-level earthquakes in base-isolated frames and confirmed that while in design-level earthquakes this method is efficient, in extreme earthquakes this is not always true34. Additionally, Bhandari et al. (2019) confirmed that earthquakes in near locations, especially in those with increased PGA to PGV ratios, have an increased potential to cause damage in base-isolated structures, highlighting sensitivity in this context35. Chalarca et al. (2024) studied the effect of fluid viscous dampers in floor acceleration response in steel moment-resisting frames to far-field ground motion and confirmed that diverse dampers’ configurations can significantly change floor acceleration response to an extent where increased floor accelerations can be achieved compared to undamped constructions36. Ziraoui et al. (2025) compared seismic response in SMRFs retrofitted by bracing systems and nonlinear viscous dampers to both near-field ground motion and far-field ground motion and confirmed that seismic risk was significantly reduced by introducing nonlinear viscous dampers in constructions where X-braced systems produced most efficient response37.

Esfandiyari R’s research team, in order to analyze the main working principle of the VD, proposed to simulate the behavior of the bypass VD using a simplified Max model and to conduct a comprehensive case study of a diagonally braced RC building fitted with this VD. The nonlinear time course study demonstrated that the bypass VD may greatly increase the SP of both structural and nonstructural elements, and that the VD can transform the input energy into heat38. Sun Y and several researchers presented a gigantic galvanic fluid damper with numerous electrodes working in shear mode to control the vibration suppression performance of smart fluid materials like galvanic and magnetorheological. With a dampening effect of 91.03% and an adjustable range of 43.8%, the megacurrent variable-fluid damper was found to have significantly suppressed vibration39. To design an optimization method for seismic strengthening of BSs, Idels O et al. proposed to construct an inelastic flexural frame using a nonlinear FVD in combination with a negative stiffness device, and to constrain the performance using an optimization objective of minimizing a cost-related objective function. The results indicated that the method effectively improved the robustness of the BS40.

In summary, although there are a lot of research results on SD of BSs and VD, the improvement of SP of buildings by the above research mainly focuses on the BS itself and under specific conditions. It is rare to find studies that use multi-objective optimization theory to optimize the placement of VD to improve the SP. Therefore, by analyzing the optimal placement and connection forms of VD in the building, the study designs displacement-based VD damping structures to further improve the SP of the BS.

Research gap and objectives

Though a great deal of research is ongoing on SD and VD, in general, research has, nevertheless, focused on the body of the structure to carry out analyses under specific situations, leaving a void in the research works for optimization of VD placement for enhancing overall SP. There has been limited research into finding, using multi-objective optimization techniques, the optimal VD distributions to minimize displacement and energy demand.

This study aims to fill the gap by proposing multi-objective optimization techniques for designing displacement-based viscous damping systems. The researchers set out to achieve the following objectives:

  1. 1.

    To develop viscous dampers with specific identify carbon parameters in enhancing the overall stiffness performance of buildings.

  2. 2.

    To devise an optimal strategy for positioning the dampers based on displacement and energy parameters.

  3. 3.

    To validate the efficiency of the presented Figure against various seismic scenarios.

Design of viscous damper damping structures

A massive galvanic fluid damper with many electrodes operating in shear mode was regulated the vibration suppression capabilities of smart fluid materials such as magnetorheological and galvanic41. It was discovered that the megacurrent variable-fluid damper greatly reduced vibration, with a 91.03% damping effect and a 43.8% adjustable range39.

Displacement-based resilience modeling of viscous damper and design of seismic-damped structures

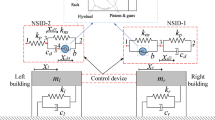
The performance of VD, which is the fundamental component of VD design, is primarily described by the RF model42. An appropriate RF model can achieve the best simulation effect, so as to accurately analyze the performance of the VD. Common RF models for VD include linear model, linear Kelvin model, linear VD (Maxwell) model, and Wiechert model. In the numerical simulation of VD, the Kelvin model and Maxwell model are usually used43. The Maxwell model, on the other hand, consists of an elastic element and a viscous element in series and is more suitable for simulating viscous fluid dampers44. Therefore, in order to more comprehensively analyze the performance of VD under various operating conditions, the study utilizes the Kelvin model in combination with the Maxwell model as the RF model of VD for simulation respectively. The Kelvin model is shown in Fig. 1.

Fig. 1
figure 1

Kelvin model diagram.

Full size image

In Fig. 1, \({F_d}\) denotes the RF provided by the VD. \({k_d}\) denotes the stiffness coefficient. \({u_d}\) and \({\dot {u}_d}\) denote the relative deformation (RD) of the two ends of the VD. \({c_d}\)denotes the damping coefficient (DC). When the Kelvin model is set to zero stiffness, the model degenerates into a viscous unit that simulates the effect of the storage stiffness of the VD on the damping produced by the linear VD36. The mathematical expression for the RF of the Kelvin model is shown in Eq. (1).

$${F_d}={k_d}{u_d}+{c_d}{\dot {u}_d}={F_0}\sin \left( {\omega t+\varphi } \right)$$
(1)

As shown in Eq. (1), this RF simulates the RF provided by the VD under sinusoidal loading. \({F_0}\) denotes the maximum outward force of the VD. \(\varphi\)denotes the phase difference between the displacement and the VD. The linear behavior of the VD under small-amplitude vibration can be accurately described in the Kelvin model, and its damping characteristics are more stable. The Kelvin model is suitable for simulating the characteristics of viscoelastic dampers and is an effective tool for designing and optimizing VD. Moreover, Maxwell model is commonly used to simulate VD, whose structure mainly consists of cylinder, piston rod, pin head and piston45. Maxwell model is shown in Fig. 2.

Fig. 2
figure 2

Maxwell model diagram.

Full size image

The Maxwell model fits the nonlinear behavior of VD with nonlinear boundary characteristics, as displayed in Fig. 246. Its damper output force is proportional to the RD of the ends, while the elastic unit output force is inversely proportional to the RD of the ends. This model focuses more on the frequency dependence of the VD and is more suitable for simulating the response behavior of BSs at higher amplitudes, higher frequencies and with less damping. The mathematical expression for the RF of the Maxwell model is shown in Eq. (2).

$${F_d}={C_0}{\dot {u}_d}$$
(2)

In Eq. (2), \({C_0}\) denotes the DC in the case of zero frequency. Conventional SD of BSs tends to cause large losses to the structure, including renovation losses and equipment losses. Therefore, in order to minimize these losses, displacement-based VD damping structures are designed by investigating the location-based adjustment of equipment to improve the SP of BSs. In this design, the study considers the VD in a BS as a single-degree-of-freedom system (SDFS). Moreover, it is given an additional damping ratio (DR) and target displacement (TD) at a set level. The response spectrum of this damper’s displacement in the vibrating environment is then used to compute the equivalent TD and the matching equivalent period. To ascertain the forces on each building floor during seismic circumstances, the base shear of the structure can then be computed and the shear forces (SF) can be distributed throughout the structure’s floors. Finally, based on the proportion of SFs carried by the VD, the SFs carried by the dampers in each floor of the BS are determined and the appropriate dampers are selected for the adjusted design. The design flow of displacement-based VD damping structures is shown in Fig. 3.

Fig. 3
figure 3

Design flow of displacement-based viscous damper damping structures.

Full size image

In Fig. 3, in the design process of displacement-based VD damping structures, a suitable performance objective is first determined and the lateral displacement (LD) distribution of the BS is calculated with this objective. At the same time, the nonlinear multi-degree-of-freedom system is equated to a SDFS. After determining the equivalent DRs corresponding to the TDs, the base shear of the BS and the seismic actions at each floor are calculated. At the same time, the DC is calculated based on the additional DR. After that, the dampers are installed in accordance with the determined DCs, and the seismic response of the structure is determined by analyzing the seismic damping effect of the BS over time using the RF model. If the structural seismic response results are unsatisfactory, then return to the TD determination stage to reset the TD. If satisfactory, the process is concluded. Equation (3) shows how the LD distribution curve is calculated.

$$D\left( x \right)=\frac{{{u_H}}}{2}\left( {\frac{{3x}}{H} - \frac{{{x^3}}}{{{H^3}}}} \right)$$
(3)

In Eq. (3), \(D\left( x \right)\) denotes the LD at \(x\).\(H\) denotes the height of the BS. \({u_H}\)denotes the displacement at the apex of the BS. This formula for calculating LDs is only applicable to frame structures that are symmetrical and have a regular arrangement of members, which is quite different from the actual situation47. Therefore, the study is based on the first-order modes of the structure to carry out the formula for calculating the LD applicable to the building steel structure, as shown in Eq. (4).

$${\Delta _i}=\frac{{{\omega _\theta }{\theta _c}{h_i}\left( {4H - {h_i}} \right)}}{{\left( {4H - {h_1}} \right)}}$$
(4)

In Eq. (4), \({\Delta _i}\) is the displacement of the ith floor BS. \({\theta _c}\) denotes the angular limit of interstory displacement. \({\omega _\theta }\) denotes the amplification adjustment factor. \({h_i}\) denotes the height of the ith floor BS from the bottom. The equivalent displacement expression for the SDFS is shown in Eq. (5).

$${\Delta _d}=\frac{{\sum\nolimits_{{i=1}}^{n} {{m_i}\Delta _{i}^{2}} }}{{\sum\nolimits_{{i=1}}^{n} {{m_i}{\Delta _i}} }}$$
(5)

In Eq. (5), \({\Delta _d}\) is the equivalent displacement. \({m_i}\) is the mass of the ith floor BS. The mathematical expression for equivalent height is shown in Eq. (6).

$${\Delta _H}=\frac{{\sum\nolimits_{{i=1}}^{n} {{m_i}\Delta _{i}^{2}{h_i}} }}{{\sum\nolimits_{{i=1}}^{n} {{m_i}{\Delta _i}} }}$$
(6)

In Eq. (6), \({\Delta _H}\) denotes the equivalent height. The mathematical expression for equivalent mass is shown in Eq. (7).

$${\Delta _m}=\frac{{\sum\nolimits_{{i=1}}^{n} {{m_i}{\Delta _i}} }}{{{\Delta _d}}}$$
(7)

In Eq. (7), \({\Delta _m}\)denotes the equivalent mass. The displacement response spectrum is mainly used to describe the maximum displacement response of a SDFS with different intrinsic periods under a given seismic excitation48. The mathematical expression for the displacement response spectrum is shown in Eq. (8).

$${S_d}={\left( {\frac{T}{{2\pi }}} \right)^2}{S_a}={\left( {\frac{T}{{2\pi }}} \right)^2}\alpha g$$
(8)

In Eq. (8), \({S_d}\) denotes the equivalent displacement response spectrum of the SDFS. \({S_d}\) denotes the self-oscillation period of the BS. \({S_a}\) denotes the acceleration response spectrum and \(\alpha\) denotes the seismic influence coefficient. \(g\) denotes the gravitational acceleration.

Design and analysis method of viscous damper damping structure based on multi-objective optimization

After the design of displacement-based VD damping structures, the structural performance of their energy dissipation and damping needs to be evaluated by using time-course analysis (TCA) method and so on. The analysis methods of VD damping structures mainly include time course analysis method and energy analysis method49. TCA analysis is a dynamic analytic technique used primarily to assess and forecast a structure’s response to dynamic loads like earthquakes. It solves a structure’s differential equations of motion through stepwise integration50. Since the seismic damping structure of a building mainly consists of energy dissipating members and main structure, the study decomposes the main body of the model into two sections, energy dissipating members and main structure, in performing the analysis of the seismic damping structure. The structural reaction of the structure at all times can be obtained by applying the time course analysis approach for building performance analysis, allowing for a more thorough evaluation of the structure’s seismic dampening effect and performance51. The dynamic equations for the time course analysis are shown in Eq. (9).

$$\left\{ {{F_{eq}}\left( t \right)} \right\}=\left\{ {{F_I}\left( t \right)} \right\}+\left\{ {{F_D}\left( t \right)} \right\}+\left\{ {{F_S}\left( t \right)} \right\}$$
(9)

In Eq. (9), \(\left\{ \cdot \right\}\) denotes the matrix, \({F_{eq}}\) denotes the elastic-plastic force. \({F_I}\) denotes the inertial force of the mass. \({F_D}\) denotes the damping force and \({F_S}\) denotes the internal force. The mathematical expression for the matrix equilibrium of the BS is shown in Eq. (10).

$$R\left( t \right)=\left\{ M \right\}a\left( t \right)+\left\{ C \right\}v\left( t \right)+\left\{ K \right\}d\left( t \right)+{R_{NL}}\left( t \right)$$
(10)

In Eq. (10), \(R\left( t \right)\) denotes the external load on the BS. \(M\), \(C\), and \(K\) denote mass, proportional damping, and stiffness, respectively. \(d\left( t \right)\), \(v\left( t \right)\), and \(a\left( t \right)\) denote the displacement, velocity, and acceleration at the moment of time node \(t\), respectively. \({R_{NL}}\left( t \right)\)denotes the sum of nonlinear cells. The energy analysis method can take into account the energy changes in the seismic case, and therefore it can well reflect the plastic damage produced by the BS under vibration conditions52. The energy analysis approach model is shown in Fig. 4.

Fig. 4
figure 4

Energy analysis approach model.

Full size image

As shown in Fig. 4, energy analysis models are generally categorized into absolute and relative displacement53. Absolute displacement analysis focuses on the energy changes of the overall structure, while relative displacement analysis focuses on the energy transfer and consumption among individual members54. Therefore energy analysis models can provide a more comprehensive assessment of the performance and damage of BSs under seismic conditions. The energy analysis model under absolute displacement is shown in Eq. (11).

$$cv^{\prime}\left( t \right)+m\bar {a}\left( t \right)+{f_1}+{f_2}=0$$
(11)

In Eq. (11), \(m\) denotes the mass factor and \(c\) denotes the damping factor. \(v^{\prime}\left( t \right)\) and \(\bar {a}\left( t \right)\) are the velocity and absolute acceleration of the SDFS relative to the ground surface, respectively. \({f_1}\) denotes the RF of the BS and \({f_2}\)denotes the RF of the energy dissipator of the VD55. The energy analysis model under relative displacement is shown in Eq. (12).

$$cv^{\prime}\left( t \right)+ma^{\prime}\left( t \right)+{f_1}+{f_2}= - mg\left( t \right)$$
(12)

In Eq. (12), \(a^{\prime}\left( t \right)\) represents the acceleration of the SDFS relative to the ground surface. The study combines the TCA analysis method with the energy analysis method, which can reflect the response of BSs under earthquakes more comprehensively. The traditional VD arrangement method fails to take into account the DC and energy distribution of the structure under seismic conditions. Therefore, the study optimizes the arrangement of VD. To obtain the optimal damping effect, a suitable objective control function is selected and the dampers are distributed logically. The problem of allocation of multiple dampers belongs to the multi-objective optimization problem. The study comprehensively applies the traditional multi-objective optimization methods such as the constraint method and the weighted coefficient summation method to design a structural design method based on multi-objective optimization for vibration damping of VD, as shown in Fig. 5.

Fig. 5
figure 5

Multi-objective optimization based structural design method for vibration damping of viscous damper.

Full size image

In Fig. 5, the DC and energy distribution of the structure are considered in the design process of VD damping structure based on multi-objective optimization. Firstly, the DCs are studied and calculated, and the DCs are reasonably distributed using the multi-objective optimization method. Meanwhile, after calculating the energy distribution, the total hysteretic return dissipation of the structure is determined. Finally, the damping performance is evaluated by combining the time course analysis method and energy analysis method. Throughout the process, it is determined whether the performance meets the requirements or not. If it is not satisfied, it is returned to the displacement-based VD damping structures design stage and re-optimized and adjusted. If satisfied, the final damping structure design solution is output. The assignment objective function of the multi-objective optimization method is shown in Eq. (13).

$${n_i}=\frac{{A \times N \times {\theta _i}}}{{\sum\nolimits_{{i=1}}^{n} {{\theta _i}} }}+\frac{{B \times N \times {a_i}}}{{\sum\nolimits_{{i=1}}^{n} {{a_i}} }}+\frac{{C \times N \times {v_i}}}{{\sum\nolimits_{{i=1}}^{n} {{v_i}} }}$$
(13)

In Eq. (13), \({n_i}\) denotes the number of VD arranged at the ith floor of the BS. \(A\), \(B\) and \(C\) all denote weighting factors and satisfy \(A+B+C=1\). \(N\) denotes the total number of VD. \({\theta _i}\) denotes the interstory displacement angle (ISDA) of the ith floor of the structure. \({a_i}\) and \({v_i}\)denote the acceleration and velocity of the ith layer structure, respectively56. The formula for the DC is shown in Eq. (14).

$${C_i}=\frac{{{F_{d,i}}}}{{2\pi {\Delta _{d,i}}}}$$
(14)

In Eq. (14), \({C_i}\) denotes the DC at the ith floor of the BS. \({F_{d,i}}\) denotes the SF on the damper arranged at the ith floor of the BS. \({\Delta _{d,i}}\) denotes the axial displacement of the damper at the \(i\) level of the BS. The formula for the displacement lateral force is shown in Eq. (15).

$${F_i}=\frac{{{V_b} \times {m_i}{\Delta _i}}}{{\sum\nolimits_{{i=1}}^{n} {{m_i}{\Delta _i}} }}$$
(15)

In Eq. (15), \({F_i}\) denotes the equivalent displacement lateral force at the ith floor of the BS. \({m_i}\) denotes the gravity load value at the ith floor. \({V_b}\) denotes the base SF. \({\Delta _i}\) denotes the TD value for the design of the ith floor.

Validation of the design of displacement-based viscous damper damping structures

The study first designs a damping structure test rig to verify the performance of the damping structures. Then the damper distribution Figure is designed according to the project profile and the displacement-based VD damping structures performance is verified by the method of controlled experiments. Finally, the practical application of the structural design is verified under natural seismic wave (NSW) conditions.

Design of vibration-damped structural test benches

In order to validate the effectiveness of displacement-based VD damping structures design, the study constructed a vibration test rig to simulate seismic conditions. To improve the effectiveness of the SD experiments, the structural frame model of the building was scaled down to a 1:3 scale using the finite element analysis software. The components in the structural frame of the vibration test bench include plates, columns, and beams in the BS. Figure 6 displays the vibration damping structure model derived from a finite element numerical simulation.

Fig. 6
figure 6

Model of vibration-damped structure based on finite element numerical simulation.

Full size image

The study first tested the mechanical characteristics of the experimental bench in order to analyze the efficiency of the output force under various working conditions. This allowed for the testing of El-Centro waves as simulated seismic waves, which helped to assess the efficacy of the vibration experiments carried out on the vibration-damped structural experimental bench. The comparison of the mechanical properties of the vibration-damped structural experimental bench is shown in Fig. 7. In the case of simulated seismic waves, the displacements generated by the experimental bench are highly consistent with the displacement waveforms simulated by the numerical simulation software. This indicates that the experimental environment is reasonably arranged and lays the foundation for subsequent experimental studies.

Fig. 7
figure 7

Comparison of mechanical properties of experimental bench with shock absorbing structure.

Full size image

Project overview and damper distribution design

The 12-story RC frame construction project is the subject of this investigation. The project has an 8 degree seismic intensity and a 0.2 g basic seismic acceleration. rating II is the site categorization, and Grade I is the seismic rating. The thickness of the building floor slab is 130 mm, and the seismic defense category is the standard defense category. The concrete strength grade of the beams, slabs and columns in the concrete frame structure is C30, and the materials of its hoop reinforcement, columns and beams are selected as HRB400. The dynamic properties of the building are summarized in Table 1. The displacement angle limit values of the different BS systems are shown in Table 2. These limit values are based on the provisions outlined in GB 50,011 − 2010 for Seismic Design of Buildings in China.

Table 1 Dynamic properties of the 12-Story RC frame Building.
Full size table
Table 2 Limit values of displacement angles for different Building structure systems.
Full size table

To verify the effectiveness of the displacement-based VD damping structures design, the study set up three different damper arrangement methods for controlled experiments. Among them, Fig. 1 is the displacement-based VD arrangement. Figure 2 arranges the VD uniformly by floor. Figure 3 arranges the damper in proportion to the displacement angle between floors.

Performance verification of displacement-based viscous damper damping structures

To verify the effectiveness of displacement-based VD damping structures design in terms of ISDA damping performance, the study comparatively analyzes the change in interstory displacement of engineered BSs in Y direction with three figures. The comparison of the change in ISDA for different arrangement figures is shown in Fig. 8. The different VD arrangement figures have a greater effect on the ISDA changes in the lower floors, especially in floor 2 where the displacement angle changes are the largest. In Fig. 8(a), the displacement angle of Fig. 1 in floor 2 is 0.0018°, which is reduced by 41.93% compared to the displacement angle of 0.0031° in the original BS. In Fig. 8(b), the displacement angle of Fig. 2 in floor 2 is 0.0021°, which is reduced by 32.25% compared to the original structure. In Fig. 8(c), the displacement angle of Fig. 3 in floor 2 is 0.0019°, which is reduced by 38.70% compared to the original structure. In summary, the design of displacement-based VD damping structures effectively reduces the ISDA of the BS under seismic conditions and improves the seismic capacity of the BS.

Fig. 8
figure 8

Comparison of the change of interlayer displacement angle for different arrangement figures.

Full size image

To further verify the SP of the displacement-based VD damping structures design, the study compares the acceleration changes of different arrangement figures as shown in Fig. 9. In Fig. 9(a), the acceleration change of Fig. 1 in floor 12 is the most significant. In this case, the acceleration of Fig. 1 is 1.44 m/s², which is 16.27% less than the 1.72 m/s² of the original BS. In Fig. 9(b), the acceleration of Fig. 2 in floor 12 is 1.54 m/s², which is a 10.46% reduction compared to the original structure. In Fig. 9(c), the acceleration of Fig. 3 in floor 12 is 1.58 m/s², which is reduced by 8.13% compared to the original structure. In conclusion, the displacement-based VD damping structures design has superior damping effect.

Fig. 9
figure 9

Comparison of acceleration changes for different arrangement figures.

Full size image

A comparison of the change in storey displacement for different arrangement figures is shown in Fig. 10. The storey displacements of the BS in the seismic environment increase with the height of the floors. There is little difference in the effectiveness of the three figures in controlling the storey displacements for the high and low floors. But for the intermediate floors, the control effect of Fig. 1 is significantly better. In Fig. 10(a), the layer displacement control effect of Fig. 1 has the best performance in floor 9. Its layer displacement is 49.9 mm, which is 6.72% less compared to 53.5 mm in the original BS. In Fig. 10(b), the layer displacement of Fig. 2 at this point is 51.0 mm, which is a reduction of 4.67% compared to the original structure. In Fig. 10(c), the layer displacement of Fig. 3 is 50.1 mm, which is a 6.35% reduction compared to the original structure. In conclusion, the storey displacement change of the BS during an earthquake is successfully decreased by the displacement-based VD damping structures design.

Fig. 10
figure 10

Comparison of layer displacement changes for different arrangement figures.

Full size image

A comparison of the change in storey shear for different arrangement figures is shown in Fig. 11. As the floor of the BS increases, the layer shear decreases gradually. The layer SF of the structure is the largest at the 1st floor, and the layer SF of the original BS is 2115KN. In Fig. 11(a), the layer SF of Fig. 1 at the 1st floor is 1430KN, which is reduced by 32.38% compared with that of the original BS. In Fig. 11(b), the layer shear at this point in time for Fig. 2 is 1526KN, which is a 27.84% reduction compared to the original structure. In Fig. 11(c), the layer shear of Fig. 3 is 1544KN, which is reduced by 26.99% compared to the original structure. In conclusion, the displacement-based VD damping structures design has superior damping performance.

Fig. 11
figure 11

Comparison of changes in layer shear for different arrangement figures.

Full size image

Practical application verification

To verify the performance of displacement-based VD damping structures design in real seismic waves, five sets of NSWs are selected for the study for experimental verification. The floor-to-floor SFs under different NSWs are shown in Table 3. The maximum storey shear of the BS in both X and Y directions occurs at the lower floors. The maximum storey shear occurs under NSW 3, which is 4704.69 KN and 4572.10 KN, respectively. The minimum storey shear generated in the X and Y directions in the high storey under NSW 2 is 821.46 KN and 848.94 KN, respectively. In conclusion, it can be observed that the displacement-based VD damping structures design has shown superior damping performance under different seismic waves.

Table 3 Floor-to-floor shear under different natural seismic waves.
Full size table

The floor LDs under different NSWs are shown in Fig. 12. In Fig. 12(a), in the X-direction, the floor LD of 12-story building under NSW 3 reaches the maximum value of 21.01 mm. In Fig. 12(b), in the Y-direction, the floor LD of the same 12-story building under NSW 3 reaches the maximum value of 22.32 mm. In conclusion, the displacement- based VD damping structures design exhibits excellent SP under actual seismic wave conditions.

Fig. 12
figure 12

Floor lateral movement under different natural seismic waves.

Full size image

The ISDAs of the floors under different NSWs are shown in Fig. 13. In Fig. 13(a), the maximum ISDA of the middle floor under seismic wave 3 in the X direction is 0.0011 rad, i.e. 1/909. This value is less than the displacement angle limit value of 1/1000, and therefore meets the code requirements for seismic-resistant structures of buildings. In Fig. 13(b), the maximum ISDA in the Y direction is also 1/909, which meets the code requirements for seismic-resistant BSs. In summary, the displacement-based VD damping structures design has enough SP under actual seismic waves to satisfy the code requirements.

Fig. 13
figure 13

Interstory displacement angle of the floor under different natural seismic waves.

Full size image

Conclusion

Building structures face considerable risk of earthquakes. The present study offers an example of the effective designs of displacement-based viscous dampers in the enhancement of seismic performance through optimization of the damping installation and configurations in tall buildings and high-rise structures. These works demonstrated quite an opportunity to reduce seismic-induced damage, enhancing compliance with seismic codes for high-rise structures.

Key Findings:

  1. 1.

    The proposed VD design based on displacement criteria helped to bring the interstory simple angle down to 0.0018°, which is a reduction of 41.93% from the original structure.

  2. 2.

    Structural acceleration fell to 1.44 m/s², which is a 16.27% decrease compared with the original design.

  3. 3.

    The displacement layers are reduced to 49.9 mm compared to the original structural capacities, 53.5 mm in total-a decrease of 6.72%.

  4. 4.

    Layer shear force reduced by 32.38% from 2115 KN to 1430 KN.

  5. 5.

    Peak story shear forces under natural seismic wave conditions were 4704.69 KN in the X-direction and 4572.10 KN in the Y-direction.

  6. 6.

    Under NSW conditions, maximum lateral displacements occurred of 21.01 mm in X and 22.32 mm in Y.

  7. 7.

    The maximum angle of interstory drift under NSW conditions was 1/909, which is still within acceptable limits according to seismic code provisions.

The results of this research have shown that displacement-based variable damping systems can minimize seismic risk. The research has yet to encompass more real-life situations, such as material variability and construction quality, which would likely bridge the applicability gap further.

Reflections on study and future recommendations

The current work provides helpful results to design viscous dampers to yield improved seismic performance in building frames. Practical implications of this work suggest that displacement-based design in viscous dampers can significantly improve structural stability in seismic loads by reducing interstory displacement angles, displacement in storesy, and acceleration. It is an economic yet efficient seismic damping method that does not require additional structural weights or additional building constructions. Furthermore, incorporation of multi-objective optimality methods provides future seismic design directions.

In future projects, several areas to be improved upon have been suggested. First, validation in reality is needed in extensive scales of building constructions in various seismic environments. Secondarily, future tests can be carried out to determine the influence of material variation and workmanship in building in influencing performance in dampers. Application of advanced algorithms in machine learning to further optimize placement in dampers and examining dynamic and complicated building systems can further enhance seismic performance prediction accuracies. Thirdly, durability over a long duration in seismic activities should be studied to prove the viability and effectiveness of the developed design in practice.

Limitations of the study

While this paper provides an overall methodology to design displacement-based viscous damper damping systems, certain limitations should be emphasized. First, this paper is predominantly based upon numerical modeling and laboratory tests in idealized conditions that can’t always represent reality in aspects of variation and complexity in field conditions. Parameters such as material properties, workmanship in construction, and effects of environmental factors weren’t studied in entirety. Second, idealized placement and response have been employed in this paper while in reality installation tolerance and maintenance can affect performance. Third, while multi-objective algorithms have been employed to optimize placement in this paper, further work is to be conducted to integrate additional aspects in reality, including cost minimization and durability over extended periods.