Introduction

Reflectarray antennas (RAs) have the advantages of simple feed network, low cost and light weight compared with phased arrays and parabolic antennas, which are suitable for satellite formation flying, especially on cheap CubeSats with high performance1. Unfortunately, the conventional medium-sized RAs suffer from the problem of narrow bandwidth2. Consequently, several representative methods have been proposed, such as multi-resonance3,4,5,6, multi-layer7,8,9,10, and subwavelength structures11,12. Significantly, broadband elements are typically implemented by combining the above three methods with traditional cell design techniques such as dimensional variation13,14, loading phase delay lines15,16, and rotating elements17,18.

Various dipoles, including rectangles, arcs, and spirals, are most commonly used to design broadband elements in virtue of their flexible shapes and diversified combinations. Although the wide bandwidth was obtained by adopting bilayer construction to avoid insufficient phase range8,19, the lower profile element is usually required in terms of the cost in the application of CubeSats. As for the single-layer configuration, the desirable phase response was optimized by adjusting the proportional relationship between different parallel rectangular or cambered dipoles 20,21,22. An even broader bandwidth could be achieved by applying those diversified combination structures with extremely high flexibility and freedom23,24, the complicated structure and the cumbersome optimization process undoubtedly increases the design complexity.

Compared to conventional dipoles, the magnetoelectric dipoles constituted by orthogonally placed patches were often employed to design wideband antenna owing to the ingenious electromagnetic complementation25,26. Moreover, simplification of the perpendicular metals with replacement by metallized vias leads to further miniaturization and ease of manufacturing, which as well introduced an efficient approach to design wideband RAs with low profile and free airgap27,28,29,30,31. Similarly, the sensitivity of the incidence angle was significantly decreased by optimizing the magnetic resonance that was beneficial to further improving broadband performance32. However, the vertical structure for magnetic resonance of the conventional magnetoelectric dipole quite increases the complexity and extremely restricts the tuning capability. In contrast to the circulating current generated by the patch-metallized via-patch structure described above, the open ring patch structure enables a planar implementation. The magnetic resonance structure generated by open rhomboid rings to acquire a planar construction was proposed in33. Nonetheless the broadband performance of the planar magnetoelectric dipole was realized in multi-polarization, the two magnetoelectric resonators were still stacked to meet sufficient phase range.

In this paper, a novel planar equivalent magnetic dipole (EMD) element with simple configuration for single layer broadband RA application is presented, eliminating the need for perpendicular metallized vias. In contrast to conventional electric dipole elements, the current distribution of the EMD element is perpendicular to the gap rather than parallel to it. Notably, the equivalent magnetic dipole is produced by the displacement current at the gap, as opposed to planar circulating currents, which offers an approach for designing single-layer, low-profile, broadband magnetic dipole elements. The reflection response is excited by constructing an equivalent magnetic current source, which reduces design complexity and offers a novel approach for designing magnetic dipoles. Furthermore, the phase continuous tuning within the whole period can be easily achieved by manipulating the physical variation along the cross-polarization direction of the proposed EMDs. An experimental RA operating at X-band is designed and fabricated to verify the broadband performance of the element. The achieved 1.5-dB gain bandwidth of 33.3% with the peak aperture efficiency of 57% indicates the excellent wideband performance of the proposed element as well as its array application.

Methods

Element configuration and operating mechanism

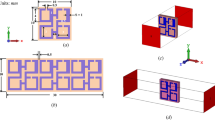
The configuration of the proposed EMD element is plotted in Fig. 1. It consists of an H-shaped patch along the x-direction and two mirrored T-shaped parasitic patches along the y-direction, and all patches are printed on the upper surface of the Rogers RT/duroid 4003 substrate (εr = 3.55, tanδ = 0.0027) with a thickness of 2 mm. An air-layer is placed between the substrate and the metal ground to smooth the phase curves and improve the stability of the phase response at different frequencies, which is beneficial to increasing the element bandwidth4. Figure 2 demonstrates the principle of equivalence when the current is strongly coupled from one patch to another. According to Maxwell’s first law, only the sum of the conduction and displacement currents are continuous in a time-varying electric field. The conduction current Js enters the plate capacitor to form a time-varying electric field that reaches the other plate in the form of a displacement current Jd. According to the equivalence theory, the displacement current can be equivalent to a magnetic current source34,35. The above analysis suggests that it is feasible to use the slot between the patches to realize the design of the magnetic current source. Therefore, double gaps between an H-shaped patch and two coupling T-shaped patches are employed as the proposed EMD resonator.

Fig. 1
figure 1

The configuration of the proposed EMD element.

Full size image
Fig. 2
figure 2

Current distribution and equivalent magnetic sources.

Full size image

In order to further explain the working mechanism of the proposed element, the surface current distribution is shown in Fig. 3(a). Clearly, the energy is coupled from the H-shaped patch into the two parasitic T-shaped patches through the gaps when excited by y-polarized electric field. Figure 3(b) describes that the electric field between the H-shaped patch and T-shaped patches is perpendicular to the gap. The charge on the equivalent capacitive plates forms a time-varying electric field between the plates, resulting in a displacement current in the slot. Furthermore, according to the duality theorem of electromagnetic fields, the phase resonance of the unit cell in y-direction occurs when the EMD resonators extend in the orthogonal direction, which contributes to maintaining the consistency of the cell size in co-polarization direction while further improving the broadband performance.

Fig. 3
figure 3

The field overlays of the EMD element when l1 = 6 mm in y- polarization. (a) The surface current distribution and (b) E-field distribution. And (c) the evolution of EMD element and the corresponding phase curves.

Full size image

The detailed evolutions of EMD element are further compared in Fig. 3(c). It is evident that the original conventional rectangular patches are pretty hard to provide enough phase due to the weak energy of the equivalent magnetic current. Next, the rectangular patch in the middle is replaced with an H-shaped patch, the energy is obviously concentrated, resulting in a significant improvement in reflective resonance. Finally, the rectangular patches on both sides are modeled as T-shaped structures, in which the linearity of the reflection curve is further enhanced to be beneficial to realizing wideband design.

Based on the above analysis, the equivalent magnetic current is determined by the gap distance l3, gap width s, as well as the width of the patch l2, and all parameters are optimized in the High Frequency Structure Simulator (HFSS) software to realize a sufficient phase range along with a linear resonance. Figure 4(a) displays the phase response at different l3. With the increase of l3 from 3 to 7 mm, the phase span decreases from 470° to 340° while the phase linearity displays the tendency of rising at the beginning and declining at the ending. It is suggested that the closer the two EM dipoles are to each other, the stronger the coupling is generated, which contributes to a dramatic variation in the phase curve. As is shown in Fig. 4(b), the phase linearity deteriorates while the range is almost constant when the width of the gap from 0.5 mm to 1.5 mm. Figure 4(c) depicts that the linearity of the phase curve increases as the l2 decreases from 10 to 4 mm. Obviously, the structural parameters around the gap are of great significance for optimizing the.

Fig. 4
figure 4

Reflected phases for different (a) l3, (b) s, and (c) w3 and w4 at 11 GHz. (d) Reflected phases for different incident angles at 11 GHz. The reflection response of the element with different frequency. (e) Reflection phase. (f) Reflection amplitude.

Full size image

broadband characteristics of the unit cell. In addition, the effect of oblique incidences on the reflection phase are also assessed. The phase responses at different incident angles are shown in Fig. 4(d) with a slight variation within 40° compared to the normal incidence. The optimized values of the element parameters are.

as follows, l2 = 4 mm, l3 = 4 mm, w1 = 1.4 mm, w2 = 3 mm, w3 = 0.5 mm, w4 = 0.5 mm, s = 1 mm, h2 = 2 mm, and p = 15 mm.

Figure 4 illustrates the reflection response of the cell between 9–13 GHz. The phase curves have excellent linearity with a range of more than 360° and the curves between the different frequencies remain parallel in Fig. 4(e), indicating that the proposed element has superior broadband characteristics. Figure 4(f) exhibits that the reflection amplitudes are higher than -0.25 dB, which means the unit cell loss is insignificant. With the purpose of analyzing the wideband performance of the proposed EMD element, the reflection phase response of different structures in the EMD element is exhibited in Fig. 5(a). Although the H-shaped patch has a large phase range, it is difficult to meet the 360° phase requirements of the reflectarray due to the single resonant structure with single layer substrate36. Therefore, the reflection phase range can be extended by adding multiple resonant structures around the patch, which is the common method for conventional electric dipoles to improve the bandwidth of the element20,21,23. On the other hand, the phase of a single T-shaped patch remains constant as the gap expands, while the phase of double T-shaped element changes greatly at large sizes, indicating that the coupling between the two patches affects the phase resonance. Importantly, Unit 3 is equivalent to Unit 4 according to the master–slave boundary model of the reflection element1, as is shown in Fig. 5(b). The gap between the two T-patches is also equivalent to an additional magnetic dipole when current is passed in y- direction, which forms a multi-magnetic resonance structure in the EMD element. Similar to conventional electric dipole elements, the bandwidth of the proposed EMD is improved by increasing the number of magnetic resonances. Significantly, the phase response at various frequencies of the classical electric dipole element20 resembles the results given in Fig. 4, which further demonstrates the implementation of broadband performance of the EMD element depends on multiple equivalent magnetic dipoles.

Fig. 5
figure 5

(a)Reflection phase of different element structure. (b) Equivalent model of the periodic element and current distribution.

Full size image

To further understand the operation mechanism, an equivalent circuit model (ECM) is introduced as a one-port circuit, as shown in Fig. 6. The H-shaped structure and T-shaped structure can be regarded as inductors, designated as L2, L1, and L3 respectively. Intervening spaces amongst these structures serve the role of capacitors, identified as C1 and C2. The surface impedances Zs are expressed as

$$Z_{s} = j\left( {\omega (L1 + L2 + L3) - \frac{1}{\omega C1} - \frac{1}{\omega C2}} \right)$$
(1)
Fig. 6
figure 6

The equivalent circuit model of the proposed EMD element.

Full size image

The air spaces are equivalent to transmission lines, and the input impedances Zin can be calculated by

$$Z_{in} = Z_{s} //jZ_{0} \tan (k_{0} h)$$
(2)

where Z0 and k0 are the characteristic impedance and propagation constant of the substrate, respectively, and “//” represents the parallel connection. When the thickness of the element is determined, the input impedances Zin depends on the surface impedances Zs. The reflective parameters are expressed as

$$S_{11} = 1 - \frac{{2Z_{0} }}{{Z_{in} + Z_{0} }}$$
(3)

As a result, the reflective performance of the element is affected by the equivalent devices. Altering the gap length along the x-axis solely modifies the equivalent capacitance, whereas the cell dimension along the y-axis remains invariant, thereby preserving the equivalent inductance, which further clarifies that the operating mechanism of the unit is to utilize an equivalent magnetic dipole rather than an electric dipole.

Reflectarray design

To verify the broadband performance of the proposed methodology, a RA consisting of 16 × 16 elements is designed, as is shown in Fig. 7(a). It is observed that the RA is fixed to the test bracket with 12 plastic screws, where a 2 mm thick gasket is used to support the substrate above the metal layer to form an air layer. A pyramidal horn antenna is placed symmetrically in front of the surface as feed to decrease the alignment error. It is worth noting that the feed blockage slightly affects the performance of the RA due to the smaller aperture size of the horn. Edge illumination level is set to be − 10 dB to balance the spillover efficiency and taper efficiency36. A focal to diameter ratio (F/D) of 0.74 is accordingly selected. The required phase distribution of the surface is realized using the following equation:

$$\phi_{{\left( {x_{i} ,y_{i} } \right)}} = k_{0} (R_{i} - (x_{i} \cos \varphi_{0} + y_{i} \sin \varphi_{0} )\sin \theta_{0} )$$
(4)

where k0 is the propagation constant in a vacuum, Ri is the distance from the horn phase center to each element, (xi, yi) is the coordinate of each element, and (θ0, φ0) is the orientation of the beam direction.

Fig. 7
figure 7

(a) Photograph of assembled broadband RA prototype. (b) Compensation phase distribution and element size distribution of proposed EMD.

Full size image

The reflectarray elements are usually selected to satisfy the required phase at the deign frequency, which indicates that the phase errors are introduced due to the mismatch between the required phase and the element phase when the frequency changes, resulting in bandwidth limitations, especially for traditional patch element. Significantly, the proposed EMD element with frequency-independent reflection phase can reduce this phase error, which is beneficial to improving the gain bandwidth. Meanwhile, the strategy of designing reflectarray is to use variable-sized unit cells as phase shifters to compensate for the required reflection phase. Figure 7(b) illuminates that the required phase of each element is calculated through expression (1). According to the phase-size curves at 11 GHz described, the detailed dimension of each element can be obtained.

Results

Due to support for hardware acceleration, CST Microwave Studio is used for reflectarary simulation to reduce computational time. The simulated 3D radiation patterns of the designed RA at 9.7 GHz, 11 GHz, and 13.2 GHz are presented in Fig. 8. Sharp pencil beams are realized in the broadside direction, exhibiting minimal pattern variations across frequencies and demonstrating stable radiation performance over a wide bandwidth.

Fig. 8
figure 8

The 3D radiation patterns of the proposed reflectarray at 9.7 GHz, 11 GHz, and 13.2 GHz.

Full size image

The radiation performance of the RA was measured by a planar near-field method in the anechoic chamber. Figure 9(a)-(f) plot the simulated and measured radiation patterns of E-plane and H-plane at three frequencies. Due to the large energy difference between the center and the surrounding area of the scanning surface, the more pronounced nulls appear between the main beam and sidelobe during the near and far field transformation. The measured results show that the sidelobe levels (SLLs) are -16 and -16.5 dB in the E-plane and H-plane at 11 GHz, respectively. The cross-polarization levels are below -37 and -40 dB in both planes. The slight discrepancies of the simulated results and measured results are caused by the fabrication tolerances and the defects in assembly accuracy. The radiation patterns for 9.7 GHz and 13.2 GHz are shown that the E-plane measured sidelobe levels are 16.5 and 18.2 dB down from the maximum and the H-plane are 13.7 and 18 dB at both edge frequencies, respectively. In addition, the measured cross-polarization levels of less than -35 dB for these planes are also observed in the results.

Fig. 9.
figure 9

2-D far-field radiation pattern for E-plane at (a) 9.7 GHz, (b) 11 GHz, and (c) 13.2 GHz and H-plane at (d) 9.7 GHz, (e) 10 GHz, and (f) 13.2 GHz. (g) Gains and aperture efficiency versus frequency.

Full size image

The gain and aperture efficiency of the designed RA are plotted in Fig. 9(g). It is seen that the discrepancies in the peak point of the curve are due to the fabrication tolerances, while the trend of the gain curve is consistent, which reveals that the measured results are in good agreement with the simulated results. Due to the difference in phase error, the gain curve decreases in a wavy shape from the center frequency rather than uniformly. The measured results show that the peak gain is 27.5 dBi with the 1.5-dB gain bandwidth of 33.3% (9.5–13.3 GHz). Furthermore, the aperture efficiency (AE) is evaluated with a peak of 57% in the band using the following definition

$$\eta_{a} = \frac{{G \cdot \lambda^{2} }}{4\pi A}$$
(5)

where G is the measured gain, A is the aperture area37. According to the directivity equation \(D = 4\pi /\lambda^{2}\),where A is the area of the aperture of the RA, the maximum ideal directive is 29.88 dBi. The feed blockage loss is approximately 0.35 dB when the area ratio between the feed and the aperture is 0.078. At the maximum, the illumination efficiency and spillover efficiency become equal, leading to identical losses of 0.8 dB for each. The element loss is 0.15 dB, and the other losses are 0.28 dB.

The comparison of the proposed design and other broadband design methods is plotted in Table 1. It is clear that the proposed planar EMD element realizes the design of wideband RA with simple configuration and ingenious tuning method. Compared with multi-resonance element in6, EMD element has simpler structure, fewer parameters, and more linear phase curve. In9, a wide phase range was easily achieved by using multi-layer element, the proliferation of various parameters escalates the design complexity, and the incorporation of dual substrates augments the cost. An achromatic RA, optimized through a convolutional algorithm, has been demonstrated to enhance bandwidth10. Nonetheless, the implementation of six trilayer unit cells introduces greater design complexity and elevates the structural profile in comparison to the EMD element utilizing a single-layer substrate. Subwavelength element11 was beneficial for reducing the phase dispersion of the aperture surface, however, the sufficient phase range is hardly realized due to the limited space. The vertical structure for magnetic resonance of the conventional magnetoelectric dipole30 increases the complexity and extremely restricts the tuning capability. The developed EMD element with a simple configuration achieves comparable performances of gain bandwidth and aperture efficiency compared to planar magnetoelectric dipole33.

Table 1 Comparison of the Proposed Reflectarray and Other Designs.
Full size table

Conclusion

A novel planar EMD element is investigated in this communication for single layer broadband RA application. The single layer EMD composed of H-shaped patch and two parasitism T-shaped patches without perpendicular metallized vias structure enjoys the advantage of low profile, wideband performance. In contrast to conventional magnetoelectric dipole elements, the equivalent magnetic current can be subtly excited through adjacent patch gaps rather than using metallized vias. Compared with electric dipole element, the current of the EMD element flows perpendicular to the gap rather than along it. Meanwhile, the variation direction of the EMD is orthogonal to the polarization direction of the element, which ensures the constant size in the polarization direction to improve the wideband performance. The measured results show that the wideband performance with high aperture efficiency is realized by employing the EMD concept. Most importantly, the proposed EMD element demonstrates significant potential for application in multi-polarization and multi-band reflectarrays, offering a simple configuration suitable for next-generation communication systems.