Introduction

Liquid–liquid extraction (LLE) is mainly used in industrial processes such as hydrometallurgy, petroleum, biotechnology and particularly in nuclear technology1,2,3,4,5,6,7. This method has become increasingly important due to the increasing demand for temperature-sensitive products, highly pure materials, more efficient equipment, and the possibility of using highly selective solvents8,9. Mass transfer in liquid-liquid systems is lower compared to gas-liquid systems. Additionally, more theoretical steps are required. Therefore, applying mechanical energy in different ways is recommended to enhance the efficiency of LLE columns10. Mechanical energy is usually added in the form of agitation or pulse to cause more turbulence on the interface of liquids and create smaller droplets, which may increase mass transfer and improve column performance. Pulsed columns (PCs) are one of the liquid-liquid extractors to which the mechanical energy input is supplied through the input pulse to the column. The input pulse acts as a mechanical agitator, produces droplets with smaller diameters, and thus, increases the column efficiency11,12,13,14,15. High separation capacity, insensitivity to common surface contamination of two phases, relatively simple design, safe and stable operation, no moving part, and being suitable for separation of radioactive and corrosive solutions due to remote control are prominent features of PCs16,17,18,19. These features make the use of PCs the first choice in the nuclear industry to purify uranium compounds20,21. In this process, the corrosion and radioactivity properties of the used solutions create serious challenges for the design of the required equipment. Therefore, in order to reduce operation costs and radiation effects and increase protection, in addition to having least number of moving parts, the equipment must have the ability to be controlled remotely, which is possibly using PCs.

PCs are planned in plate, packed, and disc & doughnut shapes. Pulsed sieve-plate columns (PSPCs) can be classified as vertical, horizontal, and vertical- horizontal (L-shaped) columns22,23,24,25 Vertical pulsed columns (VPCs) have more application than horizontal pulsed columns (HPCs) in industry. In cases where space constraints and building height are a concern, HPCs is suggested. The time needed to launch VPCs is shorter than that for HPCs. In VPCs, the throughput capacity is higher than in HPCs. The horizontal structure decreases the probability of radioactive pollution of process equipment and improves process control. These types of columns are repaired easily. In addition, HPCs are much easier than VPCs to disassemble and maintain. Recently, the third type of PSPCs has been introduced by a combination of HPC and VPC22,23,24,25. This type is named vertical-horizontal (L-shaped) pulsed columns (LPSPCs), which improve HPC and VPC performance by reducing installation height and surface area. It minimizes flooding issues by delaying accumulation26 and has throughput between VPC and HPC14. HPC and VPC have their own benefits and drawbacks; however, the combination column will represent greater benefits and will be a better option than VPC or HPC in applications with a limited area1,14.

In the extraction columns, droplet size is of great importance in the hydrodynamic behavior and mass transfer performance of the column. The dispersed phase holdup, the residence time of the dispersed phase, and maximum volumetric capacity depend on the droplet size. Therefore, the flooding behavior of the extractor is also affected by the droplet diameter. In addition, the diameter of the droplets affects the interfacial area for mass transfer. Hence, the drop size influences almost all variables affecting the hydrodynamics as well as the mass transfer in PCs1,14,25. SMD and DSD are two main parameters in the design of PCs23. SMD alone cannot fully describe phase properties in PCs, as different DSDs can yield the same mean diameter. Therefore, both SMD and DSD must be studied for accurate dispersion analysis23. Several studies have so far been accomplished on drop size in VPCs. Sreenivasulu et al. investigated DSDs for different continuous and dispersed velocities, pulsation intensities, and plate geometries in vertical pulsed sieve-plate column (VPSPC)27. They compared the experimental results of DSD with three models of distribution functions, including Mugele-evans, Weibull, and log-probability. It was found that the log-probability distribution function was well matched to the experimental data. Ousmane et al. investigated the influence of the pulsation intensity and flow rates of dispersed and continuous phase on SMD28. Yi et al. examined the effective operating parameters on SMD29. They reported that the flow rates of continuous and dispersed phases had little effect on the drop size, but pulsation intensity had the greatest effect on the droplet diameter, and increasing it reduced the drop diameter. There are only a few studies concerning the drop behavior of HPCs17,20,30,31. Khanramaki et al. studied the effects of operational parameters on the drop behavior in a horizontal pulsed sieve-plate column (HPSPC) using the central composite design (CCD) method. Pulsation intensity had the greatest effect on droplet size, and with increasing the pulsation intensity, uniform DSD and smaller droplet size were obtained20. Some suggested empirical correlations for droplet diameter expectation in PSPCs are presented in Table 1.

Table 1 The experimental correlations of SMD in PSPCs.
Full size table

In addition, some of the probability distribution functions for prediction of DSD in liquid extraction systems are listed in Table 2. In the table, d is the drop diameter, and α, and b are variables to be fitted.

Table 2 Probability distribution functions appeared in the literature for solvent extraction systems23,32.
Full size table

The only study to investigate the effect of operating parameters on SMD in LPSPC was performed by Amani et al.23. The systems investigated in this study were butyl acetate-water, butanol-water, and toluene-water; however, they did not consider the interplay of operating parameters on drop size in an LPSPC. In this paper, for the first time, four chemical systems, including water-nitric acid-kerosene-tri butyl phosphate (TBP) are investigated. Research findings show that nitric acid medium is one of the most widely used systems for uranium mining37. Nitric acid is a strong and corrosive solvent that is used in the chemical, metallurgy, and nuclear industries38. Nitrogen and phosphorus-based extractors are mainly employed to extract uranium from various acidic solutions39.

TBP is a widely used phosphorus-based extractor for uranium purification due to its high selectivity, impurity removal capability, and stability in nitric acid and radiation. However, its high density and viscosity make phase separation difficult, so it is usually diluted with kerosene. This method is the most commonly used worldwide for uranium extraction from yellow cake39. Therefore, the aqueous phase was regarded as an acidic medium (high-concentration nitric acid), and the organic phase, which serves as the uranium extractant, was considered various percentages of TBP dissolved in kerosene.

In this work, for the first time, the effect of interfacial tension, operation parameters, TBP concentration, and interaction of parameters on drop size diameter is investigated by CCD model for four chemical systems, including water-kerosene, 17% nitric acid-5% TBP/kerosene (v/v) (volume fraction tri butyl phosphate in kerosene), 17% nitric acid-15% TBP/kerosene (v/v) and 17% nitric acid-30% TBP/kerosene (v/v). Moreover, new empirical correlations are presented for prediction of SMD in each section of the column. Furthermore, the effect of operating parameters on DSD in an LPSPC is studied for the mentioned chemical systems. Finally, the applicability of probability distribution functions for prediction of DSD, including normal, log-normal, Weibull, and gamma is evaluated. By the use of experimental results, new correlations are presented to predict DSD in each section of the column and the obtained result are compared.

Experimental

Liquid-liquid system

The four liquid systems used in the present work, including water-kerosene, 17% nitric acid-5% TBP/kerosene (v/v), 17% nitric acid-15% TBP/kerosene (v/v) and 17% nitric acid-30% TBP/kerosene (v/v) were provided by the Merck company. All the experiments were carried out under the flooding conditions at the temperature of 20 °C. Before assessing the properties of chemical systems, equal volumes from both phases were allowed to saturate with each other. To achieve this, they were mixed and agitated until equilibrium was reached. After several hours, the two phases were separated, and their physical properties were analyzed. The physical properties of the systems are listed in Table 3.

Table 3 The physical properties of the chemical systems used at 20 °C.
Full size table

The density and viscosity of both phases were measured by the picometer method and the DVI-Prime viscometer, respectively. The interfacial tension was measured with the ring tear-off procedure using a Krüss tensiometer20,23.

Description of equipment

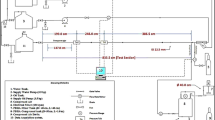
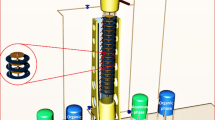
All experiments were carried out in an LPSPC. The schematic diagram of the setup is illustrated in Fig. 1. The length of each active section of the column was 146 cm and its diameter was 6 cm. In the horizontal section of the column, the 48 half-perforated sieve plates were arranged in pairs with 5 cm distance between every pair. The arrangement of two half-perforated plates in each pair was such that one of the plates is perforated at the top and the other at the bottom. This can result in better mixing of the light and heavy phases. Furthermore, it contributes to more droplet breakage. Greater droplet breakage increases in interface area and the intensity of mass transfer in this section of the column. In the vertical section, the 29 sieve plates were arranged as individuals with 5 cm distance between every plate. Plates in both sections of the column had perforations of 2 mm in diameter. Table 4 shows the column characteristics. The structure consists of vertical and horizontal sections, four tanks, two dosing pumps, one lower settler, one upper settler, one pulsating air system, and two rotameters. The two phases move in opposite directions in the column. The light and heavy phases enter the column from below and top, respectively. By compressed air, which is fed regularly to the airline connected to the lower settler of the column, the content of the column is pulsed with the considered amplitude and frequency. The interface level is controlled using the optical sensor, which is joined to the solenoid valve located at the exit of the aqueous phase. It is worth mentioning that this column is built in own laboratory.

Table 4 The geometric properties and materials used for the column.
Full size table
Fig. 1
figure 1

A schematic diagram of LPSPC.

Full size image

Both phases were saturated before conducting the experiments. Then the flow rates of both phases as well as their frequency and pulse amplitude were set to the considered values. The drop sizes were determined using a photographic approach. Ten regions of the active sections of the column were chosen for capturing the photos. For this purpose, almost 1000 drops were analyzed for each experiment. The photos were analyzed using AutoCAD software for determining SMD. Equation (1) was used to calculate SMD as follows:

$$\:{d}_{32}=\frac{\sum\:_{i=1}^{n}{n}_{i}{d}_{i}^{3}}{\sum\:_{i=1}^{n}{n}_{i}{d}_{i}^{2}}$$
(1)

Where, ni is the number of drops and di is the measured droplet diameter. The drops have mainly spherical shapes, but in some instances, ellipsoidal shapes were observed, which were characterized by measuring their minor axis (dL) and major axis (dH), representing the largest distance between the two points on the drop, and the largest length of the line at the angle of 90° to the major axis17,23. Accordingly, in order to measure the drop distortion, the drop diameter with an equivalent sphere was calculated as follows:

$$\:{d}_{i}=\sqrt[3]{{d}_{H,i}^{2}{d}_{L,i}}$$
(2)

Finally, about 20% of the drops were measured by the elliptical droplet diameter equivalent. The four photos of the drops are shown in Fig. 2 as examples.

Fig. 2
figure 2

The photos taken from the dispersed phase drops: (a) and (b) horizontal section, and (c) and (d) vertical section.

Full size image

The average absolute relative error (AARE) was adopted as an objective function to calculate the fitted parameters1:

$$\:AARE=\frac{1}{N}\sum\:_{i=1}^{N}\frac{\left|Experimental\:value-Calculated\:value\right|}{Experimental\:value}\times\:100\%$$
(3)

Response surface methodology (RSM)

Researchers are always looking for ways to get the most out of their experimental data. Response surface methodology (RSM) is used for data analysis and significant expression of independent variables on dependent variables, as well as modeling. Finally, the optimization operation is performed on the proposed model. Before performing experiments, the model selects surfaces from all possible scenarios. In fact, the middle level of all independent variables is considered the central point, and the end levels are called points + α and -α. To work with RSM, it is necessary to plan the experiments from the beginning based on the suggested points or its roadmap. RSM is introduced as a function of variables. The variables have values in a particular reach. In general, in the field of design of experiments, most models are of the second-order type. A second-order polynomial model is utilized to clarify the empirical model1,40,41,42:

$$Y={\beta _0}+\sum\limits_{{i=1}} {{\beta _i}} {X_i}+\sum\limits_{{i=1}} {{\beta _{ii}}} X_{i}^{2}+\sum\limits_{{i=1}} {\sum\limits_{{j=i+1}} {{\beta _{ij}}} {X_i}} {X_j}+\varepsilon$$
(4)

Where, Xi and Xj are the independent variables, β0 is the constant of the model, βi represents the coefficients of linear effects, βii indicates the coefficients of quadratic effects, βij shows the interactions between variables, and ε represents unexpected experimental parameters. Also Y is the predicted response (SMD)1,42. The obtained data and plots were analyzed using the Design-Expert software. The RSM-CCD method was used to specify the impact of five independent variables at five levels on the SMD. The design was made from five variables at five levels, as listed in Table 5.

Table 5 Variables and their levels based on the RSM-CCD method.
Full size table

Predicted responses for SMD based on the RSM-CCD procedure are shown in Table 6.

Table 6 Expected responses for SMD according to the RSMCCD procedure.
Full size table

Results and discussion

RSM results

Analysis of variance (ANOVA) is probatory analysis instrumentation used primarily for cause-effect analysis. The ANOVA identifies factors (X variables) with significant variation in the response (Y variables). The ANOVA results in the present research for SMDs in four systems are shown in Table 7.

Table 7 ANOVA results for both parts of the column.
Full size table

The sum of squares is one of the important parameters in the ANOVA table. Dividing the sum of squares by the degree of freedom (df) gives the mean squares. The mean squares are used to determine the F-value. In other words, the F-test determines the ratio of the mean squares (two variances). This test determines whether the variance calculated for a group of results is greater than the random variance in the data.

The importance of each of the effects is listed in the column p-value, based on which one can conclude whether or not the linear, quadratic and interaction-related effects are important. These effects can be considered significant if the value of P is less than 0.05 (with 95% probability)1,41.

The results obtained for the horizontal part showed that the F-value of the model is significant. There is only 0.01% chance that a large F-value like this could occur due to noise. P-values less than 0.05 indicate that the model terms are significant. In this case, X2 and X3 are significant model terms. Values greater than 0.1 indicate that the model terms are not significant. If there are many insignificant model terms (not counting those required to support hierarchy), model reduction may improve your model. Lack of Fit (LOF) F-value of 2.01 implies that LOF is not significant relative to the pure error. There is 14.74% chance that a large LOF F-value like this could occur due to noise. Non-significant LOF is good. The results of the vertical part of the column showed that the F-value of the model is significant. In this case, X2, X3 and X4 are significant model terms. LOF F-value of 2.84 implies that there is 5.96% chance that a large LOF F-value like this could occur due to noise. The RSM-CCD procedure suggested quadratic models based on the empirical coefficients given in Eqs. (5), and (6) for the vertical and horizontal sections, respectively (Table 8).

Table 8 RSM equations to predict SMD for LPSPC.
Full size table

These equations in terms of coded factors can be used to make predictions about the response for the given levels of each factor. By default, the high levels of the factors are coded as + 1 and the low levels are coded as -1 (according to Table 5). Coded equation is useful for identifying the relative impact of the factors by comparing their coefficients.

The coefficient of determination (R2) determines the proportionality of data with the model. In the present work, the R2 values of 0.9820 and 0.9498 were obtained for the vertical and horizontal sections, respectively, showing that the data fit well with the models. For the horizontal section, the predicted-R² of 0.9060 was in reasonable agreement with the adjusted-R² of 0.9350 (i.e. the difference was less than 0.2). Adeq precision measures the signal to noise ratio, where the ratios greater than 4 are desirable. Adeq precision of 33.476 indicates an adequate signal. The results further showed that for the vertical section, the predicted-R² of 0.9648 was in reasonable agreement with the adjusted-R² of 0.9767. Adeq precision of 57.7930 indicates an adequate signal. So this model can be used to navigate the design space. It is important to note that High R² values indicate a strong agreement between calculated and actual results. Adjusted-R² reflects the model’s fit by accounting for removed factors, while predicted-R² evaluates the model’s predictive ability. The software calculates predicted-R² by systematically omitting data points and assessing the model’s accuracy in predicting those43.

Figure 3 compares the predicted and actual values of d32 for both sections of the column. As shown, the actual and calculated values of d32 are close to each other under the experimental conditions. Therefore, the proposed RSM model is appropriate and can be used for d32 analysis and prediction.

Fig. 3
figure 3

Actual d32 values versus the predicted values of d32 for (a) horizontal and (b) vertical sections.

Full size image

Effect of model parameters on SMD

Drop size in PCs depends upon the small drops’ coalescence to larger drops and their breakage to smaller drops. The breaking of drops can occur by the turbulence created by the pulses, the hitting of drops with the wall of PCs, and the drops’ flow through the sieve-plate holes. The drops coalescence and breakage create a range of drop sizes. Thus, the mean value of the drop sizes and the way they are distributed are valid in such circumstances. 3-D response surfaces are used to show the maximum effect of two model parameters on SMD.

The effect of dispersed and continuous phase flow rates on SMD is shown in Fig. 4. It is observed that SMD increases with the increase in the flow rate of dispersed phase. It is clear that the higher flow rate of disperse phase leads to higher coalescence rate. In this study, the change in the continuous phase flow rate had little effect on SMD, may be due to the fact that as the flow rate increases, the resistance in the dispersed phase flow path increases and, the persistence of dispersed phase in the column increases slightly, resulting in more cohesion and relatively larger droplets14,23 It is worth noting that the effect of continuous phase flow rate on SMD is much less than that of dispersed phase flow rate.

Fig. 4
figure 4

The values of SMD versus the dispersed and continuous phase flow rates for (a) horizontal (b) vertical sections (TBP = 15%, σ = 22.5 Nm/m, Af = 1 cm/s).

Full size image

Figure 5 illustrates the influence of the interfacial tension and percentages of TBP on SMD. Interfacial tension plays an important role in droplet size and is directly related to surface energy. More precisely, droplet size is a function of the ratio of turbulent energy to surface energy, commonly defined as the Weber number. Pulsation intensity represents the perturbation energy and interfacial tension represents the surface energy. As shown, increasing the interfacial tension leads to an increase in the tendency of droplets to coalesce and an increase in droplet size1,14,23. In addition, increasing the percentage of TBP in the dispersed phase, the physical properties of the dispersed phase change and the diameter of the droplets decreases slightly.

Fig. 5
figure 5

The values of SMD versus the percentages of TBP and interfacial tension for (a) horizontal and (b) vertical sections (Qd= 4 l/h, Qc=4 l/h, Af = 1 cm/s).

Full size image

As shown in Fig. 6, SMD decreases with the increase of pulsation intensity, because the drop breakage increases with the enhancement in pulsation intensity due to the increase of collision between the internal walls and the dispersed liquid drops. Another point that can be concluded from Fig. 6 is that SMD in the vertical section is more than in the horizontal Sects1,14,23. Also droplets produced from the high interfacial tension systems are larger than those produced from the lower interfacial tension systems.

Fig. 6
figure 6

The values of SMD versus the interfacial tension and pulsation intensity for (a) horizontal (b) vertical sections (Qd= 4 l/h, Qc=4 l/h, TBP = 15%).

Full size image

Optimization

The deviation plot demonstrates the impact of all parameters of the model on SMD, and the center point (0) is the middle point under the operating conditions.

Fig. 7
figure 7

Deviation plots for SMD for sections (a) horizontal and (b) vertical sections.

Full size image

As shown in Fig. 7, in both sections of the column, the pulsation intensity reduces SMD, while increasing the interfacial tension causes a significant increase in SMD. In addition, the volumetric flow rate of the dispersed phase increases SMD, but its effect is much less than that of the interfacial tension. In the horizontal part of the column, as the volumetric flow rate of the continuous phase increases, SMD increases, while in the vertical part of the column, SMD decreases by increase of the volumetric flow rate. The effect of TBP percentage on SMD in the horizontal and vertical sections is also shown in Fig. 7. As indicated, it has no significant effect on the horizontal part of the column and slightly reduces the size of the droplets.

Numerical optimization can be used to determine the optimal value of each parameter of the model and response. The optimal value of each parameter and the minimum SMDs are given in Table 9.

Table 9 SMD optimization according to the RSM-CCD procedure.
Full size table

Predictive correlations for SMD

One of the main aims of this study was to develop an empirical correlation in order to predict SMD in PCs. Firstly, it is worth to mention that the correlations are mostly presented for VPSPCs and cannot be used for HPSPCs since the effect of operating variables on SMD is distinctive from that in VPSPCs. Some of the correlations in the literature for calculation of the SMD in PSPCs are compared with the experimental results of the present study. A comparison between the results of d32 with those calculated by the correlations of Khajenoori et al., Sreenivasulu et al., Mirmohammadi et al., Panahinia et al., and Kagan et al. is presented in Fig. 817,27,30,31,34. According to the values of AARE, none of the former correlations can accurately predict the experimental results in LPSPCs.

Fig. 8
figure 8

Comparison of the different correlations of SMD in a PC with the experimental results: (a) horizontal and (b) vertical sections.

Full size image

Since the former correlations are not applicable in LPSPCs, the following correlations are presented to predict SMD in both sections of the column as a function of the flow rate of both phases and pulsation intensity along with the physical properties of the systems by dimensional analysis technique as follows (In this work, we used the dimensionless analysis method via Buckingham’s π-Theorem to derive Eqs. (7) and (8)):

For horizontal section:

$$\:\frac{{d}_{32}{\rho\:}_{c\:}{Af}^{2}}{\sigma\:}=0.592{\left(\frac{Af{\mu\:}_{c}}{\sigma\:}\right)}^{0.211}{\left(\frac{Af{\mu\:}_{d}}{\sigma\:}\right)}^{0.392}{\left(\frac{{u}_{c}}{Af}\right)}^{-0.044}{\left(\frac{{u}_{d}}{Af}\right)}^{0.091}{\left(\frac{{\rho\:}_{d}}{{\rho\:}_{c}}\right)}^{0.01}$$
(7)

For vertical section:

$$\:\frac{{d}_{32}{\rho\:}_{c\:}{Af}^{2}}{\sigma\:}=1.978{\left(\frac{Af{\mu\:}_{c}}{\sigma\:}\right)}^{0.323}{\left(\frac{Af{\mu\:}_{d}}{\sigma\:}\right)}^{0.317}{\left(\frac{{u}_{c}}{Af}\right)}^{0.047}{\left(\frac{{u}_{d}}{Af}\right)}^{0.156}{\left(\frac{{\rho\:}_{d}}{{\rho\:}_{c}}\right)}^{-0.004}$$
(8)

As mentioned, we performed dimensionless analysis using Buckingham’s π-theorem. The first and most important step in dimensional analysis was to identify a complete set of independent quantities:

$$\:{d}_{32}=f({\mu\:}_{c},{\mu\:}_{d},{u}_{c},{u}_{d},Af,{\rho\:}_{c},{\rho\:}_{d},\sigma\:)$$

Next we listed the dimensions of the dependent variable (d32) and the independent variables\(\:\:({\mu\:}_{c},{\mu\:}_{d},{u}_{c},{u}_{d},Af,{\rho\:}_{c},{\rho\:}_{d},\sigma\:)\). According to base quantities and dimensions, all quantities had dimensions of the form [f] = la mb tc, where the exponents a, b and c were dimensionless numbers derived from each quantity’s definition. Then we selected complete dimensionally independent subsets from the variables and expressed the dimension of the remaining independent variables and dependent variable (d32) as a product of powers. Next, we obtained dimensionless forms of the n-k remaining independent variables by normalizing each one with the product of powers of independent subsets sharing the same dimension. Finally, when a complete relationship between dimensional physical quantities was expressed in dimensionless form, the number of independent quantities that appeared in it was reduced from the original n to n-k, where k represents the maximum number of the principal dimensions and n was the initial number of variables independent. For each chemical system, 20 experimental data points were used, totaling 80 data points for four chemical systems (for each section of the column). The selection of the dimensionless groups, exponents, and their coefficients was performed using Statistical Package for the Social Sciences) SPSS software. It is worth mentioning that sensitivity analysis was conducted on numerous dimensionless groups, and ultimately, these groups provided the best results.

The predictive ability of correlations is illustrated in Fig. 9. The AARE values of these correlations are about 6.95 and 8.29%, respectively, revealing that the data obtained by the presented equations are in good agreement with the experimental results for LPSPC in the present study. Each experiment, along with the actual values (SMDD) and the values calculated by the model, is presented in Supplementary Table 1 A (Supplementary material).

Fig. 9
figure 9

Comparison of the experimental values of SMD with the calculated values using Eqs. 7, 8 for (a) horizontal and (b) vertical section.

Full size image

Effect of operating parameters on DSD

DSD in agitated systems is mainly a function of the operating variables such as pulsation intensity, volumetric flow rate of dispersed and continuous phases, and physical properties of the system23. DSD in PCs depends on the rates of drop coalescence and breakage. In this research, the effect of pulsation intensity and volumetric flow rate of dispersed and continuous phases on DSD was investigated for four systems. The influence of pulsation intensity on DSD is displayed in Fig. 10.

Fig. 10
figure 10

Effect of pulsation intensity on DSD.

Full size image

Figure 10 shows that an enhancement in the pulsation intensity will lead to narrower ranges of DSD. The turbulence of the system and the collision energy are enhanced with increasing the pulsation intensity23. So the eddies of the liquid stream become smaller. Smaller eddies and collision energy make the pulsation intensity to be a key operational variable from the standpoint of DSD. Furthermore, DSD gets narrower for the 17% Nitric acid-30% TBP/Kerosene system (lower interfacial tension). In other words, the lower the interfacial tension, or alternatively, the higher the TBP percentage, the smaller the droplets and the narrow the curves become. The effect of pulsation intensity is stronger in the vertical section that contains larger drops. In consequence, a shift to the left is seen with increasing the pulsation intensity in DSD in both sections. The variations of DSD at different dispersed phase flow rates are illustrated in Fig. 11.

Fig. 11
figure 11

Effect of dispersed phase flow rate on DSD.

Full size image

It is seen that an enhancement in Qd leads to a wider DSD due to an increase in the flow rate of dispersed phase that increases the coalescence rate. In fact, increasing the dispersed phase flow rate leads to an increase in drag forces, which results in reduction in the droplet velocity and a subsequent enhance in the drop residence time inside PC, thereby forming larger droplets23. Hence, a smaller shift to the right in DSD is seen with increasing the flow rates of the dispersed phase in both sections of the column. The influence of continuous phase flow rate on DSD is displayed in Fig. 12.

Fig. 12
figure 12

Effect of continuous phase flow rate on DSD.

Full size image

As shown, DSD is not significantly influenced by different flow rates of the continuous phase. Thus, DSD is independent of the flow rate of continuous phase in this column.

Predictive correlations for DSD

In this study, four models of distribution functions, including normal, log-normal, Weibull, and gamma were examined for reproduction of the experimental results. The α and β parameters were obtained in terms of the dimensionless numbers. A comparison between the experimental DSDs and some of the probability distribution functions is shown in Fig. 13.

Fig. 13
figure 13

Comparison between the probability distribution functions and the experimental results.

Full size image

Probability density has been considered as the ratio of the number of drops in each group (representative drop diameter = di ± Δdi/2) to the total number of drops, where di is drop diameter (mm). New correlations are suggested to predict DSD coefficients as a function of physical properties and operational variables based on the dimensional analysis method for vertical and horizontal sections as follows:

$$\:\alpha\:\:and\:\beta\:={C}_{1}\:{{\left(\frac{{\mu\:}_{c}}{{\mu\:}_{d}}\right)}^{{C}_{2}}\left(\frac{{u}_{c}}{Af}\right)}^{{C}_{3}}{\left(\frac{{u}_{d}}{Af}\right)}^{{C}_{4}}{\left(\frac{{\rho\:}_{d}}{{\rho\:}_{c}}\right)}^{{C}_{5}}{\left(\frac{{Af\mu\:}_{c}}{\sigma\:}\right)}^{{C}_{6}}$$
(9)

The coefficients and AAREs of the correlations are presented in Table 10.

Table 10 Values of Ci in Eq. (9) for DSD functions.
Full size table

The AARE values of α and β parameters for each of the normal, log-normal, Weibull, and gamma functions were about 3.40–9.60, 11.52–17.65, 2.62-16.00, and 29.09–38.93%, respectively. According to the results, normal and then Weibull and log-normal models is acceptable orderly; however, the gamma model is not suitable for prediction of DSD. A comparison between the results of DSD coefficients with those calculated by the reported correlations in the literature is presented in Table 11.

Table 11 Comparison of the DSD coefficients a PC with the experimental results.
Full size table

The results of the above table indicate that the findings of this study do not match the DSD coefficients extracted from other literature.

Conclusion

In this research, the drop behavior of an L-shaped pulsed sieve-plate column (LPSPC) for water-kerosene, 17% nitric acid-5%TBP/kerosene, 17% nitric acid-15%TBP/kerosene, and 17% nitric acid-30% TBP/kerosene was investigated. The impacts of operating parameters such as pulsation intensity and flow rates of dispersed and continuous phases on SMD and DSD were studied. It was observed that any increase in pulsation intensity decreased the drop size, and therefore, the distribution curves of drop sizes became narrower and shifted to the left. The influence of flow rates was found to be poor compared with the effect of the pulsation intensity. Furthermore, the effect of interfacial tension and percentage of TBP in the dispersed phase on the SMD was investigated. The results showed that increasing interfacial tension leads to a greater tendency for droplets to coalesce and an increase in droplet size. In addition, with increasing the percentage of TBP in the dispersed phase, the physical properties of the dispersed phase changed and the diameter of the droplets decreases slightly. Two new empirical correlations in terms of the operating variables and physical properties of the liquid systems were presented for prediction of SMD with AARE values of 6.95 and 8.29% for the horizontal and the vertical sections, respectively. The RSM results proposed two quadratic models for SMD for the horizontal and vertical sections. The coefficient of determination (R2) for these models was 94.98 and 98.20%, respectively, indicating a good agreement between the predicted and actual data. In addition, four models of distribution functions including normal, log-normal, Weibull, and gamma were investigated to find predictive correlations for DSD. With respect to DSD, the normal and then Weibull and log-normal models were found to be acceptable, but the gamma model was not suitable for prediction of DSD. It is worth mentioning that based on the chemical systems used in this study and the application of these chemicals in uranium extraction from yellowcake using kerosene and TBP solvents, the obtained correlations can be utilized for scaling up the LPSPC from semi-industrial to industrial scale. A crucial step in designing any industrial column for metal separation is conducting experiments at a semi-industrial scale. The hydrodynamic and mass transfer relationships derived from these experiments allow for estimating the dimensions of the desired column on an industrial scale.