Introduction

In the context of today’s Internet of everything, many emerging compute-intensive mobile applications are favored by users and have been developed rapidly. The tasks generated by these emerging mobile applications also increase rapidly, and become more complex, and the latency processing requirements are increasingly high1,2,3. This makes the disadvantages of local mobile devices with limited computing resources, power and storage capacity amplified and became increasingly obvious, and it is difficult to meet the needs of these applications. Therefore, we use the computational offloading technology4 in the edge cloud to transfer some or all of the sensitive tasks of the application to the cloud for processing5,6,7, so as to reduce the application delay and alleviate the challenges brought by local devices due to their own shortcomings.

In recent years, there have been many studies on computational offloading strategies based on D2D communication techniques8,9,10. D2D technology, as a research hotspot of computational offloading in recent years, reduces the pressure of limited computational resources for local devices by offloading tasks to peers that have free time and resources. Moreover, compared with the problems of transmission distance and computational cost associated with computational offloading tasks to the edge cloud processor, offloading the processing to the neighboring peers around the local area is sometimes easier to achieve instead, and improves the computational quality of the user’s local device. However, the offloading scheme which is only carried out in the D2D framework is currently no longer able to meet the high demand of tasks from today’s users. therefore, we combine the D2D communication technology with edge cloud computing11,12,13. With the assistance of D2D technology, while taking advantage of the edge cloud processor with outstanding computing power, the appropriate execution location of the task is selected based on the actual needs of the task. Both D2D communication and edge cloud cooperate and negotiate with each other to ensure efficient execution of computational tasks while minimizing user costs.

Based on the above elaboration, this paper combines the D2D communication technique with a joint edge cloud and peer-to-peer devices to design a D2D-assisted collaboration computational offloading strategy (D-CCO), which determines the optimal offloading decision for a task by negotiating the cost of computing the task on different processors. First, a queuing system is built using stochastic optimization14 to construct a model of a queuing system with random busy arrivals of tasks by building queues on local devices, peer devices, and edge cloud processors, respectively. The Lyapunov drift14 is then utilized to minimize the queue length on each device or processor on each time slot and also to ensure the stability of this system. With this offloading policy, we can obtain the optimal offloading decision for a task and the number of tasks sent to each execution location during the offloading process. The algorithm optimizes the computational latency of the task, and also considers the waiting latency of the task computation, i.e., the backlog of tasks in each queue, and optimizes the energy consumption on this basis, so as to optimize the execution cost incurred by the computationally sensitive tasks and to improve the overall operational efficiency of the computational offloading of tasks for the local users.

The major contributions of this paper are summarized as follows:

  • By considering the characteristics of sufficient computing power and high transmission delay in edge cloud, low transmission delay but limited computational resources as well as task complexity in D2D, the D2D technology has been combined with edge cloud computing, and a queuing system model is constructed that contains local queue, peer device queue and edge processor queue in edge cloud.

  • A computational offloading strategy based on D2D-assisted collaboration (D-CCO) is proposed to derive the optimal offloading decision and offloading quantity of a task by optimizing the latency, energy consumption, and task backlog of a sensitive task, thus minimizing the computational cost to the user.

  • The algorithm is verified to have good stability through analysis and proof. The experimental results also show the stability of the D-CCO algorithm and verify that the algorithm outperforms other comparative methods in terms of reducing computational cost.

The rest of the content is organized as follows. Section two describes the related work and Section three introduces the system model, the queue dynamics and the problem formulation. In Section four, we introduce and analyze the details and performance of the D-CCO algorithm. The numerical results of this strategy are given in Section five, and Section six presents the conclusion of this paper.

Related work

With the rapid development of mobile Internet and Internet of Things technologies, edge cloud computing networks have become critical infrastructure to support various emerging applications15,16,17. In this context, as an important means to improve system performance and reduce energy consumption of mobile devices, computing offloading technology has been widely concerned by the academic community18,19,20,21,22. Niyato et al.18 used game theory to build an interaction model between users and edge devices, and users minimized their own computing costs and achieved overall cost reduction through strategy selection. From the perspective of resource allocation, Wang et al.19 studied how edge devices allocate computing resources in multi-user scenarios to meet users’ task offloading requirements and reduce latency. Liu et al.20 proposed a priority-based task offloading algorithm to make offloading decisions on edge devices according to task urgency and resource requirements. By establishing a mathematical model of edge computing network, Li et al.21 analyzed the influence of different topologies on task offloading efficiency and energy consumption. Zhang et al.22 discussed how to dynamically adjust the computing resource allocation of edge devices to meet the task offloading requirements in a mobile environment. In particular, Irtija et al.23 proposed a dynamic decision-making task offloading strategy through satisfaction game, adopting a multi-hop offloading framework. However, doing so will increase the pressure on network management and reduce the privacy and security of data. Adopting a direct end-to-end offloading scheme can achieve lower offloading latency.

The combination of D2D communication technology and computational offloading opens up a new way for the development of edge cloud computing networks24,25,26,27,28. In view of the dense distribution of mobile users, Han et al.24 proposed a computing offloading and resource allocation algorithm based on stackelberg game and genetic algorithm, which effectively improved the utility of users in need and idle users. Xu et al.25 studied the task sharing mechanism based on D2D, establishing direct data transmission links between devices to jointly complete computing tasks to reduce the overall computing time. Yang et al.26 proposes a D2D calculation offloading decision method based on signal strength, which determines whether to perform task offloading according to the strength of communication signals between devices. There are also many research achievements in the application of D2D technology to computational offloading. Wang et al.27 built an energy model for D2D computational offloading, analyzed the energy consumption under different offloading strategies, and sought an energy-saving offloading scheme. Li et al.28 explored the application of D2D technology in multi-task scenarios to achieve reasonable task allocation and parallel computation among multiple devices. However, the impact of task delay on user cost is not fully considered.

In order to meet the requirements of delay-sensitive tasks, some studies begin to focus on system stability and task wait delay. Some literature29,30,31,32,33 tries to reduce the waiting delay and improve the system performance by improving the algorithm and optimizing the network architecture. Zhao et al.29 proposed an algorithm based on queue management to reduce task waiting delay and improve system stability by optimizing task queue order. Liu et al.30 studied how to build low-latency edge computing networks from the perspective of network topology optimization to reduce task transmission and waiting time. Yang et al.31 used the predictive model to predict task demands in advance and allocate resources in advance to reduce task waiting delay and improve system response speed. Wang et al.32 proposed an adaptive task scheduling algorithm that dynamically adjusts the task execution order according to real-time network conditions and task priorities to reduce the waiting delay. Li et al.33 studies the resource reservation mechanism to reduce task waiting conflicts and ensure the stable operation of the system in the multi-user concurrent scenario. However, these methods still have some limitations when considering various user costs such as task delay, power consumption and wait delay.

In addition, there are several studies devoted to optimizing offload algorithms for more efficient resource allocation and task scheduling. Based on greedy algorithm, a fast task offloading and resource allocation algorithm34 is designed to find the best solution in a short time. Niyato et al.35 studied the resource allocation algorithm based on auction mechanism, and users obtained computing resources through bidding to achieve efficient resource allocation. Wang et al.36 proposed a task unloading algorithm based on particle swarm optimization to find the optimal offloading and resource allocation scheme through collaboration between particles. From the perspective of resource balancing, Liu et al.37 designed a task offloading algorithm for load balancing to avoid overuse of some device resources. Based on the idea of dynamic programming, a task offloading and resource allocation algorithm38 is designed which dynamically adjusts over time. However, when dealing with large-scale tasks, the algorithm has high computational complexity and insufficient guarantee for system stability.

Although some achievements have been made in the field of computational offloading, most studies fail to fully consider the task delay as a key factor when optimizing user cost, especially in the current era of delay-sensitive intelligence, this deficiency is particularly prominent. Different from the existing studies, the D2D Assisted Cooperative Computing offload strategy (D-CCO) proposed in this paper comprehensively considers various user costs such as task delay, power consumption and waiting delay. By constructing task queue system and applying stochastic optimization algorithm and back pressure algorithm, the system stability is guaranteed while the computing cost is reduced to the greatest extent. It provides a more efficient solution to the computational offloading problem in edge cloud computing network.

System model and problem construction

This section focuses on the specific analysis of the queueing system model proposed in this paper that contains local devices, peer devices, and edge cloud processors, and expands on the four aspects of the task model, local computation model, offloading computation model, and the dynamics of the queueing, and finally gives the optimization problem of this paper.

Task model

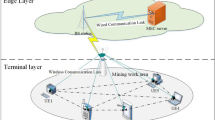
In this paper, we consider a computational offloading system with a large number of sensitive tasks arriving randomly in a joint D2D technique with edge cloud, and we investigate the task offloading problem for multiple user devices, multiple peers, and multiple edge clouds. In this system, user devices have a large number of sensitive computational tasks with high latency requirements waiting to be processed on each time slot. We define a time slot to be denoted by t, the duration of each time slot to be \(\tau\) , and set T to be the set of the indexes of the T time slots. The computational task is denoted by \({i} \in \{1,2,\ldots ,N\}\), let N be the set of N tasks, and assume that each task is a whole and cannot be partitioned into task blocks for computation. And the user task must be completed before its deadline \(F_{i}\), otherwise the user program will crash. The computational model architecture for the task is shown in Figure 1. From the system model diagram, we can see that the local device communicates with other peers as well as the edge cloud through a wireless access and offloads the task to the optimal processing location through an offloading link. At the same time, in order to fit the real-world scenarios, both the peer devices and the edge cloud have their own tasks to be processed.

Fig. 1
figure 1

The system model diagram.

Full size image

When new execution tasks are run on the local device, each task has the option of being processed either on the local device, the peer device, or in the edge cloud server. To this end, we define an offloading decision for each task that identifies where the task is to be computed. The offloading decision is defined as follows:

$$\begin{aligned} \begin{aligned}&{y_{ld}^{i}(t), y_{lm}^{i}(t)} \in \{0,1\}, \\&{y_{ld}^{i}(t)+y_{lm}^{i}(t)} \in \{0,1\}, \end{aligned} \end{aligned}$$
(1)

where \({l}\in \text {L}, {d}\in \text {D}, {m}\in \text {M}\) denote the local device, the peer device, and the edge cloud processor, respectively, \(y_{ld}^{i}(t)=1\) denotes that task i is offloaded to the peer device d for processing, and \(y_{lm}^{i}(t)=1\) denotes that task i is offloaded to the edge cloud m for execution, and when \(y_{ld}^{i}(t), y_{lm}^{i}(t)\) are both 0, it denotes that task i is processed on the local device l. And a task can only be selected to be processed on one processor and cannot be executed on any two or three of the local device, peer device or edge cloud at the same time, so \(y_{ld}^{i}(t), y_{lm}^{i}(t)\) cannot be 1 at the same time.

If the task is migrated to other peer devices in the system or processed on the edge cloud, we assume that the computational latency and energy consumption of the corresponding processor to return the result to the local user device after the computation is completed is negligible. In addition, for the computational task i arriving on the local end device, we define it with a quaternion \({\{D_{i},C_{l}^{i}.C_{ld}^{i},C_{lm}^{i}\}}\), where \(D_{i}\) denotes the size of the amount of data to be processed by the task i itself, and \(C_{l}^{i}\), \(C_{ld}^{i}\), and \(C_{lm}^{i}\) represent the number of CPU cycles to be executed for the computation of the task i on the local device, the other peer devices, and the edge cloud processor, respectively.

Local computational model

In this system, local user devices have different processing rates, while the computing power of the devices themselves is limited. We define the local device to have a large number of sensitive computational tasks arriving in each time slot, and set the transmission power of the local device to be fixed. For local devices in the system, we use the notation \({l} \in \{1,2,\ldots ,L\}\) to denote that L is the set of all local devices in the system. And we use \(f_{l}\) to represent the computing power of the local device, i.e., the number of CPU cycles per second (in GHz/s) that the local user device can execute. According to Dynamic Voltage and Frequency Scaling (DVFS)39, we can also make changes to the computation rate of the local device by adjusting the frequency of this cycle, so that the execution rate of task i on the local device in time slot t is:

$$\begin{aligned} v_{l}^{i}(t)=\eta _{l}^{i}(t)f_{l}, \end{aligned}$$
(2)

where \(0\le \eta _{l}^{i}(t) \le 1\), we define it as the ratio of the actual computing power of the local device to its computing power. Then the computational delay \(t_{l}^{i}\) for task i to process on the local device l is:

$$\begin{aligned} t_{l}^{i}=\frac{C_{l}^{i}}{v_{l}^{i}(t)}. \end{aligned}$$
(3)

In addition, we define \(\rho _{l}^{i}\) to denote the processing power of the device when the task is processed on the local device, then the energy consumption required by the task to computing on the local device can be expressed as:

$$\begin{aligned} e_{l}^{i}=t_{l}^{i}\times \rho _{l}^{i}. \end{aligned}$$
(4)

Offloading computational model

In addition to being able to compute locally, computational tasks on the local device have the option of being offloaded to other processors for processing, and this subsection focuses on the two parts of offloading tasks to peer devices or edge cloud processors specifically. The first is a computational offloading model of offloading tasks to other peers, where there are limited peer resources in the system but plenty of free computational resources. We denote it by \({d} \in \{1,2,\ldots ,D\}\) and the set of peer devices is set to D.

The computational latency of task migration to peers consists of two main phases, the link transmission latency of task offloading to other peers and the processing latency on the peers, with negligible computational latency for the return of computation results to the user locally. In this paper, we define \(f_{d}\) as the computational power of the peer device d, and \(v_{ld}^{i}(t)\) denotes the data transmission rate for offloading task i from the local to the peer device. Using the Shannon formula, the rate is defined as:

$$\begin{aligned} v_{ld}^{i}(t)=\omega log_{2}\bigg (1+\frac{\rho _{ld}^{i}h_{ld}^{i}(t)}{\sigma _{ld}^{i}}\bigg ), \end{aligned}$$
(5)

where \(\omega\) is the transmission bandwidth of the link channel in this queueing system, \(\rho _{ld}^{i}\) represents the transmission power from the local user device offloading task i to the peer device, \(h_{ld}^{i}(t)\) is the channel gain from the local to the peer device channel, and the noise power is denoted by \(\sigma _{ld}^{i}\), which is modeled as obeying additive white Gaussian noise.

In addition, we define \(v_{ld}^{max}(t)\) as the maximum transmission rate of the channel from the user’s local to the peer device. Then, the transmission delay \(t_{ld}^{i}\) computed by task i from local offloading to the peer device is denoted as:

$$\begin{aligned} t_{ld}^{i}=\frac{D_{i}}{v_{ld}^{i}(t)}. \end{aligned}$$
(6)

Meanwhile, the local execution energy consumption for task i to offload to other peers for processing is defined as:

$$\begin{aligned} e_{ld}^{i}=t_{ld}^{i} \times \rho _{ld}^{i}. \end{aligned}$$
(7)

Furthermore, on time slot t, we define the computational power of the peer device to be \(f_{d}\), and then the computational rate of task i on peer device d is:

$$\begin{aligned} v_{d}^{i}(t)=\eta _{d}^{i}(t)f_{d}, \end{aligned}$$
(8)

Where \(\eta _{d}^{i}(t) \in [0,1]\ \) represents the ratio of the actual computing power of the peer device, the processing latency of the task on the peer device can be expressed as:

$$\begin{aligned} t_{d}^{i}=\frac{C_{ld}^{i}}{v_{d}^{i}(t)}. \end{aligned}$$
(9)

And the energy consumption of task processing on the peer device is

$$\begin{aligned} e_{d}^{i}=t_{d}^{i} \times \rho _{d}^{i}, \end{aligned}$$
(10)

Where \(\rho _{d}^{i}\) indicates the processing power of the device when the task is executed on the peer device.

Next, we elaborate the computational offloading model for task offloading to edge cloud processors. Edge cloud processors have outstanding computing power compared to local devices and peers. We denote the edge cloud processor by the symbol \(m \in \{1,2,\ldots ,M\}\) and the set of processors is set to M. Similarly, the total execution latency of task offloading to the edge cloud consists of two components: the transmission latency of the task on the offload link and the processing latency on the edge cloud processor.

First, we define the transmission rate of the task during the offloading of computational communication. And \(v_{lm}^{i}(t)\) is used to denote the transmission rate at which the local user device sends the task to the edge cloud, the formula is as follows:

$$\begin{aligned} v_{lm}^{i}(t)=\omega log_{2}\bigg (1+ \frac{\rho _{lm}^{i}h_{lm}^{i}(t)}{\sigma _{lm}^{i}}\bigg ), \end{aligned}$$
(11)

where \(\rho _{lm}^{i}\) is the transmission power from the task offload to the edge cloud, \(h_{lm}^{i}(t)\) is the channel gain from the local to the edge cloud, and \(\sigma _{lm}^{i}\) represents the noise power of additive Gaussian white noise.

In addition, we further the maximum channel transmission rate from the user’s local to the edge cloud processor, denoted by \(v_{lm}^{max}(t)\). Then the transmission delay of task i offloaded from the local user device to the edge cloud m is defined as:

$$\begin{aligned} t_{lm}^{i}=\frac{D_{i}}{v_{lm}^{i}(t)}. \end{aligned}$$
(12)

Then, the energy consumption generated by the local device during that transmission is:

$$\begin{aligned} e_{lm}^{i}=t_{lm}^{i}\times \rho _{lm}^{i}. \end{aligned}$$
(13)

Meanwhile, we define the computation rate of the task on the edge cloud within the time slot as:

$$\begin{aligned} v_{m}^{i}(t)=\eta _{m}^{i}(t)f_{m}, \end{aligned}$$
(14)

where \(f_{m}\) is the computational power of the edge cloud processor and \(0\le \eta _{m}^{i}(t) \le 1\) is the ratio value of the actual processing power of that edge cloud processor. Then the computational delay of task i on the edge cloud processor m is:

$$\begin{aligned} t_{m}^{i}=\frac{C_{lm}^{i}}{v_{m}^{i}(t)}. \end{aligned}$$
(15)

Queue dynamics

This subsection focuses on the representation of the dynamism of the queue, where we define that the local device, the peer device and the edge processor process one computational task at a time, and the rest of the tasks are stored waiting in their respective queues. We then use an offloading strategy to decide where tasks should be processed to minimize the computational cost while improving the quality of the user’s experience. This queue system model is shown in Figure 1. In the following, we describe the construction of queues in this system in detail.

First, define the queue \(Q_{l}^{i}(t) \in (0,\infty ]\ \) of task i in time slot t on local device l, in which all tasks requiring computation on the local are stored. Also, we define that at each time slot t the local device has a random arrival of a large number of computational tasks that need to be processed, denoted by \(A_{l}^{i}(t)\). We assume that it obeys an independently identically distributed (i.i.d) model and define its mean as \(E[A_{l}^{i}(t)]=\lambda _{l}^{i}\), where \(\lambda _{l}^{i}\) represents the average arrival rate of task i on the local device l. Then the formula for the dynamics of the local device queue in adjacent time intervals is as follows:

$$\begin{aligned} \begin{aligned} Q_{l}^{i}(t+1)&=\bigg [Q_{l}^{i}(t)-v_{l}^{i}(t)-\sum _{d=1}^{D}y_{ld}^{i}(t)v_{ld}^{i}(t) -\sum _{m=1}^{M}y_{lm}^{i}(t)v_{lm}^{i}(t)\bigg ]^{+}+A_{l}^{i}(t), \end{aligned} \end{aligned}$$
(16)

where \([\cdot ]^{+}=max\{\cdot ,0\}\). The first term in the equation represents the current remaining unprocessed computational tasks of the local device, and is non-negative by definition, and is specifically expressed as the length of the task queue at time slot t minus the sum of the amount of locally processable tasks and the tasks offloaded to the other peer devices in the system as well as to the edge cloud processor. Thus the defining construct of this queue is the sum of the remaining unexecuted tasks and newly arriving tasks on the local device.

In addition, we define \(H_{d}^{i}(t)\in [0,\infty )\) as a queue representation of task i on peer device d in time slot t for storing computing tasks arriving on that peer device. And define \(A_{d}^{i}(t)\) obeying i.i.d to denote the random number of arrivals of tasks on peer devices in time slot t, with the average value set to \(E[A_{d}^{i}(t)]=\lambda _{d}^{i}\), where \(\lambda _{d}^{i}\) is the average arrival rate of tasks on peer device d. Then, we represent the definition of the dynamics of the queue on each peer as follows:

$$\begin{aligned} \begin{aligned} H_{d}^{i}(t+1)=\bigg [H_{d}^{i}(t)-v_{d}^{i}(t)\bigg ]^{+}&+\sum _{l=1}^{L}y_{ld}^{i}(t)v_{ld}^{i}(t)+A_{d}^{i}(t). \end{aligned} \end{aligned}$$
(17)

where the first term on the right side of the equation represents the tasks that are still waiting to be processed on the peer device, and the second term represents the tasks that have been offloaded locally to that peer device, so that the sum of the last two terms represents the total new arrivals of tasks on that peer device at time slot t.

Finally, we denote by \(H_{m}^{i}(t)\in [0,\infty )\) the queue of task i on the edge cloud processor m in time slot t. This dynamics formula can be expressed as:

$$\begin{aligned} \begin{aligned} H_{m}^{i}(t+1)=\bigg [H_{m}^{i}(t)-v_{m}^{i}(t)\bigg ]^{+}&+\sum _{l=1}^{L}y_{lm}^{i}(t)v_{lm}^{i}(t)+A_{m}^{i}(t). \end{aligned} \end{aligned}$$
(18)

In the formula, \(A_{m}^{i}(t)\) denotes the random arrivals of tasks on this edge cloud processor in slot t. Assuming that it also obeys i.i.d, and that we define \(\lambda _{m}^{i}\) as the average arrival rate of tasks on the edge cloud processor, the representation of the average value is \(E[A_{m}^{i}(t)]=\lambda _{m}^{i}\). The representation of each item in the formula is the same as above, with the first term being the tasks that have not yet been processed on the edge cloud processor, and the sum of the last two terms represents the total number of new arrivals for that processor at slot t, where the first term is then the tasks that have been offloaded from the local to that processor.

By describing and analyzing the dynamics of the three queues described above, We can find that there is a certain coupling between the above three formulas, i.e., the departure of a task on the local device queue is the arrival of a task on any of the other peer device queues or the edge cloud processor queues in the system. In this system, in order to make it more relevant to real-world scenarios, we defined each queue with newly arriving tasks, which is reflected in the latency of the computed tasks. Therefore, we assume that the item does not affect the coupling relationships described in the text. In addition, we define \(Q_{tot}^{i}(t)\) as the sum of tasks in this system at time slot t and define \(Q_{max}^{i}(t)\) as the maximum number of tasks that can be accepted by the queue, which can be expressed as:

$$\begin{aligned} \begin{aligned} Q_{tot}^{i}(t)&=Q_{l}^{i}(t)+H_{d}^{i}(t)+H_{m}^{i}(t),\\&Q_{tot}^{i}(t)\le Q_{max}^{i}(t). \end{aligned} \end{aligned}$$
(19)

In other words, this formula represents that the total number of computational tasks in time slot t is equal to the sum of the number of tasks of all three, the local device queue, the peer device queue, and the edge cloud processor queue, and that the sum does not exceed the maximum number of tasks that can be received by the queues in the system. If the maximum number of tasks is exceeded, the task may crash and the user experience will be poor. Also, the formula is an equivalent definition of the coupling relationship between queues in the system.

Problem formulation

In this section, we define the optimization problem for this queueing system model. First, we construct a quadratic equation using the Lyapunov optimization technique which combines the three sets of control queues in the system whose main roles are optimized, i.e., local queue \(Q_{l}^{i}(t)\), peer device queue \(H_{d}^{i}(t)\), and edge cloud processor queue \(H_{m}^{i}(t)\). This Lyapunov quadratic function is expressed as:

$$\begin{aligned} \begin{aligned} V(t)=\frac{1}{2}\sum _{l=1}^{L}\sum _{i=1}^{N}[Q_{l}^{i}(t)]^{2}+\frac{1}{2} \sum _{d=1}^{D}\sum _{i=1}^{N}[H_{d}^{i}(t)]^{2}+\frac{1}{2}\sum _{m=1}^{M}\sum _{i=1}^{N}[H_{m}^{i}(t)]^{2}. \end{aligned} \end{aligned}$$
(20)

Based on the definition of queue in the previous subsection, we can conclude that the function is strictly incremental. To ensure that the queues are all bounded and there is no case where a queue has an infinite size, the Lyapunov drift function is defined as:

$$\begin{aligned} \Delta (t)=E[V(t+1)-V(t)|Z(t)], \end{aligned}$$
(21)

where \(Z(t)=\big (Q_{l}^{i}(t);H_{d}^{i}(t);H_{m}^{i}(t)\big )\), denotes the queue vector on the local device, the peer device, and the edge cloud processor in time slot t. From the definition of Lyapunov optimization theory14, by minimizing the drift function, we can optimize the queue backlog on each time slot in this system, and also ensure the stability of this queue system. Therefore, below we give the definition of the optimization problem for this system:

$$\begin{aligned} \begin{aligned}&\max _{y_{ld}^{i}(t),y_{lm}^{i}(t)}\sum _{l=1}^{L}\sum _{i=1}^{N}Q_{l}^{i}(t)\Bigg (v_{l}^{i}(t) +\sum _{d=1}^{D}y_{ld}^{i}(t)v_{ld}^{i}(t)+ \sum _{m=1}^{M}y_{lm}^{i}(t)v_{lm}^{i}(t)-A_{l}^{i}(t)\Bigg )\\&\quad +\sum _{d=1}^{D}\sum _{i=1}^{N}H_{d}^{i}(t)\Bigg (v_{d}^{i}(t) -\sum _{l=1}^{L}y_{ld}^{i}(t)v_{ld}^{i}(t)-A_{d}^{i}(t)\Bigg ) \\&\quad +\sum _{m=1}^{M}\sum _{i=1}^{N}H_{m}^{i}(t)\Bigg (v_{m}^{i}(t) -\sum _{l=1}^{L}y_{lm}^{i}(t)v_{lm}^{i}(t)-A_{m}^{i}(t)\Bigg ) \end{aligned} \end{aligned}$$
(22)

subject to

$$\begin{aligned} \begin{aligned}&(a) \ (1), (19); \\&(b) \ v_{ld}^{i}(t) \le v_{ld}^{max}(t); \\&(b) \ v_{lm}^{i}(t) \le v_{lm}^{max}(t); \\&(c) \ t_{l}^{i}, t_{ld}^{i}+t_{d}^{i}, t_{lm}^{i}+t_{m}^{i}<F_{i}. \end{aligned} \end{aligned}$$

The four constraints described above denote the conditions to be satisfied for the computational offloading decision of the task, the conditions to be satisfied for the queue in the system, the conditions to be satisfied for the transmission rate of the computational task during the transmission of the task from the user’s local-end device to the peer device and during the transmission of the task from the local-end device to the edge cloud processor, and the conditions of the task completion deadline.

In addition, Eq.(22) is obtained by minimizing the \(\Delta (t)\) in Eq.(21), and by solving this optimization problem, we can minimize the average queue backlog of the tasks on each time slot in the system, improve the computational performance of the user’s tasks, and at the same time achieve the stability of the queues in the system. The concrete proof procedure of this optimization problem is shown in Appendix A. By optimizing this problem, we are able to minimize the computational delay of the task, and based on this, the energy consumption of the task is optimized to minimize the computational cost of the task. To this end, this paper proposes a D2D-assisted collaboration computational offloading strategy (D-CCO) , which comprehensively determines the offloading decisions of the tasks in this system and gets the number of tasks that can be computed at each offloading.

D2D-assisted collaboration computational offloading strategy

This section provides a detailed description for the D-CCO algorithm, which aims to minimize the delay and energy consumption of a task by negotiating the computational cost at different execution locations to determine the optimal offloading decision. First, the main steps of the algorithm are described in detail, and then the performance of the algorithm is further investigated, and the relevant theoretical proofs are also given in the paper.

Algorithm analysis

In this queueing system, we introduce the D2D communication technique, which combines D2D with the edge cloud, and propose the D2D-assisted collaboration computational offloading strategy. The strategy takes into account the processing latency of sensitive tasks and minimizes the energy consumption by adding energy consumption as a performance metric to minimize the latency. In addition, the strategy takes into account the backlog of tasks on the queues in the system, that is, the waiting delay of tasks. The details of the D-CCO algorithm are shown in Algorithm 1 in the text.

Algorithm 1
figure a

D-CCO algorithm.

Full size image

Where the main steps of the algorithm are described as follows.

Determine the tasks to be executed locally

For computational tasks arriving on local devices in the system, we optimize their computational cost to arrive at the optimal offloading decision for the task. In this step, our goal is to identify the tasks to be processed on the local device. The sum of processing latency and energy consumption for the local execution of the task is computed first, and then the sum of latency and energy consumption for the execution of the task offloaded to the peer device as well as to the edge cloud processor is computed, respectively. The results are then compared, and if the computational cost of the task on the local device is minimized, the task is placed locally for processing; otherwise, the task is placed in the set S of the offloaded task.

Determine the optimal offloading location for the task

After determining the tasks to be performed locally, this step is to determine the optimal offloading location for the task. In this subsection, we utilize the back-pressure algorithm to reduce the computational cost of a task by computing the task backlog difference, denoted by \(W_{ld}^{i}(t)\) and \(W_{lm}^{i}(t)\), between the local queue and the peer device queue as well as the edge cloud processor queue. The formula for computing the backlog difference is shown as follows:

$$\begin{aligned} \begin{aligned} W_{d}^{i}(t)&=Q_{l}^{i}(t)-H_{d}^{i}(t), \\ W_{m}^{i}(t)&=Q_{l}^{i}(t)-H_{m}^{i}(t). \end{aligned} \end{aligned}$$
(23)

We then combine the execution cost of the task with the backlog difference to jointly determine the offloading location of the task. Combined with the execution cost of the task, the optimal execution position of the task is determined by selecting the maximum value of the task backlog difference, which is expressed as follows:

$$\begin{aligned} \{y_{ld}^{i}(t),y_{lm}^{i}(t)\}=arg\max _{i\in S}\{W_{ld}^{i}(t),W_{lm}^{i}(t)\}. \end{aligned}$$
(24)

From this formula, we can get the optimal offloading decision of the task.

Algorithm performance

Theorem 1

(Queues stability). Assuming that the ratio between the performance of the D-CCO algorithm and the optimal solution is \(\frac{1}{1+\theta }\), then the capacity area will be reduced accordingly \(\frac{1}{1+\theta }\lambda _{m}{\textbf{I}}\), where \(\lambda _{m}\) is the maximum arrival rate in the system for all \(i\in N, l\in L\). Then the average length of queues in the system should satisfy

$$\begin{aligned} \lim _{T\rightarrow \infty }\frac{1}{T}\sum _{t=1}^{T}\sum _{d=1}^{D}\sum _{i=1}^{N}H_{d}^{i}(t)\le & \lim _{T\rightarrow \infty }\frac{1}{T}\sum _{t=1}^{T}\sum _{l=1}^{L}\sum _{i=1}^{N}Q_{l}^{i}(t) \le \frac{(1+\theta )B_{1}}{\varepsilon -\frac{1}{1+\theta }\lambda _{m}}, \end{aligned}$$
(25)
$$\begin{aligned} \lim _{T\rightarrow \infty }\frac{1}{T}\sum _{t=1}^{T}\sum _{m=1}^{M}\sum _{i=1}^{N}H_{m}^{i}(t)\le & \lim _{T\rightarrow \infty }\frac{1}{T}\sum _{t=1}^{T}\sum _{l=1}^{L}\sum _{i=1}^{N}Q_{l}^{i}(t) \le \frac{(1+\theta )B_{1}}{\varepsilon -\frac{1}{1+\theta }\lambda _{m}}, \end{aligned}$$
(26)

where \(\varepsilon\) is a small positive constant. The above theorem represents the stability of all queues in this system and its detailed proof is shown in Appendix B.

This subsection proves the stability of the queues in the system and the stability of the algorithm by deriving that the local queue, the peer device queue, and the edge cloud processor queue all have upper bounds, i.e., they are all less than a definite value. At the same time, due to some coupling between the queues, i.e., the departure of a task on the local device is the arrival of a task on the peer device queue or the edge cloud processor queue. In addition, there is no direct relationship between the peer device queue and the edge cloud processor queue since the peer device plays the role of a server. Therefore, in Theorem 1, the queue length of the local device is not less than the queue length of the peer device, and also not less than the length of the edge cloud processor queue, and they are both upper bounded. By proving the stability of the individual queues, i.e., the stability of the queueing systems considered in this paper is also proved.

Experiments and performance analysis

In this section, the performance index of the algorithm is evaluated by numerical simulation in the experimental environment of MATLAB R2019a, the physical platform is a person computer with an Intel Core i5 CPU(3.00 GHz), 16GB of RAM, and a 64-bit operating system. Through modeling and simulation, the performance index of the proposed algorithm is verified. In order to ensure the stability and validity of the experiment, combined with rich practical experience and a large number of paper references, we use specially designed custom data sets to simulate the environment to reflect the real scenario. We assume that in this queuing system, the local devices are randomly distributed and the peer devices and the edge cloud processors are uniformly distributed, where the peer devices are distributed around the user and the edge cloud processors are closer to the user but farther away compared to the peer devices. In addition, we define that the arrival of tasks on the local device obeys a Poisson distribution and define the arrival of 100 tasks on each device, the size of the computation of each task is 500bits, and the number of CPU cycles required to process a task locally or on a peer device is 30Mcycles. The computational power of the local device is a value among 0.6GHz, 0.8GHz, 1.0GH, 1.2GH, 1.5GHz, 1.8GHz, 2.0GHz, 2.5GHz, 3.0GHz, and the CPU frequency of the peer device ranges from 2.0GHz, 2.5GHz, 3.0GHz, 3.5GHz, and 4.0GHz, and assume that the edge cloud processor has the same computational frequency, defined as 35GHz.

In addition, we set the ratio of the computational power of each device to its actual processing power to \(\eta _{l}^{i}(t)=\eta _{d}^{i}(t)=\eta _{m}^{i}(t)=0.9\) to match the actual situation of the device. Also define the bandwidth of the channel that the task sends to the other devices as 5MHz, the channel gain is 0.1, and the noise power of the channel is set to -174dBM/Hz40. And the computational power of the task locally is set to 5mW, and the transmission power of the task sent to the peer device and the edge cloud processor is defined as 3mW and 2mW, respectively. By setting the different transmission power of the task, we can get different transmission rates to be close to the actual offloading scenarios.

Moreover, we set the task completion deadline \(F_{i}\) is 3s. If the deadline is exceeded, an error will be reported. And we assume that the average arrival rate on the local queue and the edge cloud processor queue is the same as the initial value of the task, while the peer device has a large amount of free computational resources, so we set the average arrival rate of the peer device queue to be relatively small and the initial value of this queue is reduced accordingly. The other variables covered in this paper are given in the detailed description of the performance comparison below.

Performance analysis

This section verifies the stability of the D-CCO algorithm proposed in this paper by deriving upper bounds for the local queue, the peer device queue, and the edge cloud processor queue, respectively, as shown in Figures 2. We considered 20 local devices, 10 peer devices, and 1 edge cloud processors, respectively, with an average arrival rate of \(\lambda _{l}^{i}=\lambda _{m}^{i}=6\), \(\lambda _{d}^{i}=2\) on each device. The initial value of the task is defined as \(Q_{l}^{i}(t)=H_{m}^{i}(t)=1000\) for the local queue and the edge cloud queue, and \(H_{d}^{i}(t)=200\) for the peer device queue. And the maximum number of tasks that each queue can handle is not more than 2000 to ensure the quality of user experience.

Fig. 2
figure 2

Stability of queue length.

Full size image

In Fig. 2a, we verify the stability of the local device queue. For the local queue, we choose the number of iterations to be 1000. When t is in the interval [1,650], the average backlog of the local device queue shows a fast and smooth decreasing trend, which is due to the fact that when a large number of computational tasks arrive from the local users, the other devices or processors in the system have sufficient computational resources to improve the computational efficiency by offloading the tasks to the devices or processors that have more resources and are faster in computation. However, the trend of queue backlog is flatter after \(t=650\) compared to before due to the limited transmission rate of the channel or the fact that more tasks are already stored on other queues in the system, when tasks need to be processed locally. Finally, when \(t>900\), we can see that the backlog of tasks in the local queue starts to approach a value and fluctuates within a small range, i.e., the stability of the local queue is verified.

Figure 2b verifies the stability of the peer device queue in the system. At the beginning of the iteration, there is a very short drop-off because the computing tasks on the peer devices are not crowded and they have some computing power. And then the backlog started, and that’s because some tasks on the local device are offloaded to the peer device and there are its own tasks on that queue waiting to be processed, resulting in an increased backlog of tasks on the peer device’s queue. After that, by considering the situation of tasks on all queues in the system and calculating the performance of local task execution, the optimal offloading decision for the tasks is synthesized, and as a result, the task backlog starts to decrease, showing a downward trend. Until after \(t=650\), the backlog of tasks on the peer device queue leveled off, thus validating the stability of the queue.

The experimental results in Fig. 2c show the stability of the edge queue. This queue has almost the same discount trend as the peer queue, because the peer device plays the same role as the edge cloud processor. As the iteration begins, the backlog of tasks in this queue first shows a brief rise, then begins to decline, and finally levels off. After offloading a large number of computing tasks locally to the edge cloud, the backlog of tasks in the queue starts to grow due to the large volume of transient tasks. After that, due to the high computing power of the edge cloud, the task backlog shows a trend of reduction. Finally, the stability of the edge queue is verified after \(t>660\), when the edge queue begins to fluctuate within a certain range and levels off.

Performance comparison

We have compared the performance of this D-CCO algorithm with the following five algorithms in separate numerical experiments, and each scheme is described in detail below:

  • Only-local algorithm (OL) : All tasks arriving on the local device are processed locally, and the algorithm only considers the cost of executing the task locally.

  • Random deployment algorithm (RD): The task offloading decision is determined by random matrix in this algorithm, and the task is randomly deployed on local device, peer device or edge cloud processor.

  • Back-pressure algorithm (BP)14: This algorithm uses the back-pressure algorithm to determine the offloading decision by constructing a queue system and computing the task backlog difference between queues.

  • Only local and peer device algorithm (OLP): The algorithm utilizes the stochastic optimization and the back-pressure algorithm to determine the offloading decision of the task, but only considers the task deployed on local or peer devices for processing.

  • An alternate optimization algorithm (EPSO-GA)10: A D2D-assisted alternative optimization algorithm is proposed, which uses enhanced particle swarm optimization algorithm and genetic algorithm to optimize the transmit power allocation strategy and the subtask offloading strategy, so as to obtain the offloading decision of the task.

This section mainly compares this method with the above five algorithms in terms of the performance of the local task execution cost, from the following aspects respectively: (1) the average arrival rate of local tasks; (2) the time slot; (3) the initial length of local queue; (4) the number of Local devices; (5) the number of Peer devices; and (6) the frequency of edge cloud. In order to correspond to the sensitive tasks mentioned in the paper, we made further calculations on the experimental results and concentrated them all on the delay aspect, rather than on the average queue length, so as to better express the comparative results among the algorithms. In the following, we will analyze the experimental results under different conditions separately.

Fig. 3
figure 3

Performance comparison graph.

Full size image

Figure 3a-c shows how the local task processing delay changes with the arrival rate of the local task, the size of the time slot, and the initial value of the local queue. Note that when these values change, the corresponding values of the peer device queue and edge processor queue are changed in proportion to their initial values. We set \(L=20\), \(D=10\) and \(M=1\), and we define the arrival of 100 tasks on each local device, and the CPU processing frequency of the edge processor is 35GHz. In addition, in order to facilitate the comparison of experimental evaluation values, we set the number of iterations \(T=200\).

Figure 3a compares the performance of this algorithm with other methods under different local task average arrival rates when the time slot \(\tau =60ms\) and the initial length of the local queue \(Q=1000\). By setting different average arrival rate values, the task processing delay is compared on the local device of the system. From the figure we can see that the processing latency of the tasks in this system increases as the horizontal coordinate increases, which may be due to the insufficient local computing power or the limited transmission channel. However, compared with other algorithms, the D-CCO algorithm has the smallest processing cost, i.e., the algorithm is able to efficiently compute the tasks on the local when there are a large number of arrivals, which demonstrates a greater superiority. In Fig. 3b, we study the influence of different time slot sizes on local task processing latency when \(\lambda _{l}=6\) and \(Q=1000\), and compare several comparison algorithms respectively. With the increase of \(\tau\), this algorithm can compute more local tasks, and the task processing delay of this algorithm is relatively optimal. Fig. 3c shows the change of local task processing delay at different local queue initial values. When the initial value of the local queue increases, the backlog of queues on the local device increases, and the processing latency of local tasks also increases. As can be seen from the figure, the effect of this algorithm is relatively good.

In addition to the above three cases, we also studied the change of task processing delay of the algorithm under different number of local devices, number of peer devices, and frequency of edge cloud, as shown in Fig. 3d-f. In this comparison, we set \(\lambda _{l}=6\), \(\tau =60 \, {\rm ms}\) and \(Q=1000\).

As can be seen in Fig. 3d, the processing latency of tasks in the local queue shows a slowly increasing trend. This is because although there are enough computing resources in the system to increase the local execution speed by offloading tasks to other devices or processors for computation, as the number of user devices increases, the local tasks also increase, resulting in an increase in the processing latency of local tasks. And the algorithm shows good performance in handling the task compared to other algorithms. Therefore, the algorithm can be better employed for user devices with a large number of tasks.

Figure 3e depicts the variation in task processing latency for different number of peer devices. As can be seen from the figure, with the increase in the number of peer devices, the EPSO-GA algorithm and D-CCO algorithm show a gradual decline and then a slow rise, while the OLP algorithm shows an obvious decline and then a steady rise. This is because the higher cost of computing tasks on peer devices can lead to too many tasks being offloaded to the edge cloud. As tasks continue to arrive on the local device, the backlog of tasks in the local queue increases, which increases the computing delay. In addition, the setting of the CPU frequency of the increased peer device is also one of the influencing factors.

In Fig. 3f, by varying the number of processors in the edge cloud, we investigate its impact on task processing latency. When the processor frequency increases, EPSO-GA algorithm and D-CCO algorithm have obvious changes, which have little influence on the offloading decision of other comparison algorithms. When the edge cloud processor frequency increases, its processing power also increases, which leads to more tasks being offloaded to the edge cloud processor for execution, and thus the local task processing delay decreases. And from the figure we can conclude that the D-CCO algorithm has the best experimental results and optimal performance.

Conclusion

In this paper, we study the task offloading problem under D2D-assisted collaboration. In order to optimize the computational cost of the task, we combine D2D with computational offloading and use stochastic optimization techniques to propose an optimization problem that minimizes Lyapunov drift to optimize the processing latency of the task. And based on this, the energy consumption of the task is calculated and the backlog of the task is considered to minimize the computational cost of the task. For this reason, the D-CCO algorithm is designed in this paper to minimize the user cost. However, since the paper mainly focuses on latency-sensitive tasks, in this paper, we derive the consumption by using the energy consumption formula of the tasks at different locations, and do not analyze the resource consumption in specific experiments. Moreover, due to the different computing power of each device or server, they will also generate different processing latency as well as energy consumption after choosing different computing locations, so we reduce the user’s computation cost by computing the different execution costs of the tasks to determine their optimal execution locations. In addition, a theoretical analysis of queue stability in the system is given in the paper, and experimental results verify that the algorithm minimizes the total cost of task execution when compared with other comparative methods.