Introduction

With the rapid development of the Internet of Things (IoT) technology, edge computing, as a new computing paradigm, has attracted extensive attention in recent years. Edge computing significantly reduces data transmission latency, improves data processing efficiency, and reduces network bandwidth consumption by pushing computing resources and application services from the cloud to the edge of the network1. However, in some scenarios, traditional base stations are difficult to work or provide sufficient computing resources, such as rescue operations, forest fires, disaster scenarios, and temporary large-scale events2. Taking large-scale sports events as an example, due to the increasing demand for viewing experience from spectators and the large number of computation-intensive tasks generated during the competition, the traditional network model is difficult to cope with such high demand3,4. Especially during the critical moments of the competition, the demand for real-time data updates, high-definition video streaming and other services increases sharply, which undoubtedly poses a huge challenge to the existing computing and network resources5.

Unmanned aerial vehicle (UAV)-assisted edge computing technology provides an innovative solution6. UAVs play an increasingly important role in edge computing systems due to their flexible deployment, high maneuverability, and extensive coverage. Deployed in the air, UAVs can provide better channel conditions for ground devices. Moreover, the flexible deployment capabilities of UAVs enable them to provide high-quality short-term services for temporary high-density scenarios7,8. As edge nodes, UAVs can provide fast and reliable computing and communication support for large-scale sports events, thus meeting the spectators’ demands for high-quality viewing experience9,10,11.

Although previous efforts have conducted some research on UAV-assisted edge computing in large-scale events12, there are still many challenges to face. First, numerous computation-intensive tasks are generated suddenly, and it is difficult to accurately predict the generation time of these tasks, and the communication conditions in the environment are also random, making it challenging to optimize the system without prior information. Second, the computing and communication resources of UAVs and devices are limited, requiring us to allocate these resources reasonably while ensuring system performance and cost. Finally, while the addition of UAVs can provide better communication conditions for the system, it also increases the complexity of the problem. Therefore, ensuring system performance while minimizing system energy consumption in this UAV-assisted MEC system is challenging.

This paper studies the task offloading and resource allocation problem in a three-tier UAV-assisted MEC system. We aim to minimize the energy consumption of the system while satisfying multiple constraints such as computing and communication resources. The CPU frequency and offloading power of devices and UAVs are considered as our decision variables. Since the problem is NP-hard13, we utilize mathematical methods to transform the problem and further decouple it into four subproblems. We propose the EDRA algorithm, which can stabilize the task queue of the system while minimizing system energy consumption as much as possible. Theoretical analysis proves the effectiveness of our algorithm. A series of experiments have been conducted to demonstrate that EDRA has excellent performance in solving the task offloading and resource allocation problem in UAV-assisted MEC systems.

Our main contributions are as follows:

  1. 1.

    We study the task offloading problem in a scenario that includes multiple devices, UAVs with edge servers, and a cloud server, while taking into account the randomness of tasks, channel conditions, and user locations. Under the premise of satisfying long-term constraints and system performance, we reformulate the problem as a long-term stochastic optimization problem to minimize system energy consumption.

  2. 2.

    As the problem is NP-hard, we transform it into a deterministic optimization problem through a series of mathematical manipulations. Combining rigorous proofs, we decompose the problem into multiple subproblems, each containing only one decision variable, which can achieve (approximate) optimal solutions. The efficient dynamic resource allocation (EDRA) algorithm is proposed to solve multiple subproblems online and in parallel.

  3. 3.

    Through theoretical analysis, we prove the gap between the proposed algorithm and the optimal algorithm, ensuring the performance of the proposed algorithm. Through a series of parameter analyses, we demonstrate that the proposed algorithm can adapt to different task arrival rates and device quantities. Through comparative experiments, we show that the system can effectively reduce energy consumption while ensuring the task queue length.

The structure of the remainder of this paper is as follows. Section Related work introduces related work. Section System model and problem formulation presents the system model and problem formulation. Section EDRA for task offloading and resource allocation transforms and decomposes the problem into multiple subproblems, and propose the EDRA algorithm. Section Algorithm analysis for EDRA provides a theoretical analysis of the EDRA algorithm. Section Evaluation demonstrates the performance of the EDRA algorithm in different environments through experimental results and compares it with advanced algorithms. Finally, Sect. Conclusion summarizes the paper.

Related work

Table 1 Comparison of related work based on key factors.
Full size table

Recently, many efforts have focused on task offloading and resource allocation problem in the MEC system. Ding et al.14 studied a generalized MEC system that incorporates both OMA and NOMA transmission methods. They proposed a multi-objective optimization problem to achieve minimal system energy consumption while achieving low-complexity resource allocation. Ernest et al.15 applied multi-agent reinforcement learning techniques to the computation offloading problem in MEC vehicular networks, obtaining an offloading strategy that can achieve maximum energy efficiency. Chu et al.16 studied the caching and task offloading issues in multi-access edge computing networks. They focused on maximizing user QoE by consolidating a logical resource pool, and proposed a method based on approximation and decomposition theory to solve this problem. Tang et al.17 investigated the offloading problem in multi-access edge computing. They achieved minimized offloading delay for IoT terminals by jointly optimizing computing and communication resources. However, the aforementioned studies did not take into account the randomness of channel conditions and the unpredictability of task arrivals in the environment.

Considering the dynamic variability of the environment, Liu et al.18 designed a dynamic optimization algorithm for intensive requests from terminal devices in MEC systems. This algorithm can significantly improve system performance by adjusting the offloading decisions and power allocation strategies. Ali et al.19 studied a multi-user MEC system, where they optimized the offloading decisions from a life-cycle perspective without prior information and proposed a SAC-based lifespan maximization algorithm. Li et al.20 investigated the problem of minimizing computational delay and energy consumption in MEC systems. They utilized the Lyapunov optimization framework to optimize the system while balancing both factors. Sun et al.21 studied the long-term energy-efficient task allocation and offloading in MEC systems. By decomposing the original problem into multiple subproblems, they achieved an online energy-saving strategy. However, the aforementioned works did not consider utilizing UAVs to assist edge computing, thus unable to provide edge computing for scenarios requiring temporary, intensive, and low-latency computations.

Sun et al.22 formulated the Time and Energy Minimization Communication Multi Objective Optimization Problem (TEMCMOP) for CB in UAV networks and proposed an improved Multi Objective Ant Lion Optimization (IMOLO) algorithm to solve the problem. Picano et al.23 studied the computational offloading problem in UAV-assisted MEC systems. They proposed an efficient offloading decision algorithm based on a matching algorithm while satisfying different QoS constraints. Chen et al.24 investigated a LEO Satellite-Terrestrial Edge Computing Systems with terrestrial base stations. They considered task offloading under limited resources and proposed an offloading algorithm based on potential game theory. Gao et al.25 studied the low-latency QoE problem in UAV-MEC systems. They proposed a service experience-oriented framework to cache user-required content on the edge servers on UAVs, thus improving the overall system performance. Chen et al.26 studied the scenario of using UAV to assist users in edge computing when the ground base station cannot work. A hybrid natural inspired optimization algorithm (HNIO) and its discrete optimization version were proposed to solve the energy consumption optimization problem in this scenario.

Despite significant efforts in UAV-assisted edge computing, existing works have not fully addressed the challenges of random environmental information and system stability while providing an online solution. As shown in Table 1, our work takes these issues into consideration. Compared to robust optimization and RL14,15,18,19, we balance robustness and efficiency through the dynamic transformation of the stochastic optimization framework, explicitly modeling the stochastic optimization problem. In contrast to the above works’ approaches to ensuring system performance15,17,22,27, we dynamically guarantee long-term system performance by introducing task queues.

Specifically, we formulate the Task Offloading and Resource Allocation in UAV-Assisted MEC for Large Sport Events as a stochastic optimization problem. By leveraging stochastic optimization techniques, we can provide adaptive solutions online without requiring prior knowledge of task arrival rates and channel conditions. Additionally, we ensure system stability by introducing virtual task queues and incorporating them into the optimization objective, thereby transforming the originally constrained virtual task queues into part of our optimization goal.

System model and problem formulation

System model

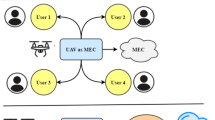
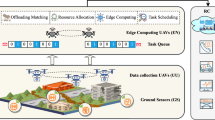
As shown in Fig. 1, this paper considers a three-tier UAV-assisted edge computing network, which includes I terminal devices, J UAVs equipped with edge servers, and a Cloud Server (CS) that can provide cloud services. To provide long-term optimization, time is divided into T equal-length discrete time slots, with each slot having a duration of \(\tau\), where \(\mathcal {T} \in \{1, 2, 3, \dots , T\}\). For convenience, \(N_{i,j}\) is used to represent the i-th device served by UAV j and \(\mathcal {I}_j\) represents the set of devices which communicating with UAV j. In each time slot, there are \(A_{j,i}(t)\) amount of tasks arriving at device \(N_{i,j}\), which is influenced by factors such as whether, position movement, etc., and the device can choose to process the tasks locally or offload them to the edge server on UAV j. The edge server can select to further transmit part of the tasks to the CS for processing based on its own task backlog. Table 2 shows the primary notations and definitions for this paper.

Fig. 1
figure 1

An example of a system model comprising multiple UAVs equipped with edge servers, multiple devices, and a cloud server.

Full size image
Table 2 Notations and definitions.
Full size table

Communication model

UAVs equipped with edge servers provide better communication conditions compared to traditional ground base stations. This is due to the higher probability of Line-of-Sight (LoS) path communication in ground-to-air communication. Therefore, this paper consider a probabilistic geometric LoS model to account for the channel gain between devices and UAVs in large-scale sports events.

We use \(H_{j}\) to represent the flight height of UAV j, and for simplicity, the height of all devices is assumed to be 0. The two-dimensional coordinates of UAV j are denoted as \((x_j(t), y_j(t))\), and the two-dimensional coordinates of device \(N_{i,j}\) are represented as \((x_{i,j}(t), y_{i,j}(t))\). The probabilistic geometric LoS channel model depends on the angle between the communication entities. We can calculate the angle between UAV j and device \((x_{i,j}, y_{i,j})\) in the t-th time slot based on the horizontal difference as:

$$\begin{aligned} \theta _{i,j}(t)=\frac{180}{\pi }\arctan (\frac{H_j}{\Vert p_j(t)-p_{i,j}(t)\Vert }). \end{aligned}$$
(1)

After obtaining the UAV j and the device’s coordinates \((x_{i,j}, y_{i,j})\), we can derive the probabilistic geometric LoS (Line-of-Sight) loss model28 between them,

$$\begin{aligned} {P}(LoS,\theta _{i,j}(t))=\frac{1}{1+a\exp (-b(\theta _{i,j}(t)-a))}, \end{aligned}$$
(2)

Where a and b are environment-dependent parameters. Additionally, the probability of NLoS link can be easily derived as \(P(NLoS,\theta _{i,j}(t)) = 1 - P(LoS,\theta _{i,j}(t))\). Moreover, during the transmission of wireless signals, there is also the free-space path loss given by:

$$\begin{aligned} FL_{j,i}(t) = 20\log _{10}||p_j(t) - p_{i,j}(t)|| + 20\log _{10}\left( \frac{4 \pi f_c}{c}\right) , \end{aligned}$$
(3)

Where this formula incorporates the path loss due to distance, related to the Euclidean distance between the UAV and the device, and the path loss caused by the diffusion of electromagnetic waves in free space. Here, \(f_c\) is the frequency, and c represents the speed of light.

In summary, similar to29,30, the path loss between the UAV and the device can be expressed as:

$$\begin{aligned} \begin{aligned} L_{j,i}(t) = P(LoS,\theta _{i,j}(t)) \times \eta ^{LoS} + P(NLoS,\theta _{i,j}(t)) \times \eta ^{NLoS} + FL_{j,i}(t), \end{aligned} \end{aligned}$$
(4)

Where \(\eta ^{LoS}\) and \(\eta ^{NLoS}\) are the additional path loss factors for LoS and NLoS conditions, respectively. Then, the channel gain is given by \(g_{j,i} = 10^{-\frac{L_{j,i}(t)}{10}}\).

Similar to31, we assume that the devices communicate with the UAVs using Frequency Division Multiple Access (FDMA) transmission. According to Shannon’s theorem32, the transmission rate in the ideal condition for a device to offload tasks to the UAV can be expressed as:

$$\begin{aligned} R_{j,i}(t) = B_j \log _2\left( 1 + \frac{g_{j,i}(t)P_{i,j}(t)}{N_0(t)}\right) , \end{aligned}$$
(5)

Where \(B_j\) is the bandwidth allocated for communication between device \(N_{i,j}\) and UAV j, \(P_{i,j}(t)\) is the transmit power of device \(N_{i,j}\), and \(N_0(t)\) is the noise power spectral density.

Task and offloading model

The system is optimized for long-term performance and divided into multiple time slots. In each time slot, tasks arrive at device \(N_{i,j}\) following a Discrete-Time Poisson Process, with the task arrival rate denoted by \(A_{i,j}(t)\). Upon receiving tasks33, the device can choose to process them locally or offload them to the edge server on the UAV. Unlike some binary offloading models, this work considers scaling the device’s CPU frequency \(f_{i,j}(t)\) and adjusting the offload power \(P_{i,j}(t)\) for more precise partial offloading. Similarly, the UAV can scale its CPU frequency \(f_j(t)\) and offload power \(P_j(t)\) to partially process tasks and offload some to the cloud. This section models the task amount and energy consumption in the system.

Energy consumption and task amount of devices

The local computation amount \(C^l_{i,j}(t)\) of the device is related to its hardware characteristics and CPU frequency, while the offloaded task amount \(C^o_{i,j}(t)\) can be changed by adjusting the offload power to alter the transmission rate. They can be expressed as follows:

$$\begin{aligned} C^l_{i,j}(t)=\frac{f_{i,j}(t)\tau }{\sigma _{i,j}},C^o_{i,j}(t) = \tau R_{i,j}(t). \end{aligned}$$
(6)

Where \(\sigma _{i,j}\) is the number of CPU cycles required by device i to process one bit of task. It is also necessary to satisfy \(C^l_{i,j}(t) + C^o_{i,j}(t) \le A_{i,j}(t)\).

The energy consumption of the device is also related to the CPU frequency and offload power34,35. According to Joule’s Law, it can be expressed as:

$$\begin{aligned} E_{i,j}(t) = \gamma _c f^3_{i,j}(t)\tau + \tau P_{i,j}(t), \end{aligned}$$
(7)

Where \(\gamma _c\) is the energy efficiency factor. The \(f_{i,j}(t)\) and \(P_{i,j}(t)\) are subject to the following constraints:

$$\begin{aligned} 0 \le f_{i,j}(t) \le f^l_{max}, \quad 0 \le P_{i,j}(t) \le P^l_{max}. \end{aligned}$$
(8)

Energy consumption and task amount of UAVs

Each UAV’s server can provide services to multiple devices, resulting in the UAV’s CPU being occupied by multiple different tasks. We logically divide the CPU frequency of the UAV into \(f^j_i(t)\) to represent the CPU frequency allocated by UAV j to device \(N_{i,j}\) in time slot t. The same applies to the offload power. Then, the task amount processed by the UAV can be expressed as:

$$\begin{aligned} D^{l,j}_{i}(t)=\frac{f^j_{i}(t)\tau }{\sigma _j}, \quad D^{o,j}_{i}(t) = \tau R^j_{i}(t), \end{aligned}$$
(9)

Where \(\sigma _j\) is the number of CPU cycles required for device i to process one bit of task. \(D^{l,j}_{i}(t)\) represents the amount of tasks processed locally, and \(D^{o,j}_{i}(t)\) represents the amount of tasks offloaded to the cloud server for processing. The energy consumption can be expressed as:

$$\begin{aligned} E_{j}(t)=\sum ^{\mathcal {I}}_{i=0} \gamma _c f^{j}_i(t)^3\tau + \tau P^j_i(t). \end{aligned}$$
(10)

Unlike devices that are only constrained by themselves, all tasks on a UAV share the computing and communication resources of that UAV, affecting each other. Task processing and offloading on the UAV need to satisfy the following constraints:

$$\begin{aligned} 0 \le \sum _{i=1}^{\mathcal {I}_j} f^j_{i}(t) \le f^l_{max}, \quad 0 \le \sum _{i=1}^{\mathcal {I}_j} P^j_{i}(t) \le P^j_{max}, \quad \forall j \in \mathcal {J}. \end{aligned}$$
(11)

Task queue model

To achieve long-term optimization of the system, we need to ensure that the system is in a state where it can process tasks normally. That is, the backlog of tasks processed by the system cannot grow indefinitely. To this end, we set up two sets of queues (they are all in a First-In-First-Out (FIFO) manner and processed one by one) to ensure that the task backlog on devices and UAVs is not excessive (the cloud service has powerful computing capabilities, so the task backlog at the cloud level is not considered for the moment). First, the queue on the device can be expressed as:

$$\begin{aligned} \begin{aligned} Q_{i,j}(t+1)=\max \{Q_{i,j}(t)+A_{i,j}(t)-C^l_{i,j}(t) -C^o_{i,j}(t),0\} \quad \forall t\in \mathcal {T}, \end{aligned} \end{aligned}$$
(12)

Where \(Q_{i,j}(t)\) represents the task backlog status of device \(N_{i,j}\) at time t, the queue entry variable is the task arrival rate \(A_{i,j}(t)\), and the exit variables are the local computation amount \(C^l_{i,j}(t)\) and the offloaded task amount \(C^o_{i,j}(t)\).

We use \(U_{i,j}\) to represent the backlog queue for the tasks of device i on UAV j, as follows:

$$\begin{aligned} \begin{aligned} U_{i,j}(t+1)=\max \{U_{i,j}(t)+C^o_{i,j}(t)-D^l_{i,j}(t) -D^o_{i,j}(t),0\} \quad \forall t\in \mathcal {T}, \end{aligned} \end{aligned}$$
(13)

Where the entry variable is the offloaded task amount \(C^o_{i,j}(t)\) from device i, and the exit variables are the local computation amount and the offloaded task amount.

Problem formulation

Given the energy consumption formula for task processing in the system, considering our optimization objective. We minimize the energy consumption of the system by optimizing the CPU frequency, offload power of devices, CPU frequency, and offload power of UAVs, while satisfying multiple constraints. This is a long-term stochastic optimization problem and can be expressed as:

$$\begin{aligned} \text {P1:} \quad&\min _{\phi _{i,j}(t)} \lim _{T \rightarrow \infty }\frac{1}{T}\sum ^T_{t=1}\sum ^J_{j=1}\sum ^{I_j}_{i=1}E_{i,j}(t)+E_{j}(t), \end{aligned}$$
(14a)
$$\begin{aligned} \text {s.t.} \quad&\lim _{T \rightarrow \infty } \sum ^T_{t=1}\sum ^J_{j=1}\sum ^{I_j}_{i=1}\mathbb {E} \{Q_{i,j}(t)\}< \infty , \end{aligned}$$
(14b)
$$\begin{aligned}&\lim _{T \rightarrow \infty } \sum ^T_{t=1}\sum ^J_{j=1}\sum ^{I_j}_{i=1}\mathbb {E} \{U_{i,j}(t)\}< \infty , \end{aligned}$$
(14c)
$$\begin{aligned}&C^l_{i,j}(t)+C^o_{i,j}(t) \le A_{i,j}(t), \forall i,j,t \end{aligned}$$
(14d)
$$\begin{aligned}&D^l_{i,j}(t)+D^o_{i,j}(t) \le C^o_{i,j}(t), \forall i,j,t, \end{aligned}$$
(14e)

(8), and (9).

Where \(\phi _{i,j}(t)=f_{i,j}(t),P_{i,j}(t),f^j_{i}(t),P^j_{i}(t)\) is a set of vector variables. \(E_{i,j}(t)\) is the energy consumption of device \(N_{i,j}\) at time slot t, \(E_{j}(t)\) represents the energy consumption of UAV j, and (14a) is our optimization goal, which is to minimize the long-term energy consumption of the devices and UAVs. (14b) and (14c) represent the long-term constraints that need to be satisfied by the device layer and the UAV layer respectively. (14d) represents the task processing capacity constraint of the devices. (14e) represents the task processing capacity constraint of the UAVs. (8) and (9) limit the CPU frequency and power of the devices and UAVs respectively.

In fact, solving this long-term stochastic optimization problem is quite challenging. Since the task arrival rate, channel conditions in the environment, and other factors are random, it is difficult to make precise predictions. Mathematically, this problem is formulated as a mixed-integer nonlinear programming (MINLP) problem, which is known to be NP-hard. Traditional mathematical methods find it difficult to provide an optimal solution within a reasonable time. Therefore, in the next section, we use stochastic optimization techniques to transform the problem into a more tractable static optimization problem.

EDRA for task offloading and resource allocation

Recall our goal of minimizing the system’s energy consumption by optimizing \(\phi _{i,j}(t)\). However, in P1, multiple variables in \(\phi _{i,j}(t)\) are coupled high-dimensional vectors. In this section, we will first transform the direct optimization of P1 into optimizing the upper bound of P1, aiming to reduce long-term energy consumption by decreasing the upper bound of P1. Additionally, we decouple the multiple variables in \(\phi _{i,j}(t)\) and decompose them into multiple independent subproblems. This also means that these problems can be solved in parallel, improving the efficiency of the solution process.

Problem transform

First, we use the vector \(\omega (t)=\{Q_{1,1}(t),\dots ,Q_{i,j}(t)\}\cup \{U_{1,1}(t),\dots ,U_{i,j}(t)\}\) to represent the overall queue backlog and stability conditions of the system at time t and \({\textbf {L}}(\omega (t))=\frac{1}{2}\sum ^J_{j=1}\sum ^{I_j}_{i=1}(Q_{i,j}^2(t)+U_{i,j}^2(t))\). Clearly, \(L(\omega (t))\) is non-negative, and we can judge the backlog situation of the system based on its magnitude. To achieve long-term stability, we can express the drift function as:

$$\begin{aligned} \Delta (\omega (t))=\mathbb {E}\{L(\omega (t+1))-L( \omega (t)\vert \omega (t)\}. \end{aligned}$$
(15)

Reducing this drift function is equivalent to reducing the backlog in the queue. However, while we stabilize the backlog in the system, we also need to minimize energy consumption as much as possible. In this case, we introduce a penalty term into the drift function to obtain the drift-plus-penalty function in order to achieve this goal.

$$\begin{aligned} D(\omega (t))=\Delta (\omega (t))+V\mathbb {E}\{E_{total}(t) \vert \omega (t)\} \end{aligned}$$
(16)

Where \(E_{total}(t)\) represents the total energy consumption of the system at time t. V is a trade-off factor used to adjust the optimization focus between the queue and energy consumption. After constructing this drift-plus-penalty function, we can optimize the overall energy consumption of the system by optimizing the upper bound of this function, while also keeping the system in a stable state. The upper bound of \(D(\omega (t))\) can be obtained by Theorem 1.

Theorem 1

If there is an upper limit \(A_{max}\) for the task arrival rate \(A_{i,j}(t)\), then the following relationship holds:

$$\begin{aligned} \begin{aligned} \Delta (\omega (t))+V\mathbb {E}\{E_{total}(t)\vert \omega (t)\}\\ \le Z + V\mathbb {E}\{E_{total}(t)\vert \omega (t) \}\\ +\sum ^J_{j=1}\sum ^{I_j}_{i=1}Q_{i,j}(t)\{A_{i,j}(t)-C^l_{i,j}(t)-C^o_{i,j}(t)\vert \omega (t)\}\\ +\sum ^J_{j=1}\sum ^{I_j}_{i=1}U_{i,j}(t)\{C^o_{i,j}(t)-D^l_{i,j}(t)-D^o_{i,j}(t)\vert \omega (t)\} \end{aligned} \end{aligned}$$
(17)

Where Z is a constant and

\(Z=\sum ^J_{j=1}\sum ^{I_j}_{i=1}[A_{i,j}^2(t)+C^l_{i,j}(t)+2C^o_{i,j}(t)C^l_{i,j}(t)+2C^o_{i,j}(t)^2+(D^l_{i,j}(t)+D^o_{i,j}(t))^2]\).

Proof

Squaring both sides of the formula (17) can yield:

$$\begin{aligned} Q_{i,j}^2(t+1) \le \{Q_{i,j}(t)+A_{i,j}(t)-C^l_{i,j}(t)-C^o_{i,j}(t)\}^2. \end{aligned}$$
(18)

Expanding the right side of the formula gives:

$$\begin{aligned} \begin{aligned} Q_{i,j}^2(t+1) \le Q_{i,j}^2(t)+A_{i,j}^2(t)+(C^l_{i,j}(t)+C^o_{i,j}(t))^2 - A_{i,j}(t)[C^l_{i,j}(t)+C^o_{i,j}(t)] +2Q_{i,j}(t)[A_{i,j}(t)-C^l_{i,j}(t)-C^o_{i,j}(t)]. \end{aligned} \end{aligned}$$
(19)

Extracting the part with upper limit and setting \(Z_1=(A_{i,j}^{max}(t))^2+(C^{l,max}_{i,j}(t)+C^{o,max}_{i,j}(t))^2\), and subtracting \(Q_{i,j}^2(t)\) from both sides, we can get:

$$\begin{aligned} \begin{aligned} Q_{i,j}^2(t+1)-Q_{i,j}^2(t) \le +Z_1 +2Q_{i,j}(t)[A_{i,j}(t)-C^l_{i,j}(t)-C^o_{i,j}(t)]- A_{i,j}(t)[C^l_{i,j}(t)+C^o_{i,j}(t)]. \end{aligned} \end{aligned}$$
(20)

Since \(A_{i,j}(t)[C^l_{i,j}(t)+C^o_{i,j}(t)]\) is always greater than or equal to 0, we can obtain the following inequality through scaling equations:

$$\begin{aligned} \begin{aligned} Q_{i,j}^2(t+1)-Q_{i,j}^2(t) \le +Z_1 +2Q_{i,j}(t)[A_{i,j}(t)-C^l_{i,j}(t)-C^o_{i,j}(t)]. \end{aligned} \end{aligned}$$
(21)

Similarly, we can get:

$$\begin{aligned} \begin{aligned} U_{i,j}^2(t+1)-U_{i,j}^2(t) \le +Z_2 +2U_{i,j}(t)[C^o_{i,j}(t)-D^l_{i,j}(t)-D^o_{i,j}(t)], \end{aligned} \end{aligned}$$
(22)

Where \(Z_2=(C_{i,j}^{o,max}(t))^2+(D^{l,max}_{i,j}(t)+D^{o,max}_{i,j}(t))^2\).

Combining the (20) and (21), the Theorem 1 is proven.

By substituting (7) and (10) into (17), we can obtain P2. According to Theorem 1, we can transform the original optimization of P1 into the optimization of P2. For brevity, we have simplified the summation and expectation of P2, and represent P2 as follows:

$$\begin{aligned} \begin{aligned} \text {P2:}\quad \min _{\phi _{i,j}(t)}V\tau [\gamma _cf^3_{i,j}(t)+ P_{i,j}(t)+\gamma _cf^{j}_i(t)^3+ P^j_i(t)]\\ +Q_{i,j}(t)[A_{i,j}(t)-\frac{f_{i,j}(t)\tau }{\sigma _{i,j}}-\tau R_{i,j}(t)] \\+U_{i,j}(t)[\tau R_{i,j}(t)-\frac{f^j_{i}(t)\tau }{\sigma _j}-\tau R^j_{i}(t)] \end{aligned} \end{aligned}$$
(23)

Decomposing subproblem

After proving that the drift function with penalty term has an upper bound, we can observe that its upper bound is a multivariate function containing four decision variables. Fortunately, after transforming it into an upper bound problem, the originally coupled four decision variables become separable. In this section, we decompose the original problem into four subproblems and solve them separately using different mathematical methods.

CPU frequency of the device subproblem

We extract the part related to CPU frequency from the upper bound problem and decouple the problem to obtain the following subproblem:

$$\begin{aligned} \begin{aligned} \text {P2-1:} \quad \min _{f_{i,j}(t)} -Q_{i,j}(t)\frac{f_{i,j}(t)\tau }{\sigma _{i,j}}+V\gamma _cf^3_{i,j}(t)\tau , \\ \text {s.t.}\quad 0 \le f_{i,j}(t) \le \min \{f^l_{max},\frac{Q_{i,j}(t)\sigma _{i,j}}{\tau }\}. \end{aligned} \end{aligned}$$
(24)

The CPU frequency determines the task execution time on each device and UAV. Higher CPU frequencies reduce task execution time but increase energy consumption due to the cubic relationship between energy consumption and CPU frequency. To optimize the CPU frequency, we formulated it as a convex optimization problem. By taking the second derivative of P2-1, we can obtain the extreme points of the function \(f_{i,j}(t)=\sqrt{[Q_{i,j}(t)/3V\gamma _c\sigma _{i,j}]}\). By observing the relationship between the extreme points and the feasible region, we can conclude:

$$\begin{aligned} \begin{aligned} f^*_{i,j}(t)= \left\{ \begin{aligned} \sqrt{\frac{Q_{i,j}(t)}{3V \gamma _c \sigma _{i,j}}}, & 0\le \sqrt{\frac{Q_{i,j}(t)}{3V \gamma _{c} sigma_i}}\le f^m \\ f^m, & otherwise, \end{aligned} \right. \end{aligned} \end{aligned}$$
(25)

Where \(f^m = \min \{f^l_{max},\frac{(Q_{i,j}(t)+A_{i,j}(t))\sigma _{i,j}}{\tau }\}\).

Offloading power of the device subproblem

By decoupling the part related to offloading power in P-2, we obtain the following subproblem:

$$\begin{aligned} \begin{aligned} \text {P2-2:} \quad \min _{P_{i,j}(t)}\quad -B_j(Q_{i,j}(t)-U_{i,j}(t))\\ \log _2(1+\frac{g_{j,i}(t)P_{i,j}(t)}{N_0(t)})+V\tau P_{i,j}(t) \\ \text {s.t.}\quad 0 \le P_{i,j}(t) \le P^l_{max}. \end{aligned} \end{aligned}$$
(26)

This is a nonlinear optimization problem. We denote the function of P2-1 as \(F(P_{i,j}(t))\), and introduce \(x_{i,j}(t)\) as a substitution for \(\frac{g_{j,i}(t)}{N_0(t)}\) and \(y_{i,j}(t)\) for \(-B_j(Q_{i,j}(t)-U_{i,j}(t))\). Then, the first-order derivative is:

$$\begin{aligned} \begin{aligned} \frac{dF(P_{i,j}(t))}{dP_{i,j}(t)}=\frac{-y_{i,j}(t)\tau x_{i,j}(t)+\tau V(1+x_{i,j}(t)P_{i,j}(t))\ln 2}{(1+x_{i,j}(t)P_{i,j}(t))\ln 2} \end{aligned} \end{aligned}$$
(27)

And the second-order derivative is:

$$\begin{aligned} \begin{aligned} \frac{dF^2(P_{i,j}(t))}{dP_{i,j}(t)^2}=y_{i,j}(t)\tau \frac{x^2_{i,j}(t)}{(1+x_{i,j}(t)P_{i,j}(t))\ln 2} \end{aligned} \end{aligned}$$
(28)

Analyzing the value of \(y_{i,j}(t)\), we have: when \(y_{i,j}(t) < 0\), the first-order derivative is always greater than 0. When \(y_{i,j}(t) = 0\), \(F(P_{i,j}(t))\) is linearly dependent on \(P_{i,j}(t)\). When \(y_{i,j}(t) > 0\), the second-order derivative is always positive, indicating a minimum occurs when the first-order derivative is 0. This minimum occurs at \(P_{i,j}(t) = \frac{y_{i,j}(t)}{V\ln 2} - \frac{1}{x_{i,j}(t)}.\) Combining these analyses, we obtain the solution:

$$\begin{aligned} \begin{aligned} P^*_{i,j}(t)=\left\{ \begin{aligned} \min \{P^{max}_{i,j},\frac{y_{i,j}(t)g_{i,j}(t)}{Vln2}-\frac{N_0(t)}{g_{i,j}(t)}\}, & V \le Z(t), \\ 0, & \text {otherwise}, \end{aligned} \right. \end{aligned} \end{aligned}$$
(29)

Where for simplicity, we use Z(t) to represent \(\frac{x_{i,j}(t)y_{i,j}(t)}{\ln 2}\).

CPU frequency of the UAV subproblem

In this subproblem, we find the optimal CPU Frequency of the UAV through solving following subproblem:

$$\begin{aligned} \begin{aligned} \text {P2-3:} \quad \min _{f^i_{j}(t)} -U_{i,j}(t)\frac{f^i_{j}(t)\tau }{\sigma _{j}}+V\gamma _cf^i_{j}(t)^3\tau , \\ \text {s.t.}\quad 0 \le \sum _{i=1}^{\mathcal {I}_j} f^j_{i}(t) \le f^l_{max}, \end{aligned} \end{aligned}$$
(30)

The CPU frequency \(f^j_i(t)\) of the UAV j needs to be decoupled, but since a UAV has to handle tasks offloaded from multiple devices, it cannot be solved as a simple convex optimization problem. Here, we utilize a combination of the knapsack problem solving approach and convex optimization. Similar to the approach for P3-1, we first find the analytical solution for the CPU frequency allocated to device i:

$$\begin{aligned} \begin{aligned} f^{i,*}_{j}(t)= \left\{ \begin{aligned} \sqrt{\frac{U_{i,j}(t)}{3V \gamma _c \sigma _{j}}}, & 0\le \sqrt{\frac{U_{i,j}(t)}{3V \gamma _c \sigma _i}}\le f^{n} \\ f^n, & otherwise, \end{aligned} \right. \end{aligned} \end{aligned}$$
(31)

Where \(f^n=\min \{f^j_{max},\frac{(U_{i,j}(t)+A_{i,j}(t))\sigma _{j}}{\tau }\}\). After obtaining the analytical solution for \(f^{i}_{j}(t)\), we treat it as weight of the task of device i and apply the knapsack problem solving method, considering the total CPU frequency of the UAV as the knapsack capacity. The specific details of the algorithm are outlined in Algorithm 1.

Offloading power of the UAV subproblem

In this subproblem, we decouple the offloading power of UAV j to establish the following subproblem?

$$\begin{aligned} \begin{aligned} \text {P2-4:} \quad \min _{P_{i,j}(t)}\quad -B_jU_{i,j}(t)\log _2(1+\frac{g^j_{i}(t)P^j_{i}(t)}{N_0(t)})\\ +V\tau P^j_{i}(t)\\ \text {s.t.}\quad 0 \le \sum _{i=1}^{\mathcal {I}_j} P^j_{i}(t) \le P^j_{max} \end{aligned} \end{aligned}$$
(32)
Algorithm 1
figure a

The Proposed EDRA Algorithm

Full size image

Similar to solving P2-3, we get an analytical solution firstly for P2-4:

$$\begin{aligned} \begin{aligned} P^*_{i,j}(t)=\left\{ \begin{aligned} \min \{P^{max}_{j},\frac{B_jU_{i,j}(t)g^j_{i}(t)}{Vln2}-\frac{N_0(t)}{g^i_{j}(t)}\}, & V \le z(t), \\ 0, & \text {otherwise}, \end{aligned} \right. \end{aligned} \end{aligned}$$
(33)

Where \(z(t)= B_jU_{i,j}(t)g^j_i(t)/N_0(t)\ln 2\).

The proposed EDRA algorithm is executed in a distributed manner across the devices and the UAVs’ edge servers. Specifically, Subproblems 1 and 2 are distributed and executed on each device, resulting in locally optimized computing and offloading decisions, with inputs that are only related to the device’s own task queue. Subproblems 3 and 4 yield the computing and offloading decisions for the UAV’s edge servers, and these subproblems are executed on the UAV. The specific algorithm design can be found in Algorithm 1.

Complexity analysis

The EDRA algorithm is designed to solve the task offloading and resource allocation in UAV-assisted MEC to optimize the energy consumption of system while maintaining the system performance. Previous work has also proposed several methods to address this issue, such as prediction-based methods and Game-based methods24,36. Unlike these methods, EDRA transforms the stochastic optimization problem into a deterministic optimization problem, eliminating the need for specially find the way to predict external environmental information. Moreover, the decoupling of the problem allows the algorithm to avoid complex iterations.

Regarding the complexity analysis of the EDRA algorithm, the algorithm has two loops. In each UAV, it is required to sort according to the offloading workload of devices and process the tasks offloaded by devices, with complexities of \(O(I\log _2I)\) and O(I), respectively. And the algorithm is currently running during T. Therefore, the overall complexity of the algorithm is \(O(I\log _2 IJT)\).

Algorithm analysis for EDRA

In this section, we prove the performance of the algorithm through rigorous theoretical analysis. By verifying that the gap between the queue length and energy consumption of the algorithm and the optimal solution is within a constant level, we ensure the performance of the algorithm.

Lemma 1

No matter what data set \(\lambda\) is provided, an optimal decision \(\alpha ^{*}\) can be obtained, which is unaffected by the length of the queue.

According to this lemma, we can get as follows:

$$\begin{aligned} \begin{aligned} \mathbb {E}\{E_{total}^{\alpha ^*}(t) \}=E_{total}^*(\lambda ),\\ \mathbb {E}\{A^{\alpha ^*}_{i,j}(t) \} \le \mathbb {E}\{C^{l,\alpha ^*}_{i,j}(t)+C^{o,\alpha ^*}_{i,j}(t)\},\\ \mathbb {E}\{C^{o,\alpha ^*}_{i,j}(t) \} \le \mathbb {E}\{D^{l,\alpha ^*}_{i,j}(t)+D^{o,\alpha ^*}_{i,j}(t)\}.\\ \end{aligned} \end{aligned}$$
(34)

Proof

The Lemma 1 can be proven by using Caratheodory’s theorem.

Lemma 2

No matter what data set \(\lambda\) is provided, we can get the following equation:

$$\begin{aligned} \begin{aligned} E_{total}^{EDRA} \le E_{total}^*+\frac{Z}{V}, \end{aligned} \end{aligned}$$
(35)

Proof

The decision \(\alpha\) and the random data set \(\lambda +\varepsilon\) are defined. Thus, we can obtain the following inequality based on Lamma 1:

$$\begin{aligned} \begin{aligned} \mathbb {E}\{E_{total}^{\alpha }(t)\}=E_{total}^*(\lambda +\varepsilon )\\ \mathbb {E}\{A^{\alpha }_{i,j}(t) \}+\varepsilon \le \mathbb {E}\{C^{l,\alpha }_{i,j}(t)+C^{o,\alpha }_{i,j}(t)\},\\ \mathbb {E}\{D^{o,\alpha }_{i,j}(t) \}+\varepsilon \le \mathbb {E}\{D^{l,\alpha }_{i,j}(t)+D^{o,\alpha }_{i,j}(t)\}.\\ \end{aligned} \end{aligned}$$
(36)

Recall the inequality (23), and the drift-plus-penalty is as follows when we substitute \(\alpha\) into decision set:

$$\begin{aligned} \begin{aligned} \Delta (\omega (t))+V\mathbb {E}\{E_{total}(t) \vert \omega (t)\} \le Z +V\mathbb {E}\{o(t) \vert \omega (t))\} \\ +\mathbb {E}\{\sum ^J_{j=1}\sum ^{I_j}_{i=1}Q_{i,j}(t)[A^{\alpha }_{i,j}(t)- C_{i,j}^{l,\alpha }(t)-C_{i,j}^{o,\alpha }(t)]\}\\ +\mathbb {E}\{\sum ^J_{j=1}\sum ^{I_j}_{i=1}H_{i,j}(t)[C_{i,j}^{o,\alpha }(t)-D_{i,j}^{l,\alpha }(t)-D_{i,j}^{o,\alpha }(t)]\}\\ \end{aligned} \end{aligned}$$
(37)

Combine (36) with (37) and simplify them, we can get:

$$\begin{aligned} \begin{aligned} \mathbb {E}\{\Delta (\omega (t))\}+V\mathbb {E}\{E_{total}(t) \vert \omega (t)\} \le Z+VE_{total}^*(\alpha +\varepsilon ) - \varepsilon \sum ^J_{j=1}\sum ^{I_j}_{i=1}\mathbb {E}\{Q_{i,j}(t)+U_{i,j}(t) \} \end{aligned} \end{aligned}$$
(38)

Taking the maximum value of t, we get:

$$\begin{aligned} \begin{aligned} V\sum ^{T-1}_{t=0}\mathbb {E}\{E_{total}(t) \vert \omega (t)\} \le ZT +VTE_{total}^*(\lambda +\varepsilon ) \\varepsilon \sum ^{T-1}_{t=0}\sum ^J_{j=1}\sum ^{I_j}_{i=1}\mathbb {E}\{Q_{i,j}(t)+U_{i,j}(t)\}. \end{aligned} \end{aligned}$$
(39)

Since both \(\varepsilon\) and \(Q_{i,j}(t)+U_{i,j}(t)\) are always greater than or equal to 0, we have the ability to scale them up:

$$\begin{aligned} \begin{aligned} V\sum ^{T-1}_{t=0}\mathbb {E}\{o(t) \vert \omega (t)\} \le ZT +VTE_{total}^*(\lambda +\varepsilon ). \end{aligned} \end{aligned}$$
(40)

Lemma 2 can be proven when both sides divide VT and set the value of T to infinity.

Lemma 3

No matter what data set \(\lambda\) is provided, we can get the following equation:

$$\begin{aligned} \begin{aligned} \overline{L} \le \frac{Z+V(E_{total}^{max}-E_{total}^*)}{\varepsilon } \end{aligned} \end{aligned}$$
(41)

Where \(\overline{L} =\lim _{T \rightarrow \infty } \frac{1}{T}\sum ^{T-1}_{t=0}\sum ^J_{j=1}\sum ^{I_j}_{i=1}\mathbb {E}\{( Q_{i,j}(t)+U_{i,j}(t)) \vert \omega (t) \}\).

Proof

Accodding to (36), we can also derive:

$$\begin{aligned} \begin{aligned} \varepsilon \sum ^{T-1}_{t=0}\sum ^J_{j=1}\sum ^{I_j}_{i=1}\mathbb {E}\{(Q_{i,j}(t)+U_{i,j}(t)) \} \le ZT +VTE_{total}^*(\lambda +\varepsilon )-V\sum ^{T-1}_{t=0}\mathbb {E}\{E_{total}(t)\vert \omega (t)\} \end{aligned} \end{aligned}$$
(42)

For any \(E_{total}(t)\), there exists \(E_{total}(t) \le E_{total}^{\max }(t) - E_{total}^{\min }(t)\). Additionally, \(V\sum ^{T-1}_{t=0}\mathbb {E}\{E_{total}(t)\vert \omega (t) \ge 0\}\) can be get. Thus, we can derive:

$$\begin{aligned} \begin{aligned} \varepsilon \sum ^{T-1}_{t=0}\sum ^J_{j=1}\sum ^{I_j}_{i=1}\mathbb {E}\{Q_{i,j}(t)+U_{i,j}(t) \} \le ZT +VT(E_{total}^{\max }(t) - E_{total}^{\min }(t)). \end{aligned} \end{aligned}$$
(43)

Similar to Lemma 2, both sides divide \(\varepsilon T\) and simplify them, then Lemma 3 is proven.

Evaluation

Experiment setup

In this section, we conduct a simulation experiment to analyze the parameters and compare the algorithms on a public EUA dataset37, and similar settings28 has been applied in experiments. The aim is to verify the adaptability of the algorithm to different operating environments and its superiority compared to other algorithms. We simulate a UAV-assisted MEC scenario with dimensions of [500,500,200], which includes 100 devices, 5 UAVs, and a cloud server. The devices are located at a height of 0, with randomly generated horizontal coordinates. Furthermore, the maximum CPU frequency of the devices is 1GHz, and the maximum offloading power is 0.1W. The five UAVs hover randomly within a height range of 100 to 200, and the edge servers on the UAVs have a maximum CPU frequency of 10GHz and a maximum offloading power of 1W. Each UAV has a total bandwidth of 1 MHz, which is allocated to connected devices through FDMA. It is assumed that the cloud server has superior computing capabilities. Devices choose the nearest UAV’s edge server for offloading, with each UAV having a maximum capacity of 20 devices. The environmental parameters a and b for communication between devices and UAVs are 4.88 and 0.43, respectively, while the coefficients for LoS and NLoS transmission are 0.1 and 21.

Parameter analysis

As shown in Figs. 2 and 3, we analyze the trade-off parameter V in the drift-plus-penalty algorithm. We use a range of \(10^{12}\) to \(9 \times 10^{12}\) as our values. V serves as a balancing factor that weighs the optimization of the queue and the optimization target (system energy consumption). Since V is the coefficient in front of the penalty term, a larger V results in a greater optimization effort for energy consumption, which in turn may lead to increased queue backlog. As V increases, both energy consumption and queue backlog gradually converge, consistent with our theoretical analysis. The figures also reflect this understanding.

Fig. 2
figure 2

The energy consumption of system vs. different trade-off parameter V.

Full size image
Fig. 3
figure 3

The queue length of system vs. different trade-off parameter V.

Full size image

In Figs. 4 and 5, we multiply the benchmark \(A_{i,j}(t)=[0,10^6]\) bits/s by coefficients of 0.8, 1.0, and 1.2, representing 80%, 100%, and 120% of the standard task arrival rate. This demonstrates the impact of task arrival rates on device energy consumption and backlog, and reflects the ability of the EDRA algorithm to handle different degrees of task arrival rates. It can be seen that under different task arrival rates, EDRA achieves convergence relatively quickly, and a higher task arrival rate leads to greater energy consumption and queue backlog. This is in line with objective conditions.

Fig. 4
figure 4

The energy consumption of system with different \(\alpha\) (scale factor of arrival rates).

Full size image
Fig. 5
figure 5

The queue length of system with different \(\alpha\) (scale factor of arrival rates).

Full size image

In Figs. 6 and 7, we test the energy consumption and queue backlog as the number of devices increases from 40 to 120, while keeping the number of UAVs, task arrival rate, and the maximum CPU frequency of each device constant. The results reflect the adaptability of the EDRA algorithm to different numbers of devices, and both energy consumption and queue backlog increase as the number of devices increases.

Fig. 6
figure 6

The energy consumption of system with the different number of devices.

Full size image
Fig. 7
figure 7

The queue length of system with the different number of devices.

Full size image

Comparative experiment

In the comparative experiment section, we prepared four algorithms:

EDRA

This is the algorithm proposed in this paper.

Local-only(LO)

This algorithm allows devices to process local computation without task offloading. It serves as one of the baseline algorithms for comparison.

Offloading-only(OO)

This algorithm allows devices to offload all tasks to the edge servers for computation. It serves as another baseline algorithm for comparison.

IDO (2022)

This algorithm is adapted from the design concept in the paper20, with some modifications to make it operable in our environment.

Figure 8 shows the performance of the four algorithms in the simulated UAV-assisted MEC system. Among the four algorithms, the OO algorithm has the lowest energy consumption and remains unchanged because when devices offload all tasks to the drones, the processing tasks exceed the maximum offloading power, causing the offloading power to operate at maximum capacity. The second-lowest energy consumption is achieved by the EDRA algorithm proposed in this paper. It can be seen that EDRA converges faster and has lower energy consumption compared to the relatively advanced IDO algorithm, as our algorithm decomposes the problem for parallel processing. The LO algorithm has the highest energy consumption, nearly double that of our proposed algorithm.

Fig. 8
figure 8

The energy consumption of system with different algorithms.

Full size image

Figure 9 shows the comparison the queue backlog of the four algorithms. It can be seen that although the LO algorithm has the lowest energy consumption, unfortunately, it achieves this at the cost of generating a significant amount of computational energy consumption. Our proposed algorithm has the second-lowest queue backlog, significantly lower than the IDO algorithm. As a baseline, the OO algorithm clearly cannot stabilize the queue length, which would lead to significant delays in the system’s task processing.

Fig. 9
figure 9

The queue length of system with different algorithms.

Full size image

Conclusion

In this paper, we investigate the task offloading and resource allocation problem in a UAV-assisted MEC system for large-scale sports events, where UAVs are deployed near the venue to provide temporary edge computing services. We formulate the system as a stochastic optimization problem and transform the original problem into an upper bound problem, then decompose it into multiple subproblems using stochastic optimization techniques. Specifically, we obtain optimal or suboptimal solutions for each subproblem through convex optimization, linear programming, and other methods. Furthermore, we prove the performance of the algorithm through theoretical analysis. We summarize a series of parameter analyses and comparative experiments to evaluate the adaptability of the problem in different scenarios and the degree of optimization for energy consumption. The experimental results show that the EDRA algorithm can effectively reduce system energy consumption by 32.4% compared to advanced algorithms, and more reliably ensure system stability. In future work, we will address the task offloading problem in UAV-assisted MEC systems by jointly optimizing UAV deployment scheduling and task resource allocation.