Optimization of energy management strategies for multi-mode hybrid electric vehicles driven by travelling road condition data

Abstract

The fuel efficiency of plug-in hybrid electric vehicle is influenced by various factors, including working conditions, driving style, and environmental variables, with the design of their energy management strategy (EMS) serving as the core and critical technology. In order to adapt to traffic environment, it is of great significance to construct driving cycles that align with driving characteristics, providing data support for the optimization of the EMS. This paper carried out research on the EMS optimization for multi-mode hybrid electric vehicle (MMHEV). Firstly, the traffic speed was established interval by using data envelopment analysis (DEA) and the urban comprehensive driving cycles based on the proportion of driving time was constructed. Then, an EMS optimized based on road condition information (RC-EMS) was developed according to the operating curves and interval thresholds of motors and engine. The initial optimal parameters for offline optimization of the EMS were obtained using a bare-bones multi-objective particle swarm optimization algorithm, with the constructed comprehensive driving cycle serving as the input information for the optimization model. After that, a fuzzy adaptive parameter optimization module (ARC-EMS) was designed to update the key parameters of the RC-EMS in real time, so as to realize the optimal dynamic energy allocation adaptively according to the road conditions. Finally, the simulation and experimental results fully showed that the proposed ARC-EMS can balance the performance more effectively. As anticipated, the strategy effectively balances energy savings and battery health, and it can be utilized to develop an EMS that enhances the overall performance of the MMHEV.

Introduction

In order to reduce dependence on fossil fuels, PHEV are widely recognized as one of the key technologies for clean transportation in the future¹. Multi-mode hybrid electric vehicle (MMHEV) is typically equipped with high-capacity power batteries whose state of charge (SoC) can vary in a wide range, where the better overall fuel economy can be achieved through capturing and storing energy from the grid to provide propulsion energy to the vehicle². The essence of EMS is to obtain the vehicle’s demand power according to the operating condition information and the driving intention of drivers, and then carry out power distribution according to the dynamic characteristics of each power source.

Literature review

PHEV powered by gasoline and electricity have been studied in a number of publications³. The flexibility of power distribution leads to more complex EMS problems yet to be well addressed, especially for MMHEV. In previous studies, the main objective of EMS was to achieve maximum overall efficiency. Rule-based is widely adopted due to the advantages of strong robustness, high operation efficiency and being easy to implement⁴. The rule-based strategy is developed based on a mathematical model, and according to the external characteristic curve of the engine, the engine is coordinated to work in the high-efficiency zone through the supplementation of the drive motor during operation, which enables efficient switching and combination of various operating modes in the operation of the vehicle, thus obtaining better fuel economy. Rule-based energy management strategies (EMS) have demonstrated remarkable advantages in the fields of PHEV and fuel cell commercial vehicles. They are capable of further enhancing the fuel economy of PHEVs, achieved through rapid calculation speeds and straightforward establishment processes⁵, as well as effectively reducing hydrogen consumption in real-time applications through rule-based learning strategies, thereby prolonging the lifespan of fuel cells⁶. Additionally, such strategies offer PHEVs more adaptable, flexible, and higher-performance EMS solutions⁷. More importantly, by utilizing rule-based algorithms, precise extraction and application of fuel cell output power rules can be achieved, ensuring that the EMS for fuel cell commercial vehicles can be implemented in real-time and optimized⁸.

Optimization-based energy management strategy is to optimize the energy management taking into account the driving conditions and driving style, in terms of offline optimization, it is mainly based on the knowledge and experience of the past or future power demand to optimize the fuel economy for a fixed route or known conditions, the main methods are reinforcement learning⁹, dynamic programming¹⁰, genetic algorithms¹¹, model predictive control¹², equivalent fuel minimum control¹³. In the research conducted on HEVs, optimized EMS based on diverse algorithms have been extensively explored. Among them, an energy management strategy for parallel HEVs grounded in optimal control has been proposed, which effectively reduces fuel consumption and battery wear, thereby extending battery life, utilizing the Principle of Pontryagin’s Maximum Principle (PMP)¹⁴. Additionally, a modularized powertrain design approach that integrates Constrained Multi-Objective Particle Swarm Optimization with dynamic programming has been introduced, significantly optimizing the economy and durability of FCHVs¹⁵. Furthermore, three real-time EMS aimed at minimizing overall operational costs have been suggested, with the strategy combining rules and optimization demonstrating superior performance¹⁶. To address uncertainties, an integrated predictive energy-dynamic programming hierarchical optimization framework has been further proposed, utilizing information entropy to provide a theoretical foundation for optimizing vehicle fuel economy and energy consumption¹⁷. Lastly, a rule-optimized energy management strategy based on the Particle Swarm Optimization (PSO) algorithm has been developed, which significantly enhances fuel economy by optimizing the mode switching and torque distribution of PHEV¹⁸.

Road conditions represent the process and state of vehicle travelling, which is usually presented through speed-time curves, and is an important reference for vehicle technology development and EMS. In the construction of working conditions, in order to solve the problem of under-representation of the standard working conditions, relevant research has carried out the construction of driving conditions, and constructed the driving conditions that meet the local roads in many cities. The commonly used methods for constructing driving conditions are short trip analysis¹⁹, random selection method²⁰Markov analysis²¹, and hierarchical clustering method²². Significant advancements have been made in the research of EMS relying on road condition information. The fuel economy and ride comfort of connected PHEV have been enhanced, and stops at traffic signals have been avoided, through the utilization of real traffic light information in conjunction with a multi-objective hierarchical optimization strategy²³.The adoption of EMS based on Cyber-Physical Systems and Deep Reinforcement Learning, coupled with the integration of multimodal traffic information, has led to optimized power flow management²⁴. Furthermore, a variable-level, multi-modal driving pattern recognition framework, proposed based on real two-dimensional vehicle-road information, has significantly improved recognition accuracy, providing support for the formulation of intelligent EMS²⁵.

In relation to the design of EMS, the collection of urban road condition data to construct driving conditions, data processing and analysis research based on data envelopment analysis, to construct comprehensive driving conditions, to provide data support for EMS and optimization. In addition, the EMS design should gradually improve from the initial single-objective optimization to real-time and intelligent multi-objective optimization (MOO). In fact, EMS performance optimization is a typical issue of MOO with the independent and balanced results. The battery pack is the energy storage system of MMHEV, and its durability has an important impact on the vehicle’s operational safety and drive ability. The battery life is largely determined by how the electrical energy is used during the trip. Therefore, it is meaningful to comprehensively consider the performance of the vehicle in terms of energy consumption, emissions and battery life, so as to achieve MOO that can balance the comprehensive performance, which is also the focus in this paper.

Motivation and innovation

This paper focused on the design and optimization of EMS for MMHEV, a fuzzy adaptive parameter optimization module (ARC-EMS) was designed to update the key parameters of the RC-EMS in real time is introduced and a MOO method is proposed, so as to realize the optimal dynamic energy allocation adaptively according to the road conditions. Promisingly, in Sect. 2, the traffic speed was established interval by using data envelopment analysis (DEA) and the urban comprehensive driving cycles based on the proportion of driving time was constructed. Section 3 describes the MOO problem, and the bare bones-multi objective particle swarm optimization (BB-MOPSO) algorithm is selected to solve MOO problem. In Sect. 4, a series of simulation and experimental bench tests are carried out to validate the effectiveness and feasibility of the proposed strategy. Conclusions are drawn in the final section. The innovations of this study are as follows: (1) The DEA method was used to establish the traffic speed interval, and the comprehensive driving cycles of urban were constructed based on the proportion of driving time, which laid the data foundation for the design and optimization of EMS. (2) A data-driven EMS based on travel conditions was designed, whose threshold parameters were optimized offline based on BB-MOPSO algorithm. (3) A real-time adaptive parameter optimization module based on fuzzy algorithm was designed to realize the multi-objective comprehensive optimal performance control which can adapt to the optimal road conditions.

Design of parameter adaptation EMS based on road condition information driven

In order to study the performance of the designed EMS, the energy distribution among the engine, motor and battery is discussed. Considering the dynamic information of the battery, a real-time optimization and parameter adjustment module based on fuzzy logic is designed.

Configuration of the studied MMHEV model and EMS optimized based on road condition

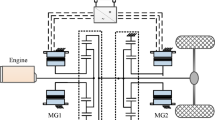
The powertrain system of the MMHEV consists of power battery, internal combustion engine (ICE), electrical machine (EM), mechanical driving mechanism and control system²⁶. Figure 1 shows the powertrain system of the MMHEV, which is selected as the research object in this paper for EMS design.

Fig. 1

Configuration of the studied multi-mode hybrid electric vehicle.

A dedicated hybrid transmission (DHT) is used to realize conversion and delivery of oil-electric energy. The power source of the MMHEV consists of ICE and two different power EMs, of which the EM1 is mainly used as a generator in the series mode, and the EM2 can be used as a drive motor to power the wheels, or as a generator to recharge the battery by regenerative braking or absorbing excess power from the ICE²⁷. The driving mode of the MMHEV can be changed by controlling the engagement and disengagement of the clutch C1 and C2. The driver mode implemented by this configuration is as follows: In the EV mode, both clutch 1 and clutch 2 are disengaged, exhibiting a characteristic where EM2 provides all the required power. In the Series mode, clutch 1 is engaged, and clutch 2 is disengaged, displaying a feature where a power-following control strategy is adopted to adjust the operating points of the ICE in the high efficiency area, and the output power of the ICE not only meets the required power of the EM2, but also outputs excess power to charge the battery. In the Parallel-CD mode, both clutch 1 and clutch 2 are engaged, exhibiting a characteristic where, under the working condition of high required power, the EM2 generates the maximum power, and the insufficient power is supplemented by the ICE. In the Parallel-CS mode, both clutch 1 and 2 are engaged, exhibiting a characteristic where the ICE always operates at the optimal torque, with excess power being used to charge the battery through EM2 and insufficient power being supplied by consuming battery energy through EM2. When the mode is engine drive mode, with both clutch 1 and 2 engaged, the system is characterized by the ICE providing all the required energy.

Establishment of traffic speed database based on DEA method

The core of driving cycle construction is to establish representative driving cycles that can reflect the actual road conditions, which means it should have high fitting precision. The research is carried out considering both time domain and space domain. Based on DEA, a non-parametric statistical estimation method, traffic speed intervals are constructed to analyze short road segments representing driving cycles, by establishing evaluation models to verify and assess the efficiency between inputs and outputs (decision making unit, DMU). The DEA method is highly inclusive of interference and uncertainty factors in the driving cycle, allowing it to objectively reflect the characteristics of driving cycles²⁸. The 1600 speed segments that were collected have been designated as decision making units (DMUs), with 700 DMUs in driving condition A, 600 DMUs in driving condition B, and 300 DMUs in driving condition C. Subsequently, the C²R model was used to calculate characteristic parameters such as velocity difference and acceleration between each pair of anchor points, as well as the average acceleration for each segment unit (DMU).

The efficiency evaluation index of the j-th decision-making unit is:

$${{\text{h}}_j}=\frac{{u_{{}}^{T}{y_j}}}{{v_{{}}^{T}{x_j}}}=\frac{{\sum\limits_{{i=1}}^{n} {{u_r}{y_{rj}}} }}{{\sum\limits_{{i=1}}^{n} {{v_i}{x_{ij}}} }},j=1,2, \ldots ,n$$

(1)

Where h_j is the weight coefficient; v_i is the i-th input metric; u_i is the r-th output metric; x_ij is the input amount of the j-th DMU for the i-th input; y_ij is the output of the j-th DMU for the r-th output.

When evaluating the j₀-th DMU, with the efficiency index of the j₀-th MDU as the objective and all DMU efficiency indices as constraints, the established optimization model is:

$$(p)\left\{ \begin{gathered} \hbox{max} \frac{{u_{{}}^{T}{y_{{j_0}}}}}{{v_{{}}^{T}{x_{{j_0}}}_{{_{{}}}}}} \hfill \\ s.t.\frac{{u_{{}}^{T}{y_j}}}{{v_{{}}^{T}{x_j}}} \leqslant 1,j=1,2 \ldots ,n \hfill \\ \end{gathered} \right.$$

(2)

Perform Charnes Cooper transformation on the above equation to obtain:

$$s=\frac{1}{{v_{{}}^{T}{x_{{j_0}}}}}>0,w=s \cdot v,{\mu _{}}=s \cdot u$$

(3)

The equivalent linear programming problem obtained from the transformation is:

$$({P_{C_{{}}^{2}R}})\left\{ \begin{gathered} \hbox{max} {h_{{j_0}}}=\mu _{{}}^{T}{y_{{j_0}}} \hfill \\ s.t.\omega _{{}}^{T}{x_j} - \mu _{{}}^{T}{y_j} \geqslant 0, \hfill \\ \omega _{{}}^{T}{x_{{j_0}}}=1, \hfill \\ \omega \geqslant 0,\mu \geqslant 0. \hfill \\ \end{gathered} \right.j=1,2 \ldots ,n$$

(4)

Its dual programming is D_C²_R, while introducing relaxation variables:

$$({D_{C_{{}}^{2}R}})\left\{ \begin{gathered} \hbox{min} \theta \\ s.t.\sum\limits_{{j=1}}^{n} {{\lambda _j}{x_j} \leqslant \theta {x_{{j_0}}},} \\ \sum\limits_{{j=1}}^{n} {{\lambda _j}{y_j} \geqslant \theta {y_{{j_0}}},} \\ {\lambda _j} \geqslant 0,j=1,2 \ldots ,n \\ \end{gathered} \right. \Leftrightarrow (D_{{C_{{}}^{2}R}}^{1})\left\{ \begin{gathered} \hbox{min} \theta \\ s.t.\sum\limits_{{j=1}}^{n} {{\lambda _j}{x_j}+S_{{}}^{ - }=\theta {x_{{j_0}}},} \\ \sum\limits_{{j=1}}^{n} {{\lambda _j}{y_j} - S_{{}}^{+}=\theta {y_{{j_0}}},} \\ {\lambda _j} \geqslant 0,j=1,2 \ldots ,n \\ S_{{}}^{ - },S_{{}}^{+} \geqslant 0 \\ \end{gathered} \right.$$

(5)

When the output result value is close to 1, it is evaluated as DEA effective, and when it is close to 0, it is evaluated as DEA invalid. By organizing the filtered data and comparing the velocity data of each group in the same time domain, the upper and lower envelope points of each positioning point can be obtained. By using MATLAB software to interpolate the data between the positioning points of units under different working conditions, the velocity time distribution at different times is formed, which is then assembled into the travel speed interval. The final velocity envelope diagram for each working condition is obtained.

Fig. 2

The comprehensive driving cycle of urban road.

The speed interval is obtained by analyzing and sorting out the data collected by the real vehicle, in which the idle stage is set as the parking point with the speed of 0. The corresponding speed around the parking point is smoothed and limited to avoid large speed fluctuations. In addition, appropriate selection of short segments is carried out to reduce the deviation of concatenation. The comprehensive driving cycle of urban road in Changchun is shown in the Fig. 2.

Design of parameter adaptation EMS based on road condition information driven

Road condition information holds great significance in the design of vehicle EMS, as it directly impacts the vehicle’s energy consumption and performance. The parameter-adaptive EMS, driven by real-time road condition information, can dynamically adjust its parameters to achieve optimal energy management and performance. Parameter-adaptive EMS design: Dynamically adjusting the cooperation mode between the engine and motor to achieve optimal energy consumption and performance. When driving on the highway, more engine power is utilized; in congested urban road conditions, more electric motors can be employed to provide power, thereby reducing emissions and energy consumption. Parameter optimization and fuzzy adaptive EMS driven by road information proposed are shown in Fig. 3.

Fig. 3

Parameter optimization and fuzzy adaptive EMS driven by road information.

As shown in Fig. 3, in the engine map, the operating modes are divided into four types, namely pure electric (EV) mode (M1), extended range (ER) mode (M2), blend drive (BL) mode (M3), and internal combustion engine (ICE) drive mode (M4). The four modes are divided by the following rules and the curves between modes are as follows: and left and right area demarcation line, the minimum value of rotational speed in the optimal working interval of the engine, set the value as the speed threshold (n_e); The mode boundary between the upper and lower parts on the left is the torque threshold (T_e); The pattern boundary between the upper and lower parts on the right is: the coupling line between the optimal operating curve of the engine and the external characteristic curve of the motor 2. The demand line above the mode on the right side: The coupling line between the external characteristic curves of motor 1 and motor 2 and the external characteristic curve of the engine. The upper and lower limits of SoC are set to SoC_H (0.8) and SoC_L (0.5), respectively, within which the internal resistance of battery charging and discharging is small and the efficiency is high. The four operating modes (M1-M4) switch based on key threshold values in different battery SoC states.

The control results of an EMS with fixed parameters may deviate from the optimal outcomes, and the trajectory of the SoC may become uncontrolled, straying completely from its normal operating range. It is necessary to take control actions accordingly by optimizing the performance index horizon to adjust parameter in real time in order to obtain the best performance. The fuzzy controller is applied as an adaptive regulator which tunes its parameters with the evaluation under the MOO framework in this section. In order to make better use of the energy between battery and engine, and thereby extend battery service life, a relatively flat SoC trajectory is important, as a hybrid energy storage system²⁹. As shown in Fig. 4, the fuzzy logic controller is employed to identify the threshold adjustment factor for the optimal control process. The ∆SoC_H and ∆SoC_L were used to update the SoC_H and SoC_L in real time according to the following equation:

$$\begin{gathered} So{C_H}=So{C_{H\_0}}+\Delta So{C_H} \hfill \\ So{C_L}=So{C_{L\_0}}+\Delta So{C_L} \hfill \\ \end{gathered}$$

(6)

Where ∆SoC_H is the threshold adjustment factor value of the SoC_H; SoC_{H _0} is the initial threshold value after the optimization decision; ∆SoC_L is the threshold adjustment factor value of the SoC_L; SoC_{L _0} is the initial threshold value after the optimization decision.

Fig. 4

Diagram of parameter adjustment based on fuzzy controller.

The fuzzy logic controller is a map from the controller inputs to outputs with a set of logic rules, which is employed to realize parameters adjustment in real time³⁰. The details of the fuzzy controller are displayed below: (1) Fuzzification: ΔSoC is the SoC difference between the real battery SoC (SoC_act) and the predefined battery SoC (SoC_pre). Power requirement (P_req) and ΔSoC are selected as two inputs in the fuzzy logic controller. ΔSoC∈[− 0.05, 0.05], P_req∈[0 kW, 160 kW]. The outputs are the threshold adjustment factor ∆SoC_H and ∆SoC_L, which ranges within [− 0.2, 0.2], and its membership function is defined as encompassing negative large (NL), negative medium (NM), negative small (NS), zero (ZO), positive small (PS), positive medium (PM), positive large (PL). (2) Rule base: The rule base of the fuzzy controller, as shown in Table 1., exemplifies a typical pattern of fuzzy logic in the M + N→W (if M and N, then W) form, where M represents the fuzzy set of ΔSoC, N represents the fuzzy set of P_req and W represents the fuzzy set of ∆SoC_H and ∆SoC_L. (3) Fuzzy reasoning and defuzzification: The Mamdani method was used to perform the fuzzy logic calculation. In order to ensure the control accuracy and calculation speed, the weighted average method is adopted in fuzzy controller for defuzzification, which is widely used in industrial control.

Table 1. The fuzzy control rules base of parameters adjustment.

Multi-objective optimization for ARC-EMS

Fuel economy and battery life are the two main objectives considered in the ARC-EMS for MMHEV. By optimizing the engine operating mode and intelligently switching power sources to optimize battery charging and discharging strategies, the optimization control of these two objectives can be achieved.

Description of MOO problem for ARC-EMS

In pursuit of the harmonious coexistence of energy consumption and battery life, we propose an innovative ARC-EMS solution based on MOO in this section. Compared to traditional methods, this approach no longer solely pursues the extreme of a certain indicator, but achieves balance and coordination among the two through carefully designed optimization strategies. In ARC-EMS, the allocation of power system work mode is no longer arbitrary or fixed, but determined by a refined system of rules. This rule system includes two key SoC thresholds (SoC_H and SoC_L) and speed and torque threshold values (n_e and T_e). By adjusting these parameters, we can flexibly and accurately control the working state of the power system, ensuring that the system can perform optimally under different operating conditions. Under multidimensional constraints, we optimized the system with the main objectives of C_{fuel_ele} (the evaluation index of fuel-electricity conversion loss rate) and Q_loss (the battery capacity loss rate). These goals do not exist in isolation, but are interrelated and interdependent. Therefore, we plan to use the PSO algorithm to obtain an optimization solution that can simultaneously meet the requirements of multiple objectives by comprehensively considering the trade-off relationship between each objective. The overall expression of this scheme can be expressed as a complex MOO function, which can comprehensively reflect the comprehensive performance of the system in terms of energy consumption and battery life. The overall expression of the objective is shown in Eq. (7):

$${J_{\hbox{min} }}[{n_e},{T_e},So{C_{H\_0}},So{C_{L\_0}}]=\arg \int_{0}^{{{T_{cyc}}}} {{I_{com\_ovp}}=\arg \int_{0}^{{{T_{cyc}}}} {\frac{1}{{{\omega _c}{C_{fuel\_ele}}{\text{+}}{\omega _Q}{Q_{loss}}}}} }$$

(7)

Where J_min represents the minimizing MOO cost function of control system I_{com_ovp}, which is the comprehensive performance evaluation index. SoC_{H_0,} SoC_{L_0}, n_eand T_e represent optimization variables. ω_C and ω_Q is the weight coefficients. This article uses the Analytic Hierarchy Process to obtain a multi-objective evaluation matrix, and calculates the weight vector result as [ω_C, ω_Q]^T=[0.63, 0.37]^T, which is based on engineering or research experience.

ICE is one of the energy sources of MMHEV, and the whole fuel consumption are produced by engine. This section describes the fuel consumption and battery capacity decay evaluation criteria. Maintaining a relatively flat SoC trajectory is beneficial for battery life, as it facilitates more efficient energy transfer between the battery and the engine. The hybrid energy storage system integrates the functions of the APU and the batteries, making it an effective solution for extending the service life of the batteries. The battery degradation model adopted in this study incorporates temperature effects, cycle count, and charge rate as variables, which was made to evaluate control strategy effectiveness while balancing computational efficiency, model complexity and data availability. Although less precise than mechanistic models, the simplified approach was chosen for its practical utility in rapid assessment. For the purpose of this investigation, taking into account the efficiency of the electric motor, the oil-to-electric conversion loss rate (C_{fuel_ele}) and battery life degradation (Q_loss) are specified is shown in Eq. (8):

$$\left\{ \begin{gathered} {C_{fuel\_ele}}=1 - \frac{{360 \cdot {\eta _{ele}}}}{{{\eta _{fuel}} \cdot \rho }} \hfill \\ {Q_{loss}}=\int_{0}^{{{T_{cyc}}}} {0.495 \times \frac{{d{I_{bat}}\left( t \right)}}{{dt}} \times \exp \left( {0.379\frac{{{I_{bat}}\left( t \right)}}{{A{h_{cell}}}}} \right) \times {N_{cyc}} \times DODdt} \hfill \\ \end{gathered} \right.$$

(8)

Where, η_fuel represents the power generation efficiency of the generator, η_fuel denotes the efficiency between the fuel consumption and the effective power output of the engine, and ρ stands for the gasoline calorific value, which is 4.6 × 107 J/kg. T_cyc is the total cycle time, I_bat(t) is the battery current; DOD is the depth of charge or discharge, DOD = 0.7; N_cyc is life cycles, Ah_cell is the cumulative capacity of the battery.

Multi-objective optimization algorithm

Traditional PSO initializes a group of particles in the feasible domain in the optimization process. Three characteristics (position, velocity and fitness function value) of each particle will be used, and the particle information features are updated by considering its own factors, individual optimality and global optimality. The speed update formula is shown in Eq. (9):

$$v_{{ij}}^{{(k+1)}}=\omega v_{{ij}}^{{(k+1)}}+{c_1}{r_1}(P_{{best\_ij}}^{{(k)}} - x_{{ij}}^{{(k)}})+{c_2}{r_2}(G_{{best\_ij}}^{{(k)}} - x_{{ij}}^{{(k)}})$$

(9)

Where v^(k)_ij is the speed of particle i at the j-th dimension component in the k-th generation, w is the inertia weight, c₁ and c₂ are the individual and social learning factors respectively.

The position update formula is shown in Eq. (10):

$$x_{{ij}}^{{(k+1)}}=x_{{ij}}^{{(k)}}+v_{{ij}}^{{(k+1)}}$$

(10)

Where x^(k)_ij represents the position of particle i at the j-th dimension component in the k-th generation. However, the traditional PSO has the disadvantage of being sensitive to control parameters, necessitating constant real time adjustment of the inertia weight and acceleration coefficients to obtain ideal solutions.

An effective bare-bones multi-objective particle swarm optimization (BB-MOPSO) method with adaptive perturbation has been adopted to realize a control-parameter-free process³¹. The BB-MOPSO algorithm integrates the principles of PSO and is specifically designed for multi-objective optimization. It simultaneously processes multiple conflicting objective functions without requiring iterative single-objective optimization or complex weight allocation, directly generating a Pareto optimal solution set (non-dominated solutions) to provide decision-makers with diverse alternatives. Effective population evolution is achieved through particle collaborative learning and controlled stochasticity. An external archive dynamically preserves non-dominated solutions, accelerating convergence while maintaining search diversity and efficiency. BB-MOPSO is adaptable to both continuous and discrete optimization problems, with optimal solutions for multi-variable decision spaces being efficiently identified through tailored fitness functions and local search mechanisms. Its modular architecture allows for customization to address application-specific constraints. Although moderate computational resources are required for complex problems, the algorithm’s high search efficiency and scalability ensure rapid convergence to high-quality solutions within practical timeframes. The BB-MOPSO algorithm with adaptive perturbation factor can improve the global exploration ability in the initial stage and local exploitation capability in the later stage. The position update formula in BB-MOPSO is presented in Eq. (11):

$$x_{{ij}}^{{(k+1)}}=\left\{ \begin{gathered} N\left( {\frac{{{r_3}P_{{best\_ij}}^{{(k)}}+(1 - {r_3})G_{{best\_ij}}^{{(k)}}}}{2},\left| {P_{{best\_ij}}^{{(k)}} - G_{{best\_ij}}^{{(k)}}} \right|+{\varepsilon _j}} \right),ifU(0,1)<0 \hfill \\ G_{{best\_ij}}^{{(k)}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{}&{} \end{array}}&{}&{}&{} \end{array}}&{}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {} \end{array}}&{}&{} \end{array}}&{} \end{array}}&, \end{array}else \hfill \\ \end{gathered} \right.$$

(11)

Where (X, Y) is a Gaussian distribution function with mean X and the variance Y; r₃ is a random number uniformly distributed within the interval [0, 1]; and U(0,1)represents a uniformly distributed random number between [0, 1]. ε_j is a disturbance factor determined by the similarity between G^(k)_best__ij and P^(k)_best__ij, and it decreases with the decrease of iteration time.

The calculation of ε_j is shown in Eq. (12):

$${\varepsilon _j}=\left\{ \begin{gathered} ({x_{j\_up}} - {x_{j\_low}}){e^{( - 5t/T)}},H>rand \hfill \\ 0\begin{array}{*{20}{c}} {}&{} \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{}&{}&, \end{array}else \hfill \\ \end{gathered} \right.$$

(12)

Where t represents the current iteration time, T is the maximal iteration time, x_{j_up} and x_{j_low} are the upper and lower limits of the j-th variable. Additionally, H is a probability factor that is calculated based on the difference between f(G^(k)_best__ij) and f(P^(k)_best__ij).

The calculation of H is shown in Eq. (13):

$$H=\frac{1}{2}(1 - \frac{1}{A}\sum\limits_{{a=1}}^{A} {\left| {\frac{{{f_a}(P_{{best\_ij}}^{{(k)}}) - {f_a}(G_{{best\_ij}}^{{(k)}})}}{{f_{a}^{{\hbox{max} }} - f_{b}^{{\hbox{min} }}}}} \right|} )$$

(13)

Where f_a^max and f_a^min are the maximal and minimal values of the a-th objective function obtained by the swarm. In a multi-cycle scenario, DEA is used to characterize urban dynamic driving patterns ^[39]. Finally, the implementation steps of the optimization algorithm are described in Fig. 5.

Fig. 5

The optimization algorithm processes based on BB-MOPSO.

Verification and discussion

In this section, in order to test the optimization effect of ARC-EMS and the ability of the proposed MOO method to balance energy consumption and emissions, simulation and experimental bench will be used to validate the EMS described in Sect. 2.

MOO simulation model

AMEsim and MATLAB/Simulink software are used to build the vehicle dynamic model and the proposed EMS respectively, and the co-simulation of the two is realized through the S-function, as shown in Fig. 6.

Fig. 6

Simulation platform of the R-EEV for the MOO problem: (a) Simulation platform of the R-EEV; (b) Control strategy model developed using MATLAB/Simulink.

The fundamental parameters of the target vehicle researched are shown in Table 2.

Table 2 Parameters of MMHEV simulation model.

The algorithm design scheme employed in the study enhances computational efficiency through the optimization of data structures, reduction of unnecessary computational steps, and utilization of parallel computing techniques. This is reflected in multiple aspects including the simplified battery degradation model, the low-computational-cost fuzzy adaptive algorithm, and the implementation of rule-based strategy control logic using pre-stored rules. Regarding implementation difficulty, both algorithmic complexity and programming feasibility have been carefully considered. The implementation complexity has been reduced through rational module partitioning and well-structured code organization. Furthermore, comprehensive validation has been conducted through unit testing, integration testing, and performance testing to ensure algorithmic stability and reliability.

Parameter optimization results based on Pareto solution sets

An optimization model was built and integrated based on the AMEsim software mentioned above, and the optimization variable results was observed. As shown in Fig. 7, the variations in optimization variables throughout the iterative process, demonstrating the trend of these variables as the iteration count increases. After approximately 120 optimization iterations, the optimization variables converge to a constant value, and during the iteration process, the paths of convergence exhibit some discrepancies, which indicate the effectiveness of the algorithm.

In the initial phase of the convergence analysis for n_e and T_e, a relatively large fluctuation range of ne, spanning from 1000 to 1650, was observed. This indicates that, during the early stages of the optimization process, the algorithm was exploring a variety of potential velocity values in order to locate the optimal solution. After approximately 40 iterations had elapsed, the fluctuation range of ne began to diminish and stabilize. This indicates that the algorithm has commenced convergence and is progressively approaching the optimal velocity value. After undergoing 60 iterations, the fluctuation ranges of n_e and T_e stabilized within [1250, 1350] and [100, 120], respectively, and converged steadily to approximately 1280 and 115. These values are likely to be the optimized velocity and torque thresholds that achieve the optimization objectives under the given constraints. This reflects the efficiency characteristics of the hybrid power system across different power operating regions. In the low-power consumption region, the system efficiency is relatively low; therefore, the optimization results tend to be oriented towards increasing the power margin values to enhance efficiency. During the convergence analysis phase for SoC_{H_0} and SoC_{L_0}, the fluctuation ranges of both SoC_{H_0} and SoC_{L_0} were initially large and exhibited a downward trend. After approximately 80 iterations had elapsed, the fluctuation ranges of SoC_{H_0} and SoC_{L_0} began to diminish and stabilize. This indicates that the algorithm has commenced convergence and is progressively approaching the optimal velocity values. After undergoing 120 iterations, the fluctuation ranges of SoC_{H_0} and SoC_{L_0} were stabilized within [0.65, 0.68] and [0.42, 0.44], respectively, and converged steadily to approximately 0.66 and 0.43. At the low SoC stage, the battery charging and discharging efficiency is relatively low; therefore, the optimization results tend to increase the proportion of charging conditions, maintaining a trend of sustaining the SoC within a higher efficiency range to enhance overall efficiency. The uniformity and rationality of the working mode distribution also demonstrate the effectiveness of the optimization algorithm. This allocation method can balance the required power range during operation, thereby ensuring the stable operation of the M-MPHV across different driving scenarios and loading conditions.

Fig. 7

Optimization variables changes during the iterative process.

This section adopts the analysis method of Pareto optimal theory, which reflects the essential features of MOO problem directly. The contradictory relationship between the two goals is comparatively analyzed in relation to evaluation indicators such as C_{fuel_ele,} Q_loss and I_{com_ovp}. Figure 8 shows the solution set of the optimal I_{com_ovp}, which is described at length later as the optimized decision result.

Fig. 8

Multi objective optimization results based on Pareto and comparative analysis: (a) distribution of the Pareto optimal solution in objective space; (b)performance comparison.

The configuration of the powertrain operating modes, specifically the manner in which the internal combustion engine, electric motor, and battery collaborate, directly leads to differences in energy consumption and battery capacity degradation. These differences are profoundly influenced by the control strategies that are implemented. In order to minimize energy consumption, strategies are flexibly adjusted based on the state of the battery: When the battery’s SoC is low, the system tends to select the range-extended mode (M2), in which the internal combustion engine operates at its optimal efficiency point to charge the battery, thereby avoiding battery operation in low-efficiency ranges, reducing energy consumption, and protecting the battery. Conversely, when the battery’s SoC is high, there is a greater tendency to adopt the pure electric mode (M1), allowing the battery to operate in a high-efficiency state and maximizing the utilization efficiency of electrical energy. When confronted with high power demands (P_req), the system is switched to the internal combustion engine drive mode (M4), leveraging the advantage of the internal combustion engine operating in its high-efficiency range to further reduce energy consumption and enhance the battery’s lifespan. It is noteworthy that when the proportion of P_req is low, the system may face the challenge of increased energy consumption. Although frequent power switching in M4 mode may result in additional fuel consumption, this mode actually reduces the frequency of battery usage, thereby contributing to the extension of battery life. The inherent contradiction between these control objectives is an inevitable issue in powertrain optimization, highlighting the importance of optimizing relevant thresholds and key parameters to achieve an optimal balance between energy consumption and battery life.

Comparison results of parameter fixation and parameter adaptation

In this section, in order to verify the universality, the parameter optimization results with the optimal I_{com_APU} are selected for comparative study, and the RC-EMS with adaptive parameter adjustment module is referred to as a revise strategy (ARC-EMS). As a result, much more engine power transients can be observed within the entire CS phases. The comparison of simulation results before and after optimization is shown in Fig. 9.

Fig. 9

The comparison of simulation results before and after optimization.

Figure 9 shows the significant differences in the switching results of the power system operating modes under RC-EMS and ARC-EMS. And the designed control logic was implemented when the power switching conditions were met, which demonstrates the excellent ability of the two comparison strategies. The addition of adaptive modules increases the working ratio of M1 and M4 under ARC-EMS. By running the ICE at its optimal efficiency point in M4, the battery is charged to avoid working in the low efficiency range, reduce energy consumption, and protect the battery; The M1 is relatively increased to drive vehicles with as much electricity as possible, while the M2 is relatively reduced to save fuel consumption. In M4 mode, ICE operation is optimized to maintain peak efficiency by the adaptive module, reducing energy waste. Dynamic adjustments to M1 and M2 modes are implemented, prioritizing electric propulsion to lower fuel consumption. ARC-EMS demonstrates superior SoC management, with smoother trajectory variations and reduced discharge depth, achieving significant improvements in both energy efficiency and battery lifespan. The SoC trajectory and battery charging and discharging current information under RC-EMS and ARC-EMS. The two SoC curves, which are considered roughly monotonic, slowly decrease to 0.631 and 0.622, respectively. Compared with RC-EMS, as expected, the SoC curve of ARC-EMS has reached a lower final SoC value, because the adaptive module will adjust the operating mode after curing according to the objective situation that the SoC value is too large, so that more battery energy can be used. According to the constraints set in the problem, the battery SoC varies within the range of [0.6, 0.7], with minimal variation during the driving cycle, achieving good tracking characteristics for SoC reference and thus extending battery life. The slight changes in SoC significantly reduce the depth of discharge, which is beneficial for achieving longer battery life and ensuring that the SoC trajectory does not exceed the lower limit, thereby avoiding damage to battery health.

Experimental test implementation and its results

Comparative study against benchmark control strategy to thoroughly evaluate the proposed ARC-EMS, the control strategies are introduced as comparison basis. The proposed ARC-EMS urges multiple energy sources to work towards more battery discharge conditions, and the robustness of its strategies is proven as the overall trend of statistical results remains similar even as working conditions become more. The developed control strategy exhibits excellent performance in terms of energy consumption, emissions, and battery life, with a particular highlight being the significant reduction in battery life attenuation that can substantially lower the overall vehicle’s service cost economically. Similar to the previous study, due to the different units and scales, before comparing the performance of the four strategies horizontally across different cycles, the normalization parameters of the performance indicators are calculated as follow:

$${\theta _{ik}}=\frac{{{\delta _{ij}} - \delta _{{ij}}^{{\hbox{min} }}}}{{\delta _{{ij}}^{{\hbox{max} }} - \delta _{{ij}}^{{\hbox{min} }}}}$$

(14)

Where ɵ_ik is the normalized index of j-th evaluation index on i-strategy; δ_ij is the index value; δ^min_ij and δ^max_ij are the index minimum and maximum value, respectively.

In addition to considering the results of the energy storage system, the simulation results of system fuel consumption, the comparison of 100 km equivalent fuel consumption (Ge) between six control strategies after the modification of terminal SoC (the SoC corrected fuel efficiencies) are shown in Fig. 10; Table 3. DP is utilized as an optimal off-line baseline under the test driving cycle, while optimal control is employed with I_{com_ovp} as the objective function. Eventually, the data domain used for normalization analysis is determined, which includes the simulation results under the above strategies and the result data under the single target based on Pareto solution set. Based on formula 15, the normalized statistical results are shown in Fig. 10.

Fig. 10

Comparison of normalized evaluation indicators.

As shown in Fig. 10, the result of the proposed strategy is closest to the best performance that can be achieved. And the performance results under each strategy show different performance, which implies that the ARC-EMS considered in this study can achieve the better balance among the two objectives.

Table 3 Test results of experimental test.

The total consumption of ARC-EMS slightly reduced by about 2.7% compared to M2, whereas the ARC-EMS is almost identical to M2 with a difference of only 1.3%, leading to the conclusion that ARC-EMS is slightly better than RC-EMS. Comparing with the results of RC-EMS and ARC-EMS with threshold parameter adjustable, there is not much difference in fuel consumption (Ge), which signifies that the proposed ARC-EMS performs well in terms of fuel economy. Based on the different operating characteristics of M-HEV in different modes, the optimized strategy will tend to operate ICE in the high-efficiency region. This mode adopts a power tracking control strategy to operate the engine at the optimal operating point corresponding to the required power. In terms of battery life, the Q_loss under ARC-EMS is relatively small, reaching 10.2%, which is 32.5% lower than the 15.1% under M1. The comprehensive index I_{com_ovp} considering energy consumption and battery life reaches the maximum value of 0.91. In summary, ARC-EMS has shown good performance in energy consumption control, engine operating efficiency, battery life, and overall performance. These advantages make ARC-EMS an energy management strategy worth considering and applying in hybrid power systems. The results demonstrate that the proposed ARC-EMS achieves comparable optimization performance to DP-based strategies. Specifically, 4% improvement in energy efficiency and 3% reduction in battery capacity degradation are observed in ARC-EMS compared to the DP-based approach. However, the advantages of ARC-EMS extend beyond these metrics. Superior performance in real-world vehicle applications is demonstrated, with computational resource requirements being significantly lower than those of DP-based algorithms. This characteristic enhances the practicality and cost-effectiveness of ARC-EMS in actual vehicular environments. Therefore, it can be concluded that while ARC-EMS matches DP in optimization outcomes, its superior real-world applicability and reduced computational demands represent a breakthrough in energy management systems. ARC-EMS not only achieves optimization effects similar to DP but also exhibits significant advantages in practical implementation and computational efficiency, solidifying its potential for high utility and broad application prospects in energy management.

Conclusion

In order to achieve the optimal energy allocation of the MMHEV from the perspective of multi-objective, a data-driven EMS based on travel conditions is proposed. Firstly, a RC-EMS was developed according to the operating curves and interval thresholds of motors and engine based on Amesim and MATLAB/Simulink platforms. The DEA was used to establish the traffic speed interval, and the comprehensive driving cycles of urban was constructed based on the proportion of driving time, which is used as the input information of the optimization model. Then, the key threshold parameters of EMS are optimized offline by using BB-MOPSO algorithm from the multi-objective perspective, and the optimal parameters obtained are used as the initial values of adaptive parameter optimization. After optimization, the comprehensive energy consumption and battery capacity decay are reduced, with the majority of the ICE operating points now concentrated in the high efficiency zone. The designed fuzzy adaptive parameter optimization module updates the key parameters of the strategy in real time, so as to realize the optimal dynamic energy allocation which can adapt to the road conditions. The simulation outcomes for various performance indicators of distinct EMS demonstrate the following: a). The adaptive module for parameter adjustment, which leverages a fuzzy algorithm, successfully fulfills the established control tasks in accordance with the predefined control logic. b). A comparison between the parameter-fixed and parameter-adaptive optimization approaches reveals that the latter exhibits superior adaptability to varying road conditions. c). The control strategy maintains robustness across different driving cycles. Furthermore, both simulation and experimental results highlight that the data-driven ARC-EMS offers a more balanced performance compared to the traditional RC-EMS. As anticipated, the strategy effectively balances energy savings and emission reductions, and serves as a viable approach for developing an EMS to enhance the overall performance of the MMHEV. Ultimately, the feasibility of this optimization method is confirmed through experimentation, demonstrating its potential benefits in practical applications. Additionally, the generalization capability of the model defined as its adaptability to diverse scenarios or datasets has been enhanced by incorporating the complexity of vehicle systems and the dynamic characteristics of traffic environments. This improvement aims to further refine the accuracy and reliability of the proposed RC-EMS particularly in scenarios involving heterogeneous urban traffic conditions, varying driver behaviors, and fluctuating vehicle states. Furthermore, extended performance metrics, such as driving comfort and vehicle acceleration, will be integrated into the optimization strategy parameter set to construct a more comprehensive evaluation framework for EMS performance.