Introduction

Nonlinear Schrödinger equations (NLSEs) can be used to model a variety of complex nonlinear physical phenomena. Such equations are used in a wide range of nonlinear physical processes, such as fluid mechanics, photonics, ocean engineering, plasma physics, electromagnetism, and more. A fascinating topic for researching soliton propagation via nonlinear optical fibers is the optical solitons theory1,2,3. In the study of optics, any optical field that remains constant throughout transmission because of a meticulous balancing act between nonlinear and linear effects in the medium is called a soliton. The transmission of ultrashort electromagnetic radiation pulses in a nonlinear medium is a multidimensional process. The interplay of multiple physical characteristics, including dispersion, material dispersion, diffraction, and nonlinear response, affects the pulse dynamics4,5.

Stochastic evolution equations are mathematical formulas that are used to describe how a system evolves over time while accounting for both random and deterministic factors6. In order to examine complex systems that display random behavior, they are extensively employed in many scientific disciplines, such as physics, biology, and finance. Economists and researchers can better comprehend the behavior and forecasts of these systems by utilizing the strong framework that stochastic evolution equations offer for studying their dynamics.

As a result, the primary emphasis of this work is the well-known three-component coupled NLS (or tc-CNLS, for short) equation. Multi-component nonlinear wave equations are being studied more than scalar NLS equations because they can yield more valuable information and lead to more applications. The three-component stochastic coupled nonlinear Schrö dinger equation is given by7

$$\begin{aligned} i\phi _{k,t}+\frac{1}{2}\phi _{k,xx}+(|\phi _{1}|^{2}+|\phi _{2}|^{2}+|\phi _{3}|^{2})\phi _{k}=i\lambda \phi _{k}\circ B_{t}, \end{aligned}$$
(1)

where \(\phi _{k}=\phi _{k}(x,t),(k=1,2,3)\) represents the wave envelopes and B(t) is a multiplicative time noise with the control parameter \(\lambda\) which is satisfies the following prosperities such as i) B(t) is a continuous function ii) \(B(0)=0\) and iii) \(B(t_{i+1})-B(t_{i})\) has standard normal distribution. The propagation of an optical pulse in a birefringent optical fiber is described by the three nonlinear complex models.

One of the key features of the three-component stochastic coupled nonlinear Schrödinger equation is that it allows for the study of complex interactions between different wave functions. In traditional quantum mechanics, wave functions are typically considered to be independent of each other. However, in systems where multiple wave functions interact, such as in certain types of matter or light waves, the behavior of each wave function can be influenced by the presence of the others. By incorporating stochastic fluctuations into the equation, researchers can gain a more nuanced understanding of how these interactions affect the overall dynamics of the system.

Chen et al. presented a succinct method for quantitatively investigated coupled stochastic nonlinear Schrödinger equations8. Kraichnan et al. described a method for dealing with nonlinear stochastic systems that may be useful in quantum mechanics and turbulence theory9. Cai et al. looked into the statistical mechanics of a complex field that the nonlinear Schrödinger equation explained. In a nonlinear medium, a propagating laser field and Langmuir waves in a plasma are explained by such fields when idealized appropriately10. In order to understand optical solitons in fiber optics, Younas et al. examined the three-component coupled nonlinear Schrödinger equation. The study of multi-component NLSE equations is becoming increasingly popular due to their capacity to represent complicated physical processes and provide dynamic solutions for localized waves11. The Darboux transformation was devised12 by Xu et al. for three-component coupled derivative nonlinear Schrö dinger equations. Kevrekidis et al. attempted to communicate a portion of the current buzz surrounding multi-component nonlinear Schrödinger models, which has been sparked by several theoretical and computational investigations as well as experimental discoveries13. Among the most active fields of study in the field of optical soliton is still the nonlinear dynamics of an optical pulse or beam, as demonstrated by Stalin et al.14. In order to regulate the propagation and interaction of optical-soliton in optical media such as multimode fibers, fiber arrays, and birefringent fibers, Jiang et al. introduced the coupled nonlinear Schrö dinger (CNLS) equations15.

Abdullah et al. explored the traveling wave solutions for explicit-time nonlinear photorefractive dynamics equation16, also, the bright and dark spatial solitons for the linear and quadratic electro-optic effects based on low amplitude approximations17. Ripai et al. worked on the solitonic characteristics of optical airy beams nonlinear propagation18, and temporal behavior of diffusion-trapped19. Moreover, they are also worked on the effect of ansatz on soliton propagation pattern in photorefractive crystals20. Raipai et al. investigated the application of the split-step Fourier method in investigating a bright soliton solution21. Chen et al. worked on the overview and recent advances of optical spatial solitons22. Conti et al. observed the optical spatial solitons in a highly nonlocal medium23.

Radhakrishnan et al. constructed an integrable set of linked nonlinear Schr ödinger equations which described the quintic nonlinearity influences the propagation of ultrashort optical soliton pulses24. Wang et al. considered the integrable coupled nonlinear Schrödinger system and investigated the exact solitary wave solutions of underlying model. The Riemann-Hilbert technique is utilized to locate N-soliton solutions in this system. The collision dynamics of two solitons are also studied25. Chan et al., used the nonlinear Schrödinger equation to generate rogue waves (RWs)26. Kanna et al., considered the Hirota technique to produce precise bright one-soliton and two-soliton solutions for the integrable three coupled nonlinear Schrödinger equations (3-CNLS) and general N-coupled Schrödinger equations27.

Brownian motion or Wiener process is one of the original stochastic processes for modelling random events, and is very important in the theory of mathematical finance. It is named as an honour to Scottish botanist Robert Brown who first noted the movement in 1827, known as brownian of individual pollen grains in water. Although the three-component nonlinear Schrödinger equation has been introduced, the study should have described more elaborately how Brownian motion impacts the optical soliton solutions of the model. It is recognized that noise affects the system and, therefore, soliton formation; nevertheless, Brownian motions (or flapping) role in determining the core characteristics of the soliton, including its amplitude, velocity, width, and stability, must be incorporated. More clarity of these effects would have provided broader understanding of the role of Brownian motion regarding soliton evolution. This clarification would enhance the scholarly applicability of the study by demonstrating how, apart from stochastic perturbations, Brownian motion alters soliton dynamics in specific ways.

In this modern era of research exact optical soliton solutions have many importance and applications. Because the stochastic evolution equations are important, many techniques have been devised to solve the including the new modified extended direct algebraic method28 , \(\phi ^{6}\)-model expansion method29, He’s semi-invers method30, Jaccobi elliptic function method31, Riccati equation mapping method32 and etc. But in this study we used the well-known method namely as generalized Riccati equation mapping method. This approach gives us the abundant families of exact optical soliton and solitary wave solutions. The novelty of this work is to acquire the closed form solitary wave solutions for the three-component nonlinear stochastic Schrödinger equation. To, gain these solution we used the generalized Riccati equation mapping method and get the solutions in the form of hyperbolic, and trigonometric function solutions. Given that the three-component nonlinear stochastic Schrö dinger equation is necessary to describe wave propagation, the solutions that were generated are significant in explaining a number of fascinating properties. Furthermore, we investigate how noise affects the precise solutions of the three-component nonlinear stochastic Schrödinger equation by utilizing the MATHEMATICA11.1 software to provide a variety of figures.

Methodology

Using a given nonlinear partial differential equation (NPDE) with independent variables \(x=(x_{0},x_{1},x_{2},...,x_{m})\) and dependent variable \(\phi\), the generalized Riccati equation mapping method works as follows.

$$\begin{aligned} F(\phi ,\phi _{t},\phi _{x},\phi _{xx},\cdots )=0, \end{aligned}$$
(2)

where \(\phi =\phi (x,t)\) is unknown function and F represents the polynomial of \(\phi\). Further Eq. (2) can be solve by using the traveling wave transformation which is taken as

$$\begin{aligned} \phi (x,t)=\psi (\varpi ),\ \ \text {where}\ \ \varpi =\varpi _{1}x-\varpi _{2}t. \end{aligned}$$
(3)

Now, Eq. (2) is converted into ODE by the help of Eq. (3) as

$$\begin{aligned} F(\psi ,\psi ^{\prime },\psi ^{\prime \prime },\psi ^{\prime \prime \prime },\cdots )=0, \end{aligned}$$
(4)

where \(\phi =\psi (\varpi )\), \(\psi ^{\prime }=\frac{d\psi }{d\varpi }\), \(\psi ^{\prime \prime }=\frac{d^{2}\psi }{d\varpi ^{2}},\cdots\). Suppose that Eq. (4) has a general solution in the following form

$$\begin{aligned} \psi (\varpi )=\sum _{j=0}^{M}\alpha _{j}\Omega ^{j}(\varpi ), \end{aligned}$$
(5)

here \(\alpha _{j}\),\((j=0,1,2,\cdots )\) are constants that are found to be later and \(\Omega (\varpi )\) must satisfy the following ODE as

$$\begin{aligned} \Omega ^{^{\prime }}(\varpi )=\kappa +\theta \Omega (\varpi )+\nu \Omega (\varpi )^{2}, \end{aligned}$$
(6)

where \(\theta\), \(\nu\) and \(\kappa\) are the constants. The general solutions of Eq. (6) is given as

Case-I: If \(M=\theta ^{2}-4\kappa \nu >0\) and \(\kappa \nu \ne 0\) then,

$$\begin{aligned} \Omega _{1}(\varpi )= & -\frac{\sqrt{M}\tanh \left( \frac{1}{2}\varpi \sqrt{M }\right) +\theta }{2\nu }, \\ \Omega _{2}(\varpi )= & -\frac{\sqrt{M}\coth \left( \frac{1}{2}\varpi \sqrt{M }\right) +\theta }{2\nu }, \\ \Omega _{3}(\varpi )= & -\frac{\sqrt{M}\left( \tanh \left( \varpi \sqrt{M} \right) +i\text {sech}\left( \varpi \sqrt{M}\right) \right) +\theta }{2\nu },\\ \Omega _{4}(\varpi )= & -\frac{\sqrt{M}\left( \tanh \left( \frac{1}{4}\varpi \sqrt{M}\right) +\coth \left( \frac{1}{4}\varpi \sqrt{M}\right) \right) +2\theta }{4\nu }, \\ \Omega _{5}(\varpi )= & \frac{\frac{\sqrt{M\left( G^{2}+H^{2}\right) }-G \sqrt{\theta ^{2}-4\kappa \nu }\cosh \left( \varpi \sqrt{M}\right) }{G\sinh \left( \varpi \sqrt{M}\right) +H}-\theta }{2\nu }, \\ \Omega _{6}(\varpi )= & \frac{-\frac{\sqrt{M\left( G^{2}+H^{2}\right) }+G \sqrt{M}\cosh \left( \varpi \sqrt{M}\right) }{G\sinh \left( \varpi \sqrt{M} \right) +H}-\theta }{2\nu }. \end{aligned}$$

where G and H are two non-zero real constants and \(H^{2}-G^{2}>0\).

$$\begin{aligned} \Omega _{7}(\varpi )= & \frac{2\kappa \cosh \left( \frac{1}{2}\varpi \sqrt{M} \right) }{\sqrt{M}\sinh \left( \frac{1}{2}\varpi \sqrt{M}\right) -\theta \cosh \left( \frac{1}{2}\varpi \sqrt{M}\right) }, \end{aligned}$$
(7)
$$\begin{aligned} \Omega _{8}(\varpi )= & -\frac{2\kappa \sinh \left( \frac{1}{2}\varpi \sqrt{M }\right) }{\theta \sinh \left( \frac{1}{2}\varpi \sqrt{M}\right) -\sqrt{M} \cosh \left( \frac{1}{2}\varpi \sqrt{M}\right) }, \end{aligned}$$
(8)
$$\begin{aligned} \Omega _{9}(\varpi )= & \frac{2\kappa \sinh \left( \varpi \sqrt{M}\right) }{ -\theta \sinh \left( \varpi \sqrt{A}\right) +\sqrt{M}\cosh \left( \varpi \sqrt{M}\right) +\sqrt{M}}. \end{aligned}$$
(9)

Case-II: If \(D=4\kappa \nu -\theta ^{2}>0\) and \(\kappa \nu \ne 0,\) then

$$\begin{aligned} \Omega _{10}(\varpi )= & \frac{\sqrt{D}\tan \left( \frac{1}{2}\varpi \sqrt{D} \right) -\theta }{2\nu }, \\ \Omega _{11}(\varpi )= & -\frac{\sqrt{D}\cot \left( \frac{1}{2}\varpi \sqrt{D }\right) +\theta }{2\nu }, \\ \Omega _{12}(\varpi )= & \frac{\sqrt{D}\left( \tan \left( \varpi \sqrt{D} \right) -\sec \left( \varpi \sqrt{D}\right) \right) -\theta }{2\nu }, \\ \Omega _{13}(\varpi )= & \frac{\sqrt{D}\left( \tan \left( \frac{1}{4}\varpi \sqrt{D}\right) -\cot \left( \frac{1}{4}\varpi \sqrt{D}\right) \right) -2\theta }{4\nu }, \\ \Omega _{14}(\varpi )= & \frac{\frac{\sqrt{D\left( G^{2}-H^{2}\right) }-G \sqrt{D}\cos \left( \varpi \sqrt{D}\right) }{G\sin \left( \xi \sqrt{D} \right) +H}-\theta }{2\nu }, \end{aligned}$$

where G and H are two non-zero real constants and \(G^{2}-H^{2}>0\)

$$\begin{aligned} \Omega _{16}(\varpi )= & \frac{2\kappa \cos \left( \frac{1}{2}\varpi \sqrt{D} \right) }{\sqrt{4\kappa \nu -\theta ^{2}}\sin \left( \frac{1}{2}\varpi \sqrt{ D}\right) +\theta \cos \left( \frac{1}{2}\varpi \sqrt{D}\right) }, \end{aligned}$$
(10)
$$\begin{aligned} \Omega _{17}(\varpi )= & \frac{2\kappa \sin \left( \frac{1}{2}\varpi \sqrt{D} \right) }{\sqrt{D}\cos \left( \frac{1}{2}\varpi \sqrt{D}\right) -\theta \sin \left( \frac{1}{2}\varpi \sqrt{D}\right) }, \end{aligned}$$
(11)
$$\begin{aligned} \Omega _{18}(\varpi )= & \frac{2\kappa \sin \left( \varpi \sqrt{D}\right) }{ -\theta \sin \left( \varpi \sqrt{D}\right) +\sqrt{D}\cos \left( \varpi \sqrt{ D}\right) +\sqrt{D}}. \end{aligned}$$
(12)

Case-III: If \(\theta =0\) and \(\kappa \nu \ne 0\), then

$$\begin{aligned} \Omega _{19}(\varpi )= & -\frac{d\nu }{q(d-\sinh (\nu \kappa )+\cosh (\nu \kappa ))}, \\ \Omega _{20}(\varpi )= & \frac{\nu (\sinh (\nu \kappa )+\cosh (\nu \kappa )) }{\kappa (d+\sinh (\nu \kappa )+\cosh (\nu \kappa ))}. \end{aligned}$$

where d is an arbitrary constant.

Exact soliton solutions via generalized Riccati equation mapping method

In this section, we convert the PDE into the ODE form by using the wave transformation39,40,41 such as

$$\begin{aligned} \phi _{k}(x,t)=\psi _{k}(\varpi )e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t},~~\text{ where }~\ \varpi =\varpi _{1}x-\varpi _{2}t,~~\varrho =\varrho _{1}x+\varrho _{2}t. \end{aligned}$$
(13)

Where \(\varrho\) and \(\psi _{k}(\varpi )\) are the real functions and \(\varpi _{1},\varpi _{2},\varrho _{1},\varrho _{2}\) are the frequencies and wave numbers while \(\lambda\) is the control parameter with \(\beta (t)\) is the Brownian motion. Taking the derivatives of the above Eq. (13) and system (1) is converted into following ODE system

$$\begin{aligned} -2\varpi _{2}\psi _{k}^{\prime }i{-\varrho _{1}^{2}\psi _{k}}-2\psi _{k}\varrho _{2}+\varpi _{1}^{2}\psi _{k}^{^{\prime \prime }}+2\varpi _{1}\psi _{k}^{\prime }i\varrho _{1}+\psi _{k}(\psi _{1}^{2}+\psi _{2}^{2}+\psi _{3}^{2})e^{2\lambda \beta (t)-2\lambda ^{2}t}=0, \end{aligned}$$
(14)

for \(k=1,2,3\). Now, comparing the real and imaginary part such as

$$\begin{aligned} \varpi _{1}^{2}\psi _{k}^{^{\prime \prime }}-(\varrho _{1}^{2}+2\varrho _{2})\psi _{k}+2\psi _{k}(\psi _{1}^{2}+2\psi _{2}^{2}+2\psi _{3}^{2})e^{2\lambda \beta (t)-2\lambda ^{2}t}=0, \end{aligned}$$

Taking the expectation into both sides39,40, we get

$$\begin{aligned} \varpi _{1}^{2}\psi _{k}^{^{\prime \prime }}-(\varrho _{1}^{2}+2\varrho _{2})\psi _{k}+2\psi _{k}(\psi _{1}^{2}+2\psi _{2}^{2}+2\psi _{3}^{2})=0, \end{aligned}$$
(15)

from the imaginary part the parametric condition is gain as \(\varpi _{2}=\varpi _{1}\varrho _{1}.\)

Assume that the general solution of the system (15) in the form of polynomial such as36,37,38,

$$\begin{aligned} \psi _{k}(\varpi )=\sum _{i=0}^{N}\alpha _{k,i}\Omega ^{i}(\varpi ), \end{aligned}$$
(16)

where \(\alpha _{k,i}\) for\(\ i=0,1,2,\cdots ,N\) are constants such that \(\alpha _{k,N}\ne 0\) and they will be defined later. The positive number N is found by applying the homogeneous balancing principle on the system (15). Consider the highest derivatives and highest power nonlinear terms in equation (15) \(\psi _{k}^{^{\prime \prime }}\) and \(\psi _{k}^{3}\). Using these term and applying the homogeneous balancing principle, we get \(N=1\). We used this value in system ( 16) and get the expression such as

$$\begin{aligned} \psi _{k}(\varpi )=\alpha _{k,0}+\alpha _{k,1}\Omega (\varpi ), \end{aligned}$$
(17)

for \(k=1,\ 2,\ 3\). Now taking the derivatives of above system (17) and substitute into the system (15) by taking the help of equation ( 6) and get the expression in polynomial \(\Omega ^{j}(\varpi ),(j=0,1,2,\cdots )\). Comparing all the coefficients of the same powers of \(\Omega ^{j}(\varpi ),(j=0,1,2,\cdots )\) and equating them equal to zero to get the system of algebraic equations. Solving this system of equations by the computational software MATHEMATICA11.1 and get the constants values such as

$$\begin{aligned} \alpha _{k,0}=\hbar \alpha _{k,1},~~\theta =\kappa \hbar ,\ \nu =\frac{ 2\kappa }{\hbar ^{2}},\ \rho _{2}=-\frac{A+\beta _{1}^{2}\left( \gamma _{0}^{2}+\rho _{1}^{2}\right) }{2\beta _{1}^{2}}. \end{aligned}$$

where

$$\begin{aligned} \hbar =\frac{1}{\sqrt{2}\alpha _{2,1}}\sqrt{\frac{A-\hbar \alpha _{2,1}^{2}\alpha _{3,0}}{\alpha _{1,1}^{2}+\alpha _{2,1}^{2}}}\text {\ \ and \ }A=\sqrt{\alpha _{2,1}^{4}\left( \alpha _{3,0}^{4}-\kappa ^{2}\omega _{1}^{2}\left( \alpha _{1,1}^{2}+\alpha _{2,1}^{2}\right) \right) }. \end{aligned}$$

Case-I: If \(M=\theta ^{2}-4\kappa \nu >0\) and \(\kappa \nu \ne 0,\) then the solutions of Eq. (1), for \(k=1,\ 2,\ 3\), are

$$\begin{aligned} \phi _{k,1}(x,t)= & \alpha _{k}\left( \hbar -\frac{\sqrt{M}\tanh \left( \frac{1 }{2}\sqrt{M}(\varpi _{1}x-\varpi _{2}t)\right) +\theta }{2\nu }\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(18)
$$\begin{aligned} \phi _{k,2}(x,t)= & \alpha _{k}\left( \hbar -\frac{\sqrt{M}\coth \left( \frac{1 }{2}\sqrt{M}(\varpi _{1}x-\varpi _{2}t)\right) +\theta }{2\nu }\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(19)
$$\begin{aligned} \phi _{k,3}(x,t)= & \alpha _{k}\left( \hbar -\frac{\sqrt{M}\left( \tanh \left( \frac{1}{4}\varpi \sqrt{M}\right) +\coth \left( \frac{1}{4}\sqrt{M}\right) \right) +2\theta }{4\nu }\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(20)
$$\begin{aligned} \phi _{k,4}(x,t)= & \alpha _{k}\left( \hbar -\frac{\sqrt{M\left( G^{2}+H^{2}\right) }-G\sqrt{\theta ^{2}-4\kappa \nu }\cosh \left( \varpi \sqrt{M}\right) }{2\nu G\sinh \left( \varpi \sqrt{M}\right) +H}-2\nu \theta \right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(21)
$$\begin{aligned} \phi _{k,5}(x,t)= & \alpha _{k}\left( \hbar -\frac{\sqrt{M\left( G^{2}+H^{2}\right) }+G\sqrt{M}\cosh \left( \varpi \sqrt{M}\right) }{G\sinh \left( \varpi \sqrt{M}\right) +H}+2\nu \theta \right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(22)
$$\begin{aligned} \phi _{k,6}(x,t)= & \alpha _{k}\left( \hbar +\frac{2\kappa \cosh \left( \frac{1 }{2}\varpi \sqrt{M}\right) }{\sqrt{M}\sinh \left( \frac{1}{2}\varpi \sqrt{M} \right) -\theta \cosh \left( \frac{1}{2}\varpi \sqrt{M}\right) }\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(23)
$$\begin{aligned} \phi _{k,7}(x,t)= & \alpha _{k}\left( \hbar -\frac{2\kappa \sinh \left( \frac{1 }{2}\varpi \sqrt{M}\right) }{\theta \sinh \left( \frac{1}{2}\varpi \sqrt{M} \right) -\sqrt{M}\cosh \left( \frac{1}{2}\varpi \sqrt{M}\right) }\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(24)

and

$$\begin{aligned} \phi _{k,8}(x,t)=\alpha _{k}\left( \hbar +\frac{2\kappa \sinh \left( \varpi \sqrt{M}\right) }{\theta \sinh \left( \varpi \sqrt{A}\right) -\sqrt{M}\cosh \left( \varpi \sqrt{M}\right) +\sqrt{M}}\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(25)

where \(\varpi =(\varpi _{1}x-\varpi _{1}\varrho _{1}t).\)

Case-II: If \(D=4\kappa \nu -\theta ^{2}>0\) and \(\kappa \nu \ne 0,\) then the solutions of Eq. (1) are

$$\begin{aligned} \phi _{k,9}(x,t)= & \alpha _{k}\left( \hbar +\frac{\sqrt{D}\tan \left( \frac{1}{ 2}\varpi \sqrt{D}\right) -\theta }{2\nu }\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(26)
$$\begin{aligned} \phi _{k,10}(x,t)= & \alpha _{k}\left( \hbar -\frac{\sqrt{D}\cot \left( \frac{1 }{2}\varpi \sqrt{D}\right) +\theta }{2\nu }\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(27)
$$\begin{aligned} \phi _{k,11}(x,t)= & \alpha _{k}\left( \hbar +\frac{\sqrt{D}\left( \tan \left( \varpi \sqrt{D}\right) -\sec \left( \varpi \sqrt{D}\right) \right) -\theta }{ 2\nu }\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(28)
$$\begin{aligned} \phi _{k,12}(x,t)= & \alpha _{k}\left( \hbar +\frac{\sqrt{D}\left( \tan \left( \frac{1}{4}\varpi \sqrt{D}\right) -\cot \left( \frac{1}{4}\varpi \sqrt{D} \right) \right) -2\theta }{4\nu }\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(29)
$$\begin{aligned} \phi _{k,13}(x,t)= & \alpha _{k}\left( \hbar +\frac{\sqrt{D\left( G^{2}-H^{2}\right) }-G\sqrt{D}\cos \left( \varpi \sqrt{D}\right) }{2\nu G\sin \left( \xi \sqrt{D}\right) +H}-2\nu \theta \right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(30)
$$\begin{aligned} \phi _{k,14}(x,t)= & \alpha _{k}\left( \hbar +\frac{2\kappa \cos \left( \frac{1 }{2}\sqrt{D}\varpi \right) }{\sqrt{4\kappa \nu -\theta ^{2}}\sin \left( \frac{1}{2}\varpi \sqrt{D}\right) +\theta \cos \left( \frac{1}{2}\varpi \sqrt{D}\right) }\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(31)
$$\begin{aligned} \phi _{k,15}(x,t)= & \alpha _{k}\left( \hbar +\frac{2\kappa \sin \left( \frac{1 }{2}\varpi \sqrt{D}\right) }{\sqrt{D}\cos \left( \frac{1}{2}\varpi \sqrt{D} \right) -\theta \sin \left( \frac{1}{2}\varpi \sqrt{D}\right) }\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(32)

and

$$\begin{aligned} \phi _{k,16}(x,t)=\alpha _{k}\left( \hbar +\frac{2\kappa \sin \left( \varpi \sqrt{D}\right) }{-\theta \sin \left( \varpi \sqrt{D}\right) +\sqrt{D}\cos \left( \varpi \sqrt{D}\right) +\sqrt{D}}\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(33)

where \(\varpi =(\varpi _{1}x-\varpi _{1}\varrho _{1}t).\)

Case-III: If \(\theta =0\) and \(\kappa \nu \ne 0\), then

$$\begin{aligned} \phi _{k,17}(x,t)=\alpha _{k}\left( \hbar -\frac{d\nu }{q(d-\sinh (\nu \kappa \varpi )+\cosh (\nu \kappa \varpi ))}\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}, \end{aligned}$$
(34)

and

$$\begin{aligned} \phi _{k,18}(x,t)=\alpha _{k}\left( \hbar +\frac{\nu (\sinh (\nu \kappa \varpi )+\cosh (\nu \kappa \varpi ))}{\kappa (d+\sinh (\nu \kappa \varpi )+\cosh (\nu \kappa \varpi ))}\right) e^{i\varrho +\lambda \beta (t)-\lambda ^{2}t}. \end{aligned}$$
(35)

Modified auxiliary equation approach

In this section, we used the MAE method to show the stability of our results42. We take the solution of eq.(15) and get the polynomials form as follows,

$$\begin{aligned} \left\{ \begin{array}{ll} \psi _{1}(\varpi )=\alpha _0+\sum _{i=1}^M \left( \alpha _i\omega ^{(z\varpi )i}+\delta _i\omega ^{-(z\varpi )i}\right) , & \\ \psi _{2}(\varpi )=\beta _0+\sum _{i=1}^M \left( \beta _i\omega ^{(z\varpi )i}+\tau _i\omega ^{-(z\varpi )i}\right) , & \\ \psi _{3}(\varpi )=\gamma _0+\sum _{i=1}^M \left( \gamma _i\omega ^{(z\varpi )i}+\sigma _i\omega ^{-(z\varpi )i}\right) , & \end{array}\right. \end{aligned}$$
(36)

where the constants \(\alpha _0\), \(\alpha _i\), \(\beta _0\), \(\beta _i\), \(\gamma _0\), \(\gamma _i\), \(\delta _i\), \(\tau _i\) and \(\sigma _i\) (i=1,2,3,...M) that are found to be later, here \(\omega (\eta )\) is simplify the solution that is given below.

$$\begin{aligned} z'(\varpi )=\frac{1}{\ln (\omega )} \bigg ( \epsilon +\mu \omega ^{z\varpi }+ \chi \omega ^{-z\varpi } \bigg ), \end{aligned}$$
(37)

here, \(\epsilon\), \(\mu\), \(\chi\) and z with \(z>0\) \(z\ne 1\) are arbitrary constants that are determine later. Homogenous balancing principle can be applied to find the value of M in the previous Eq. (15) and we can enter \(M=1\) in Eq. (36)

$$\begin{aligned} \left\{ \begin{array}{ll} \psi _{1}(\varpi )=\alpha _0+ \alpha _1 \omega ^{z\varpi }+\delta _1\omega ^{-z\varpi }, & \\ \psi _{2}(\varpi )=\beta _0+ \beta _1 \omega ^{z\varpi }+\tau _1\omega ^{-z\varpi }, & \\ \psi _{3}(\varpi )=\gamma _0+ \gamma _1 \omega ^{z\varpi }+\sigma _1\omega ^{-z\varpi }, & \end{array} \right. \end{aligned}$$
(38)

Determine the derivatives of Eq. (38) by applying the Eq. (37) and replace in the Eq. (15). After simplifying, collecting the coefficients of the same power of \(\omega ^{(z\varpi )j}\) and \(\omega ^{-(z\varpi )j}\) and set them then equal to zero in all polynomials to gain a system of equations. Apply mathematica to deal with the system of calculation and gain the family of solution as,

Family of solutions:

$$\begin{aligned} \alpha _1= & \frac{2 \alpha _0 \mu }{\epsilon }, \beta _1=\frac{2 \beta _0 \mu }{\epsilon }, \sigma _1=0, \gamma _0=-\frac{1}{2} \sqrt{-4 \alpha _0^2-4 \beta _0^2-\varpi _1^2 \epsilon ^2}, \gamma _1=-\frac{\mu \sqrt{-4 \alpha _0^2-4 \beta _0^2-\varpi _1^2 \epsilon ^2}}{\epsilon },\nonumber \\ \delta _1= & 0, \tau _1=0, \varrho _2=\frac{1}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) .~~ \text{ where } -4 \alpha _0^2-4 \beta _0^2-\varpi _1^2 \epsilon ^2>0. \end{aligned}$$
(39)

Case-I: If \(\epsilon ^2-4 \chi \mu < 0\) and \(\chi \ne 0\), then

$$\begin{aligned} \phi _{1,18}^{\pm }(x,t)= & \left( \frac{\alpha _0 \sqrt{{4 \chi \mu -\epsilon ^2 }} \tan \left( \frac{1}{2} \sqrt{{4 \chi \mu -\epsilon ^2 }} \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{\epsilon }\right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}, \end{aligned}$$
(40)
$$\begin{aligned} \phi _{2,18}^{\pm }(x,t)= & \left( \frac{\beta _0 \sqrt{{4 \chi \mu -\epsilon ^2 }} \tan \left( \frac{1}{2} \sqrt{{4 \chi \mu -\epsilon ^2 }} \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{\epsilon }\right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}, \end{aligned}$$
(41)
$$\begin{aligned} \phi _{3,18}^{\pm }(x,t)= & \left( \frac{\sqrt{{4 \chi \mu -\epsilon ^2}} \sqrt{\varpi _1^2 \left( -\epsilon ^2\right) -4 \left( \alpha _0^2+\beta _0^2\right) } \tan \left( \frac{\sqrt{{4 \chi \mu -\epsilon ^2}}}{2} \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{2 \epsilon }\right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}. \end{aligned}$$
(42)
$$\begin{aligned} \phi _{1,19}^{\pm }(x,t)= & \left( \frac{\alpha _0 \sqrt{{4 \chi \mu -\epsilon ^2}} \cot \left( \frac{1}{2} \sqrt{{4 \chi \mu -\epsilon ^2 }} \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{\epsilon }\right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}, \end{aligned}$$
(43)
$$\begin{aligned} \phi _{2,19}^{\pm }(x,t)= & \left( \frac{\beta _0 \sqrt{{4 \chi \mu -\epsilon ^2 }} \cot \left( \frac{1}{2} \sqrt{{4 \chi \mu -\epsilon ^2}} \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{\epsilon }\right) \nonumber \\ & e^{i\left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}, \end{aligned}$$
(44)
$$\begin{aligned} \phi _{3,19}^{\pm }(x,t)= & \left( \frac{\sqrt{{4 \chi \mu -\epsilon ^2}} \sqrt{\varpi _1^2 \left( -\epsilon ^2\right) -4 \left( \alpha _0^2+\beta _0^2\right) } \cot \left( \frac{\sqrt{{4 \chi \mu -\epsilon ^2 }}}{2} \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{2 \epsilon }\right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}. \end{aligned}$$
(45)

Case-II: If \(\epsilon ^2-4 \chi \mu > 0\) and \(\chi \ne 0\), then

$$\begin{aligned} \phi _{1,20}^{\pm }(x,t)= & \left( \frac{\alpha _0 \sqrt{\epsilon ^2-4 \chi \mu } \tanh \left( \frac{1}{2} \sqrt{\epsilon ^2-4 \chi \mu } \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{\epsilon }\right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}, \end{aligned}$$
(46)
$$\begin{aligned} \phi _{2,20}^{\pm }(x,t)= & \left( \frac{\beta _0 \sqrt{\epsilon ^2-4 \chi \mu } \tanh \left( \frac{1}{2} \sqrt{\epsilon ^2-4 \chi \mu } \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{\epsilon }\right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}, \end{aligned}$$
(47)
$$\begin{aligned} \phi _{3,20}^{\pm }(x,t)= & \left( -\frac{\sqrt{\epsilon ^2-4 \chi \mu } \sqrt{\varpi _1^2 \left( -\epsilon ^2\right) -4 \left( \alpha _0^2+\beta _0^2\right) } \tanh \left( \frac{\sqrt{\epsilon ^2-4 \chi \mu }}{2} \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{2 \epsilon }\right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}. \end{aligned}$$
(48)
$$\begin{aligned} \phi _{1,21}^{\pm }(x,t)= & \left( \frac{\alpha _0 \sqrt{\epsilon ^2-4 \chi \mu } \coth \left( \frac{1}{2} \sqrt{\epsilon ^2-4 \chi \mu } \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{\epsilon }\right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}, \end{aligned}$$
(49)
$$\begin{aligned} \phi _{2,21}^{\pm }(x,t)= & \left( \frac{\beta _0 \sqrt{\epsilon ^2-4 \chi \mu } \coth \left( \frac{1}{2} \sqrt{\epsilon ^2-4 \chi \mu } \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{\epsilon } \right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}, \end{aligned}$$
(50)
$$\begin{aligned} \phi _{3,21}^{\pm }(x,t)= & \left( -\frac{\sqrt{\epsilon ^2-4 \chi \mu } \sqrt{\varpi _1^2 \left( -\epsilon ^2\right) -4 \left( \alpha _0^2+\beta _0^2\right) } \coth \left( \frac{\sqrt{\mu ^2-4 \chi \epsilon }}{2} \left( x \varpi _1-\varrho _1 t \varpi _1\right) \right) }{2 \epsilon }\right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}. \end{aligned}$$
(51)

Case-III: If \(\epsilon ^2-4 \chi \mu = 0\) and \(\chi \ne 0\), then

$$\begin{aligned} \phi _{1,22}^{\pm }(x,t)= & -\left( \frac{2 \alpha _0}{\epsilon \left( x \varpi _1-\varrho _1 t \varpi _1\right) }\right) e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}, \end{aligned}$$
(52)
$$\begin{aligned} \phi _{2,22}^{\pm }(x,t)= & -\left( \frac{2 \beta _0}{\epsilon \left( x \varpi _1-\varrho _1 t \varpi _1\right) }\right) e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}, \end{aligned}$$
(53)
$$\begin{aligned} \phi _{3,22}^{\pm }(x,t)= & \left( \frac{\sqrt{\varpi _1^2 \left( -\epsilon ^2\right) -4 \left( \alpha _0^2+\beta _0^2\right) }}{\epsilon \left( x \varpi _1-\varrho _1 t \varpi _1\right) } \right) \nonumber \\ & e^{i \left( \frac{t}{4} \left( 4 \mu \chi \varpi _1^2-2 \varrho _1^2-\varpi _1^2 \epsilon ^2\right) +\varrho _1 x\right) +\lambda ^{2}t-\lambda \beta (t)}. \end{aligned}$$
(54)

Physical representation of optical solitons

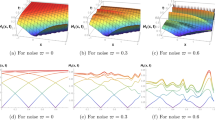
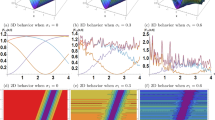
Finally, in this section, we will be analyzing the graphical representation of solutions along with a few effects of noise on the solutions. Out of all those optical solitons some of the equations are successfully solved by using the generalized Riccati equation mapping method. These solutions are expressed in dark, complex dark-bright and combined form solitons and solitary wave solution. These optical soliton have given application in the domain of optical fibers. According to the previous section, the propagation of an optical pulse in a birefringent optical fiber is characterized by the three nonlinear complex models. In some cases, these solutions are illustrate by the physical phenomena of these solutions are provided here. Despite the fact that these solitons enjoy inherent stability, they can undergo a certain fragmentation or decay in the presence of a sufficient number of perturbations. To show the physical behavior we draw some solutions in the form of 3D, 2D and corresponding contour form for the different values of parameters. Figure 1 is drawn for the solutions \(\phi _{1,1}(x,t)\) that will provided us the dark soliton solution while, Fig. 2 provided us the solitary wave solution for \(\phi _{1,14}(x,t)\). To control this randomness we take into account the Wiener process and construct their solution. The effects of noise are clearly shown in the figures that how the noise is affected our solutions. When we take \(\lambda =0\) into account moreover we increase the values of \(\lambda =0.3,0.7\) and check that how the noise is affected our solutions. If we choose \(\lambda =0\) then these solutions have no noise effect in their results. Noise greatly flattens the surface, and after a few brief minor transits, its strength increases. For the better understanding of the discussed solitary wave solutions, it is necessary to give the additional analysis of their graphical characteristics. Although amplitude plots give information about the wave shape, plotting density that is directly proportional to the square of amplitude is more useful in optics. Intensity plots were illustrated to show the energy profile of the soliton and provide a better view of the output power as well as the stability over time and space coordinates. This type of analysis provides a better possibility to identify the essential soliton properties, influencing factors, such as the intensity and width of peaks, and effect of external perturbation. Additional intensity plots together with the amplitude plots would give the overlying information on the physical specifications of the soliton, which could explain why such plots are vital complements to amplitude plots. Based on this fact that the intensity is directly related to the energy distribution that can be measured within the optical systems, this approach will provide a clearer view on other characteristics of the soliton, including the peak intensity and spatial distribution. These additions will give more details of the solitary wave behaviour and make the results support the proposed solutions more compelling. Solitons and solitary waves in the presence of noise have many potential application in contemporary optics technologies. Solitons are used as information vectors in optical systems owing to their capacity to preserve their shape and speed after migrating over large distance and resisting noise and dispersion. This property is indeed very essential in overall fiber-optic telecommunications particularly in the large distance link where repeater noises etc., are disturbances. Soliton based transmission systems require fewer repeaters and also improve the quality of the received signal. Further, the spatial soliton, found in photorefractive and nonlinear media, make it possible to develop the optical waveguides, switch and the reconfigurable photonic circuits. Solitons are immune to noise and therefore likely to be put to use in quantum communication where coherence is imperative under a noisy environment. These applications highlight the needs for understanding the effects of noise, especially the Brownian motion on the soliton stability and their performance in the real optical systems. Figure 2a–e display 3D-shape of solution \(\left| \phi _{1,13}\right|\) in Eq (30) with\(\ x\in [-4,4]\), \(t\in [0,3]\) and \(\lambda =0,\ 0.1,\ 0.3,\ 1,\ 2\) (2f) shows 2D-shape of Eq. (30) with different \(\lambda .\)

Figure 1a–e display 3D-shape of solution \(\left| \phi _{1,1}\right|\) in Eq (18) with\(\ x\in [-4,4]\), \(t\in [0,3]\) and \(\lambda =0,\ 0.1,\ 0.3,\ 1,\ 2\) Fig. 1f shows 2D-shape of Eq. (18).

Fig. 1
figure 1

Different effects of noise for the solution \(\left| \phi _{1,1}\right|\) when the constants are chooses as \(\kappa =0.8, \alpha _1=0.9, \beta _1=1.1, \gamma _1=1, \gamma _0=2.7, \rho _1=0.7, \omega _1=0.1\).

Full size image
Fig. 2
figure 2

Different effects of noise for the solution \(\left| \phi _{1,13}\right|\) when the constants are chooses as \(\kappa =1.8, \alpha _1=1.9, \beta _1=0.8, \gamma _1=1, \gamma _0=0.7, G=2, \theta =0.1, H=1, \nu =1.2, \rho _1=0.7, \omega _1=0.1\).

Full size image

Conclusions

In this manuscript we studied the three component nonlinear stochastic Schr ödinger equation analytically under the Stratonovich sense. The Birefringent optical fibers three component nonlinear stochastic Schrö dinger equation, the noise perturb the optical solitons in different ways such as, noise in the position and phase areas as well as noises in the shape and amplitude of solitons and lastly it alters the sourroundings in which solitons interact. The generalized Riccati equation mapping method is adoped to obtained the different abundant families of solitons. These solitons are explored in the dark, complex dark-bright, combined form and periodic form solutions as well. Mainly, we are focused on the effects of noise on the solitons. We have added modified auxiliary equation method to compare the results. This method is provided us only hyperbolic, trigonometric and rational solutions. So, our results are very novel for the applications of the underlying model when we take noise into account. Finally, we plot some solutions and show their behavior in 3D, 2D and corresponding contours. It is crucial for the development of fiber-optic communication technologies and ensuring the ability to keep solitons well transmitted over longer distances. Lastly, the impact of noise on the exact solutions of the three component nonlinear Schrödinger equation was illustrated using the MATHEMATICA11.1 program. We might look into additive fractional derivatives in the three-component nonlinear Schrödinger equation in the future.