Introduction

In the rapidly advancing industrial landscape, the demand for high-performance materials has significantly increased. Composite materials, characterized by their unique ability to combine properties of different constituents, have emerged as vital candidates in sectors such as aerospace, automotive, marine, and biomedical applications1. Their tailored properties, such as enhanced strength-to-weight ratio, improved thermal stability, and corrosion resistance, make them indispensable for modern industrial needs. These features enable industries to achieve operational efficiency, environmental sustainability, and economic viability2,3.

Fabrication techniques play a pivotal role in determining the properties and performance of composites. Among the various fabrication methods, solid-state techniques have gained prominence over liquid-state techniques4. While liquid-state methods, such as ultrasonic and magnetic stirring, have demonstrated improvements in the dispersion of reinforcements, their high-temperature processing often results in the formation of undesirable intermetallic compounds, adversely affecting the composite’s mechanical properties5. In contrast, solid-state techniques, particularly advanced sintering methods like microwave sintering and spark plasma sintering, offer significant advantages6. Microwave sintering enables uniform heating, reduced processing times, and energy efficiency, while spark plasma sintering allows rapid consolidation under lower temperatures with precise control over microstructural evolution. These unique features mitigate thermal mismatches and enhance the overall mechanical performance of composites7,8.

To meet the growing demand for high-performance materials in manufacturing sectors, it is imperative to accurately predict the mechanical responses of composites, which exhibit complex behavior due to the interplay of multiple factors9. In this context, machine learning (ML) techniques have garnered substantial attention from researchers and industry professionals. ML offers the capability to model non-linear relationships, analyze vast datasets, and provide accurate predictions for mechanical responses, thereby accelerating the design and optimization of composite materials10,11.

Machine learning (ML) has emerged as a powerful tool for predicting and optimizing the mechanical properties of composite materials, offering significant advantages over traditional experimental and computational methods9,12. The integration of machine learning (ML) techniques in materials science has revolutionized the way composite materials are analyzed and optimized. ML models offer a data-driven approach to predicting mechanical and tribological properties, reducing reliance on costly and time-intensive experimental trials. Various supervised learning techniques, such as Artificial Neural Networks (ANN), Support Vector Machines (SVM), Decision Trees (DT), and Random Forest (RF), have been extensively employed for predicting properties such as tensile strength, hardness, wear resistance, and fracture toughness in different composite systems. Deep learning methods, such as Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs), have been successfully employed in this field. Yang et al.13 utilized CNNs to predict the elastic properties of 3D woven composites from their microstructure images, while Zhu et al. demonstrated the effectiveness of RNNs in forecasting the stress–strain behavior of sand subjected to monotonic triaxial compression loading14,15. Regression-based models, particularly Support Vector Machines (SVMs), have also been applied to classify composite materials based on their microstructure and mechanical performance. Abuomar et al. used SVMs to categorize vapor-grown carbon nanofibre/vinyl ester nanocomposites into ten different classes based on their mechanical properties16. Feature extraction and dimensionality reduction techniques, such as Principal Component Analysis (PCA), have been widely used to reduce the complexity of microstructural data while retaining essential features17. Pathan et al.18 employed principal component regression with polynomial basis functions to predict the elastic–plastic response of composite systems with various inclusion shapes. In the realm of unidirectional fibre composites, Ren et al.19 presented a data-driven approach using supervised machine learning to predict the macroscopic stiffness and yield strength of composites loaded in the transverse plane. Their method combined image analysis of material microstructures with knowledge of constituent material properties, achieving accurate predictions without performing physical calculations. For polymer composites, Qi et al. highlighted the potential of ML in improving design and optimization, demonstrating the ability of ML techniques to predict the characteristics of novel composite materials based on their microstructures. Despite these advancements, several challenges remain in the field, including limited data availability, the need for multi-scale modeling, and improving the interpretability of ML models. Wang et al. proposed data augmentation techniques to address the data scarcity issue, while Liu et al. explored multi-scale modeling of composite materials. Zhang et al. investigated feature importance analysis techniques to enhance model interpretability, and Chen et al. demonstrated the effectiveness of hybrid approaches combining ML with physics-based models20,21,22. As research in this field continues to advance, ML techniques are expected to play an increasingly important role in the design, optimization, and understanding of composite materials, potentially revolutionizing the field of materials science and engineering.

Moreover, advanced ML techniques, such as XGBoost, Deep Learning (DL), and Convolutional Neural Networks (CNNs), have been explored for more complex materials, where feature importance analysis has played a significant role in understanding the contribution of various fabrication parameters to composite performance. Unlike traditional regression-based approaches, which assume a linear correlation between variables, ML models can capture nonlinear relationships, making them highly suitable for predicting composite behavior under varying conditions.

Kaoline has gained significant attention as a reinforcement material in aluminum composites due to its unique properties that cater to the needs of the automobile and industrial sectors. Its incorporation into aluminum alloys addresses critical performance metrics such as achieving a low wear rate and a high coefficient of friction (COF), essential for enhancing the durability and efficiency of components in demanding applications23,24.

Although several studies have focused on aluminum matrix composites reinforced with SiC, B₄C, and Al₂O₃, limited research has explored the use of Kaolin as a reinforcement in microwave-sintered aluminum composites. Kaolin, being a naturally abundant ceramic material, offers potential benefits in enhancing both mechanical and tribological properties. Furthermore, conventional studies predominantly rely on experimental characterization, whereas this work integrates machine learning (ML) methodologies to predict and optimize wear behavior and COF. The application of supervised ML models, including Support Vector Machines (SVM), Random Forest (RF), K-Nearest Neighbors (KNN), Artificial Neural Networks (ANN), and XGBoost, provides a robust framework for accurately modeling tribological performance. Additionally, a feature importance analysis has been conducted to determine the key process parameters influencing wear rate and COF, ensuring a data-driven approach to composite design and optimization. The novelty of this study lies in the combination of microwave sintering and ML-based predictive modeling, offering an innovative strategy for improving the design and performance of Al-Kaolin composites.

In this view, the present work focuses on the predictive modeling of the wear rate and COF of the AA7075/kaoline composite fabricated through a novel hybrid microwave sintering technique. The study aims to combine the advanced fabrication capabilities of microwave sintering with supervised machine learning methodologies to provide accurate predictions of mechanical responses, thereby contributing to the development of high-performance materials tailored for industrial applications.

Materials and methods

The kaolin clay was collected from the exposed areas of the Deopani deposit in Assam, situated between latitudes 26°14′27ʺ and 26°14′39ʺ, and longitudes at 93°45′54ʺ and 93°46′05ʺ. The collection was carried out by the State Directorate of Geology and Mining, Government of Assam. A representative sample of the clay was prepared in accordance with the Indian standard mixing method25. Initially, the natural kaolin clay mineral was air-dried, crushed, and ground into a fine powder using a mortar and pestle, followed by sieving through a 75 µm (∼583 mesh) sieve. The resulting powder underwent wet beneficiation using deionized water to remove impurities such as metallic oxides, organic matter, soluble salts, quartz, grits, and coarse particles, thereby refining its physical and chemical properties26,27. This process involved vigorously stirring 100 g of kaolin clay powder in 1000 mL of deionized water at room temperature for 24 h using a magnetic stirrer. The suspension was left to settle, forming a solid clay cake, which was subsequently filtered and washed three times with deionized water Deionized water with a resistivity of approximately 10 MΩ·cm at 25 °C was used for the kaolin clay purification process. The final product was air-dried overnight at 60 °C in an oven, then powdered, sieved, and stored for future use.

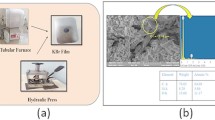
Pure aluminium powder (99% purity) and processed kaolin clay are utilized as a matrix and reinforcement material in this study. To ensure that the reinforcement is evenly distributed and diffused throughout the matrix material, the raw powder was combined with a ball-to-powder ratio of 10:1. Stearic acid (1.5 wt%) was utilized as a process control agent and the ball milling was performed at ambient temperature. The blended composite powders were uniaxially pressed by applying a 580 MPa pressure with a dwell time of 5 min. The compacted composite was heated to 530 ± 5 °C through the generated electromagnetic field inside the microwave sintering furnace (1.4 kW and 2.45 GHz) for 30 min at a heating rate of 10 °C/min in a protective argon gas atmosphere to prevent from oxidation. After that, it is allowed to cool down to room temperature in a controlled environment. An infrared pyrometer (Make Fluke 572) accurately measured sintered composite temperature. The SiC susceptor was employed to raise the cold compacts to 400 °C, facilitating the direct coupling of microwaves to the aluminum matrix to commence the heat initiation inside the composite. During microwave sintering, a SiC susceptor was utilized to enhance heat absorption and ensure uniform temperature distribution. The dimensions of the SiC susceptor used in this study were 50 mm in diameter and 10 mm in thickness. SiC is well known for its high thermal conductivity (~ 120 W/m K), low dielectric loss factor (~ 0.02 at 2.45 GHz), and excellent thermal stability, making it an ideal choice for microwave-assisted sintering. The susceptor facilitated rapid and uniform heating, minimizing thermal gradients that could lead to differential expansion and internal stresses in the composite material. The cold compacted specimens were mounted at the canter of the susceptor cavity and sintering was carried out in the multimode cavity. The composites were prepared by reinforcing 2wt%, 4wt%, and 6wt% kaolin clay in the aluminium composite.

Characterization techniques

The elemental constituents present in the as-received powders and the Al-Kaolin composites were identified through X-ray Diffraction studies performed on the Bruker DIFFRAC Plus diffractometer at a scanning of 1°/min between the scanning angle 10°–90°.

The morphology of Al and Kaolin powders, reinforcement dispersions, and elemental composition of composites were analyzed using scanning electron microscopy (SEM) and integrated with Energy Dispersive Spectroscopy EDS. The Archimedes principle was used to measure the sintered density of the Al-Kaolin composite. The Rockwell hardness of the fabricated composite was analyzed as per ASTM E18-15 standards28,29. The parameters used for the Rockwell measurement are presented in Table 1. The wear test was performed on the TR-201 CL, Ducom wear testing machine for the 12 mm diameter composite specimens. The polished Al-Kaolin composite was pressed against a rotating EN32 steel disc having 120 mm diameter and 10 mm thickness (hardness 65 HRC, surface roughness of 0.3 µm) at 450 rpm, with a constant sliding distance of 1000 m maintained during the wear test. The wear rate of the specimens was calculated using the mass loss approach, providing a quantifiable estimate of the loss of material due to the wear test. The wear rate is calculated using the Eq. (1)

$${\text{Wear}}\;{\text{Rate}} = \frac{Volume\;Loss\left( V \right)}{{Applied\;Load\left( F \right) \times Sliding\;Distance\left( D \right)}}$$
(1)

where V is the wear volume (mm3), F is the applied load (N) and D is the Sliding Distance (m).

Table 1 Optimized hyperparameters obtained through gridsearchCV techniques.
Full size table

The volume loss was calculated using the following Eq. (2)

$${\text{V}} = \frac{\Delta m}{\rho }$$
(2)

where \(\Delta m\) = Initial mass–Final mass (in gr).

The volume loss was estimated by dividing the mass loss by the density (g/mm3) of the composite.

Scale

Indenter

Load

Dwell time

Temp (°C)

B

1/16 inch

100 kgf

20 s

24 °C

Results and discussion

XRD and SEM analysis of the as-received powders and synthesized composites

Figure 1a, c depict the SEM images for the as-received Al and extracted Kaolin powders and Fig. 1b, d depict the XRD analysis of the received powders. The aluminium powders had an irregular spherical shape, and the Kaolin particles could appear as irregular flake-shaped structures with sharp corners. The particle sizes of the aluminum and kaolin were determined to be 30 microns and 40 microns, respectively, using ImageJ software (Version: 1.54 k, URL: https://imagej.net/ij/). The average particle size was calculated by considering the average of fifteen measurements for both the Al and kaolin particles. The XRD analysis of the aluminum and kaolin powders confirmed the presence of aluminum peaks at diffraction angles (2θ) 35°, 44°, 65.6°, and 78.3°. Additionally, the presence of aluminum oxide, magnesium oxide, silicon oxide, and titanium oxide indicated the successful identification of kaolin in the extracted reinforcement powder.

Fig. 1
figure 1

SEM and XRD of (a, b) received aluminium, (c, d) extracted kaolin powders.

Full size image

The XRD pattern for the microwave-sintered Al-Kaolin composites is shown in Fig. 2. The Al-2 wt%Kaolin and Al-4 wt%Kaolin composites show the presence of aluminium oxide ((110) plane), titanium oxide ((220) plane), silicon dioxide ((002) plane) potassium oxide ((311) plane), and magnesium oxide ((111) plane). However, the Al2C4 (JCPDS-96-154-0875) secondary phase was observed for the Al-6 wt%Kaolin composite. The Secondary phase formation at the composite interface significantly impacts the mechanical characteristics. During the sintering process, surplus free energy activates chemical reactions between the matrix and reinforcements. The degree of reactivity varies based on exposure time and wt% of the kaolin reinforcement30.

Fig. 2
figure 2

XRD pattern for the microwave-sintered Al-Kaolin composites.

Full size image

The SEM images for the Al-2 wt%kaolin, Al-4 wt%kaolin, and Al-6 wt%kaolin composites are shown in Fig. 3a, b, c. The kaolin particles were observed to be evenly dispersed in the aluminium materials for the 2 wt% and 4 wt% kaolin reinforcement. The addition of the kaolin of more than 4 wt% generates the Al2C4 clusters as depicted in Figure (c) and the corresponding agglomerated peak and confirmed in the XRD pattern of Figure (c) and the EDS mapping of the clustered site of the Al-6 wt%kaolin composite. The inherent properties of the different thermal expansions of the kaolin and aluminium particles accelerate the variable expansions during the microwave sintering and are susceptible to cluster formation for the Al-6 wt%kaolin composite, which in turn deteriorates the composite hardness31,32. The corresponding clusters in the Al-6 wt%kaolin composite were identified through XRD analysis and the Al2C4 element was confirmed for the Al-4 wt%kaolin composite.

Fig. 3
figure 3

FESEM and EDX spectra for the (a) Al-2 wt%Kaolin, (b) Al-4 wt%Kaolin, and (c) Al-6 wt%Kaolin.

Full size image

Hardness study for the Al-kaolin composite

The Rockwell hardness of the polished Al-kaolin composite is measured by applying a 100 kgf load. The average of six hardness readings was taken and the average readings were reported in the Fig. 4. The hardness of the composite increases from 78 RHC for the unreinforced kaolin to 96 RHC for 4wt%kaolin reinforcement, signifying a 23.07% harder than the unreinforced aluminium. This enhancement in the hardness was due to the uniform kaolin particle dispersion and the presence of the ceramic aluminium oxide and silicon oxide particles in the kaolin clay. In addition to this, the magnesium content in the kaolin improves the wettability among the aluminium and reinforced kaolin particles. The decrement in the hardness of the Al-6 wt%kaolin from 96 to 83 RHC due to the presence of the agglomerations which makes the generation of the triaxial stresses prone to the material to make indentation at lower applied loads.

Fig. 4
figure 4

Hardness of the microwave sintered (a) Al-2 wt%Kaolin, (b) Al-4 wt%Kaolin and (c) Al-6 wt%Kaolin composites.

Full size image

Generally, an increase in hardness leads to a lower wear rate due to improved resistance against plastic deformation and material removal. However, in the present study, a notable drop in hardness at 6% kaolin reinforcement was observed, which correlates with an increase in wear rate. The decline in hardness at 6% kaolin can be attributed to particle agglomeration and increased porosity. As the reinforcement content increases beyond an optimal level, particles tend to cluster together, leading to non-uniform dispersion and localized weak zones within the matrix. These regions become stress concentrators, promoting crack initiation under loading conditions. Additionally, a higher reinforcement fraction can lead to increased porosity, reducing the composite’s overall density and load-bearing capacity, which negatively impacts hardness.

Methodology and performance evaluation of machine learning models

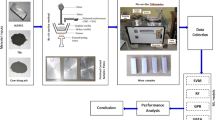
To predict the wear rate and coefficient of friction (COF) for an aluminium-Kaoline (Al/Kaoline) composite, a structured approach was taken to collect and process data. The dataset used in this study consists of 193 data points, each characterized by four input parameters: Reinforcement percentage (wt%), Angle, Pressure, and Standard of Distance (Sod), and two output parameters: Wear Rate (10−4 mm3/Nm) and Coefficient of Friction (COF). To analyze the distribution and relationships among the features, a pairplot was generated, revealing correlations between input variables and output responses. Additionally, a hexbin plot was included to illustrate the density of data distribution across different parameter ranges. To ensure high-quality data for machine learning predictions, outlier detection and removal were performed using the Z-score method. Data points with |Z|> 3 were identified as outliers and removed to prevent skewed model predictions. After outlier removal, the dataset retained 193 data points, ensuring a robust training set without extreme values. For faster model convergence and improved numerical stability, Min–Max scaling was applied to normalize the feature values between 0 and 1. This transformation ensures that all input features contribute equally during the training process, preventing dominance by features with larger numerical ranges. The dataset was systematically split into training (80%) and testing (20%) subsets, maintaining a balanced representation of the feature space.

In machine learning, hyperparameters play a major role in determining model performance. To optimize these parameters, a GridSearchCV approach was applied, allowing for systematic evaluation of parameter combinations to maximize model accuracy. With the optimized parameters, various machine learning models were trained, tested, and validated33,34.

Metric scores, such as mean absolute error, mean squared error, and coefficient of determination (R2), are essential for understanding and comparing model performance. These scores help assess model accuracy, consistency, and generalization ability on unseen data. By evaluating metrics across different models, we gain insights into each model’s strengths and limitations, enabling us to select the most reliable model for predicting wear rate and COF in Al/Kaoline composites. These metrics serve as objective indicators, guiding us to improve model accuracy and ensure practical applicability in industrial settings35,36.

To better understand the data relationships and distribution, pairplots and hexbins were employed. Pairplots, shown in Figs. 5 and 6, provide a multi-dimensional view of variable interactions within the dataset. This visualization helps highlight trends and correlations between input variables (e.g., reinforcement content, angle, pressure) and output parameters (wear rate and COF). It also helps in identifying any patterns that may impact model predictions. Starting with Wear Rate, it is evident that Reinforcement (%) plays a critical role. As the percentage of reinforcement increases, the Wear Rate decreases significantly. This can be attributed to the enhanced hardness and load-bearing capacity provided by the reinforcing particles, which resist material removal during sliding. Conversely, increasing Pressure leads to a noticeable rise in Wear Rate. This is expected as higher pressures intensify the contact forces, promoting material deformation and wear through mechanisms such as abrasive and adhesive wear. The variation of Wear Rate with Sod (sliding distance or related parameter) reveals a slight increasing trend. This could be due to the progressive material degradation or changes in surface interactions over longer distances. Interestingly, the Wear Rate shows minimal dependence on Angle, suggesting that this parameter does not significantly affect the wear behavior under the studied conditions.

Fig. 5
figure 5

Pairplot between variables with hue as wear rate.

Full size image
Fig. 6
figure 6

Pairplot between variables with hue as Coefficient of Friction (COF).

Full size image

For the COF, a similar trend is observed with Reinforcement (%), where an increase in reinforcement results in a reduction of the COF. The hard reinforcement particles create a smoother sliding interface and reduce direct metal-to-metal contact, thereby minimizing friction. However, unlike Wear Rate, the influence of Pressure on the COF is less pronounced, though a slight increase is observed. This could be due to increased material adhesion or changes in contact mechanics at higher pressures. The effect of Sod on COF follows a similar trend to Wear Rate, with a minor increase observed as Sod increases, potentially due to dynamic effects or surface energy changes over extended interactions. Like with Wear Rate, Angle exhibits negligible influence on COF, indicating that the tribological properties are largely unaffected by this parameter in the given experimental setup.

Hexbin plots, illustrated in Figs. 7 and 8, were used to display the density of data points. By binning data into hexagonal cells, these plots give a clear picture of data concentration in different regions, revealing areas where data points are densely packed or sparse. Hexbins are especially useful for identifying clusters and understanding the overall distribution in continuous datasets, helping to visually validate the effectiveness of the preprocessing steps applied to remove outliers and ensure data consistency37,38.

Fig. 7
figure 7

Hex bins representing the density of data points between input parameters versus wear rate.

Full size image
Fig. 8
figure 8

Hex bins representing the density of data points between input parameters versus Coefficient of Friction (COF).

Full size image

The selection of machine learning models in this study was based on their ability to handle nonlinear relationships, effectively process small-to-moderate dataset sizes, and provide reliable predictive performance. Five models—Support Vector Machine (SVM), Random Forest (RF), XGBoost, K-Nearest Neighbors (KNN), and Artificial Neural Networks (ANN)—were chosen due to their proven applicability in predicting material properties. SVM was selected for its capability to map nonlinear data into higher-dimensional spaces using kernel functions, making it suitable for small datasets with complex relationships. RF, a widely used ensemble learning technique, was included due to its ability to reduce overfitting and improve predictive accuracy by averaging multiple decision trees. XGBoost, an advanced gradient boosting method, was considered for its superior accuracy, computational efficiency, and ability to reduce both variance and bias, making it one of the most robust models for structured data. KNN was evaluated due to its ability to capture local patterns in the dataset, which is useful when feature interactions play a crucial role in determining composite properties. Lastly, ANN was included to explore the potential of deep learning-based approaches in modeling the nonlinear mechanical behavior of composites. While deep learning models such as Deep Neural Networks (DNNs) and Convolutional Neural Networks (CNNs) have demonstrated significant advancements in predictive modeling, they were not considered in this study due to the limited dataset size (193 data points). Deep learning models typically require many training samples to prevent overfitting and achieve optimal performance. Given the constraints of the available data, traditional ML models were more suitable for generating accurate and reliable predictions.

To optimize the performance of the selected models, hyperparameter tuning was conducted using GridSearchCV with fivefold cross-validation. This approach systematically searched for the best hyperparameter combinations, ensuring that the models were trained and validated on different subsets of the dataset, reducing the risk of overfitting. The cross-validation method allowed for a more generalized performance evaluation, ensuring that the predictive models could be effectively applied to unseen data. By implementing this structured approach, the study enhances the reliability and robustness of machine learning-based predictive modeling for composite materials.

To ensure efficient convergence during training, scaling was applied, which normalized the feature space and facilitated quicker convergence of each model. Hyperparameter optimization is key to maximizing model accuracy. GridSearchCV was employed to tune model hyperparameters systematically by searching across specified parameter values. This approach ensures each model is optimized for the dataset at hand. The optimized hyperparameters for each model are presented in Table 1, showcasing the selected values that achieved the highest performance in predictive accuracy. To evaluate the predictive performance of the machine learning models used in this study, three key metrics—coefficient of determination (R2), mean absolute error (MAE), and root mean squared error (RMSE)—were selected. Each of these metrics provides unique insights into the model’s accuracy and generalization ability. R2 was chosen as it quantifies the proportion of variance in the experimental data that is explained by the model. A value close to 1.0 indicates a strong correlation between predicted and actual values, demonstrating the model’s ability to capture data trends effectively. However, R2 alone does not indicate the magnitude of errors in predictions, which necessitates the inclusion of additional error-based metrics.

MAE was used to measure the average absolute differences between predicted and actual values. This metric provides an intuitive understanding of prediction accuracy by expressing the error in the same units as the target variable, making it straightforward to interpret. Since MAE treats all errors equally, it offers a balanced measure of overall prediction deviation. However, it does not heavily penalize larger deviations, which can be crucial in wear rate predictions where extreme values may occur.

To address this, RMSE was selected as it places greater emphasis on larger errors by squaring the deviations before averaging. This ensures that models with occasional high-magnitude errors are penalized more significantly, making RMSE a more sensitive indicator of prediction robustness. Given that tribological properties such as wear rate and coefficient of friction (COF) can exhibit nonlinear variations and extreme values, RMSE helps assess how well the model performs under such conditions. By employing a combination of R2, MAE, and RMSE, the study ensures a comprehensive evaluation of the machine learning models, balancing both goodness of fit and prediction error magnitude, thus improving confidence in the model’s predictive reliability. These metrics, displayed in Table 2, help illustrate the relative strengths of each model in capturing the wear rate and COF patterns within the data.

Table 2 Metrics of different ML models used in the present study.
Full size table

In later sections, there is a discussion regarding each model’s performance based on these metrics, identifying the model with the best generalization ability on the dataset. The discussion will also cover possible reasons for each model’s behavior with the present data, addressing both advantages and limitations. Some models may excel in minimizing error (MAE, RMSE), while others may better capture overall variance (R2), leading to different practical implications in predictive reliability.

Support vector machine (SVM)

The SVM model’s performance in predicting the wear rate and coefficient of friction (COF) for the Al/Kaoline composite was comprehensively analyzed using both regression curves and residual diagnostics, as well as key metrics including R-squared, Mean Absolute Error (MAE), and Root Mean Squared Error (RMSE). The regression plots in Fig. 9 display a strong linear relationship between actual and predicted values, with the majority of data points clustering closely along the regression line, especially for wear rate. This visual alignment reflects high predictive accuracy, further supported by the R-squared values of 0.9371 for wear rate and 0.7262 for COF. These values suggest that the SVM model successfully captured approximately 93.71% of the variance in wear rate and 72.62% of the variance in COF, with wear rate predictions showing a notably higher explanatory power.

Fig. 9
figure 9

Regression curves in SVM model for wear rate and coefficient of friction.

Full size image

The MAE and RMSE values further validate the SVM model’s predictive performance. For wear rate, MAE was 0.1623 and RMSE was 0.2408, while for COF, MAE was 0.0405 and RMSE was 0.0502. These low error metrics indicate a strong predictive fit, with wear rate predictions showing slightly higher error values, possibly due to a broader data range or more subtle influencing factors in the wear data. RMSE, which penalizes larger deviations, highlights that significant prediction errors were minimized, demonstrating the model’s effectiveness in providing reliable results for both wear rate and COF.

In Fig. 10, residual diagnostics reveal additional insights into the model’s reliability and behavior. The residuals versus predicted plots for both wear rate and COF show a random scatter around the zero line, indicating that the SVM model effectively captured the data structure without introducing systematic biases. The autocorrelation plots show minimal correlation across lags, suggesting independence in the residuals, while the QQ plots and residual histograms for both properties confirm an approximate normal distribution, with residuals symmetrically distributed around zero. This normality and lack of autocorrelation are indicative of a well-fitted model that generalized well on the dataset without overfitting.

Fig. 10
figure 10

Residual diagnostics plots of SVM model.

Full size image

Overall, the combination of visual and quantitative analyses in Figs. 9 and 10, along with the performance metrics, underscores the SVM model’s effectiveness in accurately predicting the wear rate and COF of the Al/Kaoline composite. The alignment of predicted versus actual values, low MAE and RMSE values, and favorable residual behavior affirm that the optimized SVM model provides reliable, unbiased predictions, making it suitable for applications in materials science where accurate prediction of material properties is critical.

Random forest (RF)

The Random Forest model’s performance in predicting the wear rate and coefficient of friction (COF) for the Al/Kaoline composite is effectively demonstrated through both its regression metrics and diagnostic plots, as illustrated in Figs. 11 and 12. The regression curves in Fig. 11 show a strong alignment between actual and predicted values, indicating high predictive accuracy for both wear rate and COF. The R-squared values for the Random Forest model were 0.9006 for wear rate and 0.9020 for COF, suggesting that the model successfully explained 90.06% of the variance in wear rate and 90.20% of the variance in COF. This high explanatory power reflects the model’s capacity to capture complex relationships within the data, achieving consistent accuracy across both target variables.

Fig. 11
figure 11

Regression curves in random forest model for wear rate and coefficient of friction.

Full size image
Fig. 12
figure 12

Residual diagnostics plots of random forest model.

Full size image

The Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE) values further validate the Random Forest model’s reliability. For wear rate, the MAE was 0.2328 and the RMSE was 0.3027, while for COF, the MAE was 0.0231 and the RMSE was 0.0300. These low error values demonstrate that the Random Forest model effectively minimized prediction errors, with particularly low values for COF. This discrepancy in error magnitudes between wear rate and COF could be due to differences in data distribution or complexity, but the model’s low RMSE values indicate that even larger deviations were well-controlled, reinforcing its robustness in predicting both properties.

The residual diagnostics in Fig. 12 provide further insights into the Random Forest model’s performance. The residuals versus predicted plots show a random scatter around the zero line, suggesting that the model captured the underlying patterns accurately without introducing systematic biases. The autocorrelation plots exhibit minimal correlation across lags, indicating that the residuals are independent. Additionally, the QQ plots and residual histograms reveal that the residuals approximate a normal distribution, with symmetric spread around zero, further confirming that the Random Forest model provides an unbiased fit.

In summary, the Random Forest model’s performance metrics, combined with the visual analyses in Figs. 11 and 12, highlight its effectiveness in predicting both wear rate and COF. The high R-squared values, low MAE and RMSE, and favorable residual distribution all indicate that the optimized Random Forest model provides accurate and reliable predictions, making it a strong choice for modeling wear behavior in Al/Kaoline composites.

XG boost

The XGBoost model demonstrated exceptional performance in predicting the wear rate and coefficient of friction (COF) for the Al/Kaoline composite, as illustrated in Figs. 13 and 14. The regression curves in Fig. 9 reveal a strong agreement between actual and predicted values, with data points clustering closely around the regression line for both wear rate and COF. The narrow confidence bands further emphasize the precision of the model. The R-squared values of 0.9433 for wear rate and 0.9462 for COF indicate that the XGBoost model successfully captured 94.33% and 94.62% of the variance in the respective target variables, showcasing its ability to model complex relationships effectively.

Fig. 13
figure 13

Regression curves in XG Boost model for wear rate and coefficient of friction.

Full size image
Fig. 14
figure 14

Residual diagnostics plots of XG Boost model.

Full size image

The residual diagnostics in Fig. 14 provide deeper insights into the reliability of the model. The residuals versus predicted plots exhibit a random scatter around the zero line for both outputs, confirming that the model captured the underlying data patterns without introducing systematic biases and missing significant non-linear relationships. The residual histograms further validate the model’s performance, showing a symmetric, near-normal distribution of residuals centered around zero. This suggests that prediction errors are random and unbiased. Additionally, the autocorrelation plots show minimal correlation across lags, indicating that residuals are independent. The QQ plots confirm this, as the residuals align well with the theoretical quantile line, demonstrating that the errors approximate a normal distribution with only minor deviations at the extremes.

The model’s predictive accuracy, as quantified by key error metrics, underscores its effectiveness. For wear rate, the Mean Absolute Error (MAE) was 0.1698, and the Root Mean Squared Error (RMSE) was 0.2284; for COF, the MAE was 0.0165, and the RMSE was 0.0220. These low error values highlight XGBoost’s ability to minimize prediction discrepancies. Notably, the lower RMSE values indicate that the model effectively reduced larger deviations from the actual values, further reinforcing its robustness.

The exceptional performance of XGBoost can be attributed to its gradient boosting framework, which iteratively combines weak learners (decision trees) to correct errors from previous iterations, reducing both bias and variance. The inclusion of regularization techniques, such as L1 and L2 penalties, prevents overfitting and ensures generalizability, as evidenced by the well-behaved residuals. XGBoost’s ability to handle non-linear relationships and complex interactions between input variables also played a critical role in its predictive success. Furthermore, hyperparameter optimization using GridSearchCV ensured that key parameters, such as learning rate, maximum depth, and the number of estimators, were finely tuned to maximize performance. The model’s feature importance capability likely enhanced its efficiency by focusing on the most relevant input variables for predicting wear rate and COF16,39.

K-nearest neighbours (KNN)

The performance of the K-Nearest Neighbors (KNN) model in predicting wear rate and coefficient of friction (COF) for the Al/Kaoline composite is represented in Figs. 15 and 16, showing the regression curves and residual diagnostics. These figures, along with the associated metrics, provide an in-depth view of the model’s predictive behavior and accuracy.

Fig. 15
figure 15

Regression curves in KNN model for wear rate and coefficient of friction.

Full size image
Fig. 16
figure 16

Residual diagnostics plots of KNN model.

Full size image

The regression plots illustrate a reasonably close alignment between the actual and predicted values for both wear rate and COF, with data points clustering around the regression line. However, compared to previously discussed models like XGBoost, the KNN regression curves show slightly more dispersion, particularly for wear rate, where deviations from the regression line are more pronounced. The confidence bands around the regression lines are relatively wider, indicating increased variance in the predictions. This behavior is expected, as KNN’s performance depends heavily on the distribution of data points and the selection of the optimal number of neighbors (k).

The residual diagnostics plots provide additional insights into the model’s predictive behavior and highlight areas of improvement: For both wear rate and COF, the residuals versus predicted plots display a somewhat random scatter around the zero line, indicating that the model captured the data patterns without systematic bias. However, a few noticeable deviations, especially for wear rate, suggest that the KNN model struggled with certain data points that may represent edge cases or regions of sparse data. The histograms of residuals show a near-normal distribution centered around zero for both wear rate and COF. This distribution indicates that prediction errors are relatively unbiased and randomly distributed, although there is slightly more spread in wear rate residuals compared to COF. The autocorrelation plots reveal minimal correlation for both wear rate and COF residuals, suggesting that the residuals are largely independent. This independence validates the KNN model’s ability to generalize well across the dataset. The QQ plots for both outputs demonstrate that the residuals closely follow a normal distribution, with only slight deviations at the extremes. These deviations may arise due to localized data sparsity, which can affect KNN’s performance.

The KNN model’s performance metrics further illuminate its predictive accuracy. The R-squared values were moderate, indicating that the model explained a substantial portion of the variance: 0.8750 for wear rate and 0.8850 for COF. While these values are lower than those achieved by XGBoost and Random Forest, they still highlight the model’s ability to capture meaningful patterns within the data. The Mean Absolute Error (MAE) values were 0.2851 for wear rate and 0.0357 for COF, while the Root Mean Squared Error (RMSE) values were 0.3563 and 0.0430, respectively. These error metrics suggest that the KNN model’s performance is more variable compared to ensemble-based models, especially for wear rate, where higher MAE and RMSE indicate increased prediction errors. The COF predictions, on the other hand, exhibit lower errors, likely due to the more linear and less complex relationships in the COF data. KNN’s performance is heavily influenced by its reliance on local data patterns. The model predicts an output by averaging the outcomes of the ‘k’ nearest neighbors, which makes it sensitive to the density and distribution of data points. In areas where data points are sparse, KNN may struggle, as reflected in the wider confidence bands and higher prediction errors for wear rate. The choice of the optimal ‘k’ through hyperparameter tuning mitigated some of these issues, but the model’s reliance on local proximity inherently limits its ability to generalize for more complex or less uniform datasets33,40.

Artificial neural networks (ANN)

The Artificial Neural Network (ANN) model demonstrated strong predictive capabilities for both wear rate and coefficient of friction (COF) in the Al/Kaoline composite, as evidenced by the regression curves and residual diagnostics presented in Figs. 17 and 18. The regression plots in Fig. 17 highlight a high degree of alignment between the actual and predicted values, with data points clustering closely around the regression line for both wear rate and COF. The narrow confidence bands surrounding the regression lines reflect low variance in the predictions, reinforcing the reliability and accuracy of the model. These results indicate that the ANN model effectively captured both linear and non-linear relationships within the dataset, enabling accurate predictions.

Fig. 17
figure 17

Regression curves in ANN model for wear rate and coefficient of friction.

Full size image
Fig. 18
figure 18

Residual diagnostics plots of ANN model.

Full size image

The residual diagnostics, shown in Fig. 18, provide further validation of the model’s performance. The residuals versus predicted values plots display a random scatter around the zero line for both wear rate and COF, indicating that the model successfully captured the underlying trends in the data without introducing systematic biases. However, slight deviations in certain data points suggest areas where the model could further improve, particularly for wear rate predictions. The residual histograms show a near-symmetric bell-shaped distribution centered around zero, confirming that prediction errors are unbiased and evenly distributed. Furthermore, the autocorrelation plots reveal minimal correlation across different lags for both outputs, suggesting that the residuals are independent and supporting the robustness of the ANN model. The QQ plots further confirm that the residuals are approximately normally distributed, with minor deviations at the extremes, which is expected in complex datasets.

The performance metrics of the ANN model align well with the visual observations. The R-squared values of 0.9298 for wear rate and 0.9215 for COF indicate that the model explained 92.98% and 92.15% of the variance in the respective target variables, highlighting its ability to generalize effectively. The Mean Absolute Error (MAE) values of 0.1815 for wear rate and 0.0213 for COF, along with the Root Mean Squared Error (RMSE) values of 0.2418 and 0.0274, respectively, demonstrate the model’s accuracy in minimizing prediction errors. The slightly higher error values for wear rate suggest that this target variable may exhibit greater complexity or variability, which the ANN managed well but left some room for improvement.

The ANN model’s strong performance can be attributed to several key factors. Its ability to model non-linear relationships through a multi-layered architecture enables it to capture complex interactions between input variables. The use of the backpropagation algorithm allowed for iterative weight adjustments, minimizing errors between actual and predicted values. Careful tuning of the model’s hyperparameters, such as the number of hidden layers, neurons per layer, activation functions, and learning rate, ensured a balance between underfitting and overfitting41,42. Additionally, the ANN model’s generalization ability, as evidenced by the residual independence and approximate normality of errors, demonstrates its reliability for predicting material properties in diverse datasets.

Comparative analysis of ML models

The feature importance scores of the machine learning models, as illustrated in Fig. 19, provide a comprehensive understanding of how each input feature—Sod, Pressure, Angle, and Reinforcement (%)—contributed to predicting wear rate and coefficient of friction (COF). By analyzing these scores alongside the performance metrics, it becomes evident why certain models performed better than others and how specific features influenced their predictions.

Fig. 19
figure 19

Feature importance scores of different ML models implemented in the current investigation.

Full size image

For the SVM model (Fig. 19a), Sod was identified as the most significant feature for both wear rate (32.87%) and COF (31.38%), followed by Reinforcement (%) and Angle, while Pressure had a relatively lower contribution. SVM’s reliance on feature scaling and its ability to handle non-linear relationships allowed it to prioritize dominant features effectively. However, its slightly lower R2 value for COF (0.7262) compared to wear rate (0.9371) suggests that the model struggled to capture the more complex relationships influencing COF, highlighting its limitations in datasets with intricate feature interactions.

The Random Forest model (Fig. 19b) also identified Sod as the most critical feature for both outputs, with 33.02% importance for wear rate and 32.89% for COF. Unlike SVM, Random Forest assigned substantial importance to Pressure (29.23% for wear rate and 29.36% for COF), demonstrating its ability to capture the combined effects of multiple features. This balanced feature contribution likely contributed to the model’s strong and consistent performance across both outputs, as reflected in its R2 values of 0.9006 for wear rate and 0.9020 for COF. The ensemble nature of Random Forest, which averages predictions from multiple decision trees, enhanced its robustness and ability to handle feature redundancies, although its performance was slightly lower than XGBoost.

The XGBoost model (Fig. 19c) achieved the highest accuracy, with R2 values of 0.9433 for wear rate and 0.9462 for COF, and the lowest error metrics among all models. Similar to other models, XGBoost identified Sod as the most influential feature (33.11% for wear rate and 32.87% for COF) but also highlighted the importance of Reinforcement (%) and Angle. The model’s ability to iteratively refine predictions through gradient boosting and optimize feature contributions played a key role in its superior performance. The slightly higher importance of Reinforcement (%) in XGBoost suggests that it captured subtle interactions between reinforcement content and other variables, which were critical for accurately predicting both outputs. Additionally, XGBoost’s use of regularization techniques to prevent overfitting further enhanced its predictive capability.

The ANN model (Fig. 19d) displayed a similar feature importance distribution, with Sod being the dominant feature for both wear rate (32.56%) and COF (32.88%), followed by Reinforcement (%), Angle, and Pressure. The ANN model’s ability to learn complex, multi-dimensional patterns enabled it to achieve high R2 values of 0.9298 for wear rate and 0.9215 for COF. However, its slightly higher error metrics, particularly for wear rate, suggest that it was less effective in capturing subtle feature interactions compared to XGBoost. The relatively lower importance of Pressure in the ANN model may also explain its comparatively higher error rates, indicating that further tuning of the model’s architecture or incorporating additional data could enhance its performance. For good understanding purpose comparative analysis of similar works performed on aluminium composites are listed in Table 3.

Table 3 Comparative analysis of various works like present investigation.
Full size table

In summary, the performance of each model was strongly influenced by its ability to utilize key features like Sod and Reinforcement (%), which consistently emerged as the most critical inputs. While Random Forest and ANN delivered robust and consistent results, XGBoost outperformed all models, achieving the highest R2 values and lowest error metrics. Its ability to effectively capture complex feature interactions, combined with iterative refinement and regularization, made it the most reliable model for predicting wear rate and COF in this dataset. The findings also underscore the importance of Sod and Reinforcement (%) as dominant features across all models, highlighting their critical role in predicting the target outputs.

Future scope

Future research can focus on expanding the dataset by incorporating a broader range of reinforcement compositions, sintering conditions, and wear test parameters to enhance model generalization. The inclusion of multi-source datasets from different fabrication methods and testing conditions would further improve predictive robustness. Additionally, data augmentation techniques, such as synthetic data generation using generative models, can be explored to address data scarcity issues in composite material studies. In terms of machine learning advancements, future work can investigate deep learning architectures such as convolutional neural networks (CNNs) and long short-term memory (LSTM) networks to capture complex nonlinear relationships in the dataset. Reinforcement learning approaches could also be explored to dynamically optimize process parameters for real-time wear rate prediction and adaptive manufacturing. Furthermore, ensemble learning techniques combining multiple models can be examined to further enhance prediction accuracy and model stability.

From an experimental standpoint, future research can focus on refining the microwave sintering process by optimizing power distribution, heating rates, and multi-mode cavity designs to achieve improved densification and mechanical performance. The integration of real-time monitoring systems using infrared thermography, acoustic emission analysis, and in-situ load monitoring could provide more comprehensive datasets, enabling better machine learning-driven insights into wear behavior. By addressing these aspects, future studies can further advance the predictive modeling of tribological behavior in metal matrix composites, leading to more reliable and high-performance material development.

Conclusions

In conclusion, this study successfully applied machine learning models to predict the wear rate and coefficient of friction (COF) for an Al/Kaoline composite using experimental data. Among the models evaluated—Support Vector Machine (SVM), Random Forest, XGBoost, and Artificial Neural Network (ANN)—XGBoost emerged as the most reliable and accurate model. It achieved the highest R2 values of 0.9433 for wear rate and 0.9462 for COF, along with the lowest error metrics, including MAE and RMSE. The superior performance of XGBoost can be attributed to its ability to iteratively refine predictions through gradient boosting, effectively handle complex feature interactions, and optimize feature contributions through regularization techniques. While Random Forest and ANN also demonstrated strong predictive capabilities, their slightly lower accuracy highlights the importance of the advanced boosting mechanisms employed by XGBoost.

The feature importance analysis revealed that Sod consistently emerged as the most influential feature across all models for both wear rate and COF, followed by Reinforcement (%), Angle, and Pressure. This consistent ranking underscores the critical role of these parameters in determining the wear behavior of the composite. The ability of XGBoost to capture subtle interactions between these features contributed significantly to its superior performance. SVM, on the other hand, performed well for wear rate predictions but showed limitations in handling the non-linear relationships influencing COF, while ANN’s slightly higher error rates suggested the need for further architectural optimization or additional data for improved performance.

Overall, this work highlights the potential of machine learning models, particularly XGBoost, as powerful tools for predicting material properties based on experimental data. The findings provide valuable insights into the relative contributions of key input features and demonstrate the effectiveness of machine learning in modeling complex, multi-dimensional relationships in composite materials. These results pave the way for leveraging data-driven approaches to optimize material design and performance in industrial applications. The developed Al-Kaolin composite exhibits enhanced wear resistance and mechanical properties, making it highly suitable for applications in the automotive industry, particularly in the fabrication of automobile brake discs. The improved hardness and reduced wear rate contribute to the durability and performance of braking systems under high-friction conditions.