FasNet: a hybrid deep learning model with attention mechanisms and uncertainty estimation for liver tumor segmentation on LiTS17

Abstract

Liver cancer, especially hepatocellular carcinoma (HCC), remains one of the most fatal cancers globally, emphasizing the critical need for accurate tumor segmentation to enable timely diagnosis and effective treatment planning. Traditional imaging techniques, such as CT and MRI, rely on manual interpretation, which can be both time-intensive and subject to variability. This study introduces FasNet, an innovative hybrid deep learning model that combines ResNet-50 and VGG-16 architectures, incorporating Channel and Spatial Attention mechanisms alongside Monte Carlo Dropout to improve segmentation precision and reliability. FasNet leverages ResNet-50’s robust feature extraction and VGG-16’s detailed spatial feature capture to deliver superior liver tumor segmentation accuracy. Channel and spatial attention mechanisms could selectively focus on the most relevant features and spatial regions for suitable segmentation with good accuracy and reliability. Monte Carlo Dropout estimates uncertainty and adds robustness, which is critical for high-stakes medical applications. Tested on the LiTS17 dataset, FasNet achieved a Dice Coefficient of 0.8766 and a Jaccard Index of 0.8487, surpassing several state-of-the-art methods. The Channel and Spatial Attention mechanisms in FasNet enhance feature selection, focusing on the most relevant spatial and channel information, while Monte Carlo Dropout improves model robustness and uncertainty estimation. These results position FasNet as a powerful diagnostic tool, offering precise and automated liver tumor segmentation that aids in early detection and precise treatment, ultimately enhancing patient outcomes.

Introduction

Liver cancer, particularly HCC¹, is among the most critical global health challenges, contributing significantly to cancer-related mortality worldwide^2,3. As reported by the Global Cancer Observatory (GLOBOCAN)⁴, over 830,000 lives were lost to liver cancer in 2020, ranking it as the sixth most prevalent cancer and the third leading cause of cancer-related deaths⁵. Several factors are driving the increasing prevalence of liver cancer, including chronic hepatitis B and C infections, excessive alcohol consumption, and the rising incidence of non-alcoholic fatty liver disease^6,7. Due to its aggressive nature, early and accurate identification of liver tumors is essential for improving patient outcomes, as it facilitates timely and effective treatment⁸. Liver tumors are categorized into two main types: benign and malignant. Benign tumors, such as hemangiomas, focal nodular hyperplasia, and hepatic adenomas, are generally non-life-threatening and asymptomatic⁹. However, they can sometimes lead to complications, such as excessive growth or bleeding. On the other hand, malignant tumors¹⁰, which include primary liver cancers like HCC and cholangiocarcinoma, as well as metastatic liver cancers originating in other organs, pose a considerable threat due to their potential for severe health complications. HCC is the predominant form of primary liver cancer¹¹, accounting for approximately 75–85% of cases¹².

Medical imaging methods such as ultrasound, CT, and MRI are critical tools for identifying and diagnosing liver tumors¹³. These methods provide comprehensive visualizations of liver anatomy and pathology, enabling radiologists to detect and assess liver abnormalities. Ultrasound is commonly chosen as the preliminary imaging technique due to its widespread availability and non-invasive characteristics^6,14. However, further assessment of liver abnormalities often requires advanced imaging modalities like CT or MRI, which offer greater detail and accuracy^13,15. Despite the benefits of these techniques, manual interpretation remains time-intensive and is subject to considerable variability between observers, leading to potential inconsistencies in diagnosis and treatment planning¹⁶. The need for automated and standardized approaches in medical imaging has driven significant progress in AI and deep learning technologies. These advancements have revolutionized the field by facilitating precise, efficient, and automated analysis of complex medical datasets. CNN has become an effective tool for image segmentation, surpassing traditional image-processing techniques in various medical scenarios^15,16. By reducing the workload of radiologists and enhancing the reliability and precision of liver tumor diagnoses, CNNs have proven to be highly valuable. Their ability to process hierarchical features from raw images allows them to analyze macro and micro-level details simultaneously, making them particularly suitable for segmentation tasks.

Hybrid deep learning models¹⁷, which combine the strengths of various CNN architectures, have shown great promise for improving segmentation performance. The paper presents FasNet, a new hybrid model for liver tumor segmentation that combines the ResNet-50¹⁸ and VGG-16¹⁹ architectures. FasNet aims to improve segmentation accuracy and robustness by leveraging ResNet-50’s deep feature extraction capabilities and VGG-16’s fine-grained spatial feature capture. Using residual learning from ResNet-50 and the sequential layer structure of VGG-16, FasNet effectively overcomes some of the common challenges associated with using a single CNN architecture, such as the vanishing gradient problem in deep networks.

The objective of the research work is to evaluate the high accuracy of FasNet for liver tumor segmentation using a large-scale dataset and measure performance against cutting-edge state-of-the-art techniques to be clinically applicable. FasNet is built on the combination of ResNet-50 and VGG-16 architectures by combining their complementary strengths toward achieving superior segmentation accuracy and robustness. To evaluate it, several metrics have been included, like the dice similarity coefficient, sensitivity, specificity, and computational efficiency. In addition to that, an in-depth investigation into the effect of various preprocessing and postprocessing methods on model performance is included. This work aims at establishing FasNet as a powerful tool in the battle against liver cancer, providing improved accuracy in diagnosis and treatment planning that may result in improved outcomes for patients. Further optimizations and new deep-learning techniques will be included in the model in future work to improve its performance and pertinence in real clinical scenarios. Here is a summary of the major contributions of the paper:

• 1 Development of FasNet Model: The paper presents FasNet, a novel hybrid deep learning model combining ResNet-50 and VGG-16 architectures. This integration leverages ResNet-50 for hierarchical feature extraction and VGG-16 for capturing fine-grained spatial features.

• 2 Incorporation of Attention Mechanisms: The model incorporates Channel and Spatial Attention mechanisms to enhance feature selection and focus on the most relevant spatial regions, improving segmentation accuracy and robustness.

• 3 Uncertainty Estimation: Monte Carlo Dropout enables the model to estimate uncertainty, making it more reliable for high-stakes applications like medical imaging.

• 4 Comprehensive Evaluation: The study evaluates various optimizers, batch sizes, and performance metrics (e.g., Dice Coefficient, Jaccard Index, Precision, Recall, Specificity, and F1 Score), demonstrating the robustness and effectiveness of the FasNet model.

• 5 Practical Applicability: The proposed model’s performance highlights its potential as a diagnostic tool for automated liver tumor segmentation, aiding early detection and treatment planning.

• 6 Benchmarking Against State-of-the-Art: FasNet’s results are compared with contemporary techniques, and its hybrid approach provides significant advantages for segmentation accuracy and reliability.

The paper’s organization is as follows: Sect. 2 provides an overview of recent developments in liver tumor segmentation, focusing primarily on advancements in deep learning methodologies. Section 3 elaborates on the LiTS17 dataset utilized in the research. Section 4 explains the rationale for selecting ResNet-50 and VGG-16 as the backbone encoders for the FasNet model. Section 5 details the design and structure of the FasNet model, highlighting its integration with transfer learning techniques. Section 6 presents the experimental results and evaluates FasNet’s performance across multiple metrics. Finally, Sect. 7 summarizes the key findings and suggests future research directions.

Literature review

The critical task of liver tumor segmentation in medical image evaluation facilitates accurate diagnosis, treatment planning, and liver cancer monitoring. Several methods have been suggested that utilize deep learning techniques to improve the precision and efficacy of liver tumor segmentation. This literature review investigates the most recent developments in liver tumor segmentation algorithms, emphasizing various noteworthy studies that employ different methodologies.

Chen et al.²⁰ proposed a Multi-Scale Liver Tumor Segmentation Algorithm that combined convolution and Transformer techniques to enhance segmentation accuracy by fusing local and global features. Their method, evaluated on the LiTS17 dataset, achieved Dice similarity coefficients of 0.920 for the liver and 0.748 for tumors, outperforming baseline models but potentially impacting local detail preservation. You et al.²¹ proposed the (PGC-Net) for liver tumor segmentation. This network uses contour-induced parallel graph reasoning and a Pyramid Vision Transformer to extract multi-scale features. When tested on the LiTS17 and 3DIRCADb datasets, PGC-Net achieved average Dice scores of 73.63% and 74.16%, though it struggled with indistinct lesion boundaries and target-outline correlations. He et al.²² introduced PAKS-Net, a 2D tumor segmentation model designed to overcome challenges in 3D and 2D segmentation models. The model uses the Swin-Transformer for global feature extraction and a Position-Aware module to capture spatial relationships between tumors and organs. Evaluated on KiTS19, LiTS17, pancreas, and LOTUS datasets, PAKS-Net achieved tumor DSC scores of 0.893, 0.769, 0.598, and 0.738, respectively; however, it may still face challenges with noise and inter-slice correlations. Shui et al.²³ proposed a framework of three-path networks for liver tumor segmentation using MSFF, MFF, EI, and EG modules. The framework was evaluated on the LiTS2017 dataset; its Dice index reached 85.55% with a Jaccard index of 81.11%. Cross-dataset validation on the 3Dircadb and Clinical datasets reported dice indices of 80.14% and 81.68%, respectively. Biswas et al.²⁴ introduced a GAN-driven data augmentation technique for segmentation to enhance the quality and efficiency of biomedical imaging training. Their approach showed the feasibility of producing high-quality images for the pre-segmentation stage, providing Dice scores as 0.908 on MIDAS, 0.872 on 3Dircadb, and 0.605 on LiTS datasets. However, the approach might still have to be improved regarding the reliability that conventional data augmentation techniques share. For the segmentation of liver tumors, Wang et al.²⁵ synthesized a Context Fusion Network equipped with TSA modules and MSA skip connections. Using the LiTS2017 dataset, this method obtained an 81.56% Jaccard index and an 85.97% Dice coefficient, while on the 3Dircadb dataset, this method obtained an 80.11% Jaccard index and an 83.67% Dice coefficient. Authors Muhammad et al.²⁶ suggested a hybrid ResUNet model that fused ResNet and UNet architectures for segmenting liver tumors from CT images based on the MSD Task03 Liver dataset. The authors streamlined the implementation process by leveraging the Monai and PyTorch frameworks, reducing manual scripting, and optimizing model performance. The achieved Dice coefficient was 0.98% in detecting tumors and 0.87% in segmentation. Fallahpoor et al.²⁷ suggested a deep learning technique built on the Isensee 2017, which segmented liver and liver lesions for clinical use from 3D MRI data. The model was developed using T1w and T2w MRI images from 128 patients, which, on average, attained a Dice coefficient of 88% in liver segmentation and 53% in liver tumors on 18 test cases. Wang et al.²⁸ proposed a UNet + + network for the automatic segmentation of liver and liver tumors from MRI images in hepatocellular carcinoma patients. The method attained an average DSC of 0.91 for the liver and 0.612 for liver tumors. The integration of deep learning models for enhanced medical picture segmentation, shown by FasNet, corresponds with current progress in the domain, as investigated by Z.et al.³⁰ regarding hepatic pharmacokinetics. Additionally, McGrath et al.³¹ and Mojtahed et al.³² underscore the growing reliance on semi-automated and deep learning methodologies to improve segmentation accuracy, which aligns with the objectives of FasNet in the identification of liver tumors. Additionally, Wang et al.³³ and Vaidhya Venkadesh et al.³⁴ underscore the importance of incorporating multimodal imaging and historical data to enhance deep learning models³⁵. Consequently, the efficacy of hybrid models, such as FasNet, in accurately segmenting tumors on the LiTS17 dataset is substantiated. The literature review is presented in Table 1.

Table 1 Literature review.

Input dataset

Figure 1 displays the input dataset used for liver tumor segmentation, collected explicitly from the LiTS17 dataset²⁹, which is part of the Liver Tumor Segmentation Challenge 2017. The LiTS17 dataset includes over 130 CT scans of individual patients, each accompanied by expert annotations that provide ground truth masks for liver tumors. The high-resolution images provide precise and comprehensive data for training and evaluating segmentation models. The original CT images are shown in the 1st row of Fig. 1, while the 2nd row displays the true masks, which accurately depict the tumor segmentations. Using the LiTS17 dataset al.lows for the creation of strong segmentation algorithms such as FasNet. The dataset’s extensive variety and large size ensure that the model can effectively adapt to different tumor sizes, shapes, and locations.

Fig. 1

Input dataset.

Selection of transfer learning models

Table 2 compares the specifications of two widely used transfer learning models, ResNet-50 and VGG-16. The table shows their architectural differences, number of layers, parameters, computational complexity in FLOPs, floating point operations, inference time, and top-1 accuracy achieved on the ImageNet dataset. ResNet-50 applies a network structure that contains 50 layers and 25.6 million parameters. It demands 3.8 billion floating point operations (FLOPs) and achieves a top-1 accuracy of 76.2%. Residual connections minimize the vanishing gradient issue; thus, training deep nets becomes very efficient. In stark contrast, the VGG-16 architecture is based on an entirely sequential layout of 16 layers and a configuration of 138 million parameters. Such a setup requires 15.3 billion FLOPs and reaches 71.5% for top-1 accuracy. B. Simplicity is, in fact, the precise point of strength for VGG-16 combined with the usage of compact 3 × 3 convolution filters that enable the network to catch very fine spatial details efficiently.

Table 2 Specification of transfer learning models.

In FasNet, ResNet-50 and VGG-16 models were chosen based on the complementary functionalities these two provide in feature extraction. ResNet-50 can extract complex hierarchical features with added stability because of its residual learning nature, making it highly performing for complex pattern recognition functions. Despite the VGG-16 model’s simplicity of architecture, it excels in capturing fine spatial features very well and thus is very useful for application tasks such as image segmentation. Both models also have pre-trained weights from ImageNet, making a solid basis for transfer learning and ensuring adequate training and outstanding performance on specific tasks. FasNet: A combination of a deep architecture like ResNet-50 with accurate feature extraction capabilities in VGG-16 helps in very precise and reliable segmentations. Thus, it becomes more effective for medical tasks like segmentation, especially for liver tumors.

Proposed hybrid FasNet model

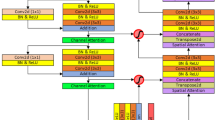
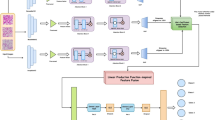
The paper introduces a deep learning model called FasNet, as shown in Fig. 2, which utilizes ResNet-50 and VGG-16 as encoder backbones for feature extraction. In addition to a robust encoder-decoder structure, FasNet incorporates Channel Attention and Spatial Attention modules to enhance feature selection and focus on relevant regions in the feature maps. The encoder is composed of two pre-trained models: ResNet-50 and VGG-16, with the final layers removed to retain only the feature extraction layers. The extracted features from ResNet-50 and VGG-16 have dimensions of 2048 and 512, respectively. These features are concatenated to form a 2560-dimensional feature map, which is then processed through channel and spatial attention modules. The attention modules refine the features by focusing on the most informative channels and spatial regions.

After the attention modules, the combined feature map is reduced to 512 channels using a 1 × 1 convolution layer. This processed feature map is further passed to the decoder network, designed to upsample features and generate segmentation maps. It starts with a 3 × 3 convolution layer followed by two transpose convolution layers progressively upscaling the feature map to nearly the exact resolution as the original input. Each of the two transpose convolution layers is followed by a Monte Carlo Dropout layer that introduces stochasticity during training and at inference time and enables it to provide uncertainty estimates in the outputs generated for segmentation. Ultimately, the upsampling layers are accompanied by a final 1 × 1 convolution that produces the number of output classes for the segmentation map. This design architecture allows FasNet to leverage multi-scale features from two different backbones while also using attention mechanisms and dropout to enhance the accuracy and robustness of the segmentation.

The FasNet class is defined with an __init__ method that sets both encoder and decoder layers, including attention modules and Monte Carlo Dropout. The forward method processes the input image with the encoder backbones, applies the attention modules, merges the features, and runs them through the decoder to produce the output segmentation map. The FasNet model is ready to train and evaluate complex segmentation tasks with all these configurations: pre-trained backbones, attention mechanisms, Monte Carlo Dropout, and the number of desired output classes.

Fig. 2

Block diagram of proposed hybrid FasNet model.

Fine-tuned ResNet50 backbone

ResNet-50 (Residual Network with 50 layers) is a convolutional neural network that addresses the vanishing gradient problem using residual blocks. Figure 3 shows the fine-tuned ResNet50 backbone with residual blocks. These blocks allow the network to learn identity mappings, making training very deep networks easier. The core concept of ResNet-50 is the residual block. A residual block can be represented in the Eq. 1:

$$\:y=F\left(x,\left\{{w}_{i}\right\}\right)+x$$

(1)

Where:

• $\:x$Is the input to the residual block.

• $\:F\left(x,\left\{{w}_{i}\right\}\right)$ is the residual mapping to be learned. Typically, F is a stack of convolutional layers.

• $\:\left\{{w}_{i}\right\}$ are the weights of the convolutional layers within the residual block.

• y is the output of the residual block.

Fig. 3

Fine-Tuned ResNet50 Backbone.

Each residual block essentially learns the difference (residual) between the input and the output, which helps the network maintain gradient flow during backpropagation.

ResNet-50 uses a bottleneck design within its residual blocks to reduce the number of parameters and computational costs. A bottleneck residual block consists of three layers: a 1 × 1 convolution, followed by a 3 × 3 convolution, and another 1 × 1 convolution. The equation for a bottleneck residual block is given in Eq. 2:

$$\:y={W}_{3}\left(\sigma\:\left({W}_{2}\left(\sigma\:\left({W}_{1}x+{b}_{1}\right)\right)+{b}_{2}\right)\right)+{b}_{3}+x$$

(2)

Where:

• $\:x$ is the input to the block.

• $\:{W}_{1}$, $\:{W}_{2}$, $\:{W}_{3}$ are the weight matrices for the 1 × 1, 3 × 3, and 1 × 1 convolutions, respectively.

• $\:{b}_{1}$, $\:{b}_{2}$, $\:{b}_{3}$ are the bias terms for the corresponding layers.

• σ represents the ReLU activation function.

• The term $\:x$ added at the end represents the skip connection, the hallmark of residual blocks.

In the FasNet model, ResNet-50 is used as one of the encoder backbones for feature extraction. The last two layers are removed to use it purely for extracting deep hierarchical features. Combined Feature Extraction Equation For the modified ResNet-50 used in FasNet is given the Eq. 3:

$$\:{F}_{ResNet50}=Flatten\left({ResBlock}_{4}\right(\dots\:{ResBlock}_{1}\left(Conv1\left(I\right))\right))$$

(3)

Where:

• $\:{F}_{ResNet50}$ is the flattened feature vector output from the modified ResNet-50.

• $\:{ResBlock}_{1}\dots\:{ResBlock}_{4}$ represents the four stages of residual blocks.

• Conv1 is the initial convolutional layer.

• $\:($I) is the input to the ResNet-50 model, typically an image with dimensions H×W×C (height, width, and channels).

Fine-tuned VGG16 backbone

The VGG16 architecture represents a convolutional neural network designed primarily for tasks involving image classification. Renowned for its straightforward design and depth, it effectively captures detailed patterns and features within images. This architecture comprises key components such as convolutional layers, max-pooling layers, and fully connected layers. For this study, modifications were made by removing the final fully connected layers to repurpose the network for feature extraction, tailoring it to suit the requirements of the FasNet model. The adjusted VGG16 backbone is depicted in Fig. 4.

Fig. 4

Fine-tuned VGG16 backbone.

Each convolutional layer applies a set of convolutional filters to the input, followed by a ReLU activation function. The equation for a convolutional layer is:

$$\:{O}_{ij}^{i}=\sigma\:({\sum\:}_{k}{W}_{k}^{l}*{I}_{k}^{l-1}+{b}^{l})$$

(4)

Where:

• $\:{O}_{ij}^{i}$ is the output feature map at position $\:(i,j)$ of layer l.

• σ represents the ReLU activation function.

• $\:{W}_{k}^{l}$​ is the weight matrix (kernel) for the k^th filter at layer $\:l$.

• $\:{I}_{k}^{l-1}$ is the input feature map from the previous layer $\:(l-1)$.

• $\:{b}^{l}$ is the bias term for the convolutional layer $\:l$.

• ∗ denotes the convolution operation.

Max-pooling layers reduce the spatial dimensions (height and width) of the input feature maps, which helps to decrease the computational complexity and prevent overfitting. The equation for a max-pooling layer is given in the Eq. (5):

$$\:{O}_{ij}^{l}={max}_{m,n}\left({I}_{i+m,j+n}^{\left(i-1\right)}\right)$$

(5)

Where:

• $\:{O}_{ij}^{l}$ is the output of the max-pooling layer at position $\:(i,j)$ for layer l.

• $\:{I}_{i+m,j+n}^{\left(i-1\right)}$ is the input feature map from the previous layer within the pooling window defined by indices m and n.

In the FasNet model, the last fully connected layers are removed from VGG16 to use it purely for feature extraction. This modified VGG16 extracts fine-grained and hierarchical features from the input images, which are then combined with features extracted from ResNet-50. Combined Feature Extraction Equation For the modified VGG16 used in FasNet is given in the Eq. 6:

$$\:{F}_{VGG16}=Flatten\left({Conv}_{5}\right(MaxPool(\dots\:{Conv}_{1}\left(I\right)\dots\:)\left)\right)$$

(6)

Where:

• $\:{F}_{VGG16}$ is the flattened feature vector output from the modified VGG16.

• $\:{Conv}_{1}\dots\:{Conv}_{5}$ represent the sequential application of convolutional and max-pooling layers.

• $\:($I) is the input to the VGG16 model, typically an image with dimensions H×W×C (height, width, and channels).

Encoder network with channel and Spatial attention

Figure 5 illustrates the encoder network of the FasNet model, designed for image segmentation tasks. The model utilizes two primary backbones, ResNet-50 and VGG16, to leverage their complementary strengths; a detailed description is already discussed in the previous sections. The outputs of these two backbones are concatenated to form a comprehensive feature vector, combining deep hierarchical features from ResNet-50 with fine-grained spatial features from VGG16. Concatenation is done by the Eq. 7:

$$\:{F}_{Combined}=Concat({F}_{ResNet50},{F}_{VGG16})$$

(7)

Where:

• F_ResNet50 is the feature vector from ResNet-50.

• F_VGG16F is the feature vector from VGG16.

Fig. 5

Encoder network with channel and spatial attention.

Channel Attention and Spatial Attention are added to convolutional neural networks to improve the model’s ability to focus on the most relevant information in an image, enhancing its decision-making capability. In complex tasks like medical image segmentation, not all feature channels (types of patterns) are equally important, and not all spatial regions (locations within the image) carry equally critical information. Channel attention operates by assigning varying levels of importance to each channel in the feature map, allowing the network to emphasize channels that capture essential characteristics (e.g., textures or structures specific to certain organs or tissues). Spatial attention focuses on regions of interest in the image that correspond to the most relevant task areas, so the model naturally leads toward crucial details potentially located at a lesion’s boundary. Channel and spatial attention enhances the segmentation as they help the model pay significant attention only to the most informative features and spatial locations. This selective attention reduces the impact of noise and irrelevant information so that the output will have cleaner and more accurate segmentations. While doing segmentation tasks, detailing in an image is essential because often, the tiny differences found here can show a big difference. Attention mechanisms allow a network to better capture intricate details or important boundaries in an image through adaptively weighting channels and spatial regions; that’s predominantly relevant in the medical imaging fields where minor errors in segmentation can result in profound implications.

The attention mechanisms help reduce overfitting by allowing the network to focus on salient features that are most crucial, rather than trying to memorize everything from the input. In medical imaging, for instance, overfitting is always a problem because the feature spaces are very high dimensional, especially with relatively small-sized datasets. The channel and spatial attention help improve this by emphasizing the most relevant aspects of every image, and the learned representations of the model become more generalizable. This ability to reduce overfitting by focusing more on critical features and spatial regions makes the network more robust, which improves its performance on unseen data necessary for any real application. Channel and spatial attention contribute to the interpretability of the model as well since they explain where in the image and which features are important to the model. This interpretability is valuable in high-stakes fields like healthcare, where understanding why the model was made and certain decisions can help build trust with clinicians. For example, spatial attention’s attention maps can be displayed visually so that regions the model focuses on line up with what a radiologist would look at. This interpretability, combined with improved localization of target structures and a more efficient focus on relevant features, makes channel and spatial attention mechanisms particularly beneficial for segmentation tasks that require accuracy and reliability.

At the end of the encoder, A 1 × 1 convolutional layer then processes this concatenated and attention module feature vector to reduce its dimensionality and further integrate the features, enhancing the model’s ability to generate accurate and high-resolution segmentation maps.

Decoder network with Monte Carlo dropout

Figure 6 illustrates the decoder network with Monte Carlo (MC) Dropout of the FasNet model, which is responsible for generating high-resolution segmentation maps from the encoded features. The decoder network begins with a 3 × 3 convolutional layer that processes the concatenated feature vector from the encoder network, refining the feature representations. Following this, the first transpose convolutional layer (also known as deconvolution or upsampling layer) increases the spatial dimensions of the feature map, effectively upsampling it to a higher resolution. The second transpose convolutional layer further upsamples the feature map, increasing the spatial resolution and ensuring that the feature maps are restored to their original spatial dimensions; after each transpose layer, the MC Dropout layer is applied to enhance the standard dropout technique. A final 1 × 1 convolutional layer integrates the upsampled feature maps. This reduces the feature channels to the number of classes in the segmentation task and produces the final output segmentation map. This map will give pixel-wise classification of the input image, showing where the regions of interest are, based on the features extracted and processed by the encoder and decoder networks. The combination of 3 × 3 convolutions, transpose convolutions, MC Dropouts, and finally a 1 × 1 convolution implies that the decoder network upsamples the feature maps with high fidelity and hence produces precise delineations of the regions of interest. This process is vital for achieving superior performance as in the tasks of liver tumor segmentation in medical imaging so that the model captures and consequently employs the deep and spatial features that the encoder network induces.

Fig. 6

Decoder network with Monte Carlo dropout.

Monte Carlo Dropout is an extension of the ordinary dropout that improves predictiveness, robustness, and uncertainty estimation. Traditionally, dropout is applied during training only to fight overfitting by randomly deactivating neurons, forcing the model to discover more general representations. But Monte Carlo Dropout does not take dropout off during inference; it still randomly drops neurons on each forward pass, making the predictions slightly different. This allows the network to simulate an ensemble effect; several “instances” make predictions that help average out noise and boost accuracy. By doing multiple forward passes with dropout enabled, MC Dropout can generate several predictions for the same input that may be averaged. On average, this type of prediction is more stable and accurate as noisy singular prediction is minimized. MC Dropout also calculates variance or spread to estimate uncertainty. The variance also indicates the points at which the model is less confident, which can be invaluable in critical applications such as medical imaging or high-performance autonomous driving, where the reliability of the model is paramount. The MC Dropout technique increases accuracy due to prediction averaging and better uncertainty estimates. Models employing MC Dropout are typically better calibrated, meaning their predicted probabilities better reflect the true likelihoods. In a setting in which the model’s predictions are at least somewhat more reliable, they are safer in high-stakes applications as well.

The specifications of the convolutional layers in FasNet, as detailed in Table 3, provide even further enhancement to the model’s effectiveness by reducing dimensionality at each stage while capturing essential features. The first layer is a 1D convolution, which minimizes the input size from 2560 to 512 with kernel size 1. The second layer is a 2D convolution that processes this output to reduce it to 256 with a 3 × 3 filter. Finally, the third layer is a 2D convolution that compresses the data into an output size of 3 with kernel size 1; the output aligns to match the dimension desired. This layered approach to the design of FasNet contributes significantly to the robustness of the segmentation performance.

Table 3 Specification of convolutional layers used in proposed model.

Results and discussion

The Results section is structured into multiple subsections to examine the model’s performance thoroughly. These include examining various optimizers, evaluating the effect of different batch sizes on the Adam optimizer, analysing training and validation loss accuracy, assessing Dice Coefficient and Jaccard Index, studying parameters in the confusion matrix, visual analysis, and comparing with cutting-edge techniques. Each subsection is dedicated to specific performance metrics and offers an in-depth examination of the model’s learning and generalization capabilities.

Analysis using different optimizers

The analysis using different optimizers, as presented in Table 4, compares the performance of five optimizers—AdaGrad, SGD, Adam, RMSProp, and AdaDelta—on various metrics, including Training Loss, Validation Loss, Accuracy, Dice Coefficient, Jaccard Index, Precision, Recall, Specificity, and F1 Score. Among the optimizers, Adam shows the best overall performance with the lowest losses (0.0251), the highest accuracy (0.9954), and superior Dice Coefficient (0.8766) and Jaccard Index (0.8487). It also excels in precision (0.8499), recall (0.8560), specificity (0.9695), and F1 Score (0.8363), indicating its robustness and effectiveness in optimizing the model compared to the other optimizers. The other optimizers, while performing reasonably well, do not match the consistent performance across all metrics exhibited by Adam.

Table 4 Analysis using different optimizers.

Figure 7 visually represents the performance of five optimizers—AdaGrad, SGD, Adam, RMSProp, and AdaDelta—across several critical metrics in training a segmentation model. Each optimizer’s performance is assessed based on Accuracy, Dice Coefficient, Jaccard Index, Precision, Recall, Specificity, and F1 Score. The Adam optimizer stands out, demonstrating the highest scores in most metrics. This aligns with the detailed analysis in Table 3, which identified Adam as the most effective optimizer with the lowest training and validation losses, highest accuracy, and superior performance in segmentation metrics. Other optimizers like AdaGrad, RMSProp, and AdaDelta show varying degrees of effectiveness. Still, none match Adam’s consistency and overall performance, making it the most robust choice for optimizing the segmentation model.

Fig. 7

Comparison of different optimizers.

Analysis of Adam optimizer using different batch sizes

The analysis of the Adam optimizer using various batch sizes, as illustrated in Table 5, highlights the impact of batch size on different performance metrics. When it comes to overall performance, the Adam optimizer has the best Dice Coefficient (0.8766) and Jaccard Index (0.8487) with a batch size of 32. It also has the highest accuracy (0.9954) and the lowest losses (0.0251). It also achieves an F1 Score of 0.8363, recall of 0.8560, specificity of 0.9695, and precision of 0.8487. Batch sizes of 16, 64, and 128 demonstrate increased losses and slightly worse performance on most metrics. Here, a batch size of 32 is the most optimal and efficient for the Adam optimizer.

Table 5 Analysis of Adam optimizer using different batch sizes.

Figure 8 presents the impact of varying batch sizes (16, 32, 64, 128) on the performance of the Adam optimizer across various key metrics, including Accuracy, Dice Coefficient, Jaccard Index, Precision, Recall, Specificity, and F1 Score. The analysis demonstrates that a batch size of 32 consistently outperforms the other batch sizes, achieving the highest values in Accuracy, Dice Coefficient, and Jaccard Index and maintaining strong performance in other metrics. This indicates that batch size 32 is the most effective for optimizing the Adam optimizer, providing the best balance between training efficiency and segmentation accuracy. Smaller and larger batch sizes, such as 16 and 128, show relatively lower performance, especially in Recall and F1 Score. This underscores the position of selecting a suitable batch size for optimal model training and performance.

Fig. 8

Comparison of different batch sizes.

Training and validation loss, accuracy analysis

Figure 9 shows the performance metrics for the segmentation model over 100 epochs, where Training & Validation Loss and Training & Validation Accuracy are presented in Fig. 9a,b. At the beginning epochs, training and validation losses are significantly changing, which is the early learning phase of the model since it tries to fit the data. The training loss starts at about 1.75, then continuously decreases until it becomes close to zero. This should be interpreted as appropriate parameter optimization. Similarly, validation loss follows a downward trend, meaning the model is improving at generalizing its ability toward new data. Simultaneously, the accuracy graph indicates an upward trajectory, where training and validation accuracy remain consistently and steadily on the increase as time progresses to stabilize close to 1.0. This improvement in accuracy and the consistent reduction in loss signifies that the model has learned effectively and is achieving high performance in both training and validation. These trends highlight the model’s successful progression from early learning adjustments to stable and reliable performance by the end of the training period.

Fig. 9

Graphical analysis (a) training & validation loss, (b) training & validation accuracy.

Dice coefficient and Jaccard index analysis

Figure 10 presents an inclusive analysis of the model’s presentation over 100 training epochs, focusing on the evolution of the Dice Coefficient and Jaccard Index for both training and validation sets. Figure 10a displays the Dice Coefficient; the training curve shows rapid improvement during the initial epochs and stabilizes around a high value of 0.90. This stable value indicates that the model is successfully learning the fundamental patterns in the training data. The validation Dice Coefficient follows a similar upward trend, eventually reaching a steady value of approximately 0.87. The close alignment between the training and validation Dice Coefficients proposes that the model performs consistently well on both datasets, indicating high segmentation accuracy and reliability. Figure 10b represents the Jaccard Index; the training curve quickly ascends, reaching a stable value of 0.98. This high Jaccard Index reflects the model’s strong ability to capture the overlap between the predicted and actual segments within the training set. The validating Jaccard Index also stabilizes at a value of 0.84, demonstrating the model’s efficiency when applied to unobserved data with considerable segmentation performance. The gradual stabilization of both metrics in training and validation depicts the strength and trustworthiness of the model in that it shows that the model can learn meaningful patterns and deliver accurate segmentations of different datasets.

Fig. 10

Graphical analysis (a) Dice Coefficient, & (b) Jaccard Index.

Confusion matrix parameters analysis

Figure 11 provides an overall impression of how the performance metrics for the segmentation model evolved at all 100 epochs, with individual graphs showing Precision, Recall (Sensitivity), Specificity, and F1-Score graphed in Fig. 11a–d. These metrics indicate that the model learned well and generalized well across the training and validation datasets. Having achieved a high level of Training Precision at 0.98, the model is accurate for true positives within the training data. The Validation Precision value of 0.84 reflected a similar striking accuracy in detecting relevant instances in unseen data that showed that the model was performing at a high level when applied out of the training set. Outstanding 0.99 was the Training Recall or Sensitivity, meaning the model successfully picked almost all instances of interest in the training data. It’s easy to see that it has low false negatives, and few cases of interest go undetected. This Validation Recall of 0.85 further ensures that the model tends to perform uniformly well on new data, capturing a lot of relevant instances, thereby showing how sensitive and good at generalization it is. Specificity, another quantity of interest for judging the model’s ability to identify true negatives correctly, gave high scores, too. At a Training Specificity of 0.99, the model has responded significantly at the exclusion of non-relevant instances within the training. Similarly, a Validation Specificity of 0.96 shows that the model performs highly in classifying unseen data with actual correctness to avoid false positives that may result from false positives in real-world applications. The F1-Score combines precision and recall to measure how well the model balances these metrics. With a Training F1-Score of 0.99, the model achieved almost the perfect balance between capturing relevant instances and maintaining the precision of its predictions, thus indicating an excellent training performance. The Validation F1-Score of 0.83 further underlines the balance and effectiveness with which the model performs in new data sources, thereby suggesting its reliability with different datasets. These metrics in Fig. 11 show that the model has high predictive capacity with stable, reliable, and consistent performance over the training and validation sets. The strong performance on multiple metrics indicates a good capacity to learn from the training data and generalize well to new, unseen data, making it suitable for deployment in practical, real-world segmentation tasks.

Fig. 11

Graphical analysis (a) Precision, (b) Recall, (c) Specificity, & (d) F1 Score.

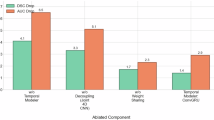
Ablation analysis

Table 6 summarizes the properties of incorporating attention mechanisms and Monte Carlo dropout on FasNet’s performance, measuring Accuracy, Dice Coefficient, Jaccard Index, Precision, Recall, Specificity, and F1 Score across model variants. The standard model, FasNet, reaches an accuracy of 0.9919 with a Dice Coefficient of 0.8659, Jaccard Index of 0.8365, and F1 Score of 0.7171, indicating high segmentation quality but with a relatively lower recall score of 0.6603, suggesting areas for improvement in detecting positive cases. Adding an attention mechanism slightly enhances performance, raising the Dice Coefficient to 0.8693, the Jaccard Index to 0.8413, and the F1 Score to 0.7520, reflecting improved feature capture and segmentation quality, though with a slight decrease in specificity. Incorporating Monte Carlo dropout alone increases model robustness, with an accuracy of 0.9902, a Dice Coefficient of 0.8676, and a Jaccard Index of 0.8437, alongside improved precision and recall scores of 0.8298 and 0.8046, respectively, illustrating the dropout’s role in balancing true positives and false positives. The model with both attention and Monte Carlo dropout achieves the highest performance across metrics, with an accuracy of 0.9954, Dice Coefficient of 0.8766, Jaccard Index of 0.8487, precision of 0.8499, recall of 0.8560, and F1 Score of 0.8363, indicating a synergistic enhancement in segmentation accuracy, consistency, and robustness across all metrics.

Table 6 Ablation study.

Visual analysis

Figure 12 presents visual analysis of original CT images, corresponding true masks, and predicted masks created by the proposed FasNet model for liver tumor segmentation. The first column showcases the original CT images, highlighting the raw input data captured through imaging techniques. The second column displays the true masks, representing the ground truth segmentations meticulously annotated by medical experts to delineate the precise boundaries of liver tumors. These true masks serve as a standard for assessing the accuracy of the model’s predictions. The third column illustrates the predicted masks produced by the FasNet model, visually reflecting its segmentation capabilities. Each row in Fig. 12 highlights a distinct set of CT images, ground truth masks, and corresponding predictions, providing a side-by-side comparison across various cases. The close resemblance between the true and predicted masks is a testament to the model’s accuracy and reliability in identifying and segmenting liver tumors. The predictions effectively capture the tumors’ overall shape, size, and position, demonstrating the model’s robustness in processing complex medical imagery. While minor discrepancies are observed in some instances, these differences are marginal and do not significantly detract from the quality of the segmentation. This detailed visual analysis underscores FasNet’s ability to deliver high-quality segmentation results, aligning closely with expert-annotated ground truth. By achieving this level of precision, the model holds great potential for assisting radiologists and medical practitioners in diagnosing liver tumors and planning appropriate treatment strategies. The findings further validate the practical applicability of FasNet in clinical environments. Overall, the visual analysis reaffirms the success of the FasNet as a reliable tool for medical image segmentation tasks.

Fig. 12

Visual Analysis of Proposed FasNet Model with Attention and Monte Carlo Dropout.

State of Art comparison

Table 7 illustrates an evaluation of the proposed FasNet model with various state-of-the-art methods. Multi-Scale Liver Tumor Segmentation Algorithm, Parallel Graph Convolutional Network (PGC-Net), and PAKS-Net are the techniques that are compared in this comparison. These techniques are evaluated on LiTS17, 3DIRCADb, KiTS19, Pancreas, and LOTUS datasets. Performance metrics utilized for comparison include the Jaccard Index (IoU) and the Dice Coefficient. In 2024, Chen et al.²⁰ employed a Multi-Scale Liver Tumor Segmentation Algorithm on the LiTS17 dataset, resulting in a Dice Coefficient of 0.748. for example. You et al.²¹ implemented PGC-Net on the LiTS17 and 3DIRCADb datasets in 2024, achieving Jaccard Indices of 73.63% and 74.16%. In addition, the 2024 He et al.²² study, which employed PAKS-Net, reported Dice Coefficients of 0.893, 0.769, 0.598, and 0.738 for various datasets. The MSFF and EG modules are also noteworthy methods implemented in 2024 Shui et al.²³. A GAN-driven data augmentation strategy was also implemented in 2024 Biswas et al.²⁴. To achieve Dice Coefficients of 85.97% and 80.11% on LiTS17 and 3Dircadb, respectively, the 2023 Wang et al.²⁵ Context Fusion Network implemented Twin-Split Attention (TSA) modules and Multi-Scale-Aware (MSA) skip connections. In contrast, the hybrid FasNet model proposed and tested on the LiTS17 dataset achieved a Jaccard Index of 84.87% and a Dice Coefficient of 87.66%, indicating that it outperformed the current state-of-the-art models.

Table 7 State of Art comparison with the proposed FasNet model with attention and Monte Carlo dropout.

Figure 13 compares the Dice Coefficient of various segmentation models, highlighting the presentation of the proposed FasNet model. Figure 13 shows that the Hybrid FasNet model achieves the highest Dice Coefficient of 87.66, outperforming other models like those by Chen et al., You et al., and Wang et al. This indicates that FasNet provides higher accuracy in liver tumor segmentation than the other methods analyzed.

Fig. 13

Comparison of dice coefficient with proposed hybrid FasNet model.

Conclusion and future work

FasNet presents a remarkable step forward in liver tumor segmentation, combining complementary deep learning techniques to overcome the weaknesses of traditional analysis of imaging data. Combining ResNet-50 and VGG-16 architectures, FasNet captures hierarchical and spatial information, both complex and critical to accurate segmentation. The novelty of the model is that it introduces channel and spatial attention mechanisms, making it even better since FasNet could selectively focus on the most relevant features and spatial regions for suitable segmentation with good accuracy and reliability. Monte Carlo Dropout estimates uncertainty and adds robustness, which is critical for high-stakes medical applications. FasNet showed impressive segmentation results on the LiTS17 dataset with a Dice Coefficient of 0.8766 and a Jaccard Index of 0.8487, thereby supporting accurate detection of liver tumors through early diagnosis and well-planned treatments. Future work will be to optimize the FasNet architecture further to achieve greater efficiency and flexibility within clinical workflows, focusing on more powerful deep learning techniques, including transformer-based models and advanced attention mechanisms, that may even make this segmentation more accurate and widen its scope to more kinds of imaging, such as MRI. Further research would be related to the interfacing of FasNet with other diagnostic devices, along with improvements in real-time processing capabilities, which can speed up the clinical implementation of FasNet. These improvements will make FasNet the reliable and scalable solution to realize accurate diagnosis of liver cancer, which forms the basis for better treatment outcomes and serves as an added tool in the fight against liver cancer.