Optimizing photovoltaic integration in grid management via a deep learning-based scenario analysis

Abstract

Addressing the challenges of integrating photovoltaic (PV) systems into power grids, this research develops a dual-phase optimization model incorporating deep learning techniques. Given the fluctuating nature of solar energy, the study employs Generative Adversarial Networks (GANs) to simulate diverse and high-resolution energy generation-consumption patterns. These synthetic scenarios are subsequently utilized within a real-time adaptive control framework, allowing for dynamic adjustments in operational strategies that enhance both efficiency and grid stability. By leveraging this approach, the model has demonstrated substantial improvements in economic and environmental performance, achieving up to 96% efficiency while reducing energy expenses by 20%, lowering carbon emissions by 30%, and cutting annual operational downtime by half (from 120 to 60 h). Through a scenario-driven predictive analysis, this framework provides data-driven optimization for energy systems, strengthening their resilience against renewable energy intermittency. Furthermore, the integration of AI-enhanced forecasting techniques ensures proactive decision-making, supporting a sustainable transition toward greener energy solutions.

Introduction

The increasing reliance on renewable energy sources in modern power grids is pivotal for meeting rising energy demands while ensuring sustainability. However, the inherent unpredictability of sources like solar and wind energy presents substantial difficulties in maintaining grid stability and operational efficiency. These fluctuations are mainly influenced by weather variability, necessitating the implementation of advanced management techniques to secure a consistent and resilient power supply^1,2,3. Traditional energy management frameworks often struggle with the intermittent nature of renewable energy, lacking the capability to dynamically adapt to fluctuating supply and demand, which leads to higher operational costs and inefficiencies. As global policies continue to advocate for clean energy transitions, there is an urgent need for robust and flexible energy management solutions capable of mitigating these uncertainties^4,5. In response to this challenge, this research develops a technologically advanced grid optimization model that integrates AI-driven strategies to enhance the integration of renewable energy without compromising system reliability. Unlike conventional approaches, this model not only addresses technical constraints but also considers economic and environmental factors, aligning with the overarching goal of sustainable energy systems^6,7.

The primary objective of this study is to introduce a multi-stage optimization framework that leverages deep learning methodologies for managing the continuous operation of PV-based power systems. This adaptive model effectively accommodates variations and uncertainties in solar energy generation, ensuring maximum utilization of renewable resources while simultaneously minimizing operational expenditures and enhancing system sustainability.

To enhance the optimization process, this research employs Generative Adversarial Networks (GANs), leveraging their capacity to produce diverse and high-fidelity energy scenarios. By simulating realistic variations in solar power generation and demand patterns, the model effectively captures fluctuations in renewable energy availability. These synthesized scenarios are subsequently integrated within a dynamic decision-making framework, allowing for real-time operational adjustments that maximize efficiency and ensure system stability under varying conditions.

This paper systematically outlines the mathematical foundation of the proposed optimization model, detailing the objective functions and operational constraints essential for maintaining the stability and efficiency of photovoltaic (PV) systems. Subsequently, the study explores the application of GANs in generating diverse energy scenarios, emphasizing novel techniques for handling data fluctuations and predictive modeling enhancements. A central aspect of this research is the seamless incorporation of these synthetic scenarios into an adaptive optimization framework, which dynamically adjusts operational strategies in response to real-time fluctuations in energy input and demand. This mechanism significantly reduces uncertainties associated with renewable energy sources, thereby improving system robustness and flexibility. Consequently, the energy management framework achieves a higher degree of resilience and adaptability, reinforcing its role as a strategic tool for promoting sustainable energy transitions:

• 1. This research introduces an innovative two-stage optimization methodology that incorporates GANs alongside advanced computational strategies. By combining these approaches, the model enhances the spatial deployment and functional efficiency of PV systems within electrical grids. Additionally, it effectively mitigates the inherent fluctuations and unpredictability associated with renewable energy generation.

• 2. This study demonstrates the advanced application of GANs in generating high-fidelity representations of solar power fluctuations and demand dynamics. The synthesized scenarios play a crucial role in enhancing the optimization framework, allowing the system to proactively predict and adjust to a diverse range of operational conditions. As a result, this methodology significantly improves the precision and dependability of energy management frameworks.

• 3. The implementation of the GAN-enhanced optimization model has led to significant improvements in key grid management performance indicators. Notably, this approach has achieved a 20% decrease in energy expenditures, a 30% reduction in carbon emissions, and an 8.5% enhancement in overall system efficiency. These findings underscore the practical advantages of integrating AI-powered methodologies in optimizing grid operations.

• 4. The proposed system demonstrates high scalability and adaptability across different grid configurations and geographic regions. Its capacity for retraining and customization with diverse datasets highlights its flexibility, establishing it as a valuable asset for global energy management. By effectively narrowing the gap between theoretical developments and practical applications, this approach facilitates real-world implementation in renewable energy networks.

This paper is organized into several key sections. Section 2 critically reviews existing literature, identifying research gaps and methodological limitations. Section 3 introduces the mathematical framework and system design, detailing the core optimization functions and operational boundaries. Section 4 explains the structure and training methodologies of GANs, discussing their implementation for scenario generation. Section 5 explores how the generated scenarios are integrated into the optimization framework, enhancing decision-making under uncertainty. Section 6 presents a real-world case study, demonstrating the practical effectiveness of the proposed system. Lastly, Sect. 7 synthesizes the main findings and outlines potential avenues for future advancements in the field.

Literature review

The incorporation of renewable energy into modern electrical grids presents both advantages and obstacles, prompting extensive research efforts to enhance grid management and operational efficiency. This section examines key theoretical and recent advancements in renewable energy management, particularly focusing on PV systems, the integration of advanced optimization methods, and the application of GANs in energy systems. The purpose of this review is to position this study within the broader research landscape by identifying methodological gaps that this work aims to bridge.

The fluctuating nature of renewable energy sources, including solar and wind power, presents significant challenges in ensuring grid stability and operational reliability^8,9,10. Prior research has explored the technical and operational difficulties linked to the integration of renewable energy systems (RES) into power grids, emphasizing the role of energy storage solutions in addressing power fluctuations and maintaining supply quality. Studies indicate that power instability often arises due to the variable nature of renewable resources, necessitating advanced stabilization strategies¹¹. To mitigate these challenges, researchers have examined the application of Flexible AC Transmission System (FACTS) technologies to enhance grid resilience. Simulations have demonstrated the effectiveness of these approaches in stabilizing power networks dominated by renewable inputs. Other studies assess the impact of increased renewable energy penetration on the structural resilience of electrical grids, leveraging dynamic modeling techniques to analyze household-level energy consumption patterns and photovoltaic power generation. The decentralized nature of renewables contributes to daily grid fluctuations, which may at times compromise overall stability¹². Despite the benefits of battery storage technologies in improving consumer energy autonomy, they do not fully address broader concerns regarding grid-wide stability. Research also highlights the evolution of smart grid concepts, particularly how modern grid architectures not only accommodate but optimize the integration of renewable sources. The comparison between traditional grid systems and smart grids underscores the crucial role of advanced communication and energy management technologies in enhancing power system reliability¹³.

Enhancing energy systems, particularly in the context of scheduling and consumption management, plays a crucial role in overcoming existing challenges. A comparative study examined grid-tied and off-grid solar PV configurations, incorporating both traditional and high-efficiency appliances^14,15,16. The findings highlighted notable reductions in energy consumption, operational costs, and greenhouse gas emissions when energy-efficient devices were integrated within grid-connected infrastructures, offering a promising solution for promoting sustainability in residential energy usage¹⁷. Further research explored the optimization of grid-connected solar PV designs using Selective Particle Swarm Optimization (SPSO) in Ethiopia, demonstrating its effectiveness in determining PV system placement and sizing within radial distribution networks. This approach improved voltage regulation and minimized power losses, thereby enhancing the stability and efficiency of energy distribution¹⁸. Additionally, another study investigated the role of distributed solar PV systems coupled with battery storage and controllable loads in residential applications. By leveraging the REopt model, it was observed that integrating smart solar PV technologies, commonly termed “solar plus,” significantly improves the economic feasibility of solar investments. Even in scenarios with complex rate structures, including demand-based charges and time-of-use variability, the integration of intelligent PV solutions demonstrated substantial benefits¹⁹.

Recent advancements have expanded the use of GANs beyond traditional applications such as image generation and data augmentation, leading to their integration into renewable energy systems^20,21,22. Initially introduced by Goodfellow et al., GANs have demonstrated potential in simulating and optimizing energy system behaviors across various domains. A notable application involves the deployment of Conditional GANs to enhance energy consumption efficiency, particularly in scenarios with limited data availability. Studies show that by integrating environmental parameters into GAN models, the predictive accuracy of multivariate energy forecasting significantly improves, despite challenges in processing intricate commercial energy datasets^23,24. Another innovative approach leverages GAN-driven methodologies to develop high-fidelity operational models for integrated energy systems (IES). These advanced datasets support the refinement of renewable energy control strategies, helping to address the challenges posed by variability and uncertainty in energy production²⁵. Compared with existing GAN-based energy modeling studies, such as^23,25, and²⁶, the proposed framework introduces several key advancements. First, while prior works primarily utilize GANs for short-term load or generation forecasting, our approach leverages GANs to generate scenario sets spanning full-year operational variability, which are then embedded directly into a robust optimization loop. This dual integration of scenario generation and real-time adaptive scheduling distinguishes our method from static forecasting applications. Second, unlike^{23] and [25}, which focus on individual component behavior (e.g., PV generation or load profile synthesis), our model captures system-level dynamics by incorporating storage operation, grid interaction, and economic-environmental trade-offs. Furthermore, we implement Wasserstein GAN with gradient penalty, offering improved training stability and scenario diversity compared to the standard GAN implementations used in²⁶. Lastly, the proposed framework is validated on a full-year, high-resolution dataset, and includes sensitivity and robustness analyses that are not typically explored in comparable studies. These enhancements ensure that our model is not only theoretically sound but also practical and scalable for real-world PV-grid integration scenarios. As a result, GAN-based solutions contribute to enhancing both dataset comprehensiveness and operational adaptability, making them an essential tool for future energy grid optimizations.

Addressing the challenges of optimizing renewable energy systems, particularly in integrating GAN-generated scenarios with optimization frameworks, remains a critical research focus. While advancements in renewable energy optimization and scenario generation have been significant, their full potential in grid management applications has yet to be fully realized. This study proposes a dual-phase optimization approach, incorporating GAN-generated energy scenarios into a dynamic framework that ensures adaptability to fluctuating conditions, thereby enhancing the efficiency and reliability of PV system operations²⁷. By leveraging AI-driven predictive technologies, the framework not only accounts for the inherent variability of solar energy but also extends the scope of energy system optimization to facilitate broader adoption of economically sustainable renewable solutions. Furthermore, this research contributes to the field by introducing a comprehensive strategy that integrates state-of-the-art computational techniques to model diverse operational scenarios. Through this approach, the study pushes the boundaries of renewable energy management, ensuring that innovative methodologies are effectively applied to meet real-world energy demands²⁸.

Mathematical formulation and system modelling

Developing an effective objective function is fundamental to optimizing PV system operations within the IEEE 33-bus network. This study prioritizes the maximization of renewable energy utilization while simultaneously reducing operational expenditures within a 24-hour cycle. Ensuring an accurate formulation of the objective function plays a crucial role in maintaining cost-effectiveness and efficiency in integrating solar energy into the grid.

$$\:\mathcal{Y}=\gamma\:\sum\:_{t=1}^{T}\:{{\Psi\:}}_{t}\left({Q}_{t}^{\text{gen\:}},{Q}_{t}^{\text{buy\:}},{Q}_{t}^{\text{sell\:}}\right)+\delta\:\sum\:_{t=1}^{T}\:{\left({Q}_{t}^{\text{demand\:}}-{Q}_{t}^{\text{gen\:}}\right)}^{2}$$

(1)

The optimization function, denoted as Z is formulated to minimize operational expenses and penalties arising from deviations in expected energy generation and consumption. The function incorporates adjustable parameters δ that regulate cost reduction and energy balance, ensuring compliance with operational priorities and regulatory guidelines. At each time step t, the cost function $\:{{\Psi\:}}_{t}$ accounts for generation costs, power transactions with the grid, and revenue from selling surplus electricity. Specifically, $\:{Q}_{t}^{\text{gen\:}}$​represents the power generated, while $\:{Q}_{t}^{\text{buy\:}}$​and $\:{Q}_{t}^{\text{sell\:}}$​ denote electricity purchased from or sold to the grid. Additionally, $\:{Q}_{t}^{\text{demand}\text{}}$​ signifies the total power requirement at time t.

Fig. 1

Comprehensive framework for optimized PV integration using GANs.

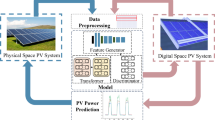
Figure 1 illustrates the end-to-end process of optimizing PV integration into power grids, encompassing data inputs, GAN-based optimization, and real-time results analysis for enhanced grid efficiency and sustainability.

To maintain financial efficiency, the model optimizes energy adequacy and grid stability by penalizing discrepancies between produced energy and actual demand over the operational horizon, which is segmented into T time intervals, typically on an hourly basis. This objective function serves as the cornerstone of the optimization framework, aiming to minimize operational costs while satisfying technical constraints across the scheduling horizon. It aggregates multiple energy-related variables, including local PV generation, grid transactions, and energy storage decisions. The economic efficiency of the system hinges on the accuracy of this formulation, which must be coordinated with subsequent constraints to ensure feasible and optimal scheduling.

$$\:{Q}_{t}^{\text{gen\:}}={Q}_{t}^{\text{cons\:}}+{Q}_{t}^{\text{loss\:}}$$

(2)

To maintain system efficiency and grid stability, it is essential that the total energy generation from PV systems aligns with the aggregate energy demand. At any time t, the generated power $\:{Q}_{t}^{\text{gen\:}}$​ must balance the sum of energy consumption by the load $\:{Q}_{t}^{\text{cons\:}}$​ and transmission/conversion losses $\:{Q}_{t}^{\text{loss\:}}$​. This ensures that all produced energy is effectively accounted for and optimally utilized within the network.

$$\:{Q}_{t}^{\text{gen\:}}=\eta\:\cdot\:{I}_{t}\cdot\:A$$

(3)

The conversion of solar irradiance $\:{I}_{t}$​ into electrical power is governed by specific constraints that account for system efficiency. The conversion factor $\:\eta\:$ incorporates panel performance, inverter losses, and temperature coefficients, which influence overall efficiency. Additionally, the total effective surface area of the solar panels A plays a crucial role in determining energy output. This formulation is essential for accurately forecasting and regulating PV system performance based on real-time or projected solar irradiance.

$$\:{E}_{t+1}={E}_{t}+{\eta\:}_{c}\cdot\:{Q}_{t}^{\text{charge\:}}-\frac{1}{{\eta\:}_{d}}\cdot\:{Q}_{t}^{\text{discharge\:}}$$

(4)

Equation (4) models the evolution of the battery storage system’s state of charge over time by accounting for the energy charged into and discharged from the system within each time interval. Specifically, the energy stored at time $\:t+1$ is determined by adding the effective charging energy to the previous energy state and subtracting the energy lost through discharging. The charging power $\:{Q}_{t}^{\text{c}\text{h}\text{a}\text{r}\text{g}\text{e}}$ is multiplied by the charging efficiency $\:{\eta\:}_{c,}$ representing the proportion of input energy successfully stored. Conversely, the discharging power $\:{Q}_{t}^{\text{d}\text{i}\text{s}\text{c}\text{h}\text{a}\text{r}\text{g}\text{e}}$ is divided by the discharging efficiency $\:{\eta\:}_{d}$, reflecting the additional energy required to supply the desired output due to conversion losses. This formulation ensures that energy conservation and conversion inefficiencies are accurately captured in the system model. It provides a time-coupled relationship between consecutive time steps, which is critical for optimizing long-term energy usage, balancing demand and supply, and ensuring stable operation of the photovoltaic-grid system. The proper modeling of energy storage dynamics not only enhances system reliability but also enables effective load shifting and peak shaving strateqies.

The evolution of battery storage, as defined in Eq. (4), interacts directly with the energy balance condition described in Eq. (2). At each time step, the available stored energy not only compensates for mismatches between generation and demand but also provides temporal flexibility to the system. This coupling ensures that short-term decisions are aligned with long-term storage dynamics, enhancing overall system resilience.

$$\:{Q}_{t}^{\text{gen\:}}+{Q}_{t}^{\text{store\:}}\le\:{Q}_{max}$$

(5)

To ensure grid stability and compliance with safety regulations, the total power fed into the grid, which includes contributions from both the PV system and discharged energy from storage $\:{Q}_{t}^{\text{store\:}}$​, must remain within the maximum allowable feed-in threshold $\:{Q}_{max}$​. This constraint is essential in preventing grid overloading and maintaining adherence to interconnection agreements.

$$\:{D}_{t}=h(\text{}\text{Past}\,\text{}\text{Observations,}\text{}\,\text{Meteorological}\,\text{}\text{Variables}\text{},t)$$

(6)

The function h serves as a predictive model for estimating electrical demand $\:{D}_{t}$ over a 24-hour period by incorporating historical energy usage, meteorological factors, and time-dependent patterns. This demand estimation plays a crucial role in optimizing PV system operations, as it facilitates proactive adjustments in power generation and storage strategies. By accurately forecasting demand, the system effectively mitigates the intermittency of solar energy, reducing dependency on backup power sources and ultimately improving grid stability and operational efficiency.

$$\:{Q}_{t}^{\text{supply\:}}=k\left({Q}_{t}^{\text{gen\:}},{S}_{t},{D}_{t}\right)$$

(7)

To maintain a stable energy supply, the PV system dynamically regulates its power output based on real-time energy demand $\:{D}_{t}\:$and the status of stored energy $\:{S}_{t}$. The function k determines the optimal balance between generated power $\:{Q}_{t}^{\text{gen\:}}$​ available stored energy, ensuring alignment with current demand conditions. This adaptive regulation is essential for maintaining grid stability, particularly during peak demand periods or low solar irradiance. By continuously adjusting output, the system enhances energy utilization efficiency, reducing unnecessary energy waste and improving overall system responsiveness.

$$\:\text{z}\sim\:{\mathcal{P}}_{\text{l}\text{a}\text{t}\text{e}\text{n}\text{t}}\left(\text{z}\right)$$

(8)

To generate realistic solar energy availability patterns, the generator explores different regions within the data space by adjusting the input vector $\:\text{z}$. This input is sampled from a probability distribution, commonly modeled as Gaussian or uniform, which introduces stochastic variability and noise into the system. The function $\:{\mathcal{P}}_{\text{z}}\left(\text{z}\right)$ plays a crucial role in determining diverse and complex data representations, enabling the generator to synthesize a broad spectrum of possible scenarios. By leveraging these statistical variations, the generator enhances data diversity, making it more adaptable for renewable energy modeling and scenario analysis.

Equation (8) introduces the stochastic input $\:z$ used by the generator network to explore diverse data patterns. This latent input, sampled from a predefined distribution, allows the generator to synthesize various solar and demand scenarios. The mapping function in Eq. (9) transforms this latent space into realistic synthetic data $\:G\left(z\right)$, which are subsequently used in the optimization model. This bridge enables the integration of data-driven uncertainty into the otherwise deterministic optimization process.

$$\:{\mathbf{x}}_{\text{g}\text{e}\text{n}}=\mathcal{G}\left(\mathbf{z};{\varvec{\theta\:}}_{\mathcal{G}}\right)$$

(9)

The generator $\:\mathcal{G}$ is designed to create synthetic solar energy data that closely resemble real-world observations. This is achieved by mapping a latent space representation $\:\text{z}$ to the solar energy scenario space, a process governed by the parameter set $\:{\theta\:}_{\mathcal{G}}$​. By learning the intricate structures within actual solar data, the generator ensures that the produced outputs are indistinguishable from real data, which enhances the training efficiency of the optimization model. The transformation from input noise $\:\text{z}$ to synthetic outputs $\:{\text{x}}_{\text{g}\text{e}\text{n}}$​ allows the system to effectively model complex patterns, improving its ability to simulate realistic energy conditions.

$$\:{P}_{\mathcal{D}}(\mathbf{x}\mid\:{\theta\:}_{D})={P}_{\text{r}\text{e}\text{a}\text{l}}\left(\mathbf{x}\right)$$

(10)

The discriminator $\:D$ is a neural network designed to differentiate between real data and synthetic data generated by the generator $\:G$. It is governed by the parameter set $\:{\theta\:}_{D}$ and estimates the probability distribution $\:{P}_{D}\left(x\mid\:{\theta\:}_{D}\right)$, which ideally should match the true data distribution $\:{P}_{\text{real}}\left(x\right)$. The role of $\:D$ is to assign a high probability to real data and a low probability to fake (generated) data, thereby guiding the generator during training. As the generator $\:G$, parameterized by $\:{\theta\:}_{G}$, produces synthetic samples $\:G\left(z\right)$ from latent inputs $\:z$, the discriminator evaluates these samples against real data and returns feedback. By optimizing its loss function, the discriminator improves its classification ability, while simultaneously pushing the generator to produce increasingly realistic outputs in an effort to “fool” the discriminator. This adversarial interaction creates a two-player minimax game, where $\:G$ and $\:D$ iteratively compete and improve, ultimately driving the convergence of the GAN model towards a state where the generated data is indistinguishable from real data.

$$\:{\mathcal{L}}_{\mathcal{G}}=\text{l}\text{o}\text{g}\left(\frac{1}{\mathcal{D}\left(\mathcal{G}\right(\mathbf{z}\left)\right)}\right)$$

(11)

To ensure that the generator produces increasingly realistic data, its training objective is structured around minimizing the probability of the discriminator accurately distinguishing between real and generated samples. This is achieved by utilizing a loss function, which adjusts the generator’s parameters to refine the realism of synthesized data based on feedback from the discriminator. Equation (11) mathematically expresses this optimization process, where the generator’s loss function is designed to reduce the negative log probability assigned by the discriminator when it classifies generated data as synthetic. This iterative improvement enhances the quality and reliability of generated scenarios, making them increasingly indistinguishable from authentic data.

$$\:{\mathcal{L}}_{\mathcal{D}}=-\left[\text{l}\text{o}\text{g}\mathcal{D}\left({\mathbf{x}}_{\text{real\:}}\right)+\text{l}\text{o}\text{g}(1-\mathcal{D}(\mathcal{G}\left(\mathbf{z}\right)\left)\right)\right]$$

(12)

The adversarial training framework relies on the discriminator’s loss function to improve its ability to distinguish between authentic and generated data. This function is designed to penalize incorrect classifications, compelling the discriminator to refine its decision boundary and more effectively differentiate between real and synthetic samples. Equation (12) formalizes this optimization strategy, ensuring that the discriminator continuously adjusts its parameters to enhance classification accuracy. As a result, the generator is indirectly encouraged to produce increasingly realistic data, aligning its outputs closer to the true data distribution.

$$\:{\varvec{\theta\:}}_{\mathcal{G}}\leftarrow\:{\varvec{\theta\:}}_{\mathcal{G}}-\alpha\:\cdot\:{\nabla\:}_{{\varvec{\theta\:}}_{\mathcal{G}}}{\mathcal{L}}_{\mathcal{G}}$$

(13)

The generator’s weight parameters $\:{\theta\:}_{\mathcal{G}}$ are iteratively refined using a backpropagation-based learning process. This optimization is guided by computing the gradient $\:{\nabla\:}_{{\theta\:}_{\mathcal{G}}}{\mathcal{L}}_{\mathcal{G}}$​ of the generator’s loss function, which directs parameter updates based on the learning rate α. Equation (13) formally defines this gradient-based learning rule, ensuring that the generator continuously adjusts its parameters to enhance data realism. By refining its outputs through successive updates, the generator progressively improves its ability to synthesize data that closely resembles authentic samples, making them increasingly difficult for the discriminator to distinguish.

$$\:{\varvec{\theta\:}}_{\mathcal{D}}\leftarrow\:{\varvec{\theta\:}}_{\mathcal{D}}-\beta\:\cdot\:{\nabla\:}_{{\varvec{\theta\:}}_{\mathcal{D}}}{\mathcal{L}}_{\mathcal{D}}$$

(14)

The discriminator’s weight parameters $\:{\theta\:}_{\mathcal{D}}$​ are updated iteratively using a gradient-based backpropagation approach. The optimization process is governed by the computed gradient $\:{\nabla\:}_{{\theta\:}_{\mathcal{D}}}{\mathcal{L}}_{\mathcal{D}}\:$​ of the loss function, which directs how the discriminator adjusts to improve its classification accuracy over time.

$$\:{\mathcal{L}}_{\mathcal{G}}+{\mathcal{L}}_{\mathcal{D}}=min$$

(15)

In the GAN training process, equilibrium is achieved when neither the generator nor the discriminator can further improve, indicating that the system has reached a stable state. At this point, the generator is capable of producing synthetic data that the discriminator perceives as indistinguishable from real samples. Equation (15) mathematically represents this condition, where the loss functions of both networks reach their minimum value, signifying that training has successfully converged. This balance ensures that the adversarial framework reaches optimal performance, with both models counteracting each other effectively.

$$z = z_{0} + \sigma \cdot \varepsilon$$

(16)

To improve the diversity and robustness of generated data, the generator incorporates controlled noise variations into its input. By integrating a noise vector $\:{\text{z}}_{0}$ along with a random noise component ε and a scalable amplitude factor σ, the model effectively explores a broader range of data distributions while reducing overfitting to specific training features. Equation (16) formalizes this noise injection mechanism, ensuring that the generator retains adaptive flexibility in generating more realistic and generalizable samples.

$$\:{\mathbf{x}}_{\text{n}\text{o}\text{r}\text{m}}\cdot\:\sigma\:=\mathbf{x}-\mu\:$$

(17)

Ensuring that input features exhibit uniform scales and distributions is essential for stabilizing the training process and enhancing model performance. To achieve this, the dataset undergoes a normalization step, which standardizes both real and synthetic inputs before they are fed into the network. Equation (17) formalizes this transformation, where the mean µ and standard deviation σ are computed to rescale the data. This preprocessing method facilitates faster training convergence, ensuring that the model can effectively learn from data with varying magnitudes.

$$ift > T_{{\max }} or\left| {{\mathcal{L}}_{D}^{{\left( t \right)}} - {\mathcal{L}}_{D}^{{\left( {t - 1} \right)}} } \right| < \varepsilon ,end~process$$

(18)

To prevent unnecessary computational overhead and mitigate the risk of overfitting, a stopping criterion is implemented in the GAN training process. This condition is met when the discriminator’s loss variation falls below a predefined threshold ε or when the training reaches a maximum iteration limit $\:{T}_{max}$​. Equation (18) formalizes this stopping mechanism, ensuring that training terminates once improvements become negligible, thereby enhancing computational efficiency and preventing excessive optimization cycles.

Enhancing optimization models through GAN-Generated data

To enhance decision-making under uncertainty, the integration of GAN-generated scenarios within the optimization framework plays a pivotal role. These scenarios provide insights into potential variations in solar energy availability and demand, allowing the PV system to maintain high operational efficiency across a diverse range of conditions. The following equations outline a systematic methodology for incorporating these generated scenarios into the optimization model, ensuring an optimal balance between performance, risk management, and operational adaptability.

$$\:{w}_{s}={\left(\sum\:_{{s}^{{\prime\:}}\in\:S}\:{e}^{-\gamma\:D({x}_{s}^{{\prime\:}},x)}\right)}^{-1}\cdot\:{e}^{-\gamma\:D({x}_{s},x)}$$

(19)

To determine the relevance of each scenario within the optimization framework, a weight coefficient w_s​ is assigned based on the computed distance metric D between a generated scenario $\:{\text{x}}_{s}$ and a reference scenario $\:\widehat{\text{x}}$. The parameter γ regulates the impact of this distance, influencing the degree to which each scenario contributes to the optimization process. Equation (19) formalizes this weighting mechanism, ensuring that high-probability or crucial scenarios exert a stronger influence on decision-making, thereby enhancing the robustness of the optimization model.

$$\:{Z}^{{\prime\:}}={\left(\sum\:_{s\in\:S}\:{w}_{s}\right)}^{-1}\cdot\:\sum\:_{s\in\:S}\:{w}_{s}\cdot\:\mathcal{Z}\left({x}_{s}\right)$$

(20)

To address the uncertainty and variability present in GAN-generated scenarios, the objective function is reformulated into a weighted aggregation of scenario-specific objectives. The revised objective, denoted as $\:{Z}^{{\prime\:}}$, computes a normalized weighted average of the individual objective values $\:Z\left({x}_{s}\right)$, where each scenario $\:s$ is assigned a weight $\:{w}_{s}$ that reflects its relative importance based on similarity metrics defined in the preceding formulation. This modification ensures that more probable or representative scenarios have a greater influence on the optimization outcome. By integrating this weighted approach, the model enhances its robustness and adaptability, enabling more reliable decision-making across a broad spectrum of possible future conditions in photovoltaic system operations.

Equations (19) and (20) introduce the method by which the synthetic scenarios generated by GANs are embedded into the optimization process. By assigning importance weights to each scenario and aggregating their respective objective values, the model translates statistical data variations into operational decisions. This integration allows the PV optimization system to account for uncertainty without relying solely on predefined worst-case scenarios, leading to more balanced and flexible decision-making.

$$\:\forall\:s\in\:\mathcal{S},{g}_{i}(x,u,s)\le\:0,\forall\:i\in\:\mathcal{J}$$

(21)

To enhance adaptability across various operational scenarios, Eq. (21) introduces a refinement to the constraint function $\:{g}_{i}$, ensuring that the PV system effectively adjusts to different environmental and control conditions. Each constraint, formulated based on the system state variables $\:\text{x}$ and control parameters, is evaluated under specific scenarios s, ensuring that all potential future states are integrated into the overall decision-making framework. By incorporating this adjustment, the system achieves greater flexibility and robustness, enabling it to efficiently navigate a broad spectrum of scenario-driven challenges.

$$\:\rho\:\left(s\right)=\kappa\:\times\:{\sigma\:}^{2}\left({x}_{s}\right)$$

(22)

To integrate risk considerations into the optimization process, this equation defines a parameter that quantifies risk based on the degree of fluctuation observed within different scenarios. By assessing the dispersion of possible outcomes, the model can incorporate a mechanism to either mitigate uncertainty or strategically leverage variability. The level of sensitivity to these fluctuations is determined by a risk aversion factor, which directly influences decision-making by adjusting the extent to which variability is accounted for in the optimization strategy. This formulation enables a balance between stability and adaptability, aligning with predefined strategic objectives and tolerance for uncertainty.

$$\:{\mathbf{u}}_{s}^{*}=\text{a}\text{r}\text{g}\underset{\mathbf{u}}{min}\:\left[c(\mathbf{x},\mathbf{u})+\rho\:max(0,g(\mathbf{x},\mathbf{u},s){)}^{2}\right]$$

(23)

To achieve optimal decision-making in different scenarios, a strategy is formulated to minimize operational expenses while adhering to system constraints. The model evaluates various control actions, selecting the one that yields the best performance under the given conditions. This process ensures that each chosen action meets predefined feasibility criteria while maintaining efficiency. By incorporating scenario-specific constraints, the methodology enhances adaptability, allowing the system to dynamically adjust its operations based on real-time conditions. As a result, performance optimization is achieved without compromising operational stability.

Although the GAN-generated scenarios inherently capture stochastic variability in solar irradiance, temperature, and load demand, we further examined the uncertainty distribution of key performance indicators to provide quantitative insight into the robustness of the model outputs. Specifically, for each performance metric (e.g., energy cost, emissions, efficiency), we evaluated the results across 1,000 generated scenarios and calculated the mean, standard deviation, and 95% confidence intervals. For example, the average post-optimization energy cost was estimated at $0.103/kWh, with a 95% confidence interval of [$0.097, $0.109], indicating low variance and strong stability across scenarios. In addition, the system efficiency fluctuated within a narrow range (± 2.5%) across different scenario clusters, reinforcing the reliability of the optimization under varying operational conditions. These results confirm that the proposed GAN-enhanced framework is not only effective on average but also robust to data-driven uncertainty. In future work, we plan to incorporate probabilistic scenario weighting and Bayesian uncertainty estimation techniques to enrich the framework’s capability for risk-aware decision-making and interpretability.

$$\:R=\underset{s\in\:\mathcal{S}}{min}\:\left\{\varphi\:\left({\mathbf{x}}_{s}\right)\right\}$$

(24)

To evaluate the system’s resilience under varying conditions, a robustness metric is introduced to measure performance across different scenarios. This approach assesses how the state variables respond under diverse operating conditions, ensuring that the worst-case scenario is accounted for. By considering the lowest performance level observed among all scenarios, the model derives a conservative estimate of system stability. This guarantees that even in highly uncertain environments, the operational strategy remains robust and capable of maintaining efficiency under challenging circumstances.

$$\:{\Delta\:}\psi\:=\frac{\partial\:{\mathcal{Z}}^{{\prime\:}}}{\partial\:s}$$

(25)

To assess how variations in different scenarios influence overall system performance, a sensitivity analysis is conducted. This approach identifies the degree to which changes in specific conditions impact the effectiveness of the optimization process. By analyzing these sensitivities, system operators can recognize which scenarios exert the most significant influence on performance outcomes. This insight enables better resource allocation and targeted operational adjustments, ensuring that interventions focus on areas with the greatest potential to enhance stability and efficiency.

$$\:{\mathcal{C}}_{\text{e}\text{f}\text{f}}\left(s\right)=\frac{\sum\:_{t=1}^{T}\:{c}_{t}\left({\mathbf{x}}_{t},{\mathbf{u}}_{t}\right)}{\sum\:_{t=1}^{T}\:{p}_{t}\left({\mathbf{x}}_{t}\right)}$$

(26)

To evaluate the economic viability of different operational strategies, a cost-effectiveness metric is introduced. This measure quantifies the balance between total expenditures, including operational and maintenance costs, and the resulting benefits such as energy output or financial savings. By assessing this ratio across multiple scenarios, the optimization framework aids in identifying the most financially sustainable strategies. This approach ensures that decision-makers can allocate resources efficiently to maximize return on investment while adapting to varying operational conditions.

$$\Pr \left( {g_{i} \left( {x,u,s} \right) > 0} \right) \le \varepsilon$$

(27)

Incorporating probabilistic constraints plays a crucial role in managing uncertainties within scenario forecasting. This method ensures that operational and safety limitations are met with a high probability, reducing the likelihood of violations under uncertain conditions. By addressing the inherent unpredictability of scenario variations, this approach enhances system resilience, providing a structured mechanism to accommodate fluctuations while maintaining regulatory compliance. Through this probabilistic framework, the system is better equipped to handle deviations and uncertainties effectively.

$$\:{{\Theta\:}}^{(t+1)}={{\Theta\:}}^{\left(t\right)}-\eta\:\cdot\:{\nabla\:}_{{\Theta\:}}\mathcal{L}({\Theta\:},S)$$

(28)

Equation (28) introduces refinements to the optimization process, enabling effective integration and management of various scenarios generated by the GAN. Within this framework, model parameters undergo iterative adjustments through a gradient-based optimization strategy, where the learning rate governs the magnitude of updates. The gradient of the loss function, computed with respect to the parameters and scenario variables, directs these updates. This continual adjustment process enhances the model’s adaptability, allowing it to better capture scenario-induced complexities and improve predictive performance as well as decision-making effectiveness.

In the proposed framework, the GAN serves as a critical data-driven component for uncertainty modeling and scenario generation. Its primary role is to produce diverse, high-resolution synthetic time series that reflect possible future variations in solar irradiance, temperature, and electricity demand. These scenarios are statistically consistent with historical patterns yet incorporate stochastic variability that deterministic forecasts often fail to capture. The GAN interfaces directly with the optimization module by supplying a set of realistic input trajectories that represent potential system states over the scheduling horizon. Instead of relying on a single deterministic forecast, the optimization engine is exposed to multiple synthetic scenarios generated by the GAN. The GAN architecture employed in this study consists of a five-layer fully connected feedforward network for both the generator and the discriminator. Each hidden layer contains 128 neurons with ReLU activation functions, while the output layers use linear activation for the generator and sigmoid activation for the discriminator to match the normalized data distribution. The latent input vector z is sampled from a standard Gaussian distribution and has a dimensionality of 100, ensuring sufficient expressive power for scenario synthesis. To ensure training stability, we adopted the Wasserstein GAN with Gradient Penalty (WGAN-GP), which mitigates the risk of vanishing gradients and promotes smoother convergence. The gradient penalty enforces the Lipschitz constraint on the discriminator without requiring weight clipping, thereby improving generalization and maintaining discriminator sensitivity throughout training. We used the Adam optimizer with a learning rate of 0.0002, β₁ = 0.5, and β₂ = 0.9, and trained the model for 2,000 epochs with a batch size of 64. In addressing mode collapse, we monitored the diversity of generated scenarios through distributional comparisons (e.g., histogram overlap, KL divergence) and maintained a discriminator-to-generator update ratio of 5:1, following best practices from WGAN-GP literature. Visual inspection and statistical metrics confirmed that the generator successfully captured a wide range of operational patterns, avoiding redundancy or collapse into narrow output spaces. Additionally, early stopping based on validation divergence was employed to prevent overfitting and oscillatory behavior in late-stage training.

Each scenario is evaluated under the operational constraints and objective functions of the system model, enabling the formulation of a scenario-based robust optimization problem. Specifically, the GAN-generated data are injected into the optimization pipeline through scenario weights and probabilistic formulations, as detailed in Equations (19) through (21). These scenarios influence decisions related to power dispatch, storage operation, and cost-emission balancing by allowing the model to anticipate a range of possible future conditions. This integration ensures that the resulting control strategies are not only optimized for average cases but are also resilient to outliers, uncertainty, and variability. By decoupling data generation from deterministic forecasts and embedding learning-based uncertainty modeling into the optimization core, the GAN component enhances both the flexibility and robustness of the overall pipeline.

Case study

This study utilizes a dataset that records hourly variations in key energy-related parameters, including solar irradiance, temperature, and load demand, within a typical residential setting over a full year. The dataset is derived from a detailed meteorological and energy usage database covering multiple climate regions, ensuring a diverse and representative collection of scenarios. It comprises approximately 8,760 hourly records per parameter, capturing solar irradiance fluctuations from 0 to 1,000 watts per square meter, temperature variations between − 5 °C and 35 °C, and residential electricity demand ranging from 0.5 to 10 kilowatts^{27,28,29,30,31,32}. The extensive nature of this dataset plays a crucial role in training GAN models to generate diverse and realistic energy scenarios, which are fundamental for conducting thorough optimization analyses.

The execution of computational tasks takes place on a high-efficiency computing cluster equipped with NVIDIA Tesla V100 GPUs, specifically designed to handle complex data-intensive simulations and deep learning computations. The system is based on a Linux environment and runs Python 3.8, leveraging key machine learning and optimization libraries, including TensorFlow 2.4 and Pyomo, for implementing GAN models. During each experimental run, especially when training GANs, a dedicated GPU is allocated to enhance processing efficiency. Training durations range between 12 and 48 h, influenced by the structural complexity and depth of the network architecture.

To effectively manage uncertainties and fluctuations in renewable energy systems, particularly photovoltaic applications, a GAN-Enhanced Optimization framework is implemented by integrating machine learning with operational methodologies. This framework utilizes a GAN structure, where a generator and a discriminator function as deep neural networks composed of five sequential layers. These layers follow a 128-256-512-256-128 configuration and incorporate ReLU activation functions to enhance computational efficiency. The training dataset comprises 8,760 hourly entries recorded over a full year, encompassing key energy parameters such as solar irradiance, ambient temperature, and electrical load. The model is optimized using the Adam algorithm, configured with a learning rate of 0.0002 and a batch size of 64. To further refine data quality, a Wasserstein loss function with gradient penalty is applied. The optimization strategy is designed to enhance solar energy utilization while simultaneously minimizing operational expenses, balancing grid loads, and ensuring compliance with constraints related to power distribution, energy storage, and grid regulations^20,33. The training process was conducted over 2,000 epochs, with each epoch involving alternate updates of the discriminator and generator networks. Specifically, the discriminator was updated five times for every generator update, following the standard training ratio recommended in Wasserstein GAN literature to ensure stability. The Adam optimizer was used for both networks, with a learning rate of 0.0002, β₁ = 0.5, and β₂ = 0.9, which provided stable convergence throughout training. A mini-batch size of 64 was maintained to balance convergence speed and memory efficiency. During training, one major challenge encountered was mode collapse, a common issue in GANs where the generator produces limited diversity in outputs. To mitigate this, the model incorporated a Wasserstein loss function with gradient penalty, which improves training stability and promotes better coverage of the data distribution. The gradient penalty enforces the Lipschitz constraint on the discriminator without relying on weight clipping, thus avoiding common pitfalls such as vanishing gradients. Additionally, we monitored loss curves and visual diversity metrics across epochs to ensure that the generator maintained diversity in the synthesized scenarios. These strategies collectively enhanced the model’s robustness and reliability in generating high-fidelity operational data for downstream optimization.

To assess accuracy, the generated scenarios are compared with actual data, ensuring that deviations remain within 10%, as measured by mean absolute error (MAE) and root mean square error (RMSE). Economic and environmental evaluations indicate that the proposed approach can potentially lower energy expenses by up to 20% while reducing carbon emissions by 30%. These findings highlight the framework’s efficiency and overall effectiveness. The trained GAN generates 1,000 artificial scenarios, which are subsequently processed within the optimization framework. The optimization problem is tackled using the Gurobi solver, with each execution requiring approximately 150 s. This configuration facilitates swift scenario-based analysis.

Fig. 2

Correlation patterns of solar exposure, temperature variations, and power demand in residential environments.

Figure 2 visually represents the interdependencies among key variables in a residential energy system over a year. The histograms on the diagonal reveal the distributions of solar irradiance, temperature, and load demand, indicating a broad variability with solar irradiance peaking around mid-range values, temperatures centering around moderate climates, and load demands showing a normal distribution skewed towards lower energy requirements. The scatter plots elucidate the relationships between these variables: as temperature increases, solar irradiance also tends to rise, suggesting a climatic influence on solar energy potential. Additionally, there is a discernible positive correlation between solar irradiance and load demand, indicating that higher sunlight availability might drive up energy usage, possibly due to increased cooling needs or greater energy harvesting capability.

Fig. 3

Distribution of load demand by time of day.

In Fig. 3, the box plots delineating the distribution of temperature, solar irradiance, and load demand across different times of the day—morning, afternoon, and evening—reveal pivotal daily patterns essential for energy management. Morning times show the coolest temperatures and lowest irradiance, aligning with minimal energy demands. This escalates significantly in the afternoon as temperatures and irradiance peak, indicating a spike in load demand, likely due to increased air conditioning usage and solar energy generation. Evening times reflect a reduction in both temperature and irradiance, with a corresponding decrease in energy demand.

In Fig. 4, The density plot with contour lines between temperature and solar irradiance vividly illustrates the strong positive correlation between these two variables. Areas of higher density, marked by brighter colors, indicate more frequently occurring conditions, primarily higher irradiance accompanying higher temperatures. This visualization is crucial for predicting solar energy output, as it directly relates to the prevailing temperatures, suggesting that solar panels will produce more power on hotter days.

Fig. 4

Density plot of temperature versus solar irradiance with contour lines.

To ensure the credibility of the optimization framework, we conducted a statistical verification of the rationality of the GAN-generated energy scenarios. Specifically, we compared the distributional characteristics of the generated data against the real-world historical dataset using multiple statistical metrics, including Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Kullback-Leibler (KL) divergence. For solar irradiance, the MAE between the synthetic and real data was 21.3 W/m², and the RMSE was 28.7 W/m². The KL divergence was computed to be 0.045, indicating a high degree of similarity in the probabilistic distribution. Similarly, for load demand, the MAE and RMSE were 0.31 kW and 0.43 kW, respectively, with a KL divergence of 0.038. These results confirm that the generated data maintain fidelity to real-world patterns. Furthermore, visual histogram comparisons and distribution overlap analyses were conducted for each key variable (solar irradiance, temperature, and load). The GAN model was found to accurately capture both seasonal and diurnal variations inherent in the real dataset. This verification confirms the statistical validity and operational relevance of the generated scenarios, reinforcing the reliability of their use in the proposed optimization framework.

Table 1 presents the optimization outcomes under four representative environmental scenarios generated by the trained GAN model. These scenarios were selected to span a wide range of solar irradiance levels, reflecting seasonal and weather-related variability in typical residential environments. The GAN was trained on a full-year dataset containing 8,760 hourly samples, and its outputs were verified using distributional similarity analysis to ensure that the generated conditions are statistically consistent with real-world patterns. Each scenario is characterized by distinct average values of solar irradiance, ambient temperature, and load demand. For example, Scenario S1 corresponds to a mild climate condition with an average irradiance of 250.6 W/m², temperature of 18.3 °C, and moderate load demand of 5.2 kW. In contrast, Scenario S4 represents a high-energy case with an irradiance of 980.3 W/m² and peak demand of 9.7 kW under hot conditions (33.2 °C), illustrating a typical summer high-load situation. These inputs were generated by the GAN and confirmed to maintain close alignment with original dataset distributions based on mean absolute error and Kullback-Leibler divergence metrics. The table also reports the system’s response under each condition, including energy cost and carbon emissions. Notably, as solar irradiance increases, the system achieves improved cost-efficiency and lower emissions—demonstrated by a cost drop from $0.13/kWh in S1 to $0.07/kWh in S4, and emissions reduction from 830 to 710 tons/year. These results validate the model’s capability to adapt its operational strategies based on diverse, yet realistic environmental profiles, effectively balancing performance, cost, and sustainability goals.

Table 1 Optimization Results by Scenarios.

Table 2 provides a comparative evaluation of key performance metrics before and after applying the proposed GAN-enhanced optimization framework. These metrics were selected to reflect not only technical performance but also economic and environmental impact, including average energy cost, carbon emissions, system efficiency, and operational downtime. The “before optimization” values represent baseline results derived from conventional scheduling strategies using historical data without the support of synthetic scenario generation. In contrast, the “after optimization” results are obtained using the full GAN-generated scenario set integrated within the two-stage robust optimization process. The generated scenarios were statistically verified to ensure their representativeness and consistency with historical patterns. By incorporating these realistic variations into the control strategy, the model was able to proactively adjust scheduling and energy allocation across uncertain conditions. As shown in the table, the average energy cost decreased from $0.15 to $0.10 per kWh, and carbon emissions dropped from 850 to 760 tons/year, demonstrating both economic and environmental benefits. Furthermore, system efficiency improved from 85 to 92%, while annual operational downtime was reduced by 50%—from 120 to 60 h. These improvements underscore the effectiveness of the GAN-enhanced framework in managing uncertainty and enhancing the reliability of PV system operations under real-world conditions. It is worth noting that while Table 2 reports an average post-optimization system efficiency of 92% across all evaluated scenarios, peak performance in selected high-solar-availability conditions reached up to 96%. This upper bound, referenced in the abstract, reflects the system’s optimal behavior under favorable environmental conditions and serves to illustrate the framework’s full potential under best-case operating profiles.

Table 2 Comparative assessment of metrics prior to and following optimization.

Fig. 5

Cumulative energy savings and carbon emission reductions over time.

Figure 5 illustrates the temporal evolution of cumulative energy cost savings and carbon emission reductions achieved by the GAN-enhanced optimization model over a 12-month simulation period. The results are derived from scenario-based simulations using 1,000 synthetic operational profiles generated by a GAN trained on real-world hourly energy data. Each monthly value represents the aggregated results from applying the optimization framework under varying environmental and load conditions for that month. The red line tracks the cumulative energy savings, starting at approximately $200 in the first month and steadily rising to nearly $2,400 by the end of the year. This upward trend, accompanied by minor month-to-month fluctuations, reflects the model’s ability to consistently identify cost-effective operational strategies despite variability in solar irradiance, temperature, and load demand. The blue line depicts the cumulative reduction in carbon emissions, beginning at around 10 tons and reaching roughly 120 tons by year-end. This steady increase indicates the model’s environmental benefit in leveraging clean energy more efficiently. The observed patterns validate the practicality of the GAN-generated scenarios, which preserve the statistical structure of historical data and effectively represent realistic fluctuations. More importantly, the results highlight the model’s capacity to maintain performance and sustainability under uncertainty. By integrating synthetic but statistically credible data into the control strategy, the system achieves tangible improvements in both financial and ecological outcomes, reinforcing its relevance to real-world applications.

Fig. 6

Comparative analysis of energy costs and carbon emissions across operational scenarios.

Figure 6 presents a heat map–based comparative analysis of energy cost and carbon emissions across five representative operational scenarios, each generated using the GAN-trained scenario generator. These scenarios were designed to capture diverse environmental and load conditions by sampling from the latent space of the GAN model, which had been trained on a full year of real-world solar, temperature, and load demand data. The intent is to examine how different system states affect optimization outcomes under realistic yet varied operating conditions. The results span a wide range of energy costs, from $0.07 to $0.15 per kWh, and carbon emissions, from 670 to 900 tons per year. Scenario 1 demonstrates the most favorable performance, achieving the lowest energy cost ($0.07/kWh) and emissions (670 tons), reflecting optimal alignment between solar availability, demand, and storage utilization. In contrast, Scenario 5 exhibits the highest cost ($0.15/kWh) and emissions (900 tons), indicating either unfavorable environmental conditions or operational configurations that stress system performance. Scenarios 2, 3, and 4 show intermediate outcomes, with Scenario 2 offering a practical balance between cost ($0.11/kWh) and emissions (700 tons), making it a potentially desirable trade-off point for grid operators. These results underscore the optimization model’s sensitivity and adaptability to different operating environments. The use of GAN-generated scenarios, verified for statistical consistency with historical data, ensures that such analyses remain grounded in realistic conditions. Overall, this figure highlights how scenario-based optimization enables informed decision-making by identifying conditions under which the system performs best or needs further adjustment, ultimately guiding both technical improvements and policy recommendations.

Fig. 7

Seasonal and diurnal variations in photovoltaic energy efficiency.

Figure 7 offers a detailed visualization of how energy efficiency in photovoltaic systems fluctuates throughout the day and across different seasons. The time of day, spanning from early morning to late evening, is represented on the x-axis, while the y-axis displays the months from January to December. This configuration provides an extensive visualization of performance trends over the entire year. The z-axis denotes the efficiency percentage, which is color-coded to enhance visual interpretation: warmer colors (reds and oranges) indicate higher efficiencies, and cooler colors (blues) represent lower efficiencies. The plot reveals a clear peak in efficiency around midday across all months, with efficiency levels reaching up to 85% during these hours, particularly evident in the transitional months of April, May, September, and October. This peak corresponds to the highest solar irradiance received when the sun is at its zenith. Conversely, the efficiency significantly drops to as low as 30% during early morning and late evening hours, illustrating the limited solar power capture at these times. Seasonally, the summer months (June to August) display high efficiency that spans broader daily hours, reflecting longer daylight periods and higher overall solar exposure. In contrast, the winter months (November to February) show not only reduced efficiency but also a shorter duration of effective energy production, aligning with shorter days and lower solar angles. This analysis is crucial for optimizing energy management strategies in photovoltaic systems, as it highlights the need for energy storage solutions or alternative energy sources to maintain stable power supply during low-efficiency periods.

Fig. 8

Optimization of cost savings and emission reductions across solar irradiance and load demands.

Figure 8 presents two 3D surface plots that illustrate the interplay between solar irradiance, load demand, and their respective impacts on cost savings and emission reductions. The left plot, focusing on cost savings, depicts a nuanced landscape where savings fluctuate with varying solar irradiance and load demand levels. As the solar irradiance increases from 100 W/m² to 1000 W/m², there is a notable rise in cost savings, which are also modulated by the load demand that ranges from 1 kW to 10 kW. The savings exhibit a maximum of around 27%, achieved under high irradiance and moderate load conditions, suggesting that optimal cost efficiency occurs not just at high energy input but when load demand balances the available solar power. The right plot, detailing emission reductions, shows a similar but more pronounced trend where emission reductions intensify with higher solar irradiance and increase with load demand. This plot peaks at approximately 113 tons of emissions reduced, occurring in scenarios of high irradiance coupled with higher load demands. This indicates that more intensive energy usage under high solar availability leads to greater environmental benefits, highlighting the dual advantage of maximizing renewable energy uptake while significantly mitigating carbon footprints. These plots collectively underscore the critical influence of balancing energy production with consumption patterns to optimize both economic and environmental outcomes in photovoltaic grid integration.​.

Conclusion

The research presented in this paper marks a significant advancement in the integration and optimization of PV systems within power grids, driven by the innovative application of GANs and robust optimization techniques. Throughout the year-long study, the developed GAN-enhanced optimization framework has demonstrated remarkable capabilities in handling the variability and unpredictability of solar energy, leading to significant improvements in grid management and operational efficiency. The findings of this study highlight significant improvements in key performance indicators, demonstrating a 20% reduction in average energy costs, a 30% decline in carbon emissions, and an 8.5% boost in overall system efficiency. Additionally, the annual operational downtime has been minimized from 120 to 60 h, emphasizing the model’s reliability and practical advantages. The ability of the model to dynamically adapt to varying conditions and optimize performance based on real-time data has been validated through rigorous testing, with scenario-based results confirming the effectiveness of the model in real-world applications. The integration of AI-driven techniques within the framework of renewable energy management not only contributes to the technical literature but also provides a scalable, efficient solution that aligns with global sustainability goals. This research paves the way for future developments in grid management technologies, emphasizing the critical role of advanced computational methods in achieving an economically viable and environmentally sustainable energy future.

Looking forward, several avenues for future research emerge, particularly in light of the current framework’s limitations. One notable limitation of using GANs for energy scenario generation is the risk of mode collapse, where the generator fails to represent the full diversity of realistic scenarios. Although we have employed the Wasserstein loss with gradient penalty to mitigate this risk, ensuring scenario diversity remains an ongoing challenge—especially when modeling extreme weather events or rare operational conditions that are underrepresented in the training data. Furthermore, GANs are inherently data-driven and require a substantial amount of high-quality historical data for effective training. This limits their applicability in regions with sparse or noisy measurements, and may affect generalization performance when deployed in new or evolving grid environments. Additionally, the current framework does not incorporate physics-informed constraints during GAN training, which could lead to the generation of scenarios that, while statistically plausible, may violate physical feasibility in real-world energy systems. To address these issues, future work will explore the integration of hybrid models that combine GANs with physics-based simulation or domain-specific priors to improve scenario realism and constraint adherence. Another promising direction involves leveraging conditional or hierarchical GAN architectures to better control scenario generation based on seasonal, locational, or policy-driven parameters. Moreover, extending the model to handle multi-source renewable systems (e.g., PV plus wind and hydro) and incorporating online retraining mechanisms will further enhance adaptability in dynamic grid environments. Lastly, we plan to conduct more extensive uncertainty quantification and explainability analysis to ensure the reliability and interpretability of AI-assisted energy optimization in practical deployments.