Abstract
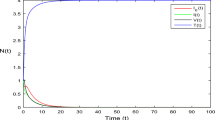
Herpes simplex virus (HSV) is a widespread infection responsible for painful blisters and ulcers. According to the World Health Organization, approximately 519.5 million people aged 15–49 years (13.3%) worldwide are infected with herpes simplex virus type II (HSV-II), the primary cause of genital herpes. In this study, we develop a nonlinear stochastic fractional delay differential equation (SFDDE) model to describe the transmission dynamics of HSV-II in a human population. The population is divided into susceptible \(\:S\left(t\right)\), exposed \(\:E\left(t\right)\), asymptomatic \(\:A\left(t\right)\), symptomatic \(\:I\left(t\right)\), HSV-infected \(\:H\left(t\right)\), and recovered \(\:R\left(t\right)\)compartments. The model’s fundamental properties, including existence, uniqueness, positivity, and boundedness of solutions, are established. Local and global stability analyses are conducted around the HSV-free and HSV-present equilibrium points, and the basic reproduction number is derived using the next-generation matrix method along with sensitivity analysis. Numerical simulations based on a stochastic nonstandard finite difference (NSFD) scheme confirm the theoretical results and demonstrate the stability of the proposed model. These findings highlight the importance of nonlinear fractional stochastic modeling in understanding and controlling HSV-II transmission dynamics.
Similar content being viewed by others
Data availability
The datasets analyzed during the current study are available from the corresponding author upon reasonable request.
References
Gurmu, E., Bole, B. & Koya, P. Mathematical model of herpes simplex Virus–II (HSV-II) with global stability analysis. Int. J. Math. Model. Comput. 5 (4), 361 (2020).
Harfouche, M. et al. Estimated global and regional incidence and prevalence of herpes simplex virus infections and genital ulcer disease in 2020: mathematical modeling analyses. MedRxiv, 2024–2006. (2024).
Edogbanya, H. O., Momoh, S. O. & Sani, U. Herpes simplex virus Type-2 (HSV-2) and HIV Co-infection dynamics with optimal control. International J. Dev. Math. (IJDM), 1(1). (2024).
Jothi, N. K., Dayalan, S. K., Giri, J., Hatamleh, W. A. & Panchal, H. Dynamic interactions of HSV-2 and HIV/AIDS: A mathematical modeling approach. AIP Advances, 14(3). (2024).
Mupedza, T. V. & Mhlanga, A. Theoretical exploration of behavioral change in disease control: sex work as a case study for HSV-2 transmission dynamics. Sci. Afr. 23, e02015 (2024).
Nahal, B., Owen, E. M., Jama, M., Obasi, A. & Clarke, E. A review of authorship in herpes simplex virus type-2 (HSV-2) research conducted in low-income and middle-income countries between 2000 and 2020. BMJ Global Health. 9 (7), e012719 (2024).
Dovrat, S. et al. Analysis of HSV1/2 infection reveals an association between HSV-2 reactivation and pregnancy. Viruses 16 (9), 1370 (2024).
Jama, M., Owen, E. M., Nahal, B., Obasi, A. & Clarke, E. Twenty years of herpes simplex virus type 2 (HSV-2) research in low-income and middle-income countries: a systematic evaluation of progress made in addressing WHO priorities for research in HSV-2 epidemiology and diagnostics. BMJ Global Health. 9 (7), e012717 (2024).
Song, P. et al. Viral etiology of aseptic meningitis and clinical prediction of herpes simplex virus type 2 meningitis. J. Personalized Med. 14 (9), 998 (2024).
Wei, M. et al. Epidemiological characteristics of three herpes virus infections in children in Nanjing, China, from 2018 to 2023. Front. Cell. Infect. Microbiol. 14, 1448533 (2024).
Wang, K. et al. A nonhuman primate model for genital herpes simplex virus 2 infection that results in vaginal vesicular lesions, virus shedding, and seroconversion. PLoS Pathog. 20 (9), e1012477 (2024).
Casto, A. M. et al. Viral genomic variation and the severity of genital HSV-2 infection as quantified by shedding rate: a viral genome-wide association study. The J. Infect. Diseases, jiae283. (2024).
Khryanin, A. A. & Sturov, V. G. Herpes virus infection and reproductive health disorders in women. Anal. Rev. Pharmateca. 31 (5), 6–15 (2024).
Ford, E. S., Li, A. Z., Laing, K. J., Dong, L., Diem, K., Jing, L., … Corey, L. (2024).Expansion of the HSV-2–specific T cell repertoire in skin after immunotherapeutic HSV-2 vaccine. JCI insight, 9(14).
Zhang, B., Li, Y., Yang, P., He, S., Li, W., Li, M., … Zhang, M. (2024). Herpes Simplex Virus Type 2 Blocks IFN-β Production through the Viral UL24 N-Terminal Domain-Mediated Inhibition of IRF-3 Phosphorylation. Viruses, 16(10), 1601.
Quadiri, A., Prakash, S., Dhanushkodi, N. R., Singer, M., Zayou, L., Shaik, A. M.,… BenMohamed, L. (2024). Therapeutic prime/pull vaccination of HSV-2-infected guinea pigs with the ribonucleotide reductase 2 (RR2) protein and CXCL11 chemokine boosts antiviral local tissue-resident and effector memory CD4 + and CD8 + T cells and protects against recurrent genital herpes. Journal of Virology, 98(5), e01596-23.
Stone, J., Looker, K. J., Silhol, R., Turner, K. M. E., Hayes, R., Coetzee, J., …Vickerman, P. (2023). The population impact of herpes simplex virus type 2 (HSV-2)vaccination on the incidence of HSV-2, HIV and genital ulcer disease in South Africa:a mathematical modelling study. EBioMedicine, 90.
Gurmu, E. D., Bole, B. K. & Koya, P. R. Optimal control strategy on transmission dynamics of HIV-HSV-II coinfection model. International J. Industrial Mathematics, 15(4). (2023).
You, S., Yaesoubi, R., Lee, K., Li, Y., Eppink, S. T., Hsu, K. K., … Rönn, M. M. (2023).Lifetime quality-adjusted life years lost due to genital herpes acquired in the United States in 2018: a mathematical modeling study. The Lancet Regional Health–Americas, 19.
Zheng, C., Wang, Y., Yan, X., Ai, W., Chen, R., Jia, Y., … Tang, W. (2023). Epidemiology of herpes simplex virus type 2 in China: Systematic review, meta-analyses, and meta-regressions.Authorea Preprints.
Mickens, R. E. (ed) Nonstandard Finite Difference Models of Differential Equations (world scientific, 1993).
Arenas, A. J., Gonzalez-Parra, G. & Chen-Charpentier, B. M. Construction of nonstandard finite difference schemes for the SI and SIR epidemic models of fractional order. Math. Comput. Simul. 121, 48–63 (2016).
LaSalle, J. P. Stability theory and invariance principles. In Dynamical Systems (211–222). Academic. (1976).
Abernathy, Z., Abernathy, K. & Stevens, J. A mathematical model for tumor growth and treatment using virotherapy. AIMS Math. 5 (5), 4136–4150 (2020).
Yang, Z. & Su, H. Probabilistic safety analysis in complex pipeline systems. In Advanced Intelligent Pipeline Management Technology 111–129 (Springer Nature Singapore, 2023).
Zhao, Q., Zhang, H., Xia, Y., Chen, Q. & Ye, Y. Equivalence relation analysis and design of repetitive controllers and multiple quasi-resonant controllers for single-phase inverters. IEEE J. Emerg. Sel. Top. Power Electronics (2025).
Liu, Y., Jiang, L., Qi, Q., Xie, K. & Xie, S. Online computation offloading for collaborative space/aerial-aided edge computing toward 6G system. IEEE Trans. Veh. Technol. 73 (2), 2495–2505 (2023).
Verma, L., Meher, R., Nikan, O. & Al-Saedi, A. A. Numerical study on fractional order nonlinear SIR-SI model for dengue fever epidemics. Sci. Rep. 15 (1), 30677 (2025).
Verma, L., Meher, R., Nikan, O. & Avazzadeh, Z. Numerical analysis on fuzzy fractional human liver model using a novel double parametric approach. Phys. Scr. 99 (11), 115202 (2024).
Acknowledgements
and Funding section: This work was supported by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID:90254), with the financial support of the European Union under the REFRESH – Research Excellence For Region Sustainability and High-tech Industries project number CZ.10.03.01/00/22_003/0000048 via the Operational Programme Just Transition.
Author information
Authors and Affiliations
Contributions
Ali Raza contributed to the conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing of the original draft, review and editing, visualization, supervision, project administration, and funding acquisition. Mansoor Alsulami contributed to methodology, Visualization, validation, and writing – review and editing. Marek Lampart contributed to resources, supervision, validation,writing – review and editing,and project administration. Umar Shafique contributed to data curation, software, methodology,validation and writing – review and editing. All authors reviewed and approved the final version of the manuscript. All authors read and approved a manuscript with the given study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Proof: First, we analyze the Lipschitz’s condition for the function. For this, we take help with the following and :
Since, \(\:{\xi\:}_{1}=\left({\beta\:}^{\alpha\:}{e}^{-{\mu\:}^{\alpha\:}\tau\:}\left({{\epsilon}}_{4}+{q}^{\alpha\:}{{\epsilon}}_{3}\right)+{\mu\:}^{\alpha\:}\right)\). Lipschitz’s condition is satisfied. Next, for \(\:{{\hslash\:}}_{2}\left(t,\:E\right)\) consider \(\:E\) and \(\:{E}_{1}\).
For, \(\:{\xi\:}_{2}=\left({\eta\:}^{\alpha\:}+{\mu\:}^{\alpha\:}\right)\). Lipschitz condition is satisfied.
Next, for \(\:{\hslash\:}_{3}\left(t,\:A\right)\) analyzing for \(\:A\) and \(\:{A}_{1}\).
For, \(\:{\xi\:}_{3}=\left({\phi\:}^{\alpha\:}+{\gamma\:}^{\alpha\:}+{\mu\:}^{\alpha\:}\right)\). Lipschitz condition is satisfied.
Next, for \(\:{\hslash\:}_{4}\left(t,\:I\right)\) analyzing for \(\:I\) and \(\:{I}_{1}\).
For, \(\:{\xi\:}_{4}=\left({\varphi\:}^{\alpha\:}+{\theta\:}^{\alpha\:}+{\mu\:}^{\alpha\:}\right)\). Lipschitz condition is satisfied.
Next, for \(\:{\hslash\:}_{5}\left(t,\:H\right)\) analyzing for \(\:H\) and \(\:{H}_{1}\).
For, \(\:{\xi\:}_{5}=\left({\delta\:}^{\alpha\:}+{\xi\:}^{\alpha\:}+{\mu\:}^{\alpha\:}\right)\). Lipschitz condition is satisfied.
Next, for \(\:{{\hslash\:}}_{6}\left(t,\:R\right)\) analyzing for \(\:R\) and \(\:{R}_{1}\).
For, \(\:{\xi\:}_{6}=\left({\omega\:}^{\alpha\:}+{\mu\:}^{\alpha\:}\right)\). Lipschitz condition is satisfied.
Next, there is constant in (13–18).
Remaining variation is as follows:
Therefore, we have
Let,
Similarly,
As required.
Appendix B
Proof
Consider the \(\:S\left(t\right),\:E\left(t\right),A\left(t\right),I\left(t\right),H\left(t\right)\:\text{a}\text{n}\text{d}\:R\left(t\right)\) are bounded. Then.
Since, \(\:S\left(t\right),\:E\left(t\right),A\left(t\right),I\left(t\right),H\left(t\right)\:\text{a}\text{n}\text{d}\:R\left(t\right)\) will converge because the system (31–36) exists and consistent. For this, consider \(\:n\) changes as \(\:{A}_{n}\left(t\right),\:{B}_{n}\left(t\right),\:{C}_{n}\left(t\right),\:{D}_{n}\left(t\right),\:{X}_{n}\left(t\right)\:\text{a}\text{n}\text{d}\:{Y}_{n}\left(t\right)\). Thus,
The result of Lipschitz condition for \(\:\left({\xi\:}_{1}\right)\) and the triangle inequality, and \(\:{\hslash\:}_{1}\) for \(\:i=\text{1,2},\text{3,4},\text{5,6}\), fulfills the Lipschitz condition.
with repetition of (55),
Next, at \(\:{t}_{\text{*}}\), one acquires
Assuming \(\:n\:\to\:\:{\infty\:}\) as the limit.
By applying the hypothesis \(\:\frac{{\xi\:}_{1}}{{\Gamma\:}\left(\alpha\:\right)}\left({t}_{\text{*}}\right)<1\), we get
Similarly,
As desired.
Appendix c
Proof
Examine how the sets \(\:{S}_{1},{E}_{1},{A}_{1},{I}_{1},{H}_{1},\:\text{a}\text{n}\text{d}\:{R}_{1}\) represent the solutions to (1–6).
.
After simplifying,
By applying the hypothesis \(\:\left(1-\frac{{\xi\:}_{1}}{{\Gamma\:}\left(\alpha\:\right)}\left(t\right)\right)>0\), we have from (66) yield.
Similarly,
Hence proved.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Raza, A., Alsulami, M., Lampart, M. et al. Nonlinear fractional stochastic delay modeling and computational analysis of herpes simplex virus type II dynamics. Sci Rep (2026). https://doi.org/10.1038/s41598-026-37658-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-026-37658-w