Introduction

We describe a variable which has hardly changed over thousands of years. Our variable is a function of basic food and drink prices. Prices are known to exhibit regularities, independent of other properties of the items being sold, which do reflect market forces (Schindler and Kibarian, 1996). Our variable belongs to this broad category.

It is well known that the value of food and drink items can be measured from many quite different points of view, and that there is no one-size-fits-all normalization for food and drink prices (Jones and Monsivais, 2016). Furthermore, food and drink items can be sold in various numbers, weights, volumes or package sizes, etc., and these choices do influence sales (Yonezawa and Richards, 2016). However, it has also been known for some time that consumers use prices as the basis of their decisions unless price-per-unit information is explicitly provided or they have the time to calculate it for themselves (Granger and Billson, 1972; Yan et al., 2014; Çakır and Balagtas, 2014). Since we use historical data covering thousands of years, one must also take into account the fact that consumers have not always had the education required to be able to perform such calculations. We have therefore decided to use retail price data as they have been reported. We ask the reader to suspend judgement on this choice until having read the description of our main result.

To provide a sense of the argument to come, it will be useful to begin with a discussion of the German hyperinflation which followed the end of the First World War. It is a phenomenon which has been a topic of discussion in economic circles since even before it happened (Keynes, 1919). Retail prices for bread, peas, beans, potatoes, beef, pork, butter, margarine, lard, sugar, eggs and milk are available (Statistisches Reichsamt, 1923, 1925), and we have included our analysis of these in Supplementary Table S1. It is well known that prices tend to become uncoupled from the real economy during a hyperinflation (Cagan, 1956), and we therefore include prices from before and after what would be technically defined as the period of hyperinflation to allow for context. In the short period beginning in April 1922 to the end of November 1923, prices for all these items increased by factors of more than ten million, but the price of the most expensive item at any given time always remained less than 250 times the price of the cheapest item. In other words, the range of relative prices was always less than 0.0025% of the variation in prices themselves over this period. The point to be made is that the range of relative prices is insignificant in comparison with the variation in prices. In Fig. 1, we show the German hyperinflation data from April 1922 to the end of November 1923, including a prewar average taken between October 1913 and July 1914 for comparison. The 1913/1914 prewar average prices are in Goldmark. All other prices are in Papiermark (“paper” Mark). The Rentenmark was introduced on November 15, 1923, and the hyperinflation stabilized soon after. The Papiermark remained in circulation until early 1924. The enormous variation in prices over this period compels us to use logarithms. What we see is that the prices form a band of more-or-less constant width, and this is the insight which lies at the basis of our investigation.

Fig. 1: The German hyperinflation.
figure 1

Circles indicate the base 10 logarithms of prices. Straight grey lines joining these show the evolution in price of individual items (such as “bread” or “milk”). Most prices tend to fall within a band, given by the mean plus or minus one standard deviation. The upper and lower limits of the band are plotted as dark grey curves which have been smoothly interpolated between dates with data. Vertical dark grey bars indicate its width at dates for which data is available.

Full size image

During the hyperinflation, potatoes are often the cheapest item, and seem not to follow the band as strictly as the other prices. This emphasizes the importance of using all available data, not just the extremes.

Motivated by this example, and wishing to avoid having to deal with differences between currencies, we have chosen to focus on ratios of prices as expressed in terms of differences in logarithms of prices. Treating log prices as if they were samples from an unknown probability distribution, the width of this probability distribution, which can be estimated by the sample standard deviation, offers itself as a robust object of study which takes all prices available at any given time into account. Note that no assumption needs to be made concerning the unknown distribution itself in order to calculate this quantity. One can always calculate the sample standard deviation of a finite set of numbers. If the unknown probability distribution were a normal distribution, one would expect 68% of samples to fall within the mean plus or minus one standard deviation. The width we are estimating may therefore be a measure of the range of most relative prices on sale at a given place and time. In Fig. 1, the mean plus or minus one standard deviation appears as dark (interpolating) curves. One can see that the difference is ~1 at all times, meaning that most prices tend to be within an order of magnitude of each other.

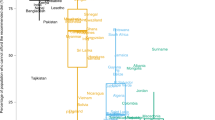
The data used in this study are taken from independent data sources, covering a wide range of countries and time periods as far back as ancient Egypt and as recent as modern day Chile. The data underlying Fig. 2 are from ancient Egypt (1135–1113 BCE), Babylon (292–78 BCE), Delhi (1351–1388 CE), Istanbul (1489–1770 CE), Germany (1850– 2000 CE), the United States of America (1920–1942 CE), the United Kingdom (1960–2004 CE), Tokyo (1957–2001 CE) and Chile (2007–2010 CE), as well as some isolated data points from ancient Rome and the Soviet Union. In Fig. 2, the full analysis is presented in the upper portion, and the individual contributions of various datasets are also individually presented in the lower portion. For Fig. 3, the data is from a single very long English time series, covering the years 1209–1914 CE.

Fig. 2: Widths of distributions of log prices.
figure 2

Conservative estimates of the width of the distribution of log prices using data from different cultures and continents, covering three thousand years. The light grey band suggests a Goldilocks principle, of neither too much nor too little width. Note that the German hyperinflation data appear as a peak with a height of ~0.3, despite the fact that the underlying log prices increased by about 10.

Full size image
Fig. 3: Log price distribution widths for a long-term time series.
figure 3

Raw estimates of the width of the distribution of log prices using data from a single time series for England (Clark, 2004) covering seven hundred years. In the upper panel, the sizes of data points correspond to the number of items for which prices are reported for the corresponding dates. Dates for which no saffron price was reported are shown as filled black discs. Where the price of saffron was reported, the width of the distributions including the saffron are shown as unfilled circles, and the width of the same distributions but excluding saffron are shown as filled black discs.

Full size image

Methods

We deal with the logarithms of positive prices, using an arbitrary base b > 1, and consider the set of all logarithms of prices at any given time as samples from an unknown distribution. It is natural to study moments of this distribution, beginning with location and width.

The first moment is

$$A_b\left( {P_1,\, \ldots ,\,P_N} \right) = \frac{1}{N}\mathop {\sum}\limits_{j = 1}^N {{{{\mathrm{log}}}}_b\left( {P_j} \right)} ,$$

and the second, which requires at least two prices (N ≥ 2), is

$$\begin{array}{*{20}{c}}{B_b\left( {P_1, \ldots ,P_N} \right) = \sqrt {\frac{{\mathop {\sum}\nolimits_{i = 1}^N {\left( {{{{\mathrm{log}}}}_b\left( {P_i} \right) \,-\, A_b\left( {P_1, \ldots ,\,P_N} \right)} \right)^2} }}{{N - 1}}} }\\\qquad\qquad\qquad\quad { = \frac{1}{{\ln \left( b \right)}}\sqrt {\frac{{\mathop {\sum}\nolimits_{i = 1}^N {\left( {\frac{1}{N}\mathop {\sum}\nolimits_{j = 1}^N {\ln \frac{{P_i}}{{P_j}}} } \right)^2} }}{{N - 1}}} .}\end{array}$$

In this empirical study, we make no assumption regarding the nature of the unknown probability distribution. However, if the unknown distribution were Gaussian, then about 68% of price logarithms would be expected to be between Ab−Bb and Ab + Bb (see Fig. 3). The ratio (R) of the raw prices (i.e. not logarithms of prices) corresponding to Ab−Bb and Ab + Bb is

$$\begin{array}{*{20}{c}}{R = b^{\left( {2B_b} \right)} = \exp \left( {\ln \left( b \right) \times 2 \times B_b\left( {P_1, \ldots ,P_N} \right)} \right)}\\ { = \exp \left( {{\displaystyle{\frac{2}{N}}} \times \sqrt {\frac{{\mathop {\sum}\nolimits_{i = 1}^N {\left( {\mathop {\sum}\nolimits_{j = 1}^N {\ln \frac{{P_i}}{{P_j}}} } \right)^2} }}{{N - 1}}} } \right)}\end{array}$$

which does not depend upon the base b. The analysis of historical data presented here suggests that B10 ≈ 0.5, so R ≈ 10 × (2 × 0.5)=10, which is one order of magnitude.

Data sources

In Fig. 2, we have made use of food and drink price data from a wide variety of sources. We have tried to cover as many geographical regions and ages as possible. We have not included data relating to food and drink purchases made by large organizations, such as hospitals, monasteries or farms, since the prices tend to be for quantities too large (such as the price of one goat) for family consumption. Most of the data sets reflect some degree of market freedom. For Fig. 2, we have selected items and dates in a conservative way which ensures that every item included has a reported price for all dates used, and done this in a way which includes the majority of data. The full datasets are provided as Supplementary Tables, including analyses based upon using all available data to demonstrate the robustness of our analysis. Furthermore, Fig. 3 has been constructed without any such conservatism, allowing the reader to see that this difference does not influence our conclusions. First, we will describe the data sets used in generating Fig. 2.

The Twentieth Dynasty was the last of the New Kingdom of ancient Egypt. Although dating is difficult (Ramsey et al., 2010), we have used two contemporaneous (appearing in the same document) pairs of spelt and barley prices (Cerný, 1933), for the fourth (or possibly fifth) year of Ramesses VII and the 17th year of Ramesses IX. We have provided the years 1135 BCE and 1113 BCE as what we believe are reasonable estimates for the respective dates. These have been supplemented with other prices, for bread, fresh fat, cream, beer, honey, salt and vegetables, from New Kingdom sources (Cerný, 1954), and the full data set we have used is to be found in Supplementary Table S2.

The prices we have used (Supplementary Table S3) from the Hellenistic period of Babylon (Van der Spek, 2005), following its conquest by Alexander the Great in 331 BCE and including the period of decline following his death, were compiled by astronomers for the purpose of divination, which is of relevance here because it suggests that the prices were not fixed, and we note that others have independently concluded that markets were relatively free during the same period (Temin, 2002). The prices are for barley, dates, mustard, cress and sesame.

Firoz Shah Tughlaq ruled over the Sultanate of Delhi during the period 1351−88 CE. In Chapter III of “Northern India under the Sultanate” (Habib, 1982), on p. 88, we find the quote “This sultan gave up all attempts at controlling prices”, and so have used prices from his reign (Haider, 2004). The prices are for wheat, barley, gram, clarified butter, sesame oil and salt. Our analysis of these prices is to be found in Supplementary Table S4.

Prices for Istanbul in the period of rule by the Ottoman Empire (Supplementary Table S5) were obtained from (Özmucur and Pamuk, 2002), where it is noted that price ceilings (“nahr”) did exist for much of this period, and that the government was involved in price formation. Thus, it cannot be said that these data correspond to entirely free market conditions. The prices are for wheat, wheat flour, bread, rice, butter, olive oil, mutton, honey, sugar, coffee and chick peas.

Price data for more recent times have been taken from (O’Donoghue et al., 2006) for the United Kingdom (Supplementary Table S6), (Metz, 2015) for Germany (Supplementary Table S7, covering the German Confederation from 1850, the German Empire, Federal Republic of Germany (West Germany) and the reunified Germany of today), Chapter IV of the NBER Macrohistory Database of the National Bureau of Economic Research (Feenberg and Miron, 1997) for the United States of America (Supplementary Table S8), and Chapter 22, Section 19, of the online version of the Historical Statistics of Japan (Japan Statistical Association, 1987) provided by the Statistics Bureau of Japan (Supplementary Table S9 and Supplementary Note).

Scraped price data (Cavallo, 2018) from a supermarket chain in Chile were downloaded from The Billion Prices Project (Cavallo and Rigobon, 2016). This data set is of an entirely different nature from what has so far been described. It contains very large numbers of daily price observations from 1025 days in the period 2007 to 2010. Of these, we used only prices from the 39 food and drink categories for which prices are available for the entire period (Supplementary Tables S10 and S11).

We have also included, for comparison, some data points corresponding to price ceilings or markets which were certainly not free:

In 301 BCE, the Roman Emperor Diocletian proclaimed an edict (Kent, 1920), which was intended to prevent dramatic rises in prices of commodities and services from continuing. The Edict of Diocletian contained a list of maximum prices, specifically including basic food and drink items, with selling beyond these price limits punishable by death. We have used these maximum prices (Supplementary Table S12) in the absence of sufficient data on actual prices.

From the Soviet Union, we have used state store retail and collective farm market prices for 1950 (Wainstein, 1954). Since Soviet state store prices were fixed by the state but farm market prices less so, we have processed the datasets separately. The list of items is the same in each case. For this reason, the corresponding symbol in Fig. 2 is elongated vertically to reflect the difference between the two price lists. That the 1950 Soviet values are very close to those from the West German data for the same year is likely due to the fact that food rationing in West Gemany, for all but sugar, ceased on the first of March of that year. Finally, we have also included Soviet prices from 1958 (Lomberg and Turgeon, 1960). Our analysis of all data we have used from the Soviet Union is to be found in Supplementary Table S13.

While our analysis does not explicitly include quantities, every price used is associated with a quantity of some kind, be it “one apple”, “100 g of beef” or “500 mL of oil”. Each dataset we have used has been compiled for a specific region and age, reflecting not only the items sold in the region at that time, but also the units used. We have respected these choices. Furthermore, most datasets are based upon generic produce (such as “200 g of butter”), whereas the Tokyo and scraped Chilean supermarket data sets are based upon specific items (such as “185 g of Mount Fuji Brand Super Plus Butter in a plastic container”). We have provided translations for the Tokyo data as a Supplementary Note. Where specific items are involved, there is a natural turnover, as companies renew their portfolio of products. It is nonetheless always possible to calculate the sample standard deviation of the log prices of items being sold at any given time.

In Fig. 2, we have included the publication date of the first edition of “The Wealth of Nations” (Smith, 1776), as a proxy for the date of emergence of modern market economies. We have done so to emphasize that, against our own initial expectations, the robustness of the width of log price distributions appears to have deeper roots than modern economic mechanisms or structures.

For Fig. 3, sample standard deviations have been calculated for all dates at which there are two or more reported prices. This is the minimum number for which the sample standard deviation can be calculated at all.

The data used for Fig. 3 comes from a long time series of prices for England (Clark, 2004), our analysis of which is provided as Supplementary Table S14. The published data includes saffron from 1265 to 1570 CE. In modern times, saffron is most commonly thought of as a relatively expensive foodstuff, but this has not always been so. In the Middle Ages in Europe, it was perhaps even more closely associated with medicine and wellness (Freedman, 2015). Indeed the possible uses of saffron extended to the use of quantities of saffron as a financial hedge (Basker and Negbi, 1983).

Discussion

We observe that the sample standard deviations of the base ten logarithms of prices (B10) fall within about 0.25 and 0.75 (0.5 ± 0.25). This is a very small range in comparison with the variation of log prices themselves, which is about 10 in the German hyperinflation dataset alone. That this stability cannot be dismissed as due to a coincidental alignment of data points, resulting from the different units used in different datasets, is already demonstrated by the internally consistent seven hundred year dataset from England (Clark, 2004) shown in Fig. 3. Thus, our variable seems to be decoupled from inflation and general price volatility (Gilbert and Morgan, 2010).

Instead, our analysis suggests that the width of the log price distribution remains essentially the same, but the prices of individual food and drink items can weave around within what appears to be a fixed probability distribution. This is illustrated in Fig. 4, which uses prices for 20 food and drink items in the UK between 1914 and 2004, and is particularly true of time series in which the list of food and drink items appearing together changes over time, such as the Tokyo and Chile supermarket datasets.

Fig. 4: Conservation of width despite changing number of items.
figure 4

Illustration of the band of logarithms (base 10) of prices within one standard deviation of the mean, using data from the UK (O’Donoghue et al., 2006). Circles indicate log prices. Straight lines joining these show the evolution in price of individual items (such as “eggs” or “milk”). The upper and lower limits of the band are plotted as dark grey curves which have been smoothly interpolated between dates with data. Vertical dark grey bars indicate its width at dates for which data is available.

Full size image

For our method of analysis to be practically useful, we do feel that it is preferable to be able to take published price lists as they are. It is also to be expected that datasets of prices of actual items sold, such as the Chile supermarket dataset we have used, will become the norm in the future as a result of increased automation of the advertising and sales processes.

Our analysis is based upon prices at a given time, and therefore differs from the classical approach of Mills (1927) (Keynes, 1928), for which rates of change of prices form the basis. The modern study of price dispersion (Lach, 2002) also involves the widths of distributions of log prices, but for individual items rather than a set of many prices. Neither quantities nor weightings appear explicitly in our analysis. It is important to stress that our empirical study covers ancient as well as modern prices, and that what can be learned from the dispersion of prices in a market economy with modern technology and ease of movement may not be automatically applicable to ancient times.

The log price distribution width does have small variations over relatively short time periods, and yet never deviates significantly from the global long-term average. This is difficult to explain in terms of memory effects, for example, since one would expect that changes in food culture or technology would at times result in lasting changes, introducing a new normal. We see no evidence of corresponding step-like changes in the sample standard deviation of log prices. Additionally, memory effects cannot account for stability over thousands of years between different cultures on different continents. One cannot expect Tokyo prices in 1970 to have been influenced by any kind of memory from ancient Egypt.

The distribution of relative prices of basic food and drink items has a width which varies so little that it suggests the existence of a universally “standard” width. We hope this observation will contribute to the extension of the theory of price distributions beyond its current scope (Weber, 2012; Koschate-Fischer and Wüllner, 2017). It is conceivable that this may require the incorporation of elements of the rapidly developing field of the economics of nutrition (Finaret and Masters, 2019). Thinking in another direction, one may even wildly speculate that humans may have an innate sense of log price distribution based upon a representation of prices as numbers on a logarithmic mental number line (Cheng and Monroe, 2013; Dehaene, 2003), a hypothesis which would at least be amenable to experiment. The bottom line is that we are not aware of any branch of contemporary economic theory which can explain our observation.

The field of econophysics applies tools from the theory of complex systems and their fluctuations to the science of economics (Stanley et al., 1999). For example, evidence for power laws in land price data has been reported (Ishikawa 2009; Blackwell, 2018). Power-law distributions are associated with a lack of scale. Our result is also scale invariant in the sense that the width of the sample standard deviation of log prices depends only upon ratios of prices. In this empirical study, we have not addressed the question of what the unknown distribution of prices may be. This is primarily due to the fact that the ancient price lists we have used contain so few items that it is difficult to justify extending the analysis beyond a measure of width. Looking beyond these practical limitations of our empirical study, it is reasonable to expect that econophysics may contribute to the construction of the necessary framework for a theoretical understanding of the nature of the log price distribution of basic food and drink items.

Conclusion

Our main result is that the width (sample standard deviation) of the distribution of logarithms of food and drink prices, a quantity which depends only upon price ratios, has remained essentially unchanged over a period of three millennia, with no large differences seen between geologically or culturally separated areas. This appears to be so without any appreciable dependence on the actual food and drink items involved, as well as being apparently independent of average incomes and expenditures, and the state of technology, transport, politics, institutions or culture.

A satisfactory explanation may need to include a regulatory mechanism which both prevents prices from drifting too far apart or from becoming too alike. Our analysis suggests that this mechanism, if it does indeed exist, has not changed over thousands of years and is essentially the same in widely separated cultures.