Introduction

In February 2018, the State Council of China formally in principle approved and agreed with the “Hohhot-Baotou-Ordos-Yulin (HBOY) urban agglomeration Development Plan“Footnote 1, which ushered in a unique development opportunity for this new type of urban agglomeration centered on the energy industry. This Plan will strengthen joint prevention and control of severe pollution in the area, promote the construction of Hong-Jian-Nao National Wetland Nature Reserve, and coordinate efforts to comprehensively control soil erosion on the Loess Plateau and accelerate the construction of a one-hour travel circle in Hohhot-Baotou-Ordos, gradually improve the level of regional aviation infrastructure construction, and deepen industrial development cooperation. All these will certainly bring significant opportunities for urban development in the region.

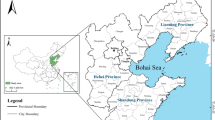
HBOY urban agglomeration is composed of Hohhot, the capital city of Inner Mongolia; Baotou, a heavy industry base of Inner Mongolia; Ordos, the resource-based city of Inner Mongolia, and Yulin in Shaanxi Province, known as the “Pearl of the Forbidden City”. There are many urban agglomerations in mainland China. The one we focused on is neither the largest nor the first established one. However, it is still noteworthy due to its economic scale and geographical location. HBOY urban agglomeration covers an area of 175,000 square kilometers and has a total population of nearly 12 million. In 2021, the total GDP of the four cities exceeded 1.65 trillion Yuan, accounting for more than 33% of the total economic output of the two provincesFootnote 2. Besides, HBOY is one of those urban agglomerations in China’s western region. It locates in the strategic urbanization layout of China’s “Two Horizontal and Three Vertical“Footnote 3 and is the northern end of the Bao-Kun Corridor on the horizontal axis of the western region. It plays a vital role in the in-depth development of the region, the formation of a new pattern of growth in the area, and the promotion of the urbanization process.

The Western part of China is less-developed areas with lower level of social-economic development, and needs more attention from the central government and the academic world to win better opportunities for its development. There are 1866 county units in China, accounting for more than 90% of the country’s total area, and 52.5% of the country’s total population. However, the GDP generated by these counties is just accounted for 38.3% of the whole country’s outputFootnote 4. The slow development of county economy has always been a dragging force for China’s economic development. The rises and falls of the county economy directly determine the economic trend and growth quality of the whole country. Accelerating the development of the county economy is an inevitable choice for China’s future regional economic development. Particularly, paying attention to the economic efficiency of the county economy is of great significance to the economic rise of the western region.

At the core of economics is the concept of efficiency. Economic efficiency measures how well a market or the firms perform (Leibenstein,1966; Qiu et al., 2016). To better understand why HBOY’s level of regional economic development is lower than many other parts of China, we need to distinguish the causes of lacking input from those of low economic efficiency. The first objective of this study is to find where the counties with lower economic efficiency lie within HBOY urban agglomeration by evaluating the economic efficiency of each county unit in this area. The second aim is to reveal the pattern of these differences in terms of economic efficiency by revealing and visualizing their spatial and temporal pattern. Therefore, we can locate the areas where improvement can be made to boost the economy of the urban agglomeration, and hopefully, this will help balance China’s national economy. This paper examines the economic efficiency of an urban agglomeration based on data from the county level. Analyzing small geographical areas will help us identify with a higher level of resolution (compared to analyses at the city or province level) the dragging areas. This study finds several significant issues that should have attracted some attention to fully understand the status quo of the development of HBOY urban agglomeration and are vital for boosting the region’s economy in the future.

Our study contributes to the existing literature by (i) paying attention to the economic efficiency of counties from under-developed areas and (ii) filling the research gap for studies focusing on spatial distribution patterns for the economic efficiency of HBOY urban agglomeration. The rest of the paper is organized as follows. In section ‘Literature review’, we conduct a literature review covering most existing studies on economic efficiency. Section ‘An overview of HBOY urban agglomeration’ introduces the study area and the data used for this analysis. Section ‘Model specification and variable selection’ presents a simple Stochastic Frontier Model and introduces the selected variables. In section ‘Results and discussion’, we evaluate the economic efficiency of the counties within HBOY urban agglomeration and then examine its temporal and spatial differentiation characteristics. After that, we conduct a spatial correlation analysis of the economic efficiency of these counties. We conclude in section ‘Research conclusions and implications’.

Literature review

A well-known problem with growth accounting in development economics is that it ignores some factors that may cause economic growth. In standard regression analysis, to estimate the average input-output relationship, a common approach is to filter out the influence of core factors by introducing control variables (such as factors of input, demographic, and geographic) to get as “clean” a white noise as possible. Based on this method, all deviations from the fitted curve are considered the contribution of statistical errors. All Decision-Making Units (DMU) production activities are usually assumed to be fully efficient or at the edge of the Production Possibility Frontier (PPF). Such a perfect efficiency assumption simplifies measurement’s complexity, but it also brings some problems.

Although many economic models assume that decision-making units are efficient, it is undeniable that there are usually quite a few inefficiencies in the real world. For example, inefficiency is caused by information asymmetry or market incompleteness in a broader sense (Greenwald & Stiglitz, 1986). To a certain extent, inefficiency exists in almost every aspect of economic activity. Owing to different management practices, inefficiencies vary in different enterprises, regions, or countries. These differences might be caused by different degrees of information asymmetry, cultural backgrounds, beliefs or traditions, or expectations (Bénabou & Tirole, 2016).

For studies with interests in economic efficiency estimation, the two methods that researchers most use are Data Envelopment Analysis (DEA) and Stochastic Frontier Analysis (SFA). Both methods evaluate efficiency by measuring the inefficiency of a DMU, which is calculated as the distance from the actual performance to the theoretically best practice that is considered perfectly efficient. However, there are some differences between these two methods. DEA is a nonparametric method that estimates efficiency by comparing unobserved true frontier to observed data and poses no assumption about the specific form of the frontier (Simar & Wilson, 2007). The issue with DEA is that it assumes no errors and deviations from the efficient frontier, meaning those errors and deviations are entirely considered part of the inefficiency. SFA models avoid some of the limitations of the DEA. Specifically, it allows the decomposition of deviations from the efficient frontier into a random error term that embodies statistical noise and a one-sided error term representing inefficiency. However, SFA requires specifying a functional form for the frontier (Newhouse, 1994).

Total Factor Productivity (TFP) is an important indicator to reflect production activities’ input and output efficiency (Van Beveren, 2012). It is used to express the part of the output that cannot be explained by factor inputs and reflects the efficiency and intensity of production activities using production factors. In 1977, scholars such as Aigner and Meeusen, respectively, published their papers and proposed the Stochastic Frontier (SF) model (Aigner et al., 1977). Since then, this model type has become one of the most appreciated essential tools in the field of efficiency analysis. SFA believes that the efficiency of all decision-making units is an empirical question, which should be tested based on statistical data, and the interference of random errors should also be considered.

Most of the research using SFA to measure efficiency will involve specific sectors or industries, such as ports, banks, energy, agriculture, transportation, and land use. Otsuka used SFA to measure the TFP of manufacturing in different regions of Japan (Otsuka, 2017). The study found that the production efficiency in regions where the manufacturing industry is concentrated is high. Introducing international competition in the manufacturing industry will improve local production efficiency. Choi et al. used SFA and DEA methods to measure the efficiency of 1471 hospitals in the United States. The study found that hospitals have a significant Bowmer Effect. As labor costs increase, the operating efficiency of hospitals has shown a downward trend (Choi et al., 2017). Ding et al., based on U.S. banking data from 2001 to 2016, used SFA to measure banks’ cost efficiency and further analyzed the relationship between the bank’s capital structure, asset portfolio risk level, and operating performance. The research found that banks with high operating efficiency are more inclined to increase capital, arrogate greater credit risk, and reduce their holdings of risk-weighted assets (Ding & Sickles, 2018).

Domestic researchers from China mainly focus on the application of the SFA method. Studies involve enterprises, universities, banks, land use, water resource use, foreign trade, etc. (Gu & Liu, 2009; Fang et al., 2018; Dong, Xing, 2020; Liu et al., 2020; Ye, 2015; Ren et al., 2018; Chai, 2018). In addition to microeconomic decision-making units (which is not the focus of our study), Chinese researchers have shown strong research interest in the evaluation of regional economic efficiency (Li & Li, 2018; Nie & Li, 2016; Huang & Pu, 2010; Liu, 2013; Ehrl, 2013). Some researchers established a three-factor stochastic frontier model based on the Cobb-Douglas production function and used maximum likelihood estimation to measure the production efficiency of 34 prefecture-level cities in the three northeastern provinces from 2000 to 2013 (Li & Li, 2018). They examined the changing trends and determining factors of production efficiency, holding government fiscal expenditures, industrial structure, and infrastructure as the core factors affecting urban production efficiency. Nie & Li (2016) used DEA to evaluate industrial circular economy efficiency for 30 provinces in China from 2010 to 2013 and found a significant difference in economic efficiency. From a provincial perspective, studies show that regional TFP has noticeable spatial differences, and the economic efficiency is significantly affected by a variety of factors, including migration (Huang & Pu, 2010), foreign direct investment (Liu, 2013), economic agglomeration (Ehrl, 2013), etc. For cities, studies show that the economic performance of a city increases steadily over time, its economic efficiency is significantly associated with its size (Yang & Wang, 2002; Huang & Guo, 2020), spatial structure (Liu et al., 2017), technological progress (Bergeaud et al., 2016), etc.

By comprehensively reviewing existing literature, we perceive that the following two issues need to be addressed. Firstly, although TFP has received wide attention from domestic scholars in recent years, the studies are mainly based on two kinds of spatial scale: one is to use data from provinces to evaluate their economic efficiency and to analyze the determinants (Wang, 2010; Liu, 2013; Qiu et al., 2016; Nie & Li, 2016; Liu & Tsai, 2021)), the other is to study the differences in the economic efficiency of different cities (Sun et al., 2015; Wang et al., 2016; Huang & Guo, 2020; Xu & Jiang, 2021). Few studies focus on the spatial scale of the county. All of these are based on data from counties from developed provinces or moderately developed provinces, like Jiangsu and Zhejiang provinces (Liu & Qin, 2009; Yuan, 2010), Chongqing municipality (Huang & Gao, 2017) and Henan province (Yuan et al., 2020), none of the researches analyze counties from under-developed areas. Existing studies paid more attention to the economic efficiency of either micro decision-making units (such as banks and universities) or provinces and cities. Less attention was paid to the economic efficiency of counties, especially for those from under-developed areas (Liu et al., 2009; Yuan, 2010; Huang & Gao, 2017; Yuan et al., 2020). Secondly, though it has been common to use spatial econometric techniques to investigate the role of location as a determinant of economic performance (see Abreu et al., 2004 for a survey), previous work on county economic efficiency, for some reason, failed to address this spatial correlation problem. Thus, a research gap exists for studies focusing on spatial distribution and correlation patterns for county-level economic efficiency. Specifically, there needs to be a study paying more attention to the spatial correlation of county economic efficiency of HBOY urban agglomeration. Hence, we conduct this research to make up for the deficiencies of existing research and enrich the achievements in the field of economic efficiency.

An overview of HBOY urban agglomeration

This paper takes the HBOY urban agglomeration as the research object. This urban agglomeration covers an area of 175,000 square kilometers and has a total population of nearly 12 million. In 2021, the total GDP of the four cities exceeded 1.65 trillion Yuan.

The observations are 30 county-level units under the jurisdiction of the urban agglomeration. These 30 decision-making units (DMU) are shown in Fig. 1.

Fig. 1: Schematic diagram of HBOY urban agglomeration.
figure 1

Different color represents different city. Area in dark blue represents Baotou, light blue for Hohhot, green for Ordos, and gray for Yulin.

Full size image

County-level economic growth

The economic growth of these counties generates different patterns, as shown in Fig. 2. Generally speaking and on average, the county-level economy of HBOY urban agglomeration has been growing for the period covered by this study. Baotou District is dominantly the largest economy among these 30 units, and the second and the third largest are Hohhot District and Jungar Banner, respectively.

Fig. 2: County-level GDP in selected years.
figure 2

County-level GDP in selected years shows the growth pattern of each county. The blue bar represents GDP in 2012, red for 2016, green for 2020.

Full size image

As for the growth rate, the fastest-growing counties are obviously not the largest ones, Hengshan District’s GDP ranked No. 9 in 2020, but it is almost seven times larger than it was in 2012. The second fastest-growing county is Fugu County, whose GDP in 2020 is more than 5.8 times larger than in 2012.

County-level population and employment

The population is the fundamental element for continued economic prosperity. 17 out of 30 Counties have experienced population growth from 2012 to 2020, as shown in Fig. 3. Ordos District, Hohhot District, and Otok Banner are the top 3 growers in population growth, among which Ordos District has shown an annual growth rate of 12.8%, 10.5% for Hohhot District, and 8.4% for Otok Banner. For the other counties with positive growth, the annual rates are lower than 5%.

Fig. 3: Average county-level population growth from 2012 to 2020.
figure 3

17 out of 30 counties have experienced positive population growth from 2012 to 2020, the rest counties have shown negative growth.

Full size image

On the contrary, the rest 13 counties have shown negative growth during the same period. The county with the fastest population decline is Wuchuan, with a negative annual growth rate of 3.9%, negative 3% for Qingshuihe County, negative 2.6% for Hangjin Banner, negative 2.4% for Damao Banner, negative 1.2% for Tumed Left Banner. As for the other counties with negative population growth rates, their annual declining rates are less than 1%.

Figure 4 is based on data on employment. Hohhot District, Baotou District, and Ordos District are the top 3 counties that provide the most job opportunities. These three counties accommodated more than 60% of all the employment opportunities within HBOY urban agglomeration in 2020. As for the annual growth rate of employment of these county units, Otok Banner ranks first with an annual growth rate of 36.7%, Jungar Banner ranks second with a rate of 29.8%, and Ordos District ranks the third with a rate of 27.4%. Nine counties have experienced negative employment growth. The fastest decline happens in Helin County, with a negative rate of 7.8%, then follows Wuchuan County, with a rate of negative 3.5%, and Qingshuihe County, with a rate of negative 3%.

Fig. 4: Employment and average growth rate from 2012 to 2020.
figure 4

The ranking is arranged in descending order by the average employment growth rate of each county from 2012 to 2020. The height of each blue bar represents the number of job opportunities provided by a specific county.

Full size image

County-level fixed assets investment

County-level fixed assets investment of HBOY urban agglomeration and its annual growth rate are shown in Fig. 5. The fixed assets investment expenditure is disproportionately concentrated in a few counties. The investment in Baotou District accounts for almost one-fourth of the total investment of the urban agglomeration in 2020. Moreover, the investment expenditure of the five counties with the most significant investment accounts for nearly 50% of the total investment of the urban agglomeration.

Fig. 5: Fixed assets investment and average growth rate from 2012 to 2020.
figure 5

The ranking is arranged in descending order by the fixed assets investment of each county from 2012 to 2020. The red line represents its annual growth rate.

Full size image

As for growth rate, the top 5 counties with the fastest growth rate in investment are all from Yulin City. The annual growth rate of investment of Jia County is 148%, the second fastest grower in investment is Suide County with an annual rate of 81%, then comes Zizhou County with a rate of 76%, Qingjian County with a rate of 55%, and Dingbian County with a rate of 50%. It is worth noting that although these five counties’ investments have been growing fast, they account for merely 5% of the total investment of the urban agglomeration.

County-level retail sales

Total retail sales refer to the number of physical goods directly sold to individuals by enterprises through transactions and sold to social groups for non-production and non-business purposes and the amount of expenditure spent for catering services. It represents the market size vitality of a region. As shown in Fig. 6, Hohhot District and Baotou District are the top 2 county units with the largest retail market. These 2 regions’ retail sales account for two-thirds of the total retail sales in HBOY urban agglomeration in 2020.

Fig. 6: Retail sales and average growth rate from 2012 to 2020.
figure 6

The ranking is arranged in descending order by the retail sales of each county from 2012 to 2020. The red line represents its annual growth rate.

Full size image

In terms of the growth rate of the size of the local market, Hengshan District’s annual growth rate is 61%. The second fastest grower is Yulin District, with an annual growth rate of 41%, and the third one is Otokqian Banner, with an annual rate of 34%. It is worth noting that Hohhot District and Baotou District have large retail markets and have proliferated since 2012.

As shown above, these demographic and economic indicators reflect the county-level development of HBOY urban agglomeration over the past decade. The development of these county units during this period needed to be balanced. Some regions grew faster, and some regions grew slower. This unbalanced development was shown in the output, population, employment, investment, and consumption. More importantly, these statistical data suggest that the difference in economic growth among these county units is not only caused by the scale of input but also caused by the change in input-output efficiency. Hengshan District is a typical example. During the period covered by this study, the output growth of the Hengshan District was the fastest. However, when we pay attention to the growth of its population, employment, and investment, we unexpectedly find that the growth of factor input of Hengshan District could be faster. The slow growth of factor input has brought about the relatively fast growth of output, probably due to the improvement of its economic efficiency.

Model specification and variable selection

Model specification

We refer to the stochastic frontier production function that Battese and Coelli proposed (Zhang et al., 2004), assuming that regional effects follow a truncated normal distribution and allow time-varying effects to exist. The basic settings of the model are as follows:

$$Y_{it} = X_{it} \cdot \beta + \left( {v_{it} - u_{it}} \right),i = 1, \ldots ,N,\,t = 1, \ldots ,T$$
(1)

where, Yit represents the logarithmic form of the output of area i in year t; Xit is a k × 1 vector representing the logarithmic form of the inputs of area i in year t; β represents a set of unknown parameters; vit is a random disturbance term, which is mutually independent and follows a normal distribution \(N\left( {0,\sigma _v^2} \right)\), and is independent of uit. uit is a non-negative random variable, representing the degree of technical inefficiency of the local production, it is assumed to be mutually independent of each other and follows a truncated normal distribution \(N\left( {\mu ,\sigma _u^2} \right)\) at the point 0, where:

$$\mu _{it} = Z_{it} \cdot \delta$$
(2)

where, Zit is a p × 1 vector of variables, which may influence the efficiency of a DMU; and δ is an 1 × p vector of parameters to be estimated. Based on the above model setting, the economic efficiency of area i in year t could be defined as:

$${\mathrm{TE}}_{it} = \frac{{Y_{it}}}{{X_{it} \cdot \beta _j + v_{it}}}$$
(3)

Input-output variable for production function

We adopt a logarithmic C-D production function according to the previous model setting. Many researchers use a two-factor C-D production function to evaluate the TFP(Pires & Garcia, 2012; Reynès, 2019; Ishikawa, 2021; Liu & Tsai, 2021). We select an augmented three-factor C-D production function to fit the real economy better, meaning three inputs and one output. The logarithmic function has a variety of advantages. It can conveniently represent large and small numbers, making it possible to calculate ratios by simple addition and subtraction (Griffin et al., 1987). Logarithmic specification of production functions is trendy in the empirical analysis found in economic journals (Kozo & Mario, 2010).

Those three inputs are Land Usage, Labor Force, and Capital Stock, and the output is the annual GDP of each county unitFootnote 5. The original data used for the empirical analysis of this article comes from the “Inner Mongolia Statistical Yearbook”, “Shaanxi Statistical Yearbook” and the official statistical data of the corresponding local statistical departments.The processing methods of each variable are described as follows:

(1) Land Usage. Owing to the lack of data on each county’s built-up area, the study uses each county’s land coverage area, which can be found in the Statistical Yearbook, as a substitute for Land Usage, the raw data for land input is calculated by “square kilometer”.

(2) Labor force. The labor force is defined as the number of employed persons in each county. The number of employed persons can also be found in the Statistical Yearbook and is calculated by “person”.

(3) Capital Stock. There are no official capital stock statistics, meaning they need to be estimated. The data on capital stock involved in this study is calculated by Perpetual Inventory Method (PIM)Footnote 6. The initial value of capital stock adopts the calculation results of China’s provinces, autonomous regions, and municipalities by Zhang Jun et al. The province-level capital stock is allocated proportionately to each county according to each county’s share of GDP. The depreciation rate is assumed to be 5%. Capital Stock is calculated by “ten thousand RMB”.

(4) Regional GDP. Each year’s real GDP is used as the only output in our evaluation, and the data is directly obtained in the Statistical Yearbook, which is calculated by “ten thousand RMB”.

Independent variable for inefficiency model

Following the specification of Battese & Coelli (1992), we choose the following four variables, which may influence the technical efficiency of a DMU.

(1) Economic Linkage. There are interdependencies across places, so what happens in one region has implications for this location and other regions. Economic linkage is an index that represents this kind of economic interdependence among these county units. It is calculated with an augmented gravity model proposed by Miao, Zeng (2020), as shown in Eq. (4). Data for this index were calculated with the same method.

$$G_{ij} = \frac{{I_iI_j}}{{T_{ij}^2}}$$
(4)

where, Gij represents the economic linkage between county i and county j; Ii and Ij represents the comprehensive level of development of county i and j, respectivelyFootnote 7; Tij is the shortest time required for one way driving between two counties.

(2) Government Involvement. Government involvement in the economic system may generate spillover benefits or costs since the market is not perfect, and government intervention is required to minimize the distortions, which result from market failure. We use government expenditure as a proxy for government involvement. The data for this variable came from the statistical yearbook. Each county’s government expenditure per capita is used as raw data and is calculated by “RMB/capita”.

(3) Market Size. The relationship between efficiency and the size of a specific region (like cities) has been recognized and studied for a long time (Alonso, 1971; Prud’homme & Lee, 1999; Meijers et al., 2016). We introduce market size as a proxy variable to capture the effects of the “size” of a county on its efficiency. The data for this variable was represented by each county’s retail scale per capita and are calculated by “RMB/capita”.

(4) Core Area or not. We introduce a dummy variable indicating whether a county is the so-called core area of a city. for example, Hohhot District is the core area of Huhhot City. Descriptive statistics of all dependent and independent variables are shown in Table 1.

Table 1 Descriptive statistics of variables.
Full size table

Results and discussion

Regression results

In the application of Frontier 4.1, the Maximum Likelihood Estimation (MLE) is obtained from estimation using Ordinary Least Square (OLS) and second phase grid search. Then it is estimated to find the Stochastic Frontier function using MLE. Table 2 shows the final estimation results of MLE with Frontier 4.1.

Table 2 Regression results.
Full size table

For the production function estimation, as we can see in Table 2, coefficient β1 shows a value of 0.3393, which indicates that every 1% increase in labor will increase the output by 0.3393% ceteris paribus. The t-value of β1 is 5.0525, meaning there is a significant influence of labor on output. The estimated value of coefficient β2 is 0.0538, and its t-value shows that the influence of land on output is not significant. The estimation for coefficient β3 is 0.5136, which means every 1% increase in capital will cause an increase in output by 0.5163%, and this influence of capital on output is significant at the level of 1%.

For the estimation of the inefficiency model, coefficient δ1 gets a value of −0.3374 at the significance level of 1%. This negative value of estimation indicates that every 1% increase in a county’s economic linkage with the other counties within the urban agglomeration will lower the economic inefficiency of this county by 0.3374%. As for government involvement, its coefficient δ2 is 0.1426, which means government involvement increases 1%, and the economic inefficiency will increase by 0.1426%, meaning the economic efficiency will decrease by the same percentage. However, this coefficient is not significantly different from 0, even at the significant level of 10%. As for market size, its coefficient δ3 is −0.1663, which indicates that every 1% increase in market size will cause the economic inefficiency drops by 0.1663%, meaning the economic efficiency will increase with the same percentage, but this estimation is only significant at 10% level. Lastly, the estimated value for coefficient δ4 is positive and significant at 1% level, and this result indicates that if a county is the core area of a city, its inefficiency will increase, which means that being a core area of a city will lower its efficiency.

It seems counter-intuitive that being the core area of a city and government involvement will lower the economic efficiency of a county. However, because government intervention may also result in inefficiency rather than efficiency in resource allocation, our findings about the core area and government involvement will bring adverse effects to a county’s economic efficiency and start to make sense. Being a core area of a region naturally attracts more attention and, therefore, more expenditure from the government. It is probably true that the local government has already spent disproportionately too much in the core area of a city, which exceeds a certain critical level and generates some adverse effects on its efficiency.

Evaluation of economic efficiency of county units in HBOY urban agglomeration

We use the stochastic frontier model to calculate the economic efficiency of each county within HBOY urban agglomeration in the years 2012, 2016, and 2020, respectively. The results are shown in Table 3.

Table 3 Economic efficiency of each county unit in HBOY urban agglomeration.
Full size table

Generally speaking, the economic efficiency of these 30 county units has increased steadily in those selected years. The overall average efficiency level of HBOY urban agglomeration has increased from 0.505 in 2012 to 0.641 in 2016 and 0.753 in 2020. From the perspective of the economic efficiency of the four prefecture-level cities, Baotou has consistently ranked at the top, followed by Ordos, Hohhot in the third place, and Yulin in the last place of the four cities. The order has stayed the same in the period concerned in this paper. In 2020, Baotou, Ordos, and Hohhot’s economic efficiency were 0.829, 0.815, and 0.804, respectively, with little difference between the three. In the same year, the economic efficiency of Yulin was only 0.662, which was significantly lower than that of the other three cities.

Regarding efficiency improvement, the three county units with the most apparent improvement are Hengshan District, Wushen Banner, and Helin County. Among them, Hengshan District experienced the fastest growth. Compared with 2012, the economic efficiency of Hengshan District in 2020 increased by 102.39%, and the economic operation efficiency of Wushen Banner and Helin County increased by 95.14% and 90.24%, respectively. These three county units are the only areas with more than 90% efficiency improvement among the 30 county units. For the improvement of the economic efficiency of these three county units, we can find some clues in the previous analysis in section ‘An overview of HBOY urban agglomeration’. As for Hengshan District, for those 8 years covered by this study, its employment annual growth rate is only 1.1%, and its annual fixed assets investment annual growth rate is a moderate 8.5%. However, its GDP in 2020 is almost seven times larger than it was in 2012, which means a nominal annual growth rate of 87.4%. Increases in inputs cannot explain this unusually fast growth rate but probably come from economic efficiency improvements.

Those three county units with the slowest efficiency improvement are Jia County of Yulin city, Hohhot district, and Baotou District. Compared with 2012, the economic efficiency of the three regions increased by 12.63%, 15.06%, and 18.01% individually in 2020, all lower than 20%. Among them, the efficiency improvement of Hohhot district and Baotou District is not evident because their efficiency levels are very close to the production frontier. In 2020, the efficiency levels of the two regions reached 0.992 and 0.993 sequentially. In contrast, the efficiency value of Jia County was only 0.32 in 2012 and slightly increased to 0.36 in 2020. Within years covered in this paper, the economic efficiency of Jia County shows two prominent characteristics: one is the low level of efficiency, and the other is the slow growth rate. This evaluation result makes sense when we look at the raw data of Jia County. During those 8 years covered by this study, Jia County’s fixed assets investment has grown by an average rate of 147.8% annually. However, this considerable input does not generate rapid output growth. Besides, this differs from the cases of Hohhot District and Baotou District. Jia County’s slow economic efficiency growth does not mean its efficiency value is close to the production frontier. Because in the past decade, a vast amount of investment was made into areas that do not create value in terms of GDP, such as planting trees, strengthening dams, building nursing homes, and returning farmland to forests.

Spatiotemporal differentiation of county-level economic efficiency in HBOY urban agglomeration

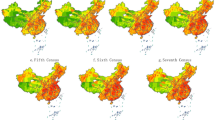
We use ArcGIS to visualize the economic efficiency of county units within HBOY urban agglomeration in 2012, 2016, and 2020 to intuitively expose the temporal and spatial differences in the economic efficiency of these 30 county units. The results are shown in Fig. 7.

Fig. 7: County-level economic efficiency in HBOY urban agglomeration in selected years.
figure 7

The darker the color of a region, the higher its economic efficiency is. The three maps from left to right illustrate the economic efficiency of each county unit in the year 2012, 2016, and 2020.

Full size image

In 2012, the overall input-output efficiency level of HBOY urban agglomeration was low. The average efficiency value was only 0.505. The District of Hohhot City had the highest efficiency (0.863), and the Otokqian Banner of Ordos City had the lowest efficiency (0.285). The efficiency values of 17 out of the 30 county units are lower than 0.5. The efficiency values of 11 regions are between 0.5 and 0.8. There are two county units with efficiency values higher than 0.8.

In 2016, the overall economic efficiency of HBOY urban agglomeration increased by a certain extent compared with 2012 and reached an average efficiency value of 0.641. Baotou District replaced Hohhot district as the economic unit with the highest economic efficiency (0.983), and Wubao County of Yulin City (0.343) had the lowest efficiency level. The efficiency values of 8 out of the 30 county units are lower than 0.5. The efficiency values of 15 county units lie between 0.5 and 0.8. There are three county units whose efficiency values are between 0.8 and 0.9. Baotou District, Dalat Banner, Hohhot District, and Jungar Banner’s efficiency values exceed 0.95.

In 2020, the overall economic efficiency of HBOY urban agglomeration was improved to an average efficiency value of 0.753. Baotou District ranked first with an efficiency value of 0.993. Dalat Banner still ranked second, with an efficiency value of 0.992. Jia County of Yulin city ranked at the bottom of 30 county units with an efficiency level of 0.350. Only 3 out of the 30 county units in the urban agglomeration had efficiency values lower than 0.5, all belonging to Yulin City. The efficiency values of 13 county units are between 0.5 and 0.8. There are three county units whose efficiency values are between 0.8 and 0.9. It is worth noting that in 2020, the economic efficiency of 11 county units in the urban agglomeration exceeded 0.9, of which the efficiency level of 5 county units exceeded 0.98, which is very close to the production frontier.

As shown in Fig. 7, in terms of the spatial distribution of efficiency, it can be concluded that in 2012, high-efficiency county units were concentrated in the middle of the urban agglomeration. Most county units in the north and southwest of the urban agglomeration and Helin county and Qingshuihe County in the east are low-efficiency areas. In 2016, high-efficiency county units are still mainly concentrated in the middle and east of the urban agglomeration, forming a gathering area of high-efficiency county units around Baotou Municipal District, Dalat Banner, and Jungar Banner. However, most county units in the north and southwest of the urban agglomeration, as well as Helin County and Qingshuihe County, are still low-efficiency areas. In 2020, the high-efficiency units with an efficiency value of more than 0.9 are mainly concentrated in the junction area of Huhhot, Baotou, and Ordos, forming a contiguous high-efficiency area in the middle and east of the urban agglomeration. This spatial distribution pattern of high-efficiency counties of HBOY is similar to what Luo Shasha has discovered in her study focusing on Fujian Province: high-efficiency areas are expanding over time and forming a spatial pattern in a continuous manner(Luo et al., 2021). Our finding about the spatial pattern of high-efficiency counties of HBOY is also consistent with the research conclusion of LIU Jiang etc. (Liu et al., 2020). That is, high-efficiency areas tend to form clusters. The southeast region of the urban agglomeration forms a region where the low-efficiency county units are concentrated. The four county units with the lowest efficiency level belong to Yulin City and are concentrated in the southeast region of the urban agglomeration.

Spatial correlation analysis of county-level economic efficiency in HBOY urban agglomeration

The economic efficiency levels of 30 county units in HBOY urban agglomeration may not be independent. There may be spatial autocorrelation between the economic efficiency levels of each county unit. Spatial autocorrelation examines the spatial correlation of a variable among observations (Lee & Li, 2017). When the values of a variable in adjacent areas are close, it is called positive spatial autocorrelation. Negative spatial autocorrelation is discovered when the observed values of adjacent areas vary greatly.

This paper uses Moran’s Index to test the spatial autocorrelation of economic efficiency of 30 county units in HBOY urban agglomeration. Moran’s Index is an index used to test the global correlation, and its calculation method is as follows:

$$I = \frac{n}{{S_0}}\frac{{\mathop {\sum }\nolimits_i \mathop {\sum }\nolimits_j w_{ij}\left( {x_i - \bar x} \right)\left( {x_j - \bar x} \right)}}{{\mathop {\sum }\nolimits_i \left( {x_i - \bar x} \right)^2}}$$
(5)

where, \(\bar x\) represents the mean value of economic efficiency of 30 county units, wij is the element in the spatial weight matrix, S0 is the sum of all elements of the spatial weight matrix, \(S_0 = \mathop {\sum }\nolimits_i \mathop {\sum }\nolimits_j w_{ij}\). Moran’s I is usually between −1 and 1. A value greater than 0 indicates positive spatial autocorrelation, and the closer it is to 1, the stronger the positive correlation. Its value less than 0 indicates negative spatial autocorrelation, and the closer it is to −1, the stronger the negative correlation. Suppose its value is equal to or very close to 0. In that case, it means the spatial distribution of observed values is random, and there is no spatial correlation between the economic efficiency of each county unit.

Table 4 shows the results of the overall Moran’s I of the economic efficiency of the county units of HBOY urban agglomeration. Regarding the robustness of the measurement results, this paper adopts two kinds of spatial weight matrices, namely the Queen adjacency matrix and the Euclidean distance matrix. The results show that the Moran’s I value measured based on the Queen adjacency matrix is slightly lower than that measured based on the Euclidean distance matrix, but the measurement results of the two consistently reflect that there is a significant positive spatial autocorrelation between the economic efficiency of each county unit of the urban agglomeration. Zhou (2020) reached a similar conclusion that the county units have shown a positive spatial correlation on the level of economic development by calculating Moran’s I using data on GDP per capita of counties from HBOY urban agglomeration. However, the author did not pay attention to the economic efficiency of county units. Except for the result in 2012 under the queen adjacency matrix, which is only significant at the significance level of 0.05, the Moran’s I values under the two spatial weight matrices in other years are greater than zero and significant at the significance level of 0.01.

Table 4 Moran’s I: Overall economic efficiency of county units in HBOY urban agglomeration.
Full size table

The three spatial autocorrelation fitting lines shown in Fig. 8 are drawn based on the Queen Adjacency Matrix, from left to right, respectively, in 2012, 2016, and 2020. The spatial autocorrelation of the economic efficiency among county units in the urban agglomeration has strengthened over time, and the significance is also improving.

Fig. 8: Spatial autocorrelation fitting line based on Queen contiguity weights matrix.
figure 8

Scatter points in the graph are mainly distributed in the first and third quadrants, representing a positive correlation. From left to right, the fitting line becomes steeper and steeper, representing the stronger spatial correlation between the economic efficiency of each county unit.

Full size image

For robustness, the three fitting lines shown in Fig. 9 are drawn based on the Euclidean distance matrix. The spatial correlation of the efficiency calculated based on the Euclidean distance matrix is stronger and more significant than the Queen adjacency matrix.

Fig. 9: Spatial autocorrelation fitting line based on Euclidean distance weights matrix.
figure 9

Scatter points in the graph are mainly distributed in the first and third quadrants, representing a positive correlation. From left to right, the fitting line becomes steeper and steeper, representing the stronger spatial correlation between the economic efficiency of each county unit.

Full size image

The Moran’s I value calculated above effectively describes the global spatial correlation of unit economic efficiency of 30 counties in HBOY urban agglomeration. However, this method cannot express the characteristics of local spatial correlation and local spatial agglomeration of county unit economic efficiency. In order to further reveal the temporal and spatial differentiation characteristics of county unit economic efficiency in the urban agglomeration, we use LISA diagram to visualize its feature in terms of local spatial correlation (Anselin, 1995).

The types of spatial autocorrelation can be expressed as geographical clusters and outliners. The former includes High-High mode (H-H) and Low-Low mode (L-L), and the latter includes Low-High mode (L-H) and High-Low mode (H-L). The H-H mode is a case of high-value clustering, meaning the observed value of a particular area is high, and the weighted average of the observed value of the surrounding area is also high. The L-L model is a case of low-value clustering, meaning the observed value of a particular area is low, and the weighted average of the observed value of the surrounding area is also low. The L-H model is a low-value outliner, which means the observed value in a particular area is low, but the weighted average of the observed value in the surrounding area is high. The H-L model is a case of a high-value outliner, which means the observed value in a particular area is high, but the weighted average of the observed value in the surrounding area is low.

As shown in Fig. 10, in 2012, 12 out of 30 county units’ economic efficiency showed significant spatial autocorrelation. Among them are four county units belonging to the “H-H” model, namely the Tumed Right Banner of Baotou City, Dalat Banner of Ordos City, Ordos Municipal District, and Yijinholo Banner of Ordos City. These four county units and their surrounding counties belong to high-efficiency units. There are five county units in the “L-L” mode, all located in the administrative divisions of Yulin City, including Hengshan District, Zizhou County, Mizhi County, Wubao County, and Qingjian County. Two county units belong to the “L-H” mode, namely Guyang County of Baotou City and Qingshuihe County of Hohhot City. Only Suide County of Yulin City belongs to the “H-L” mode. Regarding the significance of the local correlation, the high-value agglomeration between Tumed Right Banner and Ordos Municipal District and the surrounding areas has reached the significance level of 0.001. The high-value agglomeration in Dalat Banner and the high-value outliner in Suide County is significant at the significance level of 0.01; Other areas were significant at the significance level of 0.05.

Fig. 10: LISA: County-level economic efficiency in HBOY urban agglomeration.
figure 10

The patches with color on the left map represent specific types of spatial autocorrelation, while the patches with different shades of green on the right map represent their corresponding significance.

Full size image

Compared with 2012, the spatial correlation of county unit economic efficiency of HBOY urban Agglomeration was enhanced in 2016, and the economic efficiency of 15 county units showed significant spatial autocorrelation. Among them, six county units belong to the “H-H” mode. These six county units formed a prominent high-value agglomeration area of economic efficiency. Six county units belonged to the “L-L” mode, all located in the administrative divisions of Yulin City. The two county units in the “L-H” mode were still Guyang County of Baotou City and Qingshuihe County of Hohhot City. Suide County still belonged in the “H-L” mode. Regarding significance,it increased in 2016, and the high-value agglomeration of Tumed Right Banner, Dalat Banner, and Ordos Municipal District and the high-value anomaly of Suide County reached the significance level of 0.001. The significant level of spatial correlation between Yijinholo Banner in Ordos City, Hengshan District, Qingjian County, and Wubao County in Yulin City and the surrounding areas increased from 0.05 to 0.01; Other regions maintained significant spatial correlation at the level of 0.05.

Compared with 2016, the spatial correlation of county unit economic efficiency in HBOY urban agglomeration did not change significantly in 2020. The economic efficiency of 15 county units showed significant spatial autocorrelation. The number of county units with high-value agglomeration represented by the “H-H” mode was consistent with that in 2016. The spatial correlation between Guyang County and the surrounding county units was no longer significant, and Wuchuan County and Qingshuihe County showed the characteristics of “L-H” spatial autocorrelation. Jiaxian County, Mizhi County, Zizhou County, Suide County, Wubao County, and Qingjian County still belonged to the “L-L” mode, forming the spatial pattern characteristics of low-value agglomeration. Hengshan District broke away from the original low-value agglomeration and showed a new “H-L” mode.

As far as we know, no previous studies are focusing on the local spatial correlation among county units of HBOY urban agglomeration from the angle of TFP measurement using stochastic frontier analysis. Yu et al. (2012) conducted a similar study using data on the economic development level (instead of indicators for economic efficiency) of the county units of HBOY urban agglomeration to examine the local spatial correlation. They identified the geographical clusters and outliners close to our research results in 2012, but they did not report their study’s significance level.

Research conclusions and implications

Conclusions

Using data from the county units of HBOY urban agglomeration, this article has sought to evaluate the economic efficiency of 30 counties by adopting the Stochastic Frontier Model. This paper contributes to the existing literature by considering the county-level economic efficiency of such an under-developed area which attracts little attention previously, and reaches the following conclusions:

In summary, the county-level economic efficiency of HBOY urban agglomeration has steadily improved during the period covered by this study. As far as prefecture-level cities are concerned, the spatial pattern of economic efficiency has changed slightly. Baotou has always been the city with the highest efficiency level in HBOY urban agglomeration, while Yulin is the one that stays at the bottom of the four cities. At the county level, those county units with high efficiency have formed an apparent cluster in the east of the urban agglomeration. Such spatial structure characteristics were formed in 2012 and strengthened over time. The economic efficiency among county units shows a significant spatial correlation, indicating an apparent driving or spillover effect meaning high-efficiency areas could drive the surrounding areas to form high-efficiency agglomeration.

The county units with high efficiency have formed a pronounced agglomeration in the eastern part of the study area. From the perspective of spatial correlation, there is a significant positive relationship among these county units. Regarding factors that may affect economic efficiency, the empirical analysis concluded that economic linkage is the main positive factor that will increase the economic efficiency of a county. The market size is another positive factor. On the contrary, some factors will undermine the economic efficiency of a county, like its identity as the core area and government involvement (not significant).

Implications

Premised on these findings that the paper recommends, we come up with the following policy implications: First, the length of commuting time between counties is one of the core factors affecting the strength of intercounty economic linkage and consequently affects economic efficiency. Establishing and continuously upgrading a convenient transportation network can effectively shorten the “time distance” between these counties, saving commuters time, reducing transportation costs for commodities and production factors, and effectively lowering the transaction costs of various economic activities.

Second, a county’s “comprehensive level of development” is determined by its economic volume and other factors such as medical care, education technology, infrastructure, natural environment, and degree of openness. Therefore, the starting point for strengthening the intercounty economic linkage strength is to improve these counties’ “comprehensive level of development”.

Third, expanding the local market scale can improve economic efficiency. The market scale is measured by the total retail sales, which depends on the willingness and ability of residents to pay. Therefore, stimulating residents’ consumption is an effective way to improve economic efficiency.

Fourth, reducing government expenditure, especially for core areas. Empirical analysis has found that government expenditure harms economic efficiency. Excess government expenditure may lead to low marginal output or severe crowding-out effects. Therefore, appropriately reducing government participation may improve economic efficiency.

Finally, our study’s findings also have implications for future research on economic efficiency, focusing on the scale of the county economy. The findings of our study show that economic linkage is a significant determinant of county economic efficiency, and any future research on county economic efficiency or economic growth should incorporate this kind of variable in the models. Our results indicate that being a region’s core area does not necessarily gain advantages when economic efficiency is concerned. Whatever the core area of a region is attracting from the regional government or the market, it probably harms its economic efficiency, and future studies may target finding out the reasons behind this phenomenon.