Introduction

The emergence of “carbon finance” can be attributed to the evolving landscape of international climate policy and the implementation of two crucial international conventions, namely, the United Nations Framework Convention on Climate Change and the Kyoto Protocol (Ahonen et al., 2022). Carbon finance refers to the investment and financing activities associated with the low-carbon economy. It encompasses the buying and selling of carbon substances, as well as the financial mechanisms and instruments used to support climate change mitigation efforts (L. Yang and Hamori, 2021). Additionally, there is evidence that carbon finance is the key to achieving green and sustainable development (Bai et al., 2022). Since 2011, China has launched carbon emissions trading pilots in eight provinces and cities: Beijing, Shanghai, Tianjin, Guangdong, Shenzhen, Chongqing, Hubei, and Fujian (Liu et al., 2022).

Multiple criteria decision-making (MCDM) is a branch of operational research dealing with finding optimal results in complex scenarios, including various indicators, conflicting objectives, and criteria (A. Kumar et al., 2017). Within the realm of economic development analysis, multiple-criteria decision-making methods have been extensively utilized (Luczak and Just, 2020). It also gained widespread popularity across various fields and disciplines, providing valuable tools for addressing complex decision-making problems. Among the diverse range of MCDM approaches, the TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) method stands out as one of the most popular MCDM methods (Subbaraj and Thiyagarajan, 2021). The fundamental principle of TOPSIS dictates that the chosen alternative should demonstrate the shortest distance from the positive ideal solution (PIS) while also being the farthest away from the negative ideal solution (NIS) (Celikbilek and Tuysuz, 2020). Another notable MCDM method is the VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje) method; this method involves identifying a trade-off value to rank and evaluate alternatives according to conflicting criteria, allowing decision-makers to select the most favorable solution based on their preferences (Peng et al., 2020).

Considering the remarkable advancements in carbon finance within China and the significant attention given to this domain by the Chinese government, investigating the competitiveness of regional carbon finance has become a critical endeavor(Jiang et al., 2023). This analysis seeks to fill the existing research gap by examining the combined application of MCDM techniques and conducting a thorough exploration of the extent of carbon finance development in specific regions.

Through this study, we aim to shed light on the integration of MCDM methods, provide insights into addressing complex system problems, and offer a comprehensive assessment of carbon finance progress at the regional level. Furthermore, to address the complexity inherent in system ordering problems, the topological hierarchy diagram of adversarial interpretive structure modeling (AISM) is introduced to form a complete system analysis. This diagram represents a novel modeling approach that builds upon the classical interpretive structure model (ISM) while integrating principles inspired by generative adversarial networks. This method effectively solves the problem of clutter present in the ISM model.

Based on the innovative hybrid MCDM methodology and the AISM model, we found that the level of carbon finance development in China can be categorized into six echelons and that focusing on innovation, the development of the financial industry, and greater participation in ETS market transactions are important factors for development.

The present study makes several significant contributions to the field. Firstly, this study combines carbon regulation and ETS market elements for the first time, introducing a novel framework for assessing carbon finance in China. This framework provides a comprehensive evaluation system for the development of carbon finance in China. Secondly, a new hybrid MCDM method is proposed in this study. Specifically, this method combines TOPSIS and VIKOR. By incorporating VIKOR’s positive and negative distance solutions and decision intervals into TOPSIS, this integration addresses the decision error issue associated with traditional TOPSIS methods, making TOPSIS more effective in the decision-making domain. Thirdly, methodologically, the AISM is extended to economic analysis. The results of ranking China’s carbon finance pilot cities confirm that the ranking of these cities forms a rigid system. This analytical paradigm provides valuable insights for investors in making carbon finance investment decisions. Additionally, this analytical paradigm offers a method to test the effectiveness of investment decisions, which can be extended to the field of behavioral finance. The method reveals investment choices within a stable decision interval, and these contributions have practical implications for policymakers and investors in the field of carbon finance.

“Literature Review” of this paper summarizes the relevant literature that examines the combined application of the TOPSIS and VIKOR methodologies, as well as the contributions of previous researchers in exploring the development of carbon finance in China. “Reconstruction of the Carbon Finance System” reconstructs a new evaluation system for carbon financial development based on the literature by adding factors such as carbon regulation and carbon innovation. “Methodologies” introduces the innovative MCDM methodology adopted in this paper, while “Empirical Study” presents the empirical part and visualizes the ranking of the pilot cities using the AISM model. “Discussion” addresses the results. “Conclusion and Policy Recommendation” presents the conclusions of the paper and directions for further research.

Literature review

Carbon finance is progressively emerging as a significant domain influencing the economy and society. Substantial empirical evidence supports the notion that the development of carbon finance positively contributes to various aspects of the economy, including technological innovation, industrial structure, energy efficiency, and overall economic development (Hu et al., 2022; Lin and Jia, 2019; Tang et al., 2021). There are fewer studies that focus on evaluating the level of regional carbon finance. In 2014, Liu (2014) made the pioneering attempt to measure the level of provincial carbon finance development by utilizing a few criteria layers: carbon finance business, energy efficiency, and science and technology. As part of this effort, Liu constructed the provincial carbon finance development index. Li and Dong, 2018 established a panel data model to further analyse the factors affecting the level of regional carbon finance development and concluded that civil vehicle ownership, enterprise size, the proportion of tertiary industry output value, and industrial governance investment intensity have more significant effects on the level of regional carbon finance development. Chen et al. (2020) used a neoclassical theoretical model to construct a panel regression model and empirically test the factors influencing the level of carbon finance development. They found that carbon emissions trading and carbon emission reduction investment and financing are two important components of carbon finance development. Zhan et al. (2023) used the MCDM technique to accurately and quantitatively assess the level of low-carbon transportation development in China, identifying the key influencing factors.

However, the influence of the heterogeneity of provincial environments on the level of carbon finance development has not been comprehensively considered. Moreover, it is essential for indicators to encompass diverse factors, including environmental and social aspects, to measure the extent of regional carbon development accurately. Furthermore, the literature predominantly focuses on China’s carbon finance market prior to its rapid growth. Thus, there is a need for innovation in evaluating the evolving carbon market in China. With the implementation of new policies and the rapid development of the carbon market, utilizing the MCDM method becomes crucial in assessing the competitiveness of regional carbon finance.

In the context of the hybrid approach combining TOPSIS and VIKOR, several scholars have conducted comparisons of these two methods. Some scholars have independently utilized the two methods for comparative studies of decision-making problems within the same system. To validate the regional COVID-19 security assessment published in the DKG report, Hezer et al. (2021) used three MCDM methods for ranking, ultimately concluding that the TOPSIS method is closer to the ranking originally provided in the report than the VIKOR method. In addition to medical analysis, TOPSIS, and VIKOR methods can be extended to economic and environmental analysis. Sari et al. (2020) used TOPSIS and VIKOR for environmental suitability analysis. They compared the two methods, validating that the overlap between VIKOR and suitability maps was 88%, and for TOPSIS, it was 91%. Nonetheless, the aforementioned articles consistently employ the distinct methods of the two models in isolation, neglecting their potential integration. Consequently, the resulting findings confirm the disparate ranking solutions generated by the MCDM methods employed in each model. In addition, both the TOPSIS and VIKOR methods are capable of generating a ranking list of alternatives. In the case of VIKOR, the highest-ranked alternative is the one that is considered the closest to the ideal solution. While TOPSIS may provide a more comprehensive ranking, it does not necessarily guarantee that the top-ranked option is always the closest to the ideal solution (Opricovic and Tzeng, 2004).

Also, this paper incorporates the AISM approach proposed by Ni (2020), initially designed for scalable evaluation of training methods in the military domain. The AISM method offers an advantage over the ISM method by addressing the issue of clutter that arises when the level of interpretation of the evaluation object becomes more complex. Su et al. (2023) further extended the application of the AISM model to evaluate business strategies and supply chains. Building upon these previous studies, this paper seeks to expand the application of the AISM model by employing it for an integrated analysis of the regional environment and economy.

Reconstruction of the carbon finance system

In academic circles, there is currently no unified consensus regarding the overall evaluation index of carbon finance. Building upon the research perspectives of Chen et al. (2020) regarding the measurement of the regional carbon finance development level in China, we have endeavored to construct a set of carbon finance measurement index systems that possess strong regional adaptability. In this paper, a comprehensive evaluation of China’s carbon finance development is conducted by selecting a subset of representative indicators from a larger pool. This approach ensures a fair assessment of the current state of carbon finance development in China. It addresses the issues of outdated indicator selection and generalized data utilization found in previous literature. The index system comprises five benchmark layers: carbon environment, carbon regulation, carbon finance, ETS market, and carbon innovation. The indicators were chosen based on principles of rationality, representativeness, and accessibility. Detailed measurement methods for each indicator can be found in Table 1.

Table 1 Carbon finance system construction.
Full size table

Carbon environment

Carbon finance, as a financial activity aimed at mitigating greenhouse gas emissions, particularly in reducing carbon emissions, is an institutional innovation within the realm of environmental governance. It is a product of financial innovation that has emerged in the context of low-carbon economic development (Chen et al., 2021). The development of carbon finance is intricately linked to the local carbon environment, highlighting the importance of considering the carbon environment as an indicator of carbon development. Additionally, the presence of forest cover and civilian car ownership has been shown to exert a significant influence on the level of regional carbon finance development (Li and Dong, 2018). Therefore, these elements have been incorporated into the analysis.

Carbon regulation

The concept of carbon finance emerged relatively late in China, and as a result, some regions have insufficient carbon regulation measures in place. Furthermore, there is a limited body of research on carbon regulation specifically focused on China. Yang et al. (2023) have confirmed that the central government can promote low-carbon technology innovation and encourage investment expansion by implementing low-carbon policies that mitigate the potential negative impact on economic growth. This finding underscores the importance of considering carbon regulation when evaluating carbon finance, an aspect often overlooked in many previous evaluation systems.

A firm’s participation in social and environmental activities is positively and significantly rewarded by a higher level of financial efficiency (Abdi et al., 2022). Pollution control investment and environmental protection tax revenue from public companies are the most direct quantitative indicators of the government’s approach to carbon environmental management. In addition, to ensure scientific rigor, we selected two other representative environmental regulatory indices in China, the Pollution Information Transparency Index (PITI) and the Carbon Neutral Composite Index.

PITI is a significant initiative by the Chinese government aimed at promoting information disclosure in the field of environmental protection (Ding et al., 2022). This index is jointly published by the Institute of Public and Environmental Affairs (IPE) and the Natural Resources Defence Council, and it has gained widespread recognition as one of the most reputable regulatory indices in China.

In 2021, the Chinese Research Academy of Environmental Sciences (CRAES) and the IPE established a research group that regularly publishes the “Carbon Neutral Composite Index.” This index evaluates the climate ambition, low-carbon status, and emission reduction trends of cities in China based on the national strategy, utilizing publicly available information. The index reflects the commitment of local governments to establish peak carbon and carbon-neutral targets, enhance their capacity, and implement and support national policies. It considers various factors, such as economic development, energy use, carbon emissions, and other relevant aspects, to provide a comprehensive assessment.

ETS market

The establishment and development of a carbon market play a crucial role in addressing the financial challenges associated with low-carbon economic development, enhancing the carbon emissions trading system, and bolstering the core competitiveness of the national economy (Luo et al. 2021). The implementation of an emissions trading system (ETS) has emerged as a widely recognized approach for addressing carbon emissions. Over the past two decades, the ETS has garnered significant international attention and has had a profound impact on the global economy and industrial structure in the 21st century (Ritz, 2022).

Emissions trading systems (ETS) have gained recognition as effective market-based policy tools. To comprehensively summarize the experiences from the construction and operation of the first compliance cycle of the national carbon emissions trading market and to enhance the understanding of the national carbon market in the community, the Ministry of Ecology and Environment of the People’s Republic of China organized and compiled the Report on the First Compliance Cycle of the National Carbon Emissions Trading Market in 2023. This report highlights key aspects such as carbon emission allowances, carbon emission trading volume, and the average price of carbon transactions (Jin et al., 2020). These indicators have been selected as key components in this paper.

Carbon finance products

In April 2022, the China Securities Regulatory Commission issued the Carbon Financial Products (JR/T 0244-2022) as a recommended standard for the financial industry. The issuance of carbon bonds serves the purpose of financing carbon-neutral projects and supports the development of low-carbon industries. These bonds play a crucial role in providing sufficient working capital for low-carbon industries and contribute significantly to mitigating climate change (Wei et al., 2022). Consequently, the cumulative issuance of carbon bonds in each province and city has been selected as a measure to assess the activity of carbon financial products in their respective carbon markets.

Research by Sharma et al. (2023) suggests that green credit and stock markets have a significant impact on regional sustainability. Additionally, Phung et al. (2022) find a significant negative correlation between nonperforming loan ratios and bank efficiency. The effectiveness of financial markets plays a crucial role in promoting green development. However, previous literature has not yet incorporated carbon financial products into the scope of carbon finance evaluation indicators. Taking data availability into consideration, this paper selects several indicators from the CSMAR database, including the daily individual stock returns (excluding cash dividends) of carbon-neutral concept stocks, the growth rate of green loans, the nonperforming loan ratio of carbon-neutral concept stocks, and the growth rate of the financial sector within the tertiary sector. These indicators are chosen to assess stock performance and consider the growth of the financial sector.

Carbon innovation

Zhou et al. (2022) have highlighted that the underdevelopment of the tertiary sector hinders the promotion of carbon efficiency. Additionally, the implementation of low-carbon pilot city policies that prioritize innovations with higher carbon abatement potential can enhance low-carbon innovation within cities. Furthermore, the innovation environment significantly influences the effectiveness of innovation in cities (Pan et al., 2022). Both companies and governments recognize innovation as a fundamental driver of technological development, and carbon innovation is increasingly gaining importance as a component of green innovation. To measure carbon financial innovation, indicators such as R&D intensity and the value added of the tertiary industry as a proportion of GDP are selected. These indicators provide insights into the level of investment in innovative science and technology, as well as technological research and development within a region and its enterprises.

Methodologies

TOPSIS-VIKOR hybrid method

This section introduces a novel method for ranking the superior and inferior solutions that can link the distance solutions obtained in TOPSIS and VIKOR. Both methods offer ranking lists, but they differ in their suitability for different decision-making scenarios. The VIKOR method is more appropriate for selecting the optimal solution when a unique optimal solution is desired (Liu et al., 2020). On the other hand, the TOPSIS method is more inclined towards ranking and is suitable for selecting multiple alternatives (Opricovic and Tzeng, 2004). In this study, we aim to combine the two methods by starting from a distance and employing the following approach:

Step 1. Calculation of positive and negative ideal solutions

The positive and negative ideal solutions are denoted by \(x_j^ +\) and \(x_j^ -\).

$$x_j^ + = \left\{ {x_1^ + ,x_2^ + , \cdots ,x_m^ + } \right\} = \left\{ {{{{\mathrm{max}}}}\left( {\left. {n_{ij}} \right|j \in J} \right)} \right\}$$
(1)
$$x_j^ - = \left\{ {x_1^ - ,x_2^ - , \cdots ,x_m^ - } \right\} = \left\{ {{{{\mathrm{min}}}}\left( {\left. {n_{ij}} \right|j \in J} \right)} \right\}$$
(2)

Step 2. Assuming that \(D_i^ +\) is the distance to the PIS and \(D_i^ -\) is the distance to the NIS, the distance between each parameter and the positive and negative ideal points can be obtained according to the distance calculation formula, and the Euclidean distance calculation method is used in this paper.

The PIS equation is:

$$D_i^ + = \sqrt {\mathop {\sum}\limits_{j = 1}^m {w_j^2\left( {x_j^ + - n_{ij}} \right)^2} }$$
(3)

The NIS equation is:

$$D_i^ - = \sqrt {\mathop {\sum}\limits_{j = 1}^m {w_j^2\left( {n_{ij} - x_j^ - } \right)^2} }$$
(4)

Now, the VIKOR group utility and individual regret calculation. The specific calculation steps of the VIKOR method are as follows (Kumaran, 2022):

Step 4. The best (\(\max ( {n_j} )\)) and worst (\(\min ( {n_j} )\)) values of all the criteria functions were determined.

$$L_{p,j} = \root {p} \of {{\mathop {\sum}\limits_{j = 1}^n {\left\{ {\frac{{w_j\left[ {\max \left( {n_j} \right) - n_{ij}} \right]}}{{\max \left( {n_j} \right) - \min \left( {n_j} \right)}}} \right\}^p} }}\left( {1 \le p \le \infty ;j = 1,2, \cdots ,m} \right)$$
(5)

where j denotes the indicator number, i is the assessment criterion number, nij denotes the i assessment value of the j unit, \(\max ( {n_j} )\) and \(\min ( {n_j} )\) denote positive and NISs, respectively, and wj denotes the weight.

Step 5. Determine the maximize group utility (\(S_i^ +\)) and minimize individual regret (\(R_i^ +\)). The formula is as follows:

$$- S_i^ + = \mathop {\sum}\limits_{j = 1}^m {\frac{{w_j\left[ {\max \left( {n_j} \right) - n_{ij}} \right]}}{{\max \left( {n_j} \right) - \min \left( {n_j} \right)}}\left( {j = 1,2, \cdots ,m} \right)}$$
(6)
$$- R_i^ + = \begin{array}{*{20}{c}} {max} \\ {j = 1} \end{array}\left\{ {\frac{{w_j\left[ {\max \left( {n_j} \right) - n_{ij}} \right]}}{{\max \left( {n_j} \right) - \min \left( {n_j} \right)}}} \right\}\left( {j = 1,2, \cdots ,m} \right)$$
(7)

The two values indicate the distance to the PIS, i.e., the negative indicator, so a negative sign is added to the previous term (Bera et al., 2022).

The VIKOR method makes decisions based on group utility and individual regret and shares similarities with TOPSIS (Opricovic and Tzeng, 2004). Both methods make optimal decisions by determining positive and NISs, i.e., PIS and NIS. Previous literature using the VIKOR method was calculated using Eq. (6) and Eq. (7) (Akram et al., 2021). When we extend the expected and regret values of the VIKOR method in Fig. 1, we can obtain two sets and opposite signs of expected and regret values, which are extended here with Eq. (8) and Eq. (9).

Fig. 1: VIKOR Compromise Solution.
figure 1

Calculations within the feasible set.

Full size image

Step 6. Determine minimize group utility (\(S_i^ -\)) and maximize individual regret (\(R_i^ -\))

$$S_i^ - = \mathop {\sum}\limits_{j = 1}^m {\frac{{w_j\left[ {n_{ij} - \min \left( {n_j} \right)} \right]}}{{\max \left( {n_j} \right) - \min \left( {n_j} \right)}}} \left( {j = 1,2, \cdots ,m} \right)$$
(8)
$$R_i^ - = \begin{array}{*{20}{c}} {max} \\ {j = 1} \end{array}\left\{ {\frac{{w_j\left[ {n_{ij} - \min \left( {n_j} \right)} \right]}}{{\max \left( {n_j} \right) - \min \left( {n_j} \right)}}} \right\}\left( {j = 1,2, \cdots ,m} \right)$$
(9)

Equation (8) and Eq. (9) denote the distance to the NIS, which is not considered in the classical VIKOR method, and the two values are positive indicators. Suppose the two distances are used to measure the best decision. In that case, the final compromise decision indicator values should be arranged in ascending order instead of descending order as in the classical method (Sałabun et al., 2020).

From this, we can obtain the values of the three positive and NIS columns, summarized in Table 2 as follows.

Table 2 TOPSIS VIKOR ideal solution summary.
Full size table

Thus far, we can sort the samples according to their distances to the positive and NISs by averaging them. SDR+ and SDR− denote the positive and NIS averages, respectively, and Q is the final compromise solution:

$$\begin{array}{l}Q_i = \left( {1 - k} \right)\left[ {\frac{{SDR_i^ + - \min \left( {SDR_i^ + } \right)}}{{\max \left( {SDR_i^ + } \right) - \min \left( {SDR_i^ + } \right)}}} \right]\\\qquad + k\left[ {\frac{{\max \left( {SDR_i^ - } \right) - SDR_i^ - }}{{\max \left( {SDR_i^ - } \right) - \min \left( {SDR_i^ - } \right)}}} \right]\end{array}$$
(10)

According to the definition of the VIKOR method, the formula is expressed as the distance to the optimal solution, which is considered a negative indicator, and those indicators are ranked in descending order based on their magnitude (Kaya et al., 2020).

AISM operations

The ISM method solves the hierarchical process using a best-to-best approach, i.e., the hierarchical elements are placed from top to bottom from the Pareto optimal to the Pareto inferior approach in the hierarchy diagram (R. Kumar and Goel, 2022). The AISM method is the opposite, i.e., it starts from the lower level (Ni and Huang, 2020). The calculation steps are shown in Fig. 2.

Fig. 2: Schematic diagram of the AISM construction process.
figure 2

From original matrix to pareto-optimal set.

Full size image

D is a decision evaluation matrix with n rows and m columns, n represents the evaluation object and m represents the dimension. First, we process this matrix. According to the rule of a partial order, for negative indicators, i.e., the lower the value, the better the indication. If any two rows (x, y) in the decision matrix D have \(d_{x1} \ge d_{y1}\), \(d_{x2} \ge d_{y2}\), …, and \(d_{xn} \ge d_{yn}\), then the evaluation object y is better than the evaluation object x, and it is denoted as \(x \prec y\). These results are displayed in the relationship matrix \(A = \left[ a \right]_{n \times n}\). This paper indicates the results of comparing two provinces with each other under different indicator dimensions, where:

$$a_{xy} = \left\{ {\begin{array}{*{20}{c}} {1\quad x \prec y} \\ {0\quad No\,complete\,superiority\,or\,inferiority\,relationship\,or\,y \prec x} \end{array}} \right.$$
(11)

Since the relation matrix A is a Boolean matrix, its reachable matrix is calculated as follows:

$$B = A + I$$
(12)

A is the original relationship matrix, B is the multiplication matrix, I is the unit matrix, and concatenation of B yields:

$$B^k = B^{k + 1} = R$$
(13)

R is the reachable matrix in Eq. (13). The comparative relation matrix R is subjected to Boolean operations to obtain the skeleton matrix S, and the procedure is shown in Eq. (14).

$$S = R - \left( {R - I} \right)^2 - I$$
(14)

Hierarchical graph division is determined by the prior set Q, the reachable set R, and the common set T. As an example, the ei element in the relation matrix A is summarized as Table 3.

Table 3 Element extraction calculation.
Full size table

The UP-type hierarchical chart is divided into hierarchical levels according to the result priority; the rule is \(T\left( {e_i} \right) = R\left( {e_i} \right)\), and the province samples are placed in order from top to bottom. In contrast, the DOWN-type hierarchical chart is divided into hierarchical levels according to the effect priority; the rule is \(T\left( {e_i} \right) = Q\left( {e_i} \right)\), and the province samples are placed in order from bottom to top. The two extraction methods result from the opposition, with the Pareto-optimal samples placed at the top level and the worst samples at the bottom level, the superiority and inferiority represented by directed line segments, from which a more intuitive ranking of provinces can be determined.

Empirical study

Data from eight provinces and cities participating in China’s carbon pilot program were selected. The authority of provincial indicators was taken into consideration during the data collection process. The data sources include the China Statistical Yearbook, China Environmental Statistical Yearbook, WIND database, EPS database, and CSMAR database. In the empirical part, first, the indicators of each sample are normalized using the polar difference method, the corresponding weights are calculated using the entropy weight method, and the three pairs of positive and negative distance solutions (S, D, and R) are calculated according to the formula in “TOPSIS-VIKOR Hybrid Method”. The topological hierarchy diagram is obtained by the AISM operation according to the method in “AISM Operations”, and the robustness tests are performed. The following steps are detailed.

Weight calculation

This paper uses the entropy value method to measure the weight of indicators. According to the definition of information entropy, for a certain indicator, the entropy value can be used to judge the dispersion degree of a certain indicator (Teixeira et al., 2021). The information entropy value is related to the dispersion degree of an indicator, meaning that a smaller entropy value indicates a greater influence or weight of the indicator in the comprehensive evaluation. Therefore, the information entropy method can be employed to calculate the weights of each indicator, providing a basis for the comprehensive evaluation of multiple indicators. The entropy method has been widely utilized in academic analysis for determining weights in various fields (Alrasheedi et al., 2022; Chen, 2021; Qin et al., 2022). To ensure the comparability of different indicators and to eliminate the influence of varying magnitudes in the raw data, a standardization process is applied to the data obtained from the database. Once the data are standardized, the entropy weight method is employed to calculate the weight values for each secondary indicator. This enables the identification of high-weight indicators that significantly influence the development of carbon finance. The specific results can be found in Table 4.

Table 4 Entropy weights and ranking.
Full size table

TOPSIS-VIKOR methods solution results

Using the weights obtained from Table 4, the SDR of the positive and NISs and the average of the positive and NISs were determined by combining the joint method of TOPSIS and VIKOR, and Fig. 3 presents the steps of this method operation.

Fig. 3: TOPSIS-VIKOR operation.
figure 3

From Original Data to Compromise Q.

Full size image

The SDR values are calculated in Table 5, which presents the joint distance of the TOPSIS and VIKOR methods, where SDR+ is the PIS and SDR− is the NIS.

Table 5 Combined positive and negative ideal solutions.
Full size table

Next, the compromise solution Q can be determined according to Eq. (10), and according to the rule, the more distant the sample is from the NIS, the higher it is ranked. By convention, a cluster analysis should be performed at this point to determine the inflection point of K values in [0,1], and the dominance ranking changes when K values are at the inflection point (Ren et al., 2022). In this empirical evidence, two inflection points are found to exist within [0,1], and this inflection point leads to a change in the ranking of each province and city. The results are shown in Tables 6 and 7.

Table 6 Compromise value Q for each type of K value.
Full size table
Table 7 Sensitive value clustering analysis.
Full size table

To more explicitly present the rankings of the eight evaluation subjects, the AISM was introduced.

AISM solution

To more intuitively grasp the hierarchy of advantages and disadvantages among the evaluation objects, the decision matrix D, consisting of positive and NIS SDR in Table 5, is selected for calculation, leading to the relationship matrix A, derived in Table 8. The matrices are then connected using the method in “Carbon Innovation”.

Table 8 Relationship matrix A.
Full size table

According to the method mentioned above, the relationship matrix A is extracted in an effect-first and result-first manner. Under the premise of effect priority, the reachability matrix behavior of the object is 1; under the premise of result priority, the reachability matrix column of the object is 1. UP and DOWN belong to a group of opposite (adversarial) methods in topological-level graph drawing. The extracted results are shown in Table 9.

Table 9 UP and DOWN extraction hierarchy diagram.
Full size table

In this case, since the relationship between the evaluation objects is uncertain and the direction of the directed line segment is not confirmed, we need to compute the general skeleton matrix S to represent the loop structure in the simplest daisy chain. The computed results for the general skeleton matrix S are presented in Table 10.

Table 10 General skeleton matrix.
Full size table

The general skeleton matrix provides information on the direction of the directed line segments, allowing for the generation of the UP and DOWN topology hierarchy. Figure 4 represents the topological ordering of the UP and DOWN, showcasing the hierarchical relationships between the evaluation objects.

Fig. 4: UP-DOWN daisy chain.
figure 4

UP type for result priority and DOWN type for effect priority.

Full size image

According to the ranking results of the method, Guangdong and Beijing are in the first echelons, followed by Shenzhen, Shanghai, Hubei, and Fujian. Tianjin belongs to the same fifth echelon, and Chongqing is ranked last. Furthermore, by examining the AISM topological hierarchy diagram, it can be observed that the results form a rigid system, indicating a higher level of stability in the rankings.

Robustness test

In this section, based on the theory of mental accounting (Thaler, 2008), a robustness test is performed by varying the mental accounting Q-value to form different decision intervals, thus proving the robustness of the whole system in different intervals.

We intercepted the decision intervals from the original clustering intervals [0,0.1866] and [0.8099,1], shortened the decision intervals [0,1] to [0.1,0.9], and ran the clustering sensitivity value analysis again to test whether it would lead to an unstable system. This test changes both the decision interval and length and can be applied to most decision groups. The results of the robustness test are shown in Table 11.

Table 11 Robustness Test.
Full size table

Upon extracting the new clustering results, we obtain the same sorting result as the original decision interval. Furthermore, the hierarchical topology derived from the new clustering results aligns with the hierarchy presented in Table 9.

Discussion

Influences of indicator

Through the entropy weighting method, the weights of all indicators were calculated. The findings reveal that among the primary indicators, the indicators related to financial industry development (D) rank first in terms of their weight. Similarly, among the secondary indicators, R&D intensity (E1) holds the highest weight. These empirical results are considered favorable and consistent with the current state of carbon finance. The results suggest that the role of the ETS market and financial innovation should be vigorously pursued. In the future, it should actively participate in the ETS market and actively explore ways of carbon innovation.

TOPSIS-VIKOR method

We propose an MCDM method that combines the classical TOPSIS and VIKOR methods. This method extends the group utility and individual regret values in the VIKOR model, integrates the positive and NISs of evaluation objects, and derives a compromise solution Q. By leveraging the strengths of both the TOPSIS and VIKOR methods, this approach not only determines the best solution but also provides a relatively reasonable overall ranking. Through robustness testing, we found that the results obtained by this method are robust within a certain decision interval. Additionally, the method yields different sensitivity value intervals, allowing for a certain tolerance range in decision-making choices under different mental accounts.

The methodology yields an optimal investment ranking and investment decision for carbon finance in China, with Beijing and Guangdong being the optimal investment choices and remaining robust after changing the decision interval.

AISM model

We introduced the AISM model to obtain a pair of minimal hierarchical topology graphs using opposite hierarchical extraction rules. This approach allows us to maintain the system’s functionality without losing any essential information. By applying the AISM model, we obtained topological ordering with a rigid structure, which offers clearer characteristics than the ISM model. The AISM model effectively avoids the clutter problem associated with the ISM model and ensures the scientific nature of the model by extracting the UP and DOWN twice for different priority degrees.

Conclusion and policy recommendation

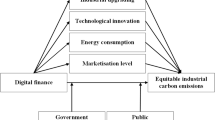
Carbon finance is a complex interdisciplinary domain that requires consideration of various factors and data. In this paper, the carbon finance system is reconstructed to align with the development status of China’s carbon finance, incorporating elements such as carbon regulation and carbon innovation to adapt to the changes in the country’s carbon market. The results of the study suggest that there is a need to strengthen innovation investment and the development of the tertiary industry to empower carbon finance. Drawing on the concept of the environmental Kuznets curve, which posits that environmental pollution tends to slow down and environmental quality improves after reaching a certain critical point of economic development (Dinda, 2004), the paper argues that focusing on green innovation and the level of the financial industry is crucial for enhancing the degree of local carbon finance development. Additionally, attention should be given to the development of the ETS market, with a particular emphasis on increasing carbon emission quotas and trading volume. Evidence from the EU-ETS demonstrates that increased intervention by enterprises and governments in the carbon market, along with enhanced market activity, can effectively reduce carbon emissions (Bayer and Aklin, 2020). Therefore, to enhance the effectiveness of carbon finance and achieve environmental goals, it is crucial to strengthen the cooperation between enterprises and governments. This can be achieved by improving the transparency of the carbon market, enhancing information disclosure, and promoting effective communication among stakeholders. By doing so, the fluidity and activity of carbon trading can be increased, leading to more efficient and impactful carbon reduction efforts.

According to the estimation results of the TOPSIS-VIKOR-AISM model, Beijing, and Guangdong are identified as cities with the highest investment potential in carbon finance. Both cities are placed in the first tier of carbon finance development. However, it is worth noting that Chongqing has a significantly lower investment potential than the other cities, even when considering different mental account expectations. This could be attributed to the relatively low activity level of the ETS market in Chongqing.

The proposed paradigm offers a novel approach to evaluating the relationship between environmental and economic development, providing practical solutions for decision-making problems. By leveraging the strengths of multiple methods, our approach enables the development of a more rational ranking scheme, facilitating optimal decision-making. This methodology can be applied to enhance the analysis of various domains, such as environmental geography (Mitra and Das, 2023), supply chain management (S. Kumar and Barman, 2021), and regional investment (Fakhrehosseini, 2019). The versatility of this approach contributes to improved decision analysis and informed decision-making processes.

While this study provides valuable insights into the level of development and investment decision-making in China’s carbon finance, it is important to acknowledge several limitations. Considering the importance of ETS markets in carbon finance and the early stage of China’s ETS market, relying solely on market transaction indicators may not provide a complete picture. Obtaining more detailed information on ETS market activities would lead to a more comprehensive understanding of carbon finance development. While the K values obtained by altering the decision interval boundaries in “Robustness Test” are reasonable, they are limited to specific demographic groups. To meet the needs of a broader range of decision-makers, future research could use statistical methods to obtain more scientifically grounded decision intervals and boundary values. For instance, incorporating happiness attenuation coefficients and pain blunting coefficients could clarify the prepayment preferences of decision-makers. Additionally, while the AISM model reveals the simplest system structure, when there are too many elements at the same hierarchical level, the simplest hierarchy may not reveal the connections within the internal hierarchy. The complexity variations in decision-making scenarios underscore the importance of further researching the internal relationships within the same hierarchy of the AISM. This contributes to ensuring this method in complex decision-making scenarios.