Introduction

Ice cloud microphysics is important for the susceptibility of Earth’s climate to human influence via tropical high cloud feedback processes1 and dehydration of air at the tropical tropopause2. Radiative transfer through cirrus is sensitive to cloud ice crystal number concentrations (ICNCs)3. Thus, dynamical and microphysical processes controlling the formation stage of cirrus clouds, in particular nucleated ICNCs, can have a strong impact on the global radiative forcing from cirrus and, ultimately, on climate sensitivity.

While mesoscale variability in updraught speeds due to internal gravity waves is known to play a crucial role in cirrus formation4,5,6,7, exactly in which conditions and to which degree microscale turbulence alters nucleated ICNCs in cirrus remains elusive. Turbulence episodes occur infrequently and in small patches8. Incidences of clear-air turbulence in the upper troposphere may increase due to climate change9. Gravity wave breaking in stratified shear layers is a key source of turbulence in this region10.

To reduce fundamental uncertainty regarding the role of cirrus clouds in the present and future climate, the impact of turbulence on cirrus formation should be fully understood. Clarifying on the process level how turbulence perturbs homogeneous freezing events (HFEs) is an essential step in this direction. Homogeneous nucleation of ice in ubiquitous supercooled solution droplets11 is a fundamental cirrus formation process. First evidence of the crucial role of homogeneous freezing for upper tropospheric cirrus formation dates back to more than three decades12,13.

While turbulence-microphysics interactions have long been studied in the case of liquid-phase clouds due to their relevance for cloud lifetime and the cloud radiative effect (CRE)14, only very recently studies have begun to explore the impact of turbulence on microphysical characteristics in cirrus with a particle-based method15. The impact of turbulence on cirrus ice formation has not yet come under scrutiny, limiting our understanding of how cirrus clouds respond to anthropogenic activities16.

The upper troposphere is characterised by stable stratification on average, the presence of significant wind shear, and a broad range of turbulence kinetic energy dissipation rates17. Turbulent mixing breaks air parcels down to smaller scales without causing irreversible mixing. The latter occurs only under the action of molecular diffusion. Viscous dissipation of mechanical flow energy and intermixing of air and its constituents as well as ice crystal nucleation and growth by deposition of water vapour take place near the dissipation (Kolmogorov) length scale (≈1 cm). In this way, cirrus formation depends on the fine structure of temperature and moisture fields which combine to define ice supersaturation, arguably the most crucial atmospheric variable affecting HFEs.

Turbulent fluctuations of relative humidity play an important role in liquid water cloud formation via water droplet activation from aerosol particles18. While the formation of such clouds takes place within a fraction of a percentage point above liquid water saturation, HFEs commence at high values in cirrus, and extend over a few percent of ice supersaturation below water saturation. No studies are available that pin down to which degree ice supersaturation fluctuations due to turbulence interact with the strong temperature- and supersaturation-dependent homogeneous freezing process19. Yet, such knowledge precedes robust studies of anthropogenic aerosol-cirrus interactions.

Cirrus formation is commonly studied with models based on ice supersaturation predicted on large spatial scales. The underlying assumption is that aerosol particles and ice crystals experience the same values of moisture and temperature in a given grid cell. For example, cloud-resolving and large-eddy simulation (LES) models typically resolve 500 m and 50 m horizontal scales, respectively, with LES capturing the cloud structure produced by large turbulent eddies by means of closure schemes that emulate effects of unresolved smaller air motions. Direct numerical simulation (DNS) resolves the dissipation scale, but the computational demand for simulating cirrus formation is large, and DNS results on HFEs are not available. Traditional air parcel models—employed to derive parametrisations of cirrus ice formation for use in global weather and climate models—do not account for spatial variability and neglect turbulence altogether. This means that the effects of turbulence on cirrus formation and subsequent impacts on the global radiative forcing from cirrus are not known.

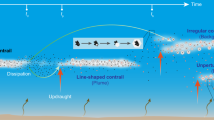
To move beyond the traditional treatment of cirrus formation and explore the role of turbulent fluctuations in HFEs in the present study, we couple a particle-based, microphysical model with the Linear Eddy Model (LEM)20. The LEM reproduces the multiscale rearrangement of fluid parcels induced by turbulence in a one-dimensional framework (‘Methods’). We have recently combined the LEM with a particle model, which we call partLEM (Fig. 1), to examine the effects of microscale turbulence on ice supersaturation in the cloud-free upper troposphere21. The partLEM can address a range of scales that is computationally infeasible for DNS and thus bridge the scale gap between DNS and LES. It allows us to treat advective turbulent mixing, diffusive molecular mixing, particle motions, and aerosol and ice microphysics as independent yet interactive processes down to the dissipation scale. Number and water mass mixing ratios, vertical positions, thermodynamic water phase, and other attributes of thousands of simulation aerosol and ice particles—each representing a multitude of physical particles—are tracked individually as they evolve over time22. HFEs are initiated by imposing a constant updraught speed characteristic of gravity wave activity23, acting as the mean forcing of ice supersaturation via adiabatic cooling.

Fig. 1: The partLEM model framework.
figure 1

An air parcel is subject to an updraught speed (w) and rises along the dry adiabatic lapse rate to an altitude (h), eventually covering a full homogeneous freezing event (HFE). The vertical parcel dimension is equal to the depth of a homogeneous freezing layer (Lf), corresponding to a narrow range of ice supersaturation (s). The high-resolution computational domain of the Linear Eddy Model (LEM) is placed vertically within the air parcel, where molecular diffusion and turbulent mixing act on temperature (T) and water vapour mass mixing ratio (qv) fields. The full partLEM model encompasses a wide range of microphysical processes involving liquid solution droplets and ice crystals derived from them via stochastic homogeneous freezing without assuming thermodynamic equilibrium. Mixing causes stochastic turbulent temperature fluctuations and similarly affects water vapour and a large number of simulation particles present at different Lagrangian LEM altitudes (z). In addition, all particles are subject to random Brownian motion and settle due to gravity. Initially, T and qv and particles are uniformly distributed across the vertical grid levels. We refer to the combination of turbulent mixing and dissipation scale processes (vapour and heat diffusion and Brownian particle motion) as ‘LEM physics’. This model set-up replicates conditions of ice formation at the top of cirrus clouds.

Full size image

Identifying and understanding intricate interactions between microphysical processes and turbulent mixing due to vertical motions calls for detailed numerical simulations. Our model framework serves as a valuable starting point to identify and understand turbulence effects on HFEs. It allows us to treat, for the first time, turbulent mixing explicitly alongside associated stochastic turbulent water vapour and temperature fluctuations; molecular diffusion of moisture and heat; Brownian motion and gravitational settling of simulation particles; hygroscopic growth of liquid aerosol solution droplets and deposition growth of ice crystals by kinetically-limited uptake of water vapour molecules (H2O); and probabilistic, non-equilibrium homogeneous droplet freezing.

We set out to investigate microscale turbulence effects on HFEs to fill an elusive knowledge gap regarding cirrus formation. Together with the quantification of the minimum spatial resolution required by models to properly simulate HFEs, we shed first light on a persistent uncertainty in the representation of cirrus in cloud and climate models and discuss ramifications of turbulence-microphysics interactions for tropical cirrus.

Results

Time and length scale analysis reveals the importance of turbulence-ice interactions

Knowing the turbulent Damköhler number, Da, for HFEs allows us to make a general statement about the response of cirrus ice formation in a turbulent environment characterised by the dissipation rate of turbulence kinetic energy, ε. We define Da as the ratio of the turbulent mixing and homogeneous freezing time scales (‘Methods’). Figure 2 shows Da as a function of ε evaluated for extratropical upper-tropospheric conditions. Da decreases with increasing ε as mixing becomes faster and eddies dissipate within the time required to complete an HFE. We find that typically Da ≈ 1 is in the range of typical upper-tropospheric turbulence levels21 (ε = 10−6–10−4 m2 s−3). This means that aerosol and ice particles experience changing temperature and moisture levels during HFEs due to mixing, or for low turbulence levels, due to sedimentation.

Fig. 2: Importance of turbulence-ice microphysics interactions.
figure 2

Turbulent Damköhler number, Da, and transition length scale, L*, for homogeneous freezing vs dissipation rate of turbulence kinetic energy, ε, estimated for conditions in the upper troposphere (220 K, 230 hPa) and evaluated for a mean updraught speed of 0.1 m/s. The grey shading marks the range of ε-values frequently observed in the upper troposphere, and the orange shading indicates the range of homogeneous freezing layer depths. Da is evaluated at an average depth of 15 m. L* is defined as the length scale at which Da = 1. The dashed curve shows L* neglecting ice crystal sedimentation. Da-values are similar for conditions in the TTL (190 K, 100 hPa), but sedimentation effects are small, so that L* approximately follows the dashed curve.

Full size image

We also show the transition length scale24, L*, below which spatial supersaturation inhomogeneities no longer affect freezing due to sufficiently fast turbulent mixing. As most cloud models assume unresolved mixing processes to be homogeneous, L* defines the minimum model resolution to properly simulate the effects of slow, inhomogeneous mixing on ice microphysics. We find that for predominant turbulence levels (ε < 10−4 m2 s−3), L* values are smaller than the typical freezing layer depth (15 m)21, i.e., below the resolution of most cirrus models. Ice crystal sedimentation increases L* at low ε-values, except in very cold regions with greatly diminished ice crystal fall speeds, such as the tropical tropopause layer (TTL).

These results underscore the importance of critically assessing how turbulence perturbs cirrus formation. The assumption of spatially uniform ice supersaturation in conventional cirrus models may only be abandoned below vertical resolutions of ~1–10 m for the range of turbulence levels typically found in the upper troposphere. Finer resolution may be required in TTL conditions.

Probabilistic HFEs lead to a distribution of nucleated ICNCs

While the traditional deterministic approach to simulate non-turbulent HFEs yields single values for nucleated ICNC and other microphysical variables for a given updraught speed based on a continuum of solution droplets, probabilistic HFEs are described here by a range of such variables caused by the inherently stochastic nature of homogeneous ice nucleation within a large population of discrete simulation aerosol particles selected randomly from a given aerosol size distribution (‘Methods’), even in the absence of turbulence.

We illustrate the stochastic variability of HFEs analysing distributions of total nucleated ICNC and maximum ice supersaturation in comparison to the traditional deterministic approach in Ext. Data Table 1 and Ext. Data Figs. 1 and 2 based on simulations in an air parcel framework. The combined standard deviation of nucleated ICNCs due to the freezing statistic and randomly selected droplet sizes (‘Methods’) is ~10% relative to the mean value.

Temperature and supersaturation fluctuations are non-Gaussian

While HFEs are traditionally simulated based on spatially uniform thermodynamic variables25 and evaluated by comparing an average value of ice supersaturation, s, or temperature, T, with a fixed threshold that characterises the onset of freezing26, turbulence causes these variables to exhibit stochastic variability.

It has been established that gravity wave activity causes non-Gaussian fluctuations in s and possibly T on the mesoscale23,27. We show that microscale turbulence generates fluctuations in s and T that also show non-Gaussian behaviour (Ext. Data Fig. 3). Such heavy-tailed distributions arise from the nonlinear redistribution of energy in the inertial subrange and associated kinematic eddy motions affecting scalar transport. The distribution tails contain fluctuations due to rare eddies with sizes up to the outer turbulence length scale, which we identify with the vertical depth of a homogeneous freezing layer.

We now apply the partLEM combining one-dimensional simulations of probabilistic HFEs with turbulence in the stratified upper troposphere to find out how the strongly s- and T-dependent homogeneous freezing process responds to microscale fluctuations in these variables. We note that most traditional simulations predict homogeneous freezing rates and liquid water content based on equilibrium ambient relative humidity. Here, we abandon this assumption, replacing it with a full non-equilibrium treatment based on aerosol water activity (‘Methods’), to properly capture the effects of fast processes that evolve on sub-second time scales.

Table 1 defines the simulation scenarios and summarises mean values and standard deviations of key cirrus microphysical properties. Base is the baseline scenario with average ε; it includes the full suite of physical processes affecting HFEs (Fig. 1). NoTurb is the reference scenario with probabilistic freezing, but without ‘LEM physics’. NoSed is a scenario identical to NoTurb, but suppresses sedimentation and thus serves as the one-dimensional analogue to traditional air parcel simulations (Ext. Data Figs. 1 and 2). Trad is identical to NoSed, but treats HFEs deterministically in line with traditional freezing simulations. Scenarios Turb are similar to Base; they are introduced to study effects of ε-variations in average upper-tropospheric turbulence conditions. These scenarios cover the effects of typical variations in stability (‘Methods’). We address the role of turbulence in tropical cirrus formation by studying scenarios Anvil and TTL. The two latter scenarios examine the effects of colder air temperatures and lower air pressures. While atmospheric conditions are more variable than representable in a process-oriented model, we do not consider variability in meteorological conditions and aerosol properties within each scenario to isolate the effect of turbulence on HFEs.

Table 1 Simulation scenarios and statistics
Full size table

Assessing the role of turbulence, sedimentation, and probabilistic freezing in cirrus formation

We characterise in more detail an HFE from the baseline scenario and demonstrate the importance of individual physical processes by comparison to scenarios NoTurb, NoSed, and Trad. Note that turbulent mixing-induced temperature fluctuations generate a dry adiabatic lapse rate and an associated ice supersaturation gradient faster with larger ε21. Mixing stops having an effect on the vertical temperature profile once neutral stability is established in the freezing layer, but continues to affect particle motions. We terminate all simulations right after ice nucleation ceases in the whole domain.

Scenario Base results in large variability of ice phase properties as indicated by skewed probability distributions of nucleated ICNC (ni) and ice crystal radius (ri) (Fig. 3), revealing a wide range of individual values of ni = 16–1072 g−1 and ri = 4–18 μm, the latter determined by the limited time available for growth in the simulations. Accordingly, the relative dispersion (ratio of standard deviation and mean, δ) of ni is large: 88.8/295.2 ≈ 30% (Table 1). Power spectra of nucleated ice crystal number and mass concentrations, which are determined by turbulent up- and downdraughts, follow Kolmogorov scaling (Ext. Data Fig. 4). A small fraction (≈3%) of available water vapour has been deposited on the freshly nucleated ice crystals when the simulations stop, equivalent to an ice mass mixing ratio of 3.4 ppm. Turbulent mixing creates vertical gradients in all ensemble-mean profiles (Ext. Data Fig. 5). In the upper part of the domain, where T-values are lower than the column-integrated mean value, relatively more ice crystals form. On average, 49/(295.2 + 49) ≈ 14% of all ice crystals have settled out of the freezing layer (Table 1), representing particles with high ri values that are no longer included in the probability distributions and vertical profiles. They are generated either in incidences of weak mixing or interrupted (prematurely terminated) HFEs.

Fig. 3: Anatomy of an HFE—role of turbulence, ice crystal settling, and freezing representation.
figure 3

For the (a, b) baseline scenario and sensitivity scenarios (c, d) NoTurb, (e, f) NoSed, and (g, h) Trad, we show probability (P) distributions of ice crystal number mixing ratio (ni) and radius (ri), respectively, derived from all vertical profiles per ensemble. Grey curves repeat the corresponding results from Base to facilitate comparison. The arrows mark the distribution core around mean ICNCs that becomes increasingly narrower when turbulence is neglected (NoTurb), when, in addition, sedimentation is neglected (NoSed), and when, furthermore, probabilistic freezing is replaced by deterministic freezing (Trad).

Full size image

Direct comparison of scenario Base with NoTurb demonstrates that microscale turbulence is responsible for the large spread in all variables. Probability distributions of ICNCs and radii are much narrower in NoTurb (Fig. 3) due to the absence of large turbulent s- and T-fluctuations. The broadening of the regions of these distributions around the most probable values is caused by stochastic freezing and random variations in droplet sizes. The relative ICNC dispersion of ≈14% is less than half that of Base (Table 1) and relatively more ice crystals (≈17%) leave the freezing layer. Vertical profiles no longer exhibit gradients (Ext. Data Fig. 5).

Scenarios NoSed and Trad neglect sedimentation, allowing a more direct comparison to traditional parcel simulations. When ice crystals stay in the domain and continue to act as efficient vapour sinks, fewer ice crystals nucleate than in NoTurb (Table 1). The standard deviation of qv is notably enhanced in NoSed relative to NoTurb, because falling ice crystals can no longer homogenise the moisture field via diffusional growth. Over 5 min of simulation time, we estimate a settling distance of ≈30 cm for ri = 5 μm ice crystals with fall speeds of ≈3 mm s−1. Thus, homogenisation occurs rather locally. Apart from this, NoTurb and NoSed led to similar results.

The mean values of all ice phase variables from scenario Trad (which replaces probabilistic with deterministic freezing) deviate substantially from NoSed, NoTurb, and Base (Table 1 and Ext. Data Fig. 2). The still significant, non-turbulent ICNC dispersion of 31.4/290.2 ≈ 11% (δHFE = 0.11) in NoSed is caused by both probabilistic freezing and random aerosol droplet size variations. Note that the mean value and standard deviation of ni from NoSed are in excellent agreement with equivalent air parcel simulations (Ext. Data Table 1). The remaining ICNC dispersion of 9.3/167.9 ≈ 6% (δaer = 0.06) in Trad is solely caused by the droplet size variation. As the dispersion values are statistically independent, we estimate the value due to probabilistic homogeneous freezing alone to be δfrz = [(δHFE)2 − (δaer)2]1/2 = 0.09.

While ice crystal number-size distributions exhibit significant variability on a case-to-case basis due to turbulent mixing, Ext. Data Fig. 6 shows that ensemble-mean size distributions are monomodal with similar widths due to fast radial growth rates of ice crystals (on the order of μm s−1 at 220 K) quickly offsetting most variations that arise during freezing. Probabilistic treatment of HFEs slightly modifies the size distribution tails. Only in scenario Trad does the size distribution width decrease substantially due to the absence of stochastic processes.

We explore how variations of the turbulence dissipation rate affect HFEs relative to Base. The number of ice crystals, nsed, that sediment out of the freezing layer (Table 1) decreases only slightly from Turb-low to Base, but more than halves from Base to Turb-high. In Ext. Data Fig. 5, we observe a positive slope in the ensemble-mean vertical profile of nucleated ICNC, brought about by gradients in temperature and supersaturation that become more pronounced with increasing ε. The impact of ε-variations on ensemble-average ice crystal distributions is small (Ext. Data Fig. 6).

Microscale turbulence significantly affects ice crystal properties

This key finding is supported by testing the statistical significance of column-average ICNC changes between scenarios, summarised in Ext. Data Table 2. The main cause of the significant differences between Base and scenarios NoTurb and NoSed is that turbulent mixing creates a wide range of nucleated ICNCs and sizes. The scenarios with modified ε are also statistically different from Base according to this metric. We are now ready to close in on the effects of turbulence on HFEs.

Turbulence enhances variability in ICNCs beyond that caused by stochastic freezing and aerosol size effects by two features that are evident in the probability distributions of ICNCs (Figs. 3–5): (i) the broadening of the core region around the most probable ICNCs caused by mixing due to numerous small eddies leading to additional nucleation and (ii) the degree to which rare large eddies generate the heavy ICNC-tails in these distributions. The widths of the distribution cores increase non-linearly with increasing ε. Very large ICNCs become more abundant when going from Turb-low to Base, but, surprisingly, upon increasing ε above the baseline value, they diminish. The latter is related to ice crystal sedimentation, as explained below.

Fig. 4: Anatomy of an HFE—impact of turbulence intensity variations.
figure 4

For the two Turb scenarios, a–d show probability (P) distributions of ice crystal number mixing ratio (ni) and radius (ri), respectively, derived from all vertical profiles per ensemble. Grey curves repeat the corresponding results from the Base to facilitate comparison. The arrows mark the distribution core around the mean ICNC that broadens with increasing turbulence intensity. e illustrates the broadening by showing the relative ICNC dispersion (δ) vs turbulence dissipation rate (ε). f shows the ratio (τ) of supersaturation quenching time over eddy turnover time vs eddy length (L) for mean and maximum ICNCs evaluated for 5 μm ice crystals. The grey shadings mark the ranges of values of ε (baseline value 10−5 m2 s−3) and L (mean value 0.25 m) represented in the simulations.

Full size image
Fig. 5: Results for tropical cirrus.
figure 5

a–d show probability (P) distributions of ice crystal number mixing ratio (ni) and radius (ri), for the Anvil and TTL scenario, respectively, derived from all vertical profiles per ensemble. e presents a snapshot of an ICNC profile with narrow layers taken from one arbitrary statistical realisation of the full TTL ensemble.

Full size image

We quantify in Fig. 4 feature (i) noting that upon increasing ε from Turb-low to Base, the broadening is hardly visible, but becomes more evident upon further increasing ε (Base to Turb-high). This behaviour can be understood by considering the turnover time, IL = (L2/ε)1/3, of size-L eddies and their associated vertical velocity, wL = L/tL = (Lε)1/3. Homogeneously nucleated ICNCs scale with updraught speeds28, w, as ni ∝ w3/2.

Decomposing ni and w into mean (nm and nm) and fluctuating components (n′ and w′ = wL) and introducing relative dispersions (δw = w′/wm and δturb = n′/nm), we derive δturb = (1 + δw)3/2–1 ≈ (3/2) δw for velocity fluctuations that are small relative to the specified mean updraught speed, wm = 0.1 m s−1. The variance of the turbulent ICNC fluctuations is statistically independent of, and can thus be added to, those due to probabilistic freezing and random aerosol sizes.

We evaluate δturb for the mean eddy size in our simulations (0.25 m, see ‘Methods’). The total ICNC dispersion, δ = [(δHFE)2 + (δturb)2]1/2, is shown in Fig. 4 as a function of ε and quantifies the trend visually inferred from the simulations. When going from low to high dissipation rates in the Turb scenarios, δ increases from 0.146 to 0.482. For very high upper-tropospheric turbulence levels (ε > 10−4 m2 s−3), δ → δturb. For very low ε < 10−6 m2 s−3, δ → δHFE set mainly by the stochasticity of the homogeneous freezing process. Recall that we do not resolve the physical dissipation scale, η = 0.9–1.6 cm depending on ε, but account for the effects of eddies smaller than the model’s smallest resolved eddy size (10 cm) by enhancing the molecular and particle diffusivities with a subgrid-scale turbulent contribution (‘Methods’).

We address feature (ii) and explain the absence of ICNCs much larger than nm that occurs when ε increases from Base to Turb-high. Owing to the short settling distances of nucleated ice crystals, only those close to the bottom of the freezing layer leave the domain; recall that nsed decreases only moderately (by 11%) when going from Turb-low to Base, but more substantially (by 44%) upon increasing ε further to Turb-high (Table 1). Also recall that more ice crystals nucleate in the upper part of the freezing layer due to the adiabatic lapse rate that develops faster with increasing ε. When turbulent mixing replaces ice crystals in the lower part of the domain with smaller ones from above, the latter are less likely to settle out, and nsed decreases accordingly.

Importantly, the larger ice crystals that were mixed into the upper (colder) part of the domain from below homogenise the supersaturation field to a larger degree than the smaller ice crystals that would otherwise be present. In turn, this reduces the occurrence of large supersaturation fluctuations there, removing the tail of the ICNC distribution in scenario Turb-high. To confirm this explanation, we ran the Turb-high scenario without sedimentation and indeed recovered very large ICNC values similar to Base.

Vertical eddy motions induced by turbulent mixing cause fluctuations in homogeneous freezing rates. Immediately after ice nucleation, deposition growth may reduce ice supersaturation within the duration of an eddy mixing event measured by the turnover time, tL, for an eddy of length L. As the eddy motions that cause these fluctuations are treated as instantaneous mapping events in the LEM, the potential quenching of ice supersaturation is not resolved. To assess this issue, we evaluate the ratio, τ = tq/tL, with the supersaturation quenching time29, tq ∝ (ni)−1. For average ε = 10−5 m2 s−3 and eddy sizes within the model’s inertial subrange (L = 0.1–15 m), we find that during mixing events, ice crystals do not significantly interact with the H2O gas phase (τ ≫ 1) across the full range of nucleated ICNCs (Fig. 4). Thus, the instant mixing assumption in the LEM does not introduce a significant error in simulated supersaturation.

Unveiling small-scale processes in tropical cirrus

Current understanding of microphysical processes in anvil and TTL cirrus is incomplete, preventing robust quantification of how tropical cirrus clouds respond to global warming30,31. Tropical cirrus evolve at colder temperatures and lower pressures than assumed in the previous scenarios, causing significant reductions in the amount of H2O available for deposition and growth rates per ice crystal, in turn causing larger nucleated ICNCs and smaller mean ice crystal sizes (Table 1). Fewer ice crystals settle out of freezing layers. The relative ICNC dispersions in scenarios Anvil (≈33%) and TTL (≈36%) are similar to Base.

Aircraft measurements have demonstrated the infrequent occurrence of vertically thin (several metres), isolated cirrus layers in the TTL and implicated high number concentrations of ice crystals (several per cm3) within them with homogeneous freezing32,33. Our simulations show that turbulent mixing can produce such layers. In the TTL case shown in Fig. 5, a single cloud layer was produced by an eddy of length 2.5 m, resulting in peak ICNC of ≈20,000 g−1 (3.5 cm−3). This feature was broken down further into three 1 m-thick layers by subsequent mixing.

Discussion

We studied how turbulence affects homogeneous freezing in cirrus clouds. When sampled from homogeneous freezing layers, turbulence causes remarkably broad distributions of nucleated ICNCs that are heavily skewed towards large number concentrations. Mean ICNC values depend strongly on whether HFEs are treated probabilistically or deterministically. Ensemble-mean ice crystal number-size distributions right after nucleation are broader than simulated in adiabatic parcel models and insensitive to turbulence intensity. Removal of falling ice crystals from the freezing layer causes an increase in total nucleated ICNC due to reduced supersaturation quenching. We identified a feedback mechanism between sedimentation and turbulent mixing that diminishes large ICNC values at high dissipation rates.

The inherently probabilistic nature of homogeneous freezing creates a spread of nucleated ICNCs even in the absence of turbulence. This challenges traditional cirrus simulations and parametrisations that do not account for stochastic solution droplet freezing. The total spread is dominated by turbulent mixing for dissipation rates exceeding the range of values commonly encountered in the upper troposphere.

Defining the atmospheric environment down to the dissipation scale with the help of DNS will allow to augment the findings reported here. Three-dimensional DNS based on a Lagrangian ensemble of simulation particles appears to be feasible to study HFEs under less idealised conditions in which turbulence evolves in the upper troposphere. However, such simulations would only cover a small number of statistical realisations.

Acquiring conclusive evidence on how turbulence alters cirrus formation from aircraft measurements is difficult, in part owing to the short duration and localised nature of homogeneous solution droplet freezing. Another experimental route to further advance our knowledge on this subject consists of measurements that create homogeneous freezing conditions in a controlled laboratory setting, ideally combined with DNS that recreates the experimental conditions34.

Aircraft measurements reveal a strong relationship between gravity waves and turbulence at cirrus altitudes35. Turbulence occurrence frequencies range from 2.5 to 20% in the TTL according to radiosonde analyses (Ext. Data Fig. 7). In concert with gravity wave activity, turbulent mixing, and associated supersaturation fluctuations may help explain the fact that homogeneous freezing in the TTL occurs in isolated, narrow layers that may influence the stratospheric water budget32,36. Such layers are affected by wave motions, wind shear, cloud ice growth, sedimentation, entrainment, and horizontal mixing7,37.

Turbulence affects microphysical process rates and likely cirrus macrostructure and lifecycle. It is conceivable that resulting effects grow over time during cloud evolution, especially in the case of anvil cirrus that have long lifetimes38 and evolve under a wide range of dissipation rates exceeding 10−4 m2 s−3. Anvil cirrus maintenance is linked to ice nucleation induced by cloud radiative heating and in-cloud convection39, influenced by gravity wave activity present even hundreds of kilometers away from tropical deep convective source regions40.

Cloud ice particles interact with shortwave and longwave radiation, leading to a CRE and resulting atmospheric heating. The latter influences the morphology and evolution of tropical anvil cirrus41. We derive a joint probability distribution of ice water content (IWC) and effective ice crystal radius (reff) based on the Anvil scenario, representative of aged anvil cirrus far away from deep convective cores (optical depth ≈ 1). Consistent with our approach to representing isotropic turbulence and HFEs, we then apply the joint distribution in a single-column radiative transfer model (Ext. Data Fig. 8) to compute a probability distribution of CRE that reflects the turbulence-induced microphysical variability. This allows us to demonstrate that turbulence-ice nucleation interactions can have an appreciable impact on anvil CRE and may, therefore, matter for climate. The magnitudes of cirrus microphysical properties and radiative effects we tested are well within the range detected by satellites and aircraft.

We compare results from multiple radiative transfer simulations based on IWC and reff values from scenario Anvil sampled from the full joint distribution and weighted according to their probability of occurrence with a reference case based on a single simulation using the mean (most frequent) values, IWC = 4.2 mg m−3 and reff = 19.6 μm. The resulting distributions of CRE and atmospheric radiative heating are shown in Fig. 6. Distribution-weighted averages differ only marginally from the reference value, because CRE responds approximately linearly to changes in IWC and 1/reff over the limited parameter ranges where most of the probability in the joint distribution is concentrated.

Fig. 6: Variability in anvil cirrus radiative response to homogeneous freezing.
figure 6

Probability distributions of cloud radiative effect (CRE) and cloud radiative heating caused by turbulence-induced variability in nucleated ice water content (IWC) and ice crystal effective radii (reff) developed after an HFE. a–c show longwave, shortwave, and net CRE, respectively. The resulting distribution of cloud-induced radiative heating averaged over vertical cloud layers is given in d. Mean values obtained as averages across the probability distributions are given in the top right in each panel; for comparison, cursive font indicates values from a single radiative transfer simulation based on the mean IWC and reff.

Full size image

However, the local radiative response to HFEs varies significantly across the turbulence-generated IWC-reff parameter space. Importantly, the radiative heating due to the perturbed cirrus has a large range of about 6 K d−1, on the order of the mean value. Such variability in heating within a single cloud system can impact cirrus lifetime and CRE, influencing the evolution of tropical cirrus systems and the larger-scale circulations in which they form in a number of ways. Examples include stronger horizontal cloud spreading and thinning caused by the pronounced in-cloud heating gradients, as well as enhanced in-cloud convection and turbulence41 possibly triggering further ice nucleation.

Turbulence-induced variability in ice numbers and the probabilistic nature of HFEs hamper the attribution of cirrus observations42,43,44 to ice nucleation mechanisms. Exactly how turbulence alters the role of heterogeneous ice-nucleating particles (INPs) in aerosol-cirrus interactions depends on the associated ice nucleation mode. In the case of efficient INPs such as mineral dust particles45 that nucleate ice with a minor stochastic component before homogeneous freezing commences46, turbulent supersaturation fluctuations cause INPs to form ice earlier. The resulting, enhanced H2O deposition losses cause fewer solution droplets to freeze homogeneously resulting in fewer total nucleated ICNCs46. However, as sedimentation of previously nucleated ice crystals out of homogeneous freezing layers may allow more ice crystals to form, both effects tend to offset each other so that, on average, nucleated ICNCs might not change much. Ice crystal settling may also affect cirrus macrostructure by quenching ice nucleation at lower cloud levels47.

Progress towards constraining Earth’s climate sensitivity requires improved representations of ice microphysics in models, in particular regarding cirrus ice nucleation mechanisms48. By turning the spotlight on small-scale turbulence and its effects on cirrus formation, the advanced process understanding reported here represents a significant step towards better understanding and constraining cirrus cloud feedbacks. However, this first attempt to identify and understand the effects of turbulence on cirrus formation presented here has limitations. The frequent co-occurrence of mesoscale waves and microscale turbulence35,49,50 along with the possibility of increased upper-tropospheric turbulence in a warmer climate9 underscores the need to study their combined effect on ice formation in cirrus and anvil cirrus evolution. Regarding the latter, small-scale processes have the potential to alter the net warming due to optically thin anvils and, thus, the global radiative forcing from tropical cirrus systems as a whole.

In view of the paramount importance of mesoscale vertical air motions to determine nucleated ice number concentrations, better observational characterisation and model representation of gravity wave forcing and aerosol-cloud interactions remain principal tasks of contemporary cloud research. In combination with a refined understanding of microscale turbulence effects on cirrus formation, this will help focus research as well as model and measurement development.

Methods

Damköhler number for HFEs

The turbulent Damköhler number, Da, is generally defined as the ratio of a macroscopic turbulent flow timescale, tm, and a physico-chemical process time scale, tµ: Da = tm/tµ. In our problem, if Da ≪ 1, particles experience the same ice supersaturation, s, during an HFE, as assumed in adiabatic parcel models (homogeneous mixing limit). If Da ≫ 1, particles experience fluctuating temperature and moisture concentrations due to turbulent mixing, and we can expect homogeneous freezing to be perturbed (inhomogeneous mixing limit).

The turbulent mixing time scale is chosen to be the eddy breakdown time, tL = (L2/ε)1/3, where L is the outer length scale of turbulence. Measurements suggest a typical range of dissipation rates of turbulence kinetic energy, ε = 10−6–10−4 m2 s−3, in the cloud-free extratropical upper troposphere21; median values in the TTL also lie in that range51. Sedimentation may contribute to homogenising the supersaturation field due to the ability of ice crystals to deposit water vapour. With the sedimentation time scale, ts = L/vt, and terminal fall speeds vt ∝ (rh)2 ascribed to the population of freshly nucleated (micrometre-sized) ice crystals, the latter have mean radii28 rh ∝ w1/2 (w is the mean updraught speed), so that vt ∝ w. We introduce the generalised mixing time scale52,

$${{\rm{t}}}_{{\rm{m}}}=1/[({{{\rm{t}}}_{{\rm{L}}})}^{-1}+{({{\rm{t}}}_{{\rm{s}}})}^{-1}]$$
(1)

This means for large ε, tm → tL ∝ w0 and for small ε, tm → ts ∝ w−1. Brownian motion mainly affects small solution droplets and contributes to homogenisation only very weakly; it is therefore not included in tm.

While the supersaturation quenching time describes the decay of ice supersaturation, s, towards ice saturation during and after an HFE, tµ only refers to the actual ice formation process that self-terminates as soon as s decreases below the value at the onset of homogeneous freezing. As a microphysical process time scale suitable for evaluating Da, we therefore choose the time required for air to ascend the full depth of a homogeneous freezing layer, Lf ≈ 15 m21, tµ = Lf /w. By setting Da = 1 and iteratively solving for L, we obtain the transition length scale24, L*, from Eq. (1). For large ε, the duration of ice formation events gets shorter relative to mixing, hence, Da ∝ w and L* ∝ w−3/2. For small ε, both Da and L* are independent of w. If L* lies in the inertial subrange of turbulence, only turbulent eddies with sizes smaller than L* mix homogeneously.

Representation of homogeneous, isotropic air turbulence

We have coupled the LEM, a parametric, stochastic turbulent mixing model20, to a cirrus column model with a novel probabilistic treatment of HFEs to study effects of turbulence on ice supersaturation in the cloud-free, stably-stratified upper troposphere. The resulting model replicates the inertial range energy cascade in a vertically oriented, rising column, encompassing the outer and inner model turbulence length scales, L+ and L−, respectively. Turbulent mixing is implemented in the LEM through randomly selected, continuous mappings of line segments of scalar fields (temperature, T, and water vapour mass mixing ratio, qv), mimicking motions of fluid elements induced by turbulent eddies with probabilities based on the Kolmogorov scaling laws. The mappings employed here53 (‘triplet maps’) are applied simultaneously for all scalar fields. Molecular diffusion smoothens sharp, mixing-induced gradients in the vertical profiles of T and qv, which combine to yield s.

The full partLEM model (Fig. 1) includes a high-level, non-equilibrium aerosol and ice microphysics scheme to enable the simulation of HFEs for various turbulence levels. Initially, T, qv, and supercooled liquid aerosol particle number-size distributions are uniformly distributed over the model domain. This allows us to compare our results with simulations of HFEs based on traditional air parcel models.

To initiate HFEs, the model is forced by a constant (mean) updraught speed with temperature decreasing along a dry adiabat (lapse rate Γ). Thus, the Lagrangian LEM domain cools at the rate −Γw and mean values of T and s change accordingly. Via turbulence, random vertical displacements of air parcels generate turbulent temperature fluctuations of average magnitude on the order of ΓL-. If air parcels in the LEM are occasionally affected by larger eddies with sizes up to the outer length scale, the magnitude of these fluctuations can be significantly larger (Ext. Data Fig. 3). Turbulent temperature fluctuations cause the lapse rate in the LEM domain to approach Γ (neutral stability) for sufficiently strong mixing, since entrainment is not included in this study.

Together with the Brunt-Väisälä (buoyancy) frequency, N, ε determines the eddy diffusivity, D = ε/(3N2), that characterises the average rate of turbulent mixing in the LEM; the latter increases ∝ D21. Our simulations start shortly before and end shortly after an HFE to ensure that we investigate the effects of turbulent mixing that occur during ice nucleation and, at the same time, minimize the likelihood of entrainment of environmental air. Variations in prescribed N merely alter D, but are not related to the initial temperature distribution. Moreover, in nature, changes in ε and N may not be independent. We therefore do not explicitly include stability variations in our study. We add that increasing (decreasing) the updraught speed results in less (more) time for turbulence to influence HFEs for given ε, meaning that the effects of updraught speed variations are at least to a degree captured by variations in ε. Thus, we do not consider variability in the mean forcing.

Representation of simulation particles

In each LEM grid cell, supercooled aqueous solution droplets are initially represented as a size-dispersed, upper-tropospheric accumulation mode background aerosol population. We apply a variant of the super-droplet method54 to represent individual simulation particles and track water phase, water mass mixing ratio (liquid or ice), and position in the vertically-oriented computational domain as simulation particle attributes. All real particles represented by a given simulation particle are exposed to the same conditions of s and T. The number mixing ratio for all simulation particles corresponds to the smallest resolved particle number concentration. Moreover, each simulation particle carries its own water-soluble core volume.

Not all solution droplets from the size distribution need to be represented as individual simulation aerosol particles, only those that are expected to freeze homogeneously. To determine which portion of the size distribution is to be represented to initialise simulation aerosol particles, we first estimate the expected homogeneously nucleated droplet number concentration, nh, based on a parametrisation28. We then multiply nh by a factor fmax > 1 to ensure that the actually nucleated ice crystal number from the simulations is not limited by the number of available simulation aerosol particles and that sufficiently many small droplets with low freezing probabilities are also included: nmax = fmax nh. Furthermore, we prescribe the minimum number concentration to be resolved as nmin = fmin nh with fmin < 1. The part of the size distribution comprising droplets within these concentration limits is discretised into 25 radial size bins, i, with widths δr(i). Droplet core radii lie in the approximate range rcore = 0.1–0.5 μm. The solution droplet number concentrations in each bin, δni(i), are partitioned into simulation aerosol particles with dry radii sampled randomly within δri(i). In each bin, we obtain particles of different size, each of which defines simulation aerosol particles with number concentration nmin and multiplicity M(i)=δni(i)/nmin. The total number of simulation aerosol particles represented in the model per vertical grid cell is NSAP = ΣiM(i) ≈ 100–1000, depending on the scenario, chosen as a compromise between reasonable computational efficiency and very accurate prediction of ICNC values and sufficient to limit variability in simulated properties due to initial particle sampling.

Solution droplet growth

The initial liquid water volume in each simulation aerosol particle, LWV, used together with the core volume to calculate the wet (total) droplet radius, rw, is determined iteratively from the Köhler equation: Sw = aw(rw) K(rw), where Sw is the bulk liquid water saturation ratio in the air (determining qv), aw is the non-equilibrium, size-dependent water activity in the solution droplet, and K is the thermodynamic Kelvin (curvature) correction to the water vapour saturation pressure. To calculate aw, we use the κ-Köhler method55 along with a hygroscopicity parameter (κ = 0.5) representative for a mixed sulphate-organic aerosol prevalent in the upper troposphere56. After initialisation, LWV, hence, the associated liquid water mass mixing ratio in each simulation aerosol particle, ql(rw), is predicted by integrating the droplet growth equations constrained by total water conservation. This means that aw is tracked over time for each simulation aerosol particle for use in the estimation of droplet freezing probabilities.

Due to the imposed mean updraught, the liquid water content evolves in a quasi-steady state, where aw lags behind Sw by a few percent (kinetically-limited uptake of H2O); aw deviates more substantially from Sw for small droplets due to the Kelvin effect.

Probabilistic, non-equilibrium HFEs

Our probabilistic method to represent homogeneous droplet freezing as a particle-based process differs from the traditional deterministic approach of integrating an ice number budget equation over time-based on continuous aerosol size distribution and assuming thermodynamic equilibrium between gaseous and liquid water phases. We simulate HFEs using a water activity-dependent nucleation rate19 to capture non-equilibrium states caused by rapid changes in local temperature and supersaturation due to turbulent mixing.

Homogeneous nucleation of ice in supercooled water turns simulation aerosol particles into simulation ice particles that increase their radius, ri, and ice water mass mixing ratio, qi, by water vapour deposition governed by second set of kinetic equations based on radial diffusional growth rates with surface-kinetic corrections. The total water mass balance coupling qv with ql and qi is solved over time57, neglecting small contributions of latent heating or cooling due to water phase changes.

HFEs and growth are modelled particle-per-particle across the vertical domain. After freezing, simulation aerosol particles change their phase attribute and are thus treated as simulation ice particles that undergo depositional growth. Ice crystals forming at high ice supersaturation (>0.5) grow rapidly, and HFEs self-terminate right after supersaturation quenching commences (‘freezing-relaxation’)28. A constant, particle-average value of the deposition coefficient, taken to be 0.758, is sufficient to resolve HFEs, as our simulations are terminated right after ice nucleation ceases while s is still high.

We use a homogeneous freezing rate coefficient, J, based on laboratory measurements19, allowing for incorporation of kinetic limitations to hygroscopic droplet growth via aw. J is very sensitive to small variations in T and aw. The predicted LWV of a given simulation aerosol particle is used to compute aw and thus the associated freezing rate, LWV·J. Homogeneous freezing is a Poisson-distributed stochastic process11, implying the survival probability p = exp(−LWV·J·Δt) after a model time step, Δt. Simulation ice particles are created, and the corresponding simulation aerosol particles removed, when a random uniform variate, distributed within [0,1], exceeds p for any given simulation aerosol particle. We note that sufficiently small droplets stay liquid because of diminishing LWV and J (via aw) due to the Kelvin effect. Moreover, the largest droplets do not contribute significantly to the total nucleated ICNC due to their low abundance and non-equilibrium water content (hence, relatively small aw). In simulations replicating the traditional deterministic framework (scenario Trad), ice nucleation is realised by creating one simulation ice particle when the condition LWV·J·Δt > 1 is met.

Particle motion

Simulation particles undergo turbulent vertical displacements, Brownian motion, and sedimentation across the computational domain (Fig. 1). Simulation aerosol particles are, and most simulation ice particles remain, small enough during HFEs to justify the use of spherical particle shapes in calculations of water uptake; in the case of ice crystals, no significant faceting develops. The resulting small Stokes numbers justify the use of the Stokes relationships59,60 to calculate size-dependent terminal settling velocities, vt ∝ r2, and Brownian diffusion coefficients, Db ∝ r−1, corrected by the Cunningham slip factor in order to account for deviations from continuum regime predictions for sub-μm particles. Terminal fall speeds of most simulation ice particles in the simulations are on the order of the Kolmogorov velocity scale, ∝ ε1/3.

After a model time step, the downward settling distance of simulation particles is given by the drift term vt Δt. Since Brownian motion is a diffusive process, the mean square particle displacement is 2DbΔt. It is fully decorrelated since associated autocorrelation times are much smaller than ∆t. Thus, simulation particles are moved across the computational grid by the size-dependent net distance

$${{{\delta }}}{{\rm{z}}}=-{{\rm{v}}}_{{\rm{t}}}\Delta {\rm{t}}+{\rm{R}}({2{\rm{D}}}_{{\rm{b}}}{\Delta {\rm{t}}})^{1/2}$$
(2)

where R is a random number taking the values −1 or +1 to represent both upward and downward displacements occurring with equal probability. Simulation particles are not allowed to leave the top of the domain. While simulation ice particles that leave the lower domain boundary are irreversibly lost, simulation aerosol particles (including their water content) are reinserted at the domain top once they leave it. The absence of notable inertial effects allows us to move simulation particles between the LEM grid cells in turbulent mixing events like the corresponding fluid elements. Hence, the same mapping rule that acts on the scalar fields is applied to emulate turbulent simulation particle motions, in addition to the random displacements described by Eq. (2).

Simulation set-up

We set the outer model length scale of turbulence, L+, equal to the average depth of a homogeneous freezing layer, L+ = Lf = 15 m21. To fully accommodate triplet map eddies, the vertical resolution of the LEM grid is L−/6, where the inner length scale of turbulence, L−, can in principle be as low as the molecular dissipation (Kolmogorov) length scale, η ≈ 1 cm, depending on ε. To allow for a large number of simulations, we set L− = 10 cm. The vertical model resolution is ~1.67 cm, the model Reynolds number is ReM = (L+/L−)4/3 ≈ 797, and the mean (resolved) eddy size is 2.5 L− = 0.25 m. Since L− > η, diffusive vapour and particle motion is enhanced to compensate for the unresolved eddies between L− and η. This is accomplished by adding D/ReM to the molecular and Brownian diffusion coefficients. The size of unresolved eddies, Lu, is given by the first moment of the eddy size distribution21: Lu = 2.5 η ξ(x) with ξ(x) = (1–x2/3)/(1–x5/3) and x = η/L− ≤ 1 (ξ(1) = 2/5).

ICNCs in HFEs are not sensitive to parameters describing upper-tropospheric liquid solution droplets28 and we may not expect notable aerosol variability across the small spatial and temporal scales considered here. Log-normal number-size distributions are used to initialise simulation aerosol particles with a total number concentration of 500 cm−3, dry modal radius of 0.02 μm, and geometric standard deviation of 1.5 in all scenarios; no ice crystals are present at the start of a simulation. We set the initial supersaturation over ice to s = 0.5 at an air pressure of 230 hPa and temperature of 220 K to characterise spatially uniform vertical profiles shortly before homogeneous freezing sets in, except in the tropical cirrus scenarios, where we use 0.52, 150 hPa, 210 K (Anvil) and 0.58, 100 hPa, 190 K (TTL). The value fmax = 3 was used for all scenarios. For scenarios starting at 220 K, fmin = 0.02, nh = 100 L−1, nmin = 2 L−1, NSAP = 150, and rcore = 0.13–0.47 μm. For the tropical cirrus scenarios, corresponding values are: 0.01, 200 L−1, 2 L−1, 300, 0.11–0.47 μm (Anvil) and 1/300, 3000 L−1, 10 L−1, 900, 0.055–0.31 μm (TTL).

To intercompare results of total nucleated ICNCs, we terminate each simulation when the domain-averaged ice supersaturation falls below the initial value, leading to parcel ascent distances of about 30 m covering an HFE. We track the number concentrations of previously nucleated particles that sediment out of the lowermost grid cell during an HFE (Table 1); the latter are not present in vertical profiles and probability distributions (Figs. 3 and 4). We disregard the upper 5 m of the vertical domain in our analyses to remove influences resulting from persistent nucleation in the top layer and use a fixed model time step of 0.5 s for all scenarios. We compute mean properties from 1,000 individual simulations per ensemble by applying different random number seeds.