Introduction

Rapidly growing global population intensifies the demand for efficient and eco-friendly energy resources. While the traditional fossil fuel-based resources continue to deplete, the climate change driven by greenhouse gas emissions poses severe risks to our ecosystems1,2,3,4,5. Currently, the technological advancements are paving the way for more efficient and accessible renewable energy solutions without environmental degradation. In addition to the environmentally benign renewable energy sources such as wind6,7, solar8, and geothermal9 energy, the recently advancing clean method of energy generation is the salinity gradient energy (SGE), also known as blue energy10,11,12,13, can act as a promising source of renewable energy. The extraction of SGE is done from a salinity gradient generated by mixing the seawater and river water, which is abundantly available on earth10,14,15,16,17.

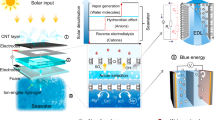
The most extensive approaches for harvesting the blue energy are pressure-retarded osmosis (PRO)18,19 and reverse electrodialysis (RED)20,21. In PRO, the river water (low-concentration) and seawater (high-concentration) solutions are separated by a semipermeable membrane, which only allows the water molecules to flow from low-concentration to high-concentration solutions. This results in volume expansion on the high-concentration side, leading to the generation of osmotic pressure and this pressure gradient is used to run the turbine for electricity production22,23 (see Fig. 1). Unlike in PRO, in RED, electricity is harnessed directly from the salinity gradient24. The seawater and freshwater are pumped into the alternate compartments containing the cation and anion exchange membranes (CEMs and AEMs). The concentration gradient induces the movement of cations and anions through cation exchange (CEM) and anion exchange membranes (AEM), respectively. Here, an ion exchange membrane (IEM) allows only the counter-ions and rejects the co-ions (i.e., CEM -allows cations and rejects anions; AEM -allows anions and rejects cations). Thus, selective ion transport due to concentration gradient generates the electrochemical potential across the membranes, which is collected at electrodes in the form of electricity25,26,27,28,29,30,31 (see Fig. 1). The main advantage of RED over PRO is that it is based on ionic movement rather than water movement. This makes the RED process easier for commercialization and industrialization. However, large-scale applications of these methods are limited by poor selectivity, low energy efficiency and power density due to low-performance membranes, high operating costs and maintenance such as fouling and scaling. Several studies have been done to improve the output power density of the RED process by modifying the membrane design and materials32,33,34,35,36,37.

Fig. 1: Extensive approaches for harvesting SGE.
figure 1

The schematic representation of pressure retarded osmosis (PRO) and reverse electrodialysis (RED). In PRO, a semipermeable membrane is used to separate the low-concentration and high-concentration solutions. A turbine is used for generating power. But in the RED, the cation and anion exchange membranes (CEMs and AEMs) are arranged, and the space between the membranes is filled with low and high-concentration solutions alternatively. The electrodes are placed across these membranes to collect the electricity. Inset: Expanded view of the selected portion.

Full size image

In recent years, it has been demonstrated that a simple creation of a nanopore on the solid-state substrate in the context of mimicking the biological channels will act as an IEM and lead to various applications38,39,40,41,42. However, the engineering of the 2D materials into the membrane (by introducing nanopores or forming lamellar membranes) shows better ion selectivity and conductivity compared to other materials43,44,45. Since the ionic and water flux varies inversely with the membrane thickness, the use of atomically thick 2D materials (like graphene, hexagonal boron nitride (h-BN), Transition metal dichalcogenides (TMDs) such as MoS2 and WS2, MXenes, Covalent organic framework (COF), and metal-organic framework (MOF)) as a membrane can help to gain more advantages over the conventional membrane with an increase in the power density and improves the output power density from a few Wm−2 to a few thousands of Wm−2 46,47,48,49,50,51,52,53,54,55,56,57,58. More specifically, 2D materials are in the limelight of SGE generation, making as a viable source of energy. Due to the developments in nanofabrication technology, many efforts are put into employing the 2D membranes on a large scale and to understand the interactions of fluidic channels in the membrane, ion-pore interactions, and surface functionalization effects. However, the attention given to the scalability of the SGE generation is not adequate and is still lacking.

In this review, we discuss the leading technologies and advancements related to salinity gradient energy (SGE). We first briefly summarize the theoretical background for osmotic power generation through 2D-nanofluidic channels and then explore the fabrication of 2D materials and nanopore fabrication techniques. We highlight the principal advancements in power generation through different 2D membranes and expand the investigation from nanopores to milli pores. Finally, we discuss challenges and future perspectives for the scalability of the osmotic energy conversion on a large scale. This review is expected to elucidate the potential utilization of 2D materials for SGE as a feasible energy source.

Theoretical background

Technology for harvesting power from salinity gradient is known as blue energy. The salinity gradient is naturally formed at the estuary where the river water meets seawater. The mixing of seawater (a high-concentration solution) with river water (a low-concentration solution) forms a moderate concentration brackish solution. From a thermodynamic point of view, the amount of energy generated from the mixing of these solutions can be quantified by the Gibbs free energy of the mixing as given below59,60,

$$\Delta {G}_{{\rm{mix}}}={G}_{B}-({G}_{H}+{G}_{L})$$
(1)

where subscripts B, H, and L refer to the brackish, high- and low-concentrated solution, respectively. Approximately the amount of energy that can be harvestable from the mixing of 1 m3 of river water with 1 m3 of seawater is 1.4 MJ at ambient conditions61,62. Overall, 3.1 TW of output power can be extracted when considering the average global river flow rate as ~37,300 km3 year−1. This output power is almost 420 times the overall capacity of available nuclear power plants in India. Extracting such a high power is impossible due to geographical disadvantages and impurities present in the river and seawater. However, controlled mixing of high and low-concentrated solutions through membranes (including nanofluidic devices) is a promising way for extracting maximum available energy.

Basic principle for power generation

A typical blue energy power generation system includes the membrane (i.e., nanopores and nanochannels) separated by the high and low-concentration solutions (see Fig. 2a). These membranes are selective to a particular type of ions (cations or anions). Owing to the concentration gradient, ions diffuse through these membranes, thereby creating a net ionic flux. The net flux of ions through the membrane is governed by the Nernst-Planck equation50,57,63:

$${J}_{i}=-{D}_{i}\nabla {C}_{i}-{z}_{i}{\mu }_{i}F{C}_{i}\nabla \phi +{C}_{i}u$$
(2)

where J is the total flux of the ionic species i, D is the diffusion coefficient, C is the concentration, μ is the ionic mobility (D/RT), R is the gas constant, F is the Faraday’s constant, ϕ is the electric potential, u is the fluid velocity and T is the thermodynamic temperature. Equation (2) describes three modes of ion transport: Diffusion (due to concentration gradient), Migration (due to electric field), and Convection (due to fluid flow). The net ionic flux creates a potential difference across the membrane, known as membrane potential, which can be approximated as49,63:

$${V}_{m}=S\frac{RT}{zF}\ln \frac{{C}_{H}}{{C}_{L}}$$
(3)

here, S represents the ion selectivity of the membrane, which can be expressed in terms of ionic flux (i.e., current) or diffusion coefficient (D) or permeability (P)50,63:

$$S=\frac{{J}^{+}-{J}^{-}}{{J}^{+}+{J}^{-}}=\frac{{D}^{+}-{D}^{-}}{{D}^{+}+{D}^{-}}=\frac{{P}^{+}-{P}^{-}}{{P}^{+}+{P}^{-}}$$
(4)

generally, S varies between −1 to 1, indicating that the membranes are selective to anions and cations, respectively. Further, S = 0 dictates that the membranes are not selective to any type of ions.

Fig. 2: Basic principles for power generation.
figure 2

a, b Schematic diagram of the typical nanofluidic RED setup used to harvest the energy from the salinity gradient and the corresponding I–V characteristics. Nanopores created on the 2D materials can act as ion exchange membranes, which are used to separate the high-concentration and low-concentration solutions. The I–V curve is offset about the origin due to the osmotic potential originating from the concentration gradient. These offset values of current and voltage are used to calculate the power. c The schematic representation of EDL covering inside the nanopore for overlapped EDL and non-overlapped EDL cases and their corresponding concentration, potential and velocity profile inside the pores. The thickness of EDL solely depends on the bulk concentration of the solution and is related through Eq. (6). c Adapted with permission from ref. 65. CC BY-NC-SA 4.0.

Full size image

The membrane potential acts as an electromotive force that drives the ions across the membrane, producing the current. As a result, I–V characteristics are observed with an offset from the origin (see Fig. 2b). The offset current and voltages are called as closed-circuit current (Iosm) and open-circuit voltage (Vosm), respectively. The energy conversion efficiency (Φ, is the ratio of Gibb’s free energy of mixing to the power extracted) can be given as59:

$$\Phi =\frac{{S}^{2}}{2}$$
(5)

which solely depends on the selectivity of the membrane.

Ion selectivity

Ion selectivity of the membrane refers to the fact that the membrane allows only counter-ions to the surface charge density of the membrane to pass through it. Whereas it repels the co-ions from the membrane. Ion selectivity solely depends on the surface charge density and thickness of the electrical double layer (EDL) formed near the surface42,48,64,65. The surface charge density is attained through the association and dissociation of the various functional groups on the surface of the membrane. The sign of the surface charge depends on the nature of the available functional group on the surface.

When the surface of the membrane is in contact with the salt solution, it attracts the counter-ions and forms layers of counter-ions near the surface in the solution to maintain electro-neutrality, forming the EDL. The thickness of the EDL can be calculated by using the Debye length65,66:

$${\lambda }_{d}={\left(\frac{{\epsilon }_{0}{\epsilon }_{r}RT}{2{F}^{2}{z}^{2}{C}_{0}}\right)}^{1/2}$$
(6)

where ϵ0 is the permittivity of free space, ϵr is the relative permittivity of the medium, R is the ideal gas constant, T is temperature, F is the Faraday’s constant, z is the valency of the ions and C0 is the bulk concentration. The thickness of the EDL inversely correlates with the bulk concentration. At 1 mM concentration, the EDL thickness is approximately 10 nm. If the radius of the nanopore is reduced to or made comparable to the EDL thickness, then the EDL from the surfaces overlaps, creating a non-zero electric potential at the center of the pore, which results in the selective transport of counter-ions. In the case of non-overlapping EDL, the electric potential from the surface of the channel decreases to zero value outside of the EDL, resulting in the presence of a bulk solution at the center of the pore (see Fig. 2c).

Diffusio-osmosis

Apart from the selective ion transport, interfacial osmotic flow, known as diffusio-osmosis, is possible near the surface even though the membrane is not perm-selective. Diffusio-osmosis is a surface phenomenon occurring within a few nanometers of EDL from the surface due to the specific interactions between salt ions and the surface. As a result, an interfacial osmotic gradient is developed inside the EDL and generates a plug-like water flow inside the membrane (see Fig. 2c). The concentration gradient along the surface creates ionic movement in the membrane, thus producing the ionic current called diffusio-osmotic current49. The osmotic current (Iosm) generated due to diffusio-osmotic flow can be expressed as follows48,49,63:

$${I}_{{\rm{osm}}}=2\pi {r}_{p}{\sigma }_{s}{u}_{{\rm{DO}}}\times N$$
(7)

here, rp is the pore radius, σs is the surface charge density, N is the number of pores in the membrane, and uDO is the diffusio-osmotic velocity is given below48,49,63:

$${u}_{{\rm{DO}}}=\frac{{k}_{B}T}{8\pi {l}_{B}\eta }.\frac{\Delta \log C}{{l}_{p}}$$
(8)

where kB, η, lp, and lB are the Boltzmann constant, fluid viscosity, pore length, and Bjerrum length. The osmotic current scales linearly with the surface charge density (Iosm ∝ σs) for the highly charged surfaces, and for the low surface charge density, it varies cubically (\({I}_{{\rm{osm}}}\propto {\sigma }_{s}^{3}\)).

Membrane conductance

The generated power from selective ion transport or diffusio-osmotic transport through the membrane under the salinity gradient can be harvested by connecting electrodes in the reservoirs to the external load (see Fig. 2a). The maximum generated power (Pmax)48,50,51,52,53,63 is given by:

$${P}_{{\rm{max}}}=\frac{{V}_{{\rm{osm}}}^{2}{G}_{m}}{4}$$
(9)

Gm is the internal conductance of the membrane. The power generation capacity of the membrane can be optimized by maximizing ion selectivity and conductance of the membrane under salinity gradient conditions. Ion selectivity and conductance depend on the intrinsic properties of the membranes. The surface charge density of the membrane (depends on the ionizable groups on the membrane surface) and the pore size determines the membrane selectivity. Similarly, the membrane conductance depends on the membrane thickness and surface charge density. In the case of nanopores, the conductance is divided into two components, i.e., surface conduction (due to the movement of ions inside the EDL created due to surface charge of nanopore) and bulk conduction (due to bulk motion of ions outside the EDL)50. For perfectly selective membranes, surface conduction will dominate inside the nanopores, whereas, for non-selective pores, both conduction plays an equal role. So, to extract the maximum power from the salinity gradient, one should carefully choose the membrane according to the above-mentioned characteristics.

New generation 2D materials as nanopower generators

Power generation from the salinity gradient is mainly dependent on the nature of membrane that conducting the ions. Commercial ion exchange membranes such as polymer and nafion membranes for osmotic power generation are highly sensitive and experience various constraints such as high cost, fouling, low lifespan, and high membrane resistance, which results in futile process efficiencies47. In recent years, it has been shown that engineering the nanopore on solid-state materials can provide high selectivity and flux as compared to commercial membranes. However, the use of 2D membranes shows superiority over other membranes since the flux and power are expected to vary inversely with the membrane thickness (according to Eqs. (7) and (8)). The use of 2D materials improves the power density above the commercialization benchmark of 5 Wm−2 51,55,56,57. New generation 2D membranes are becoming a promising candidate for nanopower generation with their merits, such as low cost, unsophisticated fabrication techniques, high surface-to-volume ratio, high ion flux, controlled mass transport, various surface functionalizations and viable high power densities.

Synthesis, growth and transfer

Typically, most of the 2D materials can be synthesized by using two methods: the exfoliation method (top-down approach)67 and the chemical vapor deposition (CVD) method (bottom-up approach)68,69. In the exfoliation method, the 2D materials are generated by breaking the bulk materials into nanosheets through the liquid exfoliation methods70,71 (using chemical reagents and ultra-sonication) or mechanical methods72,73 (using scotch tape). 2D nanosheets prepared in this method are generally dispersed in the liquids and filtered using a vacuum filter to form free-standing lamellar 2D membranes74. However, the size and phase controllability of the 2D materials in this method is poor and challenging. In contrast to top-down methods, CVD method shows great advantages for scalable growth of 2D methods in a well-controlled manner68,69.

Figure 3a, b shows the schematics of the overall CVD growth process of 2D materials. In the CVD method, the metal precursors in the form of powder, pellets and gaseous state are initially sublimated and transported to the growth chamber through the carrier gas. Here, inert gases (i.e., H2, N2, Ar, He) are generally used as carrier gases. The sublimated metal precursors in the growth chamber are adsorbed on the substrate (i.e., Silicon nitride (Si4N3), silicon, mica, sapphire, copper and platinum foils, etc.) to form the 2D material flakes through thermal decomposition at an elevated temperature. Figure 3c displays the SEM images of the various 2D material flakes grown using the CVD process. With recent developments in the CVD process, it is possible to grow monolayers of various 2D materials like graphene, TMDs (MoS2, WS2, MoSe2, WSe2), h-BN and other newly developed materials75,76,77,78,79. This process is stable and robust and is used for large-scale production of 2D materials. The properties of the as-grown 2D material depend on its size, phase, and defects present on it. These parameters can be controlled by tuning the CVD growth parameters68,69. The major parameters that influence the 2D material properties are the precursor and its concentration, carrier gas flow rate, substrate, temperature and pressure80,81,82. Recently, it has been shown that MoS2 can be grown up to a 12-inch scale by maintaining the uniform precursor concentration near the substrate and providing an additional coating of α-Al2O3 on the growth substrate83,84 (see Fig. 3e).

Fig. 3: Synthesis of 2D materials.
figure 3

a, b The schematic representation of the CVD growth process and the corresponding temperature profile for 2D materials. Precursors used in this process may be in the form of power, pellets, or gas. Generally, the inert gases are used as a carrier gas to carry the precursor atoms to the substrate where they react to form 2D materials. c SEM images of various CVD-grown 2D materials like h-BN and TMDs (MoS2, MoSe2, WS2, WSe2) and corresponding their AFM images confirming the monolayer growth. d, e Large-scale CVD growth of the graphene and MoS2 on the SiO2/Si substrate and transfer the same to flexible PET substrate. c h-BN: Reprinted with permission from ref. 75. Copyright 2015 Springer Nature. MoS2: Reprinted with permission from ref. 76. Copyright 2014 American Chemical Society. MoSe2 and WSe2: Reprinted with permission from ref. 77. Copyright 2017 American Chemical Society. WS2: Reprinted with permission from ref. 78. Copyright 2016 Royal Society of Chemistry. d Graphene islands on Cu: Reprinted with permission from ref. 79. Copyright 2012 American Chemical Society. Graphene on SiO2 and PET : Reprinted with permission from ref. 87. Copyright 2019 Royal Society of Chemistry. e MoS2 on SiO2: Reprinted with permission from ref. 83. Copyright 2023 Springer Nature. MoS2 on PET: Reprinted with permission from ref. 84. Copyright 2023 Springer Nature.

Full size image

For blue energy applications, the as-grown 2D materials are transferred to destined substrates (or supporting membranes) through wet or dry transfer and engineered to create a pore on them. The most common method for transfer is polymer-assisted wet transfer, in which as-grown material is coated with PMMA (poly(methyl methacrylate) or PDMS (polydimethylsiloxane) and transferred to a destined substrate85,86. Finally, the coated polymer material is dissolved in a solvent (like acetone) or peeled off from the destined substrate. Figure 3d displays that the graphene grown on Cu substrate is transferred to SiO2 and flexible PET substrate87. Apart from this wet transfer method, another scalable transfer method is a lamination-assisted transfer of 2D materials into another substrate88,89,90. In this method, an as-grown substrate is laminated with polymer material and transferred to another substrate. This method is very simple and fast but also requires less skilled operators90. The two methods discussed so far are promising transfer methods for large-scale CVD-grown materials.

Nanopore fabrication methods

One of the important parameters affecting the efficiency of nanopower generation is the pore size and its density. Generally, pores of size 5–15 nm are created to ensure the EDL overlap for maintaining the ion selectivity of the membrane. There are a number of ways available to drill nanopores91,92,93,94. But, for 2D materials, the controllability of pore shape and its location on the substrate at the sub-nanometer level is challenging. Transmission electron microscope (TEM) and focused ion beam (FIB) are suitable candidates for creating precise pores at the sub-nanometer level (Fig. 4a, b). TEM uses a high-intensity (107 to 108 A m−2) electron beam, and FIB uses a high-energy ion beam to drill a nanopore on the suspended substrate. Gallium (Ga+) and helium (He+) ions are the commonly available ion sources for the FIB process. These focused beams sputter away single atoms precisely and create a nanopore95,96,97. In situ imaging techniques, along with these methods, allow us to make nanopores at very precise locations. It has been demonstrated that nanopores of size 5–30 nm can be drilled in a uniform spacing to form an array on a graphene layer with the help of a helium ion microscope98.

Fig. 4: Nanopore fabrication methods and their TEM images of nanopores created on 2D materials.
figure 4

a Focused ion beam (FIB), b TEM (Focused electron beam), c Reactive ion etching (RIE), d Atomic force microscopy (AFM), e Plasma etching and f Electrochemical reaction (ECR). TEM of (a). Reprinted with permission from ref. 95. Copyright 2018 American Chemical Society. TEM of (b). Reprinted with permission from ref. 97. Copyright 2013 IOP Publishing. TEM of (c). Reprinted with permission from ref. 101. Copyright 2016 Springer Nature. TEM of (d). Reprinted with permission from ref. 112. Copyright 2021 American Chemical Society. TEM of (e). Reprinted with permission from ref. 240. Copyright 2015 Springer Nature. TEM of (f). Reprinted with permission from ref. 107. Copyright 2015 American Chemical Society.

Full size image

Apart from these methods, chemical etching is another method for creating nanopores in which heavy ions are bombarded on the substrates to create tracks known as nucleation sites for etchants to react and form a pore99,100. The pore size is monitored and controlled through ionic current variations in time. Hydrogen fluoride (HF) and Potassium hydroxide (KOH) are commonly used reactants. This method results in a random pore distribution, and covering the substrate with a mask reduces the area of exposure to the reactants. Further, the use of this method with a common lithography process known as reactive ion etching (RIE) enables us to control the precise pore locations and their density and allows us to mass production of nanopore arrays101,102,103 (Fig. 4c).

Other interesting methods for nanopore creation are plasma etching and electrochemical reaction (ECR, also known as controlled dielectric breakdown). In these methods, the defects present in the 2D materials are enlarged to form a nanopore. In the plasma etching method, a high-temperature plasma is allowed to pass and expand through the defects present in the 2D materials104,105,106 (Fig. 4e). But, in the ECR, 2D material is kept inside the electrochemical cell containing KCl solution and a voltage is applied across it (Fig. 4f). Because of the applied voltage, ions are forced to enter through the defects107,108. The resulting pore size is monitored and controlled through ionic current measurements. From the measured ionic current, the nanopore conductance is calculated and fitted with the following analytical model to estimate the nanopore size109,110:

$$G=\kappa {\left(\frac{4{l}_{p}}{\pi {d}_{p}^{2}}+\frac{1}{{d}_{p}}\right)}^{-1}$$
(10)

where κ is the conductivity of the 1 M KCl solution (105 mS cm−1). The estimated pore size estimation using Eq. (10) is found to be in close agreement with the TEM measurements.

Atomic force microscopy (AFM) is another technique to create a nanopore at a desired location111. In this method, the conductive AFM tip with the desired radius of curvature is positioned exactly at a location where the pore is to be created. A voltage source is connected to the AFM tip (positive terminal) and the substrate (negative terminal). When the voltage pulse is applied between the AFM tip and the substrate, the electric field of order 108 to 1010 V m−1 will be created on the surface of the substrate. This results in the local joule heating of the substrate and a variety of chemical reactions, which are complex and unknown, leading to the creation of the pore (Fig. 4d). The pore size depends on the applied voltage and its reaction time. Further, this method of pore creation can be used in combination with ECR, in which the AFM tip is used to localize the electrochemical reaction at a particular location112.

The mechanism of each method for pore creation is different and leads to the addition of carboxyl, hydroxyl or protonable groups at the edge of the pores. As a result, the pore possesses different surface charge densities, though the pore material remains the same. So, one cannot compare the performance of power generation based on the material unless the pore creation method or surface functional groups are mentioned. Sometimes, more than one method of pore creation may be used to enhance the performance of the power generation104.

Salinity gradient energy (SGE) generation

As discussed in the earlier section, the 2D membrane with nanopore (created using various techniques) is placed to regulate the mixing of the low (river water) and high-concentration (seawater) solution. The energy generated from mixing these solutions is harvested by placing the electrodes across the membrane (Fig. 2a, b). Implementing this power generation technique at the estuary is challenging and at early nascent stages. At the laboratory level, the artificial seawater (i.e., 0.5 M KCl, NaCl, etc. salt solutions) and artificial river water (i.e., 0.01 M KCl, NaCl, etc. salt solutions) are separated by the membrane having an area of few μm2 to mm2 as a bench scale model. The performance of the membrane is quantified by the power density (i.e., power per unit area of the membrane). In the following sections, we discuss the salinity gradient energy generation capabilities of the different 2D materials and the process of improving them.

Graphene and its derivatives

Graphene is a single-atom-thick material made up of carbon atoms bonded in a hexagonal pattern. Because of these unique arrangements of atoms, it possesses excellent characteristics like superior thermal conductivity, high surface area, high elastic strength, high conductiveness, and excellent charge carrier mobility113,114,115. The creation of nanopores on the graphene makes it a better candidate for selective ion transport106,116,117,118,119 (Fig. 5a). Due to the concentration gradient, cations and anions will diffuse into the pore without the external voltage. When one type of ion diffusion rate is higher than the other type, an osmotic current (Iosm) will be generated. The positive osmotic current indicates that the pore is cation-selective and that cations are moving from high to low concentrations. The selectivity of the pore is directly calculated from the osmotic potential using Eq. (3)109. Figure 5b shows the variation of the ion selectivity in terms of conductance of 1 M KCl and estimated pore size (estimated from Eq. (10)). When the pore size increases above 25 nm and at higher concentrations, the selectivity drops, significantly affecting the generation of osmotic power109. It is noted that the selectivity also depends on the pH of the solution, which alters the surface charge density of the nanopore (Fig. 5c). The selectivity of pores increases with the surface charge density of the membrane, resulting in higher osmotic power generation104. Also, it improves the energy conversion efficiency since it directly depends on the selectivity (see Eq. (5)). It is found that simple irradiated graphene nanopores can be generated up to 126 Wm−2 120, whereas ozone-treated pores (ozone treatment increases the defect density) can produce 700 Wm−2 power density121. Since the surface charge density and pore density of the membrane vary depending on the pore creation method.

Fig. 5: Graphene and its derivatives.
figure 5

a Nanoporous graphene used for osmotic energy generation. b Variation of ion selectivity of the graphene nanopore with pore size and conductance in terms of 1 M KCl solution. c Effect of nanopore surface charge density on the output power density and energy conversion efficiency. d Graphene oxide (GO) membrane and the SEM image of its cross-section. It is a layer-by-layer material made up of graphene nanosheets with functional groups. e, f I–V characteristics of GO/CNFs composite membrane (made of GO and cellulose nanofibers (CNFs)), GO, CNFs membranes and their output power density. The addition of CNFs to the GO membrane increases the ion transportation across the membrane, which results in higher output power density. a Reprinted with permission from ref. 120. Copyright 2019 Elsevier. b Reprinted with permission from ref. 109. Copyright 2016 Springer Nature. c Reprinted with permission from ref. 104. Copyright 2024 American Chemical Society. d Reprinted with permission from ref. 241. Copyright 2017 John Wiley and Sons. e, f Reprinted with permission from ref. 147. Copyright 2020 Royal Society of Chemistry.

Full size image

It has been demonstrated that graphene nanopores can be tuned from cation to anion selectivity by controlling the concentration of multivalent ions and inducing the charge inversion near the nanopore110. The osmotic power density is increased by 10–100 times in the case of the multivalent ions (>105 Wm−2) as compared to monovalent ions (>104 Wm−2). Nanopores decorated with carboxyl groups or other oxygen-containing groups show higher surface charge density rather than the other functional groups104,122,123,124,125,126,127. To increase the surface charge density of the nanopore further, a preanchoring method is developed to achieve the electrostatic directional modification of the functional groups near the nanopore104. Initially, as a preanchoring process, octa-ammonium-polyhedral-oligomeric-silsesquioxane (POSS, it is positively charged) made surround near the pore electrostatically. 4-carboxy benzene diazonium tetrafluoroborate (4-CBD) is attracted by the POSS and reacts with the pore to modify the surface charge density. Apart from the graphene, carbon nanotubes (CNT) are employed to harvest the energy from the salinity gradient128,129. Moreover, the power density of the CNT remains in the same range as graphene.

To a great extent, graphene provides a basis for other materials like graphene oxide (GO) and reduced graphene oxide (r-GO) (Fig. 5d), which are less expensive and easy to produce. Graphene nanosheets are oxidized to obtain the graphene oxide (GO) and are dispersed in the solution to obtain the GO membrane113,114,115. GO sheet contains <20% pristine graphene and >80% the oxidized sheets, which include the oxygen functional groups such as carboxyls, epoxides, and hydroxyl on their edges. Further, these GO sheets are converted into reduced GO sheets through chemical, electrical and thermal reduction processes130,131. The main advantages of using GO membranes are large-scale size132,133 (a few cm2 area with few μm thickness) and ease of customizing the surface functional groups125,134,135,136,137. As compared to the nanopore, the ion transport mechanism inside the GO membranes differs significantly due to the layer-by-layer arrangement of nanosheets. With the increase in the membrane thickness and number of layers, the power drastically reduces as compared to the single nanopore. Moreover, the GO membrane produces a power density of 2–3 Wm−2 under a 50 concentration gradient137,138. The power density is further boosted by undergoing the N2/H2 plasma or alkaline treatment of GO membranes to ~5 Wm−2 138,139. Further, creating asymmetric nanochannels of GO membranes enhances the power density to 5.32 Wm−2 140, which is in the same order as other treatments. Interestingly, the vertical stacking of the nanosheets of the GO membrane improves the power density up to 10 Wm−2 141, as it provides the easiest pathways for ion movement.

In addition, to improve the properties of the GO sheets, they may be combined with polymer/biological materials, forming composite structures142,143,144. GO/polymer composite membranes145,146 did not show a significant increase in the osmotic power density, whereas GO/Cellulose nanofiber (GO/CNF) membrane generated ~5 Wm−2 power density147. Figure 5e displays the I–V characteristics of GO, CNF, GO/CNF membranes. The osmotic potential is almost in the same range for GO, CNF, GO/CNF membranes, indicating the high selectivity of the membranes. However, the osmotic current increases significantly for the composite membrane (GO/CNF), explaining the fastest ion transportation of the membrane (since, adding CNF increases the interlayer spacing of GO membrane from 0.88 nm to 1.32 nm). As a result, the power density increases significantly for the GO/CNF composite membrane147 (see Fig. 5f). Similar to traditional RED, the membranes with opposite charges (for example, p-GO and n-GO membranes) are connected in series to improve power generation148. For the p-CNC/GO and n-CNC/GO pairs (CNC—cellulose nanocrystals), the power density is increased up to ~12 to 16 Wm−2 by increasing the temperature of the solutions149. Enhanced fluidic viscosity and the ionic mobilities with temperature are responsible for this increment.

Hexagonal boron nitride (h-BN)

h-BN is an insulator having the same structure as graphene150,151,152,153. The boron and nitrogen atoms are arranged alternatively in a hexagonal lattice. Due to its large band gap, h-BN is proven to be a good dielectric material. Recently, it has been shown that triangular pores on the bilayer h-BN can rectify the current, whereas hexagonal and circular pores do not154. Creating triangular pores results in nitrogen-terminated pores for one layer and boron-terminated pores for another layer. These asymmetries in the pore terminations rectify the current and make the h-BN nanofluidic diode. Further, it has been demonstrated that h-BN nanopores112 (Fig. 6a), h-BN nanotubes (h-BNNT)155 (Fig. 6b) and lamellar membranes156 can be used for osmotic power generation from the salinity gradient. The inner walls of the BNNT are shown to have a very large and pH-tunable surface charge of ~1 C/m2, which is higher than the other materials reported earlier, resulting in a high power density of 4000 Wm−2 under a 1000 concentration gradient (see Fig. 6c) which is attributed to the diffusio-osmotic flow generated due to the high surface charge of the BNNT and no overlapping of the EDL (i.e., non ion-selective)155. For a large-scale scaling, the pore density of ~108 pores/cm2 is achieved by direct growth of h-BN on a porous anodized alumina oxide (AAO) membrane through the CVD process157. However, the power density is reduced to 105 Wm−2 due to the ion concentration polarization (ICP)64,158 decreasing the local concentration near the membrane.

Fig. 6: h-BNs and TMDs.
figure 6

a, b 3 × 3 Nanopore array on h-BN/SiN substrate and the h-BN nanotubes (BNNT) embedded in SiN membrane (with the help of nanomanipulator) setup for osmotic power generation. Tip-controlled local breakdown technique (which is a combination of AFM and ECR methods) is employed to generate the nanopore arrays. c Variation of produced power density with concentration gradient and pH (5.5—yellow; 9.5—purple; 11—red). d The schematic diagram of the MoS2 nanopore used as a nanopower generator. e Variation of osmotic potential and current with pore size. The optimal value of pore size to extract the maximum size is found to be 10 nm. f Variation of output power with the number of MoS2 layers. The Y-axis shows the output power density of n layers relative to the monolayer output power density. a Reprinted with permission from ref. 112. Copyright 2021 American Chemical Society. b, c Reprinted with permission from ref. 155. Copyright 2013 Springer Nature. d–f Reprinted with permission from ref. 108. Copyright 2016 Springer Nature.

Full size image

Transition metal dichalcogenides (TMDs)

TMDs are three-layered materials represented as MX2; here, M represents the transition metal atoms, and X is the chalcogen atoms in the periodic table, i.e., one transition metal atom is sandwiched between the two chalcogen atoms forming the three-layer structure159,160,161,162,163,164. Also, TMDs are quite popular due to their adjustable bandgaps and phase- and thickness-dependent electrical and optical properties165. MoS2, MoSe2, WS2, WSe2 are the widely-used TMDs. A Nanopower generator is fabricated using single-layer MoS2 shown to generate a power density of ~106 Wm−2 (see Fig. 6d)108. This high power density value is attributed to the atomically thin membrane of MoS2 and its high surface charge density108,166. The non-monotonic variation of osmotic potential and current is observed with the nanopore size since the ion selectivity reduces with an increase in the pore size (Fig. 6e). Further, it could be explained by the depletion of ion concentration near larger pores. It is noted that the nanopore size of 10 nm is found to be optimum to achieve the higher power density. Also, the generated power density decays strongly with the number of layers of MoS2, indicating the importance of the atomically thin membrane (Fig. 6f). To extend the TMDs to a large scale, stable metallic MoS2/cellulose167 and WS2/cellulose168 composite membranes having a test area of few μm2 are fabricated. Similar to GO membranes, they also can produce power in the range of 3–7 Wm−2 due to their large membrane area and thickness.

Other 2D materials

Another interesting 2D material is mono elemental Xenes (MXenes). Similar to the TMDs, it is also a layer-by-layer material, represented as Mn + 1XnTx, n = 1–3 represents the number of layers, M is the transition metal atoms, X refers to carbon (C) or nitrogen (N) atoms, and T refers to functional groups like carboxyl or carbonyl groups169,170,171,172,173. However, synthesis of the Mxene through CVD is challenging; the mechanical exploitation method followed by filtration is employed to produce the lamellar membrane of few cm2 area for osmotic energy generation applications (Fig. 7a). The output power density of mxenes is also in the range of 3–6 Wm−2, similar to other material lamellar membranes. Moreover, this value is increased through various functionalizations174 and combining with other materials175,176,177,178. Mxene/Go179 and Ti3 C2 Tx Mxene/BN180 composite membrane increases the power density up to ~8 Wm−2 at an elevated temperature of ~333 K. Further, bioinspired Ti3 C2 Tx MXene-ionic diode membrane having positive and negative charged functional groups on the opposite sides of the membrane is designed to produce 8.6 Wm−2 181. Creating nanopores on the Ti3 C2 Tx MXene membrane enhances the power density to 17.5 Wm−2, which is almost 38% increment as compared to pristine mxene (Fig. 7c)182. Moreover, the porous membrane increases the ion transportation rate, resulting in a higher osmotic current (Fig. 7b). The selectivity almost remains the same in both cases, which is visible in terms of osmotic potential (Fig. 7b).

Fig. 7: Other 2D materials like MXenes and COF.
figure 7

a The schematic representation of osmotic energy generation setup using the MXene lamellar membrane. This membrane is prepared by liquid exploitation from the MAX phase, followed by vacuum filtration. b, c shows the I–V characteristics of pristine MXene and nanoporous MXene and the corresponding output power density. d Schematic diagram of anion-selective amine-ended zinc tetraphenyl porphyrin (ZnTPP)-COF monolayer membrane with square nanopore arrays is prepared by interfacial polymerization. e Molecular arrangement of ZnTPP-COF monolayer square nanopore. f shows the output power density of the COF membrane. High-ordered nanopore arrangement helps to achieve this high power density. a Reprinted with permission from ref. 230. Copyright 2019 American Chemical Society. b, c Reprinted with permission from ref. 182. Copyright 2022 American Chemical Society. d–f Reprinted with permission from ref. 190. Copyright 2022 Springer Nature.

Full size image

Covalent organic frameworks (COF) are crystalline porous polymeric materials with organic units arranged in high-order structures through polymerization. In this material, organic units are connected to atoms like boron, carbon, and hydrogen through covalent bonds183,184,185,186. COF membrane is a suitable candidate for osmotic power generation since the number of layers and pore parameters like density, size and surface charge are tunable by choosing the different organic units (Fig. 7d, e). Also, pore shapes can be changed to hexagonal187, triangular188 and diamond shapes189. COF membrane is fabricated via mechanical exfoliation or interfacial polymerization190. Mono-layer COF membrane generates the output power density of 102 Wm−2 191. Ultimate permeability originated from the high membrane porosity, which is responsible for this higher value. Anion-selective amine-ended zinc tetraphenyl porphyrin (ZnTPP)–COF monolayer membrane with square nanopore arrays is prepared by interfacial polymerization (Fig. 7d, e) is proved to produce up to ~150 Wm−2 power density (Fig. 7f)190. Further, it is demonstrated that the COF membrane with well-defined ion channels192, asymmetric in geometry and surface charge193 can be used as high-performance nanopower generators that can generate up to ~210–230 Wm−2 under a 50-fold concentration gradient. Compared to other material lamellar membranes, mono-layer COF membranes provide hope for large-scale scalability with enhanced selectivity. In addition, 3D COF and lamellar membranes are demonstrated to generate more than 5 Wm−2 power density, which is the benchmark set by the other materials194,195,196.

Another material similar to COF is metal-oxide frameworks (MOF), in which a periodic structure is formed by the inorganic metal ions (or clusters) and connected through organic ligands197. The MOF nanosheets are prepared by solvent-assisted exfoliation or direct formation on the substrate198,199. Like other materials, asymmetry in the membrane200 and surface charge density201, the MOF membrane can be tuned to produce power density in the range of 25–40 Wm−2. Moreover, the MOF membrane is in the initial stage of osmotic power generation. A summary of 2D materials used for osmotic power generation and their power densities are given in Table 1.

Table 1 Head-to-head comparison between the commercial and 2D nanofluidic membranes for SGE generation
Full size table

Upscaling and challenges

Scalability of the osmotic power generation from the nanoscale to large scale is important for real-time applications. The following are the techniques used for scalability of power generation: (1) Stacking of the electrochemical cells (i.e., multiple membranes/devices are connected in series, Fig. 8a, b), (2) Formation of nanopore arrays (parallel arrangement, Fig. 8c, d), and (3) Creation of nm to mm size pores (meso and macro size pores, Fig. 8e, f).

Fig. 8: Upscaling techniques for osmotic power generation.
figure 8

a, b The alternative arrangement of cation and anion exchange membranes, same as traditional RED, or addition of more cells (i.e., series connection of cell (shown in Fig. 2a) one after other). c Stacking nanopores to form an array. The semi-circle at the end of the channel represents the access region and ICP zones. d The variation of center pore current with an increase in the number of pores on the membranes. Inset: Variation of overall nanopore array conductance with the number of pores. It follows logarithmic variation and reaches its saturation value at higher pore density. e, f Creation of mm size pores. The mm size pores used for osmotic power generation and their corresponding osmotic power. SP and MP refer to single-pore and multi-pore systems, respectively. a, b Reprinted with permission from ref. 177. Copyright 2020 John Wiley and Sons. c, d Reprinted with permission from ref. 204. Copyright 2023 American Chemical Society. e, f Reprinted with permission from ref. 208. Copyright 2023 John Wiley and Sons.

Full size image

The power density of the membrane depends on the two parameters, i.e., osmotic current and voltage. The osmotic current is based on ion transportation, which can be increased by making composite or increasing the porosity of nanoporous membranes. In comparison, the osmotic potential is related to the membrane’s selectivity; in extreme cases, it is limited to ideal selectivity. An alternate arrangement of cation- and anion-selective membranes (Fig. 8a) or connecting multiple cells in series (Fig. 8b) and maintaining the concentration gradient across each membrane, similar to traditional RED, results in the enhancement of osmotic potential177. Recently, it has been demonstrated that adding more cells in a series increases the osmotic potential from a few mV to V and is used to lid the LEDs run the timers and calculators142,148,176,180,202,203. However, adding more cells leads to unnecessary voltage drops, reducing the overall output osmotic potential. One must optimize the number of cells depending on their pore/membrane size in order to extract the maximum power.

Creating multiple nanopores in an array can increase the output power density compared to a single pore system. However, the performance of individual nanopores is suppressed and limited by the ion concentration polarization (ICP) phenomenon190,204,205. Selective ion transport near the nanopore entrance creates a local decrease in the ion concentration, resulting in the ICP phenomenon, and the ICP zone (i.e., ion depletion) will be formed near each nanopore. This ICP zone affects the effective concentration gradient across the nanopore and affects its output power. If the interpore spacing is small compared to the pore size, then these ICP zones will overlap and form a single zone206. The interactions among the pores will be set up through this zone, and the osmotic current of the individual pores decreases toward the center204,207. Further, the center pore current decreases with an increase in the number of pores (i.e., pore density) due to the strong ICP phenomenon, which suppresses the overall conductance of the membrane (see Fig. 8c, d). As a result, the membrane conductance follows logarithmic scaling with a number of pores in the membrane204,205. One must be careful in choosing the interpore distance and pore density to generate the maximum output power density. Apart from this, controlling the interpore distance and number of pores is still challenging and requires more research in this field.

Recently, it has been shown that nm to mm sized copper/graphene pore is able to produce the output of a few μW range, although the membrane is non-selective208 (see Fig. 8e, f). This higher output power is attributed to the diffusio-osmosis flow originating due to the concentration gradient across the membrane. An automated system is designed to maintain the fresh high and low-concentration solutions in the reservoir and the concentration gradient209,210. In comparison to single-pore devices, individual pore performance in multi-pore devices is limited due to the depletion of local ion concentration near the pore, though an automated system is employed. This type of upscaling is in the initial stage of research. When the pore size is increased from nm to mm size and a large area lamellar membrane, maintaining the desired concentration across the membrane is challenging due to the ICP phenomena and requires the novel design of the fluidic cells with an automated system to monitor the concentration. However, the design and process parameters maintaining the concentration gradient will vary with the number of pores and membrane size. Further, the CVD growth of the 2D materials on a large scale is also at the initial research. However, for MXene, like a new class material, the growth using the CVD process is challenging and at the early stage of research. So, one should choose the 2D material that has the possibility to grow on a large scale and a well-customized automated fluidic control system to upscale the performance of osmotic energy generation through large pores.

Future perspectives and outlooks

The important element in blue energy generation is the use of ion-selective membrane. Employing the 2D materials as membranes with various techniques increases the output power density above the commercialization benchmark level of 5 Wm−2 51,55,56,57. Head-to-head comparisons between the commercial and 2D membranes are given in Table 1. Even though many research initiatives have been taken on blue energy generation using 2D materials, they are still at the laboratory scale due to their implementation challenges. However, the output power density changes drastically with the different working solutions and conditions (i.e., pH, temperature, concentration gradient), making it difficult to compare with other materials. Also, it is found that the use of the real seawater and river water combination increases the output power density ~5 times as compared to artificial seawater and river water211. To get more realistic results, one should test with real seawater and river water systems.

The deviations in the output power density can be attributed to the nature of functional groups available on the pore surface. Proper tunability of the functional groups on the 2D material is limited. Adding carboxyl, oxygen and nitrogen-containing function groups to graphene/graphene oxide membrane through various treatments improves its low surface charge density thereby elevating its output power density. Similarly, such functional groups have effect on other 2D materials like TMDs, h-BNs, and MXenes for blue energy generation, which needs to be investigated.

Photo-light-induced enhancement of blue energy generation using 2D materials is another interesting topic of research51,212,213. Depending on the location at which photo-light is introduced, this effect is divided as (1) photo-light-induced heat gradient, and (2) photo-light-induced surface charge. The introduction of photo-light on the seawater side acts as the local heat source and increases the temperature, creating a heat gradient across the membrane. This heat gradient induces the additional ionic current and improves the output power density. Similarly, the introduction of photo-light on the membrane enhances its surface charge density, resulting in higher power density. However, the study of these effects on the different 2D materials may provide an opportunity to explore further.

Additionally, it is shown that membranes having diode characteristics produce higher power density181,193. Because of its single-atom thickness, vdW interactions among the 2D layers help us to form vdW heterostructures, which can form the diode membranes and enhance the output power density. MoS2/MoSe2, WS2/WSe2, Gr/MoS2, Gr/h-BN are common vdW heterostructures available in literature. Therefore, the study of vdW heterostructures for blue energy generation may open new research avenues. In addition, different phases of the TMDs also need to be explored due to variations in the surface charge density.

In this review, we put forward the fabrication methods of 2D materials and nanopore generation techniques and their applications in the field of blue energy harvesting. We summarize that the output power density of the 2D material depends on the pore size, membrane thickness, pore density, and surface charge density. Creating the ultrathin membrane can enhance the power density, but the controllability of pore density and interpore distance is challenging and can reduce the power density by inviting the ICP phenomenon. Further, we expanded our review toward lamellar membranes and discussed the creation of composite membranes; ionic diode membranes increase the output power density on a large scale. Also, we have discussed three upscaling techniques for blue energy generation along with their challenges. Overall, it is anticipated that the use of 2D materials can make the salinity gradient energy a viable source.