A cross population study of retinal aging biomarkers with longitudinal pre-training and label distribution learning

Abstract

Retinal age has emerged as a promising biomarker of aging, offering a non-invasive and accessible assessment tool. We developed a deep learning model to estimate retinal age with enhanced accuracy, leveraging retinal images from diverse populations. Our approach integrates self-supervised learning to capture chronological information from both snapshot and sequential images, alongside a progressive label distribution learning module to model biological aging variability. Trained and validated on healthy cohorts (34,433 participants from the UK Biobank and three Chinese cohorts), the model achieved a mean absolute error of 2.79 years, surpassing previous methods. When applied to broader populations, analysis of the retinal age gap—the difference between retina-predicted and chronological age—revealed associations with increased risks of all-cause mortality and multiple age-related diseases. These findings highlight the potential of retinal age as a reliable biomarker for predicting survival and aging outcomes, supporting targeted risk management and precision health interventions.

Introduction

The world’s aging population is placing increasing strain on healthcare systems, amplifying the burden of chronic diseases and raising concerns about quality of care. While current approaches typically treat age-related conditions in isolation, the geroscience hypothesis posits that fundamental aging processes drive systemic cellular deterioration, accelerating disease onset across organ systems¹. Targeting biological aging directly could delay or prevent multiple chronic diseases simultaneously, offering a more effective strategy than traditional disease-specific interventions². However, individuals of the same chronological age exhibit substantial variability in biological aging and health status, highlighting the limitations of chronological age as a predictor of age-related risks. This underscores the urgent need for accurate biological age assessments to capture individual vulnerabilities, improve risk prediction, and enable more precise, personalized interventions^3,4.

Initial efforts to estimate biological age have relied on molecular and physiological biomarkers, including epigenetic clocks⁵, transcriptomic⁶ and proteomic signatures^7,8, and composite clinical indices³. While these methods offer valuable insights into aging mechanisms, their invasiveness, complexity, and reliance on specialized expertise limit their feasibility for large-scale clinical use. Deep learning methods have facilitated biological age estimation using non-invasive medical imaging, including chest X-ray⁹, brain MRI^10,11,12, and 3D facial imaging¹³. However, these techniques are hindered by high costs, complex infrastructure requirements, and variable clinical reliability, impeding their integration into routine health assessments. These limitations underscore the need for reliable, non-invasive, cost-effective, and widely accessible biomarkers of biological aging that can be seamlessly incorporated into clinical workflows.

Retinal age, derived from fundus imaging, has emerged as a promising biomarker in aging research^{14,15,16,17,18,19,20}. Unlike neuroimaging modalities that require specialized expertise and equipment, retinal imaging is minimally invasive, largely automated, and allows rapid image acquisition, making it particularly suitable for widespread clinical implementation. The retina’s unique composition of vascular and neural tissues, which demonstrates age-related changes paralleling those in critical organs such as the heart and brain, highlights its potential as a window into systemic aging processes^21,22,23. These characteristics position retinal age as an exceptionally valuable clinical biomarker, offering distinct advantages in accessibility, non-invasiveness, and potential for integration into routine healthcare assessments.

Several studies have developed retinal age prediction models using deep learning^14,24, however, fundamental challenges persist in capturing the complexity of biological aging. A key issue stems from the dynamic and highly variable nature of the aging process. Existing models predominantly rely on single-time snapshot retinal images and predict retinal age as a single-point value using regression methods. While straightforward, this approach oversimplifies the complexity of aging^14,24, failing to account for temporal fluctuations and individualized trajectories, which are critical for understanding biological aging²⁵. This constraint reduces both predictive accuracy and clinical relevance^14,24. Another major limitation is the lack of generalizability across diverse populations. Aging manifests differently across individuals due to genetic, environmental, and lifestyle factors. Existing studies have relied on single-source datasets, leading to models that may not adequately represent demographic variability^14,24. This focus risks introducing biases into predictions and undermines the applicability of these models to broader, heterogeneous populations^26,27. Finally, current research has primarily focused on the retinal age gap—the difference between predicted retinal age and chronological age—in relation to specific health conditions such as cardiovascular disease and kidney diseases^{14,16,19,28,29,30,31}. While these studies offer valuable insights into the predictive utility of retinal age gaps for individual diseases, they do not fully explore their potential connections to a broader range of age-related conditions. Given the systemic nature of aging, further investigation into these wider associations could establish retinal age as a robust and holistic biomarker for biological aging and health outcomes.

In this study, we aim to address these challenges by presenting a new framework for retinal age estimation that introduces several advancements. First, we employ a temporal-order self-supervised learning (TO-SSL) framework that leverages longitudinal retinal images to capture the dynamic nature of aging. By incorporating masked image modeling and temporal order tuning, our approach models aging progression over time, addressing the limitations of snapshot-based analyses. Second, we propose a two-stage label distribution learning (LDL) approach that models retinal age as a probabilistic distribution rather than a single-point estimate, reflecting the inherent variability of biological aging. To enhance generalizability across diverse populations, we introduce cross-domain ordinal constraints that ensure consistent feature alignment across datasets, mitigating demographic biases. Additionally, we validate our model across multiple populations by integrating data from the UK Biobank (UKB) and three Chinese (CHN) cohorts, demonstrating its robustness and broad applicability. Finally, we conduct a comprehensive analysis of retinal age gaps, linking them to mortality and a wide spectrum of age-related diseases (see Fig. 1), providing new insights into the systemic health implications of this biomarker.

Fig. 1: Overview of the proposed workflow for retinal aging biomarker development and evaluation.

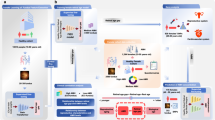
a Data collection and preparation: The training dataset comprises retinal images from the UK Biobank (UKB) and a Chinese (CHN) cohort, selected to represent a generally healthy population. These images undergo automated quality control through an image grading model. b Framework for estimating retinal age: In Stage I, snapshot images are used to train a masked auto-encoder. This is followed by a partial fine-tuning of the encoder with longitudinal images, enhancing its ability to model the temporal evolution for retinal aging. Stage II involves a sophisticated two-stage label distribution learning process, where a regression head is fused with the pre-trained encoder, enabling accurate prediction of retinal age. c Evaluation of the retinal aging biomarker: The model’s performance is tested across a varied demographic, utilizing the difference between calculated retinal age (RA) and chronological age (CA) as an innovative biomarker to predict susceptibility to age-related diseases.

Results

Study design and overview

In this study, we evaluated retinal age as a biomarker of biological aging through the development and validation of a predictive model and subsequent disease association analyses. The study was structured into three interconnected phases: data processing, model development, and clinical validation. In the data processing phase, retinal fundus images were curated and preprocessed to ensure quality and reliability. A dataset of 133,894 images from 32,282 healthy individuals aged 15–92 was collected from three CHN cohorts³² and UKB cohort A for model development. An additional dataset of 45,436 participants from UKB cohort B, representing the general population, was reserved for disease association analyses. All images underwent automated quality control using a grading model trained on the EyePACS-Q dataset³³, classifying images as good, usable, or rejected based on illumination, artifacts, and diagnostic clarity³⁴. Only gradable images (good or usable) were retained to ensure data integrity.

The model development phase centered on creating the retinal age prediction model using data from healthy individuals, under the assumption that biological age aligns with chronological age in the absence of chronic diseases^1,12. The model utilized snapshot retinal images to extract spatial features, while longitudinal images captured temporal aging patterns. We implemented a label distribution learning approach to predict retinal age as a probabilistic distribution, with model performance primarily evaluated using mean absolute error (MAE). A lower MAE reflects the model’s enhanced ability to approximate biological age, particularly in healthy individuals, where it closely tracks chronological age. Through ablation studies, we assessed individual model components’ contributions. Additionally, attention map visualizations and systematic image manipulations identified key age-predictive retinal features, while analysis of microvascular features quantified from segmented retinal images further elucidated their relationship with aging.

In the clinical validation phase, we applied the model to the general population to evaluate the retinal age gap as a potential biomarker of aging deviations. This gap, defined as the difference between predicted retinal age and chronological age, was analyzed using data from 45,436 participants in UKB cohort B. We investigated associations between the retinal age gap and various age-related conditions, spanning cardiometabolic, neurological, and ocular diseases. Using Cox proportional hazards models, we quantified associations with mortality and disease incidence, deriving hazard ratios and confidence intervals to characterize the relationship between retinal age gap and age-related health outcomes.

Evaluation of retinal age estimation in relatively healthy participants

In Fig. 2, we present the primary outcomes of retinal age estimation. Our model demonstrated impressive accuracy, achieving an MAE of 2.79 years in both the CHN and UKB cohorts. Moreover, it exhibited a strong correlation between retinal age and chronological age, with Pearson correlation coefficients of 0.954 and 0.885 for the CHN and UKB cohorts, respectively. In Fig. 2c and d, we assessed the level of agreement between the predicted retinal age (RA) and chronological age (CA) using Bland-Altman plots. Bland-Altman plots analyses revealed that the average differences between RA and CA were −0.04 (−1.96 SD −7.1 to +1.96 SD 7.19) for CHN cohort and −0.12 (−1.96 SD −7.20 to +1.96 −7.00)for UKB cohorts. We analyzed the retinal age deviations across various age groups, categorized as follows: under 20, 20–30, 30–40, 40–50, 50–60, 60–70, 70–80, and over 80 years. Predictions within the error margins (−2.79 ≤ age deviation ≤ 2.79) are considered to fall within the expected technological accuracy. Figure 2e and f show that most age groups exhibited an age deviation close to zero, and a significant proportion of cases (60%) fell within this error range. Across age groups (20–30, 30–40, 40–50, 50–60, 60–70, and 70–80), the proportion of prediction differences within the MAE varied between 53.6% and 71.9%. Lower percentages were observed in the 10–20 age group (12.5%, n = 8) and in individuals aged ≥80 years (27.4%, n = 350). The overall age deviation distribution is shown in Fig. 2g and h. We present the age label distribution for predicted retinal ages. These predictions tend to cluster around the corresponding chronological ages, as illustrated in Fig. 2i. Additionally, Fig. 2j provides a detailed examination of four distinct cases of age estimation, showcasing the respective age label distributions for each case.

Fig. 2: Result of retinal age predictions from the RLDL model on relatively healthy participants.

a, b Scatterplots for the correlation of the retinal age and chronological age for the CHN cohort (a) and the UKB cohort (b). c, d Bland-Altman plots for the agreement between retinal age and chronological age for the CHN cohort (c) and the UKB cohort (d). e, f the distribution of retinal age gap by age groups. g, h The distributions of the retinal age gap for the CHN cohort (g) and the UKB cohort (h). i The average probability distribution of the age prediction on the age labels. j Showcases of the predicted retinal age distribution for individual samples.

We then compare our model with existing popular regression methods, including the direct regression method, classification-based methods^35,36, and ranking-based methods³⁷. The Mean-variance method improves classification models by adding concentration regularization, while the ranking-based method explicitly introduces ordinal information through a combination of binary classifiers. The POE methods model uncertainty using probabilistic embeddings. In addition, we include two baseline predictors: a simple mean predictor, which predicts the mean age of the training set for all test samples, and a conditional mean predictor based on sex, which predicts the mean age for each sex group. Table 1 presents the detailed comparison results. The mean predictor and the conditional mean predictor (sex-based) serve as naïve baselines, with MAE of 9.09 years (on all data) and 6.74 years (on the UKB cohort), respectively, demonstrating the limitations of simple demographic-based approaches. Among existing methods, classification-based models outperform direct regression methods across all data cohorts, consistent with previous findings^35,38. The POE-CLS method achieves the best performance among the baselines; however, its accuracy is still inferior to our proposed model. Our method denoted as RLDL (Retinal Label Distribution Learning), achieves an MAE of 2.84 years, an RMSE of 3.70, and a Pearson’s correlation coefficient (R) of 0.950 when trained solely on snapshot images. These results highlight the superiority of our approach in capturing age-related features and improving prediction accuracy over both naïve and established baseline methods.

Table 1 Comparison of the proposed method with existing studies

Ablation study of the proposed method

Here, we present the ablation study results of our model to demonstrate the impact of various components on its overall performance. The impact of each component is summarized in Table 2, with detailed analyses provided below.

Table 2 Ablation study on the proposed method (MIM and TOL denote masked image modeling and temporal-order learning, respectively)

Initially, the base model using only the coarse age prediction stage achieved a MAE of 3.08 and a Pearson correlation coefficient (R) of 0.946. Introducing the refined age prediction stage reduced the MAE by approximately 0.2, improving the precision of the model. The refined stage further centralized the predicted age distributions around the true age, as demonstrated in Fig. 2j. Supplementary Fig. 1 illustrates additional cases, showing that the refined predictions align more closely with the true age compared to the coarse predictions. When analyzed by age groups (Fig. 3e), the refined predictions consistently outperformed the coarse predictions in groups aged 30–40, 40–50, 50–60, 60–70, 70–80, and ≥80. The refined stage yielded lower MAEs, particularly for older individuals, where the refined model provided significant gains in accuracy. In younger age groups (≤30), coarse predictions performed better, likely due to greater variability in biological aging in this demographic, where coarser age bins may provide more stable predictions.

Fig. 3: Ablation results of the proposed model.

a UMAP plot of the image features for the different pre-trained models. b Evaluation of the pre-trained features using linear probing and k-NN. c UMAP plot of the image features for the baseline model, ordinal regularized model, and ordinal-aligned model. d Adaptation result when using different training and test cohort data. e Distribution of retinal age deviation for coarse and refined predictions across age groups.

The integration of ordinal feature alignment further improved the model’s performance. While the improvement in age prediction accuracy was modest, the feature space organization showed significant enhancements, as visualized in Fig. 3c. The aligned feature space demonstrated better clustering of age-related features, highlighting the benefit of incorporating ordinal constraints. To evaluate the model’s generalizability across cohorts, we conducted experiments by training the model on one cohort (e.g., UKB cohort) and testing it on another (e.g., the CHN cohort). As shown in Fig. 3e, this cross-cohort evaluation resulted in decreased prediction accuracy due to inherent differences in dataset characteristics. However, combining data from multiple cohorts during training improved the model’s robustness and prediction accuracy, emphasizing the value of diverse training datasets.

We explored the effect of different pre-training sources by visualizing the features using UMAP plots in Fig. 3a. Features pre-trained on temporal images showed a significant improvement in aligning with the age labels compared to those pre-trained on ImageNet or solely on snapshot retinal images. pre-training the model on temporal fundus images further reduced the MAE from 2.84 to 2.79, demonstrating the effectiveness of incorporating longitudinal data. The impact of pre-training sources was visualized using UMAP plots in Fig. 3a, where features pre-trained on temporal images exhibited stronger alignment with age labels compared to features pre-trained on ImageNet or solely on snapshot retinal images. Linear probing (LP) and k-nearest neighbors (k-NN) evaluations further supported these findings, as shown in Fig. 3b. Temporal image pre-training consistently outperformed both ImageNet and snapshot retinal image pre-training in terms of MAE, across both UKB and CHN cohorts.

Model visualization and explanation

To understand which areas of the retinal image influence the model’s age prediction, we employed both attention map analysis and systematic image manipulation experiments. For attention visualization, we adopt the approach developed by Chefer et al.³⁹, which computes relevancy in Vision Transformers. This technique assigns initial relevance scores to local features using the Deep Taylor Decomposition principle and systematically distributes these scores back through the network layers. The attention maps, shown in Fig. 4, revealed that our model focuses particularly on regions surrounding major vessels and their adjacent tissue areas. Additional examples of attention map results can be found in supplementary materials.

Fig. 4: Explanation analysis of the retinal age model.

a Result of image decomposition, the model is train and evaluated with decomposed retinal images which include vessel-only images, vessel-removed images, and color-removed images. b Attention map visualization result. c Relations between the quantified microvascular features and age.

To quantitatively evaluate the importance of different retinal image components for age prediction, we conducted controlled experiments using modified retinal images. Specifically, we created three types of images: vessel-only images that retain only the vascular structures, vessel-removed images where visible vessels were eliminated while preserving other features, and color-removed images that converted images to grayscale while retaining structural information. For vessel removal, we implemented three approaches: vessel inpainting (filling vessel regions with surrounding content), vessel masking (setting vessel regions to zero), and vessel randomizing (replacing vessel structures with those from unrelated images). Results for the primary method—vessel inpainting—are shown in the main text, while additional results for vessel masking and vessel randomizing are provided in the supplementary file.

The results, summarized in Fig. 3, show that vessel removal (inpainting) had the most significant impact on model performance, increasing the MAE from 2.84 to 4.33 years. This substantial degradation highlights the critical role of vascular structures and their surrounding regions in retinal age prediction. By contrast, color removal had a relatively minor effect, with the MAE increasing to 3.04 years, indicating that structural features contribute more to age prediction than color information. When using vessel-only images, the MAE increased to 3.32 years, suggesting that while vascular patterns are essential, they alone cannot fully account for all age-related features present in retinal images.

To further explore the impact of vessel removal methods, we evaluated vessel masking and vessel randomizing (Supplementary Fig. 5). Vessel masking, where vessels were replaced with zero values, resulted in an MAE of 3.22 years. Despite the removal of vessel content, the residual vessel structures remained visible due to contrast with the surrounding tissue, partially preserving vessel-related spatial information. In contrast, vessel randomizing—where unrelated vessel patterns were introduced—led to the most severe performance drop, with MAE increasing to 5.98 years. This result indicates that biologically inconsistent vascular structures significantly disrupt the model’s ability to extract meaningful age-related features.

To validate the biological relevance of vascular parameters, we applied Automorph³⁴, a validated tool for automated retinal vascular morphology analysis. Significant correlations were observed between age and vascular metrics in healthy participants. Specifically, Fractal Dimension and Vessel Perfusion Density exhibited significant negative correlations with age (P < 0.001), with R² values of 0.310 and 0.300, respectively, as shown in Fig. 4c. These findings confirm that age-related changes in retinal vasculature are measurable and provide critical biological features for age estimation.

Associations between retinal age gap and age-related diseases

Table 3 describes the baseline characteristics of study participants for clinical value analysis. Among the 45,436 participants, 44.65% were male with mean (SD) ages of 55.67 ± 8.21 years, an interquartile range (IQR) of 49–63 years, and an age range of 40-70 years. Participants in the incidence mortality group tended to be older, more likely male, had higher levels of deprivation, and were more often current or former smokers compared to those in the non-mortality group. Additionally, they were less likely to have a college-level education, less likely to meet physical activity recommendations, and had higher BMI and comorbidity index scores.

Table 3 Characteristics of the dataset for disease association analysis

During a median follow-up of 11.4 (IQR: 11.3–11.6 years), 1143 cases of death were reported. The duration of follow-up years for thirty diseases slightly differed ranging from 11.3 years to 11.4 years due to the different eligibility of included participants for each disease. During the follow-up time, the number of newly diagnosed cases varied from 39 for multiple sclerosis (MS) to 5106 for dyspepsia. Figure 5c shows the associations between retinal age gaps and risk of mortality. The results revealed that each 1-year increase in retinal age gaps was associated with a 3% increase in the risk of mortality (hazard ratio [HR] = 1.03, 95% confidence interval [CI]: 1.01–1.05, P = 0.003) in the fully adjusted model. Furthermore, every 5-year and 10-year increase in retinal age gaps was associated with a 16% and 35% increase in the risk of mortality, respectively in the fully adjusted model (HR = 1.16, 95% CI: 1.05–1.28; HR = 1.35, 95% CI: 1.10–1.65). We also categorized retinal age gaps into four quarters and retinal age gaps in the third and fourth quartiles exhibited a 29% and 66% increased risk of mortality compared to individuals with first quartiles of retinal age gaps (HR = 1.29, 95% CI: 1.06–1.56; P = 0.012; HR = 1.66, 95% CI: 1.33–2.08; P < 0.001; respectively). Adjusted survival curves showed that higher quartiles of retinal age gaps exhibited lower survival rates compared with the lowest quartiles of retinal age gaps (Fig. 5a).

Fig. 5: Retinal age gap and its association with mortality risk and predictive performance.

a Adjusted survival curves for risk of mortality among different quarters of retinal age gaps. HR = hazard ratio; CI = confidence interval. This survival curve adjusted for age, sex, Townsend, education, body mass index(BMI), smoking status, physical activity level, and Charlson Comorbidity index (CCI) scores index. b Model performance comparison for predicting 10-year mortality risk. The horizontal bar chart displays area under the curve (AUC) values with 95% confidence intervals for different prediction models. c Association between retinal age gap with risk of all-cause mortality. Model 1 adjusted for age, gender, and Townsend. Model 2 adjusted for covariates in Model 1 + education, smoking status, physical activity, BMI, and CCI scores.

To contextualize the predictive value of retinal age gap, we compared multiple models for predicting ten-year mortality risk using held-out validation data. As shown in Fig. 5b, the baseline model using only age achieved an AUC of 0.6947 (95% CI: 0.6593–0.7279), while sex alone showed limited discriminative ability (AUC = 0.5457, 95% CI: 0.5123–0.5801). Retinal age demonstrated improved predictive performance with an AUC of 0.7298 (95% CI: 0.6977–0.7620), outperforming the model combining age and sex (AUC = 0.7041, 95% CI: 0.6711–0.7363). The highest discrimination was achieved by the combined model incorporating age, sex, and retinal age gap (AUC = 0.7380, 95% CI: 0.7066–0.7679). Sensitivity analysis showed that the associations between retinal age gap and mortality remained significant after further adjustment of age square and log(age)(Supplementary Fig. 6). In addition, the retinal age acceleration residuals were also significantly associated with incident mortality(Supplementary Fig. 7).

Among thirty age-related diseases, six out of eight cardiometabolic diseases, one out of seven neurological diseases, eight out of twelve other systemic diseases, and all three age-related eye diseases showed significant results after controlling for FDR in the fully adjusted model 2 as shown in Fig. 6 (corrected P values < 0.05). Higher retinal age gaps were associated with a higher risk of hypertension (HR = 1.01, 95% CI: 1.00–1.02), atrial fibrillation (HR = 1.02, 95% CI: 1.00–1.04), heart failure (HR = 1.03, 95% CI: 1.01–1.06), high cholesterol (HR = 1.02, 95% CI: 1.01–1.04), stroke (HR = 1.04, 95% CI: 1.01–1.06), and coronary heart diseases (HR = 1.03, 95% CI: 1.02–1.04). Additionally, every one-year increase in retinal age gaps was associated with a 6% increase in epilepsy risk (HR = 1.06, 95% CI: 1.01–1.10).

Fig. 6: Associations between retinal age gap and incidence of age-related diseases.

Forest plot showing hazard ratios (HRs) and 95% confidence intervals (CIs) per 1-year increase in retinal age gap across multiple disease categories. Analyses were conducted using two models: Model 1 adjusted for age, sex, and socioeconomic status (Townsend index), and Model 2 additionally adjusted for education, smoking status, physical activity, body mass index (BMI), and Charlson Comorbidity Index (CCI).

Other eight systemic diseases including chronic kidney diseases, bronchiectasis, COPD, psoriasis, chronic liver diseases, fracture, dyspepsia, and treated constipation showed significant positive associations with retinal age gaps. Higher retinal age gaps were also associated with higher risks of three age-related eye diseases including cataract (HR = 1.11, 95% CI: 1.09–1.12), glaucoma (HR = 1.09, 95% CI: 1.06–1.11), and AMD (HR = 1.08, 95% CI: 1.05–1.11). Further sensitivity analyses between retinal age gap and age-related outcomes showed similar results (Supplementary Fig. 8 and Supplementary Fig. 9).

To evaluate whether our improved retinal age modeling translates to enhanced clinical utility, we conducted comparative analyses against the baseline Direct Regression model, which had a higher MAE. As illustrated in Fig. 7a and b, our model consistently yielded higher odds ratios across all disease categories: +4.0% for cardiometabolic, +6.3% for neurological, +4.2% for other systemic, and +18.4% for age-related eye diseases. On average, the mean odds ratio improved from 1.10 to 1.17. To further evaluate clinical relevance, we stratified patients into quintiles based on the retinal age gap and computed risk ratios between the highest (Q5) and lowest (Q1) quintiles. As shown in Fig. 7c, d, 73.3% (22 out of 30) of the assessed diseases demonstrated improved risk stratification, with a sample-size-weighted average increase of 2.4% in quintile-based risk ratios. These findings confirm that improved model accuracy leads to measurable benefits in downstream clinical applications.

Fig. 7: Clinical relevance of improvements in retinal age modeling.

a Odds ratio comparison between baseline model (Direct regression) and our model, with lines connecting same diseases to highlight paired differences. b Mean odds ratios comparison by disease categories, with percentage improvements. c Risk stratification improvement for individual diseases, showing the percentage increase in quintile-based risk ratio (Q5/Q1) compared to baseline. d Direct comparison of risk ratios between models, with points above diagonal line indicating improvements in disease risk stratification.

Discussion

In this study, we developed a predictive model for retinal age that demonstrated improved accuracy compared to previous methods. This approach also improved the model’s generalizability across diverse populations. We achieved this by incorporating temporal information from longitudinal retinal images and progressively learning age label distributions using data from multiple healthy cohorts. The retinal age gap, defined as the difference between the retina-predicted age and chronological age, was used as a metric to assess deviations from typical aging patterns. Our analysis revealed that higher retinal age gaps were associated with an increased risk of all-cause mortality. Furthermore, retinal age gaps were linked to a range of age-related eye diseases and systemic conditions. These findings support the potential of retinal age as a robust and reliable biomarker of biological aging, with applications in risk stratification for survival and age-related diseases.

Our methodological framework addresses several fundamental limitations in existing approaches to estimating retinal age. The temporal-order pre-training strategy captures dynamic aging patterns by combining masked image modeling with temporal sequence learning, moving beyond the static patterns detected in traditional cross-sectional analyses. To handle population heterogeneity, we developed a cross-domain feature alignment mechanism that ensures consistent embedding across diverse demographic groups while preserving age-related variations. Instead of relying on traditional regression methods, our approach employs label distribution learning, shifting the focus from single-point age predictions to estimating a more nuanced estimation of age distribution, better reflecting the complexity of biological aging. These innovations culminate in an MAE of 2.79 years—a substantial improvement over previous methods that typically exceed 3.5 years^14,24,40. This accuracy gain demonstrates the value of integrating longitudinal data with advanced learning strategies.

A fundamental challenge in biological age modeling is the lack of a universal ground truth². We adopted the commonly used assumption that biological equals chronological age in healthy populations^29,41, as these individuals without chronic diseases tend to have normal aging rates. This approach provides a practical reference point by enabling standardized model training and facilitating comparison across studies in biological age estimation. By reducing modeling error and achieving a lower MAE in this healthy reference population, we enhanced our ability to detect deviations that may signal accelerated or decelerated aging. However, this approach has important limitations. Even within apparently healthy populations, individuals may harbor undiagnosed conditions that affect their biological aging rates. Natural variation in aging trajectories can arise from multiple sources, including genetic predisposition, environmental exposures, and lifestyle factors¹. Our label distribution learning framework partially addresses these limitations by modeling age as a distribution rather than a point estimate, better reflecting the inherent variability in biological aging. Future studies should explore alternative reference frameworks, such as using longitudinal health outcomes or molecular aging markers, to provide complementary insights into the aging process⁴².

While achieving lower MAE may be viewed as a modeling benchmark, our findings highlight its direct clinical relevance. First, reducing age prediction error improves the signal-to-noise ratio of the retinal age gap, making it more sensitive to deviations that signify pathological or accelerated aging. A less precise model may introduce noise that obscures these deviations, thereby diminishing the clinical informativeness of the biomarker. Second, our downstream analyses (Fig. 7) demonstrate that improved MAE is accompanied by enhanced disease association strength and risk stratification performance. For example, we observed stronger associations with cardiometabolic, neurological, and ocular diseases, and more robust stratification across risk quintiles—improving discrimination in 22 of 30 conditions with a weighted average gain of 2.4%. These findings empirically validate the clinical value of reducing prediction error in biological age estimation, potentially supporting more effective risk stratification and preventive care.

The clinical significance of our findings extends beyond the improved accuracy in age estimation. The retinal age gap independently predicts all-cause mortality risk after adjusting for traditional risk factors, suggesting it captures unique aspects of biological aging and provides valuable insights into overall health status. Unlike prior studies that focused on single conditions^14,28, our comprehensive analysis demonstrates that retinal age gaps were associated with a broad spectrum of age-related diseases, spanning both ocular and systemic pathologies, even after adjusting for chronological age and other risk factors. For ocular conditions, retinal age gaps were strongly associated with three major age-related eye diseases: cataracts, glaucoma, and AMD. This aligns with established evidence of age-related changes in retinal structure—including lens hardening, decreased optic nerve axons, reduced ganglion cells, and basement membrane thickening—which are hallmark features of these conditions⁴³. Beyond ocular pathology, the retina effectively mirrors systemic aging processes. Neuronal cell loss and degeneration, particularly thinning of the retinal nerve fiber layer, are strongly correlated with neurodegenerative diseases²². Similarly, retinal vascular alterations—including venular dilation, arteriolar narrowing, and reduced vessel density and capillary complexity—reflect systemic vascular aging²¹. These associations establish the retina as a unique window into both local and systemic aging processes.

Although we initially hypothesized a significant role for neurovascular features, the attention maps suggest a nuanced emphasis on perivascular regions. Evidence from OCT-A imaging supports the biological relevance of these areas, highlighting the presence of microvascular structures critical for aging assessment⁴⁴. To investigate further, we quantified microvascular features, including fractal dimension and vessel density, from segmented vascular images. These features showed a negative association with age, aligning with established findings that microvascular decline is a hallmark of aging. While standard fundus photography inherently limits the resolution of fine vascular details due to its imaging constraints and necessary downsampling for computational efficiency, recent studies^34,45 demonstrate that deep learning models can effectively extract meaningful vascular features from fundus images, even at reduced resolutions. To ensure reliability, we implemented standardized quality control³⁴ to preserve visible vessel structure integrity and mitigate artifact-related effects. The model’s performance and interpretation analysis suggest it captures aging-relevant microvascular features by detecting complex patterns in perivascular regions, which correlate with aging processes, rather than directly resolving smaller vessels.

Our findings have several clinical implications. At the individual level, retinal age could be applied in community-based screenings to identify individuals at risk of accelerated aging. Individuals who are exhibiting larger age gaps should be considered to have higher risks of aging and would be more likely to develop mortality and a wide range of age-related diseases. It will provide a reliable screening approach for accelerated aging and facilitate risk stratification of aged individuals in primary care settings and communities, which enables prioritizing targeted populations for anti-aging interventions. Additionally, it can boost the management of age-related chronic conditions by improving patient compliance in real-world scenarios. Considering most people are highly concerned about aging, this biological age indicator could provide a potential communication tool for achieving better health and following physicians’ pharmacy intervention⁴⁶. Moreover, the retinal age gap representing the overall aging and mortality and morbidity risks may provide a single cross-sectional end-point outcome for anti-aging risk factor exploration in clinical trials.

There are certain limitations in this study. A primary constraint is the inherent resolution limitations of fundus photography, which hinder the precise visualization and analysis of fine microvascular structures that may be critical to understanding aging processes. Although our model achieves competitive accuracy relative to other aging biomarkers^6,47,48, there remains scope for reducing prediction errors, particularly in younger and older age groups. Furthermore, while we employed diverse datasets for model development, our analysis of disease associations relies predominantly on UK Biobank data, which may limit the generalizability of findings to broader populations. The reliance on inpatient and mortality records for identifying incident cases likely underestimates true disease incidence, potentially biasing associations toward the null. Lastly, the observational nature of our study design precludes establishing causality between retinal age gaps and health outcomes, underscoring the need for further longitudinal and interventional studies to validate these relationships.

These findings lay the groundwork for several promising future research directions. While fundus imaging offers practical advantages in terms of accessibility and ease of use, investigation of higher-resolution imaging modalities, particularly OCT-A, could provide deeper insights into the vascular features driving age prediction. Technical advances in portable fundus imaging technology may enhance feasibility for home-based monitoring. Prospective studies are needed to identify modifiable factors influencing retinal age and to validate the clinical utility of retinal age assessment in risk stratification and intervention monitoring. Despite current limitations, the combination of improved prediction accuracy, robust disease associations, and practical implementation potential positions retinal age with fungus photography as a valuable biomarker for both clinical practice and aging research.

Methods

Ethical approval and data acquisition

The UK Biobank is a publicly available prospective cohort with over 50,000 UK residents recruited in 2006 (https://biobank.ndph.ox.ac.uk/showcase/browse.cgi) 45° fundus images were introduced in 2009 for the study subjects. Chinese cohort A was the normal participants from the Guangzhou Diabetic Eye Study (GDES) cohort, and Chinese cohort B was historical data recruiting healthy participants from Guangdong Provincial People’s Hospital⁴⁹. Another database is an ongoing prospective cohort study that enrolled healthy participants. Participants were invited to take part in annual follow-up assessments including fundus images. The study was in accordance with the Helsinki Declaration with informed consent from all participants. Ethics approval for this study was obtained from North West Multi-centre Research Ethics Committee (References: 11/NW/0382) and St Vincent’s Hospital Melbourne (References: 2023/SVH00014).

Dataset

To develop the retinal age prediction model and validate its clinical applications, we utilized retinal fundus photographs from three CHN cohorts and two UKB cohorts, encompassing both healthy and general populations (Fig. 8). The age prediction model was developed on a combined dataset after quality control included 133,894 images from 32,282 healthy individuals, with approximately two-thirds from the CHN cohort and one-third from the UKB cohort. The dataset comprised both disc-centered (N = 15,935) and macula-centered (N = 117,959) images, with UK Biobank images consistently captured as macula-centered (field one) with a 45° field of view (see Supplementary Fig. 2).

Fig. 8: The retinal data used for the model development.

Data from three Chinese cohorts and one UK Biobank cohort, all representing healthy individuals, were employed to train the model for estimating retinal age. The general population data from the additional segment of the UK Biobank cohort, encompassing a mix of healthy and unhealthy individuals, were utilized for the clinical disease association analysis.

To ensure statistical independence, we implemented a subject-level split for model development: 23,910 individuals (96,691 images) for training, 2391 individuals (10,732 images) for validation, and 5981 individuals (26,472 images) for testing. Additionally, longitudinal data from a subset of individuals was specifically utilized for temporal-order self-supervised learning pre-training, including 1735 individuals (13,880 images) for training and 416 individuals (3,328 images) for testing. Images from both eyes were included when available to maximize data utilization while maintaining subject-level data splits. For subsequent age-related disease analysis in the general population, we incorporated an additional UK Biobank cohort (UKB cohort B) comprising 45,436 participants.

Image quality control

A standardized quality control process was implemented for all retinal images to ensure anatomical integrity and diagnosability. This process utilized an image quality grading model based on EfficientNet-B4⁵⁰, trained on the EyePACS-Q dataset³³, as described in the previous study³⁴. Images were categorized into three quality levels—good, usable, and reject—based on illumination, artifacts, and diagnosability of general eye diseases, as assessed by two expert graders. Following the same settings from literature³⁴, ungradable images were treated as the positive class in quality grading, with the probability of the ungradable category equivalent to that of the reject quality. Conversely, the gradable category probability was defined as the sum of the good and usable quality probabilities. Using thresholds of a mean value of 0.75 and a standard deviation of 0.1, we finalized the classification of images into rectified gradable and ungradable categories. Approximately 25.6% of the images across the combined dataset were classified as poor quality and excluded from further analysis. This proportion varied between cohorts, with 8.3% of the UKB cohort images and 28.4% of the CHN cohort images being ungradable (Supplementary Fig. 3). The final dataset used for model development consisted of 133,895 gradable images (84.4% of the original dataset).

Unlike previous studies that exclusively relied on good-quality images, we also included usable images to enhance generalizability and align with real-world clinical scenarios. While excluding usable images could mitigate challenges posed by suboptimal conditions, such as dim illumination or mild artifacts, it would also reduce the size and diversity of the dataset, potentially limiting the model’s applicability. By incorporating usable images, we aimed to create a dataset reflective of clinical reality, where a significant proportion of images fall into the usable category but may not meet stringent criteria for good quality. This approach ensures that the model is robust and applicable in clinical environments, where obtaining perfectly good-quality images is not always feasible.

DL framework for retinal age estimation

Considering the complicated aging process as well as the ambiguity issue in the age label space, a natural way is to give an age estimate with a particular confidence interval, such as a Gaussian distribution with a particular mean age and a standard deviation^35,51. Therefore, we formulate the retinal age estimation as a two-stage label distribution learning problem. As shown in Fig. 1, in the first stage, the model uses global features from the image encoder ${E}_{s}\left(\cdot \right)$ to predict a coarse age distribution on roughly discretized age labels. Each coarse age prediction is associated with a query vector corresponding to an age group. Then, the model performs class attention⁵² between the age group query and local spatial features to generate fine-level features which are further combined with the coarse age prediction to give refined age predictions. Notably, when using CNNs as the image encoder, the global features and the local spatial features are the outputs from the last global average pooling layer and the last convolutional layer. While for Vits, they are class tokens and patch tokens, respectively. For ViTs, we treat the age group query as a prompt token and perform class attention with both the age group query and local patch features.

Formally, given a dataset with N images ${\mathcal{X}}={\{{x}_{i}\}}_{i = 1}^{N}$, the corresponding age labels ${\mathcal{Y}}={\{{y}_{i}\}}_{i = 1}^{N}$ range in [a, b]. The image encoder first transforms an input image x_i into a spatial feature ${{\bf{F}}}_{i}\in {{\mathbb{R}}}^{H\times W\times D}$, and a global feature ${f}_{i}\in {{\mathbb{R}}}^{1\times D}$. We discretize the age classes as ${\hat{y}}_{i}=\,\text{R}\,\left({y}_{i}/{\delta }_{d}\right)* {\delta }_{d}$, where $\,\text{R}\,\left(\cdot \right)$ denotes the round operator and δ_d is the age interval for tuning the discretization degree. Therefore, the total discretized age class number is ${C}_{{\delta }_{d}}=\,\text{R}\,\left(\frac{\left\vert b-a\right\vert }{{\delta }_{d}}\right)$. For the coarse-level age estimation, we set a large δ_d which determines the age group queries as ${{\bf{Q}}}_{coarse}\in {{\mathbb{R}}}^{{C}_{{\delta }_{d}}\times D}$. Then, we use an FC layer with softmax applied on the f_i to calculate the coarse age distribution ${p}_{i}\in {{\mathbb{R}}}^{1\times {C}_{{\delta }_{d}}}$.

Different from the previous study²⁴ using fixed label distribution as ground truth, we directly learn the distribution from training data with discretized age labels:

$${{\mathcal{L}}}_{lds}=\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}-log\left({p}_{i,{\hat{y}}_{i}}\right)+\frac{\alpha }{2N}\mathop{\sum }\limits_{i=1}^{N}{\left({y}_{i}-{m}_{i}\right)}^{2}+\frac{\beta }{N}\mathop{\sum }\limits_{i=1}^{N}\mathop{\sum }\limits_{c=1}^{{C}_{{\delta }_{d}}}{p}_{i,c}* {\left({y}_{i}-{m}_{i}\right)}^{2}$$

(1)

where m_i is the expected value of the predicted age distribution p_i, The first term is the cross-entropy loss which helps the model converge in an early training stage, the last two terms encourage the learned distribution to be centered and concentrated at the true age labels.

In the refining stage, the mean value of coarse age distribution m_i is used to select the age group query from Q_coarse to involve the computation of fine-level feature:

$${f}^{{\prime} }=\,{\text{A}}\,\left({Q}_{coarse}\left[R\left(\frac{{m}_{i}}{{\delta }_{d}}\right)\right],{{\bf{F}}}_{i};{\theta }_{a}\right)$$

(2)

where $\,\text{A}\,\left(\cdot \right)$ denote the attention block with θ_a as the parameters. The key and value vectors in the attention function come from F_i. Finally, we concatenate the ${f}^{{\prime} }$ with the mapped coarse age distribution as the final feature embedding to predict the fine-level age distribution with a small δ_d of 1:

$$z=\,{\text{concat}}\,\left({f}^{{\prime} },\,{\text{f}}\,\left({p}_{i}\odot {\hat{y}}_{1,\ldots ,{C}_{{\delta }_{d}}};{\theta }_{f}\right)\right)$$

(3)

$${p}_{i}^{{\prime} }=\,{\text{softmax}}\,\left(\,{\text{mlp}}\,\left(z;{\theta }_{m}\right)\right)$$

(4)

where $\,\text{f}\,\left(\cdot \right)$ denotes an FC layer with parameters θ_f, $\,\text{mlp}\,\left(\cdot \right)$ represents a multilayer perceptron with one hidden layer and the parameter is θ_m. The training loss is the same with Eq. (1).

Although existing studies^38,51 show that formulating regression as a classification task to learn the label distribution yields better performance, the ordinal information of age relations is lost in feature space. This issue becomes more problematic when training data originates from disparate data sources, as the domain variance further disrupts the coherence of the learned features. In Fig. 1 (b), we visualize the intermediate feature learned on our fundus image dataset by data source and age label, respectively. As can be seen, the original model produces scattered and inconsistent features for ordinal age labels, while the features exhibit a clear gap for different data sources.

To address the above issues, we propose to introduce ordinal constraints in the label distribution learning and perform feature alignment to eliminate the domain variance. The key idea of imposing ordinal constraints in embedding space is to construct a set of triplets and enforce the feature distance to be consistent with the relative age gap. Specifically, for each batch of input data {x₁, …, x_B}, we first compute their pairwise feature distance which outputs a distance matrix $D\in {{\mathbb{R}}}^{B\times B}$. Then, we construct feature triplets and calculate the distance gap by subtracting the shifted distance matrix ${D}^{{\prime} }$ from the original D. In this case, each sample will have a chance to serve as the anchor to be compared with other samples. We formulate the ordinal constraint as following margin loss:

$${{\mathcal{L}}}_{ord}=\mathop{\sum }\limits_{i=1}^{B}\mathop{\sum }\limits_{j=1}^{B}\max \left(0,D\left[i,j\right]-{D}^{{\prime} }\left[i,j\right]+m\right),\,{\text{s.t.}}\,\,i\ne j,\,{\text{and}}\,\,{\hat{y}}_{j}\ne {\hat{y}}_{{j}^{{\prime} }}$$

(5)

where $D\left[\cdot \right]$ denotes metric of Euclidean distance, m is a dynamic margin depends on the relative age gap between $\left\vert {\hat{y}}_{i}-{\hat{y}}_{j}\right\vert$ and $\left\vert {\hat{y}}_{i}-{\hat{y}}_{{j}^{{\prime} }}\right\vert$. To align image features from different data sources, we directly select samples from the same class and push them closer in the embedding space by minimizing the intra-class distance on both coarse-level features and fine-level features:

$${{\mathcal{L}}}_{align}=\mathop{\sum }\limits_{c=1}^{{C}_{{\delta }_{10}}}{{\mathbb{I}}}_{c}\left(i,j\right)d\left({f}_{i},{f}_{j}\right)+\mathop{\sum }\limits_{c=1}^{{C}_{{\delta }_{1}}}{{\mathbb{I}}}_{c}\left(i,j\right)d\left({f}_{i}^{{\prime} },{f}_{j}^{{\prime} }\right)$$

(6)

where the ${{\mathbb{I}}}_{c}\left(i,j\right)$ is an indicator function.

Compared to single snapshot images, longitudinal fundus image sequences, which inherently capture changes in the fundus structure over time, provide a more comprehensive depiction of aging processes. Modeling this temporal evolution can potentially improve retinal age prediction. However, temporal fundus images can be limited in practice because the individuals are often lost to follow-up. Learning a temporal model on such a small dataset usually degrades the model’s performance. To address this, we propose a joint pre-training strategy using both limited temporal sequences and abundant snapshot fundus images. We aim to leverage the chronological information from temporal sequences to augment our model’s feature representation.

As illustrated in Fig. 1, the proposed pre-training mechanism unfolds in two phases. Initially, an image encoder is trained with masked image modeling on snapshot images, focusing on spatial detail extraction. Subsequently, we introduce a ranking head atop the encoder, trained to discern the chronological order of temporal image pairs. Notably, during this second pre-training phase, we freeze the encoder’s lower layers to maintain their focus on spatial details, while the upper layers are trained for higher-order semantic understanding and pattern recognition.

Model training

In the absence of a universally accepted standard for biological age determination², chronological age was adopted as the reference standard in healthy populations. The training dataset consisted of 133,895 retinal images from healthy subjects without documented systemic diseases across four cohorts, including 2937 longitudinal sequences with an average of five images per sequence. The training process includes two-stages, incorporating pre-training and fine-tuning phases to optimize performance.

The pre-training stage focused on learning general retinal features through sequential steps. First, masked image modeling was employed to learn spatial features from snapshot images by randomly masking patches. This process utilized a Vision Transformer Base (ViT-B) architecture with a patch size of 16 × 16, following the settings of ref. ⁵³, and was trained for 100 epochs. Subsequently, temporal order learning was applied to sequential images to capture age-related progression patterns. During this step, the first half of the image encoder was frozen, while the remaining part, along with newly added fully connected layers, was trained for 30 epochs to optimize temporal order capturing.

In the fine-tuning stage, the pre-trained model was refined for retinal age prediction by adding a regression head to the pre-trained image encoder and training the entire network. Input images were resized to 384 × 384 pixels, and data augmentation techniques, including random resized cropping, color transformation, and image flipping, were applied to enhance generalizability. We utilized the ADAM optimizer with a batch size of 80 and a maximum of 50 epochs, with early stopping criteria to prevent overfitting. The initial learning rate was set to 3 × 10⁻⁴, with a layer-wise learning rate decay factor of 0.65 and cosine learning rate scheduling to ensure stable convergence. These training parameters were consistently applied to all comparison models and the temporal order learning step.

Evaluation metrics

The performance of the DL prediction model was assessed by its accuracy and the validity in prediction of age-related health outcomes. MAE and Pearson correlation between predicted retinal age and chronological age were used to assess the accuracy. A smaller MAE indicates a higher accuracy of the aging biomarker. Root Mean Square Error (RMSE) was also included to evaluate the accuracy. Retinal age gap defined as the deviation from the normal aging process was calculated as retina-predicted age minus chronological age. The Hazard Ratio (HR) and its corresponding 95% Confidence Interval (CI) were assessed in a Cox regression analysis to assess the associations of retinal age gaps with mortality and multiple morbidities.

Clinical value verification of disease association and mortality prediction

We evaluated the clinical relevance of the retinal age model by analyzing the association between the retinal age gap and both all-cause mortality and a wide spectrum of age-related diseases. The retinal age gap was defined as the difference between model-predicted retinal age and chronological age, with positive values reflecting accelerated biological aging. Mortality outcomes were ascertained through linkage with national death registries.

Disease status was determined using both prevalent and incident diagnoses. Baseline conditions were identified through inpatient hospital records, and participant-reported diagnoses confirmed by healthcare providers. Incident cases were captured via longitudinal hospital admission records and death registries. Each participant was followed from baseline until the earliest of disease onset, death, or censoring due to loss to follow-up. The analysis included 30 conditions spanning four major disease categories. Cardiometabolic diseases encompassed hypertension, atrial fibrillation, heart failure, peripheral vascular disease, hypercholesterolemia, stroke, diabetes, and coronary heart disease. Neurological disorders included anxiety, depression, epilepsy, multiple sclerosis, Parkinson’s disease, schizophrenia, and dementia. Additional systemic conditions—such as chronic kidney disease, chronic obstructive pulmonary disease, and various gastrointestinal disorders—were also evaluated, alongside age-related ocular diseases including cataract, glaucoma, and age-related macular degeneration. Full diagnostic classifications and coding criteria are provided in Supplementary Table 1 and Supplementary Table 2.

We assessed the predictive performance of the retinal age model for 10-year all-cause mortality using data from the UK Biobank. The dataset was randomly split into a training set (70%) and a held-out test set (30%) using stratified sampling to preserve the mortality class distribution. Logistic regression models were developed using individual risk factors (chronological age, sex, retinal age) and their combinations. In particular, retinal age was defined as the sum of chronological age and the model-predicted age gap. Continuous predictors were standardized prior to model fitting, and sex was encoded as a binary variable. To account for class imbalance, we applied inverse frequency-based class weighting during training. Model discrimination was evaluated on the test set using the area under the receiver operating characteristic curve (AUC). For each model, 95% confidence intervals for AUC were estimated via bootstrapping with 1000 iterations to enable robust comparison across predictor sets.

Clinical verification of improved retinal age estimation

To evaluate whether the improved accuracy of our retinal age model (MAE = 2.79 years) enhances clinical utility, we conducted comparative analyses against a baseline model (MAE = 3.35 years) using downstream disease prediction and risk stratification metrics. We assessed associations between retinal age gap and 10-year incidence of 30 age-related diseases using logistic regression. For each disease, we restricted analyses to eligible participants and standardized the age gap. Models were adjusted for chronological age, and odds ratios (ORs) with 95% confidence intervals were estimated for both the improved and baseline models. Percent improvements in OR strength (log OR) were calculated to quantify gains in predictive association across disease categories. To assess risk stratification capability, we divided participants into quintiles based on predicted age gaps. For each disease, we computed incidence within each quintile and derived risk ratios between the top (Q5) and bottom (Q1) quintiles. Similar analyses were performed using extreme groups (top and bottom 10%). Comparisons were made between the improved and baseline models across all diseases with sufficient case counts (≥20). We further examined statistical significance by calculating the proportion of diseases with p < 0.05 for both models. Relative improvements in odds ratios (ORs) and risk ratios were summarized across disease categories, with sample-size weighting used to compute overall improvements in stratification.

Statistical analysis

In Cox regression models, we adjusted for covariates, with Model 1 being adjusted for baseline age, gender, and Townsend, and Model 2 being additionally adjusted for education status, lifestyle factors including smoking status, physical activity, body mass index (BMI), and Charlson Comorbidity index (CCI) score. Physical activity was assessed using self-reported questionnaires from the validated short International Physical Activity Questionnaire (IPAQ). Physical activity was defined as meeting recommendations or not according to the criteria, whether a person met the UK Physical Activity Guidelines of 150 minutes of walking or moderate activity per week, or 75 min of vigorous activity⁵⁴. The CCI score, a well-established tool, was incorporated into the model to account for major comorbidities⁵⁵. The CCI is calculated by summing weighted scores assigned to specific comorbid conditions of their relative risk of mortality. An overview of the CCI calculation and the corresponding field IDs is provided in supplementary materials. All variables were assessed for the proportional hazards assumption before they were fitted into Cox proportional hazards regression models. To ensure the robustness of our findings across these multiple comparisons, we applied the Benjamini-Hochberg procedure to control the false discovery rate (FDR) at a 5% level, minimizing the risk of false positives and enhancing the reliability of our results⁵⁶. Sensitivity analyses were conducted to validate the results. Firstly, additional analysis was performed by adjusting for age square and log(age) in addition to the covariates included in Model 1(Model 3) and the covariates included in Model 2 (Model 4). We also investigated whether retinal age acceleration residuals (calculated as the residual resulting from regressing retinal age on chronological age) were associated with mortality and other age-related outcomes. A two-sided p-value of <0.05 was considered statistically significant. Analyses were performed using R (version 3.3.0, R Foundation for Statistical Computing, www.R-project.org, Vienna, Austria) and Stata (version 13, StatCorp, Texas, USA).