Predicting antidepressant response via local-global graph neural network and neuroimaging biomarkers

Abstract

Depressed mood and anhedonia, the core symptoms of major depressive disorder (MDD), are linked to dysfunction in the brain’s reward and emotion regulation circuits. To develop a predictive model for treatment remission in MDD based on pre-treatment neurocircuitry and clinical features. A total of 279 untreated MDD patients were analyzed, treated with selective serotonin reuptake inhibitors for 8–12 weeks, and assigned to training, internal validation, and external validation datasets. A hierarchical local-global imaging and clinical feature fusion graph neural network model was constructed. The model achieved 76.21% accuracy (AUC = 0.78) in predicting remission. Validation on the internal and external independent datasets yielded similar performance (accuracy = 72.73%, AUC = 0.74; accuracy = 71.43%, AUC = 0.72). Key contributing brain regions included the right globus pallidus, bilateral putamen, left hippocampus, bilateral thalamus, and bilateral anterior cingulate gyrus. These findings highlight the role of specific circuits in guiding antidepressant treatment.

Introduction

Major depressive disorder (MDD) is a significant global mental health issue, characterized by a high incidence and disability rate, imposing a substantial burden on patients and society. Antidepressants, particularly selective serotonin reuptake inhibitors (SSRIs), are widely used as the first-line treatment for depression due to their efficacy in improving depressive symptoms. However, MDD presents with high clinical heterogeneity, leading to individual variability in treatment response. In current clinical practice, antidepressant prescribing often relies on empirical, trial-and-error strategies, resulting in significant variability among clinicians^1,2. Studies have reported remission rates for first-time antidepressant treatments ranging from 36% to 48%^3,4. Insufficient remission rates can prolong illness and lead to chronic or treatment-resistant depression⁵. Therefore, identifying objective and effective methods to predict antidepressant response is crucial for achieving personalized and precise therapy.

Previous studies primarily focused on clinical or neuroimaging features independently for remission prediction. Clinical and demographic information, such as age, sex, education, and illness duration, offers insight into patients’ subjective experiences and disease backgrounds⁶. In contrast, neuroimaging features serve as objective biomarkers, reflecting changes in brain structure and function. Integrating these two modalities is essential for constructing predictive models of antidepressant efficacy.

Depressed mood and anhedonia, core symptoms of MDD, are often associated with poor treatment outcomes. SSRIs alleviate depressive mood by inhibiting 5-hydroxytryptamine (5-HT) reuptake, with low mood identified as a potential predictor of SSRIs’ efficacy⁷. Anhedonia has also been closely linked to treatment outcomes, with studies highlighting its role as a predictor of remission time in SSRIs-resistant MDD adolescents⁸. Systematic reviews have shown that monoaminergic agents, glutamatergic drugs, psychedelics, and stimulants are associated with varying degrees of improvement in anhedonia among adults with MDD⁹. Consequently, brain circuits related to depressed mood and anhedonia hold significant potential as predictors of antidepressant efficacy. This study focuses on neuroimaging circuits associated with these symptoms for feature selection.

Recent advancements in functional magnetic resonance imaging (fMRI) have enabled the study of MDD pathophysiology and the identification of biomarkers for predicting antidepressant efficacy. Studies suggest that dysfunction in the reward and emotion regulation circuits is closely associated with anhedonia and depressed mood, key mechanisms underlying depression^10,11,12. The 5-HT-mediated emotion regulation circuit includes the prefrontal cortex, hippocampus, amygdala, orbitofrontal cortex (OFC), and anterior cingulate cortex (ACC)¹². Changes in the structure and function of these regions in MDD patients are linked to symptom trajectories and serve as significant predictors of antidepressant efficacy^13,14. Similarly, the reward circuit, which includes the ventral striatum, ventral pallidum, dorsolateral prefrontal cortex (DLPFC), OFC, ACC, and thalamus, has been implicated in anhedonia^15,16. A review indicated that the reward circuit comprises several key brain areas such as the ventral striatum, ventral pallidum, DLPFC, OFC, ACC, and thalamus¹⁷. Research indicates that 5-HT levels in the insula and ventral striatum are associated with anhedonia and that SSRIs may alleviate this symptom by modulating these levels¹⁸. Structural and functional changes in these circuits following SSRIs treatment are closely associated with symptom trajectories and antidepressant efficacy^{19,20,21,22,23}.

Baseline clinical characteristics and demographic information have been associated with antidepressant outcomes²⁴. Hamilton Depression Rating Scale (HAMD) score have been proposed as predictors of early remission²⁵. Moreover, psychosocial functioning, a stable predictor of long-term prognosis, has been suggested as an indicator of long-term treatment efficacy^26,27,28. This study aims to integrate age, sex, education level, illness duration, HAMD score, Quality of Life Enjoyment and Satisfaction (QLES) Questionnaire score, and neuroimaging features to develop a predictive model for antidepressant treatment outcomes.

Machine learning (ML) based on fMRI has been increasingly applied to predict treatment responses in MDD. Previous studies primarily utilized traditional ML models such as support vector machines, random forests, or logistic regression for predicting antidepressant efficacy^29,30,31. However, these models often fail to fully explore the complex topological structures of data and the intricate dependencies between features^32,33, potentially limiting insights into the mechanisms underlying brain changes induced by antidepressant treatment. Advanced ML methods are therefore essential for improving the prediction of antidepressant efficacy.

Traditional network analysis methods, including metric indices, path analysis, and network models, have been used to evaluate macroscopic characteristics and structural properties of networks. Nonetheless, these methods struggle to capture complex network topologies and higher-order dependencies. Graph neural networks (GNNs), by contrast, update node representations by aggregating information from neighboring nodes without relying on a fixed number or order of neighbors, effectively capturing complex topological structures within graphs. Unlike traditional network analysis, which is limited to direct interactions, GNNs accommodate versatile topological structures, with nodes and edges corresponding to the brain’s regions of interest (ROIs) and their structural and functional connections. This approach has been shown to enhance prediction performance.

Recent advances in the application of GNNs to neuro-images such as fMRI have laid the groundwork for learning informative brain representations and supporting downstream tasks such as brain age prediction, sex classification, and disease diagnosis. Notably, BrainGNN³⁴ introduced ROI-aware graph convolutional layers and ROI-selection pooling, enabling adaptive learning of region-specific features and interpretable biomarker identification. Extending this progress, LGGNet³⁵ successfully adopted a local-global paradigm for brain-computer interfaces using electroencephalogram (EEG) data, learning both intra- and inter-functional brain activities. Similarly, PLI-GCNN³⁶ leveraged hybrid feature representations by combining electrode-level characteristics and global topological patterns to automate the detection of alcoholism. Building on this foundation, BNT³⁷ proposed an orthonormal clustering readout for self-supervised soft clustering, further enhancing the discriminability of node embeddings across functional brain modules. BrainRGIN³⁸ integrated clustering-based embeddings and graph isomorphism networks to better capture modular brain sub-network organization and enhance graph-level representations via attention-based readout functions. CI-GNN³⁹ proposed a Granger causality-inspired GNN to identify the most influential subgraph that is causally related to the decision.

Despite these advances, many of these models primarily focused on static, subject-specific graphs, consequently limiting their generalizability across clinically heterogeneous populations. Moreover, they often overlooked the integration of population-level information, which is crucial for understanding the diversity of brain function and pathology across individuals. In response, recent studies have explored hierarchical GNN architectures to simultaneously model intra-subject brain features and inter-subject similarities. For instance, SFC-GNN⁴⁰ combined regional graph perception with a structure feature pooling strategy, constructing population-level graphs via similarity kernels and enabling node classification through community-aware embeddings. However, these models did not support end-to-end joint optimization of local and global graphs, which can hinder the alignment between individual- and population-level learning objectives. LG-GNN⁴¹ further introduced a two-level framework in which a self-attention-based local ROI-GNN captures regional biomarkers, while a global subject-level GNN integrates both imaging and non-imaging data to enhance classification performance. This model achieved end-to-end optimization of the local-global network structure, highlighting the importance of integrating non-imaging data and subject relationships. However, it still lacked the capability to dynamically update graph structures based on task-specific signals derived from time-resolved neural features.

Alongside these developments, there has been growing attention to the temporal dimension of fMRI data, particularly the dynamic fluctuations in BOLD signals. Models such as BrainGNN and BrainRGIN treated fMRI as static snapshots, ignoring the temporal progression of neural activity. Addressing this limitation, Graph Clustered Transformer⁴² conducted a comparative analysis of resting-state functional magnetic resonance imaging (rs-fMRI) time points and resting-state functional connectivity (rs-FC) for Alzheimer’s prediction, utilizing temporal convolutional networks (TCNs) for temporal feature embedding. Deep-Spatiotemporal⁴³ integrated GNNs and temporal networks, including TCNs and LSTM, to model spatiotemporal dynamics in rs-fMRI data, and confirmed findings that RNNs and CNNs can provide similar performance. DSAM⁴⁴ further proposed a dynamic spatiotemporal attention framework that employed TCNs to extract multi-scale temporal features and leveraged self-attention to learn task-specific FC directly from the time series. These works validate the feasibility of integrating temporal features into GNN architectures and further support the construction of task-specific brain connectivity matrices.

In addition to these modeling challenges, the integration of multimodal data remains underdeveloped in the context of neuroimaging-based prediction. While Deep-Spatiotemporal⁴³ proposed an architecture combining TCNs and GNNs for spatiotemporal learning and claimed support for multimodal integration, its fusion strategy was confined to combining fMRI and structural connectivity from diffusion-weighted imaging (DWI). MS²-GNN⁴⁵ proposed a GNN-based multimodal fusion strategy, which successfully investigated the heterogeneity/homogeneity among audio and EEG modalities for the subsequent MDD detection task. Following this trend, LGMF-GNN⁴⁶ proposed the local-global multimodal fusion GNN, which jointly modeled local ROI connectivity and global population-level patterns, integrating functional and structural MRI with clinical data to enhance MDD diagnostic accuracy. These advances collectively underscore the critical importance of multimodal fusion in enhancing the predictive power and clinical applicability of GNNs.

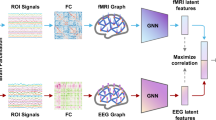
In this context, as illustrated in Fig.1, we propose a hierarchical local-global imaging and clinical feature fusion GNN (LGCIF-GNN) to predict antidepressant efficacy in the acute phase of SSRIs treatment. First, the model performs dynamic graph structure optimization by adaptively updating adjacency matrices based on pairwise similarities of ROI-level temporal embeddings extracted via a bidirectional GRU (bi-GRU) encoder. This learnable, task-driven graph construction captures richer temporal dependencies than static correlation methods and aligns graph topology with treatment prediction.

Fig. 1: Schematic overview of the LGCIF-GNN framework.

a Local graph construction and encoding. At the local level, subject-specific functional graphs are constructed from ROI-wise BOLD time series and processed via a GRU encoder and GCN-based readout to extract individual brain embeddings. In parallel, clinical variables are embedded into feature vectors. b Global graph modeling and multimodal fusion. The local embeddings are used to construct population-level functional and clinical graphs, where nodes represent subjects and edges encode modality-specific similarity between subjects. Global graph modules extract shared and unique representations across modalities, which are fused via attention and passed to an MLP for individualized prediction. c Model interpretability and marker mining. The model supports interpretation by identifying discriminative functional connections, relevant clinical features, and modality contributions to treatment outcome prediction.

Second, we introduce a local-global architecture that jointly models intra-subject ROI-level dynamics and inter-subject population-level similarities. The local network focuses on modeling fine-grained, ROI-level functional dynamics within each subject’s brain activity, encoding rich temporal dependencies that reflect neural processes underlying MDD. In parallel, the global network operates over population graphs based on functional and clinical similarity among subjects, capturing inter-individual relationships and common patterns. By integrating these two levels, the end-to-end network effectively fuses personalized features with population-wide trends. This design provides complementary, multi-angle supervision signals that enhance the model’s ability to identify both individual-specific and group-consistent features predictive of SSRIs treatment response.

Third, to bridge the longstanding gap in multimodal fusion, we integrated neuroimaging and clinical data within a unified graph-based architecture. Specifically, we constructed phenotype-informed population graphs using a clinical trait similarity encoder (CTSE) and employed specialized modules—modality-unique graph convolutional networks (MU-GCNs), modality-shared GCNs (MS-GCNs), and a modality-attention fusion block—to extract and integrate complementary information from each modality. These design choices facilitate not only improved performance in predicting SSRIs treatment response in MDD but also provide clinically interpretable insights, representing a step toward precision psychiatry.

Focused on reward and emotion regulation circuits—including the nucleus accumbens, striatum, thalamus, amygdala, hippocampus, DLPFC, OFC, and ACC—this study employed ablation analysis to evaluate the impact of radiographic features on model performance. An independent external validation set was used to confirm the model’s predictive accuracy and generalizability. It was hypothesized that clinical and neuroimaging features from the reward and emotion regulation circuits would effectively predict remission in MDD patients after 8–12 weeks of antidepressant treatment.

Results

Demographic and clinical characteristics

In the training set, 19 patients were removed due to incomplete scale data or duration information. For the internal validation dataset, 2 patients were excluded due to head movement. For the external validation dataset, 1 patient was excluded due to head movement, and an additional 2 patients were removed due to incomplete scale data. Ultimately, 279 patients were included in the final analysis.

The demographic and clinical characteristics of the training set are summarized in Table 1. The remission rate for MDD patients after 8 or 12 weeks of SSRIs treatment was 45.12% (74 out of 164 patients achieved remission). No significant differences were found between groups regarding sex, age, education level, or episode frequency (all p ≥ 0.05). Compared to the remission group, the non-remission group exhibited higher HAMD-17 scores and longer illness duration (p < 0.001 and p = 0.012, respectively), and lower QLES scores (p = 0.005). Details of demographic and medication information for the 66 MDD patients in the internal validation dataset and the 49 MDD patients in the external validation dataset are provided in the Supplementary Materials (Supplementary Tables 1 and 2).

Table 1 Demographic and clinical information of train data

Prediction model and performance validation

The area under the curve (AUC) of the prediction model was 0.78, with a sensitivity of 75.20%, a specificity of 77.48%, and an accuracy of 76.21% (Fig. 2a). Validation on the internal independent validation set yielded comparable results, with an accuracy of 72.73%, sensitivity of 73.53%, specificity of 71.88%, and AUC of 0.74 (Fig. 2b).

Fig. 2: Performance evaluation and generalizability of the LGCIF-GNN.

a The ROC of the 5-fold cross-validation. The AUC is 0.78, accuracy is 76.21%, sensitivity is 75.20%, and specificity is 77.48%. b The ROC on the internal independent validation set. The AUC is 0.74, accuracy is 72.73%, sensitivity is 73.53%, and specificity is 71.88%. c The ROC on the external independent validation set from a separate center. The AUC is 0.72, accuracy is 71.43%, sensitivity is 70.00%, and specificity is 72.41%. d The ROC of the ablation study using clinical features alone. The AUC is 0.71, accuracy is 69.41%, sensitivity is 66.01%, and specificity is 73.45%.

To further evaluate the generalizability of our approach, we tested the model on an external cohort from an independent clinical site. The LGCIF-GNN achieved an AUC of 0.72, with an accuracy of 71.43%, sensitivity of 70.00%, and specificity of 72.41% (Fig. 2c). Despite differences in imaging protocols and demographic composition, the model maintained robust predictive performance, indicating its ability to generalize across sites and capture clinically relevant patterns.

To better understand the contribution of each modality, an ablation study of imaging features was conducted. Model performance declined significantly when using only clinical features without incorporating neuroimaging data into the fusion model, resulting in an accuracy of 69.41%, sensitivity of 66.01%, specificity of 73.45%, and AUC of 0.71 (Fig. 2d). This comparison clearly demonstrates the added value provided by integrating imaging modality.

Model interpretation

The attention score for functional imaging data was 0.3312, indicating a stronger influence compared to clinical data, which had a score of 0.3284. The multimodal (MC) embedding, which integrates both modalities, achieved the highest attention score of 0.3404, underscoring its critical contribution to the model’s predictive performance.

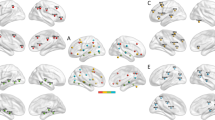
The differential rs-FC matrix identified the top five enhanced and top five diminished rs-FC characteristics within the reward and emotion regulation circuits (Fig. 3). The primary brain regions involved included the right globus pallidus, bilateral putamen, left hippocampus, bilateral thalamus, and bilateral ACC. Among these regions, the left hippocampus was the most frequently selected.

Fig. 3: Differential FC matrix and altered FC in remission and non-remission Groups.

a–c The differential FC matrix between the remission and non-remission groups. The color bar indicates the strength of functional connectivity. d The top five enhanced and the top five diminished FC were shown in a chord picture.

Feature masking analysis revealed that imaging features contributed more significantly to the model’s predictive performance than clinical features (Fig. 4). The top ten node features included brain regions such as the bilateral ACC, right globus pallidus, bilateral dorsolateral prefrontal cortex (dPFC), OFC, right hippocampus, and right thalamus. Among clinical features, HAMD item 5 (Sleep poorly) and item 8 (Retardation) showed slightly higher contributions compared to other clinical features (Fig. 4).

Fig. 4: Weight distribution of the top ten contributing clinical and neuroimaging features.

The radius or the area covered by each sector in the wind direction rose map represented the magnitude of the weight values for each feature in the classification model. The results revealed that neuroimaging features have a greater contribution to the model than clinical features.

The neural substrates showing significant alterations in rs-FC between remission and non-remission groups included the left ACC, right thalamus, and right globus pallidus. These brain regions were identified as pivotal contributors, ranking among the top ten nodes with the most substantial impact on network prediction performance, as determined by the feature masking strategy.

Discussion

The primary objective of this study was to develop a GNN model to predict the efficacy of SSRIs during the acute treatment period based on rs-fMRI features of the reward and emotion regulation circuits, along with clinical characteristics. The model demonstrated satisfactory predictive performance with an accuracy of 76.21%, and its robustness and generalizability were confirmed using an independent validation set (accuracy = 72.73%). Ablation studies revealed that neuroimaging features made a significant contribution, with the most impactful brain regions including the right globus pallidus, bilateral putamen, left hippocampus, bilateral thalamus, and bilateral ACC. These findings underscore the potential of a model combining clinical and neuroimaging features of the reward and emotion regulation circuits for predicting SSRIs response in MDD patients.

Recent advances in spatiotemporal GNNs have substantially shaped the landscape of neuroimaging-based predictive modeling. Models such as BrainGNN³⁴, BrainRGIN³⁸, and BNT³⁷ have demonstrated the utility of ROI-aware architectures or cluster representation for brain network modeling, integrating specific brain regions and subnetworks. Concurrently, spatiotemporal frameworks such as DSAM⁴⁴, Graph Clustered Transformer⁴², and Deep-Spatiotemporal⁴³ have pioneered hybrid temporal-graph approaches for capturing dynamic brain states. LG-GNN⁴¹, SFC-GNN⁴⁰, and MS²-GNN⁴⁵ have made strides toward integrating intra-subject features and population-level information or fusing features from different modalities. While building upon these foundations, our Local-Global Imaging and Clinical Feature Fusion GNN (LGCIF-GNN) offers a meaningful advancement by combining dynamic, task-adapted graph construction, local-global modeling that bridges subject-specific neurobiological precision with population-level similarity, and interpretable multimodal disentanglement and fusion.

First, unlike prior edge-enhanced GNNs such as BrainGNN³⁴ and BrainRGIN³⁸, which rely on static FC matrices or precomputed similarity graphs, LGCIF-GNN constructs subject-specific functional graphs during training by leveraging the dynamic similarity of ROI-level temporal embeddings. This approach allows the model to directly align graph topology with the treatment prediction task, improving representational specificity and model interpretability. Additionally, this design avoids hard clustering or top-k pooling strategies in previous works, such as Graph Clustered Transformer⁴² and BNT³⁷, which are sensitive to hyperparameters and risk discarding relevant features. Specifically, our attention-based mechanism enables soft graph readout, preserving critical regional information and improving robustness.

Second, previous studies have mainly defined the “spatiotemporal” or “local-global” concept within the scope of individual subjects, focusing on fine-grained temporal dynamics within single ROIs and spatial or global relationships across brain regions. For example, models like DSAM⁴⁴ and Deep-Spatiotemporal⁴³ integrate TCNs with GNNs to capture intra-subject spatiotemporal patterns using unidirectional and multi-scale temporal modeling. In contrast, LGCIF-GNN replaces the commonly used TCN modules with bi-GRU encoders, enabling the extraction of long-range, bidirectional temporal dependencies—crucial for capturing feedback and recurrent processes in emotion and reward-related circuits. Further, our framework advances this paradigm through a population-tiered hierarchy. This architecture dynamically links individual-level ROI dynamics (“local”) to population graphs constructed from functional and clinical similarity (“global”), enabling simultaneous learning from personalized neurodynamics and group-level pathophysiological patterns. This dual-scale supervision captures both individual heterogeneity and population-consistent biomarkers of treatment response in an end-to-end manner—a capability underexplored in prior local-global GNNs.

Third, while recent multimodal GNNs have started incorporating non-imaging data, they often do so in a limited manner. For instance, Deep-Spatiotemporal⁴³ replaces the adjacency matrix with DWI-derived structural connectivity, without true feature-level integration; LG-GNN⁴¹ includes only age, sex, and site as phenotypic inputs. MS²-GNN⁴⁵ recently demonstrated the promise of integrating EEG and audio data for MDD detection, but the application of GNNs to fuse fMRI and clinical features in psychiatry—especially for outcome prediction—remains underexplored. In contrast, LGCIF-GNN presents a more comprehensive and clinically grounded multimodal framework. It incorporates a diverse range of phenotype- and symptom-relevant clinical features, including age, sex, education, disease duration, and multiple clinical scale scores (HAMD, QLES, YMSR), which reflect both underlying biological vulnerability and external clinical status. Through modality-specific and shared feature extraction (MU-GCN, MS-GCN) and adaptive fusion, it achieved task-specific, interpretable multimodal integration tailored to SSRIs response prediction. This integration notably enhanced predictive performance, with the area under the receiver operating characteristic (ROC) curve (AUC) increasing from 0.71 to 0.78, a 10% improvement, after incorporating imaging features. These results highlight the added value of including neuroimaging data to enable more precise and individualized predictions of treatment response.

Moreover, previous studies on antidepressant efficacy prediction often utilized small sample sizes, unbalanced datasets, or uncontrolled polypharmacy approaches^7,30,31, leading to potential confounding in model assessments. In contrast, this study employed a larger sample size, balanced training and testing datasets, and a rigorous single-drug therapy protocol, enhancing the stability and generalizability of the predictive model. Additionally, the use of an independent validation set strengthens the model’s robustness. Unlike earlier studies relying solely on internal cross-validation, this study employed a validation dataset acquired with different scanning parameters and acquisition batches, facilitating a more comprehensive evaluation of generalization performance.

The proposed model achieved an AUC of 0.74 and an accuracy of 72.73% on the internal independent validation set, and an AUC of 0.72 and an accuracy of 71.43% on the external independent validation set, demonstrating its robustness and reliability. External validation is critical for assessing a prediction model’s adaptability to real-world scenarios beyond its development data and population⁴⁷. For comparison, a recent study by Poirot et al. developed an XGBoost model to predict sertraline response, achieving an internal cross-validation accuracy of 68% and an external validation accuracy of 65%⁴⁸, which is notably lower than the accuracy achieved by our model.

Consistent with the latest meta-study⁴⁹, neuroimaging features contributed more significantly to the model than clinical features. The ablation experiments and feature importance analysis demonstrated that resting-state brain imaging features played a more substantial role in predicting treatment outcomes compared to clinical features. Combining the results of the differential FC matrix analysis and feature masking analysis of node degrees revealed that the ACC, globus pallidus, hippocampus, and thalamus were common key features in predicting SSRIs treatment outcomes.

The right globus pallidus, a key component of the reward circuit^50,51, showed FCs with the left rostroventral area 24 and the right ventromedial putamen, forming an integrative network responsible for modulating emotional and motivational states. The globus pallidus plays a crucial role in regulating anxiety- and depression-like behaviors and can integrate and transmit signals related to motivation, reward, stress, and depression in the brain⁵². A recent study has shown that the plasticity of the cholinergic neuronal circuit in the ventral globus pallidus regulates pain-like and depression-like behaviors in mice⁵³. Another study has shown that there are structural and functional abnormalities in the putamen among patients with depression and those at genetic risk in their families, suggesting that the putamen is a potential biomarker for depression^54,55. The left hippocampus, a core component of the emotion regulation circuit¹¹, and the right thalamus, which is involved in both the reward and emotion regulation circuits^7,12,33, were also identified as critical nodes. FCs between the left rostral hippocampus and subregions of the right thalamus, the right subgenual area 32, and the right dorsolateral putamen form an integrative network mediating interactions among multiple brain systems involved in emotional and reward processing^56,57. The hippocampus plays a crucial role in emotional regulation and is closely related to the pathophysiological mechanism of depression⁵⁸. Research has shown that SSRIs promote neurogenesis in the dentate gyrus of the hippocampus and selectively act on the serotonergic pathway⁵⁹. Recently, many studies have emphasized that the pathways involving the thalamus may be the targets for the treatment of depression. Zhang et al. found a circuit from the visual cortex to the lateral posterior thalamic nucleus regulates depression-like behaviors in male mice⁶⁰. Zhang et al. found that the pathway from the thalamic reticular nucleus to the lateral habenula regulates depression-like behaviors in chronic stress and chronic pain⁶¹. In this study, our findings highlight the central role of functional alterations in the hippocampus, thalamus, and globus pallidus in predicting antidepressant efficacy. Dysfunctions in these connections may underlie core depressive and anhedonia symptoms. Antidepressant interventions likely exert their therapeutic effects by restoring functional synchrony, offering promising targets for MDD treatment strategies.

Regarding clinical features, HAMD item 5 (“Sleep poorly”) and item 8 (“Retardation”) contributed slightly more than other clinical features. Previous studies have suggested that the initial presentation of retardation and sleep disturbances may influence antidepressant efficacy^62,63,64, aligning with our findings. While neuroimaging features performed well independently, adding clinical features further enhanced model accuracy.

However, this study has several limitations. Firstly, the FC structure was initially estimated using Pearson correlation, a widely adopted approach in neuroimaging research due to its practicality and interpretability. While our model incorporates a graph structure optimization mechanism to adapt and refine the FC using temporally informed representations, future investigations into alternative FC metrics may offer additional benefits in expressiveness and biological fidelity. Second, for poorly covered masks, NaN values were replaced with the mean of non-NaN values from other MDD patient signals. Future research could explore personalized mask configurations. Lastly, this study focused solely on establishing a predictive model for SSRIs efficacy. Considering the variety of real-world medications, future studies should include additional antidepressant types to build more comprehensive efficacy prediction models.

In summary, the Local-Global Imaging and Clinical Feature Fusion Graph Neural Network (LGICF-GNN) was successfully applied to predict the acute-phase efficacy of SSRIs treatment in MDD patients, and it demonstrated consistently strong performance on the independent internal and external validation sets. The integration of clinical and functional imaging features achieved optimal predictive performance, with imaging features contributing significantly more than clinical features. These findings highlight the potential of neuroimaging features from the reward and emotion regulation circuits as predictors of antidepressant response. The current results represent an important step toward biomarkers of antidepressant response.

Methods

Participants

The MDD cohort in this study was derived from three cohort studies (ChiCTR-OOC-17012566, MR-11-23-003930, and ChiCTR2200059053) conducted at Beijing Anding Hospital, Capital Medical University, from September 2018 to October 2023. The study included 183 MDD patients in Cohorts 1 and 2, and 68 MDD patients in Cohort 3. Cohorts 1 and 2 were used as the training data, with all patients receiving SSRIs treatment for either 8 or 12 weeks. Additionally, Cohort 3 was designated as the internal validation set to assess model stability and generalization, with all patients receiving SSRIs treatment for 8 weeks. To further evaluate the model’s generalizability across different clinical sites, we included an external validation dataset comprising 52 MDD patients recruited from Shandong Daizhuang Hospital between March 2023 and February 2025, all of whom received SSRIs treatment for 8 weeks. Treatment outcomes were assessed using the same clinical criteria as in the primary cohort to ensure consistency in endpoint definition. The inclusion and exclusion criteria were consistent with those applied in the discovery cohort. This external dataset was acquired under different scanning protocols and demographic conditions, providing a realistic testbed for evaluating the model’s robustness across variations in scanner hardware, acquisition parameters, and population characteristics.

Inclusion criteria were: (1) adults aged 18–65 years; (2) Han ethnicity and right-handedness; (3) diagnosis of MDD based on the Diagnostic and Statistical Manual of Mental Disorders-IV (DSM-IV) for Cohorts 1 and 2, or the DSM-V for Cohort 3; (4) no prior antidepressant use or use for no more than seven days within the preceding 14 days; (5) willingness to undergo SSRIs treatment. Exclusion criteria included: (1) significant non-depression DSM-IV or DSM-V diagnosis ; (2) previous intolerance or lack of response to SSRIs; (3) MRI contraindications; (4) presence of psychotic symptoms.

The study was approved by the Human Research and Ethics Committee of Beijing Anding Hospital, Capital Medical University, and all participants provided informed consent (Approval No. 2017-24, 2020-106, 2022-14-202221FS-2). This study follows the STROBE statement checklist.

Treatment and clinical assessment

The HAMD-17 was used to assess depressive symptoms. Patients achieving a HAMD score ≤7 after 8 or 12 weeks of SSRIs treatment were classified as the remission group, while those with a score >7 were classified as the non-remission group. The Young Mania Rating Scale (YMRS) was used to assess manic symptoms, consisting of 11 items with total scores ranging from 0 to 44, where higher scores indicate more severe symptoms. The quality of life was measured using the 16-item QLES Questionnaire⁶⁵. The total score was calculated by summing the first 14 items, each rated on a 5-point Likert scale (1 = very poor to 5 = very good), resulting in a total score range of 14–90, with higher scores indicating better quality of life.

MRI image acquisition

Baseline neuroimaging data were collected using 3.0 T Siemens superconducting MRI scanners equipped with 64-channel head coils at two sites. Both sagittal T1-weighted magnetization-prepared rapid gradient-echo (MPRAGE) and gradient-recall echo-planar imaging (EPI) sequences were acquired. Participants were scanned in a supine position with earplugs to reduce noise, and were instructed to relax and minimize head movement. The internal and external validation cohorts followed the same scanning protocol, while the discovery cohort utilized a different protocol.

Scanning protocol of the training cohort

T1-MPRAGE sequence: repetition time (TR) = 2530 ms, echo time (TE) = 1.85 ms, flip angle (FA) = 9°, matrix = 256 × 256, slice thickness = 1 mm, gap = 0 mm, number of slices = 192, field of view (FOV) = 256 mm × 256 mm.

EPI sequence: TR = 2000 ms, TE = 30 ms, FA = 90°, matrix = 64 × 64, slice thickness = 3.5 mm, gap = 0.7 mm, number of slices = 33, FOV = 200 mm × 200 mm, 200 time points.

Scanning protocol of internal and external validation cohorts

T1-MPRAGE sequence: repetition time (TR) = 2530 ms, echo time (TE) = 4.21 ms, flip angle (FA) = 7°, matrix = 256 × 256, slice thickness = 1 mm, gap = 0 mm, number of slices = 192, field of view (FOV) = 256 mm × 256 mm.

EPI sequence: TR = 2000 ms, TE = 30 ms, FA = 90°, matrix = 64 × 64, slice thickness = 3.5 mm, number of slices = 33, FOV = 224 mm × 224 mm, 240 time points.

MRI image preprocessing

The PhiPipe tool was used for preprocessing rs-fMRI data⁶⁶. The steps included head motion adjustment using AFNI’s 3dvolreg, slice acquisition correction with AFNI’s 3dTshift, boundary-based registration with FreeSurfer’s bbregister, and masking for brain regions based on T1 processing and BOLD-T1 registration. Motion outliers were interpolated using neighboring volumes. Nuisance signals, including mean white matter and ventricle signals, and Friston’s 24-parameter head motion model, were regressed out. Bandpass filtering (0.01–0.1 Hz) was applied, and BOLD images were transformed into MNI152 standard space using combined T1‐MNI152 and BOLD‐T1 registration.

Functional connectivity analysis

FC analysis was performed using DPARSF (http://rfmri.org/DPARSF). Following preprocessing, the FC matrix of the reward and emotion regulation circuits was constructed by calculating Pearson’s correlation between the time courses of each ROI. Brain region coordinates were obtained from the Brainnetome Atlas template and relevant literature, including the nucleus accumbens, striatum, amygdala, globus pallidus, DLPFC, thalamus, OFC, ACC, and parahippocampus, totaling 70 ROIs (Supplementary Table 3).

ROIs were defined as 5 mm radius spheres around the peak coordinates of each cluster. The time series of voxels within each ROI was extracted and averaged. Rs-FC between ROI pairs was calculated using Pearson correlation, followed by Fisher R-to-Z transformation. NaN values for ROIs with poor coverage were replaced with the mean of non-NaN signals from other MDD patients.

Overall model design and computational pipeline

To predict SSRIs treatment outcomes in patients with MDD, this study introduces a hierarchical local-global imaging and clinical feature fusion graph neural network (LGCIF-GNN). The architecture integrates fine-grained brain functional activity with population-level patterns to enhance predictive accuracy and interpretability. An overview of the model architecture and computation pipeline is illustrated in Fig. 1.

LGCIF-GNN takes rs-fMRI signals and clinical variables as input, processing them through a hierarchical local-global graph framework. At the local level, subject-specific brain ROI graphs are constructed to capture individual functional dynamics across ROIs using temporal encoding and connectivity optimization. In parallel, clinical and demographic data are structured and embedded. As a result, for each subject, the model derives both functional and clinical embeddings, which serve as node features in two modality-specific population graphs. In these graphs, each node corresponds to a subject, and edges represent pairwise similarities in either FC patterns or clinical profiles. The two global population graphs are then jointly processed at the global level through modality-specific and shared GCN⁶⁷ branches, followed by an attention-based fusion mechanism. The fused representation is then passed to a final multi-layer perceptron (MLP) for individualized prediction of SSRIs treatment response (remission vs. non-remission). Importantly, the model supports interpretability by highlighting discriminative functional connections, clinically relevant traits, and relative modality contributions, thereby enabling both accurate prediction and biologically meaningful insights. In the following, we describe the key components of the framework and elaborate on the underlying computational workflow.

Initially, rs-fMRI signals are preprocessed using the DPABI toolbox to extract ROI-wise BOLD time series for each subject, using a standardized brain atlas. These ROI-specific time sequences are then fed into a bi-GRU⁶⁸ encoder, which captures the intrinsic temporal dynamics of each brain region and generates region-level embeddings. These embeddings serve as input to the graph structure optimizer, a module that learns subject-specific FC matrices in a task-driven manner. This approach yields individualized adjacency matrices that capture functionally meaningful neural interactions tailored to the treatment prediction objective, thereby addressing the limitations of conventional static, correlation-based connectivity measures. The resulting adjacency matrix defines the structure of each subject’s local ROI-level brain graph, wherein each node corresponds to an ROI defined by a standard brain atlas, and the node features are derived from the corresponding row of the Pearson correlation-based FC matrix. Subsequently, the Local GCN Readout module takes both the node features and the optimized graph structure as input, applies graph convolutional operations coupled with attention mechanisms⁶⁹ to update and aggregate regional features, producing a compact graph-level embedding that captures individual functional patterns within the reward and emotion regulation circuits. This embedding is then propagated to the global level, where each subject is represented as a node in the functional population graph.

In parallel, clinical and demographic variables—such as age, sex, clinical assessment scale scores, disease duration, and education level—are numerically encoded and concatenated into structured vectors in the Feature Encoding module. These vectors are used by the CTSE to project clinical features to a shared latent space and compute a pairwise similarity matrix across subjects, forming a clinical population graph that reflects clinical phenotypic proximity between subjects.

Both the subject-level functional embeddings and clinical features are input into the global graph modules as two population graphs. To disentangle and integrate modality-specific and modality-shared information across these population graphs, the global model employs a three-branch design: the Modality-Unique (MU) GCN block extracts distinct representations from each modality using independent multi-hop residual GCNs (MHR-GCNs); the Modality-Shared (MS) GCN block captures common cross-modal patterns via weight sharing; and the Multimodal Attention (M-Attention) block adaptively fuses the outputs of all branches into a unified representation, with attention weights reflecting their relative contributions to final treatment outcome prediction. Finally, an MLP receives the fused embedding and outputs the individualized prediction of the SSRIs treatment response. Additional details on model construction and implementation are provided in the Supplementary Tables 4 and 5.

Through this design, LGCIF-GNN achieves end-to-end optimization of both graph structures and multi-modality feature fusion, leveraging both local fine-grained functional patterns and global population-level similarities to improve the robustness and interpretability of multimodal predictive modeling.

Local graph construction and encoding

In local graphs, different functional ROIs of the reward and emotion regulation circuit, according to neurological knowledge, were defined as nodes, and the FC between these ROIs is defined as edges. Specifically, 70 ROIs were used as nodes, and the FC strength between nodes was established as edge weights to construct the local graph, with each graph corresponding to one subject. The FC derived from the correlation computations was utilized to initialize the graph structure of the local graph.

As depicted in Fig. 1a, the local ROI-based GNN consists of three main components: (1) a GRU regional time series encoder, (2) an FC matrix adjustment optimizer and graph generator, and (3) a readout module for generating graph-level embeddings and local predictions.

The temporal resolution of fMRI-derived time series signals is typically low. To extract the temporal features of the fMRI BOLD signals for each ROI while avoiding overfitting, this paper employs a lightweight bi-GRU⁶⁸ as the temporal encoder. Specifically, for an input BOLD time series $X\in {R}^{n\times t}$ of a subject, where n represents the number of ROIs and t is the length of the time series, the GRU encoder produces a regional embedding for each ROI, ${h}_{e}={Encoder}(x)$, where ${h}_{e}\in {{\mathbb{R}}}^{n\times d}$ and d is the output dimension of the GRU encoder.

To enable the graph structure defined by the FC matrix to be continuously optimized and adjusted in the network training stage, rather than being determined solely by coarse and inflexible correlation computation methods, a graph structure optimizer has been designed. This module constructs the adjacency matrix A based on the node feature vectors. The cosine similarity between the feature vectors of the ith and jth nodes is used as the weight at the position ${A}_{{ij}}$ of the adjacency matrix: ${A}_{{ij}}={h}_{e}\cdot {h}_{e}^{T}$ .

After the first two modules, the local graph structure has been learned and optimized. The local readout module updates the node features based on the GCN⁶⁷ and employs an attention mechanism to perform a weighted aggregation of the features across all nodes in the entire local graph, thereby generating a graph-level embedding. This graph-level embedding maps the functional characteristics of various brain regions and the inter-regional FC patterns within the reward and emotion regulation circuit of an individual into a hidden space. Specifically, the node feature ${h}_{i}$ of node $i$ was initialized with the ith row of the Pearson correlation FC matrix ${A}_{p}$ .

$$\begin{array}{c}{{\rm{H}}}_{l}^{0}=\left[{h}_{l1}^{0},{h}_{l2}^{0},\,\ldots ,{h}_{\mathrm{ln}}^{0}\right]{\rm{\#}}\end{array}$$

(1)

$$\begin{array}{c}{{\rm{h}}}_{{\rm{i}}}^{0}=\,{A}_{p}\left[i,:\right]{\rm{\#}}\end{array}$$

(2)

A 3-layer GCN was used to update the node feature, and the kth GCN layer is defined referring to the GCN proposed by Kipf and Welling⁶⁷ as:

$$\begin{array}{c}{H}_{l}^{k}=\sigma \left({GCN}\left({H}_{l}^{k-1},A\right)\right)=\sigma \left({D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}{H}_{l}^{k-1}{W}^{k}\right){\rm{\#}}\end{array}$$

(3)

Where $D$ is the diagonal matrix, $A$ is the adjacent matrix derived from the graph structure optimizer and ${{\rm{W}}}^{{\rm{t}}}$ is a trainable weight matrix of the kth layer, which is a two-layer MLP in our implementation. The final embedding of the whole local graph is the concatenation of node embedding weighted by the attention score.

$$\begin{array}{c}{a}_{{ROI}}={Attention}\left(A\right)={softmax}\left(\mathop{\Sigma }\limits_{j=0}^{n}{A}_{{ij}}\right)\cdot n{\rm{\#}}\end{array}$$

(4)

$$\begin{array}{c}{H}_{{lG}}={concat}\left({a}_{{ROI}}{H}_{l}^{k}\right){\rm{\#}}\end{array}$$

(5)

The local classification is determined by a 3-layer MLP classification head:

$$\begin{array}{c}\hat{{y}_{l}}={MLP}\left({H}_{{lG}}\right)\end{array}$$

(6)

Global graph construction and cross-modal fusion

Each subject was used as a node to construct two global graphs, including a functional graph and a demographic characteristics graph. The global feature vector (readout) of the subject’s fMRI signals learned from the local graph was used as the node feature of the functional graph. The demographic characteristics graph was constructed by using the subject’s age, sex, duration, education level, YMSR, HAMD, and QLE scale scores as node features. Subsequently, an attention mechanism was used to perform multimodal feature fusion of the two graphs. The node-level classification was used as the supervisory signal by the local graph.

As illustrated in Fig. 1b, the global GNN updates node features on both the functional population graph ${G}_{f}=({V}_{f},{E}_{f},{W}_{f})$ and the clinical population graph ${G}_{c}=({V}_{c},{E}_{c},{W}_{c})$, facilitating the fusion of clinical and imaging modalities, and performs node-level classification to obtain the final prediction of treatment outcome. In these population graphs, each node represents a patient, and the weights of the edges between nodes indicate the similarity between two patients in the corresponding modality. In the functional population graph, the node features are the functional embeddings generated by the local GNN, and the edge weights are the cosine similarity between the features of two nodes. In the clinical population graph, the node features remain as the functional embeddings produced by the local GNN, while the edge weights are determined by the CTSE based on clinical information such as age, sex, education level, disease duration, YSMR, QLES, and HAMD scale scores of the two patients. In the global GNN, the modality-unique GNN module is designed to extract unique features from each of the two modalities. The modality-shared GNN module is utilized to capture the common features across both modalities. Meanwhile, the modality-attention fusion module is employed to facilitate the fusion of multimodal features.

The CTSE starts by accepting the clinical feature vector ${h}_{c}$, a concatenation of age, sex, education level, disease duration, and the sub-item total scores of clinical scales, as input and maps each input to a common latent space ${h}_{{ci}}\in {{\mathbb{R}}}^{{D}_{c}}$. In the ${D}_{c}=128$ dimensional space, the cosine similarity can be better applied. The projection network is a 1-layer MLP to avoid overfitting. Thereby, the CTSE calculates the similarity between node $i$ and j as:

$$\begin{array}{c}{W}_{c}\left(i,j\right)=\displaystyle\frac{\cos \left({MLP}\left({h}_{{ci}}\right),{MLP}\left({h}_{{cj}}\right)\right)+1}{2}\end{array}$$

(7)

where $\cos$ denotes the cosine similarity between two input vectors.

In this study, we propose the MHR-GCN to address the over-smoothing issue and enhance the aggregation of multi-scale information in GCNs, inspired by the snowball GCN block. Our network architecture incorporates residual connections to facilitate the training of deeper networks, mitigating the vanishing gradient problem and enabling the training of GCNs beyond four layers. The MHR-GCN block concatenates the output of each layer before the final GCN layer to enrich feature representation, where the output of each hidden layer is a description of the center node with its different-hop neighbors. Residual connections are added after each GCN layer to learn the residual information, and the final output layer aggregates features from all hidden layers to produce node embeddings. This design allows the MHR-GCN to effectively aggregate information from various receptive fields, providing comprehensive node representations in the Subject-Graph, thus mitigating over-smoothing and enhancing the network’s ability to learn complex graph representations. The structure of snowball MHR-GCN is as follows:

$$\begin{array}{c}{H}_{g}^{0}={H}_{{lG}}\end{array}$$

(8)

$$\begin{array}{c}{H}_{g}^{l+1}={H}_{g}^{l}+{Tanh}\left({{H}_{g}^{l}W}_{l}\right),\,l=0,1,2,\ldots ,N-1\end{array}$$

(9)

$$\begin{array}{c}C={Tanh}\left(\left[{H}_{g}^{0},{H}_{g}^{1},\ldots ,{H}_{g}^{n}\right]{W}_{n}\right)\end{array}$$

(10)

$$\begin{array}{c}{H}_{{gG}}={normalize}\left({L}^{p}C{W}_{c}\right)\end{array}$$

(11)

Where $N$ is the number of MHR-GCN layers, ${W}_{l},{W}_{n},{W}_{c}$ is the trainable matrix, ${H}_{g}^{0},{H}_{g}^{1},\ldots ,{H}_{g}^{l}$ are extracted features, $p\in \left\{\mathrm{0,1}\right\}$, ${H}_{{gG}}$ is the global Subject-Graph embedding of one specific modality. When $p=0,\,{L}^{p}=I$ and when $p=1,\,{L}^{p}={L=D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$, which means that we project $C$ back onto the Fourier basis, which is necessary when the graph structure encodes much information.

The MU-GCN is applied to extract modality-unique embeddings, which are defined as follows:

$$\begin{array}{c}{H}_{u}^{f}={MHR}-{GCN}\left({X}^{f},{A}^{f}\right)={MHR}-{GCN}\left({H}_{{lG}},{A}^{f}\right)\end{array}$$

(12)

$$\begin{array}{c}{H}_{u}^{c}={MHR}-{GCN}\left({X}^{c},{A}^{c}\right)={MHR}-{GCN}\left({H}_{{lG}},{A}^{c}\right)\end{array}$$

(13)

where ${X}^{f}{\rm{and}}{X}^{c}$ are the node features for rs-fMRI and clinical modalities, respectively. And ${H}_{u}^{f}{\rm{and}}{H}_{u}^{c}$ are the modality-unique representations. The weights of the three SnowballGCN networks are independent of each other, making it possible to extract unique features more effectively.

Although the data structures and semantic information of various modalities possess distinct characteristics, it is far from trivial to completely disentangle these diverse data types. When performing the same task, data from different modalities often contain overlapping information. Extracting this shared information not only aids in distilling high-quality features for problem-solving but also reduces redundancy during the integration of multimodal information. To achieve this objective, we introduce the MS-GCN module, which facilitates the sharing of weight matrices across different modalities during the execution of the MHR-GCN operation. The specific formulations are as follows:

$$\begin{array}{c}{H}_{s}^{f}={MHR}-{GCN}\left({X}^{f},{A}^{f}\right)={normalize}\left({L}^{{fp}}{C}^{f}{W}_{{cs}}\right)\end{array}$$

(14)

$$\begin{array}{c}{H}_{s}^{c}={MHR}-{GCN}\left({X}^{c},{A}^{c}\right)={normalize}\left({L}^{{cp}}{C}^{c}{W}_{{cs}}\right)\end{array}$$

(15)

where ${H}_{s}^{f}$ and ${H}_{s}^{c}$ are the modality-common representations for rs-fMRI and clinical modalities, respectively. And ${W}_{{cs}}$ is the shared trainable matrix. By sharing weights in this way, modality-common features can be filtered out. The final common embedding is obtained by the weighted sum of the two ${H}_{s}={\alpha H}_{s}^{f}+\beta {H}_{s}^{c}$, where $\alpha$ and $\beta$ are hyperparameters measuring the importance of each modality’s common embedding. In the implementation, we set $\alpha =\beta =0.5$ to pay equal attention to all modalities.

The varying impact of various types of information on the ultimate treatment outcome prediction depends on the specific illness being targeted. In order to focus more on the informative methods and relegate the less critical ones to a supporting function, we employ an M-Attention Block on two unique embeddings ${H}_{u}^{f}$ and ${H}_{u}^{c}$ and one shared embedding ${H}_{s}$.

$$\begin{array}{c}{a}_{f},{a}_{c},{a}_{s}={Attention}\left({H}_{u}^{f},{H}_{u}^{c},{H}_{s}\right)\end{array}$$

(16)

$$\begin{array}{c}{e}_{i}={\rm{Tanh}}\left({W}_{{ai}}{H}_{u}^{i}+{b}_{i}\right)\end{array}$$

(17)

$$\begin{array}{c}{a}_{i}=\displaystyle\frac{\exp \left({e}_{i}\right)}{\exp \left({e}_{f}\right)+\exp \left({e}_{c}\right)+\exp \left({e}_{s}\right)},\,i\in \{f,c,s\}\end{array}$$

(18)

Once the attention score has been derived, the final embedding can be computed by integrating the representation with the weight as follows:

$$\begin{array}{c}H=\,{a}_{f}{H}_{u}^{f}+{a}_{c}{H}_{u}^{c}+{a}_{s}{H}_{s}\end{array}$$

(19)

Finally, an MLP layer is employed for class prediction.

$$\begin{array}{c}\hat{{y}_{g}}={MLP}\left(H\right)\end{array}$$

(20)

Training and implementation details

The optimization objective of the proposed LGCIF-GNN model integrates three complementary loss components: a classification loss, a modality-unique decorrelation loss, and a modality-shared consistency loss:

$$\begin{array}{c}L={L}_{{cls}}+{L}_{{unique}}+{L}_{{shared}}\end{array}$$

(21)

First, to supervise the predictive task, we adopt a cross-entropy loss framework. Since our architecture supports prediction at both local and global levels, the classification loss is formulated as a weighted combination of both contributions:

$$\begin{array}{c}{L}_{{cls}}={L}_{{cl}{s}_{{global}}}+\lambda {L}_{{cl}{s}_{{local}}}\end{array}$$

(22)

Here, ${\rm{\lambda }}$ is a hyperparameter regulating the influence of the local loss term. In our implementation, we set ${\rm{\lambda }}$ = 0.2 to prioritize the global classification signal during training, while still retaining local-level supervision to enhance representation learning.

Second, to disentangle modality-specific from modality-invariant information, we introduce a statistical independence constraint between the learned modality-unique embeddings ${H}_{u}$ and shared embeddings$\,{H}_{s}$. This is achieved by minimizing the Hilbert-Schmidt Independence Criterion (HSIC)⁷⁰, which quantifies dependence between distributions in a reproducing kernel Hilbert space (RKHS):

$$\begin{array}{c}{HSIC}\left({H}_{u},{H}_{s}\right)={\left(m-1\right)}^{-2}{tr}\left({K}_{s}R{K}_{u}R\right)\end{array}$$

(23)

where $K\left({H}^{i},{H}^{j}\right)=\, < \phi \left({H}^{i}\right),\phi \left({H}^{j}\right) >$ is the kernel function mapping the input embeddings into an RKHS, $R=I-\frac{1}{m}{e}{e}^{T}$ is the centering matrix, $I$ is the identity matrix, and $e$ is an all-ones vector. The total decorrelation loss aggregates HSIC values across multiple modality pairs:

$$\begin{array}{c}{L}_{{unique}}={HSIC}\left({H}_{u}^{f},\,{H}_{s}\right)+{HSIC}\left({H}_{u}^{c},\,{H}_{s}\right)\end{array}$$

(24)

Additionally, to encourage alignment among modality-invariant embeddings, we enforce similarity across shared representations derived from distinct modalities. After ${L}_{2}$-normalizing each embedding matrix, we compute pairwise differences between their similarity matrices:

$$\begin{array}{c}{N}_{s}={H}_{s}\cdot {H}_{s}^{T}\end{array}$$

(25)

$$\begin{array}{c}{L}_{{shared}}=\,{{||}{N}_{s}^{f}-{N}_{s}^{c}{\rm{||}}}^{2}\end{array}$$

(26)

The proposed model was implemented in Python 3.7 and PyTorch 1.12.1, utilizing an NVIDIA RTX 4090 GPU. For optimization, the Adam optimizer was employed with an initial learning rate of 5e-3, which was halved every 100 epochs. Across all experiments, the model was trained for a maximum of 200 epochs. The weight hyperparameter for the local classification loss was fixed at 0.2, giving precedence to the global classification loss during optimization. Detailed architectural and implementation specifications are provided in Supplementary Table 5.

Performance validation

To ensure accuracy and robustness in feature selection, the model’s performance was evaluated using 5-fold cross-validation, along with metrics including the AUC of the ROC, accuracy, sensitivity, and specificity. The training dataset was randomly divided into five equal parts. In each cycle, four parts were used as sub-training sets to build the model, and the remaining part was used to test the model’s performance. This process was repeated five times so that each subset served as a test set once. The optimal hyperparameter settings determined during cross-validation were applied to construct the final model using the entire training dataset. The final model was then tested on the internal and external validation sets for further verification. All ML analyses were conducted using Python.

To assess the model’s generalization capability, we conducted validation on two held-out datasets. The internal validation set (n = 66) provided an in-site assessment of predictive stability on temporally distinct data. In contrast, the external validation set (n = 49) served to evaluate the model’s cross-center generalizability. Specifically, it tested the robustness of the learned representations under differences in MRI scanner types, acquisition protocols, and patient population characteristics—factors known to challenge the reproducibility of neuroimaging-based biomarkers.

Additionally, an ablation study was performed to confirm the significance of radiographic features in improving model performance. During the ablation study, only the clinical features of 164 MDD patients were used in 5-fold cross-validation to assess their independent contribution.

Interpretation of functional imaging

As described in the section “Local graph construction and encoding”, the Graph Structure Optimizer in this study was designed to extract temporal sequence features from brain regions within the reward and emotion regulation circuits during training of the efficacy prediction network. This process constructs and optimizes an FC matrix specifically for predicting treatment outcomes. Through joint optimization of the local and global networks, the learned adjacency matrix encapsulates deeper temporal information while accounting for the constraints of functional brain imaging and clinical feature similarities among patients. This matrix reflects FC patterns relevant to treatment outcome prediction.

To understand the functional characteristics of the reward and emotion regulation circuits in non-remission and remission groups, FC matrices generated by the trained model for 164 subjects were analyzed. Subjects were grouped by treatment outcomes (non-remission or remission), and their FC matrices were averaged separately to obtain mean FC matrices for each group. These average matrices represent the general FC patterns within the two populations. A differential FC matrix, created by subtracting the mean non-remission FC matrix from the mean remission FC matrix, highlights differences in connectivity patterns between the groups.

The differential FC matrix was analyzed to identify brain regions and connections with the most significant differences between remission and non-remission groups. The specific rows and columns corresponding to the top five highest and lowest values in the matrix represent the FCs most enhanced or diminished in remission patients compared to non-remission patients. To determine the most impactful brain regions, the absolute values of the differential FC matrix were summed across rows to calculate node degrees. Higher node degrees indicated greater discrepancies in functional connections between the groups. Using this method, the 10 brain regions with the highest node degrees were identified as the most indicative for predicting treatment outcomes.

Assessment of modality importance

To evaluate the predictive contributions of different data modalities, the Modality-Attention (M-Attention) module within the global GNN model was utilized. This module fuses functional imaging and clinical data modalities, generating three distinct feature embeddings: unique imaging features, unique clinical features, and shared features between the two. The M-Attention module performs weighted fusion of these embeddings based on attention weights, allowing an assessment of the relative contributions of unique and shared features to the prediction process.

To compare the impact of specific clinical information and functional signals from different brain regions on treatment outcome predictions, a feature masking strategy was employed. During the inference phase on the independent test set, elements corresponding to clinical features were set to zero, or time series signals of specific ROIs were nullified. The model’s performance was evaluated using the masked features as input, and its efficacy was assessed by the AUROC.

Performance loss caused by masking individual features was visualized as a heatmap. Features with greater predictive importance caused larger reductions in AUROC, indicated by deeper blue tones in the heatmap. This analysis identified the clinical and functional features most critical to predicting antidepressant treatment efficacy.

Statistical analysis

Demographic data were analysed separately for the training and independent validation sets using SPSS Statistics 26.0. Age and clinical characteristics were compared using the Mann–Whitney U test or two-sample t-test. Chi-square tests were conducted to evaluate differences in sex and education level between the remission and non-remission groups.