Abstract
Neuropsychiatric disorders have complex causes and exhibit considerable individual variability as they develop over time. This suggests the need for a shift from a focus on observable clinical symptoms to a personalized trajectory monitoring paradigm that incorporates brain function checkups into routine primary care to allow detection of risk prior to the emergence of distress and impairment. A dynamical systems model of brain function enables quantitative snapshots of neural circuit function to be derived from electrophysiological measurements. Latent neurodynamical features can then be combined with personal and clinical data, enabling personalized neuropsychiatric trajectory monitoring. We present a general framework with recommended methods from dynamical systems theory to extract dynamical information from readily available EEG measurements. The dynamical features can then be incorporated into machine or statistical learning methods, where additional personal characteristics, experiences, and clinical data can be integrated to create risk prediction models for psychiatric conditions.
Similar content being viewed by others
Introduction
The primary purpose of psychiatric evaluation in a clinical setting is to determine a person’s mental health status to create a treatment plan that will relieve undesirable symptoms and suffering and optimize health in some way. The observed symptoms that define psychiatric diagnoses may be considered the end product of a long neurodevelopmental process1,2. Traditional classification systems are not well-suited to precision psychiatry because they focus on a single, underlying dysfunction for each diagnosis, which fails to acknowledge the complexity of psychiatric disorders and the heterogeneous expression in individuals. This limits the development of personalized therapies that consider the complex idiosyncrasies of each person’s mental health journey through life. To move beyond current clinical decision-making based on the Diagnostic and Statistical Manual (DSM) or related International Classification of Disease 11 (ICD-11) categories, Flagel et al. have developed a statistical framework that intends to incorporate multiple factors to produce a personalized, probabilistic diagnosis3. The general outline of this approach was sketched for schizophrenia4 using a Bayesian statistical model that integrates five different elements: Putative causes (such as genetics, environment, trauma, disease, medical history); “Hidden” brain physiology; latent Research Domain Criteria dimensional constructs; DSM categorical diagnoses; and measurable biomarkers, wearable data, or assessments. A key component of this model is the assumption that the bridge between causes of psychiatric disorders and the observed symptoms or behaviors are neural circuits. While this model is conceptually rich, in practice the many potential causative factors are rarely recorded in the medical record. A snapshot of brain function or the “hidden” neurophysiological bridge between putative causes and observed behaviors and diagnostic categories may enable a practical clinical implementation of this approach. Our perspective is that neural circuits create an electromagnetic field that meets the definition of a dynamical system. Direct measurements of this field using electroencephalographic (EEG) sensors enables information to be extracted as quantitative values, using dynamical systems theory. These may then be used in models of neural function to track changes that may indicate changing risk for psychiatric disorders.
Mental and neurological disorders are ultimately neural circuit disorders, with complex connections among physiology, anatomy, metabolism, and behavior that develop and change over time. That is, the pathological outcomes from brain dysfunction, whether mental or physical disease symptoms, are the end product of a developmental neurophysiological process1. Currently, psychiatric treatment typically begins near the end of this process, when symptoms become acute and observable, and often targets generic symptom clusters rather than incorporating idiographic understanding of each patient.
A paradigm shift toward precision preventive healthcare, rather than disease care, is possible if neurophysiological changes that occur in response to underlying causes can be monitored. Causes of mental health changes may include genetic predisposition, social and environmental exposures, trauma, injury, disease, and other factors that confer resilience or risk5,6. For most children and adults without overt symptoms, contact with the medical system occurs only sporadically during routine checkups. It may be impossible to monitor all the factors that affect an individual. Importantly, the link between genetic or environmental causes to cognition and behavior operates through neural circuits. Thus, monitoring neural circuit function may provide important personalized information about emerging psychiatric disorders in each individual without requiring knowledge or measurement of the underlying etiologies7.
While it is widely assumed in a general sense that the brain is responsible for all behaviors, and that observable behaviors must reflect changes in the brain, the specific physical mechanisms may be less obvious. We suggest that, fundamentally, bioelectrical forces are responsible for cognition and behavior. Support for this concept can be found in the neuroelectric fields that coordinate engram complexes responsible for memory representations8. More specifically, our hypothesis and the perspective presented here, is that computable properties of the neuroelectric field are associated with psychiatric diagnoses or symptoms that define psychopathologies. To test this experimentally, methods are required to compute appropriate properties of the neuroelectric field and statistically assess how well they correlate with specific psychiatric diseases.
Thus, the primary purpose of this paper is to present a tractable and extensible approach to incorporating measurements of neural circuit function, the “hidden” bridge between causes and outcomes, into personalized schemes for computing risk of emerging mental disorders and monitoring their course. We note that although our focus is on electromagnetic (EM) fields generated by neurons, contributions to the neuroelectric field from other physiological generators or even exogenous sources are implicitly incorporated into the measurements. Emerging evidence suggests that bioelectric sources are found in all living cells and contribute to signaling throughout the organism9,10.
A recently proposed approach to psychiatric clinical decision making suggests that a person’s mental health may be conceptualized as a trajectory through time7. From this perspective, the goal of therapy is to redirect that trajectory toward more desirable outcomes. The foundation for this framework is a data-driven model that links “underlying dimensional constructs with categorical constructs and actions”3. This model is sketched in Flagel et al.3 and presented again in an application to schizophrenia4.
Although neural circuits are explicitly identified as the bridge linking genetics and fundamental neurobiology to behavior, this neural circuit bridge is thought to be forever hidden and thus not computable in models of mental health or dysfunction2. Dynamical systems theory has been applied to psychiatric disorders previously on several different scales. On a macroscopic scale, dynamical systems concepts have been applied to the development of observable psychiatric symptoms11,12 or as a model of interacting physiological and behavioral processes on several levels13. The concept of a digital twin of the brain is also related to dynamical systems14. Multimodal imaging data, including MRI, fMRI, CT, EEG, and MEG data, are fed into machine learning models, typically recurrent neural networks (RNNs), and used to detect disease14. At the neural or synaptic scale, concepts from information theory that are related to dynamical systems have been used to model how synapses utilize stochasticity to enable learning despite ambiguous or uncertain inputs15.
Our perspective is founded on a conception of the neuroelectric field, which is generated by neural activity, with contributions from other bioelectric sources, as the driver of all behavior and cognition. We are specifically interested in the possibility of measuring the neuroelectric field on a macroscopic scale using EEG devices. EEG and magnetoencephalography (MEG) sensors measure the summed activity of many neurons and, as mentioned previously, the contribution of any other sources to the location of the sensor. A thorough discussion of clinical and research aspects of EEG can be found in authoritative sources such as Niedermeyer’s Electroencephalography, now in its seventh edition16. The primary tool for analysis of EEG measurements has been the human eye: Visual analysis of EEG time series reveals pathologies such as seizures and epileptiform spikes. The time series measured by EEG may also be analyzed using dynamical systems methods to infer dynamical properties of the neuroelectric source. In this way, dynamical properties of the neuroelectric field created by neural circuit activity can be used as a proxy for neural circuit function in the general framework proposed by Flagel3. This approach has the distinct advantage of being relatively easy and inexpensive due to the emergence of a commercial market of portable and consumer EEG devices. Thus, the application of dynamical systems theory to EEG measurements may enable neural circuit function to be measured routinely and incorporated into clinical biomarker models for psychiatric disorders.
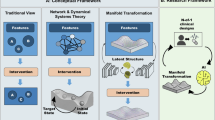
Incorporation of functional neural information into trajectory models of mental health may improve the ability of such models to detect pathological changes prior to the emergence of observable symptoms and to monitor the effects of therapy. With this goal in mind, a modified computational pipeline is shown in Fig. 1 that is inspired by the framework proposed by Flagel and Gordon3,4. Importantly, our framework explicitly includes neural circuit functional information, derived from dynamical analysis of EEG signals. We note specifically that inputs to the chosen statistical or machine learning methods include, in addition to the dynamical features from EEG signals, data that may typically be contained in the patient’s electronic health record (EHR) or other data, such as patient experiences, particularly trauma. Since the adoption of data standards for the exchange of health information, particularly Fast Health Interoperability Resources, incorporation of EHR data into personalized models has become widespread and relatively easy to accomplish.
The (neural field of the) brain is a dynamical system
The brain has been called a complex dynamical system17. This statement typically refers to the topological complexity of the network of neurons that comprise the brain. We suggest that the neuroelectric field produced by the synchronized activity of neurons and related physiology is the complex dynamical system that is the substrate for all neural systems’ functions18. The neuroelectric field is the receptor of all sensory input and the physical effector of all movement and behavior. A simple illustration of this is provided by transcranial magnetic stimulation. A type of “magnetic wand” is held above the scalp to change the neuroelectric field below the scalp, resulting in movements or sensations appropriate to that region of the brain. Change the neuroelectric field, change the mind itself. Each neuron is now recognized as a complicated computing device, further supporting the concept of the neuroelectric field as the substrate for all cognitive activity19. This field concept extends even to “simpler” organisms: The unicellular Euplotes has been shown to regulate its membrane potential, an electric field, to enable real-time control over its motor functions20.
If the neuroelectric field is a dynamical system, it can be analyzed and quantified using methods from dynamical systems theory. Data from time series measurements provided by scalp electroencephalogram (EEG) recordings are sufficient to reconstruct the essential functional dynamics of the system that produced those signals. The growing availability of easy-to-use, high-quality portable EEG devices makes it feasible to collect brief EEG recordings in routine care settings. Routine EEG measurements, analogous to blood pressure measurements, may be a relatively simple and important objective proxy for monitoring brain function related to emerging mental dysfunction, for predicting future outcomes, and for monitoring treatment effects21.
Dynamical systems are typically described by ordinary differential (continuous time) or difference (discrete time) equations. Dynamical systems that are continuous in space, such as are found, for example, in astrophysical plasmas or nuclear fusion reactors, are described by partial differential equations. In many situations, mathematical models of system dynamics are unavailable and cannot be inferred from measurements. If time series measurements of system variables are available, it may be possible to deduce properties of unmeasured dynamical values. This kind of model-free analysis of a dynamical system has been successfully applied to physical systems22 and engineered control systems23. Our approach to analyzing EEG time series uses a model-free approach to extract dynamical information about neuroelectric field dynamics for input to statistical or machine learning algorithms.
Many neurological, mental, and neurodevelopmental disorders have been described as dynamical diseases, including, but not limited to, epilepsy24,25,26, schizophrenia and bipolar disorder27,28,29,30, autism31,32,33,34, disorders of consciousness35,36, and Alzheimer’s Disease37,38,39. The conceptualization of neural circuit disorders as dynamical disorders is consistent with the view of the neuroelectric field as the physical substrate of cognitive activity or the mind. The neuroelectric field is a spatially continuous dynamical system40,41. The components that contribute to the neuroelectric field include neurons42,43, glia, and other physiological processes that modulate bioelectric fields44,45,46. This perspective is a theoretical framework that considers the neuroelectric field, coupled with neurophysiology, sensory input, and motor output, to be a dynamical system of embodied cognition from which behavior is generated by activation patterns in the continuously evolving neuroelectric field as it interacts with its environment, as well as by internal neuronal interactions47. Neural activation patterns may be described mathematically as a dynamical system as they evolve over time48,49,50.
A dynamical system is formally a mathematical system of continuous or discrete equations that describe the evolution of a coupled set of variables over time. The term may also refer to a physical, chemical, biological, or social system that can be modeled by equations that meet the mathematical definition of a dynamical system51,52,53. A dynamical system is capable of information processing, and the information processing capacity of a dynamical system is related to the complexity of the dynamical system50,54,55. This principle is now being exploited to build a new generation of information processing or AI systems in the form of physical reservoir computers56,57. The analysis of reservoir computing systems may provide additional theoretical concepts for describing the neuroelectric field using dynamical system measures40,41.
Phase space, trajectories, phase portrait
The state of a dynamical system at any given time can be represented abstractly by a vector in a high-dimensional phase space. In the context of dynamical systems, a phase space is an abstract, multidimensional space where every possible state of the system is represented as a unique point. Each axis in this space corresponds to one of the system’s variables, such as position or velocity, allowing the system’s behavior over time to be represented as a trajectory through this space. The trajectory of points through the phase space is called a phase portrait and represents the system’s dynamics without equations. A simple example is shown in Fig. 2.
If we can measure system dynamics at a scale appropriate for psychiatric (behavioral) patterns, then the sequence of state vectors through time comprises the trajectory of the neural system. The set of all possible trajectories through neural phase space is called the phase portrait of the system and is an abstract representation of all the possible sequences of the system. The phase portrait fully describes how the system may change over time. The set of trajectories shows geometrically (abstractly, if the number of dimensions exceeds three), without an explicit time variable, the progression of states through which the system can change. It is like showing a series of time-lapse photographs of the arm of a person throwing a ball. The arm moves smoothly through a certain path and cannot just randomly jump from place to place. The phase portrait is a structural or geometrical representation that completely describes the dynamics of the system. The phase portrait is a mathematical abstraction that can be analyzed and quantified in more than three dimensions.
Applying these concepts to neurons, if the potential of every one of the 80 billion or so neurons in the brain was known at this moment, the set or vector of 80 billion potential values represents the current state in the phase space of all possible values of the neural system. A moment later, the potential values of some neurons will have changed, and the new values represent another state. Although the neuroelectric field is continuous, a fine-grained representation of the state of the entire neuroelectric field at, for example, each neuron’s location, can be written as a vector of N real numbers, where N may be ~80 billion. Fortunately, such a fine-grained representation may not be necessary for capturing neural correlates of behavior or markers of neuropathology. Various approaches have been used to demonstrate that coordinated microscale dynamics can be measured as macroscale dynamics. Microscopic neural activity patterns can be interpreted using many-body physics to bridge the gap between neuron activity and microscopic brain functions that represent mental states58. Traditional concepts from statistical physics, such as spontaneous breakdown of symmetry and phase transitions are used to analyze EEG signals. A similar conceptual approach proposes that psychology and physiology provide two different descriptions of the same system; that is, psychology and physiology represent coarser- and finer-grained system states that are equally adequate59. These suggest that while neurons display stochastic dynamics at small scale scales, the larger scales measured by EEG display more coherent behavior or high-dimensional chaos60.
An important mathematical theorem concerning time series measurements was proved by Floris Takens in 198161. In essence, the theorem states that, given a smooth dynamical system and a generic observation function, the state space of the system can be reconstructed from time-delayed measurements of a single observable. The implication here is that, by measuring even one variable of a high-dimensional system, the full dynamics (up to a diffeomorphism) can be reconstructed using a computational method called time-delay embedding. This supports the idea that time series data from a single sensor may be used to reconstruct the essential features of the phase portrait of the entire system. It is important to note that the theorem does not claim that all the specific details of every part of the system can be reconstructed, but only the topological properties of the system. These properties are called dynamical invariants. Soon after this theorem was put forth, computational methods began to be developed for computing dynamical invariants from recurrence plot images that were derived from time series measurements62,63,64,65. The implications of the embedding theorems and computational methods are profoundly important for EEG measurements but have yet to be fully exploited. EEG sensors provide time series measurements of the neuroelectric field that, according to Takens’ theorem, enable the phase portrait of the neural system to be reconstructed and quantified. An open research question is to determine the quantity and nature of the dynamical invariants derived from EEG measurements and how well these can predict to detect macroscopic behaviors or diagnoses. Figure 3 illustrates the idea of phase space reconstruction by time series embedding.
Here, we review some current computational methods to derive dynamical invariants from time series measurements. We emphasize that an open research question is to determine a fundamental set of dynamical measures that fully describes the essential dynamics of a system. The set of measures described here are widely used but more continue to be developed. It may be that new approaches using unsupervised machine learning techniques may discover a different set, or additional dynamical measures, that form a basis set for describing system dynamics. Whatever future dynamical measures might be discovered, they can be incorporated into the analysis framework outlined here. We describe how to extract latent dynamical features from a larger set of multiscale dynamical invariants and then map these to behavioral measures, neurological diagnoses, or psychiatric constructs using machine learning. The resulting computed values can be used and tested as digital biomarkers.
Computing latent dynamical features
Multiscale and multifrequency decomposition
Physiological neural networks exhibit structure across many scales. Because of this multiscale structure, the electrical fields generated by neural circuits span many scales or frequency bands61. Multiscale entropy analysis introduces a scale-dependent approach to nonlinear analysis. Multiscale entropy was first introduced to analyze physiological signals associated with heart disease66,67,68. Although the use of entropy as a measure of physiological complexity was not new, the primary innovation here was recognizing that complexity across multiple scales contained important diagnostic information not available in the raw signal. In general, complexity loss was associated with aging or pathological conditions, with the degree of loss varying across frequency bands or scales69,70,71. The scales produced by the coarse-graining procedure in the multiscale entropy literature have been shown to be identical to the approximations produced by the Haar wavelet transform72. This insight has shown the relation between coarse grain scales and the standard frequency bands typically used for EEG spectral power analysis (delta, theta, alpha, beta, gamma). The relation between spectral decomposition and the low-pass filtering implemented by the coarse-graining procedure is illustrated in Fig. 4.
Spectral decomposition (a) and coarse graining (b) are illustrated. Band pass filtering is commonly used to analyze EEG signals by first decomposing the signal into distinct frequency bands using Fourier or related methods. Coarse-graining was introduced in studies of multiscale entropy, where “multiscaling” was accomplished by a coarse-graining algorithm. Coarse-graining is mathematically identical to the “approximations” of the Haar wavelet transform and is a low-pass filter, eliminating all frequencies above a specified cutoff.
EEG signals are often contaminated by various types of noise, including physiological artifacts (such as muscle activity or eye blinks) and non-physiological artifacts (including electrical interference and electrode movement)73. Filtering EEG signals to remove artifacts may be necessary for obtaining accurate and meaningful data. Common filtering techniques include low-pass filters to remove high-frequency noise, high-pass filters to eliminate slow drifts, band-pass filters to focus on specific frequency ranges, and notch filters to remove narrow bands of interference, such as power line noise74. Some nonlinear measures, such as Kolmogorov-Sinai entropy, are strongly affected by the presence of noise in signals, whereas others, such as approximate entropy, are less affected by noise75. A challenge that has not been adequately explored is to determine how these various filtering techniques alter the nonlinear properties of the actual neurophysiological signal. This is an important research topic in nonlinear signal analysis, particularly for routine clinical applications of EEG.
Computing properties of dynamical systems: nonlinear time series analysis
The term “quantitative EEG analysis” has traditionally been defined by the neurology and neurophysiology communities as “the mathematical processing of digitally recorded EEG to highlight specific waveform components, transform the EEG into a format or domain that elucidates relevant information, or associate numerical results with the EEG data for subsequent review or comparison”76. Power on multiple frequency bands (“spectral power” or, equivalently, “multiscale power”) has been valuable for inferring diagnostic information. It may be included in the list of signal features. While the next sections review some of the currently most common dynamical measures that may be computed from time series, the primary perspective should be kept in mind: The neuroelectric field generated by neural circuit activity is a dynamical system. If neural correlates of diagnostic categories or behavioral measures are sought, they may be found in quantitative measures of the dynamical system, which can be derived from EEG time series. This hypothesis can be tested empirically by computing dynamical measures from EEGs and using machine learning methods to evaluate their predictive value. The following sections review dynamical measures that have been found to be useful as psychiatric biomarkers, but the catalog presented here is almost certainly not complete.
One of the first applications of nonlinear signal analysis to a physiological system was multiscale entropy to analyze electrocardiograms or heart electrical signals66. The specific “entropy” value used was sample entropy, related to the original information entropy proposed by Claude Shannon77,78. Since then, the number of different algorithms to compute an entropy value has grown to dozens, including Sample, Approximate, Renyi, and Fuzzy entropies, to name a few79. Each has been used for many scientific applications, adding to the confusion over what entropy means80,81,82. Entropy has a physical definition (i.e., the amount of energy in a system that is unavailable to perform work) and a mathematical definition used in information theory83, initially defined by Shannon77. The mathematical definition has the same form as that used in thermodynamics, and both represent a measure of randomness, although the thermodynamic and mathematical applications are unrelated. In keeping with the goals of this paper, we interpret signal complexity or entropy as a quantitative measure of only one dynamical aspect of the system that produced the signal.
In addition to the many entropy variations, several other dynamical properties can be computed from physiological signals. These include correlation dimension84, Hurst Exponent, Lyapunov exponents, and Detrended Fluctuation Analysis85,86. This is not an exhaustive list, nor should we assume that all quantitative measures of dynamical system properties have been discovered. A remaining challenge is determining the minimal, complete set of measures to fully describe a complex system’s dynamics or phase portrait.
The many dynamical values described thus far are not entirely independent, and more may yet be discovered. An important outstanding research question is to determine a minimal set of measures needed to fully characterize the properties of a dynamical system. The answer to this may depend on the complexity of the dynamical system, which might suggest that many measures are needed to characterize brain function. This set of measures might be called a basis set for a dynamical system, borrowing the term ‘basis set’ from linear or functional analysis, where a basis set is a minimal set of vectors needed to represent all dimensions or functions in an abstract space. The framework presented allows for any number of additional nonlinear measures to be included. Before presenting a preprocessing method for extracting a set of latent factors from many multiscale dynamical measures, a graphical approach to computing nonlinear properties called recurrence plot analysis is presented.
Recurrence plot analysis
Recurrence plots (RPs) were first introduced as a means to visualize the phase portrait of a dynamical system projected onto a two-dimensional plane87. In principle, the RP contains all the essential dynamical system properties from which it was derived64. The availability of desktop computers allowed numerical computations that soon resulted in recurrence quantitative analysis (RQA), which was an attempt to quantify the essential properties of a dynamical system from a reconstructed (abstract) phase portrait. The development and application of RQA to various physical and biological systems suggested that RPs contained essential information to enable quantitative descriptions of dynamical system properties64. Examples of recurrence plots derived from time series produced by several different dynamical systems are shown in Fig. 5. The RP is a two-dimensional projection of the phase portrait of the system. In principle, it contains all of the fundamental dynamics of the measured system down to a scale presented by the sampling rate of the time series64. The RP might be considered a type of Quick Response (QR) code for brain function.
An advantage of recurrence plot analysis is that it can provide dynamical information even for short, noisy, non-stationary time series64,88. For EEG analysis of brain function, Takens’ Theorem (one of the embedding theorems) has been shown to be a special case of a more general reconstruction process from multiple time series, which may result in a more accurate reconstruction when time series are digitized or noisy. The results apply to situations having parallel time series measurements for variables related to the same dynamical manifold89. This is precisely the situation with multiple scalp sensors on a typical EEG recording.
A consequence of the embedding theorems is that the embedding dimension for the system is determined by the dimension of the system attractors, not by the frequently much higher dimensionality of the microscopic degrees of freedom90. Rather, this is a mathematical description of the neurophysiological phenomenon of many neurons synchronizing and firing together to accomplish a given task or behavior. Dynamical properties of a system can be computed from a recurrence plot by statistically characterizing the various lines and structures in the plot91,92,93. The most common measures and their meaning are summarized in Table 1.
Recurrence network analysis (RN)
A related approach to quantifying the recurrence plot is based on network analysis, where the recurrence plot is interpreted as the adjacency matrix of a complex network91,94,95. Recurrence network (RN) analysis exploits an analogy between complex network theory and nonlinear time series analysis94. This approach is complementary to RQA, resulting in additional nonlinear information that is not extracted by RQA methods95. In particular, the RN approach extracts information regarding the structure of the underlying chaotic attractors, which are not available using the conventional algorithmic methods of nonlinear time-series analysis96. Values computed from a recurrence network assess properties of system attractors using network measures, including the ε-clustering coefficient; mesoscopic measures, such as ε-motif density; path-based measures, such as ε-betweennesses; and global measures, such as ε-efficiency96,97.
Emerging time series processing methods
Foundation models have very recently achieved remarkable success in natural language processing and image analysis, but this success has not yet been demonstrated for EEG signal analysis. EEG signals are more irregular and dynamic than the structured relationships found in language or images and are thus more difficult to capture through attention mechanisms98. Some potential has been demonstrated for detecting short-term changes associated with seizures or sleep stages, or tasks that might be performed through brain-computer interfaces99. While promising, it is not yet clear if the dynamical system properties associated with mental health and disease can be discovered by these methods.
Neuromorphic computing has been attracting attention as an alternative to the deep learning paradigm, in part because it offers comparable performance at far less energy cost100. Reservoir computing (RC) is a relatively new and rapidly evolving machine learning approach that exploits dynamical systems’ information processing and adaptability capability. RCs are related to RNNs but are much faster to train because they utilize a fixed, high-dimensional dynamical system, known as the reservoir, to map input data to a simple output layer. This enables efficient pattern recognition with a readout layer that only requires minimal training, making it faster and less computationally expensive than traditional neural networks, especially for time-series data analysis. The fixed nature of the reservoir allows for implementation on diverse hardware platforms, including but not limited to optical systems and electronic circuits57,101,102.
Another aspect of RC for EEG analysis is that the reservoir can learn dynamical properties not included in the training data, a remarkable property that is believed to be related to the conjugacy between the source as a dynamical system (such as the neural circuits of interest in this paper) and the reservoir itself. The reservoir essentially learns the source dynamics from the time series, and these properties are simply read from the output layer103. Compared to deep learning and transformer methods, theory and application of RC is still in early stages. However, it is quite promising for incorporation into the framework presented here because it is completely consistent with a dynamical systems perspective on neural circuit function100.
Tensor representation of multiscale EEG features
The dynamical analysis described results in hundreds or thousands of values derived from each EEG recording. Typical values are 19 or more sensors, 6 frequency bands, and 15 dynamical measures (shown in Table 1), which yield 1710 dynamical values. High-density EEG nets used in research may have as many as 256 sensors, which would result in tens of thousands of dynamical values. These values are likely not entirely independent. For example, nearby sensors are likely to have some sources in common. Adjacent frequency bands are likely to have more in common than those farther apart. Moreover, the minimum set of dynamical measures necessary to characterize a system is not yet known. A reservoir computing device will produce a set of values in the output layer which may also be larger than desired for input into machine learning models. Latent features extracted by tensor analysis can be used as dynamical biomarkers in machine learning or regression models. This presents a computational approach to discovering a basis set of measures for characterizing the brain dynamical system from EEG signals.
The set of EEG measures described above can be arranged into a tensor, i.e., a 3-dimensional data structure (sensor, frequency band, nonlinear measure). The data from multiple patients or research participants can be represented as a fourth axis, creating a fourth-order tensor of dimensions N x Ns x Nf x Nm, where N is the number of participants. Tensors have been used to represent EEG features recently104, but supervised tensor factorization has not been proposed in this context previously. Supervised tensor factorization can be used as a preprocessing step to extract latent dynamical values that are related to the training construct or diagnosis of interest. These then become input to the statistical or machine learning algorithm as illustrated in Fig. 6.
A. EEG recordings (1) are used to compute latent dynamical factors by either multi-frequency decomposition and nonlinear feature calculation (A.2 and A.3) or reservoir computing (B.3). Output from either method is input to a (4) supervised tensor factorization algorithm to extract latent dynamical features or “hidden neurophysiology.” Other available data, such as putative causes, patient history, or lab tests, may be input as covariates to supervised tensor factorization. Resulting latent dynamical factors are input to learning models, as in Fig. 1.
The goal of tensor factorization is to identify a small number of latent variables within the EEG data that explain most of the variation in the data. Importantly, the predominant variations in the data may not be the most highly correlated with target conditions of interest. Thus, supervising on a primary target can improve the value of the identified factors. Further, in clinical contexts, the latent variables often are influenced by additional variables, such as environmental exposures or sex assigned at birth. Supervising on a primary target variable and additional covariate variables can improve the accuracy and usefulness of the discovered latent variables105.
A supervised tensor decomposition algorithm, such as the Canonical Polyadic (CP) regression algorithm in the Tensorly Python package106 or the SupCP described in the literature107, can extract latent features that are most aligned with the target and covariate variables. Tensor factorization is analogous to Singular Value Decomposition (SVC) for matrices but generalized to multiple dimensions and supervised, allowing the target outcomes to influence the factor extraction process. The extracted latent factors are analogous to principal components found by Principal Components Analysis used for matrix analysis. The result of supervised tensor factorization is the reduction of 1710 (or more) dynamical values to a much smaller set of perhaps 3 to 20 factors relevant to the condition of interest. These factors may be used as the fundamental features to train a machine learning model or statistical forecast model.
An important feature of tensor factorization is that the latent factors are interpretable. Supervised tensor decomposition can extract latent features and explore the underlying neurophysiology relevant to the labels or categories used for the supervised factorization105,108. Like the SVC for matrices, a tensor decomposition will find a reduced dimensionality feature set109,110,111. The canonical polyadic (CP) decomposition of a rank R tensor factorizes the tensor into a sum of R rank-1 tensors112. The supCP107 tensor factorization method implements a supervised version of the CP factorization algorithm in which covariates inform the latent variables. The covariates include the outcomes of interest, extracting latent structures—biomarkers—that are more accurate and interpretable than unsupervised factorization provides. Moreover, these latent factors represent dynamical information that is derived from the dynamical neuroelectric field, thus representing the underlying brain physiology.
Application roadmap and illustrations of dynamical correlates
Nonlinear analysis of EEG time series is proving to be a promising approach to functional brain analysis and biomarker discovery113,114,115. As mentioned previously, an outstanding challenge is to determine how much clinically useful information can be extracted from EEG time series by phase space reconstruction analysis. Currently, this can only be accomplished through empirical testing. The basic scheme for doing so, as illustrated in Fig. 6, is as follows: First, the raw EEG signals are decomposed into standard frequency bands. “Scales” derived from the coarse-graining procedure have been used in multiscale entropy studies; as we illustrated, these can be understood as frequency bands. Dynamical invariants can be computed from the signals using the algorithms described for entropy, Lyapunov exponents, and RQA. A promising new approach for computing these dynamical invariants is reservoir computing. Further research is needed to determine how dynamical invariants computed by reservoir computing compare to those computed by time delay embedding methods. Regardless of the method, these dynamical invariants can be mapped as quantitative features to clinical diagnoses or behavioral measures using standard machine learning methods. Given that there are many dynamical variables, feature reduction methods may be applied to reduce the number of features. We discussed tensor factorization as a promising approach, but many other approaches commonly used in machine learning methods may be used.
Our own studies have found promising correlations between dynamical measures and emerging autism spectrum disorder113,116,117, childhood anxiety118,119,120, and attention deficit disorders121,122 as well as detection of epilepsy123,124,125, monitoring the effects of anti-seizure drugs126, and sleep disorders127. Further, a review of several studies showed that those with schizophrenia exhibit altered EEG complexity, as characterized by increased entropy signals128. Individuals with major depressive disorder display distinct nonlinear EEG patterns, such as decreased fractal dimension and reduced complexity, which are thought to indicate impaired neural connectivity and information processing120,129,130. Research on bipolar disorder has identified unique nonlinear EEG markers, including variations in Lyapunov exponents, which reflect the chaotic nature of mood fluctuations in these patients131. Mood disorders associated with underlying neurological pathology, such as Parkinson’s Disease, offer another avenue for studying the correlation of neuroelectric field and psychiatric symptoms. High-resolution intracranial recording techniques have the potential to undercover the network dysfunction and cognitive processes that drive these symptoms toward a principled re-tuning of circuits132. While these studies suggest correlations between dynamical properties of the neuroelectric field, as derived from EEG analysis, and psychiatric phenotypes, we suggest that more research using comprehensive dynamical feature sets may result in more accurate biomarkers and, perhaps more importantly, be useful for understanding overlap and commonalities among the neural foundations for psychiatric and neural disorders.
Discussion
Our primary goal in this paper was to present a dynamical systems perspective on the neuroelectric field generated by neurophysiology and to present a computational approach to extracting dynamical features that might be useful in predictive or classification models of psychiatric disease. The fundamental conception of the neural field as a dynamical system, and the consequent approach to computing system properties using readily measured time series using EEG recordings, may be applicable to any approach to computing digital biomarkers for psychiatric disease or symptoms. Quantitative measures of brain function can be derived from time series (EEG) measurements of the neuroelectric field to compute dynamical properties or ‘invariants’ that can be used as diagnostic, prognostic, or monitoring biomarkers, or incorporated into trajectory models that predict changing risk for psychiatric disorders over developmental time. Supervised tensor factorization is a general methodology for organizing these EEG-derived values and for extracting latent features associated with specific disorders. Our goal here is clinically pragmatic: The neuroelectric field can be measured routinely by a new generation of portable EEG sensors relatively easily and inexpensively, characterized by the tools of dynamical systems analysis, and mapped to cognitive constructs, developmental behavioral milestones, or psychiatric conditions using supervised tensor factorization and machine learning. That is, the presented perspective on the brain as the source of the neuroelectric field is presented as the foundation for a general computational approach to incorporate functional neural circuit information in neuropsychiatric biomarker discovery and evaluation.
A significant challenge remains. Nonlinear analysis of EEG time series has been used for several decades to compute signal properties to be used as biomarkers for psychiatric disorders. However, a comprehensive perspective that seeks to find a minimal set of measures, a basis set in mathematical terms, that comprehensively characterizes (brain) system dynamics has yet to be presented. As we described above, the number of nonlinear measures that can be computed continues to increase, with more than 20 different entropies alone being defined79. We present a flexible framework that allows new nonlinear measures to be added, with the same supervised tensor factorization scheme, to extract a smaller latent set of factors most correlated with a chosen target, such as a specific disease or psychiatric construct. Identification of a minimal comprehensive set of measures that should be computed from every EEG recording would establish a common set of measures for use by the entire neurophysiology community to create a shared learning neuropsychiatric data system. This is a task for the computational psychiatry community, as different sets of factors are likely needed for predicting not only different disorders but also a given disorder at various stages of development.
Artifacts and noise in EEG measurements are known to affect spectral power values. For example, eyeblinks and facial muscle movements cause large deviations in signals from sensors near the activity from these non-neural sources. Noise introduced to the measurement and digitization process may significantly affect power values. An important question yet to be answered is how much these artifacts affect nonlinear measures. It may be that some dynamical measures are relatively immune to transient, large-amplitude muscle artifacts. On the other hand, small amplitude noise, which may have little effect on power, may significantly alter values of entropy or other dynamical measures. Importantly, the effects of filtering for noise, artifacts, or frequencies on the various dynamical measures is unknown. Since filtering is commonly applied to EEG signals, a systematic study of these effects is important for further development of dynamical analysis to neural biomarker applications.
Correlating dynamical values with specific psychiatric conditions presents several related challenges. The first is simply to find clinically useful digital biomarkers that correlate with some diagnostic label or predict later emergence of such a condition. This problem can be solved using basic machine learning algorithms, as illustrated in Fig. 1. The term ‘digital biomarkers’ is used to distinguish a weighted combination of many, multimodal input values from a single scalar value, such as fasting blood glucose level (a scalar number) as a biomarker for diabetes. Complex digital biomarkers that are output by a machine learning algorithm may be difficult or impossible for a human to review visually and interpret, but an algorithm can map these numbers to a binary outcome. A more challenging problem is to determine what outcome labels to use. The commonly used diagnostic labels found in the Diagnostic and Statistical Manual of Mental Disorders (DSM 5)133 or the International Classification of Disease134 attach a diagnostic label to symptom clusters. This approach has been criticized as not being based on neurobiology. Alternative nosologies that focus on underlying biological and psychological processes rather than symptom-based categories receive increasing attention135. Determining the proper targets for mapping dynamical values may require empirical research to solve.
The mathematical theory of dynamical systems guarantees that the phase portrait of a dynamical system can be reconstructed by a time series from any component of the system136. The theorems do not say how fine-grained of a reconstruction is possible. As discussed previously, EEG time series are composed of the action potentials of many neurons. It is likely that the sampling rate of the measuring device, the degradation of the cortical signals as they pass through the skull and scalp, and corruption of the signal by noise and artifacts will all impose limits on how precisely individual differences can be detected. If macroscale differences can be detected in neuroelectric field dynamics that distinguish major categories of mental disorders, this may be clinically useful in itself. Combining dynamical measures with genetic, historical, or other clinical data may enable more refined and personalized patient or disease characteristics to be detected. This must be determined empirically by analysis of larger clinical datasets.
Psychiatric disorders emerge over developmental time, which has led to the recommendation that a “a patient’s experience is a trajectory, and the goal must be to shift that trajectory”7. If our fundamental hypothesis is correct, that is, that changes in behavior reflect changes in neural circuit dynamics or, equivalently, neuroelectric field dynamics, then changes in dynamical measures derived from EEG time series should detect changes in the patient’s trajectory, whether from emerging disease or from the effects of therapy or medication. In the latter case, routine monitoring of neural function with EEG measurements, from which dynamical invariants can be computed, may provide a tool for monitoring therapeutic progress. This perspective is grounded on the assumption that there is a causal correlation between the electrical field that neural circuits generate and the behaviors that define psychopathological symptoms. Previously cited examples demonstrated correlations between some dynamical measures and psychiatric disorders. Inclusion of dynamical invariants in predictive or monitoring algorithms can be done with the measures discussed here, or with new measures, perhaps from new approaches such as reservoir computing, enabling characterization of neuroelectric fields with more comprehensive dynamical measures and disease.
Preliminary evidence suggests that the computational tools presented are useful for discovering potential digital biomarkers for many neuropsychiatric disorders, some of which we have explored in our own research107,113,123,124. Application, analysis, and clinical testing are needed for specific disease cases to build machine learning models derived from training data. This will require specialists from many fields, using their knowledge to properly train as well as upgrade the model framework as needed. We believe that the theoretical perspective on neuroelectric fields and the computational framework for deriving dynamical invariants from short EEG measurements will provide an important record of brain function that can be incorporated into machine learning or statistical models, including developmental trajectory models, to enable clinically useful biomarkers for monitoring many neuropsychiatric disorders to be discovered.
Data availability
No datasets were generated or analysed during the current study.
References
Insel, T. R. Mental disorders in childhood: shifting the focus from behavioral symptoms to neurodevelopmental trajectories. JAMA 311, 1727–1728 (2014).
Redish, D. & J. Gordon. Computational Psychiatry: New Perspectives on Mental Illness. (MIT Press, Cambridge, MA, USA, 2016).
Flagel, S. B. et al. A Novel Framework for Improving Psychiatric Diagnostic Nosology. In Computational Psychiatry: New Perspectives on Mental Illness (eds Redish, A. D., Gordon, J. A. The MIT Press, 2016).
Gordon, J. A., Morris, S. E. & Avenevoli, S. A framework for integration of dimensional and diagnostic approaches to the diagnosis of schizophrenia. Schizophr. Res. 242, 98–101 (2022).
Chen, L. H., Law, W., Chang, D. H. F. & Sun, D. Editorial: the bio-psycho-social approach to understanding mental disorders. Front. Psychol. 14, 1225433 (2023).
Arango, C. et al. Risk and protective factors for mental disorders beyond genetics: an evidence-based atlas. World Psychiatry 20, 417–436 (2021).
ReRedish, A. D., Gordon, J. A., Redish. From Psychiatry to Computation and Back Again. In Computational Psychiatry: New Perspectives on Mental Illness (pp. 319–330). (eds Redish, A. D., Gordon, J. A. The MIT Press, 2016).
Pinotsis, D. A. & Miller, E. K. In vivo ephaptic coupling allows memory network formation. Cereb. Cortex 33, 9877–9895 (2023).
Levin, M. Bioelectric networks: the cognitive glue enabling evolutionary scaling from physiology to mind. Anim. Cogn. https://doi.org/10.1007/s10071-023-01780-3 (2023)
Blackiston, D. et al. Revealing non-trivial information structures in aneural biological tissues via functional connectivity. PLoS Comput. Biol. 21, e1012149 (2025).
Scheffer, M., et al. A dynamical systems view of psychiatric disorders—theory: a review. JAMA Psychiatry https://doi.org/10.1001/jamapsychiatry.2024.0215 (2024).
Gauld, C. & Depannemaecker, D. Dynamical systems in computational psychiatry: a toy-model to apprehend the dynamics of psychiatric symptoms. Front. Psychol. 14, 1099257 (2023).
Durstewitz, D., Huys, Q. J. M. & Koppe, G. Psychiatric illnesses as disorders of network dynamics. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 6, 865–876 (2021).
Wang, H. E. et al. Virtual brain twins: from basic neuroscience to clinical use. Natl Sci. Rev. 11, nwae079 (2024).
Kappel, D. & Tetzlaff, C. Synapses learn to utilize stochastic pre-synaptic release for the prediction of postsynaptic dynamics. PLoS Comput. Biol. 20, e1012531 (2024).
Schomer, D. L., & Lopes da Silva, F. H. (Eds.). Niedermeyer’s Electroencephalography: Basic Principles, Clinical Applications, and Related Fields. Oxford University Press 2017.
Barabási, D. L. et al. Neuroscience needs network science. J. Neurosci. 43, 5989–5995 (2023).
Tosches, M. A. Developmental and genetic mechanisms of neural circuit evolution. Dev. Biol. 431, 16–25 (2017).
Beniaguev, D., Segev, I. & London, M. Single cortical neurons as deep artificial neural networks. Neuron 109, 2727–2739.e3 (2021).
Laeverenz-Schlogelhofer, H. & Wan, K. Y. Bioelectric control of locomotor gaits in the walking ciliate Euplotes. Curr. Biol. 34, 697–709.e6 (2024).
Shalbaf, R. et al. Non-linear entropy analysis in EEG to predict treatment response to repetitive transcranial magnetic stimulation in depression. Front. Pharm. 9, 1188 (2018).
Lu, Z. et al. Reservoir observers: model-free inference of unmeasured variables in chaotic systems. Chaos 27, 041102 (2017).
Ellis, G. Observers in Control Systems (Academic Press, 2002).
Baud, M. O., Proix, T., Rao, V. R. & Schindler, K. Chance and risk in epilepsy. Curr. Opin. Neurol. 33, 163–172 (2020).
Woldman, W., Cook, M. J. & Terry, J. R. Evolving dynamic networks: An underlying mechanism of drug resistance in epilepsy?. Epilepsy Behav. 94, 264–268 (2019).
Moraes, M. F. D., de Castro Medeiros, D., Mourao, F. A. G., Cancado, S. A. V. & Cota, V. R. Epilepsy as a dynamical system, a most needed paradigm shift in epileptology. Epilepsy Behav. https://doi.org/10.1016/j.yebeh.2019.106838. (2019)
Zhang, N. et al. Altered complexity of spontaneous brain activity in schizophrenia and bipolar disorder patients. J. Magn. Reson. Imaging 54, 586–595 (2021).
an der Heiden, U. Schizophrenia as a dynamical disease. Pharmacopsychiatry 39, S36–S42 (2006).
Scharfman, H. E. et al. Epilepsy as a Network Disorder (2): what can we learn from other network disorders such as dementia and schizophrenia, and what are the implications for translational research?. Epilepsy Behav. 78, 302–312 (2018).
Giersch, A. & Mishara, A. L. Is schizophrenia a disorder of consciousness? Experimental and phenomenological support for anomalous unconscious processing. Front. Psychol. https://doi.org/10.3389/fpsyg.2017.01659. (2017)
Belmonte, M. K. et al. Autism and abnormal development of brain connectivity. J. Neurosci. 24, 9228–9231 (2004).
Amatya, D. N. et al. Dynamical electrical complexity is reduced during neuronal differentiation in autism spectrum disorder. Stem Cell Rep. 13, 474–484 (2019).
Kessler, K., Seymour, R. A. & Rippon, G. Brain oscillations and connectivity in autism spectrum disorders (ASD): new approaches to methodology, measurement and modelling. Neurosci. Biobehav. Rev. https://doi.org/10.1016/j.neubiorev.2016.10.002. (2016)
Mohammad-Rezazadeh, I., Frohlich, J., Loo, S. K. & Jeste, S. S. Brain connectivity in autism spectrum disorder. Curr. Opin. Neurol. https://doi.org/10.1097/WCO.0000000000000301. (2016)
Bai, Y., Lin, Y. & Ziemann, U. Managing disorders of consciousness: the role of electroencephalography. J. Neurol. https://doi.org/10.1007/s00415-020-10095-z. (2020)
Cao, B. et al. Abnormal dynamic properties of functional connectivity in disorders of consciousness. Neuroimage Clin. 24, 102071 (2019).
Niu, Y. et al. Dynamic complexity of spontaneous BOLD activity in Alzheimer’s disease and mild cognitive impairment using multiscale entropy analysis. Front. Neurosci. 12, 677 (2018).
Gu, Y. et al. Abnormal dynamic functional connectivity in Alzheimer’s disease. CNS Neurosci. Ther. 26, 962–971 (2020).
Niu, H. et al. Abnormal dynamic functional connectivity and brain states in Alzheimer’s diseases: functional near-infrared spectroscopy study. Neurophotonics 6, 025010 (2019).
Damicelli, F., Hilgetag, C. C. & Goulas, A. Brain connectivity meets reservoir computing. PLoS Comput. Biol. 18, e1010639 (2022).
Enel, P., Procyk, E., Quilodran, R. & Dominey, P. F. Reservoir computing properties of neural dynamics in prefrontal cortex. PLoS Comput. Biol. 12, e1004967 (2016).
Abbott, L. F. & Dayan, P. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems (MIT Press, Cambridge, MA, USA, 2001).
Gerstner, W., Kistler, W. M., Naud, R. & Paninski, L. Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition (Cambridge University Press, https://doi.org/10.1017/CBO9781107447615. 2014).
Perea, G., Sur, M. & Araque, A. Neuron-glia networks: integral gear of brain function. Front. Cell. Neurosci. 0, (2014).
Fields, R. D. et al. Glial biology in learning and cognition. Neuroscientist 20, 426–431 (2014).
Kastanenka, K. V. et al. A roadmap to integrate astrocytes into systems neuroscience. Glia 68, 5–26 (2020).
Schöner, G., Reimann, H. & Lins, J. Neural Dynamics. in Dynamic Thinking: A Primer on Dynamic Field Theory (eds Schöner, G., Spencer, J. & Research Group, D.) 0 (Oxford University Press, https://doi.org/10.1093/acprof:oso/9780199300563.003.0001. 2015).
Freeman, W. J. Indirect biological measures of consciousness from field studies of brains as dynamical systems. Bord. Complex. 20, 59–78 (2012).
Carroll, T. L. Computing with Dynamical Systems: Reservoir Computers. NRL Memorandum Report NRL/6390/MR—2023/2. Naval Research Laboratory. https://apps.dtic.mil/sti/trecms/pdf/AD1192952.pdf (2023).
Dambre, J., Verstraeten, D., Schrauwen, B. & Massar, S. Information processing capacity of dynamical systems. Sci. Rep. 2, 514 (2012).
Alligood, K. T., Sauer, T. D. & Yorke, J. A. Chaos: An Introduction to Dynamical Systems (Springer, New York, NY Heidelberg, 1996).
Strogatz, S. H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering 2nd edn (CRC Press, Boulder, CO, 2015).
Pincus, D. Clinical psychology at the crossroads: an introduction to the special issue on nonlinear dynamical systems. Nonlinear Dyn. Psychol. Life Sci. 23, 1–15 (2019).
Kubota, T., Takahashi, H. & Nakajima, K. Unifying framework for information processing in stochastically driven dynamical systems. Phys. Rev. Res. 3, 043135 (2021).
Vettelschoss, B., Rohm, A. & Soriano, M. C. Information processing capacity of a single-node reservoir computer: an experimental evaluation. IEEE Trans. Neural Netw. Learn Syst. 33, 2714–2725 (2022).
Nakajima, K. Physical reservoir computing—an introductory perspective. Jpn. J. Appl. Phys. 59, 060501 (2020).
Tanaka, G. et al. Recent advances in physical reservoir computing: a review. Neural Netw. 115, 100–123 (2019).
Freeman, W. J. & Vitiello, G. Nonlinear brain dynamics as macroscopic manifestation of underlying many-body field dynamics. Phys. Life Rev. 3, 93–118 (2006).
Allefeld, C., Atmanspacher, H. & Wackermann, J. Mental states as macrostates emerging from brain electrical dynamics. Chaos 19, 015102 (2009).
El Boustani, S. & Destexhe, A. Brain dynamics at multiple scales: Can one reconcile the apparent low-dimensional chaos of macroscopic variables with the seemingly stochastic behavior of single neurons? Int. J. Bifurc. Chaos https://doi.org/10.1142/S0218127410026769. (2010)
Takens, F. Detecting Strange Attractors in Turbulence. in Dynamical Systems and Turbulence, Warwick 1980 (eds Rand, D. & Young, L.-S.) Vol. 898 366–381 (Springer, Berlin, Heidelberg, 1981).
Gao, J. & Cai, H. On the structures and quantification of recurrence plots. Phys. Lett. A 270, 75–87 (2000).
Marwan, N. A historical review of recurrence plots. Eur. Phys. J. Special Top. https://doi.org/10.1140/epjst/e2008-00829-1 (2008).
Marwan, N., Romano, M. C., Thiel, M. & Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 438, 237–329 (2007).
Zbilut, J. P. & Webber, C. L. Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett. A 171, 199–203 (1992).
Costa, M., Goldberger, A. L. & Peng, C. K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 89, 068102 (2002).
Costa, M., Goldberger, A. L. & Peng, C. K. Multiscale entropy analysis of biological signals. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 71, 021906 (2005).
Costa, M., Goldberger, A. L. & Peng, C. K. Broken asymmetry of the human heartbeat: loss of time irreversibility in aging and disease. Phys. Rev. Lett. 95, 198102 (2005).
Bruce, E. N., Bruce, M. C. & Vennelaganti, S. Sample entropy tracks changes in electroencephalogram power spectrum with sleep state and aging. J. Clin. Neurophysiol. 26, 257–266 (2009).
Maturana-Candelas, A., Gómez, C., Poza, J., Pinto, N. & Hornero, R. EEG characterization of the Alzheimer’s disease continuum by means of multiscale entropies. Entropy21, E544 (2019).
Pappalettera, C. et al. Approximate entropy analysis across electroencephalographic rhythmic frequency bands during physiological aging of human brain. Geroscience 45, 1131–1145 (2023).
Bosl, W. J., Loddenkemper, T. & Vieluf, S. Coarse-graining and the Haar wavelet transform for multiscale analysis. Bioelectron. Med. 8, 3 (2022).
Islam, M. K., Rastegarnia, A. & Yang, Z. Methods for artifact detection and removal from scalp EEG: a review. Neurophysiologie Clinique/Clin. Neurophysiol. https://doi.org/10.1016/j.neucli.2016.07.002. (2016)
Siddiqui, M. M., Kidwai, M. S., Srivastava, G., Singh, K. K. & Charan, P. Analysis of EEG data using different techniques of digital signal processing. Biomed. Pharmacol. J. 17, 135–139 (2024).
Natarajan, K. et al. Nonlinear analysis of EEG signals at different mental states. Biomed. Eng. Online 3, 7 (2004).
Nuwer, M. Assessment of digital EEG, quantitative EEG, and EEG brain mapping: report of the American Academy of Neurology and the American Clinical Neurophysiology Society. Neurology 49, 277–292 (1997).
Shannon, C. E. & Weaver, W. A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 (1949).
Shannon, C. E. Prediction and entropy of printed English. Bell Syst. Tech. J. 30, 50–64 (1951).
Ribeiro, M. et al. The entropy universe. Entropy 23, 222 (2021).
Tribus, M. & McIrvine, E. C. Energy and information. Sci. Am. 225, 179–190 (1971).
Vopson, M. M. The mass-energy-information equivalence principle. AIP Adv. 9, 095206 (2019).
Çengel, Y. A. On entropy, information, and conservation of information. Entropy 23, 779 (2021).
Popovic, M. Research in entropy wonterland: a review of the entropy concept. Therm. Sci. 22, 1163–1178 (2018).
Kantz, H. & Schreiber, T. Dimension estimates and physiological data. Chaos Interdiscip. J. Nonlinear Sci. 5, 143–154 (1995).
Hardstone, R. et al. Detrended fluctuation analysis: a scale-free view on neuronal oscillations. Front. Physiol. 0, 450 (2012).
Peng, C.-K., Havlin, S., Stanley, H. E. & Goldberger, A. L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 5, 82–87 (1995).
Eckmann, J., Kaphorst, S. O. & Ruelle, D. Recurrence plots of dynamical systems. Europhys. Lett. 5, 973–977 (1987).
Webber, C. L., & Marwan, N. (Eds.). (2015). Recurrence Quantification Analysis: Theory and Best Practices. Springer International Publishing Understanding Complex Systems. (2015).
Deyle, E. R. & Sugihara, G. Generalized theorems for nonlinear state space reconstruction. PLoS ONE 6, e18295 (2011).
Kantz, H. & Schreiber, T. Nonlinear Time Series Analysis (Cambridge University Press, Cambridge, UK; New York, 2004).
Donner, R. V., Zou, Y., Donges, J. F., Marwan, N. & Kurths, J. Recurrence networks-a novel paradigm for nonlinear time series analysis. New J. Phys. https://doi.org/10.1088/1367-2630/12/3/033025. (2010)
Komalapriya, C. et al. Reconstruction of a system’s dynamics from short trajectories. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 78, 66217 (2008).
Marwan, N. & Webber, C. L. Mathematical and computational foundations of recurrence quantifications. Understand. Complex Syst. https://doi.org/10.1007/978-3-319-07155-8-1 (2015)
Donges, J. F., Heitzig, J., Donner, R. V. & Kurths, J. Analytical framework for recurrence network analysis of time series. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 85, 46105 (2012).
Donges, J. F. et al. Unified functional network and nonlinear time series analysis for complex systems science: the pyunicorn package. Chaos 25, 1–28 (2015).
Jacob, R., Harikrishnan, K. P., Misra, R. & Ambika, G. Uniform framework for the recurrence-network analysis of chaotic time series. Phys. Rev. E https://doi.org/10.1103/PhysRevE.93.012202 (2016)
Harikrishnan, K. P., Misra, R. & Ambika, G. Quantifying information loss on chaotic attractors through recurrence networks. Phys. Lett. Sect. A Gen. At. Solid State Phys. https://doi.org/10.1016/j.physleta.2019.125854 (2019)
Cui, S., Lee, D. & Wen, D. Toward brain-inspired foundation model for EEG signal processing: our opinion. Front. Neurosci. 18, 1507654 (2024).
Yue, T. et al. EEGPT: unleashing the potential of EEG generalist foundation model by autoregressive pre-training. Preprint at https://arxiv.org/abs/2410.19779 (2024).
Yan, M. et al. Emerging opportunities and challenges for the future of reservoir computing. Nat. Commun. 15, 2056 (2024).
Liang, X. et al. Physical reservoir computing with emerging electronics. Nat. Electron 7, 193–206 (2024).
Kumar, P., Jin, M., Bu, T., Kumar, S. & Huang, Y.-P. Efficient reservoir computing using field programmable gate array and electro-optic modulation. OSAC 4, 1086–1098 (2021).
Hara, M. & Kokubu, H. Learning dynamics by reservoir computing (In Memory of Prof. Pavol Brunovský). J. Dyn. Diff. Equat. 36, 515–540 (2024).
Li, W. et al. Data-driven retrieval of population-level EEG features and their role in neurodegenerative diseases. Brain Commun. 6, fcae227 (2024).
Lock, E. F. & Li, G. Supervised multiway factorization. Electron. J. Stat. 12, 1150–1180 (2018).
Developers, T. CPRegressor. Available at: https://tensorly.org/stable/modules/generated/tensorly.regression.cp_regression.CPRegressor.html (2024).
Bosl, W. J., Bosquet Enlow, M., Lock, E. F. & Nelson, C. A. A biomarker discovery framework for childhood anxiety. Front. Psychiatry 14, 1158569 (2023).
Guan, L. Smooth. and Probabilistic PARAFAC Model with Auxiliary Covariates. J.Comput. Graphical Stat. 33, 538–550 (2024).
Cichocki, A. et al. Tensor decompositions for signal processing applications: From two-way to multiway component analysis. IEEE Signal Process. Mag. https://doi.org/10.1109/MSP.2013.2297439 (2015).
Zhou, G. et al. Linked component analysis from matrices to high-order tensors: applications to biomedical data. Proc. IEEE 104, 310–331 (2016).
De Wel, O. et al. Decomposition of a multiscale entropy tensor for sleep stage identification in preterm infants. Entropy 21, 1–15 (2019).
Kolda, T. G. & Bader, B. W. Tensor decompositions and applications. SIAM Rev. https://doi.org/10.1137/07070111X (2009).
Bosl, W. J., Tager-Flusberg, H. & Nelson, C. A. EEG analytics for early detection of autism spectrum disorder: a data-driven approach. Sci. Rep. 8, 6828 (2018).
Donges, J. F., Heitzig, J., Donner, R. V. & Kurths, J. Analytical framework for recurrence-network analysis of time series. Phys. Rev. E 85, 046105 (2012).
Goswami, B. A Brief introduction to nonlinear time series analysis and recurrence plots. Vibration https://doi.org/10.3390/vibration2040021. (2019)
Catarino, A., Churches, O., Baron-Cohen, S., Andrade, A. & Ring, H. Atypical EEG complexity in autism spectrum conditions: a multiscale entropy analysis. Clin. Neurophysiol. 122, 2375–2383 (2011).
Gurau, O., Bosl, W. J. & Newton, C. R. How useful is electroencephalography in the diagnosis of autism spectrum disorders and the delineation of subtypes: a systematic review. Front. Psychiatry 8, 121 (2017).
Minkowski, L., Mai, K. V. & Gurve, D. Feature extraction to identify depression and anxiety based on EEG. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2021, 6322–6325 (2021).
Schoenberg, P. L. A. Linear and nonlinear EEG-based functional networks in anxiety disorders. Adv. Exp. Med. Biol. 1191, 35–59 (2020).
Trambaiolli, L. R. & Biazoli, C. E. Resting-state global EEG connectivity predicts depression and anxiety severity. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2020, 3707–3710 (2020).
Catherine Joy, R., Thomas George, S., Albert Rajan, A. & Subathra, M. S. P. Detection of ADHD from eeg signals using different entropy measures and ANN. Clin. EEG Neurosci. 53, 12–23 (2022).
Rezaeezadeh, M., Shamekhi, S. & Shamsi, M. Attention deficit hyperactivity disorder diagnosis using non-linear univariate and multivariate EEG measurements: a preliminary study. Phys. Eng. Sci. Med. https://doi.org/10.1007/s13246-020-00858-3. (2020)
Bosl, W. J., Loddenkemper, T. & Nelson, C. A. Nonlinear EEG biomarker profiles for autism and absence epilepsy. Neuropsychiatr. Electrophysiol. 3, 1 (2017).
Sathyanarayana, A. et al. Nonlinear analysis of visually normal EEGs to differentiate benign childhood epilepsy with centrotemporal spikes (BECTS). Sci. Rep. https://doi.org/10.1038/s41598-020-65112-y. (2020)
Sathyanarayana, A. et al. Measuring the effects of sleep on epileptogenicity with multifrequency entropy. Clin. Neurophysiol. 132, 2012–2018 (2021).
Sathyanarayana, A. et al. Measuring real-time medication effects from electroencephalography. J. Clin. Neurophysiol. 41, 72–82 (2024).
Liang, X. et al. Decreased sample entropy during sleep-to-wake transition in sleep apnea patients. Physiol. Meas. 42 (2021).
Naffaa, M.M. Bridging Neuroscience and Psychiatry through Brain Complexity and Neural Circuit Dysfunctions in Anxiety, Depression, and Schizophrenia. Nat. Cell Sci. 2, 257–277 (2024).
Kaushik, P., Yang, H., Roy, P. P. & van Vugt, M. Comparing resting state and task-based EEG using machine learning to predict vulnerability to depression in a non-clinical population. Sci. Rep. 13, 7467 (2023).
Baskaran, A., Milev, R. & McIntyre, R. S. The neurobiology of the EEG biomarker as a predictor of treatment response in depression. Neuropharmacology 63, 507–513 (2012).
Bystritsky, A., Nierenberg, A. A., Feusner, J. D. & Rabinovich, M. Computational non-linear dynamical psychiatry: a new methodological paradigm for diagnosis and course of illness. J. Psychiatr. Res. 46, 428–435 (2012).
Ricciardi, L., Apps, M. & Little, S. Uncovering the neurophysiology of mood, motivation and behavioral symptoms in Parkinson’s disease through intracranial recordings. npj Parkinsons Dis. 9, 136 (2023).
Diagnostic and Statistical Manual of Mental Disorders: DSM-5TM 5th edn xliv, 947 (American Psychiatric Publishing, Inc., Arlington, VA, US, https://doi.org/10.1176/appi.books.9780890425596. 2013).
Organization, W. H. ICD 10: International Statistical Classification of Diseases and Related Health Problems Volume 1. (Amer Psychiatric Pub Inc, Geneva, 1992).
Hakak-Zargar, B. et al. The utility of research domain criteria in diagnosis and management of dual disorders: a mini-review. Front. Psychiatry 13, 805163 (2022).
Tolle, C. R. & Pengitore, M. Phase-space reconstruction: a path towards the next generation of nonlinear differential equation based models and its implications towards non-uniform sampling theory. In Proc. 2009 2nd International Symposium on Resillient Control Systems. 63–68 (IEEE, Idaho Falls, ID, USA, 2009) https://doi.org/10.1109/ISRCS.2009.5251347.
Mandelbrot, B., Hudson, R. L. The Misbehavior of Markets: A Fractal View of Financial Turbulence. Basic Books: New York, 2006.
Zhang, H.-Y., Feng, Z.-Q., Feng, S.-Y. & Zhou, Y. Typical Algorithms for Estimating Hurst Exponent of Time Sequence: A Data Analyst’s Perspective. IEEE Access 12, 185528–185556 (2024).
Hilborn, R. C. Lyapunov exponents: a tool to explore complex dynamics. Phys. Today 70, 62–63 (2017).
Acknowledgements
This research was supported by the National Institute of Health (R01 MH078829) and a Tommy Fuss Center Innovation Award from the Tommy Fuss Center for Neuropsychiatric Disease Research at Boston Children’s Hospital (WB, MBE). The content is solely the responsibility of the authors and does not necessarily represent the official views of any granting agencies.
Author information
Authors and Affiliations
Contributions
W.B. contributed to the conception and design of the methods, algorithm design, and wrote software associated with the methods discussed. M.B.E. contributed to the design and conception of this project and wrote sections of the Introduction. M.E. and C.N. conceived of and secured funding for data collection in the Emotion Project, which provided data to develop ideas for this study. All authors reviewed, edited, and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Bosl, W.J., Enlow, M.B. & Nelson, C.A. A dynamical systems framework for precision psychiatry. npj Digit. Med. 8, 586 (2025). https://doi.org/10.1038/s41746-025-01984-6
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41746-025-01984-6