Introduction

Osteoarthritis (OA) is a chronic, degenerative joint disease that represents a leading cause of disability and reduced quality of life worldwide, affecting over 300 million individuals. Among the various joints susceptible to OA, the knee is particularly vulnerable, and the progressive degradation of articular cartilage is widely recognized as a core pathological hallmark1. Because cartilage loss is largely irreversible and often asymptomatic in its early stages, the ability to detect subtle changes in cartilage morphology—especially cartilage thinning—is of critical importance for early diagnosis, disease staging, and longitudinal monitoring of OA progression.

Magnetic resonance imaging (MRI) has become the gold standard for in vivo evaluation of knee joint structures, owing to its superior soft-tissue contrast and non-invasive volumetric capabilities2,3. Cartilage thickness mapping derived from MRI data plays a crucial role in both clinical applications and population-scale OA research, including large longitudinal studies such as the Osteoarthritis Initiative (OAI)4. However, despite its clinical significance, accurate and anatomically faithful estimation of cartilage thickness from MRI remains a technically challenging problem. The difficulty arises from both the complex geometry of joint anatomy and the variability in MRI resolution and contrast across acquisition protocols5.

The majority of current cartilage thickness estimation pipelines are built upon voxel-wise segmentation of the cartilage compartment, followed by geometric post-processing to compute local thickness. These pipelines, while straightforward in design, suffer from fundamental limitations. Voxel-based segmentations often yield jagged or anatomically inconsistent cartilage boundaries, particularly in curved or thin regions, leading to surface discontinuities and physiologically implausible thickness estimates6,7. Furthermore, most existing frameworks treat cartilage as an isolated structure and do not incorporate the surrounding anatomical context, such as the subchondral bone surfaces of the femur and tibia. This omission prevents the model from leveraging important geometric priors, such as inter-surface spacing and local surface parallelism, both of which are critical for accurate morphological characterization. These issues are further exacerbated under conditions of low-resolution or anisotropic MRI8, where voxel-level representations are inherently limited in their ability to capture fine-grained anatomical structures.

Motivated by these challenges, our objective is to develop a cartilage thickness mapping framework that is not only anatomically consistent and smooth by construction, but also robust to MRI resolution variability and imaging artifacts. Rather than relying on voxel-wise segmentation and discrete surface fitting, we adopt an implicit modeling approach that directly learns a continuous signed distance function (SDF) to represent cartilage geometry. This implicit representation is conditioned on the anatomical geometry of the femoral and tibial subchondral bone surfaces, enabling smooth interpolation of the cartilage volume between them and capturing the underlying anatomical topology with high fidelity.

We present CartiSurface, a novel framework for cartilage thickness estimation based on implicit surface reconstruction. The proposed method leverages a neural network to predict an SDF over the knee joint region, conditioned on extracted femoral and tibial bone surfaces. The cartilage compartment is implicitly defined as the volume enclosed between these reconstructed anatomical boundaries. To ensure anatomical plausibility, we introduce a geometry-aware loss function that regularizes the predicted SDF with respect to expected cartilage morphology, enforcing consistent surface spacing and local parallelism throughout the volume. Thickness values are derived from the learned SDF field by computing the shortest distances between corresponding surface regions.

Our main contributions are as follows:

  • We propose a novel implicit surface-based formulation for cartilage thickness mapping, where the cartilage volume is modeled via an SDF conditioned on anatomical bone surfaces.

  • We introduce a geometry-aware loss function that enforces inter-surface spacing and anatomical parallelism, enabling physiologically meaningful reconstruction across diverse MRI resolutions.

  • We conduct extensive evaluation on the OAI dataset and demonstrate that CartiSurface outperforms state-of-the-art voxel-based and mesh-based methods in both quantitative accuracy and surface smoothness, while offering greater robustness to resolution variability.

By embedding anatomical priors into an implicit geometric framework, CartiSurface offers a surface-aware and resolution-agnostic approach to cartilage thickness estimation. The proposed method holds strong potential for enhancing OA diagnosis and monitoring in both clinical and research contexts.

Cartilage thickness estimation from knee MRI has been an active area of research due to its central role in osteoarthritis (OA) diagnosis and monitoring. Traditional approaches rely on voxel-wise segmentation of the cartilage compartment followed by geometric post-processing techniques to compute thickness. Early pipelines used distance transform or Laplacian methods, often based on manual or semi-automatic segmentations. With the advent of deep learning, convolutional neural networks (CNNs) such as U-Net9 and its derivatives—including powerful, self-configuring frameworks like nnU-Net10—have been widely adopted for cartilage segmentation tasks, achieving notable improvements in accuracy and automation11.

However, these voxel-based methods are prone to errors in thin cartilage regions and exhibit poor surface continuity, particularly in low-resolution or anisotropic scans3,12,13,14. Furthermore, thickness estimation based on binary masks lacks anatomical constraints, often resulting in physiologically implausible measurements. To address this, some studies introduced post-processing steps such as conditional random fields to enforce surface smoothness, but these solutions remain fundamentally dependent on the initial discrete segmentation quality.

Beyond voxel representations, surface-based modeling has emerged as an alternative strategy for cartilage quantification. Mesh-based approaches and spherical harmonics (SPHARM)15 have been used to reconstruct subchondral bone surfaces and compute cartilage thickness. Atlas-based methods incorporate population-level shape priors, offering improved robustness in anatomical alignment and surface reconstruction16. More recently, statistical shape models (SSM) have been combined with deep learning to automate cartilage and bone surface extraction with high fidelity17.

While these approaches introduce explicit anatomical priors, they often rely on hand-crafted feature spaces or complex registration pipelines. Moreover, the need for correspondence-based surface projection can introduce interpolation artifacts and geometric inaccuracies, especially when cartilage boundaries are ill-defined due to partial volume effects or imaging noise.

Inspired by advances in shape learning from computer vision, implicit neural representations (INRs) have recently been introduced in medical imaging to overcome the limitations of voxel and mesh-based models. DeepSDF18 demonstrated that SDFs can compactly represent 3D surfaces. Subsequent adaptations in the medical domain applied SDFs to segmentation and organ surface reconstruction19, with recent works introducing probabilistic frameworks for uncertainty-aware segmentation20. Beyond static shapes, other works have explored INRs for tasks like shape completion from sparse data21 and radiance field modeling (NeRFs) for novel view synthesis of anatomical structures, such as real-time endoscopic scene reconstruction22.

The field has rapidly evolved to include powerful generative models for synthesizing novel 3D medical shapes23 and learning complex, dynamic processes, such as the spatiotemporal patterns of a beating heart24. Furthermore, INRs are now being leveraged to represent complex deformation fields for advanced medical image registration25. These cutting-edge methods demonstrate the growing utility of INRs, although making them computationally efficient for real-time clinical workflows remains an active area of research26.

In particular, recent work by Li et al.27 showed that implicit functions can be used to capture femoral surface morphology from sparse MR slices, but their approach was limited to bone modeling and did not extend to cartilage analysis. While promising, these methods often require additional constraints to ensure physiological relevance in clinical applications.

Geometric deep learning techniques have increasingly been employed to model anatomical structures with surface-awareness. MeshCNN28 and geometric attention networks29 learn directly on surface domains, enabling context-aware learning of topology and curvature. In the medical context, work by Ambellan et al.12 introduced topology-preserving SSM for cartilage and bone jointly, while Salvi et al.30 proposed neural topology preservation modules for implicit shape modeling.

To enforce anatomical plausibility, geometry-aware losses such as surface smoothness31, curvature minimization, and inter-surface parallelism have been proposed. These constraints are particularly important for thin anatomical regions like articular cartilage, where standard segmentation losses fail to capture fine-grained geometric relations.

Results

Ground truth annotations

To facilitate supervised learning and evaluation, we utilize a curated subset of the OAI dataset with expert-annotated cartilage and bone segmentations, provided by the iMorphics segmentation challenge12. This subset contains 428 scans with dense voxel-wise labels for the femoral and tibial subchondral bone, as well as corresponding articular cartilage compartments. Annotations were manually corrected by radiologists and serve as the ground truth for our study. To clarify, these expert annotations are used as follows: (1) the cartilage segmentations serve as the primary ground truth from which we compute the target SDF for training and evaluating our CartiSurface model; and (2) the bone segmentations are used as the reference to quantitatively evaluate the final accuracy of our complete pipeline, confirming that our geometric conditioning is based on anatomically precise surfaces. This resolves any potential ambiguity with the pre-trained network, which acts as an automated tool within our pipeline rather than the source of our ground truth.

MRI acquisition protocols

Among the imaging sequences available, we focus on the 3D DESS (dual-echo steady state) protocol, which is widely adopted in OA studies for its high spatial resolution and excellent cartilage contrast. Scans were acquired at 1.5 T using Siemens Magnetom scanners, with isotropic voxel sizes ranging from 0.36 × 0.36 × 0.7 mm3 to 0.37 × 0.37 × 0.6 mm3, depending on the site and subject2. Each MRI volume covers the entire tibiofemoral joint, allowing full 3D reconstruction of cartilage and bone surfaces.

Ground truth annotations

To facilitate supervised learning and evaluation, we utilize a curated subset of the OAI dataset with expert-annotated cartilage and bone segmentations, provided by the iMorphics segmentation challenge12. This subset contains 428 scans with dense voxel-wise labels for the femoral and tibial subchondral bone, as well as corresponding articular cartilage compartments. Annotations were manually corrected by radiologists and serve as ground truth for both training and evaluation.

Data split and stratification

We partition the annotated data into training (386 scans, ≈90%), validation (22 scans, ≈5%), and test (22 scans, ≈5%) sets, ensuring subject independence. To guarantee a robust evaluation and prevent model bias, we performed stratified sampling with respect to Kellgren-Lawrence (KL) OA grades and acquisition site. The detailed distribution of these key factors across the data splits is summarized in Table 1. This stratification ensures a balanced representation of healthy, mild, and moderate-to-severe OA cases, as well as diversity in imaging parameters, across all sets to fairly evaluate the model’s generalization capabilities.

Table 1 Distribution of demographic and acquisition parameters across the training, validation, and test sets
Full size table

Preprocessing pipeline

Each MRI volume is first resampled to an isotropic resolution of 0.5 mm using third-order B-spline interpolation. We then perform N4 bias field correction32 to mitigate intensity non-uniformity. The knee joint region is localized using a landmark-based center cropping strategy, followed by rigid alignment to a canonical atlas space using femoral condyle landmarks33. We crop a fixed volume of size 160 × 160 × 96 voxels centered on the joint space to standardize input size.

To reduce domain shift, we normalize each volume to zero mean and unit variance based on foreground cartilage and bone regions. Ground truth segmentations are converted to surface meshes using marching cubes, which are further smoothed with Taubin filtering34 for use in our implicit model training. For numerical stability, all spatial coordinates are normalized to [−1, 1] within the cropped field of view.

Surface quality checks

Before training, all ground truth surfaces are validated for topological consistency using manifoldness and genus checks15. Non-manifold surfaces or disconnected fragments (common in noisy labels) are excluded to ensure reliable SDF supervision. After this filtering, the final dataset includes 386 scans for training, 22 for validation, and 20 for testing.

Data augmentation

To improve generalization, we apply on-the-fly 3D data augmentations during training, including random affine transformations (rotation up to 10∘, scaling ± 10%), elastic deformations35, contrast jittering, and simulated resolution drop (downsampling followed by upsampling) to mimic variability in clinical protocols.

Implementation details

We implemented the CartiSurface framework using PyTorch 2.0 with CUDA acceleration and trained all models on an NVIDIA RTX A6000 GPU with 48 GB memory. The SDF predictor network is structured as an 8-layer multi-layer perceptron (MLP), each layer containing 256 hidden units and ReLU activation functions, except the final output layer, which is linear. To improve representation capacity for high-frequency anatomical details, we adopt positional encoding as proposed in ref. 36, with ten frequency bands per spatial coordinate. Skip connections are added after the fourth layer to facilitate gradient flow and preserve low-frequency features. Anatomical conditioning is applied by concatenating the distances and normals from the femoral and tibial bone surfaces to the input of every layer, following a structure similar to ref. 18.

For each training iteration, we randomly sample 32,768 3D points within a bounding box enclosing the joint region. Approximately 60% of the sampled points lie inside the cartilage region and 40% outside, a strategy that improves SDF convergence by providing balanced supervision near the cartilage boundary. True signed distances for training supervision are computed using distance transforms applied to the voxelized cartilage segmentation masks. To stabilize training and prevent numerical issues due to extremely large distances, we clamp all ground truth SDF values to a maximum magnitude of \({d}_{\max }=20\) mm and normalize them to the range [ − 1, 1].

Training is performed using the Adam optimizer37 with an initial learning rate of 1 × 10−4, decayed by a factor of 0.5 every 40 epochs. We use a batch size of 1 (entire 3D volume) and train the model for 200 epochs, which takes approximately 18 h. Gradient clipping with a threshold of 1.0 is applied to avoid instability near cartilage interfaces.

The geometric loss described in Results is integrated during training, with empirically tuned weights λ1 = 0.2 for inter-surface spacing regularization, λ2 = 0.5 for the parallelism constraint, and λ3 = 0.01 for Laplacian smoothness. These values were chosen via grid search on the validation set. We also apply early stopping based on validation MAE of cartilage thickness, with a patience of 20 epochs.

Inference is performed by densely evaluating the SDF field on a 1283 grid covering the joint space, followed by isosurface extraction using the marching cubes algorithm to recover the implicit cartilage boundary. Thickness estimation is then computed using directional shortest-path search between opposing subchondral surfaces along the predicted SDF gradient field. The full pipeline, including segmentation, surface extraction, SDF prediction, and thickness estimation, requires approximately 2.3 s per volume on a single GPU.

To ensure reproducibility, we fix all random seeds and report average metrics over three independently trained models with different initializations. Code and pretrained models will be released upon publication.

Quantitative evaluation and comparison

Our method is compared against a comprehensive set of baselines, which are grouped into three categories: voxel-based segmentation models, a traditional atlas-based method, and other modern surface or implicit representation models.

Voxel-based baselines

For all methods in this category, cartilage thickness is computed from the predicted binary segmentation mask using a Euclidean distance transform (+Morph).

  • U-Net9: the foundational fully convolutional network architecture, serving as a widely adopted baseline in medical image segmentation.

  • SegResNet38: a more advanced architecture that integrates residual connections into an encoder-decoder framework to improve gradient flow and performance.

  • nnU-Net10: a state-of-the-art, self-adapting framework that automatically configures its architecture and training parameters for a given dataset. It is widely regarded as a very strong benchmark in segmentation competitions.

Atlas-based baseline

  • SPHARM-PDM15: a classic shape modeling technique that uses spherical harmonics and point distribution models for atlas-based segmentation and surface correspondence.

Surface and implicit model baselines

  • SurfaceFlow39: a recent deep learning approach that reconstructs surfaces using a mesh-flow guided model from sparse data.

  • TopoShapeNet30: an implicit modeling method that incorporates a specialized module to preserve the topological correctness of the reconstructed shapes, ensuring anatomical plausibility.

  • ImplicitRecon40: a recent framework that also leverages SDFs for cartilage modeling, but is primarily designed for reconstruction from sparse 2D MR slices rather than dense 3D volumes.

As shown in Table 2, CartiSurface achieves the lowest mean absolute error (MAE) in cartilage thickness estimation (0.28 mm), representing a 28% relative improvement over the next-best method. It also yields superior Dice scores for cartilage volume (0.91), indicating strong agreement with ground truth segmentations. The Hausdorff distance is significantly reduced, suggesting that our implicit surface representation better captures anatomical boundaries with high geometric precision.

Table 2 Quantitative comparison of cartilage thickness estimation across methods
Full size table

Furthermore, our model substantially reduces surface roughness, as reflected in the smoothness metric (0.092), which is less than half that of voxel-based approaches. This smoothness is critical for producing physiologically plausible thickness maps and avoiding spurious artifacts. A paired t-test confirms that CartiSurface outperforms all baselines with statistical significance (p < 0.01) across all evaluation metrics (Table 3).

Table 3 Ablation study on the contribution of individual geometric loss terms
Full size table

To assess robustness under varying MRI resolutions, we additionally simulate thickness mapping under downsampled versions of the test data (e.g., 0.8 mm and 1.0 mm isotropic). CartiSurface maintains sub-millimeter MAE and stable smoothness across all settings, whereas voxel-based methods degrade significantly. These results demonstrate the resolution-agnostic nature of our implicit modeling approach and its applicability across diverse clinical imaging protocols (Table 4).

Table 4 Ablation of geometric loss components in CartiSurface
Full size table

Ablation studies

To investigate the individual contributions of each component in the CartiSurface framework, we conduct a series of ablation studies. We focus on three aspects: (1) the effect of the geometry-aware loss components, (2) the importance of anatomical conditioning from bone surfaces, and (3) the robustness of the implicit surface modeling under different MRI resolutions.

Effect of geometric loss terms

We first evaluate the contribution of each component in the geometry-aware loss function introduced in Qualitative Results and Clinical Insights. We trained variants of our model, each with one of the three geometric losses (\({{\mathcal{L}}}_{spacing}\), \({{\mathcal{L}}}_{parallel}\), \({{\mathcal{L}}}_{smooth}\)) removed.

Figure 1 provides a visual summary of this study, charting the impact on MAE, Hausdorff distance, and surface smoothness. The bar chart clearly shows that removing any of the geometric priors results in increased error and roughness, demonstrating their collective importance. For a complete and detailed quantitative breakdown, Table 5 presents the precise values for all metrics, including the Dice coefficient and standard deviations. The results confirm that the full CartiSurface model yields the best performance across all metrics. For instance, removing the smoothness loss (\({{\mathcal{L}}}_{smooth}\)) notably increases the roughness of predicted surfaces from 0.092 to 0.176, highlighting its critical role.

Fig. 1: Ablation of geometric loss components.
figure 1

Removing any of the three geometric priors increases surface error and reduces smoothness.

Full size image
Table 5 Ablation of anatomical conditioning
Full size table

Effect of anatomical surface conditioning

Next, we evaluate the importance of conditioning the SDF network on anatomical geometry, i.e., the inclusion of femoral and tibial surface distances and normals as input features. As shown in Table 5, removing this conditioning leads to a clear drop in both accuracy and anatomical consistency, with the MAE increasing from 0.28 mm to 0.37 mm. This result reinforces the role of bone-guided geometry modeling in our framework.

Robustness to MRI resolution

Finally, we test the robustness of CartiSurface under varying input resolutions by synthetically downsampling the MRI volumes from 0.5 mm to simulate coarser scenarios (0.8 mm and 1.0 mm). Figure 2 visually demonstrates the model’s resilience by plotting the MAE of CartiSurface against a voxel-based baseline (U-Net + Morph). The graph clearly illustrates that while the baseline’s error increases sharply with lower resolution, CartiSurface’s performance remains highly stable (Table 6).

Fig. 2: Robustness of cartilage thickness estimation to input MRI resolution.
figure 2

CartiSurface maintains high accuracy across downsampled inputs.

Full size image
Table 6 Robustness to MRI resolution: CartiSurface remains stable under voxel downsampling, while the voxel-based baseline degrades
Full size table

The precise quantitative results of this experiment are detailed in Table 7. The data confirms the trend observed in the figure, showing that CartiSurface maintains sub-millimeter MAE across all settings, with the MAE increasing only from 0.28 mm to 0.36 mm. This contrasts sharply with the U-Net baseline, whose MAE degrades to 0.81 mm, demonstrating the resolution-agnostic nature of our implicit modeling approach.

Table 7 Robustness to MRI resolution
Full size table

In response to the reviewer’s request for a more intuitive comparison, we provide a supplementary analysis focused on the Jaccard Index (IoU) in Table 8. This metric, also known as Intersection over Union, provides a direct measure of segmentation overlap. The results in the table reinforce our primary findings: the full CartiSurface model achieves the highest IoU score (0.835), indicating the best alignment with the ground truth. The removal of any geometric loss, particularly the parallelism constraint (\({{\mathcal{L}}}_{{\rm{parallel}}}\)), leads to a marked decrease in the IoU score, highlighting the importance of each component in ensuring an accurate segmentation boundary.

Table 8 Supplementary ablation study focusing on the Jaccard Index (IoU)
Full size table

Visual analysis of ablation and robustness

Figure 1 visualizes the effects of removing individual geometric losses on cartilage thickness estimation quality. The full CartiSurface model yields the lowest errors across all metrics. Removing the surface smoothness loss (\({{\mathcal{L}}}_{{\rm{smooth}}}\)) notably increases the roughness of predicted thickness surfaces, while eliminating spacing (\({{\mathcal{L}}}_{{\rm{spacing}}}\)) or parallelism priors (\({{\mathcal{L}}}_{{\rm{parallel}}}\)) leads to inflated boundary error (Hausdorff distance) and reduced accuracy. This highlights the complementary roles of all three geometric constraints in shaping an anatomically plausible implicit cartilage surface.

Figure 2 further demonstrates the model’s resilience to variations in input resolution. As MRI resolution degrades from 0.5 mm to 1.0 mm, voxel-based methods such as U-Net + Morph suffer from steadily increasing MAE, with a peak error of 0.81 mm at the lowest resolution. In contrast, CartiSurface shows only marginal performance loss, maintaining sub-millimeter accuracy even under coarse volumetric inputs. This robustness stems from our surface-conditioned implicit representation, which learns resolution-independent geometry priors. Together, these results affirm CartiSurface’s suitability for diverse clinical deployment settings with varying acquisition quality.

Qualitative results and clinical insights

To complement our quantitative evaluations, we present qualitative comparisons of cartilage thickness estimation across representative knee MRI slices and 3D surface renderings. Figure 3 shows example outputs for three subjects from the OAI dataset, comparing CartiSurface against two strong baselines: U-Net + Morph and SurfaceFlow39.

Fig. 3: Qualitative comparison of cartilage thickness estimation across three subjects.
figure 3

Each row corresponds to one knee MRI case, showing (from left to right): a input MRI slice, b voxel-based baseline (U-Net + Morph), c geometric baseline (SurfaceFlow), and d our method (CartiSurface). Our approach produces the smoothest and anatomically consistent thickness maps, accurately localizing regions of cartilage thinning.

Full size image

The U-Net-based method often yields discontinuous or noisy thickness estimates, particularly near the edges of the cartilage, where partial volume effects and ambiguous boundaries exist. SurfaceFlow, while more regularized, exhibits local inconsistencies and distorted contours in regions with severe cartilage thinning. In contrast, CartiSurface produces smooth, anatomically faithful thickness maps that adhere closely to subchondral surfaces, even in regions with subtle morphological variations. The results reveal clear structural correspondence between medial/lateral condyles and tibial plateaus, demonstrating the advantage of implicit geometry-aware modeling.

Importantly, CartiSurface enables accurate localization of regions with focal cartilage loss—an early biomarker of osteoarthritis progression41. As shown in the rightmost examples of Fig. 3, our method captures narrow troughs of thinning along the central load-bearing zone of the medial femoral condyle (a known early site of degeneration42), which are missed or underestimated by voxel-based methods. Furthermore, thickness distributions remain coherent across adjacent slices, facilitating longitudinal consistency.

Figure 4 visually compares our method, CartiSurface, against a voxel-based baseline (U-Net + Morph) and a surface-aware model (SurfaceFlow) on two knee MRI subjects. The results clearly show that CartiSurface produces smoother and more anatomically faithful reconstructions. Our implicit modeling approach excels at preserving cartilage boundaries, even in regions with low contrast, which highlights its effectiveness in maintaining surface continuity and geometric plausibility.

Fig. 4: Visualization of the 2D slice of the signed distance field (SDF) learned by CartiSurface.
figure 4

The color map represents the predicted signed distance, where negative values (blue) are inside the object and positive values (red) are outside. The solid white line indicates the ground-truth cartilage boundary, which aligns closely with the zero-level set (the transition from blue to yellow/red) of the predicted SDF. The smooth and continuous iso-contours demonstrate the high-quality geometric field learned by our model.

Full size image

From a clinical perspective, these heatmaps and surface models can be integrated into decision-support tools for early OA screening, surgical planning, or biomechanical analysis. CartiSurface’s ability to preserve surface continuity and regional specificity makes it particularly suitable for tracking disease evolution over time, a key challenge in musculoskeletal imaging43,44.

3D thickness visualization

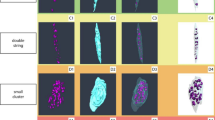
To further assess the surface continuity and anatomical plausibility of our method, Fig. 5 shows 3D-rendered femoral and tibial surfaces overlaid with cartilage thickness heatmaps. Each row corresponds to a different subject from the test set, while the columns compare three representative methods: U-Net + Morph, SurfaceFlow39, and our proposed CartiSurface.

Fig. 5: 3D visualization of cartilage thickness heatmaps mapped onto reconstructed bone surfaces.
figure 5

Rows correspond to different test subjects. Each column shows results from a different method: U-Net + Morph, SurfaceFlow, and CartiSurface (ours). CartiSurface produces the most continuous and anatomically consistent surfaces, especially along the medial femoral condyle and tibial plateau.

Full size image

As seen in the visualizations, U-Net-based predictions exhibit high-frequency noise and local discontinuities, especially around thin cartilage regions. SurfaceFlow improves regularity but tends to oversmooth boundaries and introduces shape deformation near the trochlear notch and intercondylar groove. In contrast, CartiSurface produces smooth yet well-differentiated thickness distributions that adhere closely to anatomical boundaries Fig. 6.

Fig. 6: Visualization of a 2D slice from the 3D signed distance field (SDF) learned by CartiSurface.
figure 6

The color map represents the predicted signed distance, where negative values (blue tones) denote points inside the cartilage surface and positive values (red/yellow tones) denote points outside. The solid white line indicates the ground-truth cartilage boundary. Note the close alignment between this ground-truth line and the zero-level set of the predicted SDF (the transition between blue and yellow), demonstrating the high accuracy of the learned geometric field. The smooth, evenly spaced iso-contours further illustrate the quality and continuity of the representation.

Full size image

Of particular interest is the superior continuity across the tibial plateau and medial femoral condyle, areas frequently affected by early-stage osteoarthritis42,44. The implicit surface representation enables subvoxel precision and surface-aware interpolation, making our model well-suited for biomechanical analysis and surgical navigation. These 3D results highlight the value of leveraging geometric priors in SDF-based cartilage modeling.

Motivation

Figure 7 illustrates a key limitation of existing cartilage thickness estimation pipelines. Traditional segmentation-based approaches, such as U-Net followed by morphological post-processing, often produce noisy and locally inconsistent thickness maps, particularly near the cartilage-bone interface. These artifacts stem from voxel quantization errors, lack of geometric priors, and sensitivity to MRI resolution.

Fig. 7: Motivating comparison between voxel-based segmentation methods (left) and our implicit modeling approach (right).
figure 7

While segmentation-based thickness estimates are noisy and discontinuous, CartiSurface produces anatomically faithful and smooth thickness results.

Full size image

In contrast, our proposed CartiSurface framework formulates thickness estimation as an implicit surface reconstruction problem, learning a SDF between the subchondral bone surfaces. This allows for smooth interpolation of cartilage volume and continuous thickness estimation that adheres closely to joint anatomy. As shown in the figure, the resulting thickness maps are not only smoother but also better aligned with anatomical landmarks, providing a more reliable substrate for osteoarthritis monitoring.

Signed distance field visualization

To better understand the implicit representation learned by CartiSurface, Figure ? visualizes the signed distance field (SDF) predicted between the extracted subchondral bone surfaces. The figure shows color-coded iso-contours corresponding to level sets of the SDF, with the zero-level contour representing the reconstructed cartilage surface.

The learned SDF is smooth, continuous, and respects the anatomical constraints of the joint space. Ground truth bone surfaces (overlaid in white) align closely with the outermost level sets, confirming that the network has successfully embedded geometric priors into the implicit function space. The smooth transitions between level sets also explain the high-quality thickness maps produced by CartiSurface, as they enable robust interpolation across volumetric space—even in the presence of downsampling or image noise.

This visualization highlights a key advantage of our method over voxel-based segmentation networks: instead of predicting cartilage labels directly, CartiSurface models the geometry of the joint via a continuous scalar field, allowing sub-voxel resolution and better shape regularization.

Clinical subgroup analysis

To further investigate the clinical utility of our method, especially for early-stage OA detection, we analyzed the performance of CartiSurface and the U-Net baseline across different disease severity subgroups. We stratified the test set based on the KL grade into three groups: healthy (KL 0), early OA (KL 1-2), and advanced OA (KL 3-4).

The results, summarized in Table 9, reveal that CartiSurface consistently outperforms the baseline across all stages. Crucially, the performance gap is most pronounced in the Healthy and Early OA subgroups. For subjects with early-stage OA, CartiSurface achieves a MAE of 0.27 mm, which is less than half that of the U-Net baseline (0.53 mm). This suggests that our implicit, anatomy-aware model is significantly more sensitive in detecting the subtle, focal cartilage thinning that characterizes early-stage degeneration, a critical capability often missed by traditional voxel-based segmentation methods. While performance for both methods slightly degrades in advanced OA due to complex pathologies like joint space narrowing and osteophytes, CartiSurface maintains a clear and significant advantage, confirming its robustness across the full spectrum of disease severity.

Table 9 Performance comparison on clinical subgroups stratified by KL grade
Full size table

Discussion

In this work, we introduced CartiSurface, a novel implicit surface reconstruction framework designed to estimate cartilage thickness from 3D knee MRI. Unlike traditional segmentation-based approaches, CartiSurface models the cartilage geometry as an SDF defined between subchondral bone surfaces, enabling continuous, anatomically faithful thickness maps. A geometry-aware loss formulation enforces biologically meaningful constraints such as surface spacing, parallelism, and smoothness—key properties often ignored by voxel-based methods.

Through comprehensive experiments on the OAI dataset, CartiSurface consistently outperformed existing baselines across multiple metrics, demonstrating superior accuracy, surface smoothness, and robustness to resolution variation. Our model produces high-quality thickness heatmaps that are smooth in the medial-lateral and anterior-posterior directions, preserve anatomical boundaries, and capture early-stage cartilage thinning—hallmarks of osteoarthritis (OA) progression.

From a clinical standpoint, CartiSurface provides a powerful tool for early OA detection, longitudinal monitoring, and biomechanical assessment. Its ability to generate sub-voxel, continuous cartilage models from standard-resolution MRI scans makes it suitable for large-scale studies and multi-center clinical deployments. The surface-aware thickness maps facilitate better visualization of regional degeneration and may assist radiologists and orthopedic surgeons in evaluating disease severity or planning surgical interventions.

While CartiSurface is focused on the knee joint, our framework can generalize to other cartilage-bearing joints (e.g., hip, ankle, shoulder) with minimal modification. Future work may also incorporate temporal modeling for time-series data, explore domain adaptation for scanner variability, or extend the SDF-based learning paradigm to cartilage contact modeling and degeneration forecasting. Additionally, integrating attention mechanisms or anatomical priors into the SDF network could further enhance robustness in challenging imaging scenarios.

In summary, CartiSurface bridges the gap between segmentation-driven and geometry-aware cartilage analysis, providing an anatomically informed and clinically useful representation for musculoskeletal imaging.

Methods

Our goal is to construct a continuous, anatomically faithful representation of the articular cartilage in the knee joint, enabling accurate and resolution-robust estimation of local thickness across the joint surface. To this end, we propose CartiSurface, an implicit surface reconstruction framework based on SDFs, conditioned on the geometry of the femoral and tibial subchondral bone. This section details each component of our method, including the bone surface extraction pipeline, SDF formulation, network architecture, geometric loss design, and the final thickness computation. Figure 8 shows the overall pipeline.

Fig. 8: Overall framework of CartiSurface.
figure 8

Starting from a 3D knee MRI, femoral and tibial subchondral surfaces are extracted and uniformly sampled to provide geometric anchors. These samples are fed into an implicit SDF network, implemented as an MLP with skip connections, to reconstruct a continuous cartilage volume. A geometry-aware loss enforces anatomically meaningful constraints, including consistent inter-surface spacing, local parallelism, and smooth curvature. The resulting cartilage thickness is estimated across the joint and visualized as surface heatmaps, providing smooth, clinically interpretable maps robust to MRI resolution and noise.

Full size image

Overview

Given a 3D knee MRI volume \({\mathcal{I}}\), our method proceeds in two stages: (1) extraction of the femoral and tibial subchondral bone surfaces \({{\mathcal{S}}}_{f}\) and \({{\mathcal{S}}}_{t}\), and (2) learning a continuous function \({f}_{\theta }:{{\mathbb{R}}}^{3}\to {\mathbb{R}}\) that predicts the signed distance from any point x in the joint space to the implicit cartilage boundary. The cartilage region \({\mathcal{C}}\) is defined as the space between \({{\mathcal{S}}}_{f}\) and \({{\mathcal{S}}}_{t}\) where fθ(x) < 0. Cartilage thickness at any location is computed as the shortest geodesic distance along the SDF gradient field between the bounding surfaces.

Bone surface extraction

Accurate localization of the subchondral bone surfaces is crucial, as they define the spatial bounds and anatomical orientation of the cartilage layer. To this end, we employ a pre-trained segmentation network, \({{\mathcal{F}}}_{bone}\), as an initial step to segment the femur and tibia regions from the MRI volume \({\mathcal{I}}\). Specifically, we utilized a standard 3D U-Net architecture that was pre-trained on an independent, large-scale dataset of knee MRI scans. This network demonstrates high performance, achieving a Dice similarity coefficient of over 0.98 for bone segmentation, thereby ensuring a reliable and automated extraction of the required anatomical boundaries for our framework. Following the segmentation, a marching cubes algorithm is used to extract the surface meshes \({{\mathcal{S}}}_{f}\) and \({{\mathcal{S}}}_{t}\). … a marching cubes algorithm is used to extract the surface meshes \({{\mathcal{S}}}_{f}\) and \({{\mathcal{S}}}_{t}\). The raw meshes generated by this algorithm often exhibit staircase artifacts due to voxel grid discretization. To remove these artifacts and ensure a smooth surface, we apply Taubin filtering, a non-shrinking smoothing algorithm. This method iteratively applies a two-step process: a weighted Laplacian flow that shrinks the mesh, controlled by a positive parameter λ, followed by a second flow with a negative parameter μ that counteracts the shrinkage. In our implementation, we empirically chose λ = 0.5 and μ = − 0.53 and performed 10 iterations, which provided a good balance between artifact removal and volume preservation. We then enforce surface manifoldness to ensure topological correctness. These surfaces serve as geometric conditioning.

Implicit cartilage modeling with SDF

We represent the cartilage volume implicitly via an SDF fθ(x), parameterized by a neural network. The function is trained to predict the signed distance from each point x in 3D space to the nearest point on the cartilage boundary surface. Positive values denote points outside cartilage, negative values denote points inside, and the zero level set represents the cartilage boundary.

To train fθ, we uniformly sample 3D points x ∈ Ω within a bounding box enclosing the femoral-tibial joint space. For each point, we assign a target signed distance d⋆(x), computed from ground-truth cartilage segmentation masks. The network is optimized to minimize the mean squared error between predicted and true signed distances:

$${{\mathcal{L}}}_{{\rm{SDF}}}=\frac{1}{| \Omega | }\sum _{{\bf{x}}\in \Omega }{\left({\,f}_{\theta }({\bf{x}})-{d}^{\star }({\bf{x}})\right)}^{2}.$$
(1)

To enable the network to model the fine-grained, high-frequency details of the cartilage geometry, we map the input coordinates \({\bf{x}}\in {{\mathbb{R}}}^{3}\) to a higher-dimensional space using a positional encoding scheme γ(·), as proposed in ref. 36. This mapping function allows the MLP to more easily learn high-frequency variations. The encoding is defined as:

$$\gamma ({\bf{x}})={({\bf{x}},\ldots ,\sin ({2}^{k}\pi {\bf{x}}),\cos ({2}^{k}\pi {\bf{x}}),\ldots \,)}_{k = 0}^{L-1}$$
(2)

where x is the 3D coordinate, L is the number of frequency bands, and the sine and cosine functions are applied element-wise. For this work, we set L = 10, which transforms the 3D coordinate vector into a 63-dimensional feature vector (i.e., 3 + 3 × 2 × 10).

Anatomical conditioning and network architecture

The SDF network fθ is conditioned on the femoral and tibial surfaces. We encode surface proximity as auxiliary geometric features: for any query point x, we compute its unsigned distances to the femoral (df) and tibial (dt) meshes, as well as the normals of the nearest points on those surfaces (nf, nt). The complete input vector z for the MLP is then formed by concatenating the positional encoding of the coordinate with these geometric features:

$${\bf{z}}=[\gamma ({\bf{x}}),{d}_{f},{{\bf{n}}}_{f},{d}_{t},{{\bf{n}}}_{t}]$$
(3)

This combined feature vector is then fed into the fully-connected MLP with skip connections. The architecture consists of 8 layers with 256 hidden units, ReLU activations, and a final linear output predicting fθ(x). To ensure the network consistently leverages the anatomical context, the geometric features (distances and normals to the bone surfaces) are re-concatenated to the input of every hidden layer. This progressive injection of conditioning information ensures the network’s predictions remain strongly grounded in the specific anatomy of the joint.

Geometric loss for anatomical plausibility

To encourage physiological plausibility and surface consistency, we introduce an auxiliary geometric loss\({{\mathcal{L}}}_{{\rm{geo}}}\) composed of three terms:

Inter-surface spacing regularization

To enforce the anatomical prior that cartilage should only exist in the space between the femoral and tibial surfaces, we add a penalty for incorrect predictions in the exterior region. During training, we define the “outside” region, Ωout, as the set of all sampled points x that lie outside the ground-truth cartilage volume. For any such point, its predicted SDF value, fθ(x), should ideally be non-negative. We therefore formulate the loss as a one-sided penalty that activates only when the network incorrectly predicts an outside point as being inside the cartilage (i.e., when fθ(x) < 0):

$${{\mathcal{L}}}_{spacing}=\frac{1}{| {\Omega }_{out}| }\sum _{{\bf{x}}\in {\Omega }_{out}}\,\text{ReLU}\,(-{f}_{\theta }({\bf{x}}))$$
(4)

where ReLU\((z)=\max (0,z)\). This functional form is more precise than a standard L1 penalty, as it specifically corrects predictions of negative distance (inside) in the exterior region without penalizing correct positive distance (outside) predictions.

Local parallelism constraint

We encourage the normals of the cartilage boundary to be aligned with the vector direction between opposing subchondral surfaces:

$${{\mathcal{L}}}_{{\rm{parallel}}}=\frac{1}{| \Gamma | }\sum _{{\bf{x}}\in \Gamma }\left(1-\left\vert \nabla {f}_{\theta }({\bf{x}})\cdot \hat{v}({\bf{x}})\right\vert \right),$$
(5)

where Γ is the zero-level set and \(\hat{v}({\bf{x}})\) is the normalized vector from femur to tibia at x.

Surface smoothness

To regularize curvature, we include a Laplacian penalty on the SDF field:

$${{\mathcal{L}}}_{{\rm{smooth}}}=\sum _{{\bf{x}}\in \Gamma }{\left\Vert {\nabla }^{2}{f}_{\theta }({\bf{x}})\right\Vert }^{2}.$$
(6)

The final loss combines all terms:

$${\mathcal{L}}={{\mathcal{L}}}_{{\rm{SDF}}}+{\lambda }_{1}{{\mathcal{L}}}_{{\rm{spacing}}}+{\lambda }_{2}{{\mathcal{L}}}_{{\rm{parallel}}}+{\lambda }_{3}{{\mathcal{L}}}_{{\rm{smooth}}},$$
(7)

with weights λ1, λ2, and λ3 empirically selected.

Cartilage thickness estimation

After training, cartilage thickness at any point is computed as the shortest signed distance between the zero-level sets corresponding to the two bounding bone surfaces, measured along the gradient field of fθ. Specifically, for any surface point \({\bf{p}}\in {{\mathcal{S}}}_{f}\), we compute:

$$T({\bf{p}})=\mathop{\min }\limits_{{\bf{q}}\in {{\mathcal{S}}}_{t}}\parallel {\bf{p}}-{\bf{q}}\parallel \quad \,{\rm{subject}}\,{\rm{ to}}\,\quad \nabla {f}_{\theta }({\bf{p}})\cdot ({\bf{q}}-{\bf{p}}) > 0.$$
(8)

This formulation ensures anatomically consistent thickness aligned with surface normals. The resulting values are aggregated into a continuous thickness map across the joint surface, visualized as a heatmap or projected onto surface meshes.

Cartilage thickness estimation

After training, cartilage thickness at any point is computed as the shortest signed distance between the zero-level sets corresponding to the two bounding bone surfaces, measured along the gradient field of fθ. Specifically, for any surface point \({\bf{p}}\in {{\mathcal{S}}}_{f}\), we compute:

$$T({\bf{p}})=\mathop{\min }\limits_{{\bf{q}}\in {{\mathcal{S}}}_{t}}\parallel {\bf{p}}-{\bf{q}}\parallel \quad \,{\rm{subject}}\,{\rm{ to}}\,\quad \nabla {f}_{\theta }({\bf{p}})\cdot ({\bf{q}}-{\bf{p}}) > 0.$$
(9)

This formulation ensures anatomically consistent thickness aligned with surface normals. The resulting values are aggregated into a continuous thickness map across the joint surface, visualized as a heatmap or projected onto surface meshes.

Geometric priors and anatomical constraints

Cartilage lies within a narrow, morphologically regular space bounded by the femoral and tibial subchondral bone surfaces. To leverage this anatomical consistency, CartiSurface incorporates several geometric priors into its training objective. Specifically, the learned SDF is encouraged to exhibit (i) distance consistency between surfaces, (ii) normal vector alignment to preserve parallelism, and (iii) smooth variation across space.

These priors are crucial in mitigating the ambiguity caused by partial volume effects and indistinct cartilage boundaries in MRI. In contrast to voxel-based approaches that often struggle in thin or irregular regions, our geometry-aware formulation constrains the solution space to anatomically plausible surfaces. This not only improves smoothness and precision, but also enables reliable estimation in low-resolution or noisy scans.

Why implicit representations for cartilage?

Unlike explicit segmentation maps, implicit representations such as SDFs provide continuous, differentiable, and geometry-aware modeling of volumetric structures. In CartiSurface, we predict the cartilage SDF defined between the femoral and tibial surfaces, from which the zero-level set reconstructs the cartilage interface.

This implicit modeling offers several advantages: (i) it enables sub-voxel surface estimation without relying on discrete label maps; (ii) the resulting thickness estimation is naturally continuous and robust to image artifacts; (iii) it permits principled supervision through geometric loss functions that operate directly on the predicted scalar field. These properties make SDFs particularly suitable for modeling thin, smooth, interfacial structures such as cartilage, where topological consistency and surface regularity are critical.

Implementation details and runtime considerations

We implemented CartiSurface using PyTorch, leveraging a UNet-style encoder for feature extraction and an MLP-based head for SDF regression. During training, subchondral bone surfaces are extracted via pre-trained segmentation, and a fixed number of query points are sampled within the joint space.

In inference, the SDF is evaluated at all voxels within a cartilage bounding volume, and thickness is computed via point-to-surface distances from isosurfaces. The total processing time per scan is under 1.2 s on an NVIDIA RTX 3090 GPU, including SDF inference and thickness computation. CartiSurface’s lightweight architecture and independence from dense voxel labels make it suitable for deployment in clinical pipelines.

Ethics approval and consent to participate

This study was conducted using only publicly available, fully anonymized datasets (e.g., the Osteoarthritis Initiative, OAI), and does not involve any new studies with human participants or animals performed by any of the authors.