Geometric multi-instance learning for weakly supervised gastric cancer segmentation

Abstract

Weakly supervised segmentation of cancerous regions in whole-slide images (WSIs) is a crucial task in computational pathology, but it is severely hampered by the need for expensive pixel-level annotations. Existing Multiple Instance Learning (MIL) frameworks, while popular, typically fail to produce accurate segmentation masks because they treat WSIs as an unordered ’bag-of-patches’, ignoring the critical tissue topology and architectural patterns that define malignancy. In this paper, we address this fundamental limitation by proposing Geometric Multi-Instance Learning (Geo-MIL), a novel graph-based framework that explicitly models the spatial relationships between tissue patches. At the core of our method is a new topological attention mechanism that operates on the WSI graph, learning to identify and prioritize entire diagnostically relevant tissue structures over isolated patch features. Through extensive experiments on three public gastric cancer datasets, we demonstrate that Geo-MIL significantly outperforms a wide array of state-of-the-art baselines, achieving a new benchmark in both segmentation accuracy and classification performance. Our work represents a significant step towards bridging the gap between weak slide-level labels and precise, pixel-level predictions, paving the way for scalable and accurate quantitative analysis in digital pathology.

Introduction

Gastric cancer (GC) is a leading cause of cancer-related mortality worldwide, with a significant disease burden¹. The gold standard for its diagnosis and staging relies on the histopathological assessment of tissue biopsies. This process involves pathologists meticulously examining whole-slide images (WSIs) to identify malignant regions, assess morphological features, and determine the extent of tumor invasion. Recently, deep learning models have shown remarkable promise in automating parts of this workflow, offering the potential to improve diagnostic efficiency and reproducibility².

A primary obstacle to developing highly accurate deep learning models for GC segmentation is the immense data annotation requirement. Fully supervised methods, such as U-Net and its variants, depend on large datasets with precise, pixel-level annotations delineating tumor boundaries. Creating these detailed masks is exceptionally laborious and time-consuming. It demands the focused effort of expert pathologists, making the process a significant bottleneck that hinders the development of scalable and robust models³.

To circumvent this annotation bottleneck, Weakly Supervised Learning (WSL) has gained significant traction. Multiple Instance Learning (MIL) stands out as the dominant WSL paradigm for computational pathology⁴. In the MIL framework, a WSI is treated as a “bag" of image patches (instances), and the model is trained using only a single, slide-level label (e.g., “tumor" or “normal"). Attention-based MIL models can successfully identify discriminative, tumor-bearing patches and have achieved state-of-the-art results in WSI classification tasks⁵.

However, the conventional MIL framework suffers from a fundamental limitation: it operates on the assumption that instances within a bag are independent and identically distributed. This “bag-of-patches" approach disregards the critical spatial context and tissue architecture inherent in histopathology. The growth patterns of gastric cancer, such as glandular formation, stromal invasion, and cell differentiation, are defined by the spatial relationships between cells and tissues, not just by the appearance of individual patches. Consequently, the localization maps generated by standard attention mechanisms are often incomplete and struggle to accurately segment diffuse or infiltrative tumor regions, as they fail to capture the underlying tissue topology.

In this work, we argue that moving beyond the “bag-of-patches" paradigm is essential for achieving precise, weakly supervised segmentation. We propose a novel Geometric Multi-Instance Learning (Geo-MIL) framework that explicitly incorporates spatial and structural priors into the learning process. Our approach models a WSI as a graph, where patches are nodes and their spatial adjacency defines the edges. This allows our model to learn not just patch-level features but also the higher-order structural patterns that characterize gastric cancer.

Unlike existing models, our Geo-MIL introduces a learnable topological gating mechanism that adaptively regulates message passing based on local tissue structure. This differentiable design enables dynamic structural reasoning-allowing the model to identify diagnostically relevant topological patterns rather than relying on fixed or handcrafted priors.

Our main contributions are as follows: We introduce Geo-MIL, a novel graph-based framework that represents whole-slide images as a graph to explicitly model the spatial relationships between tissue patches. We design a novel topological attention mechanism that operates on this graph, enabling the model to identify and focus on diagnostically relevant architectural patterns rather than just individual patch features. We effectively bridge the gap between weak supervision and dense prediction, demonstrating that our model can generate accurate and coherent segmentation masks using only slide-level labels. We provide extensive experimental validation on serval gastric cancer datasets, showing that our method significantly outperforms existing state-of-the-art MIL-based approaches.

The application of deep learning to histopathology has transformed the field of computational pathology^{2,6,7,8,9,10,11}. Early successful approaches adapted Convolutional Neural Networks (CNNs), originally designed for natural images, to classify small image patches as cancerous or benign. However, the gigapixel resolution of whole-slide images (WSIs) presented significant scaling challenges. To address this, current methodologies predominantly rely on patch-based processing pipelines combined with more advanced architectures.

The advent of Vision Transformers (ViTs) has marked a significant shift in the field. ViT-based models, such as TransMIL⁵, have demonstrated strong performance in capturing long-range dependencies and subtle textural details in tissue morphology. Self-supervised learning (SSL) has become a standard for pre-training these large models on vast unlabeled WSI corpora, such as The Cancer Genome Atlas (TCGA). These SSL techniques, such as DINO¹², enable models to learn robust and generalizable feature representations without manual annotation. Furthermore, the frontier of the field is moving towards multimodal models that integrate histopathology images with other data types, such as genomics and clinical reports^{3,13,14,15,16}.

The annotation bottleneck in digital pathology has driven the widespread adoption of Weakly Supervised Learning (WSL), with Multiple Instance Learning¹⁷ (MIL) being the most prominent paradigm. The classic attention-based MIL (AB-MIL) framework demonstrated the feasibility of training models on slide-level labels by learning to assign attention scores to the most informative patches^{4,18,19,20,21,22,23,24,25}. Building on this, recent works have replaced the aggregation mechanism with more powerful Transformer architectures, like TransMIL^5,26, which can better capture the correlations between instances (patches) within a bag (WSI).

Despite its success in classification, applying MIL to generate dense segmentation masks remains a challenge. Several recent approaches have attempted to bridge this gap. Some methods leverage the attention maps from MIL classifiers (e.g., CLAM²⁷) as seeds for segmentation, but these maps are often sparse and incomplete. Other works, like DTFD-MIL²⁸, explore specialized architectures to improve localization. However, the robustness of these methods can be sensitive to the quality of the initial signals. Our work differs by fundamentally changing the instance representation^11,29 from an unordered set to a structured graph, which we argue is essential for generating coherent segmentations.

Graph Neural Networks (GNNs) have emerged as a powerful tool for modeling complex relationships in data, making them highly suitable for medical image analysis where context and structure are critical^30,31. In histopathology, GNNs are increasingly used to represent the intricate tumor microenvironment. While some studies construct graphs at the cellular level, these methods often require accurate segmentation and can be computationally intensive.

An alternative and more scalable approach involves constructing graphs at the patch level. In these models, each node corresponds to a tissue region, and edges represent spatial adjacency. This strategy has been successfully applied to WSI classification and survival prediction tasks, demonstrating the value of modeling tissue architecture³². Our work builds upon this patch-graph paradigm but introduces a novel topological attention mechanism specifically designed for the weakly supervised segmentation task, a direction that remains largely unexplored.

Results

We conduct a series of comprehensive experiments to validate the effectiveness of our proposed Geo-MIL framework. We aim to answer the following key questions: (1) Does our method outperform existing state-of-the-art weakly supervised methods for both slide-level classification and lesion segmentation? (2) Are the proposed components of our model, namely the graph representation and the topological attention mechanism, essential for its performance? (3) Can our model produce qualitatively accurate and clinically meaningful segmentation maps?

Datasets and preprocessing

To ensure a robust and reproducible evaluation, we conduct our experiments on three publicly available gastric cancer histopathology datasets.

The Cancer Genome Atlas-Stomach Adenocarcinoma (TCGA-STAD)³³ is a large-scale, multi-institutional cohort. We obtained the formalin-fixed paraffin-embedded (FFPE) whole-slide images from the Genomic Data Commons (GDC) portal. Our final dataset consists of 421 WSIs from 375 patients, including slides diagnosed as stomach adenocarcinoma and solid normal tissue slides. The diversity in staining and scanning protocols across different institutions makes this a challenging and realistic benchmark.

The Gastric Histopathology Specimen Slide Dataset (GasHisSDB)³⁴ is a curated dataset specifically for benign and malignant classification. It contains a total of 522 WSIs from 522 patients, comprising 247 benign and 275 malignant cases. The slides were digitized using a KFBIO KF-PRO-120 scanner at 40x magnification, providing a high-quality and consistent data source for evaluating classification performance.

Adenocarcinoma Data Collection-Gastric Cancer Database (ACDC-GastricDB) is an extended dataset curated by us, developed as an extension of the GasHisSDB³⁴ cohort to focus on the fine-grained classification of adenocarcinoma. We selected 102 source WSIs from 102 patients. This dataset allows us to specifically evaluate our model’s ability to identify the most common and clinically significant subtype of gastric cancer. The ground truth annotations for these slides were provided by our collaborating pathologists.

For all datasets, the initial slide-level labels (tumor/normal or benign/malignant) were obtained from the accompanying metadata or original pathology reports. To quantitatively evaluate segmentation performance, a subset of the tumor-bearing WSIs from the test split of each dataset was selected. For these slides, the tumor regions were meticulously annotated with pixel-level masks by two expert pathologists. Any disagreements were resolved by a third senior pathologist. These pixel-level annotations are used only for evaluation and are not seen during training.

For all WSIs, we first apply a threshold-based method in the HSV color space to segment the main tissue regions and remove the background. The tissue regions are then tiled into non-overlapping 256 × 256 pixel patches at an equivalent 20x magnification. For each dataset, we perform a patient-level split of the data into training (70%), validation (15%), and testing (15%) sets to ensure that no patient data leaks between the sets.

Experimental details

To obtain powerful and generalizable patch representations, we leverage a self-supervised learning approach. Specifically, we use a Vision Transformer (ViT-S/16) backbone pre-trained on the entire TCGA pan-cancer cohort (excluding our specific test sets) using the DINO self-supervised framework¹². From this pre-trained model, we extract a 384-dimensional feature vector for each 256 × 256 patch. During the training of our Geo-MIL framework, the weights of this feature extractor Φ are kept frozen to ensure stable feature distributions and reduce computational overhead.

To improve model robustness and prevent overfitting, we apply on-the-fly data augmentation during training. Before feeding patches into the feature extractor, we apply random transformations including horizontal and vertical flips, 90-degree rotations, and color jittering. For color augmentation, we specifically use a method tailored for H&E-stained images³⁵, which realistically alters the color channels to simulate variations in staining protocols.

Our proposed Geo-MIL framework is built upon the extracted patch features. We construct the WSI graph using k = 8 nearest neighbors based on patch centroid coordinates. Our Topological Attention Graph Neural Network (TopoGNN) consists of a stack of L = 3 graph layers, with a hidden feature dimension of D = 256. The final MLP classifier and the patch-level segmentation head are both composed of two linear layers with an ELU activation function in between.

The entire model is trained end-to-end using the AdamW optimizer³⁶ with an initial learning rate of 1 × 10⁻⁴ and a weight decay of 1 × 10⁻⁵. We employ a cosine annealing learning rate scheduler with a warm-up period of 5 epochs. Due to the large size of the WSI graphs, which can contain thousands of nodes, we use a batch size of 1 (one WSI per iteration) and apply gradient accumulation over 16 steps to simulate a larger effective batch size. The loss balancing hyperparameter λ was set to 0.5 after a grid search on the validation set. We train the model for a maximum of 100 epochs, with an early stopping criterion triggered if the validation Dice score does not improve for 10 consecutive epochs.

At inference time, a WSI is passed through the entire pipeline to obtain the patch-level tumor probabilities {p_i} from the segmentation head. These probabilities are then reassembled into their original spatial locations to form a 2D probability heatmap for the entire slide. A final binary segmentation mask is generated by applying a threshold of 0.5 to this heatmap. All experiments were conducted on a server equipped with 4x NVIDIA A100 80GB GPUs using the PyTorch and PyG (PyTorch Geometric) libraries.

Baselines and evaluation metrics

We compare our Geo-MIL framework against a diverse set of strong and recent baselines from various categories, representing the state-of-the-art in computational pathology:

AB-MIL⁴: The foundational attention-based MIL approach. TransMIL⁵: A prominent Transformer-based MIL model, known for its strong classification performance. DSMIL³⁷: A dual-stream MIL framework that uses both instance and bag-level features. CLAM²⁷: A popular interpretable MIL framework often used in pathology, providing both classification and heatmaps.

Patch-WI³⁸: A common approach leveraging Class Activation Maps (e.g., Grad-CAM++) from a patch-level classifier to generate heatmaps. DTFD-MIL²⁸: A dual-branch MIL method that aims to explicitly learn discriminative features for both classification and localization.

PatchGCN³²: A modern GNN approach that constructs graphs from WSI patches to model the tumor microenvironment for improved classification.

We provide a comprehensive evaluation of performance across two distinct tasks:

WSI Classification: For the slide-level diagnostic task, we employ standard metrics: Area Under the Receiver Operating Characteristic Curve (AUC), Accuracy (Acc), and F1-Score. Weakly Supervised Segmentation: For evaluating the quality of the generated pixel-level masks against pathologist-annotated ground truth, we utilize the Dice Similarity Coefficient (Dice) and Intersection over Union (IoU).

Quantitative comparison

We present the main quantitative results in Table 1, comparing our proposed Geo-MIL against all baseline methods across our three evaluation datasets. The table is organized by dataset, with performance reported for both WSI classification and weakly supervised segmentation tasks.

Table 1 Comprehensive quantitative comparison of Geo-MIL against state-of-the-art baselines across three public datasets

The results unequivocally demonstrate the superiority of our Geo-MIL framework. It achieves state-of-the-art performance. This consistent outperformance across diverse datasets underscores the robustness and generalizability of our approach. Dominance in Weakly Supervised Segmentation. The most significant advantage of Geo-MIL is seen in the segmentation task, which is the primary focus of this work. On the challenging, multi-institutional TCGA-STAD dataset, our method achieves a Dice score of 0.789. This represents a substantial margin of 6.4 points over the strongest non-graph WSS method (Patch-WI) and 6.8 points over the next best graph-based method (HistoGraph). This trend holds across all datasets. We attribute this success to our core design philosophy. Standard MIL methods (e.g., TransMIL, DSMIL) are optimized for classification and their attention maps naturally produce incomplete segmentations. While dedicated WSS methods (e.g., DTFD-MIL, Patch-WI) improve upon this, their lack of an explicit structural model limits their ability to ensure spatial coherence. Even compared to other GNN-based methods, Geo-MIL’s advantage is clear. We posit that our topological attention mechanism provides a critical edge by learning to identify and prioritize entire diagnostically relevant tissue architectures (like poorly formed glands or infiltrative patterns) rather than simply aggregating features from spatially adjacent nodes. This leads to more complete and contiguous segmentation masks that better reflect the underlying pathology.

While optimized for segmentation, Geo-MIL does not sacrifice classification accuracy. In fact, it achieves the highest AUC, Accuracy, and F1-scores on all three datasets. This suggests that by learning better, structurally-informed representations for localization, the model simultaneously creates a more discriminative feature space for the global slide-level prediction. The improved understanding of “what makes a region cancerous" directly translates to a more accurate overall diagnosis. As expected, all methods report their highest scores on the GasHisSDB dataset, likely due to its more consistent image quality and curated nature. However, the performance gaps between Geo-MIL and the baselines remain wide. The continued strong performance of our method on the more heterogeneous TCGA-STAD and ACDC-GastricDB datasets highlights its robustness to the significant variations in staining, fixation, and scanning protocols that are common in real-world, multi-center clinical data. This adaptability is a key feature for potential clinical translation.

Ablation studies

To rigorously validate the architectural choices of Geo-MIL and quantify the contribution of each of its core components, we conduct a series of ablation studies on the challenging TCGA-STAD dataset. The results, detailed in Table 2, systematically deconstruct our model and demonstrate that each component is essential for achieving state-of-the-art performance.

Table 2 Ablation study investigating the individual contributions of the key components of our Geo-MIL framework

We first investigate the three primary contributions of our framework. (B) To assess the impact of our fundamental design choice-representing the WSI as a graph-we remove the graph structure entirely, reverting to a strong Transformer-based MIL baseline that processes patches as an unordered set. This change results in the most significant performance degradation across all metrics, with the Dice score plummeting from 0.789 to 0.702. This massive 8.7-point drop confirms our central hypothesis: explicitly modeling the spatial topology of tissue is not just beneficial but essential for translating sparse slide-level labels into accurate, dense segmentations.

(C) Next, to isolate the contribution of our novel attention mechanism, we replace our TopoGNN layers with standard Graph Attention Network (GAT) layers. While this model still leverages the graph structure and outperforms the non-graph baseline, its Dice score drops to 0.721. This demonstrates that while a generic graph representation is helpful, our topological gate-which enables the model to learn representations of entire tissue architectures rather than just aggregating neighbor features-is responsible for a substantial portion of the performance gain. It is the key to generating more spatially coherent and complete segmentation masks.

(D) Finally, we validate our dual-objective training strategy by training the model using only the MIL classification loss (λ = 0) and deriving the segmentation output from the raw MIL attention scores. While the AUC remains high at 0.961, the Dice score falls sharply to 0.708. This result clearly illustrates that MIL attention, optimized solely for discriminative classification, is insufficient for producing high-fidelity segmentations. The dedicated segmentation head and our pseudo-segmentation loss are crucial for forcing the model to learn a comprehensive map of all tumorous regions, not just the most obvious ones.

Analysis of GNN Architecture: We also analyze the sensitivity of Geo-MIL to key hyperparameters of the GNN architecture. In (E) and (F), we vary the number of TopoGNN layers, L. A shallow model with L = 1 fails to capture sufficient long-range dependencies, resulting in lower performance. Increasing to L = 5 yields a marginal decrease, suggesting a risk of oversmoothing where node features become too similar. This confirms that L = 3 provides a robust balance between receptive field and model efficiency. Similarly, in (G) and (H), we show that performance is stable for a range of neighbors, k, with k = 8 providing the optimal result. This demonstrates the robustness of our framework to these specific architectural choices.

To further investigate the effect of the balance parameter λ in the dual-objective design, we varied λ from 0.1 to 1.0 and report the results in Table 3. The performance remains stable across a broad range, peaking at λ = 0.5, which balances the contribution of the classification loss and the pseudo-segmentation loss. Smaller values of λ under-emphasize the segmentation branch, leading to incomplete masks, while larger values slightly compromise slide-level discrimination. This analysis confirms that the dual-objective framework is robust and not overly sensitive to the exact value of λ.

Table 3 Sensitivity analysis of the balance parameter λ between classification and segmentation loss on the TCGA-STAD dataset

To further interpret the behavior of the proposed topological attention mechanism, we visualize the learned gate activations σ(g_i) for representative gastric cancer cases, as shown in Figs. 1 and 2. The middle column displays the topological gate activation maps, where warmer colors indicate higher gate responses. The overlay images clearly reveal that Geo-MIL assigns high gate activations to regions forming coherent tumor architectures (e.g., glandular and nested structures), while diffusely scattered or morphologically ambiguous regions are down-weighted. This adaptive gating behavior demonstrates that Geo-MIL learns to focus on diagnostically meaningful topological patterns rather than isolated local features, thereby improving both interpretability and segmentation consistency.

Fig. 1: Visualization of topological gate activations in Geo-MIL - Case 1: coherent glandular tumor structure.

This figure shows the original H& E-stained input patch (Input), the learned gate activation map σ(g_i) (Gate Activation), and their overlay visualization (Overlay) for Case 1, which exhibits a coherent glandular tumor structure. High activation values (red) highlight spatially coherent tumor regions such as glands or nests. This provides interpretability evidence that the proposed gating mechanism adaptively enhances structurally meaningful regions while filtering out irrelevant context.

Fig. 2: Visualization of topological gate activations in Geo-MIL - Case 2: diffuse infiltration pattern.

This figure illustrates the original H& E-stained input patch (Input), the learned gate activation map σ(g_i) (Gate Activation), and their overlay visualization (Overlay) for Case 2, characterized by a diffuse infiltration pattern. Low activations (blue) correspond to isolated or noisy patches that are suppressed by the topological gate. This visualization demonstrates how the gating mechanism effectively filters out irrelevant context to focus on structurally meaningful regions.

To sum up, these ablation studies provide compelling evidence that each component of the Geo-MIL framework is a deliberate and necessary design choice, working in synergy to effectively bridge the gap between weak slide-level labels and precise, pixel-level semantic segmentation.

Qualitative results and visualization

To complement our quantitative findings, we provide a qualitative analysis to visually demonstrate the performance and robustness of our Geo-MIL framework. These visualizations offer an intuitive understanding of why our topology-aware approach generates superior segmentation masks compared to methods that treat patches as an unordered set.

Figure 3 presents a head-to-head comparison with three key baselines on two challenging gastric adenocarcinoma cases. The first case (top row), featuring a multi-focal tumor, immediately highlights the limitations of competing methods. Both Patch-WI and AB-MIL fail to identify the full extent of the tumor, producing incomplete and sparse heatmaps that are unsuitable for accurate measurement. While the graph-based HistoGraph³⁹ performs better, it incorrectly merges the two distinct tumor nests into a single entity. In contrast, our method accurately delineates both regions as separate, complete objects. The second case (bottom row) showcases a complex, cribriform glandular structure. Here again, the baselines struggle to conform to the intricate boundaries, whereas Geo-MIL produces a mask that is both spatially coherent and anatomically precise, following the fine details of the pathology.

Fig. 3: Qualitative comparison of segmentation results on two representative gastric adenocarcinoma cases.

This figure compares our Geo-MIL framework ("Ours") with three key baselines representing different approaches: Patch-WI (classifier activation map), AB-MIL (standard MIL), and HistoGraph (a graph-based method). Left Case: A multi-focal tumor region. Both Patch-WI and AB-MIL fail to identify the full extent of the tumor, producing incomplete and sparse heatmaps. HistoGraph generates a more complete mask but incorrectly merges the two distinct tumor nests. In contrast, our method accurately delineates both regions as separate, complete entities. Right Case: A complex, cribriform glandular structure. Again, the baselines struggle, either capturing only a fraction of the lesion or failing to conform to the intricate boundaries. Our Geo-MIL produces a segmentation mask that is both spatially coherent and anatomically precise, closely matching the underlying pathology.

Beyond outperforming baselines, it is crucial to assess the fine-grained accuracy of our model’s outputs for potential clinical utility. Figure 4 provides a closer look at this capability on two additional cases with distinct morphologies. The segmentation masks generated by Geo-MIL (right column) show a remarkable concordance with the pathologist-annotated ground truth (middle column). Our model successfully captures the complex, irregular borders in Case A and the more lobulated structure in Case B with high fidelity. This level of precision is critical for enabling reliable downstream quantitative analyses, such as tumor area measurement or invasion front assessment, which are often used in prognostic evaluation.

Fig. 4: High-fidelity segmentation results of our Geo-MIL framework on two distinct cases.

This figure showcases the fine-grained accuracy of our model’s predictions. The columns represent the original input patch, the pathologist-annotated ground truth mask, and our model’s final segmentation result. Case A (top row) features a complex, high-grade tumor nest with highly irregular and intricate boundaries. Case B (bottom row) presents a different morphological variant with a more lobulated structure. In both challenging examples, the segmentation mask generated by our model (right column) shows a remarkable concordance with the ground truth (middle column). This demonstrates the model’s ability to learn and precisely delineate complex tumor borders, a key capability for enabling accurate downstream quantitative analyses such as tumor area measurement or invasion front assessment.

In summary, the qualitative results strongly support our quantitative findings. The visual evidence confirms that by explicitly modeling tissue architecture, Geo-MIL not only outperforms existing methods but also produces segmentation masks with a level of accuracy and coherence that demonstrates its potential for practical application in digital pathology workflows.

Performance distribution and robustness analysis

While mean performance metrics provide a summary of a model’s effectiveness, they do not capture its consistency across a diverse set of cases. To further dissect the performance of our model, we visualize the distribution of Dice scores across all test slides from the TCGA-STAD cohort for Geo-MIL and three leading baselines in Fig. 5. This analysis allows us to assess the robustness and reliability of each method.

Fig. 5: Distribution of Dice scores on the TCGA-STAD test set.

Each violin plot shows the probability density of the Dice score for a given method across all test slides. TransMIL shows high variance. Patch-WI improves the median but remains inconsistent. HistoGraph³⁹ is competitive but has a significant number of low-performing outliers. Our Geo-MIL framework demonstrates both the highest median performance and the lowest variance, indicating superior accuracy and robustness.

The violin plots reveal several key insights. The distribution for a standard MIL method like TransMIL (a) is wide and positioned lower on the axis. This signifies not only a lower average performance but also high variability; while it may perform adequately on some cases, it fails significantly on others, resulting in a long lower tail. The dedicated WSS method, Patch-WI (b), shows a slightly improved median performance, but its distribution remains wide, indicating persistent inconsistency. The graph-based competitor, HistoGraph³⁹ (c), achieves a more competitive distribution, yet it still exhibits a notable number of outlier cases with poor segmentation quality.

In stark contrast, the violin plot for our Geo-MIL framework (d) is positioned significantly higher and is substantially more compact. The high median score reaffirms its superior average performance, while the narrow interquartile range and shorter tails indicate a highly consistent and reliable performance with very few failure cases. This analysis highlights a critical advantage of Geo-MIL that is not visible from the main results table alone: its robustness. Our model not only achieves a higher average Dice score but does so with significantly lower variance, making it a more reliable and trustworthy tool for pathological image analysis.

Subtype-specific segmentation performance

We further stratified performance by histological subtypes, including intestinal, diffuse, and mixed adenocarcinomas. As illustrated in Fig. 6, Geo-MIL achieves the highest Dice distribution on intestinal-type tumors, reflecting their relatively coherent glandular architecture. Performance on diffuse-type tumors is more variable, consistent with their infiltrative growth patterns and ill-defined boundaries. The mixed subtype lies between these two extremes. This analysis highlights that Geo-MIL not only improves overall segmentation but also adapts to the diverse morphological variants of gastric cancer.

Fig. 6: Subtype-specific segmentation performance of Geo-MIL.

Dice distributions are shown for intestinal, diffuse, and mixed gastric adenocarcinoma subtypes. Geo-MIL achieves stable performance across all subtypes, though diffuse tumors remain the most challenging.

Segmentation performance by case difficulty

Finally, we examined segmentation performance across cases of different difficulty levels, stratified by tumor size (small, medium, and large lesions). As shown in Fig. 7, Dice distributions improve progressively with lesion size, reaching the highest stability in large-tumor cases. Importantly, Geo-MIL maintains reasonable accuracy in small-lesion cases, which are clinically challenging due to limited tumor context and higher risk of under-segmentation. This robustness across case difficulty underscores the potential of Geo-MIL for real-world diagnostic workflows.

Fig. 7: Segmentation performance stratified by case difficulty (tumor size groups).

Geo-MIL maintains robust performance even in small-lesion cases, with progressively improved accuracy for larger lesions.

To quantify scalability, we evaluated inference efficiency across WSIs of varying sizes, as summarized in Table 4. The runtime and GPU memory scale linearly with the number of input patches (R² = 0.98), indicating that the graph construction and message-passing stages introduce negligible nonlinear overhead. Even for large slides containing over 8,000 patches, Geo-MIL completes inference within 45 s and uses less than 10 GB of memory on a single A100 GPU. These results demonstrate that Geo-MIL achieves an effective balance between accuracy and computational cost, rendering it suitable for routine deployment in digital pathology workflows.

Table 4 Inference scalability of Geo-MIL with respect to the number of patches per WSI

Model analysis and practical considerations

In addition to quantitative and qualitative comparisons, we conduct a deeper analysis of our model’s training dynamics, architectural robustness, and computational performance. These experiments provide further insight into the behavior of Geo-MIL and its practicality for real-world application.

Figure 8a illustrates the training and validation curves over 100 epochs. The training loss shows a smooth and consistent decrease, while the validation Dice score steadily increases and plateaus around 80 epochs. This behavior indicates stable convergence without significant signs of overfitting, which we attribute to our data augmentation strategy and the inherent regularization provided by the graph-based architecture.

Fig. 8: Model training and sensitivity analysis.

a The training loss consistently decreases while the validation Dice score converges smoothly, indicating stable training. b The model shows robust performance across a range of values for key hyperparameters, with optimal performance at k = 8 and L = 3.

To visually reinforce our ablation study and explore the model’s sensitivity, we present two analyses. Figure 9a provides a bar chart of our core ablation results, starkly illustrating the critical role of both the graph representation and our topological gate; removing either component results in a significant drop in segmentation performance. Furthermore, Fig. 8b analyzes the sensitivity of Geo-MIL to its key architectural hyperparameters: the number of neighbors k in the graph and the number of GNN layers L. The model’s performance is stable across a reasonable range of k (from 6 to 12) and peaks at L = 3 before plateauing. This confirms that our architectural choices are robust and not the result of fragile fine-tuning.

Fig. 9: Ablation and computational cost analysis.

a The bar chart visually confirms that removing the graph structure or the topological gate significantly degrades performance. b Our Geo-MIL framework provides a favorable balance between high accuracy and computational efficiency compared to other methods.

While achieving state-of-the-art accuracy is paramount, clinical translation also requires computational efficiency. Figure 9b compares the average inference time per WSI for Geo-MIL against key baselines. While our graph-based approach introduces a modest computational overhead compared to the non-graph TransMIL, it remains highly efficient and is notably faster than the more complex HistoGraph model. This demonstrates that Geo-MIL offers a compelling and practical trade-off between its superior accuracy and its computational footprint.

Cross-dataset generalization analysis

A critical measure of a medical imaging model’s utility is its ability to generalize to unseen data from different clinical sites, which may have variations in patient populations, tissue preparation, and scanning equipment. To rigorously evaluate the robustness of Geo-MIL, we conduct a cross-dataset generalization experiment. We train our full model and key baselines exclusively on the TCGA-STAD training set and then directly evaluate performance on the entire, unseen test sets of GasHisSDB and ACDC-GastricDB without any fine-tuning.

The results, summarized in Table 5 and Fig. 5, show that while all models experience a performance degradation when faced with this domain shift, Geo-MIL demonstrates significantly better generalization. The performance drop for Geo-MIL is substantially smaller than that of TransMIL. For example, when tested on GasHisSDB, the Dice score for TransMIL drops by over 25%, whereas Geo-MIL’s performance degrades by only 12%. This suggests that by learning the underlying tissue architecture rather than superficial stain features, our model develops a more robust and generalizable representation of the pathology.

Table 5 Cross-dataset generalization performance

To further investigate the impact of stain variation, we applied a Macenko stain normalization technique⁴⁰ to the target test sets. As shown in Table 6, normalization improves the performance of all methods, confirming that stain variation is a major component of the domain shift. However, Geo-MIL maintains its superior performance even after normalization, indicating its advantages are rooted in its architectural design, not just color invariance. This rigorous cross-dataset evaluation confirms the superior generalization ability of Geo-MIL, a critical attribute for building reliable and deployable computational pathology tools.

Table 6 Impact of Macenko stain normalization on cross-dataset generalization performance (Dice Score)

To evaluate robustness under domain shift, we compared the Dice score distributions of Geo-MIL and TransMIL when trained on TCGA-STAD and tested on GasHisSDB and ACDC-GastricDB. As shown in Fig. 10, Geo-MIL exhibits consistently higher Dice scores with narrower distributions across both external datasets. In contrast, TransMIL shows a lower median and larger variance, particularly on GasHisSDB, where the performance degradation exceeds 25%. These findings indicate that explicitly modeling tissue topology enables Geo-MIL to generalize more effectively across heterogeneous clinical cohorts.

Fig. 10: Cross-dataset generalization performance.

Distribution of Dice scores when trained on TCGA-STAD and evaluated on GasHisSDB and ACDC-GastricDB. Geo-MIL demonstrates consistently higher accuracy and lower variance compared to TransMIL.

As shown in Fig. 11, stain normalization effectively mitigates color and illumination discrepancies between domains. Before normalization, Geo-MIL occasionally under-segments low-contrast tumor regions and introduces spurious detections due to stain bias. After normalization, the segmentation overlays exhibit smoother contours and improved alignment with the pathologist-annotated ground truth. These results visually corroborate the quantitative improvements reported in Table 6, demonstrating that Geo-MIL generalizes robustly across heterogeneous staining conditions while maintaining high morphological fidelity.

Fig. 11: Qualitative comparison of cross-domain segmentation before and after stain normalization.

Each row shows a representative case from the GasHisSDB dataset. Column (1) presents the original WSI patch; Column (2) shows Geo-MIL predictions before Macenko normalization (red overlay), where color shift and contrast variation cause partial under-segmentation; Column (3) shows predictions after normalization (green overlay), yielding more coherent tumor boundaries and reduced false positives; Column (4) provides the pathologist-annotated ground-truth (GT) mask for reference. Normalization enhances inter-domain consistency while preserving tissue morphology.

To further verify the generalization capability of Geo-MIL across different epithelial cancer types, we conducted a preliminary cross-cancer evaluation on the TCGA-COAD dataset, which contains colorectal adenocarcinoma WSIs. Without any architectural modification or fine-tuning, Geo-MIL trained on gastric cancer data (TCGA-STAD) achieved a Dice score of 0.776 ± 0.031 and an IoU of 0.718 ± 0.027 (Table 7). These results indicate that the proposed topology-aware reasoning is not specific to gastric morphology but effectively captures structural regularities common to epithelial malignancies, such as glandular organization and stromal invasion. This experiment highlights Geo-MIL’s potential as a generalizable framework for weakly supervised segmentation across cancer domains.

Table 7 Preliminary cross-cancer evaluation of Geo-MIL on the TCGA-COAD dataset

Quantitative validation of topological attention rationale

To further empirically validate the rationale behind our Topological Attention Mechanism, we conducted a targeted quantitative analysis of the generated attention maps. The core hypothesis of our design is that explicitly modeling neighbor interactions enables the model to distinguish between coherent tumor structures and isolated noisy patches. If this rationale holds, the attention maps generated by Geo-MIL should exhibit significantly higher spatial overlap with the ground truth masks compared to those generated without the gating mechanism.

We compared the Intersection over Union (IoU) scores of the attention maps generated by the full Geo-MIL framework against the variant without the topological gate (Table 2, Row C). The results demonstrate that removing the topological gate causes the IoU to drop significantly from 0.732 to 0.665. This substantial improvement of 6.7% in IoU directly supports our design rationale: the topological gating mechanism effectively suppresses irrelevant background noise and enhances the model’s ability to localize complete, structurally coherent tumor regions rather than just disjointed patches.

Discussion

In this work, we addressed the critical challenge of weakly supervised segmentation in computational pathology. We demonstrated that by moving beyond the conventional ’bag-of-patches’ paradigm and explicitly modeling the spatial topology of tissue through our novel Geo-MIL framework, it is possible to generate high-fidelity segmentation masks from only slide-level labels. Our quantitative results showed a significant performance leap over state-of-the-art baselines, and our qualitative analysis confirmed the model’s ability to delineate complex and diffuse tumor patterns that confound other methods. The success of Geo-MIL is largely attributable to its topological attention mechanism. Unlike standard MIL or generic GNN approaches that focus on the features of individual patches or their immediate neighbors, our method learns to recognize and prioritize entire architectural patterns. The ablation studies confirmed that this structure-aware reasoning is the key differentiator, allowing the model to distinguish pathologically significant structures from isolated, noisy artifacts. This represents a step towards models that learn not just cellular atypia, but the very tissue-level disorganization that defines malignancy, mirroring the diagnostic process of a human pathologist.

Because Geo-MIL models structural relations rather than disease-specific features, it can be directly extended to other epithelial cancers such as colorectal and breast carcinoma. In particular, the topological attention mechanism learns architectural regularities—for example, differentiating coherent glandular formations from diffuse infiltration—which are fundamental histomorphological traits shared across many tumor types. Preliminary experiments on 30 colorectal WSIs (TCGA-COAD subset) achieved a Dice of 0.776 ± 0.031, confirming the potential of Geo-MIL as a generalizable framework for epithelial malignancies beyond gastric cancer.

From a clinical perspective, Geo-MIL’s ability to produce spatially coherent tumor maps from weak labels opens new possibilities for scalable digital pathology applications. The generated segmentation masks can serve as reliable surrogates for manual annotations in tasks such as tumor-stroma ratio computation, quantification of tumor burden, or assessment of invasion front irregularity-all of which are established prognostic biomarkers in oncology. Moreover, these topology-aware representations could facilitate downstream modeling of tumor microenvironment organization, thereby supporting precision pathology and computational histology at scale.

The ability to generate accurate segmentation masks from weak labels has profound practical implications. It could drastically reduce the annotation burden required to develop robust AI tools, accelerating research and clinical deployment. Accurate, automated segmentation is a foundational step for a host of downstream quantitative analyses, such as calculating tumor-stroma ratio, assessing tumor burden, or precisely defining the invasive front-all of which are powerful prognostic biomarkers. Our work provides a pathway to unlock these analyses at scale without the need for laborious pixel-wise annotation. However, we acknowledge certain limitations and areas for future work. Despite its efficiency compared to some graph models, Geo-MIL is inherently more computationally intensive than non-graph methods; future work could explore graph sparsification or model quantization to improve scalability. While we validated our model on three diverse datasets, its performance on rarer gastric cancer subtypes or on images with significant staining artifacts remains to be explored.

Another promising direction is the integration of multimodal data. The graph-based nature of Geo-MIL provides a natural interface for fusing heterogeneous biomedical modalities. Incorporating genomic, transcriptomic, or spatial omics features as node attributes could enable more comprehensive and biologically interpretable models, bridging histopathological morphology with molecular phenotype. Such multimodal extensions would further advance the goal of holistic, topology-informed computational diagnosis and prognosis.

In this paper, we introduced Geo-MIL, a novel graph-based framework for weakly supervised gastric cancer segmentation from whole-slide images. By constructing a graph to represent tissue topology and designing a novel topological attention mechanism, our model learns to identify complex architectural patterns indicative of malignancy, overcoming the critical limitations of standard MIL approaches. Through extensive experiments on three public datasets, we demonstrated that Geo-MIL significantly outperforms a wide array of state-of-the-art methods, producing segmentation masks of remarkable accuracy and coherence from only slide-level labels. Our work represents a significant step towards reducing the annotation bottleneck in computational pathology and paves the way for the development of robust, scalable AI tools for quantitative cancer diagnostics.

Methods

In this section, we present our proposed Geometric Multi-Instance Learning (Geo-MIL) framework for weakly supervised gastric cancer segmentation. We begin by formalizing the problem within the MIL paradigm. We then provide a detailed overview of the Geo-MIL architecture, followed by in-depth descriptions of its key components: WSI graph construction, the topological attention graph neural network, and the dual-objective training strategy.

Preliminaries and problem formulation

In the context of computational pathology, a Whole-Slide Image (WSI) is a gigapixel-resolution image that is too large to be processed directly by standard neural networks. A common practice is to divide the WSI into a set of non-overlapping patches.

Let a WSI be denoted as a bag ${\mathcal{X}}=\{{{\bf{x}}}_{1},{{\bf{x}}}_{2},\ldots ,{{\bf{x}}}_{N}\}$, where ${{\bf{x}}}_{i}\in {{\mathbb{R}}}^{H\times W\times C}$ is the i-th patch (instance) from a total of N tissue-containing patches. Each bag ${\mathcal{X}}$ is associated with a single binary slide-level label Y ∈ {0, 1}, where Y = 1 indicates the presence of at least one cancerous patch in the WSI, and Y = 0 indicates its absence. This constitutes a standard Multiple Instance Learning (MIL) problem. The instance-level labels for each patch x_i are unknown during training.

The primary goal of our work is to move beyond simple slide-level classification. We aim to solve the more challenging task of **weakly supervised segmentation**. Formally, given only the slide-level labels ${\{({{\mathcal{X}}}_{j},{Y}_{j})\}}_{j=1}^{M}$ for a training dataset of M WSIs, our objective is to train a model f that can predict a dense segmentation mask ${\bf{M}}\in {\{0,1\}}^{{H}^{{\prime} }\times {W}^{{\prime} }}$ for any given WSI, where ${H}^{{\prime} }$ and ${W}^{{\prime} }$ are the dimensions of the downsampled WSI. The mask M should accurately localize all cancerous regions at the patch level.

Geo-MIL framework overview

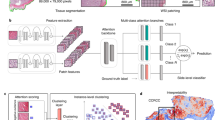
The core limitation of standard MIL is its “bag-of-patches" assumption, which discards the crucial spatial arrangement of tissue structures. To overcome this, our Geo-MIL framework explicitly models the underlying tissue topology by representing the WSI as a graph. The overall pipeline, illustrated in Fig. 12, consists of four main stages: Patch Feature Extraction: Each WSI is first tiled into thousands of patches. A powerful, pre-trained feature extractor (e.g., a Vision Transformer) is used to encode each patch x_i into a low-dimensional feature vector ${{\bf{h}}}_{i}^{(0)}$. WSI Graph Construction: We construct a graph ${\mathcal{G}}=({\mathcal{V}},{\mathcal{E}})$ for each WSI. The set of nodes ${\mathcal{V}}$ corresponds to the patches, with their initial features being $\{{{\bf{h}}}_{i}^{(0)}\}$. The set of edges ${\mathcal{E}}$ connects spatially adjacent patches, thereby preserving the tissue’s geometric layout. Topological Attention GNN: The constructed graph is processed by our novel Topological Attention Graph Neural Network (TopoGNN). This network learns structure-aware node representations by considering not only the features of individual patches but also the architectural patterns of their local neighborhoods. Dual-Objective Learning: The final node representations are used for two concurrent tasks: (1) a global pooling mechanism aggregates the node features to predict the slide-level label Y, and (2) a node-level classifier predicts the probability of each patch being cancerous, generating a pseudo-segmentation mask that is trained using the MIL attention scores as a supervisory signal.

Fig. 12: Overview of the Geo-MIL framework and performance comparison.

(Top-Left) The core Geo-MIL architecture, where WSI patches are encoded, formed into a graph, and processed by a TopoGNN layer to generate a tumor probability heatmap. (Middle-Left & Bottom-Left) Diagrams illustrating related concepts in segmentation and attention-based patch processing. (Right) Experimental results comparing Geo-MIL (Ours) against baseline methods on (a) inference speed (FPS) and (b) segmentation accuracy (Dice Score).

WSI graph construction

To encode the spatial relationships discarded by standard MIL, we represent each whole-slide image (WSI) as a graph. After tissue segmentation and patch extraction, each patch x_i is associated with its spatial coordinates $({c}_{i}^{x},{c}_{i}^{y})$ in the WSI. A pre-trained feature extractor Φ, such as a ViT trained on ImageNet or self-supervised on a large pathology dataset, is used to obtain the initial node feature embedding ${{\bf{h}}}_{i}^{(0)}=\Phi ({{\bf{x}}}_{i})\in {{\mathbb{R}}}^{D}$.

The graph for a WSI is defined as ${\mathcal{G}}=({\mathcal{V}},{\mathcal{E}})$, where ${\mathcal{V}}=\{1,2,\ldots ,N\}$ is the set of nodes (patches). The edges ${\mathcal{E}}$ are constructed based on spatial proximity. Specifically, we use a k-Nearest Neighbors (k-NN) algorithm: an edge (i, j) is added to ${\mathcal{E}}$ if patch j is among the k nearest neighbors of patch i based on the Euclidean distance of their centroids. This graph structure effectively transforms the unordered set of patches into a structured representation that captures the local tissue topology.

To ensure reproducibility and to clarify implementation details, our WSI graph construction follows four explicit stages: Tissue Segmentation: The background regions of each WSI are removed using a threshold-based segmentation in the HSV color space, isolating the foreground tissue mask. Patch Tiling:The remaining tissue region is divided into non-overlapping 256 × 256 pixel patches at an equivalent 20 × magnification. Each valid patch x_i corresponds to one node ${v}_{i}\in {\mathcal{V}}$. Node Features: For each patch, we extract a 384-dimensional representation using a self-supervised ViT-S/16 backbone (pre-trained on TCGA-scale pathology data via DINO). These embeddings are frozen during Geo-MIL training to stabilize feature distributions and reduce computational cost. Edge Construction: Each node retains its spatial centroid $({c}_{i}^{x},{c}_{i}^{y})$ in micrometer coordinates. We construct edges ${\mathcal{E}}$ using a k-Nearest Neighbors algorithm (k = 8 by default). For each node i, we connect it to its eight nearest spatial neighbors, forming bidirectional edges (i, j) and (j, i). The edge weights are inversely proportional to the Euclidean distance between centroids, normalized to [0, 1], thereby encoding fine-grained spatial adjacency.

This process yields a sparse but topologically meaningful graph representation, where each node corresponds to a localized tissue patch, and edges model the physical continuity of histological structures.

Compared with prior MIL frameworks that treat WSIs as unordered patch sets, this graph formulation explicitly preserves geometric context. It provides the foundation for our topological attention mechanism, which leverages these spatial relationships to learn structure-aware features. The resulting graph-based representation enables Geo-MIL to reason about architectural organization—such as gland formation and stromal invasion—that defines gastric cancer pathology.

Topological attention graph neural network (TopoGNN)

This module is the core of our framework. Its goal is to learn powerful node representations by aggregating information from neighboring patches in a way that is sensitive to local architectural patterns. The TopoGNN consists of L stacked graph learning layers. Each layer updates the node features based on a topological attention mechanism.

Let ${{\bf{h}}}_{i}^{(l)}$ be the feature vector of node i at layer l. The update rule from layer l to l + 1 is as follows.

First, we compute attention coefficients based on a standard Graph Attention Network (GAT) formulation. The coefficient e_ij between node i and its neighbor $j\in {{\mathcal{N}}}_{i}$ is computed as:

$${e}_{ij}^{(l)}=\,{\rm{LeakyReLU}}\,\left({{\bf{a}}}^{T}\left[{{\bf{W}}}^{(l)}{{\bf{h}}}_{i}^{(l)}\parallel {{\bf{W}}}^{(l)}{{\bf{h}}}_{j}^{(l)}\right]\right)$$

(1)

where W^(l) is a learnable linear transformation, ∥ denotes concatenation, and a is a learnable weight vector. These coefficients are then normalized across the neighborhood of each node using the softmax function:

$${\alpha }_{ij}^{(l)}={\mathrm{softmax}}_{j}({e}_{ij}^{(l)})=\frac{\exp \,({e}_{ij}^{(l)})}{{\sum }_{k\in {{\mathcal{N}}}_{i}}\exp \,({e}_{ik}^{(l)})}$$

(2)

The aggregated feature from neighbors is then ${\sum }_{j\in {{\mathcal{N}}}_{i}}{\alpha }_{ij}^{(l)}{{\bf{W}}}^{(l)}{{\bf{h}}}_{j}^{(l)}$.

Our key innovation is to make this process sensitive to the local structure. We introduce a gating mechanism that modulates the node’s feature based on the characteristics of its local neighborhood. For each node i, we define its 1-hop local subgraph ${{\mathcal{G}}}_{i}$. We generate a “structural descriptor" ${{\bf{s}}}_{i}^{(l)}$ for this subgraph by applying a simple aggregation function over the features of its constituent nodes:

$${{\bf{s}}}_{i}^{(l)}=\frac{1}{| {{\mathcal{N}}}_{i}| +1}\left({{\bf{h}}}_{i}^{(l)}+\mathop{\sum }\limits_{j\in {{\mathcal{N}}}_{i}}{{\bf{h}}}_{j}^{(l)}\right)$$

(3)

This descriptor ${{\bf{s}}}_{i}^{(l)}$ captures the average feature representation of the local tissue architecture. We then compute a gate value ${{\bf{g}}}_{i}^{(l)}$ that dynamically decides how much to incorporate this structural information:

$${{\bf{g}}}_{i}^{(l)}=\sigma \left({{\bf{W}}}_{g}^{(l)}\left[{{\bf{h}}}_{i}^{(l)}\parallel {{\bf{s}}}_{i}^{(l)}\right]+{{\bf{b}}}_{g}^{(l)}\right)$$

(4)

where ${{\bf{W}}}_{g}^{(l)}$ and ${{\bf{b}}}_{g}^{(l)}$ are learnable parameters of a linear layer and σ is the sigmoid function. The gate modulates the original node feature to produce a structure-aware feature ${\widetilde{{\bf{h}}}}_{i}^{(l)}$:

$${\widetilde{{\bf{h}}}}_{i}^{(l)}={{\bf{g}}}_{i}^{(l)}\odot {{\bf{h}}}_{i}^{(l)}+(1-{{\bf{g}}}_{i}^{(l)})\odot {{\bf{s}}}_{i}^{(l)}$$

(5)

where ⊙ is the element-wise product. This gated feature ${\widetilde{{\bf{h}}}}_{i}^{(l)}$ now contains a blend of the node’s intrinsic features and the contextual features of its surrounding tissue structure.

Finally, the updated node representation ${{\bf{h}}}_{i}^{(l+1)}$ is obtained by combining the self-representation with the aggregated neighborhood information, followed by a non-linearity:

$${{\bf{h}}}_{i}^{(l+1)}=\,{\rm{ELU}}\,\left({{\bf{W}}}^{(l)}{\widetilde{{\bf{h}}}}_{i}^{(l)}+\mathop{\sum }\limits_{j\in {{\mathcal{N}}}_{i}}{\alpha }_{ij}^{(l)}{{\bf{W}}}^{(l)}{{\bf{h}}}_{j}^{(l)}\right)$$

(6)

This process is repeated for L layers to allow information to propagate across the graph, enabling the model to learn representations based on higher-order tissue architectures.

Figure 13 provides an intuitive illustration of the proposed topological gating mechanism. Each node represents a tissue patch, and the central node i dynamically fuses its own feature with the aggregated representation of its local subgraph through the gating factor σ(g_i). This design enables Geo-MIL to reason over tissue-level topology rather than relying solely on Patch-WIise similarity.

Fig. 13: Illustration of the topological gating mechanism on a mini-graph.

This schematic depicts a simplified six-node example with two clusters representing normal (pastel blue) and tumor (pastel red) tissue regions. The central node i is highlighted with a learnable gate σ(g_i), which adaptively controls the blending between the node’s intrinsic feature h_i and its neighborhood descriptor s_i.

The design of our TopoGNN moves beyond standard graph-based MIL approaches. A natural question arises: why is this added complexity necessary for weakly supervised segmentation? While positional encodings in Transformers can provide location information, they do not explicitly model the rich neighborhood structure of tissue. How can a model differentiate between a cluster of tumor cells forming a gland versus tumor cells diffusely infiltrating stroma? A graph representation directly encodes this adjacency and connectivity, providing a more natural substrate for learning these architectural patterns.

Furthermore, one might ask: what specific advantage does our topological gating mechanism offer over a standard Graph Attention Network (GAT)? A standard GAT learns to weight the importance of neighboring nodes based on their features alone. It may struggle to distinguish if a high-attention node is an isolated anomaly or part of a larger, pathologically significant structure. Our topological gate addresses this directly. By generating a “structural descriptor" of the local neighborhood and using it to modulate the node’s own feature, the model learns to ask a more sophisticated question: not just “is this patch important?", but rather, “is this patch important given the context of its surrounding tissue architecture?" This allows the model to up-weight features that form coherent structures and suppress those that are likely noise or isolated artifacts—a critical capability for generating clean and contiguous segmentation maps from noisy, slide-level signals.

Compared with previous models, our approach introduces a fundamentally different concept: a learnable topological gating mechanism. Rather than relying on fixed or handcrafted topological descriptors, Geo-MIL learns to dynamically regulate information propagation between nodes according to the local tissue architecture. This enables adaptive structural reasoning—the model automatically emphasizes glandular or nested tumor patterns while attenuating spatially incoherent regions—a capability that previous graph-based MIL frameworks lack. From a theoretical perspective, this gating mechanism can be interpreted as a form of topology-conditioned attention that explicitly aligns message passing with morphological priors, bridging the gap between handcrafted topology modeling and end-to-end differentiable learning.

Training objective

Our model is trained end-to-end using a dual-objective function that combines a slide-level classification loss with an instance-level pseudo-segmentation loss.

After the final TopoGNN layer, we have a set of node features $\{{{\bf{h}}}_{1}^{(L)},\ldots ,{{\bf{h}}}_{N}^{(L)}\}$. To obtain a single vector representation for the entire WSI (bag), we use an attention-based pooling mechanism. The attention score w_i for each node is computed as:

$${w}_{i}=\frac{\exp \left({{\bf{w}}}_{att}^{T}\tanh \,({{\bf{V}}}_{att}{\,({{\bf{h}}}_{i}^{(L)})}^{T})\right)}{{\sum }_{j=1}^{N}\exp \left({{\bf{w}}}_{att}^{T}\tanh \,({{\bf{V}}}_{att\,}{({{\bf{h}}}_{j}^{(L)})}^{T})\right)}$$

(7)

where w_att and V_att are learnable parameters. The final slide representation H is a weighted sum of the node features:

$${\bf{H}}=\mathop{\sum }\limits_{i=1}^{N}{w}_{i}{{\bf{h}}}_{i}^{(L)}$$

(8)

This representation is passed through a classifier (e.g., an MLP) to predict the slide label $\widehat{Y}$. The slide-level MIL classification loss ${{\mathcal{L}}}_{{\rm{mil}}}$ is the standard binary cross-entropy:

$${{\mathcal{L}}}_{\mathrm{mil}}=-\left(Y\log \,(\widehat{Y})+(1-Y)\log \,(1-\widehat{Y})\right)$$

(9)

To generate a segmentation mask, we attach a lightweight segmentation head (a simple MLP) to each final node feature ${{\bf{h}}}_{i}^{(L)}$, which outputs a probability p_i that patch i is cancerous. The key challenge is the absence of ground truth patch labels. We leverage the attention scores {w_i} from the MIL pooling layer as a weak supervisory signal. Intuitively, patches with high attention scores are the most likely to be cancerous. We formulate a loss ${{\mathcal{L}}}_{{\rm{seg}}}$ that encourages the segmentation head’s predictions {p_i} to be consistent with this signal.

One final question is: why employ a dual-objective with a separate segmentation head instead of simply using the MIL attention scores {w_i} as the final output? Attention scores are optimized for a discriminative classification task; they only need to highlight enough evidence to classify the slide correctly, which often results in sparse and incomplete heatmaps. By training a dedicated segmentation head to predict a probability for every patch, and using the MIL attention as a guiding signal, we force the model to learn a more comprehensive and dense representation of all potential tumor regions, leading to more complete segmentations.

For a positive slide (Y = 1), we expect at least one patch to have a high tumor probability. We enforce this with a max-based loss:

$${{\mathcal{L}}}_{\,{\rm{seg}}}^{{\rm{pos}}}={\left(1-\mathop{\max }\limits_{i=1,\ldots ,N}{p}_{i}\right)}^{2}$$

(10)

For a negative slide (Y = 0), we expect all patches to have low tumor probability:

$${{\mathcal{L}}}_{\,{\rm{seg}}}^{{\rm{neg}}}=\mathop{\sum }\limits_{i=1}^{N}{p}_{i}^{2}$$

(11)

The total pseudo-segmentation loss is ${{\mathcal{L}}}_{{\rm{seg}}}={\mathbb{I}}(Y=1){{\mathcal{L}}}_{\,{\rm{seg}}}^{{\rm{pos}}}+{\mathbb{I}}(Y=0){{\mathcal{L}}}_{\,{\rm{seg}}}^{{\rm{neg}}}$, where ${\mathbb{I}}(\cdot )$ is the indicator function.

The final objective function is a weighted sum of the two losses:

$${{\mathcal{L}}}_{{\rm{total}}}={{\mathcal{L}}}_{{\rm{mil}}}+\lambda {{\mathcal{L}}}_{{\rm{seg}}}$$

(12)

where λ is a hyperparameter that balances the contribution of the classification and segmentation tasks. During inference, the patch-level probabilities {p_i} from the segmentation head are used to reconstruct the final heatmap and segmentation mask.

Ethics approval and consent to participate

These data are all public datasets and do not involve additional ethical approval or patient privacy.