Main

Precise control over lattice defects in monolayer (ML) crystals of transition metal dichalcogenides is essential to achieve intrinsic two-dimensional (2D) carrier transport that is free of carrier scattering and phase decoherence1,2,3,4. A prominent strategy for the wafer-scale production of single-crystalline transition metal dichalcogenide MLs is epitaxial growth on vicinal substrates (that is, substrates that have been cut slightly off one of their main crystallographic axis, resulting in a series of atomically high steps)5,6,7,8,9,10,11,12. These commonly use the unidirectional coalescence growth of multiple grains, where the local nucleation and ensuing unidirectional grain growth are registered on the vicinal steps and terraces, facilitating single-crystalline textures that are free of grain boundaries (Supplementary Table 1 provides a comparison of the reported growth schemes and properties).

Nonetheless, local defects inevitably persist when multiple grains coalesce due to growth kinetics instabilities and atomic stoichiometry4,13,14, which then obscure coherent 2D transport. It is, therefore, critical to address these local defects during growth and to recognize their impacts on the carrier transport characteristics15,16,17. In this Article, we identify the local dislocation cores associated with one-dimensional extended and zero-dimensional point defects in such single-crystalline textures, which can cause shallow-angle (<1–2°) misalignments for the case of ML molybdenum disulfide (MoS2) grown on two-inch sapphire wafers. We then develop a growth scheme in which the dislocation cores and point defects are eliminated by the careful kinetic control of coalescence epitaxy. Low-temperature transport in the resulting MoS2 films shows coherent 2D carrier transport, as manifested by weak localization and the onset of quantum Hall effects, along with a high Hall mobility of 1,200 cm2 V−1 s−1. We use the films as the channel material in field-effect transistor (FET) arrays and show that the resulting devices exhibit an average room-temperature mobility of ~100 cm2 V−1 s−1 and subthreshold swing (SS) of 65–75 mV dec−1.

Vicinal van der Waals epitaxy towards grain-boundary-free textures

We used c-plane sapphire substrates, cut with varying vicinal angles towards the A axis of 0°, 2°, 10° and 15° (Fig. 1a–c and Supplementary Figs. 1 and 2) for the vicinal epitaxy at a growth temperature (TG) of 810–850 °C. MoS2 MLs possess three-fold in-plane rotation symmetry, and their epitaxial stacking on the planar c-plane sapphires results in two crystallographic variants with an equivalent formation energy6,7. Such variants are 60° rotated from one another, as indicated by the blue and red triangles in Fig. 1b, forming mirror-twin boundaries. In other words, they naturally crystallize bicrystals on the planar c-plane sapphires18,19. It is at the atomic steps at which unidirectional nucleation is initiated, as reported for various transition metal dichalcogenide single-crystal MLs5,6,7,8,9,10,11,12. However, for unidirectional coalescence growth, the role of such step edges on vicinal substrates is yet to be fully understood. Epitaxial growth on substrates with varying vicinal angles—and thus the step and terrace density systematically vary—enables us to take a closer look at the progression of nucleation and growth (Fig. 1b,c). For example, nucleation occurs predominantly on the terrace, when the terrace width (the distance between the adjacent steps) of the 2° vicinal substrate is ~6 nm. It is, however, much shorter than 1 nm for the 15° vicinal substrate, where nucleation is solely on the atomic steps (Supplementary Fig. 2). Here we maintained a slow lateral growth rate of <0.5 μm min−1 by controlling the flow rate of metal–organic sources under lower partial pressures (pMo(CO)6 ≈ 10−6 torr and p(C2H5)2S ≈ 10−3 torr) in the near-equilibrium growth regime20,21,22. We observed systematic variation in the size and shape of the individual crystal facet on substrates with different vicinal angles, as summarized below. First, the facet size and shape gradually change from a larger triangle to a smaller trapezoid on the denser steps. Second, the total numbers of facets increase on the denser steps. Third, the facet in-plane orientation becomes unidirectional at higher vicinal angles, facilitating mirror-twin-boundary-free single-crystal textures, as statistically plotted in Fig. 1d (Supplementary Figs. 3–7 provide more details). This indicates that the vicinal steps, as the preferential nucleation sites, primarily promote unidirectional growth, consistent with previous studies6,7,8,9,10,11. In addition, our observations directly verify the anisotropic growth variations in a quantitative manner. That is, by examining variation in the individual facet shapes, we measure the directional growth rate (Va and Vb), in parallel (La) and perpendicular (Lb) to the step edges (Fig. 1e), where Va is always greater than Vb at all vicinal angles and both Va and Vb are greater at lower vicinal angles (Fig. 1f,g). This reveals that the vicinal step also acts as the diffusion barrier of the adatoms23, particularly for perpendicular growth depicted in Fig. 1e (Supplementary Figs. 8 and 9 show the analyses of the anisotropic growth profile on vicinal c-plane sapphire substrates).

Fig. 1: Vicinal van der Waals epitaxy towards grain-boundary-free textures.
figure 1

a, Schematic of the c-cut sapphire substrates with diverse vicinal angles of 0° (top), 2° (middle) and 15° (bottom) towards the A axis. b,c, Optical images (b) and schematic (c) of MoS2 ML facet crystals grown on the vicinal substrates (0° – A, 2° – A, 10° – A and 15° – A). Two crystallographic variants of the MoS2 facets are represented by blue and red colours. The terrace width is defined as the distance between the adjacent atomic steps. d, Statistical distribution of the two MoS2 variants (blue and red facets in c) on different vicinal angle substrates. e, Anisotropic geometry of a MoS2 facet on a vicinal sapphire substrate: La denotes the bottom length of the trapezoidal grain, which is parallel to the atomic steps, and Lb denotes the side length, perpendicular to the atomic steps. f, Variation in La and Lb with growth time on sapphire substrates of different vicinal angles. Shaded circles, squares, upward triangles and downward triangles denote La values at 0° – A, 2° – A, 10° – A and 15° – A, respectively, whereas the corresponding unshaded symbols denote Lb values for each substrate. Data were obtained from 20 crystals and are presented as mean ± standard deviation (s.d.). Error bars represent the s.d. (n = 20). g, Growth rates in the parallel (Va) and perpendicular (Vb) directions. The aspect ratios (Lb/La) of the facet grains on different vicinal angle substrates are also plotted. Upward triangles, downward triangles and squares denote Va and Vb and the aspect ratio, respectively. Data are presented as mean ± s.d. Error bars represent the s.d. (n = 20).

Full size image

Dislocation cores and point-defects-free crystalline textures

During unidirectional grain coalescence in the apparently single-crystalline textures, any deviation from the perfect orientational alignment of each grain can lead to local dislocation lines7,13,14, often accompanied by the presence of point defects and/or their clusters along the subunit-cell translations. This is qualitatively different from usual grain boundaries with distinct tilt angles, extended over several micrometres in poly-crystalline MLs, and is hidden under electron microscopy. Figure 2a illustrates an example of such local deformation near a Mo pentagon–heptagon (5/7) point defect, known to be the most energetically favourable point defects with the smallest Burgers vector24. The presence of a (5/7) point defect causes the two adjoining MoS2 local grains, indicated by pink and green triangles, to deviate by a misfit angle (θd), along the defect direction vector x. In our growth, this misfit angle can be as large as 1–2°, as verified by high-angle annular dark-field (HAADF) scanning transmission electron microscopy (STEM) images (Fig. 2b). These local defects can be formed for several reasons, such as in-plane strain, unwanted out-of-plane tilting and off-stoichiometry during the growth13. Then, we optimized the growth conditions by carefully tuning the TG value and precursor flow rate. In general, the higher TG value facilitates proper stoichiometry with reduced composition uncertainty and, thus, reduced off-stoichiometric defects25,26, as well as allows adatoms to migrate over longer distances to energetically favourable sites to release the residual stress at the grain boundaries27,28. The degree of this local deformation on the ML crystals was assessed by selective-area electron diffraction (SAED) patterns from 16 box regions of 50 × 50 μm2, which are 100 µm apart within a single-crystal film, grown at TG values of 810 °C, 830 °C and 850 °C (Supplementary Fig. 10 provides more details). As shown in Fig. 2c,d, we overlaid the 16 SAED patterns from each sample to examine the misfit dispersion by closely analysing the fifth-order peak (030). In Fig. 2d (insets, bottom), we observed that the width of the streaky (030) patterns is progressively larger at lower TG. Figure 2e shows the statistical distribution of the misfits, calculated by measuring the angles between each peak (indicated by red dots) and the median peak (indicated by the yellow line). For TG = 850 °C, we found the minimum misfit distribution down to ±0.41°, which can be regarded as the optimum single crystal, free from both dislocations and point defects, for our low-temperature transport investigations. We also verified a low sulfur-vacancy density of 3–6 × 1012 cm−2 in our epitaxial MoS2 single crystals by scanning tunnelling microscopy (STM) and HAADF-STEM images (Supplementary Figs. 11 and 12, respectively).

Fig. 2: Dislocation cores and point-defects-free crystalline textures.
figure 2

a,b, Schematics (a) and HAADF-STEM images (b) of a local dislocation core near a Mo (5/7) point defect. The misfit angle (θd) represents the deviation between two adjoining grains, depicted as pink and green triangles. c, Acquisition of the collection of SAED patterns in the 16 growth patterns. d, Overlaid SAED patterns from epitaxial MoS2 single-crystal MLs grown at different TG values, with the magnified fifth-order (030) peaks shown in the insets. Schematics (top) illustrate the elimination of local deformation and point defects at different TG values. e, Angle deviations of the (030) peaks from the epitaxial single-crystal MoS2 MLs grown at different TG values, showing the cleanest crystallinity at TG = 850 °C.

Full size image

Crystal and electronic structures of MoS2 single-crystalline MLs in wafer scales

Having optimized the growth conditions for the cleanest MoS2 ML single crystals at TG = 850 °C, we fabricated the selectively patterned MoS2 ML channels (50 × 50 μm2) into square SiO2 windows on two-inch-wafer c-sapphire substrates with a vicinal angle of 15°. Figure 3a shows the schematics of the selective growth (Supplementary Figs. 13 and 14 show a comparison of the growth behaviour with/without SiO2 masks)29, where we patterned square SiO2 trenches to define the growth areas of c-sapphire substrates, as well as the corresponding optical images (Methods). We verified that, within the growth panels, the trapezoidal MoS2 ML grains gradually coalesce and seamlessly stitch into the single-crystalline films (Fig. 3b,c and Supplementary Fig. 15). The in-plane crystal orientation in each pattern was confirmed by second-harmonic generation (SHG) measurements (Supplementary Figs. 16 and 17). The low-energy electron diffraction (LEED) pattern, obtained using a submillimetre-sized electron beam from the synchrotron source at beamline 4A2 of the Pohang Light Source, reveals three bright spots that indicate C3 symmetry (Fig. 3c, inset (right)), and it is consistent over the different spots, which are 1 mm apart from each other across the entire sample (Supplementary Fig. 18). The epitaxial relation to the c-plane sapphire was examined by cross-sectional STEM (Fig. 3d), showing that the MoS2 MLs are epitaxially aligned along the <\(10\bar{1}0\)> orientation of the 15° vicinal sapphire. The electronic structures of our epitaxial MoS2 single-crystal MLs were directly measured with angle-resolved photoemission spectroscopy (ARPES) with a synchrotron X-ray radiation (hv = 60 eV) beam size of ~50 µm (Fig. 3e and Methods), where we clearly found the band dispersions along the \({\bar{\Gamma}}-{\bar{\rm{M}}}\) high-symmetry directions of the Brillouin zone (data for the \({\bar{\Gamma}}-{\bar{\rm{K}}}\) direction are shown in Supplementary Fig. 19a). Note that the left half-panel shows its second derivative. The absence of split bands at \(\bar{\Gamma }\) indicates ML homogeneity without unwanted bilayer overgrowth30. Distinct single-band dispersion without mixing for each \({\bar{\Gamma }}-{\bar{\rm{M}}}\) and \({\bar{\Gamma}}-{\bar{\rm{K}}}\) direction illustrates the uniform orientation of multiple grains, confirming the exact single-crystal texture31. This is also consistent with the Fermi map at E – EF = –3.9 eV (Supplementary Fig. 19b). In particular, the 2D curvature plot of the upper valence band is consistent with the computed bands32, with the minimal energy compression indicating fewer defects, doping and stress30.

Fig. 3: Pattern growth of single-crystal MoS2 MLs in wafer scales and their electronic structures.
figure 3

a, Patterned growth of single-crystal MoS2 MLs on a two-inch, 15° c-sapphire wafer. The patterns were lithographically defined with SiO2 windows. Schematics (top) and optical images (bottom) of the samples before and after the selective growth. b,c, Optical images of single-crystal MoS2 MLs grown on the SiO2 patterns in the early growth stage (b) and after growth (c). Top inset: a representative LEED pattern; bottom inset: an in-plane HAADF-STEM image. d, Cross-sectional HAADF-STEM image and the corresponding atomic structure of an epitaxial MoS2 ML on a 15° sapphire substrate. e, ARPES band map and 2D curvature of the epitaxial single-crystal MoS2 MLs along the \({\bar{\Gamma }}-{\bar{\rm{M}}}\) high-symmetry direction, with the density-functional-theory-based band calculations30 plotted as the orange dotted lines.

Full size image

Coherent transport in epitaxial MoS2 single-crystal ML films

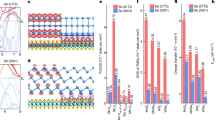
Our MoS2 single-crystalline ML channels (the growth patterns are shown in Fig. 3) were configured to a 5 × 10 μm2 Hall bar to be measured for carrier transport under an out-of-plane magnetic field (B) at low temperatures. Figure 4a shows a schematic and optical image of the Hall bar, where the MoS2 ML is encapsulated between the top and bottom hexagonal boron nitride (hBN) layers with Ti/Au edge contacts1,33. Figure 4b shows the perpendicular (Rxy) and longitudinal (Rxx) resistances at 1.5 K, leading to a high Hall mobility (µHall) of ~1,200 cm2 V−1 s−1, when the carrier density (n) was induced to be 1.7 × 1013 cm−2 at Vg = 60 V in the n-type regime (Supplementary Fig. 20 shows the result at a different carrier density and Supplementary Fig. 21 shows a larger-sized Hall-bar measurement). This µHall value is comparable with that of a single-crystal flake of chemical-vapour-deposition-grown MoS2 ML (~1,400 cm2 V−1 s−1; ref. 1) and to the theoretical calculation34 of ~1,500 cm2 V−1 s−1 at the reduced charged impurity density of 5 × 1011 cm−2. In comparison, a low-temperature Hall mobility of ~5,000 cm2 V−1 s−1 has been achieved on exfoliated flakes3. In Fig. 4b, the Rxx value at Vg = 40 V begins to decline from the constant value at B > 10 T, diverging from the classical Hall effect, which can be attributed to the onset of Shubnikov–de Haas oscillations; when µHall is ~1,000 cm2 V−1 s−1, we estimate the onset of the Shubnikov–de Haas oscillation, Bonset > µ−1 (ref. 35), to begin at ~10 T. The µHall versus T curve is given in Fig. 4c, where we observe that µHall monotonously increases with decreasing T and eventually saturates to a constant value at low temperatures. At T > 100 K, the carrier transport is primarily dominated by optical phonon scattering36, as described by a power law (µHall ≈ T−γ), where γ varies from 1.5 to 2.1. At low temperatures, where phonon scattering becomes negligible with a constant µHall value, the carrier transport is governed by either long-range Coulomb scattering or short-range scattering caused by lattice defects. The unintentional Coulomb potential from interfacial charge impurities can be effectively screened by charge carriers in the channels; thus, an increase in the charge carrier density, n, leads to enhanced mobility37,38. However, short-range scattering results in a µHall value that is less sensitive to n (refs. 39,40). In our case (Fig. 4c), the pronounced increase in the saturated µHall values with n, which we tuned by the applied gate voltage, suggests that the short-range scattering from point defects and disorders is minimized in our optimum-growth single crystals. In fact, we found the overall degradation of µ in the entire T range when the growth was performed at 810 °C (Supplementary Fig. 22), thereby allowing a larger fraction of dislocation cores and point defects (Fig. 2).

Fig. 4: Coherent transport in epitaxial single-crystal MoS2 ML films.
figure 4

a, Schematics and optical image of the Hall-bar device, where the single-crystal MoS2 ML channel is encapsulated between the top and bottom hBN layers. Scale bar, 10 μm. b, Rxx (red curves) and Rxy (blue curves) of the Hall device as a function of the magnetic field at different gate voltages (Vg), measured at 1.5 K. The light-coloured curves represent Vg = 40 V, and the deep-coloured curves correspond to Vg = 60 V. c, μHall as a function of temperature for different n values. For T > 100 K, μHall follows a power-law relationship with temperature, where μHall ≈ T−γ, with the exponent γ ranging from 1.5 to 2.1. d, Magnetoconductance ΔG*(B), defined as ΔG*(B) = [Gxx(+B) + Gxx(–B)]/2 – Gxx(B = 0 T), measured at n = 1.3 × 1013 cm−2 and T = 1.5 K, where Gxx is the longitudinal conductance. The solid black line is a fit using the HLN model within the range of –1.5 T and 1.5 T. Inset: ΔMR = [Rxx(B) – Rxx(B = 0 T)]/Rxx(B = 0 T) × 100% for 1.5 K (purple) and 50 K (red), where Rxx(B) is the symmetrized longitudinal resistance, given by Rxx(B) = [Rxx(+B) + Rxx(–B)]/2.

Full size image

The magnetoresistance (MR) at 1.5 K in our Hall bar does not follow a simple quadratic B dependence. Instead, it displays a noticeable cusp at B = 0 T (Fig. 4d). This negative low-field MR correction is a signature of weak localization, where the quantum interference effectively increases the channel resistivity near B = 0 T. Within the Hikami–Larkin–Nagaoka (HLN) model for 2D weak localization41, we extracted the phase coherence length (Lφ) in our Hall device (Methods) to be around 90 nm for n = 1.3 × 1013 cm−2 at 1.5 K. This is again comparable with those measured in exfoliated MoS2 single crystals under similar conditions42,43,44, ensuring the quantum-grade crystal quality of our MoS2 MLs, free from scattering defects. This low-field MR feature disappears at higher temperatures, where the phase coherence is lost in the classical diffusive regime (Fig. 4d, inset).

Performance of epitaxial MoS2 ML FET arrays

We integrated our MoS2 ML channel patterns into FET arrays, by transferring onto HfO2 (10 nm)/p+-Si substrates (Fig. 5a). Note that the FET channels are not hBN passivated for practical applications. We achieved ohmic contacts with bismuth as the source/drain contacts45, as verified by the I–V characteristics (Fig. 5b). Figure 5c shows the transfer characteristics (I–Vg) of an FET, where the channel length and width are ~2.2 μm and 5.0 μm, respectively, demonstrating the sharpest SS of 65 mV dec−1 at room temperature and on/off current ratio exceeding ~107. We plot the statistical distribution of the FET mobility (µFE) and the SS, measured on 64 FETs within the array (Fig. 5d,e), where we attained an average µFET of ~100 cm2 V−1 s−1, with an SS of 65–75 mV dec−1 (Supplementary Fig. 23). We highlight the FET performance metrics, with the SS being close to the theoretical limit of ~60 mV dec−1, and µFET being superior to those of the recent demonstrations on wafer-scale epitaxial MoS2 MLs6,8,10,11. For example, earlier examples of epitaxial MoS2 ML single crystals on c-plane sapphire made by similar coalescence growth schemes demonstrated FET arrays with an average µFET of 78 cm2 V−1 s−1 and SS of ~120 mV dec−1. The near-ideal SS value is also related to the substantial reduction in defect density within our single-crystal MoS2 MLs, in that the charge trap process at the defects can cause a less-steep SS46,47,48,49.

Fig. 5: High performance of epitaxial MoS2 ML FET arrays.
figure 5

a, Schematics and optical images of the FET arrays on single-crystal MoS2 MLs patterns, transferred onto a HfO2 (10 nm)/p+-Si substrate. The bottom-left optical image shows the full array, whereas the right image shows a close-up view of 16 FETs within the array. Scale bars, 100 μm. b,c, Output (b) and transfer (c) characteristics of a representative FET, measured at room temperature. d, Transfer characteristics of all 64 FETs measured at VDS = 0.01 V. e, Benchmark plot, comparing μFE and SS of the FET arrays of this work (red stars) with FETs using epitaxially coalesced single-crystalline (SC) MoS2 MLs from earlier works (indicated as Ref. A, Ref. B and Ref. C, adapted from refs. 6,8,11, respectively).

Full size image

Conclusions

We have reported an optimized growth technique for MoS2 on vicinal substrates that can reduce kinetic instabilities and off-stoichiometry defects. In particular, by controlling the coalescence kinetics of multiple unidirectional grains, we were able to create wafer-scale, single-crystalline MoS2 MLs with coherent quantum transport. Investigations of large-scale Hall-bar geometries at low temperatures showed a Hall mobility of 1,200 cm2 V−1 s−1 and a signature of weak localization. When the coherent layers were integrated into arrays of FETs, the resulting devices exhibited an average room-temperature mobility of ~100 cm2 V−1 s−1 and minimum SS of ~65 mV dec−1. Our work provides an approach to grow quantum transport platforms at wafer scales, offering a new avenue to develop 2D quantum electronics at the circuit level, as well as advanced 2D semiconductor technology.

Methods

Epitaxial growth of MoS2 ML crystals on c-plane sapphire substrates of varying vicinal angles

MoS2 ML crystals were epitaxially grown on c-plane sapphire substrates with varying vicinal angles (0°, 2°, 10° and 15°) relative to the A axis, using a custom-built metal–organic chemical vapour deposition system. The substrates were placed in a hot-walled 2.6-inch quartz tube, and the furnace was ramped up to TG = 850 °C for 20 min. The total pressure was maintained at 1.3 torr under a carrier gas flow of 80 s.c.c.m. for Ar (99.9999%) and 4 s.c.c.m. for H2 (99.9999%). During the growth process, Mo(CO)6 and (C2H5)2S precursors were supplied by individual mass flow controllers. The flow rates of the precursors were optimized at 0.3 s.c.c.m. for Mo(CO)6 and 0.6 s.c.c.m. for (C2H5)2S. Note that both precursors were kept in bubbler-type canisters at a constant pressure of 400 torr with Ar at room temperature. The growth of MoS2 ML films on the various vicinal sapphire substrates was conducted for 40–90 min. The growth time of MoS2 ML films on a vicinal 15° substrate was the longest (90 min) due to atomic steps acting as diffusion barriers, whereas it reduces to 40 min for growth on 0° substrates.

Fabrication of SiO2 windows on c-plane sapphire substrates for pattern growth

For the fabrication of SiO2 windows on two-inch sapphire wafers, conventional photolithography was used. A lift-off resist was initially spin coated onto the sapphire wafers to facilitate the lift-off process, followed by a layer of positive photoresist (AZ MIR 701), which was patterned using a contact aligner (MA/BA8 Gen4). A 20-nm layer of SiO2 was then deposited onto the photoresist-coated sapphire wafers via electron-beam evaporation. The lift-off process was carried out by soaking the wafers in acetone for 1.5 h with sonication. Afterwards, the wafers were rinsed in isopropanol with sonication for 5 min, soaked in AZ 300 MIF developer for 2 min to eliminate the lift-off resist layer and finally rinsed in deionized water for 2 min.

Transmission electron microscopy analysis

For in-plane transmission electron microscopy (TEM) observations, MoS2 ML SCs were transferred onto Cu TEM grids (holey carbon film grids for dark-field TEM imaging and QUANTIFOIL grids for STEM analysis) using a polymethyl methacrylate (PMMA)-assisted wet-transfer technique. Cross-sectional TEM specimens were prepared using a focused ion beam (Helios NanoLab G3 CX, FEI). To protect the specimens, a 20-nm-thick amorphous carbon layer was deposited using a carbon coater. STEM images and SAED patterns (Figs. 2b,d and 3c,d and Supplementary Figs. 10, 12 and 15) were obtained using a JEOL JEM-ARM 200F device with a Cs-corrected probe operated at 80 kV.

LEED and ARPES measurements

The ARPES and LEED measurements were carried out at the 4A2 undulator beamline of Pohang Light Source. Air exposure was minimized to a few seconds to avoid surface contamination, and the samples were also annealed at 400 °C for 2 h to remove the contamination layer before the measurement. The ARPES spectra were collected using a Scienta DA30L electron analyser using horizontally linearly polarized photons with an energy of 65 eV. The electrical contact to the ground was made by covering a part of the sample surface with Au foil and the Fermi energies were referred to that of the foil. The photon beam size was 20 × 20 μm2 and the base pressure of the ARPES chamber was maintained below 10−10 torr during the measurements.

SHG measurements

SHG signals were measured under ambient conditions using a femtosecond Ti:sapphire laser with a central wavelength of 800 nm and a pulse repetition rate of 80 MHz. An objective lens with a numerical aperture of 0.6 was used to focus the laser beam to a spot size of approximately 1 μm and to collect the SHG signals in the backscattering geometry. For spatial mapping of the SHG signals, a piezo-actuated stage was used.

STM sample preparation and analysis

Single-crystal MoS2 film was loaded into the STM (Omicron) chamber under ultrahigh-vacuum (UHV) conditions (10−7–10−10 torr). Initially, the sample was annealed at 523 K for 10 h to remove the contaminants. Subsequently, Au was deposited at a controlled rate of ~100 nm s−1 under UHV conditions. The sample was then removed and reloaded upside down to detach the MoS2/Au stack from the sapphire substrate under UHV conditions in the load-lock chamber (base pressure, <10−7 torr). STM investigation of the single-crystal MoS2 ML was performed in the main UHV chamber at 300 K.

Fabrication of MoS2 Hall-bar device

We used a thermoplastic methacrylate copolymer (Elvacite 2552C, Lucite International) stamp to assemble the hBN/MoS2/hBN stacks in an all-dry manner. The stack assembly process involved heating the stamp to 77 °C during the pick-up stage and heated to 180 °C for release. After the stack was successfully transferred, the stamp was dissolved in hot acetone (~100 °C) for 1 min. Following this, PMMA was spin coated onto the stack, and it was patterned into a Hall-bar structure using electron-beam lithography and reactive ion etching with a gas mixture of CF4 and O2. To ensure clean MoS2 edges that are free from contamination, the stacks were treated with in situ Ar+ sputtering within an electron-beam evaporation chamber. Subsequently, Ti/Au electrodes were deposited via electron-beam evaporation. Once the lift-off process was completed, the Hall devices were subjected to an annealing treatment in an Ar + H2 environment at 300 °C for 3 h to improve the Ti–MoS2 edge interface, improving the electrical contact quality.

Fabrication of MoS2 FET arrays

As-grown MoS2 ML square channels on c-sapphire substrates with patterned SiO2 trenches were first spin coated with PMMA. These MoS2 channels were then transferred onto clean HfO2 (10 nm)/p+-Si substrates using a water-assisted transfer method. After the transfer, the PMMA layer was removed by soaking the sample in acetone, followed by recoating with a fresh layer of PMMA resist. Electron-beam lithography was used to define the source/drain contact areas, and 10-nm Bi/40-nm Au contacts were deposited via electron-beam evaporation, followed by a lift-off process. To achieve channel isolation, an additional PMMA coating was applied, and electron-beam lithography was conducted to expose and etch away the undesired MoS2 regions using O2 plasma, resulting in well-defined MoS2 channels.

Electron transport measurements

Room-temperature d.c. measurements were performed using a four-probe vacuum station (PS-100) with a base pressure below 10−5 torr, connected to a semiconductor parameter analyser (Keithley 4200). For low-temperature electrical measurements, an Oxford Teslatron PT system (TESPT-12-L) was utilized. During Hall measurements, a constant current bias was applied to the channel using a d.c. source (Yokogawa 7651), whereas the gate voltage was controlled by a source measure unit (Yokogawa GS610). Voltage drops across the channel were recorded with voltage amplifiers (ithaco 1201) and digital multimeters (Keithley 2000).

Extraction of phase coherence length from HLN model

The physical parameters describing the weak localization effect can be extracted by using the HLN formula, expressed as

$$\Delta \sigma \left(B\right)=\sigma \left(B\right)-\sigma \left(B=0\right)=\frac{\alpha {e}^{2}}{{\rm{\pi }}h}\left[\mathrm{ln}\left(\frac{{B}_{\varphi }}{B}\right)-\varPsi \left(\frac{1}{2}+\frac{{B}_{\varphi }}{B}\right)\right],{B}_{\varphi }=\frac{h}{8e{\rm{\pi }}{L}_{\varphi }^{2}},$$

where \(\varPsi\) represents the digamma function, \({B}_{\varphi }\) is the characteristic magnetic field, \({L}_{\varphi }\) is the phase coherence length, \(h\) is Plank’s constant and \(e\) is the elementary charge. By fitting the magnetoconductance data in Fig. 4d to the HLN equation (black solid curve), \({L}_{\varphi }\) was extracted. This allows for a precise quantification of quantum interference effects in the system.